Crystal growth and aggregation in suspensions of δ-MnO₂ nanoparticles: implications for surface reactivity

Abstract

Birnessite (layer-type Mn oxide) is a key reactive phase in soils and sediments and its sorption and oxidative properties render it attractive for use in technical applications. The most widely used synthetic analog of natural and biogenic birnessite in laboratory studies is nanocrystalline δ-MnO₂. However, a wide range of physicochemical properties have been reported in the literature for δ-MnO₂. In this study, we produced several batches of δ-MnO₂ and identified the mechanisms leading to significant variations in particle size, as probed by X-ray diffraction (3 to 7 nm), dynamic light scattering (85 to 501 nm) and N₂(g) BET specific surface area (SSA: 119 to 259 m² g⁻¹) measurements. Both the coherent scattering domain (CSD) size in the ab plane and the wet-aggregate size decreased with increasing suspension pH and Na content, which is consistent with base-catalyzed oxidation and nucleation at high pH and growth by oriented attachment at low pH. The increase in the CSD size upon sample acidification but not basification provides further evidence for OA as a crystal growth mechanism. Finally, the sample SSA was not related to the crystallite size, but instead was inversely correlated to the suspension pH and Na : Mn content. The surface charge and counter-cation content of δ-MnO₂ control the aggregate structure, where low pH (low Na : Mn) favored high surface area structures and high pH (high Na : Mn) favored low surface area structures. The reversibility of SSA upon the acidification or basification of parent suspensions and the crystal growth only upon suspension acidification confirmed that the primary crystallite size and the aggregate/agglomerate size are highly sensitive to solution chemistry and surface charge and has direct implications for δ-MnO₂ nanoparticle reactivity towards organic and inorganic contaminants in environmental systems that can encompass a dynamic range of pH values and ionic compositions.

---

Environmental significance

Birnessite nanosheets are widespread in surface environments and play a major role in the biogeochemical cycling of trace elements and contaminant fate. The present study shows that changes in suspension pH and particle counter-ion content drive irreversible changes in the crystallite size of δ-MnO₂ but lead to reversible changes in physical properties such as SSA. The agglomeration of crystallites with high Na : Mn contents into low SSA particles may lower the accessibility of aqueous species to these surface sites and thus lower the overall reactivity of the particles with respect to contaminant sorption or oxidation.

Introduction

Birnessite-type minerals (layer-type Mn oxides) are among the most common Mn oxides in the environment.¹ They occur often in association with other mineral phases (e.g. Fe oxides) in desert varnishes, sediments, soil and ocean nodules, as mineral/rock coatings or in association with microorganisms.^1–4 Birnessite found in soils and sediments is composed of randomly stacked sheets of edge-sharing MnO₆ octahedra held together by interlayer cations and water, which compensate for the structural charge arising primarily from the presence of layer Mn(IV) vacancies and layer Mn(III) that can occupy Mn(IV) sites.¹ Such a birnessite tends to be nanocrystalline and have hexagonal layer symmetry,⁴ although orthogonal symmetry can be attained depending on the content and distribution of layer Mn(III) octahedra.^5,6

Due to its nanoscale dimensions and the presence of reactive surface sites at the particle edges and basal surface, birnessite participates in numerous environmental reactions with organic and inorganic compounds.^4,7,8 Consequently, a large number of laboratory studies have aimed at determining the mechanisms through which birnessite adsorbs toxicant metals such as Pb, Zn, Cd, and Ni (ref. 9–16) as well as adsorbs and oxidizes elements such As(III), Co(II), and Cr(III).^17–22 Manganese oxides are also considered as promising oxidants for a broad range of organic compounds including antibacterial agents, endocrine disruptors, and other pharmaceuticals.⁸ In addition, the sorption and redox properties of birnessite have been investigated in technical systems for their potential use in remediation strategies^7,23,24 or as water oxidation catalysts.^25,26 The majority of these studies have employed δ-MnO₂ as an analog for natural birnessite with hexagonal sheet symmetry and nanoscale dimensions.^1,9,14,27

The most common pathway for δ-MnO₂ synthesis is the “redox” method, which involves the oxidation of Mn(II) by Mn(VII) in an alkaline medium.²⁸ The nanoparticles obtained from the “redox” method are typically less than 10 nm across the ab plane and consist of 2 to 3 turbostratically stacked layers.^28,29 However, this preparation can lead to samples with SSA values that range from 120 to 315 m² g⁻¹,^{2,17,28,30–32} and Mn(III) content varying between 0 and 31%.^2,33 While the Mn(III) content of the products stems from the Mn(VII) : Mn(II) ratio employed in the synthesis,² the underlying cause for the large variations observed in SSA values is not known. Furthermore, mineral surface reactivity has been correlated to SSA values, often measured with BET theory N₂(g) adsorption.^2,8,14 Although mineral surface reactivity has been correlated to SSA values,^2,8,14 the relationship among SSA, particle size in aqueous suspension, and crystallite size has not been investigated to date despite its influence on the kinetics, mechanisms, and retention of trace elements on Mn oxides in natural and engineered settings.³⁴

The objective of the present study is to investigate how the physicochemical properties of δ-MnO₂ vary as a function of the reagent addition rate and base concentration used in its synthesis. Both variables can influence the kinetics of nucleation³⁵ and hence impact the crystallite size. Six batches of δ-MnO₂ were thus synthesized by varying the speed of MnCl₂ addition and the amount of NaOH used to control synthesis pH. The synthesis products were characterized according to chemical composition (alkali-to-Mn ratio, Mn(III) content, and average Mn oxidation number – AMON), water content, and crystal structure. In addition, the crystallite and particle size estimates were obtained from X-ray diffraction (XRD), dynamic light scattering (DLS), and specific surface area (SSA) measurements. Finally, the reversibility of the physicochemical properties of the as-synthesized products was assessed by equilibrating two suspensions to several pH units above or below the synthesis pH value, respectively.

Materials and methods

Synthesis protocol

All solutions, unless specified otherwise, were prepared using ACS-grade reagents and fresh MQ water (18 MΩ cm⁻¹). A detailed protocol for the synthesis of δ-MnO₂ is provided in the ESI.† Briefly, six batches of δ-MnO₂ were prepared by adding a solution of MnCl₂ to a KMnO₄ and NaOH mixture at a 0.67 Mn(VII) : Mn(II) molar ratio under vigorous stirring. A total suspension volume of 940 mL was used in each synthesis: 300 mL of 0.3 M MnCl₂, 300 mL of 0.2 M KMnO₄ and 340 mL of NaOH. The MnCl₂ solutions were prepared using MnCl₂·4H₂O (≥99%, ReagentPlus®) and nitrogen-purged MQ water. Prior to use, the Mn(II) concentration was measured by ICP-OES. Potassium permanganate (KMnO₄) was purchased as a standardized 0.2 M solution (Sigma-Aldrich). Finally, the concentration of NaOH was varied from 0.4 M to 0.6 M to encompass the range of [OH⁻] used in previous studies,^2,28 and the addition speed of MnCl₂ to the KMnO₄ and NaOH mixture was varied between 18 mL min⁻¹ and 72 mL min⁻¹. The δ-MnO₂ batches are identified by a letter–number scheme where the letter indicates the molar concentration of the NaOH solution used (A = 0.4 M, B = 0.5 M, and C = 0.6 M) and the number indicates the MnCl₂ addition speed (1 = 18 mL min⁻¹, 2 = 36 mL min⁻¹, and 3 = 72 mL min⁻¹). The A3 synthesis was repeated to ensure the reproducibility of the protocol; this sample is referred to as A3_b.

All syntheses were carried out in wide neck 1 L Erlenmeyer flasks. Reagents were added using a Cole-Parmer Masterflex peristaltic pump and Tygon© tubing (Fig. S1†). The flask contents were mixed vigorously using an overhead paddle. Once the addition of reagents was completed, the suspension was left to settle for 30 min and 100–200 mL of clear supernatant were siphoned. The remaining suspension (800–900 mL) was transferred to 250 mL centrifuge bottles for washing (27 500 RCF, 20 min, 25 °C). Five washing cycles using 1 M NaCl to exchange Na⁺ for K⁺ were followed by up to 10 washing cycles using MQ water to remove excess Na⁺ from the solution. After each washing cycle, the pH of the supernatant was measured with Merck Millipore pH paper. The electrical conductivity of the supernatant was also measured (Mettler EL30 conductivity meter) after each MQ washing cycle. To avoid losing significant amounts of the product, no further washing steps were conducted once the conductivity of the supernatant fell below 30 μS cm⁻¹. Typically, five washing cycles were sufficient to meet this criterion.

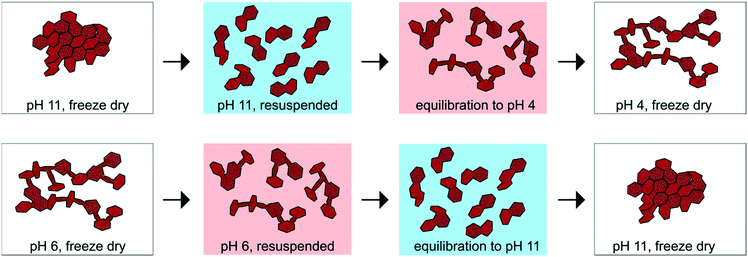
After synthesis, half of the suspension was freeze dried and stored at −20 °C, whereas the remaining half was stored in suspension at room temperature and in the dark without further pH equilibration. In a separate set of experiments, an aliquot of sample C2 (0.6 M NaOH) was equilibrated to pH 4 and an aliquot of sample A2 (0.4 M NaOH) was equilibrated to pH 11 for 7 days to test the stability of the physicochemical properties measured for the “as-synthesized” products. The suspension pH was kept constant using a Metrohm 718 STAT Titrino with either 50 mM NaOH or 50 mM HCl. The C2 and A2 samples equilibrated at pH 4 and pH 11 are denoted as C2_H and A2_OH, respectively.

Chemical analyses

The chemical composition of δ-MnO₂ was characterized with respect to the alkali metal content, Mn(III) content, AMON and water content. The Na,K : Mn ratio was measured by inductively coupled plasma optical emission spectrometry (ICP-OES, Perkin Elmer Optima 8300) from the aliquots digested in a 3% HNO₃ and 0.05 M H₂C₂O₄ solution. The AMON was determined using a three-step potentiometric titration that yields a concentration-independent measure of AMON^36,37 with a Metrohm 888 Titrando automatic titrator equipped with a Pt potentiometric electrode as described previously.^13,38 The measured AMON values were accurate within 0.05 AMON units of the theoretical oxidation numbers for reference minerals, which are equivalent to a 5% uncertainty in the Mn(III) and Mn(IV) content for the samples containing exclusively Mn(III) and Mn(IV). A reproducibility of 0.02–0.04 AMON units was determined from the standard deviation of triplicate measurements on the synthesis products (Table 1). The total Mn(III) content of the samples was determined as the amount of Mn(III) extractable by pyrophosphate (PP), as described in the ESI.†^39–41 Detailed protocols for AMON titrations and PP extractions, as well as method validation results, are provided in the ESI.†

Table 1 Physicochemical properties of synthesized samples

Sample name	Na/Mn [%]	EC^a [μS cm^−1]	Susp. pH^a	Mn(III)-PP^b ± SD [%]	AMON^b ± SD	SSA^b ± σ [m^2 g^−1]	FWHM of 02,31 band	CSD^c (ab plane) from XRD [nm]	Unit-cell b parameter (Å)	DLS^dZ average size (polydispersity index) [nm]
a The electrical conductivity (EC) and pH were measured in the supernatant at the end of the synthesis. The precision of the pH measurement was ±1. b Standard deviations (SDs) were calculated from triplicate measurements; σ indicates instrument error. c CSD sizes determined from the modeling of the 20,11 band as the radius of disks within the ab plane. d Polydispersity is defined as (width/mean)^2 of the particle size distribution obtained from the replicate measurements.
δ-MnO2_A1	16.1	4	6	2.57 ± 0.92	4.03 ± 0.03	196 ± 10	0.56084			501.7 (0.735)
δ-MnO2_A2	16.6	8	6	1.99 ± 0.29	4.02 ± 0.02	190 ± 10	0.55524			538.2 (0.711)
δ-MnO2_A3	16.0	4	6	2.07 ± 0.38	4.03 ± 0.01	259 ± 13	0.56743	7.2 ± 0.5	2.838 (1)	403.7 (0.661)
δ-MnO2_A3b	16.7	4	6	1.77 ± 0.03	4.06 ± 0.04	257 ± 13	0.59156
δ-MnO2_B2	30.2	10	8	2.07 ± 0.52	4.03 ± 0.01	163 ± 8	0.66675	3.8 ± 0.5	2.840 (1)	127.5 (0.288)
δ-MnO2_B3	28.9	10	8	2.14 ± 0.79	4.02 ± 0.01	167 ± 8	0.68685			121.7 (0.235)
δ-MnO2_C2	35.1	433	11	4.05 ± 0.26	4.00 ± 0.02	119 ± 6	0.84570	2.8 ± 0.5	2.848 (1)	85.98 (0.327)
δ-MnO2_A2_OH	—	—	11	2.88 ± 0.35	3.99 ± 0.01	117 ± 6	0.52955
δ-MnO2_C2_H	—	—	4	5.66 ± 1.58	3.92 ± 0.01	213 ± 11	0.58791

---

To determine the amount of water strongly sorbed at the particle surface, thermogravimetric analyses (Mettler Toledo TGA/SDTA 851e) were performed by heating approximately 30 mg of sample in an alumina crucible between 30 °C and 480 °C at a rate of 10 °C min⁻¹. The water content was determined by subtracting the TGA curve of an empty crucible from the TGA curve of the sample and normalizing this mass loss value to the initial sample mass. The structural water content was obtained by measuring the weight loss percentage between 80 °C and 250 °C.²⁹

Structural characterization

Freeze-dried δ-MnO₂ samples were used to characterize their crystal structure, intermediate-range structure (<2 nm), and specific surface area. The local bonding environment of Mn (<6 Å) was characterized using wet pastes obtained from initial suspensions filtered onto 0.45 μm nitrocellulose membranes, whereas the hydrodynamic size range was measured from diluted suspensions.

Synchrotron-XRD (SR-XRD) patterns for all the samples were acquired at the Swiss-Norwegian beamline of the European Synchrotron Radiation Facility (BM01B – ESRF) from powders packed into Kapton® polyimide capillaries mounted on a goniometric stage, which was spun at 50–100 rpm during data acquisition. Diffraction patterns were acquired with the SPEC software (Certified Scientific Software ©) on a 2D CCD plate using a 0.54 Å wavelength. Data reduction was carried out with FIT-2D⁴² using a LaB₆ standard for calibration. The XRD patterns were extracted from the background-subtracted azimuthal images using the custom routines in PyFAI.⁴³

Additional XRD patterns were collected over the 5–80° 2θ angular range using a Bruker D8 diffractometer, which was equipped with a SolXE solid-state detector from Baltic Scientific Instruments and Cu Kα radiation (λ = 1.5418 Å). The counting time was 80 s per 0.04° 2θ angular step. These data were modeled to determine the crystallite size and crystallographic parameters including the vacancy content. A specific trial-and-error method^44–46 was used because the XRD patterns of the turbostratic structures such as δ-MnO₂ exhibit only unresolved hk diffraction bands and 00l Bragg peaks.^46–48 Over the past two decades, this approach has been applied extensively to determine the structure of defective and turbostratic phyllomanganates.^29,49–51 This method precludes the calculation of a covariance matrix and thus the estimation of uncertainties. To overcome this limitation, several authors have assessed the sensitivity of diffracted intensity to layer symmetry, coherent scattering domain (CSD) size (i.e. crystallite size) both in the ab plane and along the c* axis (i.e. the number of layers stacked parallel to each other), lattice parameters or atomic position and site occupancy.^20,29,33,51 The sensitivity to the composition of the interlayer space and to lattice parameters has also been reported.^17,52–54

In the current study, all atomic positions within the unit cell were taken from previous studies^13,33 to reduce the number of adjusted parameters. The abundance of interlayer sodium was constrained from chemical analyses, whereas the number of interlayer H₂O molecules was refined within the limits of thermogravimetric analyses. A limited number of interlayer Mn(III) cations were allowed to account for the uncertainty in potentiometric titrations. The refined parameters were thus limited to the position of the interlayer Na⁺/H₂O molecules in the ab plane, the b unit-cell parameter 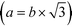, the CSD sizes in the ab plane and the site occupancies (except for layer oxygen, whose occupancy was constrained to 1). The fit quality was evaluated with the usual R_wp factor.⁵⁵

X-ray absorption spectra were collected at the Swiss Light Source (SLS) in Villigen, Switzerland, at beamline X10DA (SuperXAS), with a beam current of 400 mA. Manganese K-edge spectra were acquired at room temperature in transmission mode using a quick-scanning Si(111) double crystal monochromator oscillating about the Mn K-edge (6.4–6.9 keV) at a frequency of 1 Hz. X-ray energy was calibrated with a Mn metal foil by setting the first inflection point in the first derivative of the X-ray absorption spectrum to 6539 eV. The wet-paste samples were mounted on acrylic sample holders sealed with polyimide tape. The spectra were inspected to verify that no beam-induced damage occurred and then averaged using the JAQ software.⁵⁶ All data reduction was performed in ATHENA,⁵⁷ a GUI built on the IFEFFIT engine,⁵⁸ to obtain the X-ray absorption near edge structure (XANES) and extended X-ray absorption fine structure (EXAFS) spectra. The averaged spectra were background subtracted and normalized by fitting the pre-edge region with a linear function and the post-edge region with a quadratic function, and setting E₀ = 6554 eV, Rbkg = 1.0 Å, no clamps, k-weight = 3, normalization order 3. The EXAFS spectra were deglitched by removing one point in χ(k) around 7.6 Å⁻¹.

The specific surface area for all samples was determined by a standard 5-point BET theory N₂ adsorption isotherm at 77 K (Micromeritics Gemini 2375). Measurement uncertainty was taken as the instrument error (5%). Finally, the hydrodynamic range (Z-average particle size and polydispersity) of the as-synthesized suspensions was measured by DLS on a Zetasizer (Malvern Instruments, Nano ZS) run in backscattering mode (173°) at 25 °C after instrument calibration with 300 nm microbeads.⁵⁹ Initial suspensions were diluted with MQ water to obtain an optical density of approximately 0.3 absorption units at a wavelength of 633 nm and measured immediately after dilution. Generally, each measurement lasted 2 to 5 minutes and included 10 to 30 replicates.

Results

Chemical composition

Table 1 summarizes the physicochemical characteristics of the different δ-MnO₂ samples. At the end of reagent addition but before washing, the supernatant pH was close to 4, 8 and 12 for the A–C sample series, respectively. At the end of the MQ washing steps, the supernatant pH increased to a value of 6 for the A samples, whereas the supernatant pH decreased to 11 for the C samples. The electrical conductivity decreased from ∼10 mS cm⁻¹ to <10 μS cm⁻¹ after 5 washing steps, except in the high pH synthesis (C2). For this sample, the supernatant contained colloidally stable particles after the third washing step, with a conductivity of 433 μS cm⁻¹.

After freeze-drying and gentle grinding in an agate mortar, all samples were of comparable color, between dark brown and black. Chemical analysis showed that the Na : Mn molar ratio increased from 16% to 35% as the synthesis pH increased from 4 to 12, whereas the K : Mn molar ratio was less than 0.1% in all samples after Na-for-K exchange. The AMON measurements gave values between 4.00 ± 0.02 at high pH and 4.06 ± 0.04 at low pH. These AMON values, which are accurate within 0.05 AMON units, are consistent with the low amount of Mn(III) determined from PP extractions. About 2% PP-extractable Mn(III) was measured in all samples, except for batch C2, which showed 4.05% ± 0.26% Mn(III) (Table 1). Because PP is a non-redox active chelating agent,³⁹ any aqueous Mn(III) must derive from the mineral as Mn(III). However, the production of additional Mn(III) cannot be excluded for sample C2 when the pH was lowered from the initial value of 11 to 6.5 during the PP extraction. Finally, the structural water content as determined from the TGA curves (Fig. S2†) was comparable between the samples: decreasing from 17% (sample A3) to 12% (sample C2) on a mass basis as the synthesis pH increased from 4 to 12. Based on these measurements, a chemical formula of the form Na_xMn^3+,4+O₂·yH₂O was calculated for each sample without making any assumptions about the distribution of Na between interlayer or edge sites, the distribution of Mn(III) between layer or interlayer positions or the vacancy content. The absence of structural constraints, however, produces a charge-imbalanced chemical formula. The Na content was determined directly from the ICP-OES measurements, whereas the molar water content was obtained by scaling the TGA water content using the formula weight for the solid, and Mn(III) was determined from PP extractions:

δ-MnO2_A Na_0.16Mn³⁺_0.02Mn⁴⁺_0.98O₂·1.03H₂O (1)

δ-MnO₂_B Na_0.30Mn³⁺_0.02Mn⁴⁺_0.98O₂·0.92H₂O (2)

δ-MnO₂_C Na_0.35Mn³⁺_0.04Mn⁴⁺_0.96O₂·0.72H₂O (3)

For comparison, the product obtained by Villalobos and coauthors,² which was synthesized under conditions closest to those of our product B2, had the following formula:

Na_0.24Mn(IV)_0.94□_0.06O₂·0.72H₂O (4)

where the vacancy site content was determined by simulation of XRD patterns.²⁹

Structural characterization

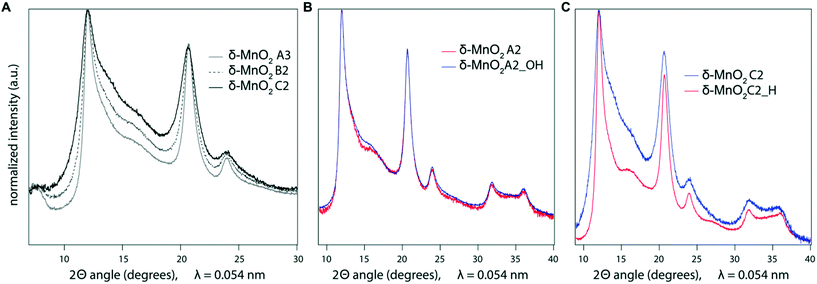
In Fig. 1, the powder SR-XRD patterns for the different δ-MnO₂ samples show the broad and asymmetric 20,11 and 02,31 bands at ∼2.44 and ∼1.42 Å characteristic of turbostratic (i.e., lacking 3D ordering) phyllomanganates.² The ratio between the positions of these two bands is close to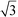 , which indicates a hexagonal layer symmetry, consistent with the 02,31 band profile. The high-angle profile of the 20,11 band is sensitive to the layer structure and, more specifically, to the content and atomic coordinates of the interlayer species. These structural parameters were thus derived from the modeling of the XRD data (Fig. 2 and Tables 1 and S1†). The structure models obtained for all three samples have 0.08–0.11 vacancies per octahedral site, the deficit of charge being compensated for by 0.05–0.06 Mn³⁺ sorbed mainly as triple-corner-sharing surface complexes above/below the vacant layer sites (TC sites) and hydrated interlayer Na⁺ (0.15–0.31). The amount of interlayer alkali cations steadily decreased with decreasing pH, which is consistent with previous studies.² The optimized coordinates for these cations, associated H₂O molecules (O3), and extra H₂O molecules (O4) are similar to those reported in earlier studies (Table S2†).^29,51,60 However, the actual distribution and the exact nature of Na⁺ and H₂O species over the two sites remain ambiguous, owing to the similar scattering factors of the two species, which host the same number of electrons. The decrease of unit cell parameter b from 2.848 Å at pH 11 (sample C2, 0.08 vacancies per octahedral site) to 2.838 Å at pH 6 (sample A3, 0.11 vacancies per octahedral site) is consistent with previous reports,⁶⁰ although slightly larger.

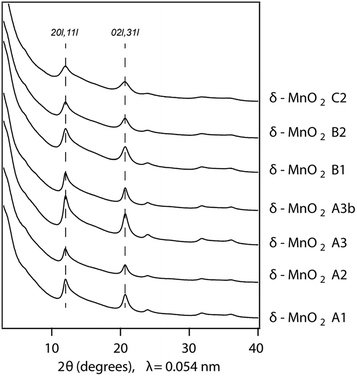Fig. 1 Comparison of SR-XRD patterns for the different δ-MnO₂ samples. The diagnostic broad diffraction peaks at 0.245 and 0.142 nm are visible and represent the 20,11 and 02,31 bands, respectively.

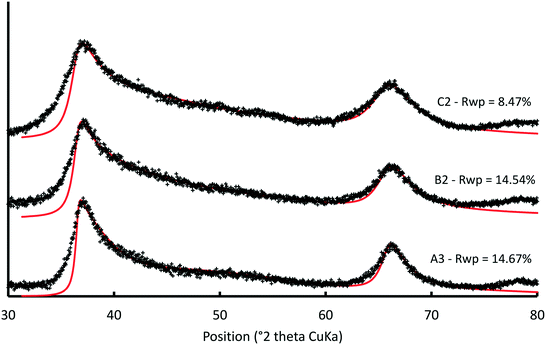Fig. 2 Comparison between experimental and calculated XRD patterns for selected δ-MnO₂ samples. Experimental and calculated XRD patterns are shown as crosses and solid lines, respectively. The 40,22 band at ∼78.5° was not calculated. Structural parameters optimized for the selected samples are listed in Table S2.†

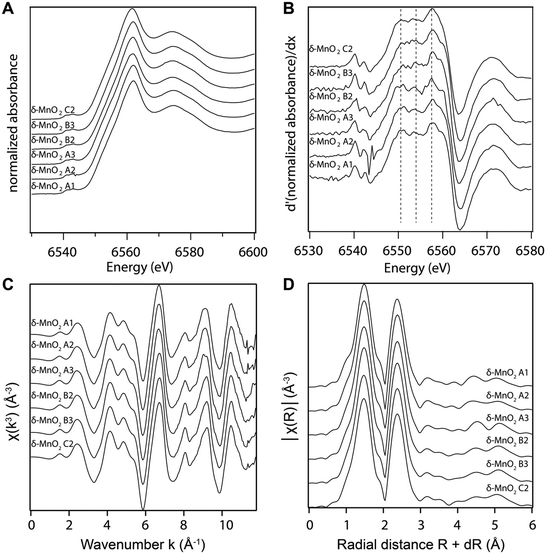
The manganese K-edge XANES and EXAFS spectra collected from all samples are shown in Fig. 3A and C, respectively. Consistent with wet chemical data, the XANES spectra and their first derivative (Fig. 3B) show that Mn(IV) is the dominant oxidation state in all samples. The white line position at 0.5 absorption units is 6551.9 eV, which is consistent with the value reported previously for δ-MnO₂.⁶¹ The EXAFS spectra and Fourier transforms of the EXAFS spectra from the different samples (Fig. 3C and D) are also in good agreement with the published EXAFS spectrum of δ-MnO₂.¹¹ In particular, the “staircase” feature between 4 and 6 Å⁻¹ indicates a mineral from the phyllomanganate family. The presence of a single peak at ∼8 Å⁻¹ instead of two symmetric oscillations around 7.8 and 8.1 Å⁻¹ in the “indicator” region between 7.8 and 9.6 Å⁻¹ indicates the absence of Mn(III) rows in the octahedral layer,⁶² whereas the position of the oscillation in this range (8.07 Å⁻¹) indicates a low overall proportion of Mn(III). Finally, the EXAFS spectra are consistent with the XANES spectra, AMON titrations and PP extraction results, which show Mn(III) amounts below the 5–10% detection limit of XAS.⁶³

Fig. 3 A) Normalized XANES spectra for the various samples. B) First derivative of the XANES spectra shown in A. C) EXAFS spectra collected from all samples. D) Fourier transform of the EXAFS spectra shown in C.

Physical characterization

The estimates of the crystallite size, wet-particle, and freeze-dried particle size were obtained from XRD, DLS, and SSA measurements, respectively. The XRD patterns of the synthesis products indicate contrasting CSD sizes. The broadening of the 02,31 band, which is insensitive to the structural parameters, is mainly related to the CSD size.⁴⁹ The decrease in the CSD size in the ab plane with higher synthesis pH is shown in Fig. 4A, where a subset of the diffraction patterns are compared, and in Fig. 5, where the FWHM of the 02,31 band is plotted against the Na content (which is also proportional to synthesis pH). This trend is confirmed by the modeling of XRD patterns that show the CSD sizes in the ab plane decrease from 7.2 ± 0.5 nm to 2.8 ± 0.5 nm when the pH increases from 6 to 11 (Table 1).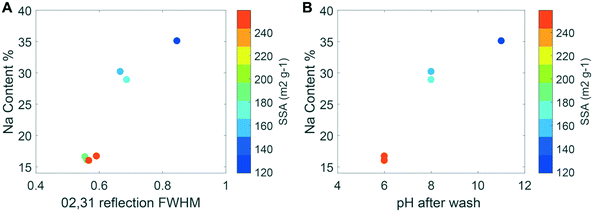

Fig. 4 SR-XRD patterns showing the 20,11 and 02,3 bands in a subset of samples show contrasting broadening. A) Data normalized to the maximum intensity of the reflection at 12° 2Θ for the three synthesis batches chosen as endmembers based on BET-SSA (δ-MnO₂ A3, B2 C2). B) SR-XRD of δ-MnO₂ A2 and A2_OH. C) SR-XRD of δ-MnO₂ C2 and C2_H.

Fig. 5 (A, left) Specific surface area as a function of Na content (Na : Mn on a molar basis from wet chemical measurements) and FWHM of the 02,31 diffraction band from SR-XRD patterns for the minerals in Table 1, which is inversely proportional to the coherent scattering domain size within the ab plane. (B, right) SSA as a function of pH (equivalent to the NaOH concentrations of 0.4 M, 0.5 M and 0.6 M, respectively) and reagent addition speed for the different samples. The samples A3b and A3 are overlaid, given the small differences in the Na content and pH. Both images exclude the basified and acidified samples.

The hydrodynamic particle size ranged from 86 to 538 nm as the suspension pH values varied from 11 to 6. These values followed the same trend as the XRD-derived crystallite size, with decreasing suspension pH leading to larger hydrodynamic radii (Table 1). All mineral suspensions were characterized by a moderate to high polydispersity, with a polydispersity index ranging from 0.235 and 0.735.⁶⁴ This value suggests that all suspensions had a relatively broad distribution of particle sizes, this breadth increasing with decreasing suspension pH and decreasing Na content (Table 1). However, the layer-type structure of δ-MnO₂ and the factor of 2–3 increase in the aspect ratio of the crystallites in the A samples relative to the C samples may confound further interpretation of the polydispersity index.

In contrast to the CSD and hydrodynamic sizes, the SSA of the freeze-dried synthesis products increased as the amount of NaOH employed in the synthesis decreased (Fig. 5). In other words, the largest particle size, as approximated by the SSA measurements, was obtained for the synthesis product with the smallest CSD size within the ab plane, which corresponds to the sample with the highest suspension pH and Na : Mn ratio. This inverse trend between the SSA and the CSD size, as indicated by the FWHM of the 02,31 band, is also shown in Fig. 5A. The measurements of SSA also increased with the MnCl₂ addition rate for the A samples (Fig. 5B), although to a lesser extent than the increase caused by the NaOH concentration used in the synthesis.

Discussion

Manganese valence and range of sodium content displayed by δ-MnO₂

The systematic prevalence of Mn(IV) in all samples (% Mn(III)-PP ≈ 2 averaged across all samples; Table 1) shows that neither the MnCl₂ addition speed nor the NaOH concentration influence significantly the average oxidation state of Mn in δ-MnO₂. The manganese valence in the products is governed instead by the initial Mn(VII) : Mn(II) ratio, such that lowering the Mn(VII) : Mn(II) ratio from 0.67 to 0.52 leads to a decrease in the AMON value from 4.02 to 3.70–3.80.^2,31,65 Evidently, reagent standardization provides control over the Mn(VII) : Mn(II) ratio used in the synthesis and allows for the formation of nanoparticles with at most trace-level Mn(III) contents. The only sample with a slightly larger Mn(III) content was sample C2_H (% Mn(III)-PP = 5.66 ± 1.58; AMON = 3.92 ± 0.01). The increase in Mn(III) content upon acidification of the parent sample C2 (Table 1) supports the hypothesis that a limited proton-promoted reduction of Mn(IV) occurs under acidic conditions,²⁸ with an electron potentially deriving from water or Cl⁻ ions.⁶⁶ This hypothesis is supported by both the thermodynamic stability of MnO₂ against water as a function of pH (Fig. S3†), where the stability range of MnO₂ straddles the water stability line across a large part of the pH range, and the decrease of AMON values with decreasing pH reported for a set of δ-MnO₂ suspensions equilibrated at different pH values.⁶⁰

In contrast to the similarity observed for AMON values, δ-MnO₂ spanned a broad range of Na : Mn ratios (0.16–0.35), such that Na : Mn increased with increasing suspension pH. This result is consistent with the literature² and can be rationalized chemically and geometrically. With a point of zero charge (PZC) value of ∼2–3,²⁸ δ-MnO₂ has a negative surface charge over the entire pH range investigated and any charge deficit must be balanced by Na⁺ cations. Protons have been proposed to adsorb at vacancy sites, but only when the amount of Na⁺ or Mn(III) present was insufficient to balance the negative charge of the vacancies.⁶⁷ As the solution pH increases, the proton activity decreases and Na⁺ can compete more effectively for negatively charged surface sites. This effect should be especially pronounced at the edge sites, for which the PZC value has been proposed to lie between pH 6 and 7.^12,68,69 The similar Na : Mn ratios across the B (pH 8) and C (pH 11) samples are consistent with the deprotonation of edge sites in these samples. Thus, the data suggest that the negative charge at the edge sites of δ-MnO₂ is mainly balanced by Na⁺ under alkaline conditions.

The measured Na : Mn ratios were also consistent with the crystallite size. Based on geometric constraints, the proportion of surface sites at the particle edges increases as the particle size decreases. Consequently, the magnitude of the surface charge arising from the edge sites also increases with decreasing particle size. To show the relationship between the surface charge and the particle size, single-layer MnO₂ nanodisks were generated in Crystalmaker®⁷⁰ using the XRD-derived estimates of the CSD size in the ab plane and the layer site occupancy (Tables 1 and S2†) and excluding proton adsorption. For each particle, the amount of Na⁺ needed to balance the negative charge arising from all undersaturated oxygen atoms was calculated assuming 4 Na⁺ cations per vacant layer site (+4 charge deficit) and 1 or 2 Na⁺ cations per edge site depending on whether the oxygen atom was doubly or singly coordinated to Mn, respectively. As the crystallite size decreased from 4 nm to 3 nm, the calculated Na : Mn ratio increased by 22%. This value is in close agreement with the 20% increase measured in the C sample (2.8 nm) relative to the B sample (3.8 nm). Both samples originated from the suspensions where pH > PZC of the edge sites and showed no significant structural evolution from the analysis of X-ray absorption spectra and X-ray diffraction patterns. Thus, the increase in Na in sample C relative to sample B should derive from the decrease in the crystallite size. Although XRD modeling assigned all Na⁺ cations to interlayer positions, the amount of interlayer Na could be overestimated in the structural model because the similar scattering factors of Na⁺ and H₂O prevent their unambiguous distinction.

Crystallite size and crystal growth

The CSD sizes within the ab plane estimated through modeling of the XRD patterns decreased significantly from 7.2 to 2.8 nm as the synthesis pH was increased from 4 to 12. On the other hand, all samples exhibited weak to absent 00l reflections, indicative of a limited extension of CSDs along the c* axis (2–3 layers), consistent with previous reports.^2,29 The smaller CSD size obtained in the high-pH synthesis is consistent with base-catalyzed oxidation of Mn, which favors the nucleation of δ-MnO₂ and limits crystal growth.^28,71 At lower pH values, however, rapid nucleation is less favoured. Moreover, the protonation of edge surface sites at low pH can promote H-bonding between crystals and favor oriented attachment (OA) within the ab plane.^72,73 However, the greater crystallite size of the δ-MnO₂ samples washed and equilibrated at pH values different from the synthesis pH further supports our conclusion that OA may be a likely crystal growth mechanism at low pH conditions. Specifically, the reduced broadening of the SR-XRD pattern obtained for the acidified C2 sample (C2_H, pH 4) compared to sample C2 (pH 11) indicates larger CSD sizes within the ab plane (Fig. 4C). Thus, the protonation of δ-MnO₂ edge sites upon sample acidification and subsequent OA may account for the observed increased crystal size.⁷³ The basified sample (A2_OH, pH 11), on the other hand, showed no change in the CSD size with respect to the parent mineral (Fig. 4B), suggesting that crystal growth through OA is irreversible. By analogy, greater amounts of Na⁺ at the particle edges limit OA and inhibit the growth of the crystals formed at high pH values.

Aggregation of δ-MnO₂ nanoparticles

The 30–60 fold increase in the hydrodynamic radius relative to the CSD size in the ab plane indicates that crystallites undergo moderate aggregation in suspension (Table 1). For instance, suspensions composed of vanishingly small crystallites (2.8 ± 0.5 nm) formed particles in suspension characterized by a 90 nm hydrodynamic radius, whereas the larger crystallites (7.2 ± 0.5 nm) formed particles with a hydrodynamic radius of about 400 nm. This non-linear scaling between the hydrodynamic radius (R_H) and the CSD size or FWHM of the 02,31 band in the XRD patterns could be approximated by a power law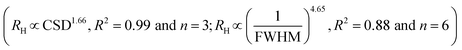 . These relationships also describe the dependence of the hydrodynamic radius on the aspect ratio because all samples had about the same thickness in the c* direction. Finally, consistent with the inverse relationship between the crystallite size and the Na : Mn ratio (Fig. 5A), the samples with the highest Na : Mn ratios formed the aggregates with the smallest hydrodynamic radii and vice versa (R_H ∝ Na^−2.22, R² = 0.98 and n = 6), indicating that the efficiency of aggregation was proportional to the counter-cation (Na⁺) content.

The non-linear scaling between the hydrodynamic radius and the aspect ratio may arise from the mode(s) of particle–particle associations in suspension, which can vary with particle shape and surface charge.⁷⁴ In montmorillonite suspensions, random edge-to-face interactions are favored when opposite surface charges develop on the basal and edge surfaces and when the electrical double layer thickness is small relative to the particle thickness.^74,75 In addition, the formation of ordered packets of montmorillonite lamellae (face-to-face interactions) is limited by decreasing suspension pH.⁷⁴ For δ-MnO₂, opposite charge between the basal and edge surfaces may develop under acidic conditions when pH < pH_pzc,edge because the structural charge (σ_o), which is always negative due to the presence of vacancy sites, causes the basal surface to be negatively charged and the proton charge (σ_H), which varies with pH, causes the edges to bear a net positive charge. Therefore, conditions favoring random edge-to-face interactions (i.e. attraction) are met in the A samples, which have protonated edge sites (i.e. σ_H > 0) and low Na : Mn ratios. By contrast, the low proton and high Na : Mn content in the B and C samples (30–35% Na : Mn) favor the formation of more compact aggregates.

The surface charge and counter-cation content are also the primary drivers of particle size as measured by BET-SSA calculation. Typically, large surface areas reflect small particle sizes and vice versa, but BET-SSA calculation measures only the N₂(g)-accessible surface area. In addition, if aggregation creates microporosity that cannot be accessed by N₂(g), the BET method cannot distinguish between aggregate and crystallite size.⁷⁶ The C constant in the BET equation provides a measure of the interaction energy between sorbent and adsorbate, and high values such as those systematically computed for the samples under study (C > 200) can indicate the presence of microporosity in the samples.⁷⁶ Inspection of the CSD and BET-SSA values for the δ-MnO₂ samples shows that SSA measurements are not consistent with the crystallite size. First, all the as-synthesized samples showed particle sizes as measured by the SSA that were inversely proportional to the CSD size in the ab plane and the hydrodynamic radius (Fig. 5A and Table 1). Second, the SSA measured on sample A2 decreased significantly following equilibration at pH 11 (190 ± 10 m² g⁻¹ and 117 ± 6 m² g⁻¹ for samples A2 and A2_OH, respectively; Table 1) without any associated increase in CSD size (Fig. 4B). In other words, low SSA values were measured for samples with both small (sample C2) and large (A2_OH) crystallite sizes. Third, both the CSD size within the ab plane (Fig. 4C) and the SSA increased significantly in sample C2 upon suspension acidification (119 ± 6 and 213 ± 11 m² g⁻¹, for samples C2 and C2_H, respectively; Table 1). To sum up, these results suggest that BET-SSA is not directly related to either the crystallite size or the hydrodynamic radius.

On the other hand, across all samples, the BET-SSA was inversely proportional to the Na content. This proportionality suggests that Na promotes the aggregation of primary crystallites and/or wet aggregates into low surface area structures (e.g., dense or closed structures) that are retained upon freeze-drying. However, this aggregation is reversible (i.e., agglomeration⁷⁷) as shown by the reversal of the BET-SSA of samples A2 and C2 upon equilibration at high and low pH, respectively (Table 1). These results indicate that for δ-MnO₂, the BET-SSA is a dynamic property that can be modified readily in response to changes in adsorbed proton or ion charge, presumably through their influence on the aggregate/agglomerate structure.

Implications for nanoparticle reactivity

The reactivity of birnessite with respect to metal and metalloid sorption^9,14,17 and organic compound oxidation⁸ has been proposed to correlate with the BET-SSA. However, surface processes, including sorption, desorption, and dissolution, depend on particle size and particle aggregation, which may or may not be captured well by BET-SSA measurements.^21,78–82 Evidently, precise definitions of particle size and careful characterization of the mineral structure are necessary.^79,83,84 In addition, mineral characterization must be done on samples prepared under conditions relevant to those used in reactivity studies. This point is highlighted by the results from this study on birnessite and others on ferrihydrite,^78,85 which reveal the interconnectedness of solution chemistry, particle surface charge and structural properties (e.g., crystallite size, BET-SSA, and aggregate or agglomerate structure). Finally, the formation of open versus closed structures upon nanoparticle aggregation or agglomeration has important implications for ion sorption by nanoscale oxides and merits further investigation. For example, one study showed that Fe oxide aggregates retained copper more strongly than dispersed nanoparticles,⁸⁶ even though the adsorption capacity of aggregates was lower than that of dispersed nanoparticles.³⁴

Conclusions

This work elucidated the underlying mechanisms that give rise to a range of chemical compositions and structures of δ-MnO₂ nanoparticles prepared by a “redox” method. In addition, to the extent of our knowledge, this is the first study that investigates the difference between the hydrodynamic particle size, the crystallite size and the dry specific surface area in layer-type Mn oxides. A schematic summarizing the conditions that govern crystallite growth as well as crystallite aggregation and/or agglomeration in δ-MnO₂ suspensions is presented in Fig. 6. Briefly, changes in the suspension pH and particle counter-ion content drive irreversible changes in the crystallite size but lead to reversible changes in physical properties such as SSA. The agglomeration of primary crystallites with Na⁺ adsorbed at the particle edges into low SSA particles may lower the accessibility of aqueous species to these surface sites and thus lower the overall reactivity of the particles with respect to contaminant sorption or oxidation. Future studies to decouple the effects of nanoparticle aggregation or agglomeration, which may lower the reactivity of edge surface sites, and of solution pH, which enhances the adsorption of cations but diminishes the adsorption of oxyanions, are needed to elucidate the controls on solute-accessible surface area.^12,14,69 Cryo-TEM or HR-TEM techniques, which have been applied successfully to investigate the oriented aggregation of Fe oxide nanoparticles,^85,87,88 may provide valuable mechanistic information on the dynamics of δ-MnO₂ nanoparticle aggregation and agglomeration. Furthermore, variations in the vacancy content of the different δ-MnO₂ batches could be probed by collecting and modelling EXAFS data from trace metal-sorbed δ-MnO₂ in order to determine the local coordination environment of the sorbate.¹⁴

Fig. 6 Schematic representation of the effects of the samples equilibrated to pH 4 (above) and pH 11 (below) and freeze drying on the aggregation state of the minerals. For simplicity, the effects on the CSD size are omitted.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded by the Swiss National Science Foundation (Grant # 200021_143742). We thank Imelda Doussou Etui and Dr. Anna Simanova for their contributions to the synthesis and characterization of the samples as well as for useful discussions, and Prof. Tamar Kohn of the Ecole Polytechnique Federale de Lausanne for the use of the DLS instrument. We also acknowledge Dr. Benjamin Legg for helpful discussions on particle aggregation. We are grateful to Michela Brunelli and Emerich Hermann at the Swiss-Norwegian beamline (BM01B) of the European Synchrotron Radiation Facility (Grenoble, France) for their assistance with X-ray scattering measurements and Maarten Nachtegaal at the SuperXAS beamline (X10DA) of the Swiss Light Source (Villigen, Switzerland) for his assistance with XAS data collection.

References

1. J. Post, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 3447–3454.
2. M. Villalobos, B. Toner, J. Bargar and G. Sposito, Geochim. Cosmochim. Acta, 2003, 67, 2649–2662.
3. W. Stumm and J. J. Morgan, Aquatic chemistry: chemical equilibria and rates in natural waters, Wiley, 1996.
4. B. M. Tebo, J. R. Bargar, B. G. Clement, G. J. Dick, K. J. Murray, D. Parker, R. Verity and S. M. Webb, Annu. Rev. Earth Planet. Sci., 2004, 32, 287–328 and references therein.
5. V. A. Drits, E. Silvester, A. I. Gorshkov and A. Manceau, Am. Mineral., 1997, 82, 946–961.
6. A. C. Gaillot, V. A. Drits, A. Plancon and B. Lanson, Chem. Mater., 2004, 16, 1890–1905.
7. Z. M. Wang and D. E. Giammar, ACS Symp. Ser., 2015, 1197, 29–50.
8. C. K. Remucal and M. Ginder-Vogel, Environ. Sci.: Processes Impacts, 2014, 16, 1247–1266 and references therein.
9. M. Villalobos, J. Bargar and G. Sposito, Environ. Sci. Technol., 2005, 39, 569–576.
10. A. Manceau, B. Lanson and V. A. Drits, Geochim. Cosmochim. Acta, 2002, 66, 2639–2663.
11. M. A. Marcus, A. Manceau and M. Kersten, Geochim. Cosmochim. Acta, 2004, 68, 3125–3136.
12. C. M. van Genuchten and J. Pena, Environ. Sci.: Processes Impacts, 2016, 18, 1030–1041.
13. S. Grangeon, A. Manceau, J. Guilhermet, A. C. Gaillot, M. Lanson and B. Lanson, Geochim. Cosmochim. Acta, 2012, 85, 302–313.
14. A. A. Simanova, K. D. Kwon, S. E. Bone, J. R. Bargar, K. Refson, G. Sposito and J. Pena, Geochim. Cosmochim. Acta, 2015, 164, 191–204.
15. C. L. Peacock and D. M. Sherman, Chem. Geol., 2007, 238, 94–106.
16. R. J. Zasoski and R. G. Burau, Soil Sci. Soc. Am. J., 1988, 52, 81–87.
17. B. J. Lafferty, M. Ginder-Vogel and D. L. Sparks, Environ. Sci. Technol., 2010, 44, 8460–8466.
18. E. Silvester, L. Charlet and A. Manceau, J. Phys. Chem., 1995, 99, 16662–16669.
19. D. L. Crowther, J. G. Dillard and J. W. Murray, Geochim. Cosmochim. Acta, 1983, 47, 1399–1403.
20. A. Manceau, V. A. Drits, E. Silvester, C. Bartoli and B. Lanson, Am. Mineral., 1997, 82, 1150–1175.
21. P. S. Nico and R. J. Zasoski, Environ. Sci. Technol., 2000, 34, 3363–3367.
22. A. A. Simanova and J. Peña, Environ. Sci. Technol., 2015, 49, 10867–10876.
23. D. G. Beak, N. T. Basta, K. G. Scheckel and S. J. Traina, Environ. Sci. Technol., 2008, 42, 779–785.
24. V. Ettler, V. Knytl, M. Komarek, L. Della Puppa, M. Mihaljevic and O. Sebek, EGU General Assembly 2012, 2012, vol. 14, p. 8532.
25. M. Wiechen, I. Zaharieva, H. Dau and P. Kurz, Chem. Sci., 2012, 3, 2330–2339.
26. R. K. Hocking, R. Brimblecombe, L. Y. Chang, A. Singh, M. H. Cheah, C. Glover, W. H. Casey and L. Spiccia, Nat. Chem., 2011, 3, 461–466.
27. Y. Wang, X. H. Feng, M. Villalobos, W. F. Tan and F. Liu, Chem. Geol., 2012, 292, 25–34.
28. J. W. Murray, J. Colloid Interface Sci., 1974, 46, 357–371.
29. M. Villalobos, B. Lanson, A. Manceau, B. Toner and G. Sposito, Am. Mineral., 2006, 91, 489–502.
30. W. Buser and P. Graf, Helv. Chim. Acta, 1955, 38, 830–834.
31. O. W. Duckworth and G. Sposito, Chem. Geol., 2007, 242, 497–508.
32. K. L. Godtfredsen and A. T. Stone, Environ. Sci. Technol., 1994, 28, 1450–1458.
33. S. Grangeon, B. Lanson, M. Lanson and A. Manceau, Mineral. Mag., 2008, 72, 1279–1291.
34. E. J. Kim, J. Kim, S. C. Choi and Y. S. Chang, Environ. Sci.: Processes Impacts, 2014, 16, 1519–1525.
35. N. T. K. Thanh, N. Maclean and S. Mahiddine, Chem. Rev., 2014, 114, 7610–7630.
36. J. J. Lingane and R. Karplus, Ind. Eng. Chem., 1946, 18, 191–194.
37. K. J. Vetter and N. Jaeger, Electrochim. Acta, 1966, 11, 401–419.
38. F. F. Marafatto, M. L. Strader, J. Gonzalez-Holguera, A. Schwartzberg, B. Gilbert and J. Pena, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 4600–4605.
39. J. Klewicki and J. Morgan, Geochim. Cosmochim. Acta, 1999, 63, 3017–3024.
40. Y. Wang and A. T. Stone, Abstr. Pap. Am. Chem. Soc., 2003, 226, U471.
41. J. E. Kostka, G. W. Luther and K. H. Nealson, Geochim. Cosmochim. Acta, 1995, 59, 885–894.
42. A. P. Hammersley, FIT2D: An Introduction and Overview, 1997.
43. G. Ashiotis, A. Deschildre, Z. Nawaz, J. P. Wright, D. Karkoulis, F. E. Picca and J. Kieffer, J. Appl. Crystallogr., 2015, 48, 510–519.
44. V. A. Drits, G. Besson, R. Setton, A. Guinier, A. S. Bookin, C. Tchoubar, F. Rousseaux, B. A. Sakharov and D. Tchoubar, X-Ray Diffraction by Disordered Lamellar Structures: Theory and Applications to Microdivided Silicates and Carbons, Springer, Berlin Heidelberg, 2012.
45. A. Plançon, J. Appl. Crystallogr., 2002, 35, 377–377.
46. R. Giovanoli, Miner. Deposita, 1980, 15, 251–253.
47. G. Brindley, in Crystal structures of clay minerals and their X-ray identification, Mineralogical Society, 1980, vol. 5, pp. 411–438.
48. B. Warren, Phys. Rev., 1941, 59, 693.
49. S. Grangeon, B. Lanson, N. Miyata, Y. Tani and A. Manceau, Am. Mineral., 2010, 95, 1608–1616.
50. V. A. Drits, B. Lanson and A. C. Gaillot, Am. Mineral., 2007, 92, 771–788.
51. B. Lanson, M. A. Marcus, S. Fakra, F. Panfili, N. Geoffroy and A. Manceau, Geochim. Cosmochim. Acta, 2008, 72, 2478–2490.
52. H. Yin, W. F. Tan, L. R. Zheng, H. J. Cui, G. H. Qiu, F. Liu and X. H. Feng, Geochim. Cosmochim. Acta, 2012, 93, 47–62.
53. H. Sun, G. H. Qiu, Y. Wang, X. H. Feng, H. Yin and F. Liu, Mater. Chem. Phys., 2014, 148, 783–789.
54. H. Yin, K. D. Kwon, J. Y. Lee, Y. Shen, H. Y. Zhao, X. M. Wang, F. Liu, J. Zhang and X. H. Feng, Geochim. Cosmochim. Acta, 2017, 208, 268–284.
55. S. Howard and K. Preston, in Reviews in Mineralogy - Modern Powder Diffraction, Mineralogical Society of America, 1989, vol. 20, pp. 217–275.
56. O. Muller, M. Nachtegaal, J. Just, D. Lutzenkirchen-Hecht and R. Frahm, J. Synchrotron Radiat., 2016, 23, 260–266.
57. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
58. M. Newville, J. Synchrotron Radiat., 2001, 8, 322–324.
59. M. J. Mattle, B. Crouzy, M. Brennecke, K. R. Wigginton, P. Perona and T. Kohn, Environ. Sci. Technol., 2011, 45, 7710–7717.
60. S. Grangeon, B. Lanson and M. Lanson, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2014, 70, 828–838.
61. J. R. Bargar, B. M. Tebo, U. Bergmann, S. M. Webb, P. Glatzel, V. Q. Chiu and M. Villalobos, Am. Mineral., 2005, 90, 143–154.
62. A. Manceau, M. A. Marcus, N. Tamura, O. Proux, N. Geoffroy and B. Lanson, Geochim. Cosmochim. Acta, 2004, 68, 2467–2483.
63. J. R. Bargar, B. M. Tebo and J. E. Villinski, Geochim. Cosmochim. Acta, 2000, 64, 2775–2778.
64. W. Brown, Dynamic light scattering : the method and some applications, Clarendon Press, New York, 1993.
65. F. F. Marafatto, PhD Dissertation, University of Lausanne, 2017.
66. M. Grätzel, J. Kiwi, C. L. Morrison, R. S. Davidson and A. C. Tseung, J. Chem. Soc., Faraday Trans. 1, 1985, 81, 1883–1890.
67. B. Lanson, V. A. Drits, E. Silvester and A. Manceau, Am. Mineral., 2000, 85, 826–838.
68. J. W. Tonkin, L. S. Balistrieri and J. W. Murray, Appl. Geochem., 2004, 19, 29–53.
69. M. Villalobos, ACS Symp. Ser., 2015, 1197, 65–87.
70. D. C. Palmer, CrystalMaker®: a crystal and molecular structures program for Mac and Windows, CrystalMaker Software Ltd, 2.7.7, Oxford, England, 2014.
71. J. J. Morgan and W. Stumm, J. Colloid Sci., 1964, 19, 347–359.
72. M. Raju, A. C. T. van Duin and K. A. Fichthorn, Nano Lett., 2014, 14, 1836–1842.
73. X. R. Liang, Z. X. Zhao, M. Q. Zhu, F. Liu, L. J. Wang, H. Yin, G. H. Qiu, F. F. Cao, X. Q. Liu and X. H. Feng, Environ. Sci.: Nano, 2017, 4, 1656–1669.
74. E. Tombacz and M. Szekeres, Appl. Clay Sci., 2004, 27, 75–94.
75. S. L. Swartzen-Allen and E. Matijevic, Chem. Rev., 1974, 74, 385–400.
76. K. S. W. Sing, D. H. Everett, R. A. W. Haul, L. Moscou, R. A. Pierotti, J. Rouquerol and T. Siemieniewska, Pure Appl. Chem., 1985, 57, 603–619.
77. A. D. McNaught and A. Wilkinson, IUPAC. Compendium of Chemical Terminology, 2nd ed., Blackwell Scientific Publications, Oxford ( 1997),  DOI:10.1351/goldbook..
78. B. Gilbert, R. K. Ono, K. A. Ching and C. S. Kim, J. Colloid Interface Sci., 2009, 339, 285–295.
79. J. Liu, D. M. Aruguete, M. Murayama and M. F. Hochella, Environ. Sci. Technol., 2009, 43, 8178–8183.
80. K. M. Kuhn, J. L. DuBois and P. A. Maurice, Environ. Sci. Technol., 2014, 48, 8664–8670.
81. C. A. Lanzl, J. Baltrusaitis and D. M. Cwiertny, Langmuir, 2012, 28, 15797–15808.
82. K. J. T. Livi, M. Villalobos, R. Leary, M. Varela, J. Barnard, M. Villacis-Garcia, R. Zanella, A. Goodridge and P. Midgley, Langmuir, 2017, 33, 8924–8932.
83. P. J. Vikesland, A. M. Heathcock, R. L. Rebodos and K. E. Makus, Environ. Sci. Technol., 2007, 41, 5277–5283.
84. D. M. Cwiertny, R. M. Handler, M. V. Schaefer, V. H. Grassian and M. M. Scherer, Geochim. Cosmochim. Acta, 2008, 72, 1365–1380.
85. B. A. Legg, M. Q. Zhu, L. R. Comolli, B. Gilbert and J. F. Banfield, Langmuir, 2014, 30, 9931–9940.
86. J. G. Dale, J. P. Stegemeier and C. S. Kim, Geochim. Cosmochim. Acta, 2015, 148, 100–112.
87. V. M. Yuwono, N. D. Burrows, J. A. Soltis and R. L. Penn, J. Am. Chem. Soc., 2010, 132, 2163–2165.
88. D. S. Li, M. H. Nielsen, J. R. I. Lee, C. Frandsen, J. F. Banfield and J. J. De Yoreo, Science, 2012, 336, 1014–1018.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7en00817a

---