Emerging investigator series: methylmercury speciation and dimethylmercury production in sulfidic solutions†
Abstract
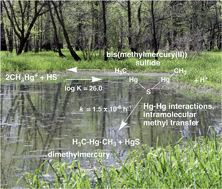
Alkylated mercury species (monomethylmercury, MeHg, and dimethylmercury, DMeHg) exhibit significant bioaccumulation, and pose significant risks to ecosystems and human health. Although decades of research have been devoted to understanding MeHg formation and degradation, little is known about the DMeHg formation in aquatic systems. Here, we combine complementary experimental and computational approaches to examine MeHg speciation and DMeHg formation in sulfidic aqueous solutions, with an emphasis on the formation and decomposition of the binuclear bis(methylmercuric(II)) sulfide complex (CH3Hg)2S. Experimental data indicate that the reaction 2CH3Hg+ + HS− ⇄ (CH3Hg)2S + H+ has a log K = 26.0 ± 0.2. Thus, the binuclear (CH3Hg)2S complex is likely to be the dominant MeHg species under high MeHg concentrations typically used in experimental investigations of MeHg degradation by sulfate-reducing bacteria (SRB). Our finding of a significant abiotic removal mechanism for MeHg in sulfidic solutions through the formation of relatively insoluble (CH3Hg)2S suggests careful reexamination of reported “oxidative demethylation” of MeHg by SRB and perhaps other obligate anaerobes. We provide evidence for slow decomposition of (CH3Hg)2S to DMeHg and HgS, with a first-order rate constant k = 1.5 ± 0.4 × 10−6 h−1. Quantum chemical calculations suggest that the reaction proceeds by a novel mechanism involving rearrangement of the (CH3Hg)2S complex facilitated by strong Hg–Hg interactions that activate a methyl group for intramolecular transfer. Predictions of DMeHg formation rates under a variety of field and laboratory conditions indicate that this pathway for DMeHg formation will be significant in laboratory experiments utilizing high MeHg concentrations, favoring (CH3Hg)2S formation. In natural systems with relatively high MeHg/[H2S]T ratios (the oxic/anoxic interface, for example), DMeHg production may be observed, and warrants further investigation.
- This article is part of the themed collections: Emerging Investigator Series, Best Papers 2018 – Environmental Science: Processes & Impacts and Mercury Biogeochemistry, Exposure, and Impacts


 Please wait while we load your content...
Please wait while we load your content...