Passive sampling of DDT, DDE and DDD in sediments: accounting for degradation processes with reaction–diffusion modeling†
A. Patricia
Tcaciuc‡
 *ab,
Raffaella
Borrelli
c,
Luciano M.
Zaninetta
d and
Philip M.
Gschwend
ab
*ab,
Raffaella
Borrelli
c,
Luciano M.
Zaninetta
d and
Philip M.
Gschwend
ab
aMIT/WHOI Joint Program in Chemical Oceanography, USA
bDepartment of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA. E-mail: paty@alum.mit.edu
cENI Renewable Energy & Environmental R&D, Donegani Institute, Novara, Italy
dSyndial, Piazza M. Boldrini 1, 20097 San Donato Milanese, Italy
First published on 11th December 2017
Abstract
Passive sampling is becoming a widely used tool for assessing freely dissolved concentrations of hydrophobic organic contaminants in environmental media. For certain media and target analytes, the time to reach equilibrium exceeds the deployment time, and in such cases, the loss of performance reference compounds (PRCs), loaded in the sampler before deployment, is one of the common ways used to assess the fractional equilibration of target analytes. The key assumption behind the use of PRCs is that their release is solely diffusion driven. But in this work, we show that PRC transformations in the sediment can have a measurable impact on the PRC releases and even allow estimation of that compound's transformation rate in the environment of interest. We found that in both field and lab incubations, the loss of the 13C 2,4′-DDT PRC from a polyethylene (PE) passive sampler deployed at the sediment–water interface was accelerated compared to the loss of other PRCs (13C-labeled PCBs, 13C-labeled DDE and DDD). The DDT PRC loss was also accompanied by accumulation in the PE of its degradation product, 13C 2,4′-DDD. Using a 1D reaction–diffusion model, we deduced the in situ degradation rates of DDT from the measured PRC loss. The in situ degradation rates increased with depth into the sediment bed (0.14 d−1 at 0–10 cm and 1.4 d−1 at 30–40 cm) and although they could not be independently validated, these rates compared favorably with literature values. This work shows that passive sampling users should be cautious when choosing PRCs, as degradation processes can affect some PRC's releases from the passive sampler. More importantly, this work opens up the opportunity for novel applications of passive samplers, particularly with regard to investigating in situ degradation rates, pathways, and products for both legacy and emerging contaminants. However, further work is needed to confirm that the rates deduced from model fitting of PRC loss are a true reflection of DDT transformation rates in sediments.
Environmental significanceSediment contamination with hydrophobic organic compounds (HOCs), such as PCBs, DDTs, PAHs and others, is a problem worldwide that requires risk assessments and remedial efforts. Passive samplers are greatly improving our ability to measure freely dissolved concentrations, which are key inputs in evaluating HOC-associated risks and defining the most problematic locales. However, for HOCs that degrade in the environment (e.g., DDT), long term fate assessment also requires information about their transformation rates. Herein we demonstrate that when used in conjunction with reaction–diffusion modeling and carefully chosen performance reference compounds, passive samplers can provide estimates of in situ degradation rates. The methods and models described can be applied to investigate the environmental fate of other legacy and emerging contaminants. |
Introduction
Sediment contamination with hydrophobic organic compounds (HOCs), such as PCBs, PAHs and others, is a problem at numerous US Superfund sites as well as throughout the world. At sites of concern, the risk associated with these chemicals depends on their availability for transport or uptake into organisms, which is in turn related to their freely dissolved concentrations (Lydy et al.1 and references therein). But for certain HOCs that are known to degrade in the environment, modeling of their long term fate requires information, not only about their freely dissolved concentration, but also about their transformation rates, preferably under in situ conditions. One such example is dichlorodiphenyltrichloroethane (DDT) which, upon release to aquatic environments, is subject to transformations, producing two major degradation products, dichlorodiphenyldichloroethylene (DDE) and dichlorodiphenyldichloroethane (DDD). The degradation of DDT in sediments has been reported to occur with half-lives from days2,3 to years,4,5 and the DDE and DDD degradates themselves may be susceptible to transformations.4,6 Hence, assessing the risks associated with DDT-contaminated sediments requires both information suited to estimating fluxes as well as reactivities.Passive sampling is becoming a widely used tool for assessing freely dissolved concentrations of HOCs in environmental media. When used in situ, passive sampling is typically used in conjunction with PRCs, which are often isotopically labeled compounds that are preloaded in the sampler before deployment and whose losses are used to adjust the measured build ups of target compounds to their equilibrium values. PRCs have been used successfully to determine porewater concentrations of PCBs7,8 and PAHs,9 as well as for DDE and DDD.10,11
The successful use of PRCs with in situ passive sampling relies on the key assumption that the transport of the PRCs and corresponding target compounds is symmetric. But various environmental processes may affect the validity of this assumption including in situ degradation or sorption kinetics.12 PRC degradation processes in the sediments can lead to accelerated loss of the reactive PRC from the sampler relative to non-reactive PRCs and may lead to erroneous interpretations of the PRCs' losses (e.g., complete PRC loss indicative of complete equilibration of the corresponding target compound). This in turn could lead to an overestimation of the fractional equilibration of the target, and potential underestimation of concentration of the reactive analyte in the environment. Some of these problems may be avoided by choosing PRCs that do not react on deployment timescales. It should be recognized, however, that this may not always be possible because reactivities of compounds may depend on environmental conditions (site or depth dependent) and may not be known a priori.
Although PRC reactivity in sediments may create problems for passive sampling applications, it also offers the opportunity for new applications of passive sampling in investigating the fates of organic chemicals in sediments. Specifically, if the measured PRC loss(es) could be evaluated with a reaction–diffusion model, passive samplers could be used to obtain information about in situ reaction rates. The sampler may also accumulate degradation products of the PRC which are produced in the sediment but can diffuse back into the sampler, as well as further into the sediment bed. Identifying the degradation products accumulated in the sampler may, in turn, provide insight into degradation pathways. In the laboratory, polymeric samplers have already been used as dosing phases during investigations of PAH biotransformations13 and recently, Belles et al.14 have also proposed that passive samplers could be used as semi-quantitative indicators of in situ degradation of nitro-PAHs. A reaction–diffusion model would thus be helpful for quantitative interpretation of field measurements (i.e., estimation of in situ reaction rates) and for studying in situ transformations of other classes of reactive compounds.
This paper investigates the application of passive sampling for measuring in situ degradation rates of DDT in sediments by using PRC-loaded PE in both field and laboratory conditions. The goals of this study were: (1) to determine if reactive processes can have a measurable impact on the transfer of PRCs between passive samplers and sediments, (2) to build a reaction–diffusion model which could be used to determine in situ degradation rates based on the measured PRC loss, and (3) to investigate implications for passive sampling applications for measuring reactive compounds. In this paper, we employed a combination of labeled PCBs and DDXs (taken here to mean any of the 2,4′ and 4,4′ isomers of DDT and their degradation products, DDE and DDD) as PRCs, in order to identify patterns in the PRC loss that are consistent with diffusion or reaction–diffusion transport for both field deployed polyethylene (PE) samplers as well as static laboratory incubations. Lastly, we investigated DDT reactivity in the test sediments with incubations of sediment slurries with a labeled DDT substrate.
Theoretical models
PE/sediment bed 1D diffusion model
Applying Fick's law to a PE membrane in an unmixed sediment bed, and employing Laplace transforms, Fernandez et al.9 developed a model for the exchange kinetics of chemicals between polymer membranes and static sediment beds. According to this model, a typical PRC loss curve is characterized by a fast, initial decrease in PRC concentration, followed by a slow decline as diffusion through the sediment bed becomes increasingly limiting. The diffusion rate into the sediment bed depends on the fraction of the chemical present in the porewater, and the sediment's porosity and tortuosity. Since porosity can be measured and tortuosity can be approximated based on porosity,9 the PRC transport can be ultimately modeled based on Kd, the sediment/water partition coefficient, which is also sometimes referred to as sediment/water distribution coefficient. Lastly, for PRC and target compounds differing only in isotopic label, the fractional equilibration of a target chemical should be, at any time, equal to the fraction of PRC lost from the PE, and this behavior has been supported by previous studies.8,9Development of 1D reaction–diffusion model
Assuming that degradation of a target compound and/or PRC takes place in a sediment bed, we can write the following governing equations: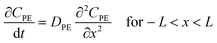 | (1) |
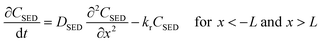 | (2) |
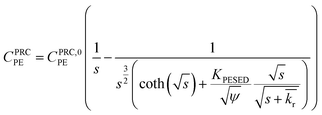 | (3) |
 is the reaction rate in non-dimensional units (=krL2/DPE). For a target chemical diffusing into PE and reacting in the sediment bed, the concentration in PE is given by:
is the reaction rate in non-dimensional units (=krL2/DPE). For a target chemical diffusing into PE and reacting in the sediment bed, the concentration in PE is given by: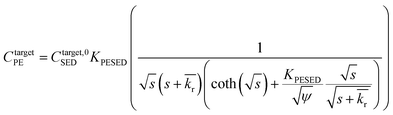 | (4) |
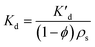 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd (cmw3 gsed−1) values determined from PE/sediment tumbling experiments (Kd,Ta), and from fits of diffusion model to PRC loss from field deployed (Kd,Fb) and PRC loss from static laboratory incubation of PE (Kd,Lc) in various sediments collected from the study site
Kd (cmw3 gsed−1) values determined from PE/sediment tumbling experiments (Kd,Ta), and from fits of diffusion model to PRC loss from field deployed (Kd,Fb) and PRC loss from static laboratory incubation of PE (Kd,Lc) in various sediments collected from the study site
| Sediment | F1 | F2 | CM | LM | ||||
|---|---|---|---|---|---|---|---|---|
| K d,T | K d,F | K d,T | K d,L | K d,T | K d,L | K d,T | K d,L | |
a
K
d,T = CSED/CPE × KPEW, with KPEW values from Hale et al.29 Error in Kd values estimated from duplicate experiments was <0.05![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units. Even when considering heterogeneity in sediment concentration from triplicate CSED measurements, error in Kd was still less than 0.1 log units. Even when considering heterogeneity in sediment concentration from triplicate CSED measurements, error in Kd was still less than 0.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units across all sediments.
b
K
d,F and standard error calculated from fitting the diffusion model (see ESI-2) to PRC losses measured at 10 and 30 days in field deployed PE (0–10 cm depth into sediment).
c
K
d,L and standard error calculated from fitting the diffusion model (see ESI-2) to PRC losses measured at various timepoints in static laboratory PE/sediment incubations.
d Not determined because 2,4′-DDE concentration in F1 sediment was below detection limit of 0.7 ng g−1 dry weight. log units across all sediments.
b
K
d,F and standard error calculated from fitting the diffusion model (see ESI-2) to PRC losses measured at 10 and 30 days in field deployed PE (0–10 cm depth into sediment).
c
K
d,L and standard error calculated from fitting the diffusion model (see ESI-2) to PRC losses measured at various timepoints in static laboratory PE/sediment incubations.
d Not determined because 2,4′-DDE concentration in F1 sediment was below detection limit of 0.7 ng g−1 dry weight.
|
||||||||
| 2,4′-DDE | n.d.d | 4.4 | 3.9 | 3.9 | ||||
| 4,4′-DDE | 4.3 | 4.5 ± 0.1 | 4.3 | 3.9 ± 0.1 | 3.9 | 3.7 ± 0.1 | 3.9 | 3.4 ± 0.3 |
| 2,4′-DDD | 3.8 | 3.9 | 3.7 | 3.6 | ||||
| 4,4′-DDD | 4.0 | 4.0 ± 0.3 | 4.1 | 4.1 ± 0.1 | 3.8 | 3.7 ± 0.1 | 3.8 | 3.5 ± 0.1 |
| f OC (%) | 2.4 ± 0.2 | 2.2 ± 0.1 | 1.42 ± 0.02 | 1.26 ± 0.03 | ||||
| f BC (%) | 0.35 ± 0.01 | 0.33 ± 0.04 | 0.26 ± 0.03 | 0.17 ± 0.03 | ||||
Materials and methods
For solvents and sources of chemicals and materials, the reader is referred to ESI-2.†PRC selection
The PRCs used were four 13C labeled PCB congeners (13C PCB 28, 13C PCB 47, 13C PCB 111, 13C PCB 153), 13C 2,4′-DDT, and two degradation products, 13C 4,4′-DDE and 13C 4,4′-DDD. The choice of PRCs reflected the predominant contaminants at the site, where previous measurements had indicated that DDE and DDD levels were high relative to their parent, DDT, and that levels of the 4,4′ isomers were higher than the 2,4′ isomers (Table S1†). The 13C 2,4′-DDT PRC was chosen instead of the 13C 4,4′-DDT such that its degradation products (i.e. the 2,4′ isomers of DDE and DDD) could be distinguished from the other PRCs. Lastly, the PCB PRCs were used as representative compounds for diffusion-only transport between PE and the sediment bed, although we recognize that PCBs may undergo reductive dechlorination in anoxic sediments,18 albeit typically requiring much longer times than the month-long PE deployments used here.PRC loading into PE
The PE was loaded with PRCs from an 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 methanol
20 methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water mixture under continuous shaking at 100 rpm for 7 d, according to the method of Booij et al. (2002).19 The methanol
water mixture under continuous shaking at 100 rpm for 7 d, according to the method of Booij et al. (2002).19 The methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) water loading solution was prepared by first adding aliquots of PRCs dissolved in nonane to methanol, followed by brief agitation to ensure complete mixing, and ultimately by addition of the volume of water required to achieve the 80
water loading solution was prepared by first adding aliquots of PRCs dissolved in nonane to methanol, followed by brief agitation to ensure complete mixing, and ultimately by addition of the volume of water required to achieve the 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 methanol–water ratio by volume. The ratio of PE to loading solution employed was 6 g of PE to 1 L of loading solution (limited by the ability to closely pack the PE in the loading jar while ensuring contact with loading solution throughout). At this phase ratio, the loading efficiency was only 0.3–0.6% (given partition coefficients between PE and 80
20 methanol–water ratio by volume. The ratio of PE to loading solution employed was 6 g of PE to 1 L of loading solution (limited by the ability to closely pack the PE in the loading jar while ensuring contact with loading solution throughout). At this phase ratio, the loading efficiency was only 0.3–0.6% (given partition coefficients between PE and 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 loading solution of ∼0.5–1 for compounds with log
20 loading solution of ∼0.5–1 for compounds with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow between 5.5 and 7, Booij et al.19). Nonetheless, this method of loading the PRCs into PE was chosen because it ensures fast equilibration times (≪7 days compared to several weeks when loading from water) and uniform PRC concentrations throughout the membrane (by removing the issue of poor solubility encountered when loading PRCs from water). After removal from the loading solution, the PE strips were placed in a clean jar with water and placed on the shaker table overnight for removal of residual methanol before use in the laboratory incubations or field deployments.
Kow between 5.5 and 7, Booij et al.19). Nonetheless, this method of loading the PRCs into PE was chosen because it ensures fast equilibration times (≪7 days compared to several weeks when loading from water) and uniform PRC concentrations throughout the membrane (by removing the issue of poor solubility encountered when loading PRCs from water). After removal from the loading solution, the PE strips were placed in a clean jar with water and placed on the shaker table overnight for removal of residual methanol before use in the laboratory incubations or field deployments.
Initial concentrations of PRCs in PE
After loading with PRCs, one strip of PE (sectioned in 5 pieces before extraction) was stored in the laboratory in a small amber vial filled with water to minimize volatilization losses (40 mL Milli-Q water for 0.5 g of PE) and was used for measurement of initial PRC concentrations in the field deployed PE. The PE used in laboratory (both static ex situ and tumbling of sediment slurries) incubations was loaded with the same PRCs as the field deployed PE, but at different initial concentrations (Table S2†). This difference was due to different PE to loading solution ratios used when loading the laboratory and field PE strips. The PE used in the laboratory was used within a few days of loading. In order to characterize initial PRC concentrations in the PE used in laboratory experiments, five pieces of blank PE were set aside when the static incubations were started and immediately extracted with solvent.Field deployment of PE
The PRC-loaded PE was transported in person to ENI Donegani Institute and stored at room temperature in foil packets for 1 month. The PE was mounted in metal frames and deployed at the sediment–water interface in June of 2013, in a subalpine lake in Northern Italy containing historical DDT contamination. The sampler extended 40 cm into the sediment bed and 20 cm above the sediment–water interface. Sediments from the near vicinity of the sampler (F1) and ∼10 m away from the sampler (F2) were also collected via a grab sampler, and stored in amber jars with foil-lined caps at 4 °C, until used either for sediment analysis or ex situ incubations with PE (see below). The F1 sediment was used in ex situ tumbling incubations, while F2 sediment was used in both ex situ static and tumbling incubations. Half of the in situ samplers were retrieved after 10 d and the rest after 30 d. After retrieval, the PE was cleaned with a Kimwipe to remove any sediment that adhered to the surface, cut from the frame and stored in foil packets at 4 °C for ∼2 month, until sub-sectioned into 10 cm slices, and extracted with solvent. The PE deployed in the sediment did not exhibit any visible signs of biofilm or precipitate (no surfaced coloration, no changes in appearance upon wiping), and therefore no special precautions were taken to clear any potential biofilm from the surface of the PE (besides briefly wiping with water and Kimwipes).Static ex situ incubations
We performed jar incubations of PE in three sediments collected from the field site to determine if the behavior of the PRC and target compounds matched what we observed in the field-deployed PE. Because only two time points could be obtained from the field deployments (10 and 30 days), the goal of the static incubations was to obtain PRC loss curves with more timepoints that would allow us to better evaluate whether the transfer was diffusion and/or reaction driven. For this, we used three different sediments previously collected from the lake (F2 sediment, as well as CM and LM sediments previously collected from other locations in the lake and stored in a freezer until use). In each case, the number of samples collected over time was limited by the amount of sediment available. The CM and LM sediments were chosen because they appeared to have similar sorption properties (Table 1), but differed in level of DDX contamination (∑DDX was ∼7 fold higher in LM compared to CM sediment, Table S1†) and redox properties (LM sediment was black with the exception of a thin light brown layer at the top, whereas CM sediment was light brown throughout, suggesting conditions in LM were more reducing).For the static incubations with F2 sediment, pre-homogenized F2 sediment (∼550 g wet weight) was placed into three 500 mL jars, and two pieces of PE (2.5 by 2.5 cm and 25.4 μm thickness) were added to each jar (total of 6 pieces). In each jar, the two pieces of PE were placed horizontally with ∼3 cm of sediment between each other and the top or bottom of the jar. The pieces of PE were removed from the sediment after 5, 10 (duplicates), 20, and 30 (duplicates) d, rinsed with Milli-Q water to remove any sediment that might have adhered to the PE, wiped with a Kimwipe, and then extracted with solvent (ESI-2†). The top pieces were removed first from each jar (5 day and the 10 day duplicates), and the bottom pieces were removed at 20 and 30 day (duplicates).
The jar incubations with the CM and LM sediments were done in 125 mL amber jars. A total of four jars for LM sediment and three jars for CM sediment were set up with ∼150 g of sediment (wet weight) and one PE piece (∼20 mg) placed horizontally in each jar. The PE pieces were removed at 4, 20 and 40 days for CM and 4, 14, 20 and 40 days for LM sediment and processed in the same way as the described above for the F2 incubations. No discoloration was observed in any of PE pieces after the ex situ static incubations and no special precautions were taken to remove any biofilm that may have been present on the surface of the PE. The PRC losses from field deployed and laboratory incubated PE were fit using the PE/sediment diffusion model9 and a simplified version developed by Apell et al.20 (see also ESI-2†).
Tumbling experiments
To determine the equilibrium concentrations of target analytes in the three sediments (F2, CM, LM), and infer the apparent sediment–water partition coefficients for DDE and DDD, a set of PE/sediment incubations was performed under continuously mixed conditions.21 In short, a ground glass stoppered round bottom flask was filled with 30–40 g of wet sediment (∼20 g dry sediment), 100 mL Milli-Q water, and ∼50 mg PRC-loaded 25 μm thick PE. Duplicate flasks were tumbled at room temperature, inside a light-excluding cardboard drum on a roller table. After 1 month, the PE was removed from each flask, wiped with a Kimwipe, extracted with solvent, and analyzed for DDD and DDE isomers (ESI-2†). An aliquot of the sediment slurry from each experiment was dried overnight in a 60 °C oven, and saved for chemical analysis.Suspecting that DDT was susceptible to degradation, two additional sets of tumbling experiments were performed with F2 sediment spiked with a mixture of d8 4,4′-DDT and 13C PCB 153. In the first experiment, about ∼45 g of F2 sediment (wet weight) were added to four 125 mL pear shaped flasks. Two of the flasks were then autoclaved and after the two autoclaved sediments reached room temperature, all four flasks were spiked with a mixture of d8 4,4′-DDT and 13C PCB 153 (25 μL of a spiking solution of 13C PCB 153 and d8 4,4′-DDT in hexane). About ∼100 mL of Milli-Q water was then added to each flask (headspace < 1 mL) and the flasks were tumbled in the dark for ∼2 h. Once shaken, the spike appeared to mix thoroughly with the slurry and did not phase separate. A piece of PE (∼40 mg) was then added to each of the four flasks, and tumbled in a light-excluding drum for 1 month. Each flask was capped with a ground glass stopper and had a minimal amount of headspace (<1 mL).
In the second experiment, a tumbling time course was performed for 60 days with spiked F2 sediment but without PE. The experimental setup, analytical methods and results of this experiment are described in more detail in ESI-2.† The concentration of the spiked chemicals was quantified in PE for the first experiment and the sediments for the second (ESI-2†).
PE extraction
Field deployed PE strips and laboratory blanks (also used to characterize initial PRC concentrations) were extracted and analyzed according to previously described procedures,17 which are also summarized in the flowchart in Fig. S1.† In short, PE samples were spiked with surrogate standards (13C PCB 70, 13C PCB 105, d8 2,4′-DDT and d8 4,4′-DDD) and extracted three times with dichloromethane (DCM). We chose d8 2,4′-DDT as a surrogate standard to determine if any degradation of 2,4′-DDT PRC was occurring during the PE extraction or GC analysis steps (see also Chemical analysis section). The combined DCM extracts were concentrated by rotary evaporation, and then solvent exchanged to hexane. Finally, the volume was adjusted to 50–250 μL under a gentle stream of nitrogen. Prior to GCMS analysis, the extracts were spiked with injection standard (13C PCB 97 and 13C PCB 167). The laboratory PE samples (tumbling and jar incubations) were extracted in a similar fashion (see also flowchart in Fig. S1†), but with a slightly different combination of recovery (13C PCB 19, 13C PCB 97, 13C PCB 170, d8 2,4′-DDT and d8 4,4′-DDD) and injection compounds (13C PCB 167). The set of recovery compounds used in the laboratory PE samples were selected to better capture the range of volatility of the PRCs and DDX analytes (as estimated from GC retention times). As such, 13C PCB 19 and 13C PCB 170 were employed because they bracket both the PRCs and the target analytes in volatility (i.e., GC retention time, Tables S3 and S4†). In addition, 13C PCB 97 was used because it is close in volatility to many of the DDX PRCs and target analytes (Tables S3 and S4†).Sediment characterization
For each sediment (F2, CM, LM) used in laboratory experiments, we characterized the water content, the fractions of organic carbon (fOC) and black carbon (fBC), and the bulk concentration of DDXs. The fOC and fBC were measured according to standard procedures,9 noting that the sediment used for fBC determination was combusted at 375 °C according to the chemo-thermal oxidation method (also known as CTO-375) directly in the silver capsule used for subsequent elemental carbon, hydrogen and nitrogen (CHN) analysis. For DDX analyses, aliquots of 1 g of ground oven dried (60 °C, 24 h) sediment were loaded into metal extraction cells, spiked with the same surrogate standards as the field PE samples, and extracted using an accelerated solvent extractor (Dionex ASE 200, Sunnyvale, CA), with a mixture of 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 DCM
10 DCM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) methanol, at 100 °C and 1000 psi. Drying at 60 °C has been used previously in our laboratory for analytes of like volatility (e.g. PAHs, PCBs) and was not found to cause significant losses.8 In addition, previous analyses of DDX contaminated sediments from our laboratory did not show any differences between oven dried and freeze-dried sediments for DDD and DDE concentrations, but showed lower recoveries of DDT in oven dried versus freeze dried sediments. However, this was not a concern for the native sediments used in this study because DDT was previously documented to be below detection using freeze dried samples. In addition, for labeled DDT analyses, the spiked DDT sediment samples from the tumbling time course were freeze dried instead of oven dried before extraction (see ESI-2†). The solvent extracts were concentrated under a gentle stream of nitrogen to a volume of ∼1 mL, treated with activated copper (granular copper, 20–30 mesh, JT Baker) for removal of elemental sulfur, and spiked with injection compounds prior to GCMS analysis.
methanol, at 100 °C and 1000 psi. Drying at 60 °C has been used previously in our laboratory for analytes of like volatility (e.g. PAHs, PCBs) and was not found to cause significant losses.8 In addition, previous analyses of DDX contaminated sediments from our laboratory did not show any differences between oven dried and freeze-dried sediments for DDD and DDE concentrations, but showed lower recoveries of DDT in oven dried versus freeze dried sediments. However, this was not a concern for the native sediments used in this study because DDT was previously documented to be below detection using freeze dried samples. In addition, for labeled DDT analyses, the spiked DDT sediment samples from the tumbling time course were freeze dried instead of oven dried before extraction (see ESI-2†). The solvent extracts were concentrated under a gentle stream of nitrogen to a volume of ∼1 mL, treated with activated copper (granular copper, 20–30 mesh, JT Baker) for removal of elemental sulfur, and spiked with injection compounds prior to GCMS analysis.
Chemical analysis
Quantifications of DDXs in the PE and sediment samples (with the exception of spiked sediments, see ESI-2†) were done on an Agilent 6890 GC coupled with a mass spectrometer (JEOL GCmate, JOEL Ltd, Tokyo, Japan), operated at parameters summarized in ESI-2.†17 To minimize the potential for DDT degradation during GC analysis, a cold-on-column injection method was used, in which the sample was injected directly onto an inert guard column connect to the separation column via an inert connector. The guard column was used because repeated sample injections can deposit nonvolatile components of the sample at the site of injection, which causes poor separation and degradation of analytes. The guard column can thus be trimmed periodically to remove the contaminated portion without affecting the length of the separation column (and hence the separation of the target analytes). The use of d8 2,4′-DDT as a recovery standard, without any of its potential degradation products (d8 2,4′-DDE or d8 2,4′-DDD) added to the sample, ensured that the amount of instrument-related DDT degradation could be evaluated in each sample (as opposed to relying on detecting the presence of degradation in separate injections of DDT-only standard solutions). Typically, if samples showed any measurable DDT degradation (seen as appearance of a d8 2,4′-DDD peak), the guard column was cut and the analysis was repeated.Results and discussion
PRC loading and detection limits
The PRC concentrations ranged from 100 to 400 ng g−1 PE, more than a factor of 100 higher than the limits of detection (Table S2†). The variability in the loaded PE (N = 5), was less than ±6% for all the PRCs in the blank PE used to quantify PRC concentrations in the field deployed PE, and less than ±10% for most PRCs in the blank PE used to quantify PRC concentrations in the laboratory PE, with the exceptions of 13C PCB 28 (±13%), 13C PCB 111 (±11%) and 13C PCB 153 (±15%). No evidence of degradation of the DDT-PRC was observed in analyses of the two sets of blank PE. The potential degradation products of the DDT PRC were below detection in both cases (Table S2†). Further, the concentration of the DDT PRC in the loaded PE was like that seen for other PRCs (recognizing differences in PE:solvent partition coefficients), which suggests that the DDT PRC did not degrade during loading.Fractional loss of PRCs after field deployment
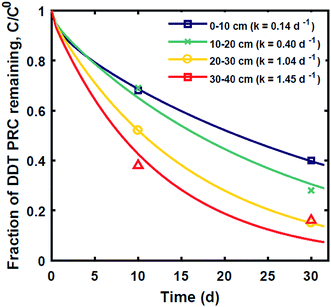
The measured PRC losses after the 10 and 30 d deployments of PE into the sediment bed at the field site for the PCB PRCs, as well as that of 13C 4,4′-DDE and 13C 4,4′-DDD, were consistent with solely diffusive losses for the whole set of PRCs (Fig. 1). The fractions of each PRC remaining were also consistent with using Kd values (cmw3 gsed−1) ranging from 103.6 to 104.2 for DDD and 104.2 to 104.7 for DDE in the model of Fernandez et al.9 Furthermore, the Kd values deduced from the PRC loss from the PE strip deployed at 0–10 cm into the sediment (104.5 for DDE and 104.0 for DDD), were within 0.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units of the independently measured Kd values from ex situ tumbling experiments with F2 sediment (Table 1). The measured Kd value for DDE was larger than that for DDD which was consistent with the magnitude of Kow values for the same compounds (Kow of DDE and DDD are 106.5 and 106.0, respectively22). Kd values are dependent on sorption to organic carbon and black carbon, which are both correlated with Kow values.23 Furthermore, across the four depth horizons (0–10, 10–20, 20–30 and 30–40 cm), the PRC losses varied at most by 10%, suggesting that Kd does not significantly vary with depth at this site (Fig. 1).
log units of the independently measured Kd values from ex situ tumbling experiments with F2 sediment (Table 1). The measured Kd value for DDE was larger than that for DDD which was consistent with the magnitude of Kow values for the same compounds (Kow of DDE and DDD are 106.5 and 106.0, respectively22). Kd values are dependent on sorption to organic carbon and black carbon, which are both correlated with Kow values.23 Furthermore, across the four depth horizons (0–10, 10–20, 20–30 and 30–40 cm), the PRC losses varied at most by 10%, suggesting that Kd does not significantly vary with depth at this site (Fig. 1).
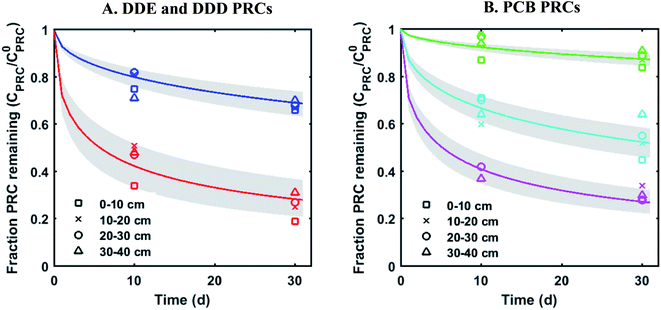 | ||
Fig. 1 Fractional PRC remaining in PE as a function of time (panel (A) DDE and DDD PRCs; panel (B) PCB PRCs), after in situ deployment in sediment at various depth horizons: 0–10 cm (squares), 10–20 cm (crosses), 20–30 cm (circles), and 30–40 cm (triangles). Solid lines represent the expected PRC release using the diffusion model of Fernandez et al.,9 assuming Kd (cmw3 gsed−1) values of 103.9 (13C 4,4′-DDD), 104.3 (13C 4,4′-DDE), 104.6 (13C PCB 28), 104.5 (13C PCB 47) and 105.4 (13C PCB 111). Shaded envelopes represent the results of the same diffusion model, using ±0.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units log log units log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd values. The measured losses of each PRC compound are consistent with diffusion-driven transport. Kd values. The measured losses of each PRC compound are consistent with diffusion-driven transport. | ||
PRC loss and target uptake in static ex situ incubations
For DDE/DDD and PCB PRCs, the losses of PRCs measured in laboratory incubations were similar to those observed in the field PE. For example, although there was some difference (∼10%) in the amount of PRC loss measured in field PE versus the PE incubated in F2 sediment (collected from the vicinity of samplers), the overall shape of loss curve was similarly well captured by the diffusion model9 (Fig. 2). This was also the case for the PE incubated in two additional sediments, CM and LM (Fig. S2†).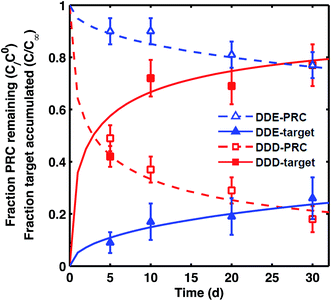 | ||
| Fig. 2 Fraction of PRC remaining (empty symbols) and fraction of target compound accumulated (filled symbols) after static laboratory incubation of PE with F2 sediment for 4,4′-DDE (blue triangles) and 4,4′-DDD (red squares). Fractional accumulation was calculated as the ratio of concentration of target analyte measured in PE from static incubation divided by the concentration of the same analyte in tumbled PE. Lines represent the diffusion model of Fernandez et al.9 for PRCs (dashed lines) and target analytes (solid lines) with Kd (cmw3 gsed−1) for DDE of 104.0 and for DDD of 104.2. Error bars for fraction of PRC remaining calculated based on one SD of PRC concentration in T = 0 PE, and for fraction of target accumulation based on one SD of instrument error. For the target accumulations, each data point corresponds to the ratio of two single PE measurements (one field PE and one tumbled PE), and the instrument error was used as an estimate of uncertainty. | ||
The transfers between PE and sediment of PRC and target analytes were isotropic for both DDE and DDD in all three static sediment incubations (Fig. 2 and S2†), as expected for diffusion-mediated transport. The sum of observed fractional PRC loss and corresponding target accumulation was 1 ± 0.1 across all sampled time points (e.g., 1.02 ± 0.03 for DDE, and 0.98 ± 0.08 for DDD for PE in F2). The diffusion model fit the PRC loss well and provided an estimate of the Kd values for the sediment (Kd, L values in Table 1). The root mean squared errors (RMSE) of the diffusion model fits were 0.04–0.05 and 0.02–0.06 for DDD and DDE PRCs, respectively. Interestingly, the Kd values that fit the measured PRC loss (Fig. 2) were up to 0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units smaller than the Kd values measured from tumbling experiments (e.g., for DDE in LM, tumbling-Kd 103.9vs. PRC-Kd 103.4, Table 1). Such differences are not large when compared with typical uncertainties associated with Kd values estimated from equilibrium partition models, where input KOC and KBC values can vary by more than 0.5
log units smaller than the Kd values measured from tumbling experiments (e.g., for DDE in LM, tumbling-Kd 103.9vs. PRC-Kd 103.4, Table 1). Such differences are not large when compared with typical uncertainties associated with Kd values estimated from equilibrium partition models, where input KOC and KBC values can vary by more than 0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units each.24 It was also possible, however, that the differences between PRC-derived Kd and tumbling-Kd could reflect local sorptive depletion and disequilibrium in the static ex situ incubation relative to the tumbling setup.
log units each.24 It was also possible, however, that the differences between PRC-derived Kd and tumbling-Kd could reflect local sorptive depletion and disequilibrium in the static ex situ incubation relative to the tumbling setup.
Thus, though potentially susceptible to chemical transformations in the sediment, the exchange of DDE and DDD between passive samplers and sediment beds appears to be diffusion-mediated. This implies that any potential transformations of DDE and DDD in both field and laboratory conditions were slower than the rates of diffusion in the sediment bed. PE/sediment exchange timescales were on the order of weeks (70 d for DDE and 15 d for DDD) while previous measurements of degradation rates imply half-lives on the order of years (3–30 years for DDE6 and 10 years for DDD in sediment beds25).
Reaction-driven DDT PRC loss
In contrast, the losses of the DDT PRC measured in the field deployed PE (Fig. 3), and in the laboratory incubations (Fig. S3†), were not consistent with diffusion-mediated transport. The loss of DDT PRC did not slow down with time, as it would be the case for diffusive loss (Fig. 3, panel A). Furthermore, since Kd is usually correlated with Kow, and DDE and DDT have similar Kow values (106.5 and 106.8, respectively22), we would expect both compounds to have similar Kd values and implicitly, similar PRC losses. In contrast, the DDT PRC was lost to a substantially greater extent than the DDE PRC (more than a factor of 2 after 30 d). Also, the Kd values (105 to 106, Fig. 3) that would be required to fit the accelerated DDT-PRC losses with a diffusion-only model (i.e., the simplified diffusion model of Apell et al.20 as described in ESI-2†), were 1–2 orders of magnitude larger than the Kd value of DDE in F1 and F2 sediments (104.3, Table 1), which is inconsistent with the fact that the two compounds have similar Kow values. In addition, the RMSEs associated with the best-fits for DDT PRC losses using diffusion-only model for each depth were also significantly higher (RMSE of 0.07–0.17) than those for the DDE (RMSE of 0.02–0.07) or DDD (RMSE of 0.02–0.10) PRCs. Lastly, the amount of DDT-PRC recovered in the PE was found to decrease significantly with depth, more than it could be explained by loading variability (∼2%), and inconsistent with the losses of all other PRCs, which varied little with depth (Fig. 1).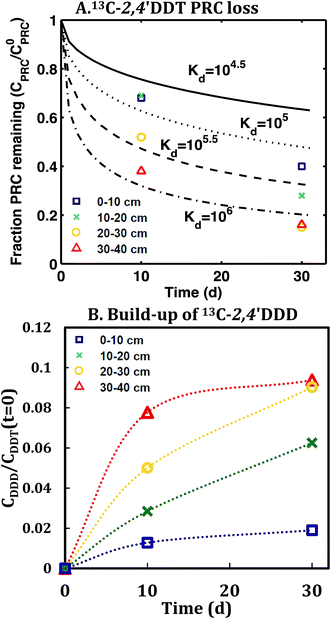 | ||
| Fig. 3 (A) Fraction of 13C 2,4′-DDT PRC remaining in PE, and (B) accumulation of degradation product 13C 2,4′-DDD expressed as a fraction of the initial 13C 2,4′-DDT PRC concentration in PE after in situ deployment in sediment at various depth horizons: 0–10 cm (squares), 10–20 cm (crosses), 20–30 cm (circles), and 30–40 cm (triangles). Lines in panel (A) represent the expected PRC release using the diffusion model of Fernandez et al.,9 assuming Kd (cmw3 gsed−1) values of 104.5 (solid), 105.0 (dot), 105.5 (dash), and 106 (dot-dash). As opposed to PRCs in Fig. 1, the measured DDT PRC losses varied significantly with depth. In addition, the PRC losses from 10–20 and 20–30 cm depth horizons were not consistent with the shape of a diffusion profile. For the 0–10 cm and 30–40 cm, the PRC loss was consistent with diffusion into a sediment with a Kd value of 105 and 106, respectively. Dotted lines in panel (B) figure are drawn to guide the eye and are not model fits. | ||
Similar to the field deployment case, the losses of the DDT PRC measured in PE strips from the static ex situ incubations, were also not consistent with solely diffusive transport. While the loss of the DDE PRC (similar size and Kow to DDT, as mentioned above) varied at most by 10% across the PEs incubated in three different sediments (e.g., 8–18% lost after 20 d, Fig. 2 and S2†), the DDT PRC loss differed greatly (e.g., after 20 d lost 43% in CM-PE, and more than 90% in LM-PE, Fig. S3†). The variable loss of DDT PRC across the different sediment incubations supports the hypothesis that reactive processes occurring in the sediment, as opposed to inside the PE, were accelerating the PRC loss.
Other hypotheses for the observed loss of the DDT PRC were also considered, but these were all ruled out for several reasons. The passive sampling process involves several steps such as loading, storage before and after deployment, extraction and chemical analysis and we considered whether degradation of the DDT PRC could have occurred at other times except during the exposure to the sediment. Degradation during loading of the PRCs into the PE was considered very unlikely because no degradation products were measured in the blank PE, and levels of the DDT PRC were comparable to those of the other PRCs (suggesting no degradation occurred during loading). Degradation during loading would also not explain the variable PRC loss observed across the field-deployed PE and laboratory-incubated PE. Degradation during GC analysis (documented in Foreman et al.26) was ruled out by using d8 2,4′-DDT as a recovery standard, which allowed us to monitor instrument-related degradation in each sample. As described in the Materials and methods section, if any instrument-related degradation was observed, the guard column was cut and the analysis was repeated.
Degradation of the DDT PRC during the storage of the PE was also considered as a potential explanation for the observed DDT PRC loss, but was unlikely for several reasons. First, degradation during storage should have led to the same extent of degradation in all field deployed PE which were all stored in the same way (i.e., for one month before deployment and two months after deployment and before analysis). In contrast, as shown in Fig. 3 and 4, the extent of the DDT PRC loss was clearly different across the various PEs deployed in the field or exposed to sediments in the laboratory. Further, the DDT PRC loss observed in PE deployed in the water column during the same field campaign,17 did not appear to be degradation-driven and the retrieved PE did not show accumulation of any PRC degradation products. Similarly, the portion of the PE from the same samplers that was above the sediment–water interface (and hence exposed to oxic bottom water) did not show any evidence of DDT-PRC degradation. Finally, degradation during storage would not explain the observed degradation of the DDT PRC in ex situ static incubations in which the PE samples were used within a few days of being loaded with PRCs and were extracted with solvent immediately after removal from the sediment.
Accumulation of PRC degradation products in the PE
The conclusion that the loss of the 13C 2,4′-DDT PRC was driven by reactions was strongly supported by the corresponding accumulation in the PE of its degradation product, 13C 2,4′-DDD. The concentration 13C 2,4′-DDD in PE increased with depth into the sediment (Fig. 3), ranging between 2 and 20 ng g−1 PE, at least 10 times more than the limit of detection (Table S2†). The identity of the degradation product was confirmed by its retention time and the observed ratio of the confirming and quantitation ion intensities. The measured PRC degradation product likely came from reactions occurring in the surrounding sediment, and not degradation during the PE extraction or GC-MS analysis. The degradation of d8 2,4′-DDT recovery standard, added to PE prior to extraction, was closely monitored and analysis conditions were carefully maintained such that d8 2,4′-DDD was always below detection. Accumulation of the PRC degradation product, 13C 2,4′-DDD, was also observed in the laboratory incubations, and the measured concentration of 13C 2,4′-DDD in PE increased with time and with the amount of observed DDT PRC loss (Fig. S3†). In both field and laboratory incubations, up to 13% of the initial DDT PRC concentration was recovered as 13C 2,4′-DDD in the PE (Fig. 3 and S3†).Instability of DDT in F2 sediment on timescales of days to weeks was also confirmed by the poor recovery of a labeled DDT spike in the tumbling time course performed with F2 sediment (only 1–18% of initial d8 4,4′-DDT spike recovered after 4–60 days, versus 91 ± 12% of spiked 13C PCB 153, see ESI-2 and Fig. S4†). The time course data were not suitable for fitting a first order reaction rate because the recovery of the two spiked compounds was variable and because >80% of the d8 4,4′-DDT appeared to have degraded after only 4 days implying a rate of 0.4 d−1 (see ESI-2 and Fig. S4†). The variability in the data could have been due to incomplete mixing or differences in the amount of headspace (and hence redox) conditions established in each flask.
In the tumbling experiments performed with spiked sediment and with PE, we found that no labeled DDT was measurable in PE after 30 days of tumbling, even when the sediment was autoclaved prior to spiking with d8 4,4′-DDT and 13C PCB 153, which suggests that the degradation may be abiotic. In contrast, the spiked 13C PCB 153 accumulated in the PE at similar levels in both the autoclaved and non-autoclaved sediments. The lack of native DDT in the field-collected F1 and F2 sediments further supports the assumption of DDT reactivity in these sediments. For an average sedimentation rate of 0.5 cm per year,27 the average age of the upper 10 cm would be about 10 years (0 at the top and 20 years at 10 cm), implying that DDT reacts on timescales shorter than 10 years.
Reaction–diffusion model
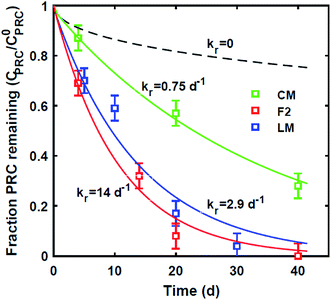
Lastly, we evaluated whether a reaction–diffusion model could fit the behavior of the DDT-PRC (eqn (3) inverted with Matlab code in ESI-3†). Since the observed PRC loss was due to both diffusion of the PRC into the sediment bed and reaction in the sediment, the reaction rate can only be deduced from a model fit for a given Kd (which affects KPESED and Ψ in eqn (3)). Applying the reaction–diffusion model to the observed PRC loss from the field deployed PE, and assuming the same value of Kd of DDT as the model-derived (Fig. 1) Kd value of DDE, we obtain best-fit reaction rates that increase with depth into sediment bed: 0.14 d−1 at 0–10 cm to 1.4 d−1 at 30–40 cm (Fig. 4). The model fit of PRC loss over time is greatly improved by using the reaction–diffusion model (RMSE of 0.0003–0.09) over using the diffusion-only model (Fig. 4vs.3, panel A; RMSE of diffusion only model of 0.07–0.18). Previous studies found that DDT degradation in sediment slurries depended on oxidation reduction potential (kr ranged from 0.3 to 0.03 d−1 for Eh values of −150 to 450 mV), and that DDD was the major degradation product in strongly reducing conditions.2 Thus, the magnitude and increase with depth of the best-fit reaction rate were reasonable given that (1) the redox potential was likely more reducing with depth into sediment bed28 and (2) the amount of 13C 2,4′-DDD degradation product measured in the PE also increases with depth (Fig. 3).Fits of PRC losses observed in laboratory incubations of PE in the sediments yielded reaction rates that were larger than for the field PE, ranging from 0.75 d−1 (CM) to 15 d−1 (LM). As was the case for modeling the results of the field deployments, the fits to the DDT PRC improved over using a diffusion-only model (RMSEs of 0.22, 0.15, 0.20 for diffusion-only versus RMSEs of 0.15, 0.03, and 0.09 for reaction–diffusion model fits for F2, CM and LM, respectively; also compare Fig. S3† with Fig. 5). The fitted reaction rate deduced from the PRC loss measured from PE incubated in the laboratory in static conditions with F2 sediment (1.4 d−1) was an order of magnitude larger than the fitted reaction rate from the field PRC loss (0.14 d−1 at 0–10 cm, Fig. 4). The difference in reaction rates could be a consequence of the assumptions made in fitting the model (e.g., lower Kd values needed to explain PRC loss from laboratory incubated PE versus field deployed, see captions of Fig. 1 and 2, and Table 1), or may actually reflect more favorable conditions for degradation of DDT in the laboratory, due to higher temperatures or changes in redox potential of the sediment after removal from the field.
The amount of degradation product (13C 2,4′-DDD) measured in the PE at the end of the field or laboratory exposures, was consistent with the amount expected to diffuse back into the PE based on the reaction–diffusion model. In order to do this calculation, we employed the fitted Kd and kr values derived in this study to calculate the concentration versus distance profiles of the DDT-PRC in PE and in the sediment bed over 30 days. Based on the distribution of the DDT-PRC in the sediment bed (Fig. S5†), most of the degradation of the DDT-PRC was occurring in the vicinity of the PE at distances between 0.1 and 0.5 cm. Using these distances and the KPEW and Kd values for 2,4′-DDD of ∼104.9 (Hale et al.29) and 103.9 (Table 1), respectively, we estimate that if all the degraded 13C 2,4′-DDT transformed into 13C 2,4′-DDD, then ∼2% to 11% of the initial 13C 2,4′-DDT should diffuse back into PE as 13C 2,4′-DDD. This is in good agreement with the observed amount of 13C 2,4′-DDD accumulated in the PE after field deployment (2–9%, Fig. 3) and after laboratory incubations (6–13%, Fig. S3†).
Discussion of model assumptions
The reaction–diffusion model was built on the assumption that the degradation of the DDT-PRC occurred in the sediment, as opposed to in the PE or at the PE–sediment interface. Several lines of evidence suggested that degradation occurred in sediment and not in the PE (i.e., the sediment-dependent loss of DDT-PRC, the accumulation of DDT-PRC degradation products in the PE consistent with back-diffusion expectations, the lack of degradation of the DDT-PRC in PE deployed in the water column, and the instability of DDT in sediments spiked with labeled DDT). Furthermore, in order for the reaction to take place inside the PE, the reductant would need to diffuse into the PE. If the reaction was mediated by microbes, it is unlikely that the microbes could penetrate the PE due to size limitations, and if the reaction was abiotic, the reductant would likely be a polar species like Fe2+ or reduced organic mediators30 which would not diffuse into PE due to their polarity. As noted before, the PE retrieved from sediment did not show any signs of a biofilm (no discoloration or growth) and such films are more commonly observed by us in water column deployments. Therefore, we did not make any distinction in the model between degradation that might have occurred in the near vicinity of the PE (i.e., a potential biofilm, if present) and in the sediment bed, and the exterior most layer of the PE was assumed to be always equilibrated with the adjacent sediment, as originally done by Fernandez et al.9The first order reaction rates derived from fitting the reaction diffusion model to the PRC loss could not be directly validated in this work. Firstly, because the sediments collected at the field site did not contain any native DDT, it was not possible to derive a DDT degradation rate by measuring the sediment concentration during the static incubation of the sediment with PE. Secondly, although we observed a very fast initial degradation of DDT in the tumbling time course performed with spiked sediment (Fig. S4†), the data were not suitable for fitting a degradation rate. Even if a degradation rate could have been calculated, the tumbling conditions would likely not be representative of the static PE exposures because the tumbling containers had <1 mL of headspace and were sealed in order to prevent leakage. As a result, the sediment may become more reducing during tumbling than would otherwise be. Another option considered was performing a static incubation with a spiked sediment. However, preparing a sediment with a homogenous spike is challenging because the mixing time has to be long enough to ensure sorption equilibrium, but not too long so as to prevent the DDT spike from being completely degraded. This difficulty was documented by other researchers when attempting to spike DDT in sediments.10
The range of fitted reaction rates from both field and laboratory PE (0.09 d−1 to 14 d−1) is in line with degradation rates previously measured in anaerobic sediment slurries2,31 or in aqueous systems amended with zero valent iron.32 However, the best fit reaction rates were fast compared to other studies which report much slower degradation rates, (0.08–2 per year).4,25 and it is worth considering whether the model assumptions could lead to an overestimation of the first order reaction rate.
One of the key assumptions used when deriving the best fit reaction rate is that the Kd of the DDT-PRC is equal to the Kd of the DDE PRC (derived from the DDE-PRC loss). This assumption was used because the reaction–diffusion model is under-constrained (two unknowns and limited number of time points available for the fits). The Kd of DDT was assumed to be equal to that of DDE based on the similarity in Kow values of DDE and DDT values. We evaluated the implications of this assumption by performing a sensitivity analysis in which we recalculated the best fit kr for values of Kd that were ±0.4 units away from the Kd value of DDE (which was used for the fits in Fig. 4 and 5). This analysis was done for both the field deployed PE PRC data (Fig. S6†) as well as for the laboratory incubated PE data (Fig. S7†) and showed that the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kr was inversely proportional to the log
kr was inversely proportional to the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd with a slope of ∼1. In other words, an uncertainty of ± 0.2
Kd with a slope of ∼1. In other words, an uncertainty of ± 0.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units in Kd value translated directly into about a factor of 2× uncertainty in the fitted kr. The RMSE of the fits did not consistently increase or decrease with log
log units in Kd value translated directly into about a factor of 2× uncertainty in the fitted kr. The RMSE of the fits did not consistently increase or decrease with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kd for all the field and laboratory data (Fig. S6 and S7†). This suggests that the model fits could not have been consistently improved by using a higher or lower value of Kd for the DDT PRC relative to that measured for the DDE PRC.
Kd for all the field and laboratory data (Fig. S6 and S7†). This suggests that the model fits could not have been consistently improved by using a higher or lower value of Kd for the DDT PRC relative to that measured for the DDE PRC.
Other model assumptions could also impact the magnitude of the best fit first order reaction rate for the DDT-PRC, but a closer look at these assumptions suggests that the reaction rate might be underestimated rather than overestimated by the reaction–diffusion model. For example, if the degradation of the DDT PRC were to take place only in the porewater (as opposed to in the bulk sediment as currently assumed in eqn (2)), the estimated first order reaction rate needed to explain the observed PRC loss would necessarily have to be higher in order to compensate for the smaller amount of DDT available for reaction (fraction of DDT PRC in the porewater expected to be very low compared to bulk sediment). In addition, our model also assumed that the reaction would take place everywhere in the sediment, but it is possible that the reaction takes place at the PE–sediment interface. However, specifying a finite distance of reaction zone would also lead to an increase in the necessary rate needed to explain the observed PRC loss because of similar reasons (the smaller amount of DDT available for reaction). Lastly, it is possible that the assumption of sorption equilibrium between the porewater and the sediment is not accurate. This would lead to an underestimation of the diffusion driven release of the PRCs from PE, which could cause an overestimation of the reaction rate. However, this artifact, if present should impact the DDE-PRC behavior to a similar extent, and the use of the Kd for the DDE-PRC in the reaction diffusion model for the DDT-PRC should minimize this effect on the fitted reaction rate.
Implications for interpretation of PRCs and measuring reactive compounds
For field deployments aimed at assessing DDX, PRCs must be chosen to avoid overlap in isotopic label or isomer state between the DDT PRC and DDE/DDD PRCs (e.g., 2,4′-DDT should be used with 4,4′-DDE and 4,4′-DDD). Using a combination of reactive and non-reactive PRCs can help us understand the processes occurring in the sediment. If a DDT-PRC is used, and there is no reactivity in the sediment, e.g., the DDT PRC behaves similarly to PCB or DDE PRCs, then the PRC loss can be interpreted similarly to the PRC loss of DDE and DDD.11 But if reactivity is present, then we can use the reaction–diffusion model to investigate how the accumulation of target compounds is affected. Assuming the same reaction rate applies to a target compound, the calculated “diffusive-PRCs corrected” accumulation of target chemical will be inaccurate. For example, a reduced uptake of target chemical could be observed when using passive sampling for other organochlorine pesticides which react in sediments on timescales similar to DDT, such as chlordane or dieldrin.25 The reaction–diffusion model could then be used to calculate the fractional equilibration of the target compound (and hence its sampling rate) using the inputs obtained from the fitting of the PRC-loss (i.e., the Kd and reaction rate for the PRC). In addition, if the reactive processes are fast enough to accelerate the PRC losses (Fig. 1 and 4, e.g., diffusion timescales of weeks to months for DDE and DDD, but reaction timescales of DDT of days), then the PRC losses in conjunction with eqn (3) could be used to evaluate in situ degradation rates. Although further work is needed to confirm that the rates interpreted from the model fitting of PRC loss are a true reflection of DDT transformation in sediments, this application warrants further investigation because it could advance our understanding of transformations of chemicals under environmental conditions.Conclusion
Altogether, the reactivity of DDT in the sediments was confirmed by (1) accelerated loss over other PRCs with similar properties, (2) accumulation of the PRC degradation product, 13C 2,4′-DDD (3) larger accumulation of 13C 2,4′-DDD with increasing reducing conditions, and (4) instability of DDT in a sediment slurry. The reaction rates estimated from the reaction diffusion model fitted to PRC losses from field and laboratory PE (0.09 d−1 to 14 d−1) could not be directly validated, but were similar to degradation rates previously measured in anaerobic sediment slurries,2,31 or in aqueous systems amended with zero valent iron.32 However, the rates estimated herein were significantly faster than degradation rates of DDT reported in sediment beds (0.08–2 per year)4,25 and more work should be performed to validate this approach. Overall, the results suggest that passive sampler users should be cautious when targeting reactive species such as DDT, but also that, with additional validation work, applying passive sampling to reactive species may also be a way to obtain information about in situ reactivity of compounds in sediments that occur on timescales of days to months.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funding for this research was provided by ENI S.p.A (through the MIT Energy Initiative). We also thank our three reviewers for several helpful comments.References
- M. J. Lydy, P. F. Landrum, A. M. Oen, M. Allinson, F. Smedes, A. D. Harwood, H. Li, K. A. Maruya and J. Liu, Integr. Environ. Assess. Manage., 2014, 10, 167–178 CrossRef CAS PubMed.
- R. P. Gambrell, C. N. Reddy, V. Collard, G. Green and W. H. Patrick, J. - Water Pollut. Control Fed., 1984, 56, 174–182 CAS.
- T. C. Chiu, J. H. Yen, T. L. Liu and Y. S. Wang, Bull. Environ. Contam. Toxicol., 2004, 72, 821–828 CrossRef CAS PubMed.
- T. Eggen and A. Majcherczyk, Chemosphere, 2006, 62, 1116–1125 CrossRef CAS PubMed.
- M. S. Connor, J. A. Davis, J. Leatherbarrow, B. K. Greenfield, A. Gunther, D. Hardin, T. Mumley, J. J. Oram and C. Werme, Environ. Res., 2007, 105, 87–100 CrossRef CAS PubMed.
- R. P. Eganhouse and J. Pontolillo, Environ. Sci. Technol., 2008, 42, 6392–6398 CrossRef CAS PubMed.
- J. E. Tomaszewski and R. G. Luthy, Environ. Sci. Technol., 2008, 42, 6086–6091 CrossRef CAS PubMed.
- J. N. Apell and P. M. Gschwend, Environ. Sci. Technol., 2014, 48, 10301–10307 CrossRef CAS PubMed.
- L. A. Fernandez, C. F. Harvey and P. M. Gschwend, Environ. Sci. Technol., 2009, 43, 8888–8894 CrossRef CAS PubMed.
- L. J. Bao, F. Jia, J. Crago, E. Y. Zeng, D. Schlenk and J. Gan, Environ. Toxicol. Chem., 2013, 32, 1946–1953 CrossRef CAS PubMed.
- H. H. Liu, L. J. Bao, K. Zhang, S. P. Xu, F. C. Wu and E. Y. Zeng, Environ. Sci. Technol., 2013, 47, 9866–9873 CrossRef CAS PubMed.
- Y. Choi, Y. Wu, R. G. Luthy and S. Kang, J. Hazard. Mater., 2016, 318, 579–586 CrossRef CAS PubMed.
- K. E. Smith, A. Rein, S. Trapp, P. Mayer and U. G. Karlson, Environ. Sci. Technol., 2012, 46, 4852–4860 CrossRef CAS PubMed.
- A. Belles, C. Alary, J. Criquet and G. Billon, Chemosphere, 2016, 164, 347–354 CrossRef CAS PubMed.
- K. J. Hollenbeck, INVLAP.M: A Matlab function for numerical inversion of Laplace transforms by the de Hoog algorithm, http://www.isva.dtu.dk/staff/karl/invlap.htm.
- J. M. Thompson, C. H. Hsieh and R. G. Luthy, Environ. Sci. Technol., 2015, 49, 2270–2277 CrossRef CAS PubMed.
- A. P. Tcaciuc, J. N. Apell and P. M. Gschwend, Environ. Toxicol. Chem., 2015, 34, 2739–2749 CrossRef CAS PubMed.
- V. S. Magar, G. W. Johnson, R. C. Brenner, J. F. Quensen III, E. A. Foote, G. Durell, J. A. Ickes and C. Peven-McCarthy, Environ. Sci. Technol., 2005, 39, 3538–3547 CrossRef CAS PubMed.
- K. Booij, F. Smedes and E. M. van Weerlee, Chemosphere, 2002, 46, 1157–1161 CrossRef CAS PubMed.
- J. N. Apell, A. P. Tcaciuc and P. M. Gschwend, Integr. Environ. Assess. Manage., 2016, 12, 486–492 CrossRef CAS PubMed.
- R. Lohmann, J. K. Macfarlane and P. M. Gschwend, Environ. Sci. Technol., 2005, 39, 141–148 CrossRef CAS PubMed.
- ATSDR, Toxicological Profile for DDT, DDE and DDD, A. f. T. S. D. Registry, US Department of Health and Human Services, 2002 Search PubMed.
- A. Accardi-Dey and P. M. Gschwend, Environ. Sci. Technol., 2003, 37, 99–106 CrossRef CAS PubMed.
- Z. Gerstl and U. Mingelgrin, J. Environ. Sci. Health, Part B, 1984, 19, 297–312 CrossRef.
- J. E. Leatherbarrow, N. David, B. K. Greenfield, J. J. Oram and J. A. Davis, Organochlorine pesticide fate in San Francisco Bay, in RMP Technical Report: SFEI Contribution #433, San Francisco Estuary Institute, Oakland, CA, 2006 Search PubMed.
- W. T. Foreman and P. M. Gates, Environ. Sci. Technol., 1997, 31, 905–910 CrossRef CAS.
- V. Putyrskaya, E. Klemt and S. Röllin, J. Environ. Radioact., 2009, 100, 35–48 CrossRef CAS PubMed.
- A. S. Madison, B. M. Tebo, A. Mucci, B. Sundby and G. W. Luther III, Science, 2013, 341, 875–878 CrossRef CAS PubMed.
- S. E. Hale, T. J. Martin, K.-U. Goss, H. P. H. Arp and D. Werner, Environ. Pollut., 2010, 158, 2511–2517 CrossRef CAS PubMed.
- R. P. Schwarzenbach, P. M. Gschwend and D. M. Imboden, Environmental Organic Chemistry, Wiley, NY, 3rd edn, 2017 Search PubMed.
- T. C. Chiu, J. H. Yen, T. L. Liu and Y. S. Wang, Bull. Environ. Contam. Toxicol., 2004, 72, 821–828 CrossRef CAS PubMed.
- E. F. Pirnie, J. W. Talley and L. S. Hundal, Chemosphere, 2006, 65, 1576–1582 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Mathematical derivation (ESI-1), details on materials and methods (ESI-2), sample Matlab codes (ESI-3) as well as additional tables and figures. See DOI: 10.1039/c7em00501f |
| ‡ Currently at Gradient, Cambridge, MA. |
| This journal is © The Royal Society of Chemistry 2018 |