Evaluating parameter availability for physiologically based pharmacokinetic (PBPK) modeling of perfluorooctanoic acid (PFOA) in zebrafish†
Manoochehr
Khazaee
 and
Carla A.
Ng
and
Carla A.
Ng
 *
*
University of Pittsburgh, Department of Civil and Environmental Engineering, 3700 O'Hara St, Pittsburgh, PA 15261, USA. E-mail: carla.ng@pitt.edu; Tel: +1-412-383-4075
First published on 8th December 2017
Abstract
Physiologically based pharmacokinetic (PBPK) models are considered useful tools to describe the absorption, distribution, metabolism and excretion of xenobiotics. For accurate predictions, PBPK models require species-specific and compound-specific parameters. Zebrafish are considered an appropriate vertebrate model for investigating the toxicity of a wide variety of compounds. However, no specific mechanistic model exists for the pharmacokinetics of perfluoroalkyl acids (PFAAs) in zebrafish, despite growing concern about this class of ubiquitous environmental contaminants. The purpose of this study was to evaluate the current state of knowledge for the parameters that would be needed to construct such a model for zebrafish. We chose perfluorooctanoic acid (PFOA) as a model PFAA with greater data availability. We have updated a previous PBPK model for rainbow trout to simulate PFOA fate in zebrafish following waterborne exposure. For the first time, the model considers hepatobiliary circulation. In order to evaluate the availability of parameters to implement this model, we performed an extensive literature review to find zebrafish-specific parameters. As in previous approaches, we broadened our search to include mammalian and other fish studies when zebrafish-specific data were lacking. Based on the method used to measure or estimate parameters, or based on their species-specific origin, we scored and ranked the quality of available parameters. These scores were then used in Monte Carlo and partial rank correlation analyses to identify the most critical data gaps. The liver, where fatty acid binding proteins (FABPs) and plasma proteins are considered, represented the best model-data agreement. Lack of agreement in other tissues suggest better parameters are needed. The results of our study highlight the lack of zebrafish-specific parameters. Based on sensitivity and uncertainty analysis, parameters associated with PFAA–protein interactions and passive diffusion need further refinement to enable development of predictive models for these emerging chemicals in zebrafish.
Environmental significanceOur evaluation of parameter availability for zebrafish PBPK modeling is timely and important: zebrafish are routinely used in experimental studies as surrogates for human and wildlife responses to environmental contaminants. Despite this, very little work has been done on toxicokinetic models in zebrafish. To the best of our knowledge, only one other PBPK model for zebrafish has been published, which is not appropriate for fluorinated acids like PFOA because it relies on the octanol–water partition coefficient to describe tissue distribution. Our work considers how toxicokinetic models can be used as predictive tools for an important class of emerging contaminants and evaluates the critical data gaps that currently hinder out ability realize the full potential of zebrafish as a “model” organism. |
1. Introduction
An organism is a complex and integrated system with many interdependent characteristics. The whole body of an organism is an interconnected system of different compartments and fluids (blood, bile, lymph, etc.). The circulating blood system has the important role to distribute different compounds through vessels to various tissues. In different compartments, compounds may bind to receptors, be transformed by enzymes, passively accumulate, or be eliminated without metabolism. A physiologically based pharmacokinetic (PBPK) model describes the absorption, distribution, metabolism and excretion of chemicals in the body of an organism based on the specific physiology of the organism and on the physicochemical properties of the substance. A PBPK model thus connects the concepts of anatomy, physiology, and biochemistry to understand the fate and transport of xenobiotics in the body of organisms. Through the development of PBPK models, many researchers have tried to describe the behavior of drugs and other chemical substances in humans, mammals, birds, and fish, using actual physiological parameters such as body weight, blood flow rates, cardiac output, tissue volumes and surface area, breathing rates, etc.1–7 PBPK models can help predict the concentrations of different xenobiotics in inaccessible organs and simulate the concentration–time profiles of various compartments with minimal data.8 Moreover, PBPK models aid researchers to obtain mechanistic insight into toxic characteristics and also reduce the time, cost and need for animals in laboratory experiments.1,9Recently, Cheng and Ng (2017) and Ng and Hungerbühler (2013) showed that PBPK modeling could be particularly useful to understand and simulate the toxicokinetics and tissue distribution of perfluorinated alkyl acids (PFAAs), an important class of emerging chemicals, in rats and fish.3,4 PFAAs, including perfluoroalkyl carboxylic acids (PFCAs) and perfluoroalkane sulfonic acids (PFSAs), are man-made industrial chemicals that have been in use since the 1940s. PFAAs contain high-energy carbon–fluorine (C–F) bonds that make them highly persistent, and some are also bioaccumulative.10 They have wide commercial and consumer applications due to their unique physicochemical characteristics such as thermal stability and amphiphilic properties.11,12 Some PFAAs, such as PFOS, have been classified as persistent organic pollutants (POPs) due to their bioaccumulation potential, toxicity, and extreme persistence.13 However, PFAAs are quite different in their toxicokinetics from traditional POPs, and as such typical models that rely on partitioning do not apply. Toxicokinetic models that explicitly incorporate protein interactions and active transport produce much better predictions of tissue distribution and bioaccumulation potential.4
Many investigations have shown that the accumulation propensity of PFAAs increases with increasing length of the carbon chain.14–16 PFAAs have been observed in both aquatic and terrestrial food chains and are bioavailable in plants and animals.17 Studies have reported PFAAs in the atmosphere,12 soils,18 wildlife,13,17,19 surface water and groundwater,20 and in municipal wastewater effluent,21 indicating they are ubiquitous in the environment. Physiological disturbances (impaired organ function, effects on reproductive hormones, and mortality) and developmental malformations in mammals and fish due to exposure to PFAAs have been detected in different studies.5,13,17,22–25 Moreover, previous studies have shown that some PFAAs, such as perfluorooctanoic acid (PFOA), undergo enterohepatic circulation in both mammals and fish, and accumulate to different degrees and have different half-lives in males and females.15,26–28
The zebrafish (Danio rerio), a cyprinid teleost, is a small freshwater fish and has been considered as an appropriate vertebrate model for investigating the toxicity of compounds.7,29–31 There are several advantages for the use of zebrafish as a toxicological model species such as their size, easy husbandry, early morphology, high fecundity, short generation time, transparency of their embryos, and fully sequenced genome.31 The functions and structures of zebrafish compartments such as liver, kidney, muscle, brain, pancreas, intestinal tract, and heart, analogous to those found in humans, encourage researchers to use them in studies.30
A review of previous work that applied PBPK models for bioconcentration of different chemicals revealed that mammals were more frequently studied than fish.1 Zaharko et al. (1972) proposed the first PBPK model for fish (sting rays), which was adapted from rodent models.32 Subsequently, other studies have developed PBPK models for different fish such as trout,4,7,9,33–35 roach,7 fathead minnow,9,36 Japanese medaka,36 catfish,37 and dogfish shark,38 among others. PBPK models are rather scarce for zebrafish in comparison with other fish, particularly trout, for which there are many studies that investigate and measure various physiological parameters via different techniques.33,39–41 However, to date, no comprehensive study has been performed to determine different physiological parameters in zebrafish.
A challenge in the prediction of fate and distribution of contaminants in organisms is the availability and the quality of physiological parameters. Many studies that have applied PBPK models to simulate the behavior of different chemicals in the body of fish used physiological parameters associated with either mammals or other species of fish.4,42 The ability of PBPK models to accurately simulate chemical fate and distribution in an organism can depend strongly on the quality of the physiological information used. In order to prioritize and highlight the availability and quality of physiological parameters for zebrafish, we assess our ability to parameterize a PBPK model for zebrafish. Our assessment is based on the framework of a previous model for the bioconcentration of PFOA in rainbow trout that explicitly considers both passive diffusion and protein interactions.4
Rather than present a validated working model for prediction of PFOA toxicokinetics in zebrafish, the main purpose of this work is to investigate the current state of knowledge for the parameters that would be needed to construct such a model in a mechanistic way. In order to construct the model, extensive bibliographic research was performed to find all available parameters. After compiling the parameters, the model was assessed using two experimental datasets for zebrafish.24,43 Next, we scored the quality of available parameters based on the way that they were measured or estimated and based on the species for which the parameter was available (with parameters specifically measured in zebrafish receiving the best score). These scores were then incorporated into an uncertainty and sensitivity analysis. In this way, we used the model as a framework to identify critical parameters, and ranked their importance through sensitivity analysis.
2. Material and methods
2.1 Model structure
The model consists of 10 compartments: blood (B), adipose interstitial fluid (AF), adipose tissue (AT), muscle interstitial fluid (MF), muscle tissue (MT), liver interstitial fluid (LF), liver tissue (LT), kidney interstitial fluid (KF), kidney tissue (KT), and bile (Bi). The extracellular component of each tissue (interstitial fluid compartments) and the blood contain proteins, to which PFOA can bind.44 These compartments were identified as important components in an earlier model for PFAA bioconcentration in rainbow trout.4 The PFOA–protein exchanges and transfers between water, blood, and other compartments of the model are shown in Fig. 1.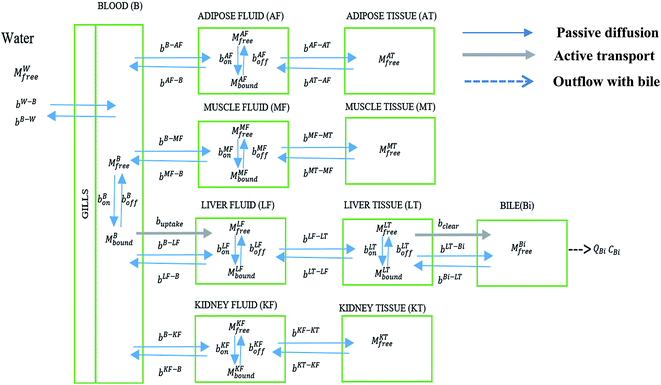 | ||
| Fig. 1 PFOA transfer and interaction with proteins in different compartments of the zebrafish PBPK model. | ||
In mammals, PFOA is known to bind to albumin.45 In zebrafish, which lack albumin, this role is likely fulfilled by apolipoprotein in plasma.44 The PFOA in plasma then enters different tissues via passive diffusion or facilitated transport. We assume liver contains fatty acid binding proteins (FABPs) to which PFOA can bind to and dissociate from. Newly included in this model is hepatobiliary circulation, which is considered important in mammals26,46–48 but has not been fully explored for PFAA toxicokinetics in fish. Additionally, we consider facilitated transport of PFOA from blood to liver and liver to bile by membrane transporters. Lack of data restricts our consideration of membrane transporters to the liver, but we acknowledge that they might have a significant role in other tissues.
In contrast with the model for the rainbow trout, a freshwater fish, the volume of urine excretion in zebrafish is extremely small.49,50 We therefore excluded urinary excretion as an elimination route and assumed that the role of transporters in eliminating PFAAs is negligible in the kidney. However, FABPs are known to be expressed in kidney tissues of other species, so that kidney tissue could still serve as a potential sink for PFAAs. In addition, since the kidney plays a central role in PFAA disposition in other species, we retain the kidney compartment in the current model to evaluate the availability of physiological parameters and as a placeholder for when additional protein interaction data become available.
2.2 PFOA mass balance equations and mass transfer coefficients
The physiological and protein-related parameters we collected were implemented in the zebrafish toxicokinetic model using the same mass balance approach originally established in Ng and Hungerbühler (2013).4 These mass balance equations are described in detail in the ESI.† The following sections focus on our search for and evaluation of the parameters included in these mass balance equations.2.3 Model parameterization
Constructing a model in a mechanistic way requires collecting a large amount of data. In order to find the needed parameter values, we performed a review of scientific literature. Our search mainly focused on papers dealing with zebrafish characteristics. In the case of lack of zebrafish-specific data, we also reviewed studies associated with other fish or with mammals. JSTOR, ISI Web of Science, and Google Scholar were used as search engines to find related papers. Based on this search, we reviewed 96 papers published between 1956 and 2017, which included parameter descriptions for more than 8 species. 35 of the 96 papers were specifically for zebrafish. The following keywords were used in our parameter search: “zebrafish, PBPK models, volume, surface area, kidney, liver, adipose, muscle, biliary system, blood, blood flow rate, cardiac output, fluid volume, concentration of proteins [in different compartments], FABPs, membrane transport protein, active transport, passive diffusion, blood perfusion rate.”Detailed descriptions of parameter derivation and final values used in the model are provided in the ESI Section S3.†
2.4 Parameter assessment
Parameters were extracted from the literature as described above and in the ESI.† Here we present our system for ranking and scoring to evaluate the quality of compiled parameters. The collected parameters used in the model were scored and then ranked based on the method used to measure or estimate them, or based on the species-specific origin. Further, we distinguished between direct experimental measurement versus estimation (e.g. based on allometry), and whether estimation methods were direct or indirect. We also scored parameters based on species of origin: zebrafish (most reliable), other fish, or mammals (least reliable). In our ranking, the most reliable score is 1, indicating that the parameter is extracted from an experimental method specifically for zebrafish, and the least reliable score is 4.5, indicating that the parameter is derived from indirect estimation associated with mammalian species.2.5 Uncertainty and sensitivity analysis
We use our PBPK model as a framework through which we evaluate the relative importance of the parameters we have collected and assessed above. Our model, similar to other PBPK models, contains a large number of parameters, many of which are interdependent. These parameters were generated using assumptions (e.g. relating different species or sizes), approximations, and unit conversions that involve uncertainty, as well as variability and uncertainty related with experimental measurements.Monte Carlo uncertainty and sensitivity analysis was conducted to quantify the relative importance of parameters. Monte Carlo analysis has been widely applied to determine the propagation of uncertainty through a model and provide feedback on parameter sensitivity, including for PBPK models.3,6,51–54 Moreover, by calculating the contribution of each parameter distribution to the variance in the model output distributions using correlation coefficients, the Monte Carlo analysis simultaneously provides information on uncertainty and sensitivity.55 We assumed parameters were independent and log-normally distributed, following previous analyses,3,54,56,57 with geometric means derived from the literature-based estimates or measurements described in detail in ESI Section S3.† The confidence factors describing the level of uncertainty associated with each parameter was based on the scoring procedure described in Section 2.4, with a range of 1 (least uncertain) to 4.5 (most uncertain).
Random sampling of parameters from their lognormal distributions was performed for 1000 runs.54 Next, the sensitivity of the model for all 35 input parameters was quantified from the outputs of the Monte Carlo sampling using partial rank correlation coefficient analysis between the model's output and the sampled parameters.
2.6 Experimental datasets used for comparison
Two experimental datasets were used to evaluate the model predictions in relation to the quality (uncertainty) of collected parameters and the model sensitivity. Ulhaq et al. (2015) exposed male and female zebrafish to 10 μg L−1 of radiolabeled perfluorooctanoic acid (14C-PFOA) for 40 days.24 Chen et al. (2016) conducted a 48 day bioconcentration study (24 day uptake, 24 day depuration) in which female zebrafish were exposed to PFOA.43 In both studies, zebrafish absorbed PFOA via gills from water.The size of the fish used in the Chen et al. (2016)43 study (mean initial fish mass) was 0.8 g, which was used for simulation in the model. Based on this study, fish were exposed to PFOA including a low dose and a high dose exposure group.43 We used the high dose exposure group in the model, for which the average exposure concentration of PFOA in water was 6.64 μg L−1. The uncertainty and sensitivity analysis was performed based on simulating the PFOA waterborne exposure experiment described in Chen et al. (2016).43 Although Chen et al. (2016) used only female zebrafish in their study, we simulate the exposure experiment for both genders and the average adult zebrafish for comparison.
3. Results and discussion
3.1 Parameters compiled
Table 1 summarizes all available parameters compiled or estimated for zebrafish and their sources. Based on the values available, a complete set was selected as being the best available estimates for use in the PBPK model for further evaluation of sensitivity and uncertainty.| Parameter | Abb | Male | Female | Adult | Reference value or method of estimating | Fish studies | Mammalian studies |
|---|---|---|---|---|---|---|---|
| a (z) indicates the study is specific to zebrafish. # indicates the parameter is used in the model. | |||||||
| Body weight | BW# | 0.41 g | 0.82 g | 0.6 g | Male = 0.41 g | (z)58 | — |
| Female = 0.82 g | |||||||
| Liver weight | LW | 8 × 10−34 g | 0.036 g | 0.019 g | Males ∼ 2.10% BW Females ∼ 4.51% BW | (z)59 | — |
| Liver weight | LW | 7 × 10−3 g | 0.015 g | 0.01 g | 1.83% body weight | (z)60 | — |
| Muscle weight | MW | 0.24 g | 0.49 g | 0.36 g | 60% body weight | (z)61 | — |
| Liver volume | VL# | 5.53 × 10−4 mL | 5.53 × 10−4 mL | 5.53 × 10−4 mL | 0.535 mm3 for adult | (z)59 | — |
| Liver volume | VL | 8 × 10−3 mL | 0.036 mL | 0.019 mL | Assuming the density of fish 1 g mL−1 | — | |
| Liver volume | VL | 7 × 10−3 mL | 0.015 mL | 0.01 mL | Assuming the density of fish 1 g mL−1 | — | |
| Muscle volume | VM# | 0.24 mL | 0.49 mL | 0.36 mL | Assuming the density of fish 1 g mL−1 | — | — |
| Kidney volume | VK# | 1.46 × 10−4 mL | 1.46 × 10−4 mL | 1.46 × 10−4 mL | Estimation based on two studies | (z)62 | — |
| (z)63 | |||||||
| Adipose volume | VA# | 1.02 × 10−3 mL | 6.32 × 10−3 mL | 3.67 × 10−3 mL | Extracted from graphs (control group) | (z)64 | — |
| Blood volume | VB# | 9 × 10−3 mL | 17 × 10−3 mL | 13 × 10−3 mL | Male = 9 μL | (z)58 | — |
| Female = 17 μL | |||||||
| Bile volume | VG# | 9.95 × 10−5 mL | 9.95 × 10−5 mL | 9.95 × 10−5 mL | 18% of liver volume | (z)59 | — |
| Liver fluid volume | VLF# | 1.7 × 10−3 mL | 4.24 × 10−3 mL | 2.83 × 10−3 mL | Based on VF/WT ratio | 41 | — |
| Kidney fluid volume | VKF# | 1.38 × 10−3 mL | 2.39 × 10−3 mL | 1.81 × 10−3 mL | Based on VF/WT ratio | 41 | — |
| Muscle fluid volume | VMF# | 0.013 mL | 0.026 mL | 0.019 mL | Based on VF/WT ratio | 41 | — |
| Adipose fluid volume | VAF# | 1.77 × 10−4 mL | 1.09 × 10−3 mL | 6.38 × 10−4 mL | Based on VF/WT ratio | 41 | — |
| Liver surface area | AL# | 1.9 cm2 | 1.9 cm2 | 1.9 cm2 | Based on spherical shape of hepatocyte and its diameter | (z)59 | — |
| Liver surface area | AL | 2.26 cm2 | 3.18 cm2 | 2.72 cm2 | Using trout data and Ng & Hungerbühler approach | 4 and 65 | — |
| Kidney surface area | AK# | 0.103 cm2 | 0.103 cm2 | 0.103 cm2 | Based on spherical shape of glomerulus and its diameter | (z)62,63,66 | — |
| Muscle surface area | AM# | 720 cm2 | 1440 cm2 | 1080 cm2 | Based on cylindrical shape of fiber and its diameter | (z)67 | — |
| Adipose surface area | AA# | 0.17 cm2 | 10.82 cm2 | 6.28 cm2 | Based on spherical shape of adipocyte and its diameter | (z)68 | — |
| Gallbladder surface area | AB# | 4.51 × 10−3 cm2 | 9.02 × 10−3 cm2 | 6.6 × 10−3 cm2 | 11 cm2 kg−1 (trout) | 69 | — |
| Gill surface area | AG# | 8.59 cm2 | 8.59 cm2 | 8.59 cm2 | Based on ratio of gill to liver surface area | 4 | — |
| Biliary flow rate | QBi# | 9.84 × 10−4 mL per day | 1.96 × 10−3 mL per day | 1.44 × 10−3 mL per day | 0.1 mL kg−1 h−1 for trout | 70 | — |
| Gill ventilation rate | QW# | 811.8 mL per day | 1623.6 mL per day | 1188 mL per day | 0.55 mL min−1 for 0.4 g cyprinid fish | (z)42 | — |
| Blood flow rate | QB# | 13.1 mL per day | 26.21 mL per day | 19.18 mL per day | 11.1 μL min−1 for 0.5 g zebrafish | (z)42 | — |
| Liver blood perfusion rate | QBL# | 0.38 mL per day | 0.65 mL per day | 0.55 mL per day | 2.9% cardiac output | 40 | — |
| Kidney blood perfusion rate | QBK# | 0.73 mL per day | 1.46 mL per day | 1.07 mL per day | 5.6% cardiac output | 33 | — |
| Muscle blood perfusion rate | QBM# | 3.30 mL per day | 6.60 mL per day | 4.83 mL per day | 25.2% cardiac output | 33 | — |
| Adipose blood perfusion rate | QBA# | 1.07 mL per day | 2.14 mL per day | 1.57 mL per day | 8.2% cardiac output | 33 | — |
| Plasma protein concentrations | CPB# | 0.57 mmol L−1 | 0.8 mmol L−1 | 0.62 mmol L−1 | Male = 37.7 mg mL−1 | (z)44 | — |
| Female = 53.1 mg mL−1 | |||||||
| FABP concentrations in liver | CFABPLT# | 0.05 mmol L−1 | 0.05 mmol L−1 | 0.05 mmol L−1 | 0.05 mol m−3 | 71 | — |
| Liver fluid protein concentrations | CPL# | 0.29 mmol L−1 | 0.4 mmol L−1 | 0.31 mmol L−1 | 0.1 mmol L−1 | — | 72 and 73 |
| Kidney fluid protein concentrations | CPK# | 0.29 mmol L−1 | 0.4 mmol L−1 | 0.31 mmol L−1 | Assuming the same liver protein concentration | — | 72 and 73 |
| Muscle fluid protein concentrations | CPM# | 0.17 mmol L−1 | 0.24 mmol L−1 | 0.19 mmol L−1 | Albumin in human adipose interstitial fluid/human serum = 0.3 | — | 74 |
| Adipose fluid protein concentrations | CPA# | 0.08 mmol L−1 | 0.12 mmol L−1 | 0.09 mmol L−1 | Albumin in human adipose interstitial fluid/human serum = 0.15 | — | 74 |
| Uptake rate constant via active transport | b uptake # | 2.75 × 10−5 s−1 | 3.17 × 10−5 s−1 | 2.95 × 10−5 s−1 | Based on the flux measured for NTCP and OSTα/β | — | 75 |
| Clearance rate constant via active transport | b clear # | 2.31 × 10−6 s−1 | 2.76 × 10−6 s−1 | 2.49 × 10−6 s−1 | Based on the flux measured for ASBT | — | 75 |
| Plasma protein association constants | K P # | 55 × 103 M−1 | 55 × 103 M−1 | 55 × 103 M−1 | Based on the geometric mean of the values reported in different studies | — | 45 and 76–78 |
| FABP association constants | K FABP # | 5.6 × 104 M−1 | 5.6 × 104 M−1 | 5.6 × 104 M−1 | Based on extrapolation from the values provided for C5–C9 PFCAs | — | 79 and 80 |
| Effective membrane permeability | P eff # | 1.13 × 10−9 m s−1 | 1.13 × 10−9 m s−1 | 1.13 × 10−9 m s−1 | — | — | 28 |
| Steady-state cell–water concentration ratio | CRC–wSS# | 1.62 | 1.62 | 1.62 | — | — | 28 |
| Water to blood uptake rate constant | k W–B# | 9.7 × 10−13 m3 s−1 | 9.7 × 10−13 m3 s−1 | 9.7 × 10−13 m3 s−1 | 1.23 L per kg per day | 4 | — |
| Rate constant for diffusion from blood back to water | k B–W# | 5.99 × 10−13 m3 s−1 | 5.99 × 10−13 m3 s−1 | 5.99 × 10−13 m3 s−1 | 0.59 L per kg per day | 4 | — |
In ESI Section S4 and Table S10,† we also provide a comparison of availability of species-specific physiological parameters for the rat (most parameters available), rainbow trout (many parameters available), and zebrafish (few parameters available).
3.2 Parameter evaluation through PBPK modeling
There are different ways to evaluate the level of confidence in a toxicokinetic model, including comparing the results with other experimental studies, performing uncertainty and sensitivity analysis, or evaluating model robustness, and plausibility.81 To evaluate model performance, we first compare model predictions to the concentration of PFOA in the liver tissue from Ulhaq et al. (2015) and in the liver, muscle, bile, and blood compartments from Chen et al. (2016), extracted at the end of uptake phase (Table 2).24,43 Model-based simulations of the Chen et al. study (2016) indicated that the prediction of the model in the compartments follows this pattern: liver > kidney > blood > adipose ≈ muscle > bile, while the distribution pattern in Chen et al. (2016)43 study is bile > liver ≈ blood > muscle (no data were available for the kidney). According to the model predictions, the concentration of PFOA in the liver of females is substantially higher than in males. In contrast, the concentration of PFOA is higher in other compartments for male than female. In Chen et al. (2016), the data were available only for female zebrafish, thus we could not compare the predicted concentration of PFOA in both genders with observations.43 In comparison with Ulhaq et al. (2015), the model-predicted geometric mean PFOA concentration in the liver of female zebrafish is overestimated by a factor of 3.75, while it falls within the range of measured concentrations for the liver of male zebrafish.24 Based on the Chen et al. (2016) dataset,43 our model underestimates the levels of PFOA to a smaller extent (by a factor of 1.4) in liver tissue. Generally, the liver tissue, where FABPs and plasma proteins are considered, represents the best model-data agreement among other compartments. However, the model is unable to predict PFOA distribution and concentration in blood, muscle and bile compartments. Our model predictions differ from the results of Chen et al. (2016) by a factor of 7 in blood and a factor of 20 in muscle, indicating lack of appropriate parameterization.43 In bile the model underestimates PFOA concentration by a factor of more than 500. Bile is clearly an important sink for PFOA in zebrafish in a way that is not captured by our current parameterization of the biliary system.| Tissue | Prediction based on Ulhaq et al. (2015) | Prediction based on Chen et al. (2016) | Results of Ulhaq et al. (2015) | Results of Chen et al. (2016) | |
|---|---|---|---|---|---|
| a It was assumed based on the average concentration of PFOA in the liver of both genders. | |||||
| Liver | Male | 1030 | 587.83 | 918 | — |
| Female | 2893.1 | 1291.7 | 770 | 1769 | |
| Adult | 1787.7 | 912.45 | 844a | — | |
| Blood | Male | 480.6 | 279.88 | — | — |
| Female | 484.85 | 239.9 | — | 1730 | |
| Adult | 463.98 | 248.03 | — | — | |
| Adipose | Male | 30 | 17.13 | — | — |
| Female | 24.86 | 12.24 | — | — | |
| Adult | 26.89 | 14.33 | — | — | |
| Muscle | Male | 24.07 | 13.98 | — | — |
| Female | 18.85 | 9.28 | — | 191 | |
| Adult | 21.36 | 11.38 | — | — | |
| Kidney | Male | 1595.4 | 638.26 | — | — |
| Female | 1397.4 | 431.49 | — | — | |
| Adult | 1561.4 | 544.28 | — | — | |
| Bile | Male | 11.41 | 6.48 | — | — |
| Female | 8.76 | 3.88 | — | 4627 | |
| Adult | 10.06 | 5.39 | — | — | |
Comparing the predicted values of PFOA in bile with the results of the Chen et al. (2016) study is particularly illustrative of the lack of agreement and issues with parameterization.43 To our knowledge, no other PBPK model considers hepatobiliary circulation of PFAAs in fish. Our model includes hepatobiliary circulation facilitated by membrane transporters. Lack of data compelled us to derive PFOA uptake rates by NTCP, OSTα/β, and ASBT transporters from mammalian studies, which may be responsible for low predicted levels of PFOA in bile relative to measured values (by a factor of 1192). In contrast to the model prediction and in agreement with Chen et al. (2016)43 observations of high bile accumulation, Ulhaq et al. (2015)24 reported the highest labeling of 14C-PFOA in bile and intestines of zebrafish, indicating substantial enterohepatic circulation of PFOA. Previous studies reported the presence of many proteins in human,82 rat,83,84 and fish85,86 bile. Indeed, proteins are the third most abundant solids in human bile.87 Therefore, it is possible that bile, similar to plasma, could be considered as an important sink for PFAAs. Thus, lack of considering biliary proteins could result in the differences between predicted and experimental PFOA concentrations in zebrafish bile.
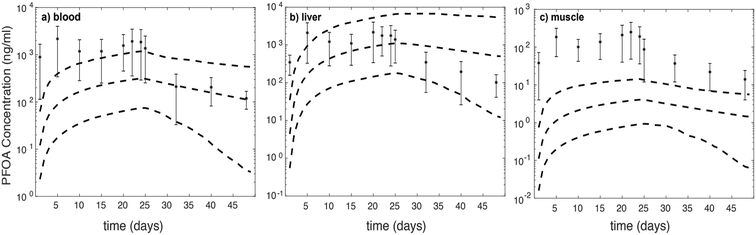
We further assess model-data agreement in the time-course data collected by Chen et al. (2016) and predicted by our model. The concentrations of PFOA in different compartments in both uptake and depuration phases (days: 1, 5, 10, 15, 20, 22, 24, 25, 32, 40, and 48) of the Chen et al. (2016) study43 were extracted and together with the 95% confidence intervals of simulations for female zebrafish (Fig. 2).
For liver (throughout the experiment) and blood (during the depuration phase) the experimental data fall approximately within the 95% confidence interval. For the muscle compartment and during the uptake phase for the blood compartment, predictions fall outside of 95% confidence intervals, which are around two orders of magnitude lower than experimental data.43 It is likely that considering FABPs and plasma proteins interactions with PFOA in the liver may account for the best model-data agreement compared to other compartments. However, based on concentration–time profile figures, the model is unable to predict PFOA distribution and concentration in blood and muscle. In comparison with the experimental dataset, the predicted PFOA concentration–time profile in blood is higher by about 1 to 1.5 order of magnitude in the uptake phase. Moreover, in the muscle compartments, the profile differs by about two orders of magnitude in the uptake phase and around one order of magnitude in the depuration phase.
3.3 Parameter assessment
Table 3 illustrates our system of ranking parameters employed in the study. Note that the minimum score is for the ideal condition of an experimental study of zebrafish, which will have a score of 1. Any deviation from this will add to the score, as indicated in Table 3 (e.g. +1 for studies for other fish species).| Num. | Abb. | References | Species | Method | Score | ||||
|---|---|---|---|---|---|---|---|---|---|
| Zebrafish | Other fish (+1) | Mammalian (+2) | Estimation | Experimental | |||||
| Direct (+1) | Indirect (+1.5) | ||||||||
| 1 | VL | 59 | * | — | — | — | — | * | 1 |
| 2 | VM | 61 | * | — | — | * | — | — | 2 |
| 3 | VK | 62 and 63 | * | — | — | — | * | — | 2.5 |
| 4 | VA | 64 | * | — | — | — | — | * | 1 |
| 5 | VB | 58 | * | — | — | — | — | * | 1 |
| 6 | VG | 59 | * | — | — | * | — | — | 2 |
| 7 | VLF | 41 | — | * | — | * | — | — | 3 |
| 8 | VKF | 41 | — | * | — | * | — | — | 3 |
| 9 | VAF | 41 | — | * | — | * | — | — | 3 |
| 10 | VMF | 41 | — | * | — | * | — | — | 3 |
| 11 | AL | 59 | * | — | — | — | * | — | 2.5 |
| 12 | AK | 62, 63 and 66 | * | — | — | — | * | — | 2.5 |
| 13 | AM | 67 | * | — | — | — | * | — | 2.5 |
| 14 | AA | 68 | * | — | — | — | * | — | 2.5 |
| 15 | AB | 69 | — | * | — | — | — | * | 2 |
| 16 | AG | 4 | — | * | — | — | * | — | 3.5 |
| 17 | QBi | 70 | — | * | — | — | — | * | 2 |
| 18 | QW | 42, 88 and 89 | * | — | — | * | — | — | 2 |
| 19 | QB | 42 | * | — | — | * | — | — | 2 |
| 20 | QBL | 33 and 40 | — | * | — | — | — | * | 2 |
| 21 | QBK | 33 and 40 | — | * | — | — | — | * | 2 |
| 22 | QBM | 33 and 40 | — | * | — | — | — | * | 2 |
| 23 | QBA | 33 and 40 | — | * | — | — | — | * | 2 |
| 24 | CPB | 44 | * | — | — | — | — | * | 1 |
| 25 | CFABP | 71 | — | * | — | — | — | * | 2 |
| 26 | CPL | 72 and 90 | — | — | * | — | — | * | 3 |
| 27 | CPK | — | — | — | * | — | * | — | 4.5 |
| 28 | CPM | 74 | — | — | * | — | — | * | 3 |
| 29 | CPA | 74 | — | — | * | — | — | * | 3 |
| 30 | K P | 45 and 76–78 | — | — | * | — | * | — | 4.5 |
| 31 | K FABP | 79 | — | — | * | — | — | * | 3 |
| 32 | P eff | 28 | — | — | * | — | — | * | 3 |
| 33 | CRC–wSS | 28 | — | — | * | — | — | * | 3 |
| 34 | b clear | 75 | — | — | * | — | — | * | 3 |
| 35 | b uptake | 75 | — | — | * | — | — | * | 3 |
There are different values available for the liver volume of zebrafish, two based on assuming fish density equal to 1 g mL−1 and another based on the ultrastructural mapping technique that Cheng et al. (2016) applied in their experiment.59 They used a combined biomolecular imaging technique to explore the gastrointestinal system, biliary system, liver and other compartments in zebrafish. Due to the novelty of the approach and the quality of their study, we used their biliary system and liver volume values in our model. Thus, the score of liver and biliary system volumes is 1 in our ranking. The volume of blood (score 1) was extracted from Zang et al. (2013), who applied a novel technique to collect the maximum blood from adult zebrafish.58 Since the muscle volume was extracted by considering fish density equal to 1 g mL−1 and then converting the muscle weight (60% of body weight of zebrafish) to volume, it was categorized as a direct estimation (score of 2). Moreover, Hasumura et al. (2012) developed an experiment to investigate the effects of green tea extract on adiposity in diet-induced obese zebrafish.64 The volume of adipose was extracted from the control group of this study and given a score of 1 in our ranking. By considering the number of nephrons, glomerulus, and podocytes in the kidney of zebrafish, we estimated their kidney volume. Since the volume of the kidney was estimated based on the collection of basic data from different studies, it was considered an indirect estimation (score of 2.5).
The direct estimation of interstitial fluid sub-compartment volumes was derived from Buschnell et al. (1998).41 They measured the interstitial fluid volumes of different compartments in trout by using EDTA ([58Co] EDTA) to explore extracellular compartment. Because these were direct estimates, but for fish species other than zebrafish, interstitial fluid volumes all received a score of 3.
Despite our extensive literature review, we could not find any zebrafish-specific values for surface area of different compartments. As described before, we make some substantial simplifications to estimate indirectly the surface area of liver, kidney, adipose, and muscle by using the diameter of the hepatocyte, glomerulus, adipocyte, and muscle fiber, respectively.59,62,63,66–68 Moreover, in accordance with the proposed simplification by Ng and Hungerbühler (2013), we estimated the surface area of liver.4 This method requires the volume of blood in each tissue compartment, which was not available in literature except for liver. Thus, we chose to not use the surface area of liver estimated by this method. Accordingly, we give a score 2.5 to the surface area of liver, muscle, kidney and adipose, since they were estimated indirectly, and the diameter of cells were compiled from studies of zebrafish. It should be noted, however, that comparison of the two methods for deriving the surface area of the liver resulted in estimates that differ by less than a factor of 2 (see Table 2).
Grosell et al. (2000) developed a technique to collect the hepatic bile continuously for days in rainbow trout by employing starvation.69 For this purpose, they measured the surface area of gallbladder by using graph paper. Based on the results for trout, we calculated the gallbladder surface area for zebrafish and gave it a score of 2 in the ranking. In addition, we used the proposed surface area of gill for trout in Ng and Hungerbühler (2013), due to lack of data.4 By using a number of allometric relationships, they calculated the area of gill for trout from different literature sources.91–93 Our score 3.5 for the gill surface area indicates that it was estimated indirectly and derived from studies not associated with zebrafish.
Péry et al. (2013) estimated the cardiac output for 0.5 g zebrafish at 26 °C by using the number of beats per minute in adult zebrafish and the ratio between stroke volume and weight for trout.42 Moreover, they extrapolated the gill ventilation rate for adult zebrafish by using the proposed relationship from Yamamoto (1991) (under normal oxygenation conditions in the fish) that at 25 °C, the volume of the gill = 1.035 BW0.771 and the oxygen uptake rate data from Vergauwen et al. (2013) for zebrafish.88,89 Thus, the blood flow rate and gill ventilation rate were estimated directly by considering the body weight of zebrafish in our model. The blood perfusion rates for liver, adipose, kidney, and muscle were reported from experiments. Barron et al. (1987) employed an experimental approach by using the indicator dilution and microsphere methods to measure the blood perfusion rates in internal organs of rainbow trout.40 Later, Nichols et al. (1990) proposed scaling factors based on highly and poorly perfused compartments for trout in their experiments.33 As described previously, the biliary flow rate for zebrafish was derived from Schmidt and Weber (1973).70 They used the organic anion sulfobromophthalein (BSP) to study the general processes of biliary excretion in trout.
Except for the concentration of total protein in plasma and the concentration of FABPs in liver, other levels of proteins in interstitial fluid of adipose, kidney, liver, and muscle were extracted from literature for mammals. Li et al. (2016) conducted an experiment to examine and analyze the proteomic profiles of zebrafish plasma.44 They employed conventional shotgun LC-MS/MS to detect the proteomic profile of plasma followed by the sequential window acquisition of all theoretical (SWATH) fragment-ion spectra approach to determine the levels and differences of plasma proteins in male and female zebrafish. Hence, the score for this parameter is 1 (zebrafish, direct estimation). The level of FABPs in the liver compartment receive a score of 2, as it was derived directly from a different fish species using the study of Londraville et al. (1996).71 In their experiment, they use a combination of bicinchoninic acid and scanning densitometry to quantify the level of FABPs in striped bass (Morone saxatilis). Based on our scoring system, the concentrations of proteins in interstitial fluid of the kidney get a score of 4.5, the least reliable score, because of indirect estimation from the interstitial fluid of liver from mammals. Since the interstitial fluid of adipose and muscle in the model were derived from Ellmerer et al. (2000), a combined experimental approach using open-flow microperfusion and the no-net-flux calibration method (based on determining the transport of analyte mass across a dialysis membrane as a function of the perfusate concentration94), the score for these parameters is 3.74
To consider the hepatobiliary circulation in the model, we used mammalian studies to determine the active transport of PFOA.75 Zhao et al. (2015) conducted an experiment to identify the role of active transporters in hepatobiliary circulation and in disposition of PFAAs.75 They investigated the uptake of PFAAs in rat and human hepatocytes in the absence or presence of sodium. Since they used an experimental method on mammals, both the buptake and bclear parameters receive a score of 3.
In the model, the plasma protein association constant (KP) and fatty acid binding protein association constant (KFABP) describe the equilibrium binding of PFOA to proteins in plasma and FABPs in the liver, respectively. As outlined earlier, the total protein concentration in the plasma of zebrafish was considered in the model as available for PFOA binding. We also assumed that these proteins would behave similarly to albumin. Hence, we calculated the geometric means of reported Kalb values (see ESI Section S4†) and used them as an estimate of KP in the model. Since there are no experimental methods to determine KP in either mammalian or fish studies (“P” consisting primarily of apolipoprotein), the indirect estimation of KP from described studies results in a low reliability score of 4.5 for KP. Thus, KP and the concentration of proteins in the interstitial fluid of kidney have the least reliable scores based on our ranking scheme.
K FABP was extrapolated directly based on Woodcroft et al. (2010) and Zhang et al. (2013) experiments on rat and human cells, respectively.79,80 Woodcroft et al. (2010) determined binding affinities of liver FABPs and their interactions with C5–C9 PFCAs fluorimetrically, followed by isothermal titration calorimetry and electrospray ionization combined with tandem mass spectrometry techniques. Accordingly, it was categorized as a parameter derived from experimental techniques from mammalian studies. Also, Zhang et al. (2013) investigated the binding affinity and interactions of 17 perfluorinated compounds with human liver-FABPs by using a direct ligand binding assay, a ligand displacement assay, molecular docking analysis, and circular dichroism spectroscopic measurements.80 The value of KFABP therefore received a score of 3 (mammalian, experimental).
As in the previous rainbow trout PBPK model, Peff and CRC–wSS were estimated directly from Weaver et al. (2010).28 They developed an experiment to determine the role of organic anion transporters by exposing cells expressing rat renal transporters to various perfluorinated carboxylates (PFCAs). They used four PFCAs with different chain lengths to inhibit the organic anion transporters, followed by kinetic analysis to elucidate the role of transporters in renal elimination of PFCAs. Accordingly, the score of 3 for Peff and CRC–wSS indicates that they are estimated directly from experimental studies for mammalian transporters.
3.4 Uncertainty and sensitivity analysis
The comparison of model predictions to experimental data is not the only—or necessarily best—means to judge the performance of a model.95 In mass balance models, such as the proposed model, representing the uncertainties of parameters is also very important. Identifying influential parameters with the highest uncertainties helps to focus future studies. We therefore used our scoring system with Monte Carlo analysis to identify those parameters that considerably affect the model outputs and require more attention. The model comprises 23 physiological parameters (10 related to tissue and fluid volumes, 6 related to surface areas, and 7 related to flow and perfusion rates), 2 for passive diffusion, and 10 protein interaction parameters (2 for active transport, 2 equilibrium association constants for binding to PFOA, and finally 6 related to protein concentrations). As described earlier, Monte Carlo and partial rank correlation coefficient analyses were employed to identify the uncertainties and sensitivity in the model by considering all parameters used to simulate the PFOA bioconcentration experiment for female zebrafish by Chen et al. (2016).43 In our simulations, a confidence factor (Cf) (in some studies called dispersion factor or operational uncertainty factor) was used to represent the variance in the log-normal distributions for each parameter.96 We assumed the Cf for all 35 parameters based on their scores in the ranking described above. For example, the score of KP is 4.5; we assumed this value as the Cf. The results of the Monte Carlo-based PBPK model simulations are shown in ESI Section S6,† illustrating the 95% confidence intervals of predicted concentration–time profiles of PFOA in blood, liver, and muscle (Fig. 2).Next, partial rank correlation coefficient analysis was performed to determine the sensitivity of the model output to each parameter (ESI Fig. S2–S10†). The five most significant parameters for each compartment in male, female and adult zebrafish are shown in Fig. 3.
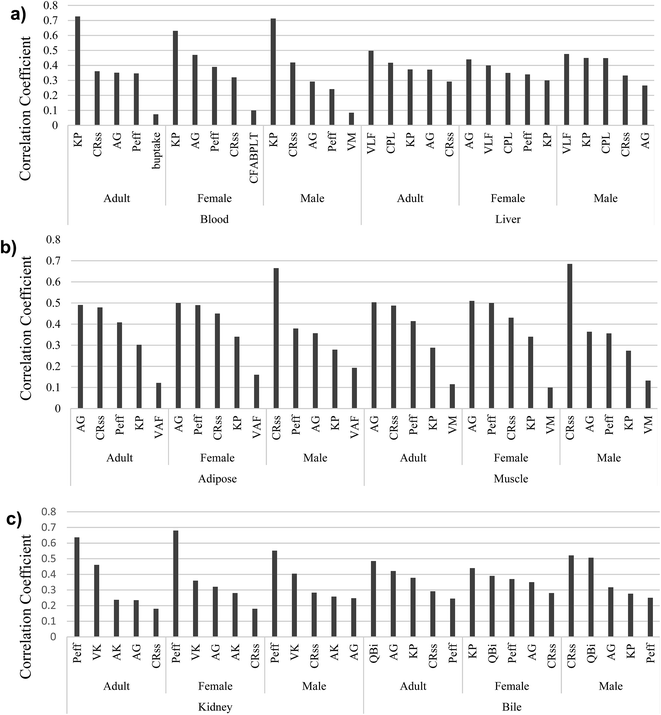 | ||
| Fig. 3 The five most influential model parameters in (a) blood and liver, (b) adipose and muscle, and (c) kidney and bile. | ||
For the blood, KP, CRC–wSS, AG, and Peff are the most important parameters for both genders and for the average adult zebrafish (Fig. 3a). In liver, we find the most important parameters to be VLF, CPL, KP, and AG, which are observed in male, female and adult zebrafish. Moreover, in contrast to female, VLF is observed in the top uncertain parameters of adult and male.
In adipose and muscle compartments (Fig. 3b), parameters playing a significant role in passive diffusion, CRC–wSS, AG, and Peff are the most important parameters, as well as VM in muscle and VLF in adipose of zebrafish. Furthermore, KP is also one of the most uncertain parameters in these two compartments.
P eff is the most important parameter in the kidney compartment of both sexes and adult zebrafish (Fig. 3c). Two parameters associated with kidney physiology, VK and AK, come into play in the kidney compartment. Moreover, AG, Peff, and CRC–wSS in the kidney of male, female, and adult zebrafish show high uncertainties. Like for other compartments, Peff, KP, AG, and CRC–wSS are the most important parameters in bile, as is QBi.
As Fig. 3 clearly illustrates, AG, Peff, CRC–wSS, and KP appear more often than other parameters. In fact, two major categories of parameters—those associated with PFOA–protein interactions and with passive diffusion—show higher overall sensitivity and uncertainty than others. Three important parameters, AG (AB–W), Peff, and CRC–wSS control uptake via passive diffusion in the gills. In addition, protein binding parameters, including the protein association constant (KP), the concentrations of FABPs in liver, and the concentration of proteins in interstitial fluid of different compartments have a significant effect on the output of the model. In comparison with these two categories, physiological parameters were less important. Moreover, AG, Peff, CRC–wSS, and KP parameters were derived from other fish or mammalian studies. Our results are in accordance with the original Ng and Hungerbühler (2013) model, which was most sensitive to parameters describing the albumin binding and passive diffusion.4 This is not surprising as our model uses the same general structure as a foundation.
4. Conclusion
Zebrafish are widely considered an important experimental animal model in different research fields. As we have outlined, they possess a variety of features that make them very attractive for research. Despite the high application of zebrafish in investigations, no detailed survey has been conducted to critically assess the availability of physiological parameters for zebrafish. Moreover, in contrast to adult zebrafish, embryos are more often used in experimental studies. In this study, an extensive literature review was performed to compile various parameters for constructing a PBPK model to predict the distribution of PFOA in different compartments of male, female, and average adult zebrafish. To collect the parameters, our priority was to compile data that were specific to zebrafish physiology. In the case of lacking data, other studies focused on mammals or other fish species were reviewed.Predictions from a PBPK model, parameterized with the resulting values, fail to capture the observed toxicokinetics, except for the concentration of PFOA in the liver of male zebrafish, which are in good agreement with Ulhaq et al. (2015)24 and Chen et al. (2016).43 This indicates the model predictions in the liver, where the protein binding is described in greatest detail, are closest to the experimental data. In contrast, in the muscle compartment where protein binding was not considered important, the predictions were not good. Consideration of protein interactions with PFAAs in other tissues may help improve the prediction of the model. This appears to be particularly relevant for bile. Moreover, the lack of zebrafish-specific parameters very likely affects the model's predictive power. Based on the systematic parameter assessment we have presented here, those parameters that showed highest sensitivities and uncertainties (derived mainly from mammalian studies), should be considered as priorities for further research.
To overcome these limitations, we suggest more research focus, including both in vitro and in vivo information, in highlighted areas. One important subject requiring more attention is to determine which proteins in zebrafish plasma interact with PFAAs, like the albumin identified as an important PFOA sink in mammals and other fish. Quantitative estimates of equilibrium association constants are needed for these proteins.
Altogether, the results of our study highlight the lack of zebrafish-specific parameters and identify the most important parameters affecting our ability to predict PFOA distribution in different tissues of zebrafish. Accordingly, further efforts are necessary to provide more zebrafish-specific parameters. The frequent use of zebrafish in research experiments, and the need to better understand and predict the fate of emerging contaminants like PFAAs in organisms, further underline the implications of this study.
Conflicts of interest
There are no conflicts of interest to declare.References
- I. Nestorov, Whole Body Pharmacokinetic Models, Clin. Pharmacokinet., 2003, 42(10), 883–908 CrossRef CAS PubMed
.
- F. Khalil and S. Läer, Physiologically based pharmacokinetic modeling: methodology, applications, and limitations with a focus on its role in pediatric drug development, J. Biomed. Biotechnol., 2011, 2011, 907461 Search PubMed
.
- W. Cheng and C. A. Ng, A Permeability-limited Physiologically Based Pharmacokinetic (PBPK) Model for Perfluorooctanoic Acid (PFOA) in Male Rats, Environ. Sci. Technol., 2017, 51(17), 9930–9939 CrossRef CAS PubMed
.
- C. A. Ng and K. Hungerbühler, Bioconcentration of Perfluorinated Alkyl Acids: How Important Is Specific Binding?, Environ. Sci. Technol., 2013, 47(13), 7214–7223, DOI:10.1021/es400981a
.
- F. Fàbrega, V. Kumar, M. Schuhmacher, J. L. Domingo and M. Nadal, PBPK modeling for PFOS and PFOA: Validation with human experimental data, Toxicol. Lett., 2014, 230(2), 244–251 CrossRef PubMed
.
- R. S. Thomas, W. E. Lytle, T. J. Keefe, A. A. Constan and R. S. Yang, Incorporating Monte Carlo simulation into physiologically based pharmacokinetic models using advanced continuous simulation language (ACSL): a computational method, Fundam. Appl. Toxicol., 1996, 31(1), 19–28 CrossRef CAS PubMed
.
-
M. Brinkmann, Uptake and effects of dioxin-like compounds in fish: in vitro–in vivo and cross-species extrapolation using physiologically based toxicokinetic models, RWTH Aachen University zur Erlangung, 2015 [cited 2017 Dec 1], https://d-nb.info/1127143719/34 Search PubMed
.
- X. Liu, B. J. Smith, C. Chen, E. Callegari, S. L. Becker and X. Chen,
et al., Use of a Physiologically Based Pharmacokinetic Model to Study the Time to Reach Brain Equilibrium: An Experimental Analysis of the Role of Blood-Brain Barrier Permeability, Plasma Protein Binding, and Brain Tissue Binding, J. Pharmacol. Exp. Ther., 2005, 313(3), 1254–1262 CrossRef CAS PubMed
.
- J. Stadnicka, K. Schirmer and R. Ashauer, Predicting Concentrations of Organic Chemicals in Fish by Using Toxicokinetic Models, Environ. Sci. Technol., 2012, 46(6), 3273–3280, DOI:10.1021/es2043728
.
-
J. P. Giesy, J. E. Naile, J. S. Khim, P. D. Jones and J. L. Newsted, Aquatic Toxicology of Perfluorinated Chemicals, 2010, pp. 1–52, http://link.springer.com/10.1007/978-1-4419-1157-5_1 Search PubMed
.
- W. Zhang, Y. Zhang, H. Zhang, J. Wang, R. Cui and J. Dai, Sex Differences in Transcriptional Expression of FABPs in Zebrafish Liver after Chronic Perfluorononanoic Acid Exposure, Environ. Sci. Technol., 2012, 46(9), 5175–5182, DOI:10.1021/es300147w
.
- K. Prevedouros, I. T. Cousins, C. Robert, A. Buck and S. H. Korzeniowski, Sources, Fate and Transport of Perfluorocarboxylates, Environ. Sci. Technol., 2005, 40(1), 32–44, DOI:10.1021/es0512475
.
- J. W. Martin, D. M. Whittle, C. G. Derek, A. Muir and S. A. Mabury, Perfluoroalkyl Contaminants in a Food Web from Lake Ontario, Environ. Sci. Technol., 2004, 38(20), 5379–5385, DOI:10.1021/es049331s
.
- N. Kudo, E. Suzuki, M. Katakura, K. Ohmori, R. Noshiro and Y. Kawashima, Comparison of the elimination between perfluorinated fatty acids with different carbon chain length in rats, Chem.-Biol. Interact., 2001, 134(2), 203–216 CrossRef CAS PubMed
.
- K. Ohmori, N. Kudo, K. Katayama and Y. Kawashima, Comparison of the toxicokinetics between perfluorocarboxylic acids with different carbon chain length, Toxicology, 2003, 184(2–3), 135–140 CrossRef CAS PubMed
.
- N. Kudo, E. Suzuki-Nakajima, A. Mitsumoto and Y. Kawashima, Responses of the Liver to Perfluorinated Fatty Acids with Different Carbon Chain Length in Male and Female Mice: In Relation to Induction of Hepatomegaly, Peroxisomal β-Oxidation and Microsomal 1-Acylglycerophosphocholine Acyltransferase, Biol. Pharm. Bull., 2006, 29(9), 1952–1957 CAS
.
- K. Kannan, A. Se Hun Yun and T. J. Evans, Chlorinated, Brominated, and Perfluorinated Contaminants in Livers of Polar Bears from Alaska, Environ. Sci. Technol., 2005, 39(23), 9057–9063, DOI:10.1021/es051850n
.
- J. G. Sepulvado, A. C. Blaine, L. S. Hundal and C. P. Higgins, Occurrence and fate of perfluorochemicals in soil following the land application of municipal biosolids, Environ. Sci. Technol., 2011, 45(19), 8106–8112, DOI:10.1021/es103903d
.
- A. K. Greaves, R. J. Letcher, C. Sonne and R. Dietz, Brain region distribution and patterns of bioaccumulative perfluoroalkyl carboxylates and sulfonates in East Greenland polar bears (Ursus maritimus), Environ. Toxicol. Chem., 2013, 32(3), 713–722, DOI:10.1002/etc.2107
.
- F. Suja, B. K. Pramanik and S. M. Zain, Contamination, bioaccumulation and toxic effects of perfluorinated chemicals (PFCs) in the water environment: a review paper, Water Sci. Technol., 2009, 60(6), 1533–1544 CrossRef CAS PubMed
.
- B. G. Loganathan, K. S. Sajwan, E. Sinclair, K. Senthil Kumar and K. Kannan, Perfluoroalkyl sulfonates and perfluorocarboxylates in two wastewater treatment facilities in Kentucky and Georgia, Water Res., 2007, 41(20), 4611–4620 CrossRef CAS PubMed
.
- H. Liu, N. Sheng, W. Zhang and J. Dai, Toxic effects of perfluorononanoic acid on the development of Zebrafish (Danio rerio) embryos, J. Environ. Sci., 2015, 32, 26–34 CrossRef PubMed
.
- M. Shoeib, T. Harner and P. Vlahos, Perfluorinated Chemicals in the Arctic Atmosphere, Environ. Sci. Technol., 2006, 40(24), 7577–7583, DOI:10.1021/es0618999
.
- M. Ulhaq, M. Sundström, P. Larsson, J. Gabrielsson, Å. Bergman and L. Norrgren,
et al., Tissue uptake, distribution and elimination of 14C-PFOA in zebrafish (Danio rerio), Aquat. Toxicol., 2015, 163, 148–157 CrossRef CAS PubMed
.
- D. M. Consoer, A. D. Hoffman, P. N. Fitzsimmons, P. A. Kosian and J. W. Nichols, Toxicokinetics of perfluorooctane sulfonate in rainbow trout (Oncorhynchus mykiss), Environ. Toxicol. Chem., 2016, 35(3), 717–727, DOI:10.1002/etc.3230
.
- J. D. Johnson, S. J. Gibson and R. E. Ober, Cholestyramine-enhanced fecal elimination of carbon-14 in rats after administration of ammonium [C]perfluorooctanoate or potassium [C]perfluorooctanesulfonate, Toxicol. Sci., 1984, 4(6), 972–976 CrossRef CAS
.
- J. J. Lee and I. R. Schultz, Sex differences in the uptake and disposition of perfluorooctanoic acid in fathead minnows after oral dosing, Environ. Sci. Technol., 2010, 44(1), 491–496 CrossRef CAS PubMed
.
- Y. M. Weaver, D. J. Ehresman, J. L. Butenhoff and B. Hagenbuch, Roles of Rat Renal Organic Anion Transporters in Transporting Perfluorinated Carboxylates with Different Chain Lengths, Toxicol. Sci., 2010, 113(2), 305–314 CrossRef CAS PubMed
.
- A. J. Hill, H. Teraoka, W. Heideman and R. E. Peterson, Zebrafish as a Model Vertebrate for Investigating Chemical Toxicity, Toxicol. Sci., 2005, 86(1), 6–19 CrossRef CAS PubMed
.
- J. R. Goldsmith and C. Jobin, Think small: zebrafish as a model system of human pathology, J. Biomed. Biotechnol., 2012, 2012, 817341 CAS
.
- J. M. Spitsbergen and M. L. Kent, The State of the Art of the Zebrafish Model for Toxicology and Toxicologic Pathology Research—Advantages and Current Limitations, Toxicol. Pathol., 2003, 31(suppl. 1), 62–87, DOI:10.1080/01926230390174959
.
- D. S. Zaharko, R. L. Dedrick and V. T. Oliverio, Prediction of the distribution of methotrexate in the sting rays Dasyatidae sabina and sayi by use of a model developed in mice, Comp. Biochem. Physiol., Part A: Mol. Integr. Physiol., 1972, 42(1), 183–194 CrossRef CAS
.
- J. W. Nichols, J. M. McKim, M. E. Andersen, M. L. Gargas, H. J. Clewell and R. J. Erickson, A physiologically based toxicokinetic model for the uptake and disposition of waterborne organic chemicals in fish, Toxicol. Appl. Pharmacol., 1990, 106(3), 433–447 CrossRef CAS PubMed
.
- D. J. Nichols, Fluid volumes in rainbow trout, Salmo gairdneri: Application of compartmental analysis, Comp. Biochem. Physiol., Part A: Mol. Integr. Physiol., 1987, 87(3), 703–709 CrossRef CAS
.
- J. W. Nichols, J. M. McKim, G. J. Lien, A. D. Hoffman, S. L. Bertelsen and C. M. Elonen, A physiologically based toxicokinetic model for dermal absorption of organic chemicals by fish, Fundam. Appl. Toxicol., 1996, 31(2), 229–242 CrossRef CAS PubMed
.
- G. J. Lien and J. M. McKim, Predicting branchial and cutaneous uptake of 2,2′,5,5′-tetrachlorobiphenyl in fathead minnows (Pimephales promelas) and Japanese medaka (Oryzias latipes): Rate limiting factors, Aquat. Toxicol., 1993, 27(1–2), 15–31 CrossRef CAS
.
- J. W. Nichols, J. M. McKim, G. J. Lien, A. D. Hoffman, S. L. Bertelsen and C. A. Gallinat, Physiologically-based toxicokinetic modeling of three waterborne chloroethanes in channel catfish, Ictalurus punctatus, Aquat. Toxicol., 1993, 27(1–2), 83–111 CrossRef CAS
.
- P. M. Bungay, R. L. Dedrick and A. M. Guarino, Pharmacokinetic modeling of the dogfish shark (Squalus acanthias): Distribution and urinary and biliary excretion of phenol red and its glucuronide, J. Pharmacokinet. Biopharm., 1976, 4(5), 377–388 CrossRef CAS PubMed
.
- W. Gingerich, R. Pityer and J. Rach, Estimates of plasma, packed cell and total blood volume in tissues of the rainbow trout (Salmo gairdneri), Comp. Biochem. Physiol., Part A: Mol. Integr. Physiol., 1987, 87(2), 251–256 CrossRef CAS
.
- M. G. Barron, B. D. Tarr and W. L. Hayton, Temperature-dependence of cardiac output and regional blood flow in rainbow trout, Salmo gairdneri Richardson, J. Fish Biol., 1987, 31(6), 735–744, DOI:10.1111/j.1095-8649.1987.tb05276.x
.
- P. G. Buschnell, D. J. Conklin, D. W. Duff and K. R. Olson, Tissue and whole-body extracellular, red blood cell and albumin spaces in the rainbow trout as a function of time: a reappraisal of the volume of the secondary circulation, J. Exp. Biol., 1998, 201(9), 1381–1391 Search PubMed
.
- A. R. R. Péry, J. Devillers, C. Brochot, E. Mombelli, O. Palluel and B. Piccini,
et al., A Physiologically Based Toxicokinetic Model for the Zebrafish Danio rerio, Environ. Sci. Technol., 2013, 48(1), 781–790, DOI:10.1021/es404301q
.
- F. Chen, Z. Gong and B. C. Kelly, Bioavailability and bioconcentration potential of perfluoroalkyl-phosphinic and -phosphonic acids in zebrafish (Danio rerio): Comparison to perfluorocarboxylates and perfluorosulfonates, Sci. Total Environ., 2016, 568, 33–41 CrossRef CAS PubMed
.
- C. Li, X. F. Tan, T. K. Lim, Q. Lin and Z. Gong, Comprehensive and quantitative proteomic analyses of zebrafish plasma reveals conserved protein profiles between genders and between zebrafish and human, Sci. Rep., 2016, 6, 24329 CrossRef CAS PubMed
.
- X. Han, T. A. Snow, R. A. Kemper and G. W. Jepson, Binding of Perfluorooctanoic Acid to Rat and Human Plasma Proteins, Chem. Res. Toxicol., 2003, 16(6), 775–781, DOI:10.1021/tx034005w?journalCode=crtoec
.
- R. A. Kemper and D. L. Nabb,
In vitro studies in microsomes from rat and human liver, kidney, and intestine suggest that perfluorooctanoic acid is not a substrate for microsomal UDP-glucuronosyltransferases, Drug Chem. Toxicol., 2005, 28(3), 281–287 CrossRef CAS PubMed
.
- J. P. Vanden Heuvel, B. I. Kuslikis, M. J. Van Rafelghem and R. E. Peterson, Tissue distribution, metabolism, and elimination of perfluorooctanoic acid in male and female rats, J. Biochem. Toxicol., 1991, 6(2), 83–92 CrossRef CAS
.
- B. I. Kuslikis, J. P. Vanden Heuvel and R. E. Peterson, Lack of evidence for perfluorodecanoyl- or perfluorooctanoyl-coenzyme a formation in male and female rats, J. Biochem. Toxicol., 1992, 7(1), 25–29 CrossRef CAS
.
- G. J. Lieschke and P. D. Currie, Animal models of human disease: zebrafish swim into view, Nat. Rev. Genet., 2007, 8(5), 353–367 CrossRef CAS PubMed
.
- S. Christou-Savina, P. L. Beales and D. P. S. Osborn, Evaluation of zebrafish kidney function using a fluorescent clearance assay, J. Visualized Exp., 2015, 96, e52540 Search PubMed
.
- R. Heredia Ortiz, A. Maître, D. Barbeau, M. Lafontaine and M. Bouchard, Use of physiologically-based pharmacokinetic modeling to simulate the profiles of 3-hydroxybenzo(a)pyrene in workers exposed to polycyclic aromatic hydrocarbons, PLoS One, 2014, 9(7), e102570 Search PubMed
.
- R. S. Thomas, R. S. Yang, D. G. Morgan, M. P. Moorman, H. R. Kermani and R. A. Sloane,
et al., PBPK modeling/Monte Carlo simulation of methylene chloride kinetic changes in mice in relation to age and acute, subchronic, and chronic inhalation exposure, Environ. Health Perspect., 1996, 104(8), 858–865 CrossRef CAS PubMed
.
- K. H. Watanabe, Z. Li, K. J. Kroll, D. L. Villeneuve, N. Garcia-Reyero and E. F. Orlando,
et al., A Computational Model of the Hypothalamic-Pituitary-Gonadal Axis in Male Fathead Minnows Exposed to 17α-Ethinylestradiol and 17β-Estradiol, Toxicol. Sci., 2009, 109(2), 180–192 CrossRef CAS PubMed
.
- F. Yang, H. W. Liu, M. Li, H. Z. Ding, X. H. Huang and Z. L. Zeng, Use of a Monte Carlo analysis within a physiologically based pharmacokinetic model to predict doxycycline residue withdrawal time in edible tissues in swine, Food Addit. Contam., Part A: Chem., Anal., Control, Exposure Risk Assess., 2012, 29(1), 73–84 CrossRef CAS PubMed
.
-
A. Saltelli, M. Ratto, T. Andres, F. Campolongo, J. Cariboni and D. Gatelli, et al., Global Sensitivity Analysis, The Primer, John Wiley & Sons, Ltd, Chichester, UK, 2007 [cited 2017 Dec 6], DOI:10.1002/9780470725184
.
- L. Lacey, O. Keene, J. Pritchard and A. Bye, Common Noncompartmental Pharmacokinetic Variables: are they normally or log-normally distributed?, J. Biopharm. Stat., 1997, 7(1), 171–178 CrossRef CAS PubMed
.
- J. Buur, R. Baynes, G. Smith and J. Riviere, Use of probabilistic modeling within a physiologically based pharmacokinetic model to predict sulfamethazine residue withdrawal times in edible tissues in swine, Antimicrob. Agents Chemother., 2006, 50(7), 2344–2351 CrossRef CAS PubMed
.
- L. Zang, Y. Shimada, Y. Nishimura, T. Tanaka and N. Nishimura, A Novel, Reliable Method for Repeated Blood Collection from Aquarium Fish, Zebrafish, 2013, 10(3), 425–432 CrossRef PubMed
.
- D. Cheng, G. J. Shami, M. Morsch, R. S. Chung and F. Braet, Ultrastructural Mapping of the Zebrafish Gastrointestinal System as a Basis for Experimental Drug Studies, BioMed Res. Int., 2016, 2016, 1–13 Search PubMed
.
- S. Örn, P. L. Andersson, L. Förlin, M. Tysklind and L. Norrgren, The Impact on Reproduction of an Orally Administered Mixture of Selected PCBs in Zebrafish (Danio rerio), Arch. Environ. Contam. Toxicol., 1998, 35(1), 52–57 CrossRef
.
- I. A. Johnston, N. I. Bower and D. J. Macqueen, Growth and the regulation of myotomal muscle mass in teleost fish, J. Exp. Biol., 2011, 214(10), 1617–1628 CrossRef CAS PubMed
.
- K. K. McCampbell, K. N. Springer and R. A. Wingert, Atlas of Cellular Dynamics during Zebrafish Adult Kidney Regeneration, Stem Cell. Int., 2015, 2015, 1–19 CrossRef PubMed
.
- W. Zhou and F. Hildebrandt, Inducible podocyte injury and proteinuria in transgenic zebrafish, J. Am. Soc. Nephrol., 2012, 23(6), 1039–1047 CrossRef CAS PubMed
.
- T. Hasumura, Y. Shimada, J. Kuroyanagi, Y. Nishimura, S. Meguro and Y. Takema,
et al., Green tea extract suppresses adiposity and affects the expression of lipid metabolism genes in diet-induced obese zebrafish, Nutr. Metabol., 2012, 9(1), 73 CrossRef PubMed
.
- A. A. Soldatov, Organ blood flow and vessels of microcirculatory bed in fish, J. Evol. Biochem. Physiol., 2006, 42(3), 243–252 CrossRef
.
- G. Ahuja, I. Ivandic, M. Saltürk, Y. Oka, W. Nadler and S. I. Korsching, Zebrafish crypt neurons project to a single, identified mediodorsal glomerulus, Sci. Rep., 2013, 3, 2063 CrossRef PubMed
.
- P. R. Biga and F. W. Goetz, Zebrafish and giant danio as models for muscle growth: determinate vs. indeterminate growth as determined by morphometric analysis, Am. J. Physiol.: Regul., Integr. Comp. Physiol., 2006, 291(5), R1327–R1337 CrossRef CAS PubMed
.
- D. Imrie and K. C. Sadler, White adipose tissue development in zebrafish is regulated by both developmental time and fish size, Dev. Dynam., 2010, 239(11), 3013–3023, DOI:10.1002/dvdy.22443
.
- M. Grosell, M. J. O'Donnell and C. M. Wood, Hepatic versus gallbladder bile composition: in vivo transport physiology of the gallbladder in rainbow trout, Am. J. Physiol.: Regul., Integr. Comp. Physiol., 2000, 278(6), R1674–R1684 CrossRef CAS PubMed
.
- D. C. Schmidt and L. J. Weber, Metabolism and Biliary Excretion of Sulfobromophthalein by Rainbow Trout (Salmo gairdneri), J. Fish. Res. Board Can., 1973, 30(9), 1301–1308, DOI:10.1139/f73-210
.
- R. L. Londraville and B. D. Sidell, Cold acclimation increases fatty acid-binding protein concentration in aerobic muscle of striped bass, Morone saxatilis, J. Exp. Zool., 1996, 275(1), 36–44 CrossRef CAS
.
- D. Levitt, The pharmacokinetics of the interstitial space in humans, BMC Clin. Pharmacol., 2003, 3(1), 3 CrossRef PubMed
.
-
T. Peters, All about albumin: biochemistry, genetics, and medical applications, Academic Press, 1995, p. 432, https://books.google.com/books?hl=en%26lr=%26id=i1DC3KlTAB8C%26oi=fnd%26pg=PP2%26dq=All+about+Albumin:+Biochemistry,+Genetics,+And+Medical+Applications%3B%26ots=WXAicT7pbd%26sig=zv2Po0Qf6F6L4Z4zv533GXhG-jQ#v=onepage%26q=AllaboutAlbumin%3ABiochemistry%2CGenetics%2CAn Search PubMed
.
- M. Ellmerer, L. Schaupp, G. A. Brunner, G. Sendlhofer, A. Wutte and P. Wach,
et al., Measurement of interstitial albumin in human skeletal muscle and adipose tissue by open-flow microperfusion, Am. J. Physiol. Endocrinol. Metabol., 2000, 278(2), E352–E356 CrossRef CAS PubMed
.
- W. Zhao, J. D. Zitzow, D. J. Ehresman, S.-C. Chang, J. L. Butenhoff and J. Forster,
et al., Na +/Taurocholate Cotransporting Polypeptide and Apical Sodium-Dependent Bile Acid Transporter Are Involved in the Disposition of Perfluoroalkyl Sulfonates in Humans and Rats, Toxicol. Sci., 2015, 146(2), 363–373, DOI:10.1093/toxsci/kfv102
.
- Y. M. Chen and L. H. Guo, Fluorescence study on site-specific binding of perfluoroalkyl acids to human serum albumin, Arch. Toxicol., 2009, 83(3), 255–261 CrossRef CAS PubMed
.
- H. N. Bischel, L. A. MacManus-Spencer and R. G. Luthy, Noncovalent interactions of long-chain perfluoroalkyl acids with serum albumin, Environ. Sci. Technol., 2010, 44(13), 5263–5269 CrossRef CAS PubMed
.
- L. A. MacManus-Spencer, M. L. Tse, P. C. Hebert, H. N. Bischel and R. G. Luthy, Binding of perfluorocarboxylates to serum albumin: A comparison of analytical methods, Anal. Chem., 2010, 82(3), 974–981 CrossRef CAS PubMed
.
- M. W. Woodcroft, D. A. Ellis, S. P. Rafferty, D. C. Burns, R. E. March, N. L. Stock, K. S. Trumpour, J. Yee and K. Munro, Experimental characterization of the mechanism of perfluorocarboxylic acids' liver protein bioaccumulation: The key role of the neutral species, Environ. Toxicol. Chem., 2010, 29(8), 1669–1677 CAS
.
- L. Zhang, X.-M. Ren and L.-H. Guo, Structure-Based Investigation on the Interaction of Perfluorinated Compounds with Human Liver Fatty Acid Binding Protein, Environ. Sci. Technol., 2013, 47(19), 11293–11301, DOI:10.1021/es4026722
.
-
WHO, Principles of Characterizing and Applying Physiologically-based Pharmacokinetic and Toxicokinetic Models in Risk Assessment, Harmonization of World Heal Organ Geneva, 2008 Search PubMed
.
- A. Reuben, Biliary Proteins, Hepatology, 1984, 4(S2), 46S–50S, DOI:10.1002/hep.1840040808
.
- G. Kakis and I. M. Yousef, Protein composition of rat bile, Can. J. Biochem., 1978, 56(5), 287–290 CrossRef CAS PubMed
.
- P. P. Godfrey, M. J. Warner and R. Coleman, Enzymes and proteins in bile. Variations in output in rat cannula bile during and after depletion of the bile-salt pool, Biochem. J., 1981, 196(1), 11–16 CrossRef CAS PubMed
.
- N. Wu, Y.-L. Song, B. Wang, X.-Y. Zhang, X.-J. Zhang and Y.-L. Wang,
et al., Fish gut-liver immunity during homeostasis or inflammation revealed by integrative transcriptome and proteome studies, Sci. Rep., 2016, 6(1), 36048 CrossRef PubMed
.
- P. J. Vuorinen, M. Keinänen, H. Vuontisjärvi, J. Baršiene, K. Broeg and L. Förlin,
et al., Use of biliary PAH metabolites as a biomarker of pollution in fish from the Baltic Sea, Mar. Pollut. Bull., 2006, 53(8–9), 479–487 CrossRef CAS PubMed
.
- K. Yamazaki, S. P. Powers and N. F. LaRusso, Biliary proteins: assessment of quantitative techniques and comparison in gallstone and nongallstone subjects, J. Lipid Res., 1988, 29(8), 1055–1063 CAS
.
- Y. Ken-Ichi, Relationship of respiration to body weight in the carp Cyprinus carpio under resting and normoxic condition, Comp. Biochem. Physiol., Part A: Mol. Integr. Physiol., 1991, 100(1), 113–116 CrossRef
.
- L. Vergauwen, D. Knapen, A. Hagenaars, G. De Boeck and R. Blust, Assessing the impact of thermal acclimation on physiological condition in the zebrafish model, J. Comp. Physiol., B, 2013, 183(1), 109–121 CrossRef PubMed
.
-
T. Peters, All about albumin: biochemistry, genetics, and medical applications, Academic Press, 1996, p. 432, https://books.google.com/books?hl=en%26lr=%26id=i1DC3KlTAB8C%26oi=fnd%26pg=PP2%26dq=All+about+albumin:+biochemistry,+genetics,+and+medical+applications%26ots=WXAhdW7vem%26sig=3Tkwrd3JcI1IaKWbxLwqLsa-_SE#v=onepage%26q=Allaboutalbumin%3Abiochemistry%2Cgenetics%2Candm Search PubMed
.
- R. J. Erickson, J. M. McKim, G. J. Lien, A. D. Hoffman and S. L. Batterman, Uptake and elimination of ionizable organic chemicals at fish gills: I. Model formulation, parameterization, and behavior, Environ. Toxicol. Chem., 2006, 25(6), 1512–1521 CrossRef CAS PubMed
.
-
M. Palzenberger and H. Pohla, Gill surface area of water-breathing freshwater fish, Reviews in Fish Biology and Fisheries, 1992, vol. 2, pp. 187–216 Search PubMed
.
- M. C. Barber, A review and comparison of models for predicting dynamic chemical bioconcentration in fish, Environ. Toxicol. Chem., 2003, 22, 1963–1992 CrossRef CAS PubMed
.
- Y. Song and C. E. Lunte, Comparison of calibration by delivery versus no net flux for quantitative in vivo microdialysis sampling, Anal. Chim. Acta, 1999, 379(3), 251–262 CrossRef CAS
.
- A. Rescigno, J. Beck and A. Thakur, The use and abuse of models, J. Pharmacokinet. Biopharm., 1987, 15(3), 327–340 CrossRef CAS PubMed
.
- M. MacLeod, A. J. Fraser and D. Mackay, Evaluating and expressing the propagation of uncertainty in chemical fate and bioaccumulation models, Environ. Toxicol. Chem., 2002, 21(4), 700–709, DOI:10.1002/etc.5620210403
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7em00474e |
| This journal is © The Royal Society of Chemistry 2018 |