Is secondary organic aerosol yield governed by kinetic factors rather than equilibrium partitioning?†
Chen
Wang
 a,
Frank
Wania
a,
Frank
Wania
 a and
Kai-Uwe
Goss
a and
Kai-Uwe
Goss
 *bc
*bc
aDepartment of Physical and Environmental Sciences, Department of Chemistry, University of Toronto Scarborough, 1265 Military Trail, Toronto, ON M1C 1A4, Canada
bDepartment of Analytical Environmental Chemistry, Centre for Environmental Research UFZ Leipzig-Halle, Permoserstraße 15, Leipzig, D-04318, Germany. E-mail: kai-uwe.goss@ufz.de; Tel: +49 341 235 1411
cInstitute of Chemistry, University of Halle-Wittenberg, Kurt-Mothes-Straße 2, Halle, D-06120, Germany
First published on 12th December 2017
Abstract
The numerical description of the formation of secondary organic aerosol (SOA) in the atmosphere relies on the use of particle yields, which are often determined in chamber experiments. What is sometimes not appreciated is that such yields (i) can be defined in different ways and (ii) depend on atmospheric conditions. Here we show with the help of hypothetical scenario simulations that the differential SOA yield upon addition of oxidation products to an atmosphere already containing such products and SOA is more relevant in the ambient atmosphere than the commonly used integrative yield from chamber studies. Furthermore, we suggest that the SOA formation scenarios that have been studied so far comprise merely a subset of possible atmospheric situations. In particular, while in the standard scenarios factors such as volatility and aerosol loading are important, scenarios can be envisaged where these factors become less important while the differential yield approaches unity for all oxidation products. Finally, we suggest aerosol growth in the atmosphere should be seen as being determined by a dynamic situation arising from many simultaneously occurring kinetic processes rather than a thermodynamic equilibrium process.
Environmental significanceSecondary organic aerosol (SOA) comprises a major fraction of atmospheric fine particles. Predicting the formation of SOA in atmospheric models is essential for evaluating their influence on climate and human health. SOA yield as an important parameter describing the efficiency of a precursor in generating aerosol materials in chamber studies, has been proposed and used for decades, despite its limitations when applied to the ambient atmosphere. A complex and dynamic system, the atmosphere's (gas and particle) composition is a result of competing kinetics of continuous emissions as well as chemical and physical processing. In this work, we emphasize the significance of the dynamic nature of the atmosphere and suggest the use of the differential SOA yield when describing SOA formation in realistic scenarios. We demonstrate the importance of the differential SOA yield with a model approach using the α-pinene SOA system as an example. |
1. Introduction
As a major component of atmospheric fine particles, secondary organic aerosol (SOA) plays a significant role in atmospheric processes relevant to climate and human health.1 One of the primary goals of SOA research is the prediction of the quantity of SOA being formed, which is a major challenge because of the complex composition and constant transformation of compounds in the atmosphere.2 The concept of particle yield is central in this effort. Studying simplified systems using both experimental and computational methods contributes to our understanding of the amount and composition of SOA formed in the atmosphere.3Laboratory studies relying on smog chambers often examine SOA formation and aging processes of individual precursors to understand their relative contributions in regional and global SOA budgets. They can be conducted in batch or continuous flow mode.4 Precursor compounds are introduced into a chamber and oxidized at specific conditions (temperature, RH, oxidants, light, seed particles, etc.). At the end of the experiment (usually when the SOA concentration reaches a plateau because of a decrease in precursor concentration), the formed particles are characterized and a SOA yield is derived. Flow reactors have also been employed to study SOA formation.5,6 Such studies improve the understanding of SOA formation under relatively simple and controllable conditions, but do not completely represent realistic atmospheric conditions. Limitations of such techniques include limited residence time, insufficient levels of oxidation, and the wall loss of gas phase compounds and particles.5,7
Models of SOA formation usually also rely on simplifications.1 One common simplification is to ignore individual molecular species and instead use surrogates to represent the complex mixtures present in aerosol. These models, including the two-product model and the volatility basis set (VBS) approach, predict SOA mass based on volatility distribution of oxidation products experimentally derived in chamber studies.8,9 More recently models have been developed that take into consideration the molecular identity of the particle-forming compounds.10–15 Such models predict SOA formation without relying on experimental SOA parameterizations. However, computational requirements currently limit the application of these more explicit approaches and prediction of SOA formation in most operational, large-scale models relies on either the two-product model or VBSs.16–19 Therefore, the models, too, may be affected by the limitations of the chamber studies that generated the parameters calibrating those approaches.
Here we will argue that some of the paradigms in SOA-formation-research need to be revisited. The concept of SOA yield needs to be clarified because the integrative yield that is commonly determined from chamber experiments (i.e. the mass of SOA produced per mass of reacted precursor) is different from the differential yield (i.e. the mass of SOA formed upon addition of oxidation products to an atmosphere already containing such products and SOA) and the latter is more relevant in the ambient atmosphere. Jiang20 first introduced such a concept under the name “instantaneous SOA yield” in 2003. He defined a mathematical expression of this new concept and applied the two-product form of the equation to calculate SOA yield in chamber experiments. Here, we try to introduce this concept again using the term “differential yield” which we find more intuitive. We do not aim to calculate the differential yield using mathematical formulas as have been introduced and discussed by Jiang,20 instead our objective is to raise awareness that the scenarios for which SOA yields have been studied experimentally so far are not necessarily those that are realistic in an atmospheric context. Most approaches to obtaining SOA mass in chamber studies do not account for the dynamic nature of SOA formation, i.e., the process of continuous emission and oxidation of precursor compounds and its effect on the gas-particle partitioning of the oxidation products and thus the formation of SOA. In a more realistic scenario, SOA precursors are continuously emitted to the atmosphere, which usually contains a considerable amount of particles, volatile organic compounds (VOCs), and semi-volatile organic compounds (SVOCs). There are potentially large uncertainties when applying SOA parameterization (based on either two-product model or VBS) from unrealistic experimental scenarios to the ambient atmosphere. In this study, we use a hypothetical experiment to study a scenario of SOA formation in which precursor is supplied and oxidized continuously. This is not necessarily more realistic than the scenarios studied in the literature already but it shows that other scenarios might be possible and that in these other scenarios SOA formation might follow other rules than those deemed important so far. In addition, with our modeling approach, we were able to investigate the differential yield for individual SOA forming compounds with different properties and their varying behavior upon changes of the atmosphere (especially a compositional change of the absorbing phase). Finally, we argue that SOA formation can only be understood correctly if it is viewed as a result of many competing kinetic processes.
2. Method
Our approach considers a hypothetical scenario involving a parcel of the atmosphere (1 m3, containing a fixed amount of water and ammonium sulfate) that is assumed to receive a mixture of oxidation products of α-pinene ozonolysis (of constant composition, details in Table S1 and Fig. S1†), yet experiences neither loss of chemicals and particles nor is being diluted with clean air. SOA is formed from the equilibrium partitioning of those products between the gas and the condensed phase, which is assumed to separate into an organic-enriched phase and an aqueous-electrolyte enriched phase. 1 μg aliquots of the mixture of oxidation products are added to the atmospheric parcel repeatedly (for a total of 200 times), and are allowed to achieve equilibrium partitioning after each addition step. The longer this model “experiment” runs, the more is SOA yield and composition expected to differ from the very beginning of the experiment. By explicitly considering the molecules involved in SOA formation we can investigate the SOA yield of individual oxidation products with different volatilities and the yield change upon addition of more oxidation products. We disregard time in this hypothetical scenario because we (i) focus on the formation of SOA as a function of the amount of added oxidation products/precursors and (ii) assume instantaneous equilibrium partitioning between gaseous and particulate phase.The gas-particle partitioning equilibrium calculations were performed using the commercial software COSMOtherm,21,22 as described previously in Wang et al.10 The focus here is on the calculated yields, and the procedure used for quantifying gas-particle partitioning is secondary and therefore only provided in the ESI.†
3. Results
3.1 Definition of SOA yield
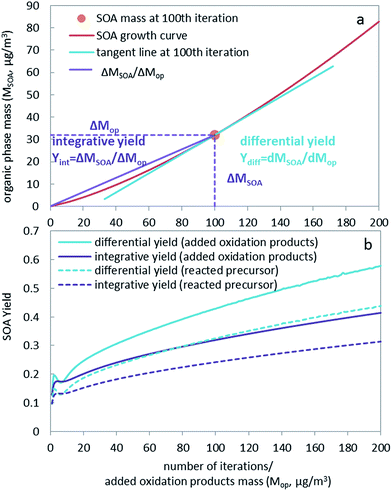
The concept of SOA yield is an important parameter in modeling the formation of SOA. SOA yield (Yint,p) is often defined as the amount of SOA formed (ΔMSOA) from certain amount of precursor reacted (ΔMp).8,23 We call this an integrative yield based on reacted precursors (Yint,p):| Yint,p = ΔMSOA/ΔMp | (1) |
Another way to define the integrative yield (Yint,op) is to describe the SOA mass formed (ΔMSOA) from certain amount of oxidation products (ΔMop), i.e. the fraction of oxidation products that end up making SOA mass:
| Yint,op = ΔMSOA/ΔMop | (2) |
Because the reaction yield of each oxidation product of α-pinene was assumed constant in this study (Table S1†) and the ratio between the mass of oxidation products formed (ΔMop) and the mass of α-pinene reacted (ΔMp) is 1.32 (calculated from reaction yield in Table S1†), Yint,op equals 1.32 Yint,p for this study.
However, in the atmosphere formation of aerosol is continuous, without an explicit beginning and end. An integrative yield cannot be a suitable parameter for describing this ongoing aerosol formation process. What is needed instead is the yield, which describes how much aerosol is formed in the system upon addition of reaction products at its actual state. Accordingly, we define the differential yield (Ydiff) as the fraction that partitions to the organic phase (dMSOA) when a small amount of oxidation products (dMop) is added to the system at a specific loading of the atmosphere.
| Ydiff,op = dMSOA/dMop | (3) |
The differential yield can also be calculated with respect to the reacted amount of precursor, which is the yield of SOA (Ydiff,p) after a small amount of precursor has reacted (dMp).
| Ydiff,p = dMSOA/dMp | (4) |
The curves showing the growth of the SOA organic phase mass during the iterations of our hypothetical experiment (Fig. 1a) illustrate the difference between integrative and differential yield. The slope of the purple line in Fig. 1a represents the integrative yield. The first derivative of the growth curve (i.e. the tangent of the red line in Fig. 1a) represents the differential yield at this point of the curve, which is the slope of the blue line in Fig. 1a. Fig. S3† similarly displays the total mass of SOA formed against the reacted amount of precursor. The integrative and differential yields based on oxidation products and reacted precursors for our hypothetical experiment are plotted in Fig. 1b. SOA yields are also plotted against total organic phase mass and compared with laboratory generated yields as chamber studies usually report SOA yields at different aerosol loadings (Fig. S4 and S5†). There is a general agreement between our prediction and laboratory studies, showing increasing yields with increasing SOA loading (Fig. S5†). Interestingly, because the SOA growth curve is convex, the differential yield is always higher than the corresponding integrative yield (see also Jiang20). This is because the slope of the tangent line at one point is always larger than the slope of the line from this point through the origin.
The aqueous phase's contribution to the aerosol loading is quite small and becomes relatively insignificant as the mass of the organic phase increases for the α-pinene SOA system (Fig. S2†). In the discussion and comparison of SOA yields, the aqueous phase contribution to the overall SOA yield is therefore not included, i.e., the term SOA yield refers to the yield in the organic phase, which usually dominates overall SOA growth, especially at higher loadings. However, for other aerosol systems, the contribution of aqueous phase and multiphase chemistry can be significant, such as glyoxal SOA, for which aqueous phase chemistry, i.e. reactive uptake other than equilibrium partitioning, needs to be considered. Note that below we are using the differential yield based on oxidation products.
Similar to the definition of overall differential and integrative yields in eqn (1)–(4), we can define the yield for an individual compound i based on the added amount of this oxidation product as follows:
| Ydiff,i = dMSOA,i/dMop,i | (5) |
| Yint,i = ΔMSOA,i/ΔMop,i | (6) |
3.2 Hypothetical SOA formation experiment
In the ambient atmosphere SOA is formed constantly with no clearly defined start or end. Oxidation products are continuously formed in an atmosphere that already contains particles of various loadings, compositions and sizes (which are quite different from seed particles used in chamber experiments) and at the same time particles are subject to constant removal by wet or dry deposition, evaporation or condensation due to temperature change, or dilution or concentration by mixing processes. Thus realistic atmospheric conditions are quite different from the scenarios that have typically been studied in the lab. The scenario we describe here, in which oxidation products are constantly added to an atmosphere, is not a realistic scenario either, because, for example, it ignores particle deposition and disregards the element of time. Nevertheless, it helps to explore the range of possible scenarios in aerosol formation and how they may differ from scenarios that have been studied so far.In order to do this, 15 α-pinene oxidation products, which are continuously added to an atmosphere as described in the Methods section, partition into the aerosol phase to form SOA. At equilibrium the mass of compound i (i = 1 to 15) in the organic phase (MSOA,i) can be described by the following equations when partitioning into an aqueous phase is ignored:
| MSOA,i = Mop,i/(1 + 1/(Korg/gas,i × MSOA/ρ)) | (7) |
| MSOA = ∑(MSOA,i) | (8) |
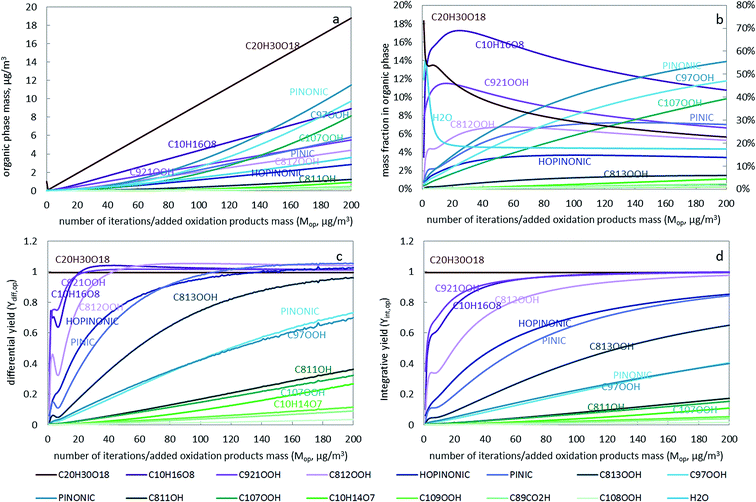
To study the contribution of an individual oxidation product to the growth of SOA and the influencing factors, the growth curve of individual compounds, the SOA composition and the individual SOA yield are plotted in Fig. 2. Generally, both the differential and integrative SOA yields increase with increasing number of iterations (Fig. 2c and d). The differential yield for each component is always higher than the integrative yield, except for C20H30O18, and the difference is larger for more volatile compounds (See Fig. S6†). There are some fluctuations in the first few iterations, which are due to the initially rapid compositional change (as shown in Fig. 2b). During the first few iterations the change of phase composition depends on the composition and mass of the organic seed assumed to be present initially (see ESI†). However, these initial conditions quickly lose their influence on the partitioning properties when the SOA mass increases.
C20H30O18, an extremely low volatile compound (ELVOC), has a differential yield of 1 at different SOA loadings (the dark red line in Fig. 2c). Similarly, the integrative yield is also 1 (Fig. 2d). This is reasonable because as long as it is formed it will prefer the condensed phase due to its extremely low volatility. The partitioning behaviour of such ELVOCs is largely independent of vapor pressures or partitioning coefficients and existing particle mass and composition. Thus, the difference between their differential and integrative yield is small. Even though C20H30O18 has a very low reaction yield (molar yield in Table S1†), it is still the dominant component in the organic phase due to its high Korg/gas (Fig. S7†). Its contribution is decreasing as more SVOC compounds with lower Korg/gas start to partition into the condensed phase at higher organic phase loadings (Fig. 2b). These SVOCs such as C107OOH, PINONIC and C97OOH have relatively high reaction yields (molar yield of 0.2385, 0.140 and 0.115 in Table S1†). The mass fraction of these three compounds in the particulate phase is increasing from the first to the last iteration (Fig. 2b).
Some compounds, such as C10H16O8, C921OOH, C812OOH, and after the 100th iteration also HOPINONIC and PINIC, have differential yields exceeding 1, i.e., the amount of a compound that partitions to the organic phase is higher than the amount added in that iteration. The “excess” amount is compound from previous iterations that had been stored in the gas phase but that now partitions into the particle phase in addition to the amount just added. Reasons for differential yields above 1 are the increasing loading of the organic phase and a changing organic phase composition that becomes more favorable for some of the compounds. For instance, there is an increase in Korg/gas (and a decrease in activity coefficient) for C10H16O8, C812OOH and PINIC with more iterations (Fig. S7 and S8†), indicating that the particle phase composition becomes more favourable for their solvation. Obviously, the differential yield of any compound that transitorily exceeds unity has to drop back to unity eventually at higher loadings. The integrative yield can never exceed 1 (Fig. 2d).
Once a compound starts to build up higher and higher gas phase concentrations, more of any additionally added amount of this compound will sorb to the condensed phase no matter its volatility. The volatility of a compound only determines when it reaches a differential yield of 1, with less volatile compound reaching that threshold earlier. For example, in Fig. 2c the ELVOC C20H30H18 reaches a differential yield of 1 immediately after it starts to form particles and the differential yield for other relatively low volatility compounds such as C10H16O8, C921OOH, C812OOH (with log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Korg/gas higher than 11 in Fig. S7†) increases quickly to 1 and above. Eventually, when enough gas phase species have accumulated and when the SOA loading is high, even relatively volatile compounds will approach a very high differential yield. While this may seem counter-intuitive at first, it becomes clearer if one realizes that any single compound continuously added to a finite gas phase will eventually approach its saturation vapor pressure and from that point onwards any additionally added amount would condense into its own pure liquid phase i.e. have a differential yield of unity, no matter how volatile it is and no matter how much particulate phase is available. Because SOA formation involves organic mixtures, eventually not a pure phase of a single chemical is formed but an azeotropic mixture. The “saturated” gas phase concentrations at which every newly formed product immediately and completely “condenses” into the azeotrope are typically much smaller than the saturation vapor concentrations of all the single components themselves. Compounds with Korg/gas (or vapor pressures) differing by orders of magnitude will eventually have similar differential yields if the particulate phase comes close to an azeotropic mixture. For example, C20H30H18, C10H16O8, C921OOH, C812OOH, HOPINONIC, PINIC and C813OOH all have differential yields around 1 at the 200th iteration, even though their Korg/gas varies from 1010 to 1019 (Fig. S7†). If we had continued our calculations in Fig. 2 much further then eventually all oxidation products, even the most volatile ones, would have reached a differential yield of unity and the particulate phase would have become an azeotrope mixture whose composition would not change any more when more oxidation products (of constant composition) were added. In this situation the growth of the particle phase would be identical to the addition of oxidation products so that compounds with the highest reaction yield would also dominate aerosol formation. This agrees with the statement from Seinfeld and Pankow25 that “the SOA yield approaches a constant value as the amount of particulate organic into which the gaseous products absorb reaches large values, and this asymptotic amount is determined purely by reaction stoichiometry”. Apart from the widely known aerosol loading effect as proposed by Seinfeld and Pankow,25 we were also able to demonstrate the effect of changing composition (i.e. the activity of organic products in the condensed phase) and gas phase accumulation on SOA formation.
Korg/gas higher than 11 in Fig. S7†) increases quickly to 1 and above. Eventually, when enough gas phase species have accumulated and when the SOA loading is high, even relatively volatile compounds will approach a very high differential yield. While this may seem counter-intuitive at first, it becomes clearer if one realizes that any single compound continuously added to a finite gas phase will eventually approach its saturation vapor pressure and from that point onwards any additionally added amount would condense into its own pure liquid phase i.e. have a differential yield of unity, no matter how volatile it is and no matter how much particulate phase is available. Because SOA formation involves organic mixtures, eventually not a pure phase of a single chemical is formed but an azeotropic mixture. The “saturated” gas phase concentrations at which every newly formed product immediately and completely “condenses” into the azeotrope are typically much smaller than the saturation vapor concentrations of all the single components themselves. Compounds with Korg/gas (or vapor pressures) differing by orders of magnitude will eventually have similar differential yields if the particulate phase comes close to an azeotropic mixture. For example, C20H30H18, C10H16O8, C921OOH, C812OOH, HOPINONIC, PINIC and C813OOH all have differential yields around 1 at the 200th iteration, even though their Korg/gas varies from 1010 to 1019 (Fig. S7†). If we had continued our calculations in Fig. 2 much further then eventually all oxidation products, even the most volatile ones, would have reached a differential yield of unity and the particulate phase would have become an azeotrope mixture whose composition would not change any more when more oxidation products (of constant composition) were added. In this situation the growth of the particle phase would be identical to the addition of oxidation products so that compounds with the highest reaction yield would also dominate aerosol formation. This agrees with the statement from Seinfeld and Pankow25 that “the SOA yield approaches a constant value as the amount of particulate organic into which the gaseous products absorb reaches large values, and this asymptotic amount is determined purely by reaction stoichiometry”. Apart from the widely known aerosol loading effect as proposed by Seinfeld and Pankow,25 we were also able to demonstrate the effect of changing composition (i.e. the activity of organic products in the condensed phase) and gas phase accumulation on SOA formation.
4. Discussion
A realistic scenario of SOA formation has to consider that usually different levels of oxidation products have accumulated in the gas phase, precursors are emitted constantly and new oxidation products are formed continuously. Fig. 2 illustrates that neither the yield nor the composition of gas and particle phase at higher loadings can be easily extrapolated from those measured at lower loadings or vice versa. The formed SOA mass will be higher than traditionally calculated based on chamber experiment fits (either using the two product model or the VBS approach) by using the differential yield, when considering the continuous emission of precursors and their oxidation products in the atmosphere.Conventional chamber experiments aid in understanding reaction pathways and kinetics but they are not providing the SOA formation parameters most relevant to the situation in the real atmosphere. That situation is dynamic, i.e., varies temporally and spatially with different loadings of particles and gas phase compounds. When oxidized compounds are formed in a clean atmosphere without many pre-existing particles, low volatility compounds will partition to the condensed phase first and the formed particles consist of compounds with low volatility. Relatively volatile products will remain in the gas phase. In this situation the differential SOA yield for individual products depends strongly on their partition coefficient and the concentration of already available sorbing particles. The total yield (i.e. integrated over all reaction products) depends on the individual yields weighted by the mole fraction that they contribute to the sum of all reaction products. Thus, quite different total yields are to be expected for different types and amounts of seed particles but also for different reaction pathways that may lead to various species and amounts of oxidation products.
While the particle grows, more volatile compounds start to partition and contribute to SOA and thus the SOA yield for individual compounds increases (Fig. 2c). This is similar to oxidation products being emitted to an atmosphere with some pre-existing particles. For example, partitioning of the compounds to the particles at the 80th iteration is very different from partitioning into the initial particle, because of the different mass (24 μg vs. 0.5 μg) and composition (Fig. 2a and b) of the organic phase. In the extreme, the scenario eventually converges towards a situation where all oxidation products have a differential yield of unity independent of their volatility and independent of the amount of available sorbing phase. In this final state the composition of the particle approaches that of an azeotrope mixture and the products with the highest reaction yields govern particle growth.
In general, we can conclude that close to the source of precursors and with a stable atmosphere (limited mixing and removal), e.g. a smog situation, the atmosphere is likely to build up substantial gas phase concentrations of partitioning species and thus achieve rather high yields. The type and amount of existing SOA then has diminished influence on the yield and even the volatility of the reaction products will become less important. If the atmosphere is rather clean, well mixed and further away from the emission of precursors, the SOA formation might be closer to that in the chamber experiments. In summary we conclude that there might exist scenarios in the atmosphere in which the differential SOA yield is not as dependent on compound volatility and existing particle mass as has been indicated by chamber experiments and theoretical investigations previously.
5. Looking forward
Fig. 2 illustrates how much the equilibrium partitioning of oxidation products between gas and particle phase can change if more and more oxidation products are added. The curves in Fig. 2 change somewhat for different temperatures, relative humidity and/or with different precursors/oxidation products. However, all of these curves still do not resemble the situation in the real atmosphere, because the dimension of time is ignored in our “experiment”. The concentration of gaseous organic compounds depends on their emission or formation rate in the air compared to the removal rate by sorption, mixing, reaction or deposition. Similarly, while particles are formed and grow, they are – at the same time – removed from an air parcel by gravitational settling or washing out or they are exchanged with neighboring air parcels by turbulent mixing. A realistic treatment cannot separate these processes from the formation of particles because the amount of existing particles has an immediate feedback on the formation of new particles. In order to understand aerosol formation in the atmosphere in qualitative and quantitative terms, it will therefore be necessary to consider the kinetics of many relevant processes even if one finds that the partition process itself is so quick that it can still be treated as an instantaneous equilibrium. If an air parcel can be considered stable for a while, a steady-state situation may arise for which a differential yield could then be calculated. It might be quite challenging though to establish where this steady-state is located, because it requires knowledge of the emission rate of precursor gases and primary particles, the reaction rate constants for all relevant reactions of the precursors, as well as the rate constants for atmospheric mixing, dry and wet deposition, and particle coagulation. Such an analysis will have to consider the simultaneous existence of particles of differing size and composition, which also differ in their growth and elimination.Due to the non-linear nature of many of the involved processes, rather small changes in the boundary conditions may lead to different, stable steady-state situations. Note that SOA parameterization based on single or a few chamber experiments (i.e. using the volatility distribution obtained from chamber experiments in the treatment of SOA formation in most current atmospheric models, e.g. the two-product or VBS approach) may not describe SOA growth in such a kinetically controlled system in a meaningful way. Such kinetically controlled systems are far from the thermodynamic considerations that dominate the discussion of aerosol formation in the literature. We believe research on SOA formation needs to focus on these kinetic questions and problems. It will be an interesting but also highly demanding task to unravel the factors that dominate aerosol formation in the real atmosphere. For example, recent studies have investigated the sensitivity of SOA evolution to different processes and parameterizations, including emissions, removal processes (such as dry deposition, photolysis and heterogeneous chemistry) and particle-phase transformations of SOA to compounds of low volatility. These studies demonstrate that SOA is a far more dynamic system and a subset of complex and uncertain processes is governing the lifecycle of SOA.19,26,27 The ultimate goal is to identify mechanisms and processes that are most influential in affecting the evolution of SOA and to understand how different parameters contribute to the overall uncertainty.28
It is unrealistic to assume the composition and volatility distribution of the oxidation products in the chamber experiments is the same as in the ambient atmosphere for a specific precursor. Instead, a direct and explicit prediction of SOA formation is required.24 Nevertheless, there is still a use for the SOA yield as a quantitative measure in comparing the efficiency of aerosol formation under different scenarios for different precursors. In this context it is certainly important to acknowledge that the differential yield is preferable over the integrative yield.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge financial support from the Natural Sciences and Engineering Research Council of Canada, an Ontario Graduate Scholarship and a Special Opportunity Travel Fellowship from the Department of Chemistry at the University of Toronto. We thank Arthur Chan and Jon Abbatt for comments on our manuscript. C. W. is grateful for Stephen Wood's help with coding.References
- M. Hallquist, J. C. Wenger, U. Baltensperger, Y. Rudich, D. Simpson, M. Claeys, J. Dommen, N. M. Donahue, C. George, A. H. Goldstein, J. F. Hamilton, H. Herrmann, T. Hoffmann, Y. Iinuma, M. Jang, M. E. Jenkin, J. L. Jimenez, A. Kiendler-Scharr, W. Maenhaut, G. McFiggans, T. F. Mentel, A. Monod, A. S. H. Prevot, J. H. Seinfeld, J. D. Surratt, R. Szmigielski and J. Wildt, The formation, properties and impact of secondary organic aerosol: current and emerging issues, Atmos. Chem. Phys., 2009, 9, 5155–5236 CrossRef CAS.
- M. Glasius and A. H. Goldstein, Recent discoveries and future challenges in atmospheric organic chemistry, Environ. Sci. Technol., 2016, 50, 2754–2764 CrossRef CAS PubMed.
- E. A. Bruns, I. El Haddad, A. Keller, F. Klein, N. K. Kumar, S. M. Pieber, J. C. Corbin, J. G. Slowik, W. H. Brune, U. Baltensperger and A. S. H. Prévôt, Inter-comparison of laboratory smog chamber and flow reactor systems on organic aerosol yield and composition, Atmos. Meas. Tech., 2015, 8, 2315–2332 CAS.
- J. E. Shilling, Q. Chen, S. M. King, T. Rosenoern, J. H. Kroll, D. R. Worsnop, K. A. McKinney and S. T. Martin, Particle mass yield in secondary organic aerosol formed by the dark ozonolysis of α-pinene, Atmos. Chem. Phys., 2008, 8, 2073–2088 CAS.
- A. T. Lambe, P. S. Chhabra, T. B. Onasch, W. H. Brune, J. F. Hunter, J. H. Kroll, M. J. Cummings, J. F. Brogan, Y. Parmar, D. R. Worsnop, C. E. Kolb and P. Davidovits, Effect of oxidant concentration, exposure time, and seed particles on secondary organic aerosol chemical composition and yield, Atmos. Chem. Phys., 2015, 15, 3063–3075 CrossRef CAS.
- A. T. Lambe, A. T. Ahern, L. R. Williams, J. G. Slowik, J. P. S. Wong, J. P. D. Abbatt, W. H. Brune, N. L. Ng, J. P. Wright, D. R. Croasdale, D. R. Worsnop, P. Davidovits and T. B. Onasch, Characterization of aerosol photooxidation flow reactors: heterogeneous oxidation, secondary organic aerosol formation and cloud condensation nuclei activity measurements, Atmos. Meas. Tech., 2011, 4, 445–461 CrossRef CAS.
- X. Zhang, C. D. Cappa, S. H. Jathar, R. C. McVay, J. J. Ensberg, M. J. Kleeman and J. H. Seinfeld, Influence of vapor wall loss in laboratory chambers on yields of secondary organic aerosol, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 5802–5807 CrossRef CAS PubMed.
- J. R. Odum, T. Hoffmann, F. Bowman, D. Collins, R. C. Flagan and J. H. Seinfeld, Gas/particle partitioning and secondary organic aerosol yields, Environ. Sci. Technol., 1996, 30, 2580–2585 CrossRef CAS.
- N. M. Donahue, A. L. Robinson, C. O. Stanier and S. N. Pandis, Coupled partitioning, dilution, and chemical aging of semivolatile organics, Environ. Sci. Technol., 2006, 40, 2635–2643 CrossRef CAS PubMed.
- C. Wang, K.-U. Goss, Y. D. Lei, J. P. D. Abbatt and F. Wania, Calculating equilibrium phase distribution during the formation of secondary organic aerosol using COSMOtherm, Environ. Sci. Technol., 2015, 49, 8585–8594 CrossRef CAS PubMed.
- A. Zuend and J. H. Seinfeld, Modeling the gas-particle partitioning of secondary organic aerosol: the importance of liquid-liquid phase separation, Atmos. Chem. Phys., 2012, 12, 3857–3882 CrossRef CAS.
- J. Li, M. Cleveland, L. D. Ziemba, R. J. Griffin, K. C. Barsanti, J. F. Pankow and Q. Ying, Modeling regional secondary organic aerosol using the Master Chemical Mechanism, Atmos. Environ., 2015, 102, 52–61 CrossRef CAS.
- J. F. Pankow, M. C. Marks, K. C. Barsanti, A. Mahmud, W. E. Asher, J. Li, Q. Ying, S. H. Jathar and M. J. Kleeman, Molecular view modeling of atmospheric organic particulate matter: Incorporating molecular structure and co-condensation of water, Atmos. Environ., 2015, 122, 400–408 CrossRef CAS.
- B. Aumont, R. Valorso, C. Mouchel-Vallon, M. Camredon, J. Lee-Taylor and S. Madronich, Modeling SOA formation from the oxidation of intermediate volatility n-alkanes, Atmos. Chem. Phys., 2012, 12, 7577–7589 CrossRef CAS.
- J. Lee-Taylor, S. Madronich, B. Aumont, A. Baker, M. Camredon, A. Hodzic, G. S. Tyndall, E. Apel and R. A. Zaveri, Explicit modeling of organic chemistry and secondary organic aerosol partitioning for Mexico City and its outflow plume, Atmos. Chem. Phys., 2011, 11, 13219–13241 CrossRef CAS.
- A. G. Carlton, P. V. Bhave, S. L. Napelenok, E. O. Edney, G. Sarwar, R. W. Pinder, G. A. Pouliot and M. Houyoux, Model representation of secondary organic aerosol in CMAQv4.7, Environ. Sci. Technol., 2010, 44, 8553–8560 CrossRef CAS PubMed.
- H. O. T. Pye, A. W. H. Chan, M. P. Barkley and J. H. Seinfeld, Global modeling of organic aerosol: the importance of reactive nitrogen (NOx and NO3), Atmos. Chem. Phys., 2010, 10, 11261–11276 CAS.
- S. C. Farina, P. J. Adams and S. N. Pandis, Modeling global secondary organic aerosol formation and processing with the volatility basis set: Implications for anthropogenic secondary organic aerosol, J. Geophys. Res.: Atmos., 2010, 115, D09202 CrossRef.
- K. Tsigaridis, N. Daskalakis, M. Kanakidou, P. J. Adams, P. Artaxo, R. Bahadur, Y. Balkanski, S. E. Bauer, N. Bellouin, A. Benedetti, T. Bergman, T. K. Berntsen, J. P. Beukes, H. Bian, K. S. Carslaw, M. Chin, G. Curci, T. Diehl, R. C. Easter, S. J. Ghan, S. L. Gong, A. Hodzic, C. R. Hoyle, T. Iversen, S. Jathar, J. L. Jimenez, J. W. Kaiser, A. Kirkevåg, D. Koch, H. Kokkola, Y. H. Lee, G. Lin, X. Liu, G. Luo, X. Ma, G. W. Mann, N. Mihalopoulos, J. J. Morcrette, J. F. Müller, G. Myhre, S. Myriokefalitakis, N. L. Ng, D. O'Donnell, J. E. Penner, L. Pozzoli, K. J. Pringle, L. M. Russell, M. Schulz, J. Sciare, Ø. Seland, D. T. Shindell, S. Sillman, R. B. Skeie, D. Spracklen, T. Stavrakou, S. D. Steenrod, T. Takemura, P. Tiitta, S. Tilmes, H. Tost, T. van Noije, P. G. van Zyl, K. von Salzen, F. Yu, Z. Wang, R. A. Zaveri, H. Zhang, K. Zhang, Q. Zhang and X. Zhang, The AeroCom evaluation and intercomparison of organic aerosol in global models, Atmos. Chem. Phys., 2014, 14, 10845–10895 Search PubMed.
- W. Jiang, Instantaneous secondary organic aerosol yields and their comparison with overall aerosol yields for aromatic and biogenic hydrocarbons, Atmos. Environ., 2003, 37, 5439–5444 CrossRef CAS.
- A. Klamt and F. Eckert, COSMO-RS: a novel and efficient method for the a priori prediction of thermophysical data of liquids, Fluid Phase Equilib., 2000, 172, 43–72 CrossRef CAS.
- A. Klamt, From Quantum Chemistry to Fluid Phase Thermodynamics and Drug Design, Elsevier, Amsterdam, 2005 Search PubMed.
- J. F. Pankow, An absorption model of the gas/aerosol partitioning involved in the formation of secondary organic aerosol, Atmos. Environ., 1994, 28, 189–193 CrossRef CAS.
- E. M. Knipping, R. J. Griffin, F. M. Bowman, B. Pun, C. Seigneur, D. Dabdub and J. H. Seinfeld, Comment on “Instantaneous secondary organic aerosol yields and their comparison with overall aerosol yields for aromatic and biogenic hydrocarbons” by Weimin Jiang, Atmos. Environ., 2004, 38, 2759–2761 CrossRef CAS.
- J. H. Seinfeld and J. F. Pankow, Organic atmospheric particulate material, Annu. Rev. Phys. Chem., 2003, 54, 121–140 CrossRef CAS PubMed.
- A. Hodzic, P. S. Kasibhatla, D. S. Jo, C. D. Cappa, J. L. Jimenez, S. Madronich and R. J. Park, Rethinking the global secondary organic aerosol (SOA) budget: stronger production, faster removal, shorter lifetime, Atmos. Chem. Phys., 2016, 16, 7917–7941 CAS.
- M. Shrivastava, C. Zhao, R. C. Easter, Y. Qian, A. Zelenyuk, J. D. Fast, Y. Liu, Q. Zhang and A. Guenther, Sensitivity analysis of simulated SOA loadings using a variance-based statistical approach, J. Adv. Model. Earth Syst., 2016, 8, 499–519 CrossRef.
- M. Shrivastava, C. D. Cappa, J. Fan, A. H. Goldstein, A. B. Guenther, J. L. Jimenez, C. Kuang, A. Laskin, S. T. Martin, N. L. Ng, T. Petaja, J. R. Pierce, P. J. Rasch, P. Roldin, J. H. Seinfeld, J. Shilling, J. N. Smith, J. A. Thornton, R. Volkamer, J. Wang, D. R. Worsnop, R. A. Zaveri, A. Zelenyuk and Q. Zhang, Recent advances in understanding secondary organic aerosol: Implications for global climate forcing, Rev. Geophys., 2017, 55, 509–559 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Additional information on the description of method, information for the organic compounds, aqueous phase composition, comparison with laboratory studies, contribution of water in the organic phase, comparison with previous studies, and additional tables and figures referenced in the text is provided. See DOI: 10.1039/c7em00451f |
| This journal is © The Royal Society of Chemistry 2018 |