The merit of perovskite's dimensionality; can this replace the 3D halide perovskite?
Abstract
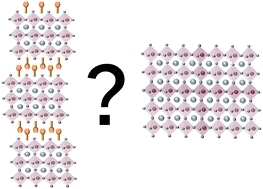
This perspective paper focuses on the dimensionality of organic–inorganic halide perovskites and their relevant advantages over 3D perovskites. The charges in two-dimensional (2D) materials are restricted in their movement to the two-dimensional plane; however, their confined structure allows one to tune the optical and electronic properties by varying their thickness. Here we focus on the main advantages of 2D halide perovskites including their enhanced stability; several recent reports discussing this point are summarized. It was observed that 2D perovskites exhibit enhanced moisture resistivity, starting from films to complete solar cells. The power conversion efficiency of photovoltaic solar cells based on 2D- and quasi-2D perovskites (2D + 3D perovskites) as light harvesters has been increasing but still not as much as 3D perovskites. However, their other advantages (e.g., stability, tuning of optical and electronic properties, and the large amount of possible organic cations that can be integrated into their structure) make them a stable alternative for efficient and large-scale module solar cells, which may constitute the next step for commercializing perovskite-based solar cells. To sum up, several strategies for improving the photovoltaic performance of low dimensional perovskites are discussed.
- This article is part of the themed collection: 2018 Energy and Environmental Science HOT Articles


 Please wait while we load your content...
Please wait while we load your content...