Using lead chalcogenide nanocrystals as spin mixers: a perspective on near-infrared-to-visible upconversion
Abstract
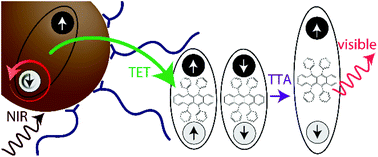
The process of upconversion leads to emission of photons higher in energy than the incident photons. Near-infrared-to-visible upconversion, in particular, shows promise in sub-bandgap sensitization of silicon and other optoelectronic materials, resulting in potential applications ranging from photovoltaics that exceed the Shockley–Queisser limit to infrared imaging. A feasible mechanism for near-infrared-to-visible upconversion is triplet–triplet annihilation (TTA) sensitized by colloidal nanocrystals (NCs). Here, the long lifetime of spin-triplet excitons in the organic materials that undergo TTA makes upconversion possible under incoherent excitation at relatively low photon fluxes. Since this process relies on optically inactive triplet states, semiconductor NCs are utilized as efficient spin mixers, absorbing the incident light and sensitizing the triplet states of the TTA material. The state-of-the-art system uses rubrene with a triplet energy of 1.14 eV as the TTA medium, and thus allows upconversion of light with photon energies above ∼1.1 eV. In this perspective, we review the field of lead sulfide (PbS) NC-sensitized near-infrared-to-visible upconversion, discuss solution-based upconversion, and highlight progress made on solid-state upconversion devices.
- This article is part of the themed collections: 2018 Frontier and Perspective articles and Metal Complexes and Nanoparticles for Energy Upconversion


 Please wait while we load your content...
Please wait while we load your content...
