Enhancement of catalytic activity of Pd-PVP colloid for direct H2O2 synthesis from H2 and O2 in water with addition of 0.5 atom% Pt or Ir†
Abstract
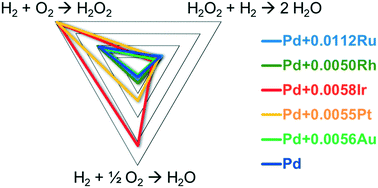
Catalytic activity of Pd-polyvinylpyrrolidone (PVP) colloid for the reaction of H2 and O2 to H2O2 in the presence of H2SO4 and NaBr was greatly enhanced with the addition of a very small quantity of Pt or Ir. In contrast to ordinary alloy catalysts, the activity of Pd was doubly increased with the addition of only 0.5 atom% Pt or Ir, although the selectivity for the H2O2 formation somewhat decreased. Addition of Ru, Rh, or Au affected little the activity. Kinetic analyses of the reactions over modified Pd-PVP indicated that the high H2-activating abilities of Pt and Ir increased the H2–O2 reaction rate, which was supported by DFT study. In contrast, H2O2 hydrogenation rates were almost constant irrespective of Pt or Ir addition, indicating little participation of the hydrogen activated on Pt or Ir in H2O2 destruction. Pt-modified Pd-PVP showed a discontinuous change in catalytic activity in the time dependency measurement, resulting in higher H2–O2 reaction rates and lower H2O2 selectivity. Lower partial pressure of hydrogen under the reaction conditions or higher temperatures in the absence of H2 accelerated the change. Structures of the Pt- and Ir-loaded Pd-PVP catalysts were suggested to change during the reaction; the Pt or Ir atoms would initially be located at coordinatively more unsaturated sites of the Pd particles and move into the surface Pd lattice to be stabilized. It is shown that the amount of H2O2 produced reaches several wt% when estimated using the Pt- and Ir-loaded Pd-PVP catalysts under an O2 partial pressure of 360 kPa.


 Please wait while we load your content...
Please wait while we load your content...