Performance of edges on carbon for the catalytic hydroxylation of benzene to phenol†
Ya-Jing
Lyu
 ac,
Ting
Qi
ac,
Ting
Qi
 b,
Hua-Qing
Yang
b,
Hua-Qing
Yang
 *b and
Chang-Wei
Hu
*b and
Chang-Wei
Hu
 *a
*a
aKey Laboratory of Green Chemistry and Technology, Ministry of Education, College of Chemistry, Sichuan University, Chengdu, Sichuan 610064, P.R. China. E-mail: changweihu@scu.edu.cn
bCollege of Chemical Engineering, Sichuan University, Chengdu, Sichuan 610065, P.R. China. E-mail: huaqingyang@scu.edu.cn
cSchool of Science, Xihua University, Chengdu, Sichuan 610039, P.R. China
First published on 1st November 2017
Abstract
Carbon catalyst is regarded as an efficient and environment-friendly material for the direct oxidation of benzene to phenol. However, the essence and detailed performances of the active sites are still unclear at the molecular level. In the present study, the role of typical defect sites on carbon for benzene hydroxylation to phenol with hydrogen peroxide as the oxidant was theoretically investigated at M06-2x/6-311++G(d, p) level in acetonitrile solution. The carbon with defect sites was modeled with armchair and zigzag edges. The turnover frequency analysis indicated that the rate-controlling step was associated with the HO–OH bond cleavage in the H2O2 moiety for the formation of hydroxyl radical. For both the armchair and zigzag edges on carbon material, the defect site plays an essential role in the hydroxyl radical formation from H2O2. In the presence of water, the defect site of carbon could readily be hydrated, where the zigzag defect site could be more easily hydrated to hydroquinone than the defect armchair site. Furthermore, the zigzag defect carbon exhibits better catalytic performance than the armchair defect carbon. Based on activation strain analysis, there is a stronger stabilizing transition state interaction in the zigzag defect carbon than that in the defect armchair carbon, which arises from a narrower HOMO–LUMO gap. The present study could shed some light on the essence and function of active sites on carbon for the benzene hydroxylation to phenol.
1. Introduction
Recently, the transformation of benzene into oxygen-containing aromatic compounds such as phenol under mild conditions has been one of the most active topics in both applied and fundamental catalytic research.1 Benzene is a very important bulk chemical in the energy and industry fields, and the C–H bond is one of the most stable to be activated. Phenol, as a crucial bulk commodity chemical, is currently produced in industry by a three-step cumene process, which has drawbacks such as high pollution, high-energy consumption, and relatively low selectivity towards phenol.2 To address these issues, a direct one-step benzene oxidation approach with H2O2 as the oxidizer is highly desired.3The development of innovative catalytic technologies to transform benzene into phenol is attracting increasing interest. In this process, many catalysts including Fe-containing zeolite, palladium membrane, titanium-containing mesoporous molecular sieves, modified titanium silicalite, vanadium-substituted phosphomolybdate, and metal-free activated carbon (AC) have been developed.4–17 Among them, carbon-based catalysts were reported as environment-friendly and promising catalysts with hydrogen peroxide as the oxidant because of its physical properties and surface functional groups.6–17 However, less information is available regarding the reaction mechanism and the essence of the active sites owing to the complex surface structure (e.g., oxygenated groups, curved sp2-hybridized carbon surface, defects, or graphene layers) and the presence of metal impurities.6,7,18–20 Ma et al. demonstrated that the nitric acid treated graphene acts as an excellent catalyst, in which the outstanding catalytic performance has been attributed to the appropriate H2O2 activation rate, good benzene adsorption ability, and consequently the balanced kinetic control over the oxidation reaction of the novel catalyst.7 Su et al. successfully identified the armchair defect as one type of active defect, which is responsible for the formation of active oxygen species.6 Despite the present research situation and existing issues, how the defect on AC, as an active site, exhibits the catalytic performance remains elusive at the molecular level.
Commonly, the functionalized carbon materials include the oxygenated groups (e.g., C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, O
O, O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–O, and C–OH) and defects. Another aspect of the carbon materials chemistry, which is often overlooked, is the dependence of the chemical and physical properties of the material under consideration on its spin state (i.e. multiplicity).21 Carbon materials depend on the presence of certain active sites on their surface, and their accessibility, which will permit the interface reaction. Two distinct types of sites can be considered in this structure: the basal plane sites and the edge plane sites. The edge plane sites are usually considered as chemically/electrochemically active sites, whereas the basal plane sites are relatively inactive.22 Unsaturated carbon atoms can chemisorb oxygen, water or compounds such as ammonia, generating some groups on the carbon surface that can act as active sites in different reactions. Among these surface groups, oxygenated groups are of great importance since they are the most abundant and consequently can modify the behaviour of the AC.23 AC can promote hydrogen peroxide decomposition through the formation of hydroxyl radicals.24–26 In general, basic or reduced AC promotes faster hydrogen peroxide decomposition, whereas the presence of surface oxygen groups inhibits the reaction.26–28 Bahamonde et al. proposed that the surface of AC promotes H2O2 decomposition to an extent depending on related-structural features and on the amount and nature of surface oxygen groups; also, a lower ordering of the carbon structure with less developed graphene layers leads to a higher decomposition rate due to higher surface concentration of unpaired electron active sites. In ACs with a similar structural ordering, the presence of acidic surface oxygen groups inhibits the decomposition of hydrogen peroxide.29 Despite the heightened effort to probe the reaction mechanism, a clear understanding of the role of active sites on carbon materials is lacking for the catalytic hydroxylation of benzene to phenol with H2O2, particularly for the formation of the hydroxyl radicals from H2O2 on the carbon materials at the molecular level.
C–O, and C–OH) and defects. Another aspect of the carbon materials chemistry, which is often overlooked, is the dependence of the chemical and physical properties of the material under consideration on its spin state (i.e. multiplicity).21 Carbon materials depend on the presence of certain active sites on their surface, and their accessibility, which will permit the interface reaction. Two distinct types of sites can be considered in this structure: the basal plane sites and the edge plane sites. The edge plane sites are usually considered as chemically/electrochemically active sites, whereas the basal plane sites are relatively inactive.22 Unsaturated carbon atoms can chemisorb oxygen, water or compounds such as ammonia, generating some groups on the carbon surface that can act as active sites in different reactions. Among these surface groups, oxygenated groups are of great importance since they are the most abundant and consequently can modify the behaviour of the AC.23 AC can promote hydrogen peroxide decomposition through the formation of hydroxyl radicals.24–26 In general, basic or reduced AC promotes faster hydrogen peroxide decomposition, whereas the presence of surface oxygen groups inhibits the reaction.26–28 Bahamonde et al. proposed that the surface of AC promotes H2O2 decomposition to an extent depending on related-structural features and on the amount and nature of surface oxygen groups; also, a lower ordering of the carbon structure with less developed graphene layers leads to a higher decomposition rate due to higher surface concentration of unpaired electron active sites. In ACs with a similar structural ordering, the presence of acidic surface oxygen groups inhibits the decomposition of hydrogen peroxide.29 Despite the heightened effort to probe the reaction mechanism, a clear understanding of the role of active sites on carbon materials is lacking for the catalytic hydroxylation of benzene to phenol with H2O2, particularly for the formation of the hydroxyl radicals from H2O2 on the carbon materials at the molecular level.
To study the role of specific groups and defects, two model catalysts with armchair and zigzag edges were constructed to mimic carbon with oxygenated groups (e.g., C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and C–OH) and/or defects. Herein, we report the catalytic mechanism for the benzene catalytic hydroxylation to phenol on carbon in acetonitrile solution. The goals are as follows: (a) to ascertain the catalytic nature of the defect on carbon materials for hydrogen peroxide decomposition, (b) to gain a deep insight into determining the transition state (TDTS) and the intermediate (TDI) of the turnover frequency (TOF), (c) to elucidate the role of an active defect on carbon, and (d) to compare the catalytic performance of armchair and zigzag edges.
O and C–OH) and/or defects. Herein, we report the catalytic mechanism for the benzene catalytic hydroxylation to phenol on carbon in acetonitrile solution. The goals are as follows: (a) to ascertain the catalytic nature of the defect on carbon materials for hydrogen peroxide decomposition, (b) to gain a deep insight into determining the transition state (TDTS) and the intermediate (TDI) of the turnover frequency (TOF), (c) to elucidate the role of an active defect on carbon, and (d) to compare the catalytic performance of armchair and zigzag edges.
2. Computational details
All calculations were performed with the Gaussian 09 program package.30 A polarized continuum model (PCM-SMD) was utilized to simulate the solvent effect of acetonitrile.31,32 Geometry optimizations were run to locate all the stationary points and transition states (TSs) using the M06-2x density functional theory method with the 6-311++G(d, p) basis set for all atoms, namely, M06-2x/6-311++G(d, p).33,34 For the reaction pathway analysis, every transition structure has only one imaginary frequency; the connections between transition states and corresponding intermediates were verified through intrinsic reaction coordinate (IRC) calculations.35,36 The natural charges, dominant occupancies of natural bond orbitals, and dominant stabilization energies E(2) between donors and acceptors for some species have been analysed with the help of the natural bond orbital (NBO) analysis.37,38 Unless otherwise mentioned, the Gibbs free energy of formation (ΔG) is relative to the initial ground state reactants obtained at the M06-2x/6-311++G(d, p) level in acetonitrile solution under atmospheric pressure and experimental temperature (1.0 atm and 343 K).8The turnover frequency (TOF) of the catalytic cycle determines the efficiency of the catalyst. Based on the transition state theory, TOF can be calculated by eqn (i) and (ii),39–42 in which δE (the energetic span)43,44 is defined as the energy difference between the summit and trough of the catalytic cycle.
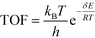 | (i) |
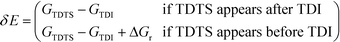 | (ii) |
3. Results and discussion
Based on the functionalized carbon materials with the oxygenated groups (e.g., C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and C–OH) and/or defects, we designed two carbon models with armchair and zigzag edges, namely, hydroquinone, semiquinone, quinone, and defect, denoted as a/z-2OH, a/z-OH–O, a/z-2O, a/z-O, respectively, to simulate the active sites. The optimized geometric structures for the active sites in acetonitrile solution are depicted in Fig. S1 in the ESI.† Herein, we studied the catalytic roles of the above active sites for the formation of hydroxyl radical and subsequently phenol in acetonitrile solution.
O and C–OH) and/or defects, we designed two carbon models with armchair and zigzag edges, namely, hydroquinone, semiquinone, quinone, and defect, denoted as a/z-2OH, a/z-OH–O, a/z-2O, a/z-O, respectively, to simulate the active sites. The optimized geometric structures for the active sites in acetonitrile solution are depicted in Fig. S1 in the ESI.† Herein, we studied the catalytic roles of the above active sites for the formation of hydroxyl radical and subsequently phenol in acetonitrile solution.
3.1 Formation of hydroxyl radical from hydrogen peroxide
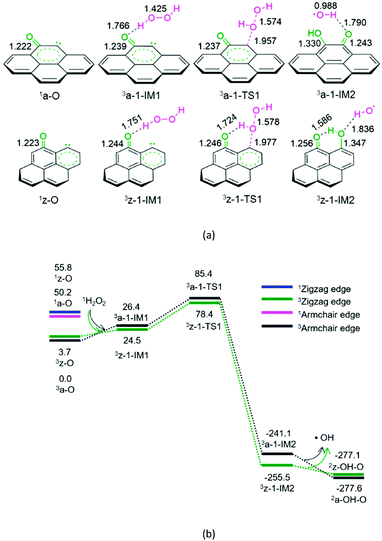
As shown in Fig. 1, for the defect armchair model of carbon, a-O, the singlet state 1a-O is located 50.2 kJ mol−1 above the ground triplet state 3a-O. Then, for P1-a, the minimal energy reaction pathway (MERP) should start at the ground triplet state. At the beginning, H2O2 interacts with 3a-O through H-bonding, forming a molecular complex 3a-1-IM1. Next, the O–O bond homolytic cleavage of the H2O2 moiety takes place via a linear three-membered transition state 3a-1-TS1, resulting in a ˙OH-containing molecular complex 3a-1-IM2. Finally, 3a-1-IM2 sets the ˙OH radical free, leaving behind the o-semiquinone 2a-OH–O. The reaction pathway P1-a possesses the EHHP of 85.4 kJ mol−1 at 3a-1-TS1.
As depicted in Fig. 1, for the defect zigzag model of carbon, z-O, the singlet state 1z-O lies 52.1 kJ mol−1 above the ground triplet state 3z-O. Therefore, for P1-z, the MERP should begin at the ground triplet state. Initially, H2O2 interacts with 3z-O through H-bonding, generating a molecular complex 3z-1-IM1. Then, the O–O bond homolytic cleavage of H2O2 moiety occurs via a linear three-membered transition state 3z-1-TS1 with an intramolecular H-bonding, leading to a ˙OH-containing molecular complex 3z-1-IM2. Finally, 3z-1-IM3 liberates the ˙OH radical, leaving behind the m-semiquinone 2z-OH–O. The reaction pathway P1-z comprises an EHHP of 78.4 kJ mol−1 at 3z-1-TS1.
Upon comparing with the reaction pathways P-S2, Pa-S3, Pa-S4, and P1-a in the absence of catalyst, it could be noted that the reaction pathways P1-a and P1-z over the armchair and zigzag defect carbon models are kinetically more preferable because of their lower EHHP (85.4 and 78.4 vs. 225.0, 276.4, and 231.5 kJ mol−1, respectively). This indicates that both the armchair and zigzag defect carbon models should exhibit superior catalytic performance toward the H2O2 decomposition. Moreover, compared with P1-a, P1-z is kinetically more favourable because of its lower EHHP (78.4 vs. 85.4 kJ mol−1). This can be attributed to the fact that there is one intramolecular H-bonding in 3z-1-TS1 and not in 3a-1-TS1.
3.2 Formation of phenol from benzene and hydroxyl radical
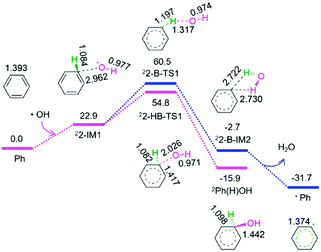
As shown in Fig. 2, from benzene and the above released hydroxyl radical, there are two reaction pathways, i.e., formation of hydroxybenzene radical and benzene radical denoted as P2-HB and P2-B, respectively. For P2-HB, the hydroxyl radical initially interacts with benzene, generating a molecular complex 22-IM1. Next, the C–O bond forms via a linear two-membered 22-HB-TS1, resulting in hydroxybenzene radical (Ph(H)OH). The P2-HB involves an EHHP of 54.8 kJ mol−1 at 22-HB-TS1. Alternatively, for P2-B, from 22-IM1, the C–H bond cleavage occurs via a quasilinear three-membered 22-B-TS1, producing a H2O-containing molecular complex 22-B-IM2. Finally, 22-B-IM2 releases the free water molecule, leaving behind the benzene radical. The P2-B possesses an EHHP of 60.5 kJ mol−1 at 22-B-TS1.
As compared to P2-B, P2-HB is kinetically more favourable because of its lower EHHP (54.8 vs. 60.5 kJ mol−1). This indicates that the hydroxybenzene radical should be more feasibly generated than benzene radical in the reaction of hydroxyl radical with benzene.
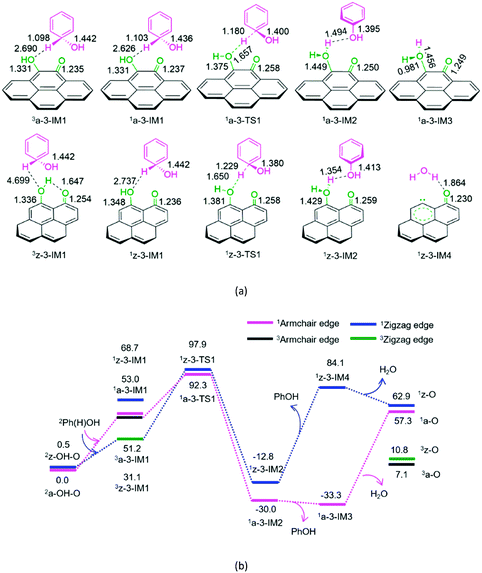
The geometric structures and the schematic energy diagrams for the hydroxybenzene radical attacking the oxygen atom of hydroxyl and carbonyl groups on the armchair and zigzag semiquinones of carbon in acetonitrile solution are shown in Fig. 3 and 4 and denoted as P3-a, P3-z, P4-a, and P4-z.
As depicted in Fig. 3, for P3-a and P3-z, at the beginning, the Ph(H)OH radical interacts with the oxygen atom of hydroxyl group in semiquinone 2a-OH-O or 2z-OH-O, forming a molecular complex 3a-3-IM1 or 3z-3-IM1, respectively. Next, C–H bond cleavage takes place via a rectangular five-membered 1a-3-TS1 or 1z-3-TS1, producing a phenol- and H2O-containing molecular complex 1a-3-IM2 or 1z-3-IM2, respectively. Then, 1a-3-IM2 or 1z-3-IM2 liberates the free phenol and H2O molecules, regenerating the defect armchair 1a-O or 1z-O, respectively. Finally, the singlet–triplet spin-crossing should take place via the minimum energy crossing point (MECP) between 1a-O and 3a-O or between 1z-O and 3z-O, regenerating the defect armchair 3a-O or zigzag 3z-O, respectively. The reaction pathways, P3-a and P3-z, possess EHHPs of 92.3 and 97.9 kJ mol−1 at 1a-3-TS1 or 1z-3-TS1 for the C–H bond cleavage, respectively.
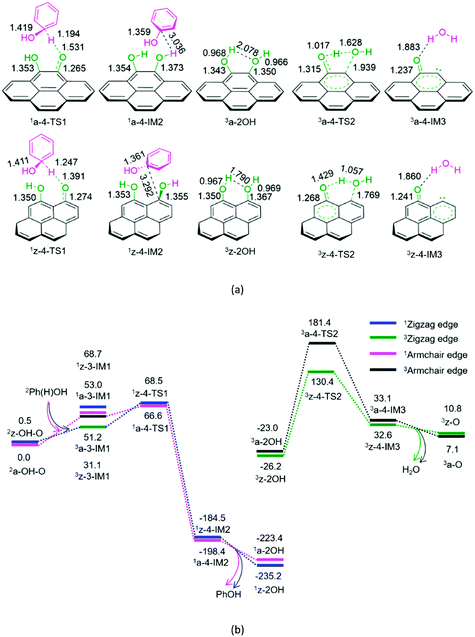
As shown in Fig. 4, for P4-a and P4-z, as mentioned earlier, the Ph(H)OH radical initially interacts with the oxygen atom of the carbonyl group in semiquinone 2a-OH–O or 2z-OH–O, generating a molecular complex 3a-3-IM1 or 3z-3-IM1, respectively. Next, the C–H bond cleavage occurs via a rectangular five-membered 1a-4-TS1 or 1z-4-TS1, producing a phenol-containing molecular complex 1a-4-IM2 or 1z-4-IM2, respectively. Following this, the molecular complex 1a-4-IM2 or 1z-4-IM2 releases the free phenol molecule, setting aside the armchair 1a-2OH or zigzag 1z-2OH, respectively. Then, the singlet–triplet spin-crossing should occur via MECP between 1a-2OH and 3a-2OH or between 1z-2OH and 3z-2OH. Subsequently, from 3a-2OH or 3z-2OH, a [1,4]-H shift or a [1,5]-H shift takes place via a five-membered ring 3a-4-TS2 or via a six-membered ring 3z-4-TS2, forming a H2O-containing molecular complex 3a-4-IM3 or 3z-4-IM3, respectively. Finally, the complex 3a-4-IM3 or 3z-4-IM3 set the H2O molecule free, recovering the defect armchair 3a-O or zigzag 3z-O, respectively. The reaction pathways P4-a and P4-z possess EHHPs of 181.4 and 130.4 kJ mol−1 at 1a-4-TS2 and 1z-4-TS2 for the C–O and O–H bond cleavages, respectively.
Compared with P4-a and P4-z, P3-a and P3-z are kinetically more favourable, because of their lower EHHP (92.3 and 97.9 vs. 181.4 and 130.4 kJ mol−1, respectively). This indicates that the intermolecular H-shift for the H2O formation both in 1a-3-TS1 and 1z-3-TS1 is kinetically favourable than the intramolecular H-shift for the H2O formation both in 3a-4-TS2 and 3z-4-TS2, respectively. In other words, for the regeneration of the carbon catalyst, the intermolecular dehydration is superior to the intramolecular dehydration. This phenomena is similar to that reported for the dehydration of fructose.46
3.3 Branched reactions
As mentioned earlier, the hydroxyl radical can be easily formed from H2O2 on the defect active sites 3a-O or 3z-O. As shown in Fig. 5, once the hydroxyl radical is produced, it could trigger the interconversion from hydroquinone to semiquinone and to quinone of carbon.
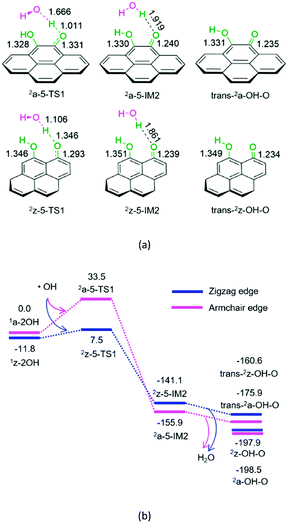
For P5-a or P5-z, from hydroquinone to semiquinone oxidized by hydroxyl radical, the hydroxyl radical initially interacts with hydroquinone on the armchair or zigzag carbon. Next, the O–H bond cleavage occurs via a linear-like three-membered 2a-5-TS1 or 2z-5-TS1, resulting in a H2O-containing molecular complex, 2a-5-IM2 or 2z-5-IM2, respectively. Finally, 2a-5-IM2 or 2z-5-IM2 releases the free water molecule, leaving behind the semiquinone 2a-OH-O or 2z-OH-O. The reaction pathway P5-a or P5-z includes an EHHP of 33.5 or 7.5 kJ mol−1 at 2a-5-TS1 or 2z-5-TS1, respectively. Such a low EHHP oxidizes hydroquinone readily to semiquinone via hydroxyl radical.
In short, once hydroquinone is generated, it could be readily oxidized to semiquinone and consume the hydroxyl radical.
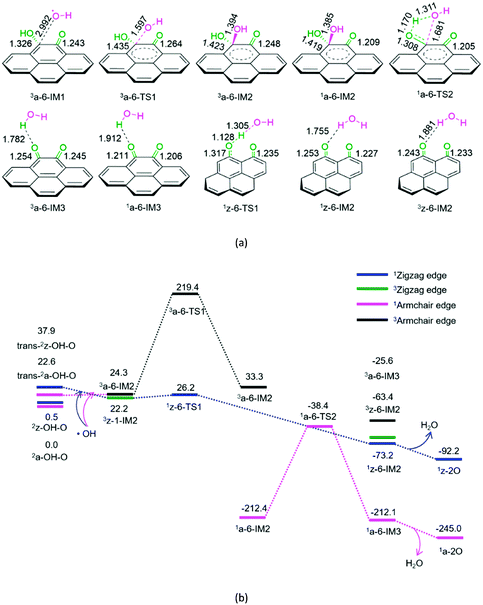
As shown in Fig. 6, for P6-a, initially, hydroxyl radical attacks the carbon atom of the –COH group on semiquinone, forming a molecular complex 3a-6-IM1. Next, C–O bond formation takes place via a three-membered ring 3a-6-TS1, leading to a dihydroxyl-containing complex 3a-6-IM2. Next, the triplet–singlet spin-crossing could occur via MECP between 3a-6-IM2 and 1a-6-IM2, resulting in the ground-state 1a-6-IM2. Subsequently, a [1,3]-H shift takes place via a four-membered cyclic 1a-6-TS2, generating a H2O-containing molecular complex 1a-6-IM3. Finally, 1a-6-IM3 sets the H2O molecule free, leaving behind quinone 1a-2O. The reaction pathway P6-a possesses the EHHP of 219.4 kJ mol−1 at 3a-6-TS1 and the HEB of 195.1 kJ mol−1 at the reaction step of 3a-6-IM1 → 3a-6-TS1.
As shown in Fig. 6, for P6-z, from semiquinone to quinone oxidized by hydroxyl, the reaction pathway is similar to that for P5-z from hydroquinone to semiquinone oxidized by hydroxyl. The reaction pathway P6-z involves an EHHP of 26.2 kJ mol−1 at 1z-6-TS1 and a HEB of only 4.0 kJ mol−1 at the reaction step of 3z-1-IM2 → 3z-6-TS1.
Compared to P6-a, P6-z is kinetically more favourable, because of its lower EHHP (26.2 vs. 219.4 kJ mol−1) and HEB (4.0 vs. 195.1 kJ mol−1). This indicates that the armchair semiquinone should be more easily oxidized to quinone than the zigzag semiquinone by consuming the hydroxyl radical.
It is evident that once the semiquinone is formed, it could react with hydroxyl radical or hydroxybenzene radical. Thus, these reactions are competitive. Herein, we list the EHHPs for the reactions of semiquinone or quinone with hydroxyl and/or hydroxybenzene radicals in Table 1.
| EHHP | P3 | P4 | P6 | P7 |
|---|---|---|---|---|
| Armchair | 92.3 | 181.4 | 219.4 | 72.4 |
| Zigzag | 97.9 | 130.4 | 26.2 | 162.2 |
As shown in Table 1, for the armchair semiquinone, the EHHP of P3-a is the lowest among the three reaction pathways of semiquinone with hydroxyl or hydroxybenzene radical (P3-a, P4-a, and P6-a). This indicates that the armchair semiquinone would rather react with the hydroxybenzene radical and then regenerate the active defect of AC than react with hydroxyl radical and then be oxidized to quinone. The armchair configuration defect was successfully identified experimentally.6 Besides, we would discuss the reaction pathway P7, vide infra.
In addition, as shown in Table 1, for the zigzag semiquinone, the EHHP of P6-z is the lowest among the three reaction pathways of semiquinone with hydroxyl or hydroxybenzene radical (P3-z, P4-z, and P6-z). This indicates that the zigzag semiquinone prefers to react with the hydroxyl radical and then be oxidized to quinone. Once the zigzag semiquinone is formed, it could be also easily oxidized to quinone and then consume the hydroxyl radical.
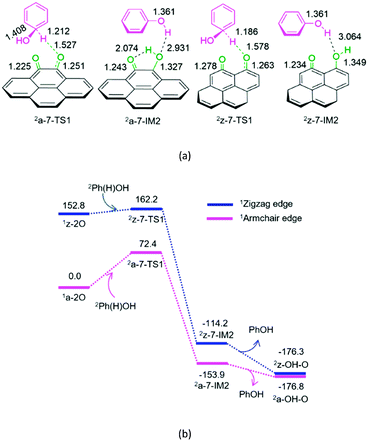
As shown in Fig. 7, for P7-a and P7-z, at the beginning, the Ph(H)OH radical attacks the oxygen atom of carbonyl in quinone 2a-2O or 2z-2O, respectively. Then, the C–H bond cleavage occurs via a linear three-membered 2a-7-TS1 or 2z-7-TS1, leading to a phenol-containing molecular complex 2a-7-IM2 or 2z-7-IM2, respectively. Subsequently, the molecular complex 2a-7- IM2 or 2z-7-IM2 liberates the free phenol molecule, leaving behind the armchair 2a-OH–O or zigzag 2z-OH–O, respectively. The reaction pathway P7-a or P7-z possesses an EHHP of 72.4 or 162.2 kJ mol−1 at 2a-7-TS1 or 2z-7-TS1 with a HEB of 72.4 or 9.4 kJ mol−1, respectively.
As mentioned earlier, once the hydroxybenzene radical is formed, it could react with the semiquinone or quinone. Furthermore, the two reactions are competitive. As shown in Table 1, the EHHPs and HEB for the armchair and zigzag quinones on carbon, which reacted with hydroxybenzene (P7), are markedly lower than those for the armchair and zigzag semiquinones (P3 and P4), respectively. This indicates that the hydroxybenzene radical should consume quinone more easily than semiquinone. Therefore, once the quinone is formed, it could easily react with the hydroxybenzene radical and then be reduced to semiquinone, yielding phenol.
3.4 Comparison of four main reaction pathways over carbon
Based on the above results, on the defect armchair 3a-O, there are two catalytic cycles for the entire reaction of benzene + H2O2 → phenol + H2O. One is composed of P1-a, P2-HB, and P3-a, and another is composed of P1-a, P2-HB, and P4-a and denoted as CA-1 and CA-2, respectively. Through TOF analysis using the energetic span model, for CA-1, the TDI and TDTS are 1a-3-IM3 and 3a-1-TS1 for the hydroxyl radical formation, respectively. Furthermore, for CA-2, the TDI and TDTS are 1a-2OH and 3a-4-TS2 for the regeneration of defect active sites, respectively. Herein, the rate constant kCA-1 of 3a-O + 1H2O2 → 3a-1-TS1 and the rate constant kCA-2 of 1a-2OH → 3a-4-TS2 are representative of the total reaction constant. Over the 313–353 K temperature range, the rate constants kCA-1 (in s−1 mol−1 dm3) and kCA-2 (in s−1) can be fitted by the following expressions:kCA-1 = 6.528 × 105![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−35 exp(−35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 994/RT) 994/RT) | (iii) |
kCA-2 = 6.927 × 1013![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−410 exp(−410![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 362/RT) 362/RT) | (iv) |
It is evident that the activation Gibbs free energies in kCA-2 are about 10 times higher than that in kCA-1, over the 313–353 K temperature range. It emphasizes that the catalytic cycle CA-1 is kinetically more favourable than CA-2. In other words, once the armchair hydroquinone is formed, it would not be beneficial for further reaction for the recovery of active defects.
In addition, on the zigzag defect 3z-O, there are two catalytic cycles. One comprises P1-z, P2-HB, and P3-z, and another comprises P1-z, P2-HB, and P4-z and denoted as CZ-1 and CZ-2, respectively. By TOF analysis using an energetic span model, for CZ-1, the TDI and TDTS are 1z-3-IM2 and 3z-1-TS1 for the hydroxyl radical formation, respectively. Moreover, for CZ-2, the TDI and TDTS are 1z-2OH and 3z-4-TS2 for the regeneration of defect active site, respectively. Therefore, the rate constant kCZ-1 of 3z-O + 1H2O2 → 3z-1-TS1 and the rate constant kCZ-2 of 1z-2OH → 3z-4-TS2 are characteristic of the total reaction constant. Over the 313–353 K temperature range, the rate constants kCZ-1 (in s−1 mol−1 dm3) and kCZ-2 (in s−1) can be adapted by the following expressions:
kCZ-1 = 1.603 × 105![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−23 exp(−23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 984/RT) 984/RT) | (v) |
kCZ-2 = 2.594 × 1013![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−367 exp(−367![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420/RT) 420/RT) | (vi) |
It could be noted that the activation Gibbs free energies in kCZ-2 is about 14 times higher than that in kCZ-1, over the 313–353 K temperature range. It echoes that the catalytic cycle CZ-1 is kinetically more preferable than CZ-2. In other words, once the zigzag hydroquinone is generated, it would be not advantageous for further reaction for the recovery of active defect.
Overall, both the zigzag and armchair defect sites show good catalytic performance. Besides, the ratio of kCZ-1/kCA-1 is calculated to be about 25–15, over the 313–353 K temperature range. This indicates that the zigzag defect 3z-O exhibits better catalytic performance than the armchair defect 3a-O.
3.5 Origin of catalytic activity difference between armchair and zigzag carbon
The results of the activation strain analysis are listed in Table 2. As shown in Table 2, the activation energy, ΔE≠, decreases from 33.9 kJ mol−1 (3a-O) to 22.9 kJ mol−1 (3z-O). The activation strain, ΔE≠strain, increases from 23.6 kJ mol−1 (3a-O) to 24.8 kJ mol−1 (3z-O). The substrate H2O2 activation-strain term, ΔE≠strain [H2O2], increases from 22.8 kJ mol−1 (3a-O) to 24.4 kJ mol−1 (3z-O), whereas the ΔE≠strain [Cat] value is so low that it could be neglected both for 3a-O and 3z-O. It is apparent that the activation strain is related to the percent extent of HO–OH bond stretching in the TS. Furthermore, the H2O2 activation strain, ΔE≠strain [H2O2], correlates nearly with the activation strain, ΔE≠strain, which increases in the same order. Moreover, the activation strain ΔE≠strain is in the reverse order as the activation energy ΔE≠. Furthermore, the stabilizing TS interaction ΔE≠int decreases from 10.4 kJ mol−1 (3a-O) to −2.0 kJ mol−1 (3z-O).
| Catalyst | TS | Length in H2O2 | Length in TS | Stretching in TS | Stretching in TS (%) | ΔE≠strain [H2O2] | ΔE≠strain [catalyst] | ΔE≠strain | ΔE≠int | ΔE≠ |
|---|---|---|---|---|---|---|---|---|---|---|
| Armchair | 3a-1-TS1 | 1.421 | 1.574 | 0.153 | 10.8 | 22.8 | 0.7 | 23.6 | 10.4 | 33.9 |
| Zigzag | 3z-1-TS1 | 1.421 | 1.578 | 0.157 | 11.0 | 24.4 | 0.4 | 24.8 | −2.0 | 22.9 |
Overall, the lower activation energy stems primarily from the strengthening of the stabilizing TS interaction by 12.4 kJ mol−1, whereas the activation strain changes by only 1.2 kJ mol−1. Therefore, the stabilizing TS interaction ΔE≠int almost correlates with the activation energy ΔE≠. This could be ascribed to the fact that there is one H-bonding in 3z-TS1 and not in 3a-TS1.
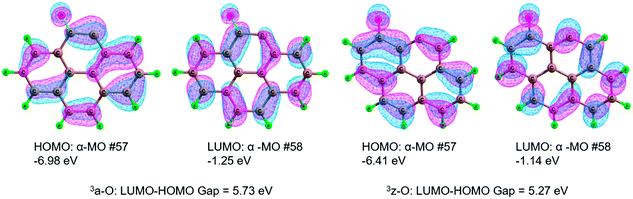 | ||
| Fig. 8 Highest occupied molecular orbital (HOMO), lowest unoccupied molecular orbital (LUMO) and the HOMO–LUMO energy gap for the defect 3a-O and 3z-O. | ||
In summary, from the MERPs for the oxidation reaction of benzene to phenol, the catalytically active site of both 3a-O and 3z-O is referred to the defect, which can play a central role of the HO–OH bond cleavage of H2O2. Furthermore, the defect 3z-O exhibits better catalytic performance than the defect 3a-O, which stems from a narrower HOMO–LUMO gap in 3z-O than in 3a-O.
4. Conclusions
The catalytic performance of the defect site on carbon for the hydroxylation of benzene to phenol in acetonitrile solution has been theoretically investigated. The following conclusions can be drawn from the present calculation.Two model catalysts of armchair and zigzag edges have been optimized to mimic carbon materials with the defect site. For both the armchair and zigzag carbons, neither hydroquinone nor semiquinone exhibits any catalytic performance toward the decomposition of H2O2. The active defect plays an essential role in the hydroxyl radical formation from H2O2, which is the rate-determining step for the benzene hydroxylation to phenol in the presence of H2O2.
Both the zigzag and armchair defect sites should show excellent catalytic performance. Furthermore, the zigzag defect on carbon exhibits better catalytic performance than the armchair defect. Through activation strain analysis, there is a stronger stabilizing TS interaction in the zigzag defect carbon than that in the armchair defect carbon, which arises from a narrower HOMO–LUMO gap in 3z-O than in 3a-O. We are actively studying the larger system of carbon materials to simulate the real reaction environment, to gain deeper insight into the catalytic nature for the hydroxylation of benzene to phenol.
Author contributions
The manuscript was written through contributions of all authors. Y.-J. Lyu is responsible for the main computation, T. Qi for part of the computation, H.-Q. Yang for part of the computation, analysis, and writing, and C.-W. Hu for design and revision. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful for financial support by the National Natural Science Foundation of China (No: 21372167) and the 111 Project (B17030).References
- Y. Morimoto, S. Bunno, N. Fujieda, H. Sugimoto and S. Itoh, J. Am. Chem. Soc., 2015, 137, 5867–5870 CrossRef CAS PubMed.
- R. J. Schmidt, Appl. Catal., A, 2005, 280, 89–103 CrossRef CAS.
- G. Centi and S. Perathoner, Catal. Today, 2009, 143, 145–150 CrossRef CAS.
- S.-I. Niwa, M. Eswaramoorthy, J. Nair, A. Raj, N. Itoh, H. Shoji, T. Namba and F. Mizukami, Science, 2002, 295, 105–107 CrossRef CAS PubMed.
- L. Balducci, D. Bianchi, R. Bortolo, R. D'Aloisio, M. Ricci, R. Tassinari and R. Ungarelli, Angew. Chem., 2003, 115, 5087–5090 CrossRef.
- G.-D. Wen, S.-C. Wu, B. Li, C.-L. Dai and D.-S. Su, Angew. Chem., Int. Ed., 2015, 54, 4105–4109 CrossRef CAS PubMed.
- J.-H. Yang, G. Sun, Y.-J. Gao, H.-B. Zhao, P. Tang, J. Tan, A.-H. Lu and D. Ma, Energy Environ. Sci., 2013, 6, 793–798 CAS.
- J.-Q. Xu, H.-H. Liu, R.-G. Yang, G.-Y. Li and C.-W. Hu, Chin. J. Catal., 2012, 33, 1622–1630 CrossRef CAS.
- C.-H. Chen, J.-Q. Xu, M.-M. Jin, G.-Y. Li and C.-W. Hu, Chin. J. Chem. Phys., 2011, 24, 358–364 CrossRef CAS.
- S.-Q. Song, H.-X. Yang, R.-C. Rao, H.-D. Liu and A.-M. Zhang, Catal. Commun., 2010, 11, 783–787 CrossRef CAS.
- Y.-K. Zhong, G.-Y. Li, L.-F. Zhu, D.-Y. Tang and C.-W. Hu, Chem. J. Chin. Univ., 2007, 28, 1570–1572 CAS.
- Y.-K. Zhong, G.-Y. Li, L.-F. Zhu, Y. Yan, G. Wu and C.-W. Hu, J. Mol. Catal. A: Chem., 2007, 272, 169–173 CrossRef CAS.
- M. Jian, L.-F. Zhu, J.-Y. Wang, J. Zhang, G.-Y. Li and C.-W. Hu, J. Mol. Catal. A: Chem., 2006, 253, 1–7 CrossRef CAS.
- J. Zhang, Y. Tang, J.-Q. Xie, Z.-R. Song, L. Wang and C.-W. Hu, React. Kinet. Catal. Lett., 2005, 85, 269–276 CrossRef CAS.
- J. Zhang, Y. Tang, J.-Q. Xie, J.-Z. Li, W. Zeng and C.-W. Hu, J. Serb. Chem. Soc., 2005, 70, 1137–1146 CrossRef CAS.
- J. Zhang, Y. Tang, G.-Y. Li and C.-W. Hu, Appl. Catal., A, 2005, 278, 251–261 CrossRef CAS.
- J. Zhang, Y. Tang, Q. Luo, M. Jian and C.-W. Hu, Chin. J. Inorg. Chem., 2004, 20, 935–940 CAS.
- W. Qi, W. Liu, B.-S. Zhang, X.-M. Gu, X.-L. Guo and D.-S. Su, Angew. Chem., Int. Ed., 2013, 52, 14224–14228 CrossRef CAS PubMed.
- D. Chen, A. Holmen, Z.-J. Sui and X.-G. Zhou, Chin. J. Catal., 2014, 35, 824–841 CrossRef CAS.
- D. Deng, L. Yu, X. Pan, S. Wang, X. Chen, P. Hu, L. Sun and X. Bao, Chem. Commun., 2011, 47, 10016–10018 RSC.
- O. V. Khavryuchenko, V. D. Khavryuchenko, V. V. Lisnyak and G. H. Peslherbe, Chem. Phys. Lett., 2011, 513, 261–266 CrossRef CAS.
- W. Jiang, T. Tran, X. Song and K. Kinoshita, J. Power Sources, 2000, 85, 261–268 CrossRef CAS.
- F. Rodriguez-Reinoso, Carbon, 1998, 36, 159–175 CrossRef CAS.
- L. C. A. Oliveira, C. N. Silva, M. I. Yoshida and R. M. Lago, Carbon, 2004, 42, 2279–2284 CrossRef CAS.
- A. Georgi and F.-D. Kopinke, Appl. Catal., B, 2005, 58, 9–18 CrossRef CAS.
- V. P. Santos, M. F. R. Pereira, P. C. C. Faria and J. J. M. Orfao, J. Hazard. Mater., 2009, 162, 736–742 CrossRef CAS PubMed.
- F. Lucking, H. Koser, M. Jank and A. Ritter, Water Res., 1998, 32, 2607–2614 CrossRef CAS.
- L. B. Khalil, B. S. Girgis and T. A. Tawfik, J. Chem. Technol. Biotechnol., 2001, 76, 1132–1140 CrossRef CAS.
- A. Rey, J. A. Zazo, J. A. Casas, A. Bahamonde and J. J. Rodriguez, Appl. Catal., A, 2011, 402, 146–155 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford CT, 2010 Search PubMed.
- M. Cossi, G. Scalmani, N. Rega and V. Barone, J. Chem. Phys., 2002, 117, 43–54 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed.
- C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161 CrossRef CAS.
- C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527 CrossRef CAS.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- S. Kozuch and S. Shaik, J. Am. Chem. Soc., 2006, 128, 3355–3365 CrossRef CAS PubMed.
- S. Kozuch and S. Shaik, J. Phys. Chem. A, 2008, 112, 6032–6041 CrossRef CAS PubMed.
- A. Uhe, S. Kozuch and S. Shaik, J. Comput. Chem., 2011, 32, 978–985 CrossRef CAS PubMed.
- S. Kozuch and S. Shaik, Acc. Chem. Res., 2011, 44, 101–110 CrossRef CAS PubMed.
- C. Amatore and A. Jutand, J. Organomet. Chem., 1999, 576, 254–278 CrossRef CAS.
- S. Kozuch, ACS Catal., 2015, 5, 5242–5255 CrossRef CAS.
- L.-K. Ren, H.-Q. Yang and C.-W. Hu, Catal. Sci. Technol., 2016, 6, 3776–3787 CAS.
- B. Xiang, Y. Wang, T. Qi, H.-Q. Yang and C.-W. Hu, J. Catal., 2017, 352, 586–598 CrossRef CAS.
- F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114–128 CrossRef CAS.
- W.-J. van Zeist and F. M. Bickelhaupt, Org. Biomol. Chem., 2010, 8, 3118–3127 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Sum of electronic and thermal free energies (Gc, hartree), and relative energies (Gr, kJ mol−1) various species with respect to the ground reactants calculated at M06-2x/6-311++G(d, p) level in acetonitrile solution under atmospheric pressure and experimental temperature (1.0 atm and 343 K). The standard orientations of various species calculated at M06-2x/6-311++G(d, p) level for the catalytic hydroxylation of benzene to phenol over the carbons with armchair and zigzag defects. Arrhenius plots of calculated rate constants for the crucial reaction step for the catalytic hydroxylation of benzene to phenol over the carbons with armchair and zigzag defects. See DOI: 10.1039/c7cy01648d |
| This journal is © The Royal Society of Chemistry 2018 |