Cation-exchanged zeolites for the selective oxidation of methane to methanol†
Ambarish R.
Kulkarni
 *ab,
Zhi-Jian
Zhao
abc,
Samira
Siahrostami
ab,
Jens K.
Nørskov
ab and
Felix
Studt
*ab,
Zhi-Jian
Zhao
abc,
Samira
Siahrostami
ab,
Jens K.
Nørskov
ab and
Felix
Studt
 *de
*de
aSUNCAT Center for Interface Science and Catalysis, Department of Chemical Engineering, Stanford University, 450 Serra Mall Stanford, California 94305, USA. E-mail: ambarish@stanford.edu
bSUNCAT Center for Interface Science and Catalysis, SLAC National Accelerator Laboratory, Menlo Park, California 94025, USA
cKey Laboratory for Green Chemical Technology of Ministry of Education, School of Chemical Engineering and Technology, Tianjin University, Collaborative Innovation Center of Chemical Science and Engineering, Tianjin 300072, People's Republic of China
dInstitute of Catalysis Research and Technology, Karlsruhe Institute of Technology, Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany. E-mail: felix.studt@kit.edu
eInstitute for Chemical Technology and Polymer Chemistry, Karlsruhe Institute of Technology, Engesserstr. 18, 76131 Karlsruhe, Germany
First published on 19th October 2017
Abstract
Motivated by the increasing availability of cheap natural gas resources, considerable experimental and computational research efforts have focused on identifying selective catalysts for the direct conversion of methane to methanol. One promising class of catalysts are cation-exchanged zeolites, which have steadily increased in popularity over the past decade. In this article, we first present a broad overview of this field from a conceptual perspective, and highlight the role of theory in developing a molecular-level understanding of the reaction. Next, by performing and analyzing a large database of density functional theory (DFT) calculations for a wide range of transition metal cations, zeolite topologies and active site motifs, we present a unifying picture of the methane activation process in terms of active site stability, C–H bond activation and methanol extraction. Based on the trade-offs of active site stability and reactivity, we propose a framework for identifying new, promising active site motifs in these systems. Further, we show that the high methanol selectivity arises due to the strong binding nature of the C–H activation products. Finally, using the atomistic and mechanistic insight obtained from these analyses, we summarize the key challenges and future strategies for improving the performance of cation-exchanged zeolites for this industrially relevant conversion.
Main text
Natural gas, composed primarily of methane, is likely to remain a major player in the international energy market.1,2 The projected U.S. production alone is estimated to exceed 40 trillion cubic feet by 2040, with ∼70% of total capacity being generated from remote and distributed shale gas and tight oil plays.3 As power generation and methane reforming are large scale, capital intensive industries, flaring of natural gas is usually more economical at these remote locations. The development of simple processes for the upgrading of natural gas to value added chemicals is therefore highly desirable.Selective oxidation of methane to methanol is one such process that has received significant interest. Due to the high stability of the C–H bond in methane4–7 and the propensity of over-oxidation to CO2, this still remains an unresolved challenge in catalysis,8–12 despite the exploration of many material classes and process variants.6,13,14 While initially inspired by their similarity to enzymatic systems,15–17 transition metal exchanged zeolites are now being increasingly studied due to their high methanol selectivity. Various oxidants have been successfully employed, including N2O,16,18–23 H2O2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24–28 and O2,15,29–31 with utilization of O2 being the most desirable for an industrial process. Encouragingly, recent results also report the use of H2O as an oxidant.32
24–28 and O2,15,29–31 with utilization of O2 being the most desirable for an industrial process. Encouragingly, recent results also report the use of H2O as an oxidant.32
Since the early successes with Fe/ZSM-5,18,19,22,23 Cu/ZSM-516 and Cu/MOR15 catalysts, a large number of zeolites have been experimentally shown to be active for partial methane oxidation. Although zeolites exchanged with Fe,24–28 Co,33–35 Ni36 and Zn37–39 have also been considered, the majority of the work using O2 as an oxidant has focused on Cu-exchanged materials.15,16,21,29,31,40–52 Additionally, as a larger diversity of zeolite topologies, active sites and process configurations have been studied for Cu-based systems, we limit our discussions here to Cu-exchanged zeolites. Importantly, however, zeolites exchanged with other cations (e.g. Fe) have also shown promise, and we will hence discuss their similarities and differences to Cu-exchanged zeolites later on.
So far two different strategies have emerged to achieve partial oxidation of methane in copper-exchanged zeolites, a stepwise15 and continuous21,52 process. In the former, methane oxidation is carried out in three separate steps: (a) activation of the copper-exchanged zeolite using an oxidant (ideally O2), (b) reaction of the activated zeolite with CH4 to form methanol and (c) methanol extraction using water or steam. These three steps are commonly facilitated at varying temperatures and require several hours for one turnover. In contrast, a continuous process would potentially have the advantage of higher space-time-yields. The challenge here is the need to avoid over-oxidation of formed methanol, which typically limits the reaction to low conversions (0.001%52–0.1%,21 for >10% methanol selectivity), with higher conversions (>10%) leading to a significant increase in the formation of the undesired oxidized products CO and CO2.21
As indicated earlier, the majority of these processes have been reported for Cu-exchanged zeolites, where the proton or cation next to the aluminum is substituted with copper ions to form the active site. Notably, a wide range of zeolite topologies have been experimentally tested for this process. Usually, a low molar yield of methanol is reported as the active site often does not constitute the majority of the copper species in the materials investigated. Despite these limitations, it is encouraging that the performance of Cu-exchanged zeolites (using mol-methanol per mol-Cu as a metric, see Fig. 1) has steadily improved over the past decade. Fig. 1 also highlights some of the notable milestones in identification and characterization of active site motifs, improvements in zeolite syntheses and optimization of activation and extraction procedures. A more detailed timeline is available in Table S1† and in other reviews.8,10,61
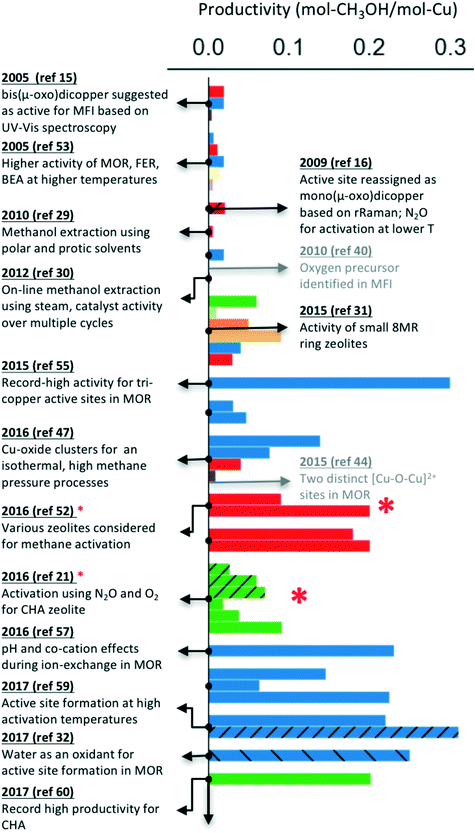 | ||
| Fig. 1 Improvements in the performance of Cu-exchanged zeolites (mol-methanol per mol-Cu) over the past decade for the stepwise process.15,16,21,29–32,40,44,47,48,52–60 The hatched bars indicate catalyst activation using N2O or H2O (instead of O2). The studies indicated by a red * also report a continuous process (multiple turnovers per active site), but only the data for the stepwise process is presented for comparison. Color schemes: MFI (red), MOR (blue), CHA (green), SAPO-34 (light green), AFX (orange), AEI (light orange), FAU (purple), EMT (brown), BEA (light purple). | ||
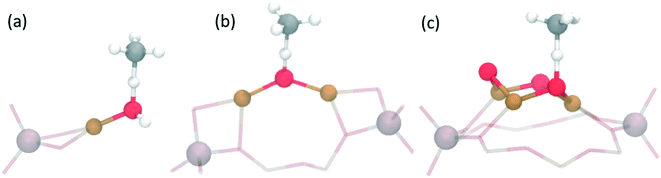
Interestingly, the exchange with copper cations can create a variety of different active site motifs after activation with O2 and/or N2O. So far, for the stepwise process, bis(μ-oxo)dicopper,15,53 mono(μ-oxo)dicopper,16 tri-copper [Cu3(μO)3]2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55–57,62 and mono-copper [Cu–OH]+
55–57,62 and mono-copper [Cu–OH]+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 63,64 species have all been observed and suggested based on spectroscopic and theoretical work in various zeolites (see Table 1, and Fig. 2). Although the bis(μ-oxo)dicopper site had been suggested originally,15,53 more recent work suggests the existence of [Cu–O–Cu]2+.16 Beyond the stoichiometrically well-defined species, dehydrated copper oxide nanoclusters (∼1 nm) have also been proposed as active species at lower activation temperatures (∼200 °C).47,49,50,65 This variety of possible active sites arises due to differences in zeolite topologies, synthesis conditions (e.g. Si/Al and Cu/Al ratios) and activation protocols (e.g. temperature, N2O vs. O2).56,62 One challenge for copper-exchange zeolites is that one usually forms a variety of different copper-species, making the identification of the active site motif difficult, while also limiting the methanol yield. It is therefore not surprising that for many systems, the exact active site composition has not yet been conclusively established.31,52 Further, to the best of our knowledge, the active site for the continuous process21,52 has not yet been confirmed.
63,64 species have all been observed and suggested based on spectroscopic and theoretical work in various zeolites (see Table 1, and Fig. 2). Although the bis(μ-oxo)dicopper site had been suggested originally,15,53 more recent work suggests the existence of [Cu–O–Cu]2+.16 Beyond the stoichiometrically well-defined species, dehydrated copper oxide nanoclusters (∼1 nm) have also been proposed as active species at lower activation temperatures (∼200 °C).47,49,50,65 This variety of possible active sites arises due to differences in zeolite topologies, synthesis conditions (e.g. Si/Al and Cu/Al ratios) and activation protocols (e.g. temperature, N2O vs. O2).56,62 One challenge for copper-exchange zeolites is that one usually forms a variety of different copper-species, making the identification of the active site motif difficult, while also limiting the methanol yield. It is therefore not surprising that for many systems, the exact active site composition has not yet been conclusively established.31,52 Further, to the best of our knowledge, the active site for the continuous process21,52 has not yet been confirmed.
Given the diversity of suggested active site motifs, it is worthwhile to investigate and compare how they facilitate the activation of methane. In this respect, density functional theory (DFT) is a useful tool as it can be used to calculate activation barriers for various combinations of transition metals and active site motifs in different zeolites. It is thus not surprising that a number of computational studies have targeted this reaction step as summarized in Table 2.
| Active site motif | Zeolite | Method | Activation barriersb (kJ mol−1) | Ref. |
|---|---|---|---|---|
| a Enthalpic barriers for [Cu–O–Cu]2+/MFI (66 kJ mol−1)16 and [Cu–O–Cu]2+/MOR (61 kJ mol−1, 46 kJ mol−1)44 have been measured experimentally and the active site has also been characterized, simultaneously. Other studies21,52 where the activation barriers are measured, but the active site is not known have not been included. b Only enthalpic energy barriers. c Less stable [Cu–O–Cu]2+ located in the double 5MR of the straight channel. d Surface stabilized pathway. e Different cluster sizes of MFI. f Various locations of the active site motif. g Different active oxygen atoms of the representative copper-oxide cluster model. h Hydroxylated version of the tri-copper [Cu3(μO)3]2+ site. | ||||
| [Cu–O–Cu]2+ | MFI | Cluster/B3LYP | 78 | 16 |
| MFI | PBE | 93, 68c | 62 | |
| MFI | PBE | 43, 82d | 66 | |
| MFI | Cluster/B3LYP | 94–126e | 67 | |
| MFI | PBE | 68 | 68 | |
| PBE-D2 | 71 | |||
| MOR | BEEF-vdW | 68, 32–93f | 69 | |
| CHA | PBE | 50 | 68 | |
| PBE-D2 | 48 | |||
| AEI | PBE | 45 | 68 | |
| PBE-D2 | 39 | |||
| AFX | PBE | 53 | 68 | |
| PBE-D2 | 49 | |||
| [Cu3(μO)3]2+ | MFI | PBE | 63 | 62 |
| MOR | PBE | 74 | 55 | |
| MOR | BEEF-vdW | 17–32g | 70 | |
| [Cu–OH]+ | CHA | BEEF-vdW | 76 | 64 |
| [Cu6O7]2+ | MOR | BEEF-vdW | 70–95g | 70 |
| [Cu–O]+ | MFI | PBE | 27 | 71 |
| CHA | BEEF-vdW | 18 | 64 | |
| [Cu3(μOH)2(μO)]2+ | MFI | PBE | 71h | 62 |
| [HO–Cu–O–Cu–OH]2+ | MFI | Cluster/B3LYP | 44 | 67 |
| [HO–Cu–OH–CuO]2+ | MFI | Cluster/B3LYP | 33 | 67 |
Methane activation barriers are calculated to range from ∼27–126 kJ mol−1 over the large variety of proposed active site motifs. Interestingly, the transition state geometries for C–H bond activation for a range of different active site motifs in zeolites are found to be almost identical, with the active oxygen abstracting a hydrogen from methane (via homolytic cleavage) leading to a methyl radical located and weakly bound to the hydrogen as shown schematically in Fig. 2 (see also Fig. 4 below). The similarities in activation barrier energies thus do not seem surprising.
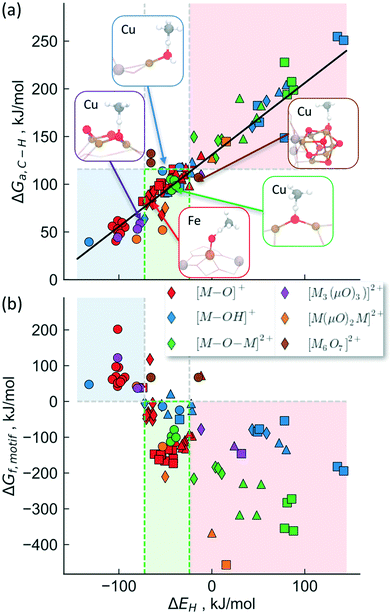
To provide a unified picture of the methane activation in cation exchanged zeolites, we performed DFT calculations (GGA level, BEEF-vdW functional,72 see methods for details) in order to compare various C–H bond activation steps. While we limit our analysis to calculations on the GGA level, which have been shown to yield similar results as hybrid functionals,69 we note that cluster calculations may be necessary to accurately describe the electronic structure of complex motifs in some cases.73,74 We expect, however, that the error induced through the GGA-approximation will not change the trends that we are interested in qualitatively. Specifically, this analysis includes [M–O]1+,2+, [M–OH]1+,2+, [M–O–M]2+, [M(μO)2M]2+ and [M3(μO)3]2+, [Cu6O7]2+ motifs, transition metal cations: Fe, Co, Ni and Cu, zeolite topologies: AEI, AFX, CHA, MAZ, MOR, MFI, TON, FAU as well as binding sites in 6-, 8-, 10- and 12-membered rings. Depending on the specific system being considered, we find that the calculated activation free energy varies considerably between 40 kJ mol−1 (for [Cu–OH]2+/CHA) and 255 kJ mol−1 ([Fe–OH]+/CHA).
We will now examine in detail the various factors that affect C–H bond activation energies. Here we focus on the effect of (i) the transition metal cation, (ii) the zeolite topology and (iii) the active site motif. A closer examination of Fig. 3a indicates that the choice of metal cation has a dramatic effect on ΔGa. For a given motif, going from left to right in the periodic table (from Fe to Cu) typically decreases ΔGa. For instance, for the [M–O–M]2+ motif (averaged across CHA, FAU, MOR, MFI topologies, see Fig. 3a), ΔGa decreases by 107 kJ mol−1 going from Fe > Co > Ni > Cu. Analogous trends for the other motifs are presented in Fig. S1,† indicating that Cu-motifs are the most active towards methane. Similar trends have been reported recently for the [M–O–M]2+ active sites in MFI using cluster calculations.66
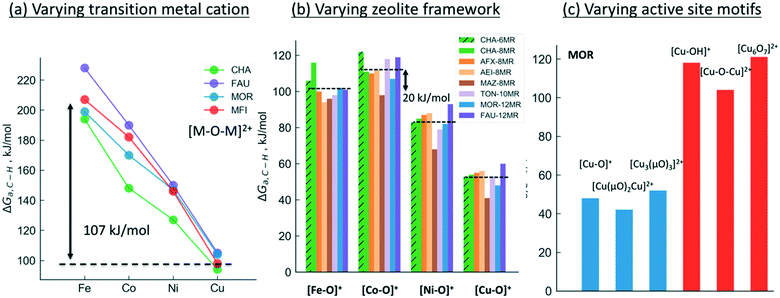 | ||
| Fig. 3 Effect of (a) transition metal cation, (b) zeolite framework and (c) active site motif on the calculated C–H bond activation energy. The lower activation barriers of [Fe–O]+ compared to [Co–O]+ in Fig. 3b is due to the differences in high-spin vs. low-spin configurations as discussed in Table S2 and Fig. S2.† | ||
Next, we analyze the effect of topology and binding site for a fixed transition metal and active site motif. For the single-cation species such as [M–O]+, the zeolite framework and cation location has a smaller effect on the calculated activation barriers (order of ∼23 kJ mol−1, standard deviation ∼7 kJ mol−1) than the choice of cation (see Fig. 3b). For more complex motifs such as [M–O–M]2+ the effect of topology is more noticeable as the Al positions and the binding site of the cations affect the ∠M–O–M angle, which in turn changes ΔGa (Fig. 3a and Table S3,† CHA vs. rest). Similar confinement and cation locations effects have been discussed recently.44,68,69,75
Given that various motifs can be formed under different activation conditions for the same zeolite, we also explore the activity of different motifs within a given framework. As both di-copper15,16 and tri-copper55 species have been previously suggested for MOR, we choose the MOR framework to compare the different motifs as shown in Fig. 3c. In agreement with calculations for MFI,62 we predict [Cu3(μO)3]2+ to be more active than [Cu–O–Cu]2+. More importantly, the active site motifs can be classified into two groups based on their reactivity towards methane. For a given number of cations, the motifs with higher reactivity (blue, Fig. 3c and Table S4†) tend to have a less negative charge on the active oxygen (qbader = −0.4e − −0.8e) than the less active motifs (red, qbader = −0.8e − −1.4e). Moreover, as shown in Fig. S3† for the [M–O]+ motif, qbader also correlates the activity for different cations, reinforcing the idea that charge depletion leads to a more active oxygen.76 This observations are consistent with the higher reactivity of the oxygen radical anions, [O˙]−.73,77 Similar results for Ni-based motifs are shown in Fig. S4.†
The activity trends discussed above arise due to the similarity of the transition states for C–H bond breaking step. As the transition state structure usually consists of a methyl radical located and weakly bound to the hydrogen, it is likely that the transition state energy will correlate with the strength with which oxygen binds to hydrogen. In fact, this hydrogen affinity (or bond strength) has been identified recently to be a good descriptor for the magnitude of the activation barrier, with a stronger O–H bond leading to a smaller activation barrier.70,76,78Fig. 4a shows the calculated transition state free energies (T = 423 K) as a function of the hydrogen affinity (ΔEH) for the various transition metals cations, active site motifs, zeolite topologies and cation binding sites considered in this study. As discussed in the Methods section, the zero-point energies and entropy corrections were calculated separately for different motifs and are summarized in Tables S5 and S7.
The proposed active site motifs for copper-exchanged zeolites16,55,64 are shown as insets and are all found to exhibit free energy barriers of <110 kJ mol−1. For a zeolite to have sufficient activity for methane oxidation, we estimate an upper bound of ∼115 kJ mol−1 for the reaction free barrier (red shaded area in Fig. 4). This value is chosen as it represents a turnover frequency (TOF) of 0.5 s−1 which corresponds to an almost complete reaction in <1 min for the methane activation step (see ESI† for details). We note, however, that the less reactive motifs may still show experimentally measurable activity at higher reaction temperatures and/or at longer reaction times.
While the excellent correlation between ΔGa and ΔEH highlights the general applicability of ΔEH as a descriptor to examine the activity of an active site motif,70 another consideration focuses on their relative stabilities as one governing factor determining the distribution and availability of active sites. Although a few spectroscopic studies have studied the activation step,40,42,63 a molecular understanding of the formation mechanism of the different active site motifs is still in its infancy. Assuming that long activation times will lead to a Boltzmann distribution of various species, one can simplify the analysis using thermodynamic arguments for the estimation of the fraction of cations in different active site motifs.64,69,79 Choosing an ideal reference state (e.g. bare cation in zeolite, bulk metal oxide or bulk metal) for the various different materials present in the data presented in Fig. 4 is complicated by the variety of motif stoichiometries and range of cations considered.55,62,69 Here, the bare cation in the reduced form (e.g. M+ for [MIIOH]+) is chosen as the reference.64,69 We justify this choice as it mimics the experimental activation process, thus enabling comparison of relative stabilities for different cations for a given structural motif. We note that alternative approaches have used transition metal oxides as the reference, which allow for comparison of different motifs for a given transition metal.55,62
Fig. 4b shows the stability calculated using the approach outlined above for the classes of investigated active site motifs (ΔGf, formation energies calculated at 723 K) as a function of ΔEH. Importantly, this is the same descriptor used to correlate the transition state energy of methane activation (ΔGa, see Fig. 3a). We observe that ΔGf becomes less negative with decreasing ΔEH, essentially stating that as the active site motifs become more active (by binding e.g. H stronger or equivalently smaller activation barrier, ΔGa) they also become less stable. While the overall correlation in Fig. 4b is rather rough, we note that the trend within a given motif family is much more pronounced (e.g. an excellent correlation is observed for [M–O–M]2+ for different cations, see Fig. S5†). These differences in the quality of the correlation arise mainly due to the different reference states used for different motifs (see ESI† for a more detailed discussion). We note that while the choice of the reference state is somewhat arbitrary, the general conclusion that stability and activity are inversely correlated seems to hold over all materials considered herein.
Considering the inverse correlation between formation energy of the motif and its reactivity towards methane, it becomes obvious that the choice of an ideal active site motif presents a trade-off between high activity (through a low methane activation barrier) and high stability (through a thermodynamically favorable formation of the active site motif). Our analysis suggests an optimal window (the green shaded area in Fig. 4) as having active site motifs to be both sufficiently stable and active. We note that our analysis identifies all known Cu-active site motifs within (or close to) this favorable region. In addition to known Cu species, this analysis also captures the recently characterized [Fe–O]2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 and suggests [M–O]+ (M = Ni, Co, Fe), [M–OH]2+ (M = Co, Fe), [Cu(μO)2Ni]2+ and [Ni(μO)2Ni]2+ as promising active site motifs in various zeolites. The descriptor (ΔEH) based analysis used in Fig. 4 thus provides a set of necessary (but not sufficient) characteristics that a transition-metal exchanged zeolite catalyst must obey to be suitable for methane activation in the stepwise process.
20 and suggests [M–O]+ (M = Ni, Co, Fe), [M–OH]2+ (M = Co, Fe), [Cu(μO)2Ni]2+ and [Ni(μO)2Ni]2+ as promising active site motifs in various zeolites. The descriptor (ΔEH) based analysis used in Fig. 4 thus provides a set of necessary (but not sufficient) characteristics that a transition-metal exchanged zeolite catalyst must obey to be suitable for methane activation in the stepwise process.
We will now briefly discuss the limitations that make the above analysis necessary but not sufficient. Our thermodynamic analysis is based only on the stability of individual motifs. Since a variety of different active site motifs can in principle be simultaneously formed after activation, it is possible that formation of active site motifs is driven by kinetics rather than thermodynamics.64 The distribution of various species will hence also depend on the synthesis conditions (secondary building units of the zeolite, Si/Al ratio, cation/Al ratio, Al location, temperature etc.). A detailed analysis of the kinetics of active site formation is thus desirable for future studies.56,57,64
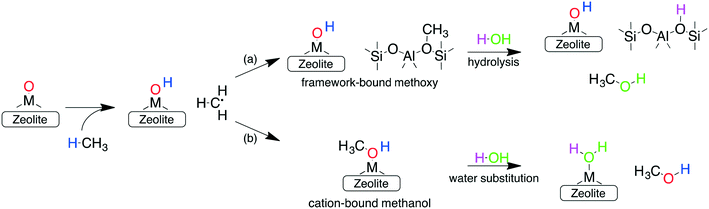
In addition to forming a large number of stable and active species, the other requirements for an ideal catalyst is its ability to selectively oxidize methane to methanol, while preventing over-oxidation. One reason for the sustained interest in cation-exchanged zeolites is their high methanol selectivity when employing the stepwise process. In such a configuration, the active sites formed during the activation step (step 1) react with methane (during step 2) to form either (a) framework chemisorbed methoxy species62 or (b) adsorbed methanol (via an oxygen rebound mechanism).69 Once formed, both these species are very strongly bound to the framework or the cation and cannot react further (see below), thus preventing their over-oxidation. Subsequent extraction with water or steam (step 3) is then required to obtain the final product. This delineation of the methane oxidation step (step 1) with the methanol extraction step (step 3) is responsible for the high selectivity of cation-exchanged zeolites.
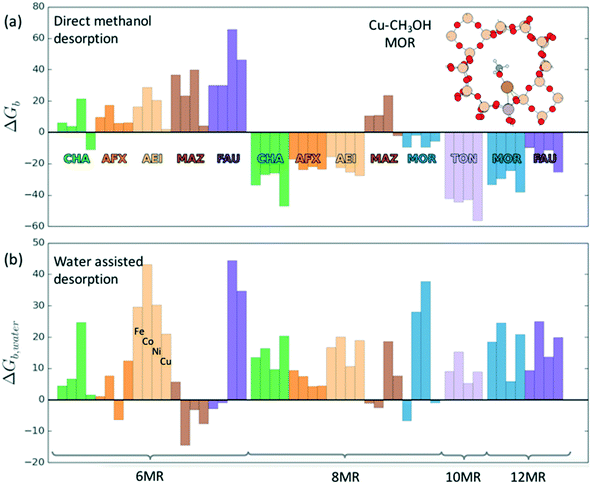
Investigations of the extraction of methanol from the catalytic system reveal two distinct pathways as shown in Scheme 1. In the methoxy route (path (a)), the addition of water hydrolyses the Brønsted methoxy group to form methanol. This pathway also explains the formation of acetic acid (via a formyl intermediate) when a mixture CO + H2O is fed after methane activation.80 The transition states for the hydrolysis of methoxy species are presented in Fig. S6† (using SSZ-13 as an example) and have also been discussed in the literature recently.81 The second pathway involves the direct addition of the methyl radical to form adsorbed methanol (path (b)), where the addition of water drives the release of methanol.69 Interestingly, methanol itself has been observed to bind rather strongly to the metal of the active site (e.g. binding energy of ∼100 kJ mol−1 on Cu-exchanged/SSZ-13).55,62,64,69 Further insight into the nature of this interaction is presented in Fig. 5 where calculations for a range of methanol adsorption energies using the [M–O]+ active site motif as an example are shown. Binding energies of methanol (ΔHb) are calculated to range from ⋍50 kJ mol−1 to ⋍150 kJ mol−1 (see Table S8† for other motifs). The binding energy depends on the choice of transition metal and the cation location (6-, 8-, 10- or 12-MR), with the latter having the more significant contribution. A good example is SSZ-13 (CHA), where the weaker binding of methanol in the 6MR can be explained by the higher stability of the bare transition metal cations in the smaller zeolite ring.64Fig. 5a shows the adsorption free energies (ΔGb, see ESI† for details) of methanol at 523 K, indicating that spontaneous desorption of methanol is unfavorable for most active site motifs (with the exception of 6MR binding sites).69 When the system is exposed to water, however, an interchange of methanol with water is possible. Here, DFT calculations predict spontaneous methanol desorption for all binding sites considered herein (Fig. 5b). As both methanol and water bind to the active site through the oxygen atom, the methanol binding energies scale with those of water with their binding energy being almost similar (Fig. S7†). This indicates that a small partial pressure of water should in principle be sufficient to remove the adsorbed methanol for most catalytic systems.
Outlook and perspectives
We will briefly summarize and address the continuous process for methane activation before discussing the stepwise process. A continuous process will involve simultaneous active site formation, methane activation and methanol desorption. The selectivity towards methanol is thus limited by the relative rates of methane and methanol oxidation on the same active site. Since the activation energy for the hydrogen abstraction from methane and methanol are correlated with a difference in the activation energies of ∼50 kJ mol−1 for all materials exhibiting a radical-like transition state, over-oxidation will always be problematic (see ESI†).70 A simple kinetic analysis reveals that at 423 K, a 106 times higher partial pressure of methane is required to achieve comparable reaction rates between hydrogen abstraction from methane and methanol, effectively setting an upper bound on methane conversion of ∼0.01%, in good agreement with the highest conversions observed experimentally.21 A continuous process for methane partial oxidation will hence be limited by ultra-low conversions unless confinement or steric effects on the transition state of methane vs. methanol can be exploited effectively.In contrast, the stepwise process faces completely different challenges. The main difficulty is related to improving the quantity of methanol that can be produced. Improving the space-time yields requires (a) maximizing the gravimetric (or volumetric) density of active sites and (b) reducing the overall cycle time. Taking Cu-exchanged CHA (with Si/Al = 11, Cu/Al = 1) with 1 [Cu–OH]+ species occupying the 8MR rings as an example (i.e. a hypothetical situation with no Cu+ species),64 we obtain a maximum achievable methanol yield of 0.04 g-methanol per g-catalyst (or 1250 μmol per g-catalyst) per cycle (see ESI†). Given that the typical experimentally measured number is ∼30–160 μmol per g-catalyst,31,55 this simple estimation shows that there is considerable opportunity to improve the performance of the stepwise process. However, assuming 1 h per cycle for the direct process, our theoretical estimate (0.04 g-methanol per g-catalyst per h) is almost two orders of magnitude lower than the commercial Cu/ZnO/Al2O3 methanol synthesis catalysts (1–3 g-methanol per g-catalyst per h).82 Currently, cycle times ranging from 1–12 h have been explored for the different reaction steps of the partial oxidation process.60
To summarize, we have shown a comprehensive overview of this small but emerging field of methane selective oxidation to methanol using transition-metal exchanged zeolites. Based on the insight obtained to date, key bottlenecks in improving the direct methane to methanol process are presented below.
1. Improving the active site motif: Identifying active site motifs that are both active (methane activation barrier below ∼115 kJ mol−1) and stable requires further optimization. Importantly, both quantities are inversely correlated and can be described using the same observable, the hydrogen binding energy to the oxygen of the active site. This binding energy can be obtained easily using quantum chemical calculations. A large number of active site motifs and topologies of the surrounding zeolite can be potentially screened for this purpose, keeping in mind that a variety of species can be formed simultaneously.
2. O2 activation and active site formation: In contrast to the large numbers of studies that have focused on the C–H bond activation step of the reaction, the O2 activation and active site formation process is not well understood. While thermodynamic analyses are useful in estimating the distribution of various active sites, a molecular level understanding of the kinetics is required to identify the key bottlenecks of the activation step. Detailed investigations of experimental activation protocols coupled with molecular simulations will give an insight on the atomic scale, which will allow to design materials and activation protocols that effectively reduce the duration and/or temperature of the activation step and thus improve the space-time-yield.
3. Methanol extraction: Methanol extraction is usually achieved through extensive steaming. This is undesirable for two reasons. Firstly, this process leads to a diluted methanol solution in water, requiring costly separation. In addition, the process conditions usually destroy the active site motif, that then needs to be restored using extensive oxidation at high temperatures (see also point 2). Moreover, as the temperatures for oxidation (450–550 °C), methane reaction (200 °C) and methanol extraction (135 °C) are quite different, a related challenge is to engineer the process so as to enable isothermal operation and subsequently, shorter overall cycle times.
Computational methods
Periodic DFT calculations were performed using the BEEF-vdW72 functional as implemented in the Vienna Ab initio Package (VASP) code.83 We use a plane wave cutoff of 400 eV, force convergence of 0.03 eV Å−1, and the Γ-point in k-space for all calculations. The harmonic entropy contributions for the various active site motifs, transition states, methanol and water binding were individually calculated for a range of systems (see ESI† for details). Other calculation details are similar to our previous work.70Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the support from the U.S. Department of Energy, Office of Sciences, Office of Basic Energy Sciences, to the SUNCAT Center for Interface Science and Catalysis. We also acknowledge the computing resources from Carbon High-Performance Computing Cluster at Argonne National Laboratory.References
- International Energy Outlook, 2016, http://www.eia.gov/forecasts/ieo/pdf/0484(2016).pdf.
- Natural gas-fired electricity generation expected to reach record level in 2016, https://www.eia.gov/todayinenergy/detail.cfm?id=26552.
- Most natural gas production growth is expected to come from shale gas and tight oil plays, https://www.eia.gov/todayinenergy/detail.cfm?id=26552.
- J. A. Labinger and J. E. Bercaw, Nature, 2002, 417, 507–514 CrossRef CAS PubMed.
- R. H. Crabtree, Chem. Rev., 1995, 95, 987–1007 CrossRef CAS.
- R. A. Periana, D. J. Taube, S. Gamble, H. Taube, T. Satoh and H. Fujii, Science, 1998, 280, 560–564 CrossRef CAS PubMed.
- B. Ensing, F. Buda, M. C. Gribnau and E. J. Baerends, J. Am. Chem. Soc., 2004, 126, 4355–4365 CrossRef CAS PubMed.
- A. I. Olivos-Suarez, À. Szécsényi, E. J. M. Hensen, J. Ruiz-Martinez, E. A. Pidko and J. Gascon, ACS Catal., 2016, 6, 2965–2981 CrossRef CAS.
- R. Horn and R. Schlögl, Catal. Lett., 2015, 145, 23–39 CrossRef CAS.
- B. Wang, S. Albarracín-Suazo, Y. Pagán-Torres and E. Nikolla, Catal. Today, 2017, 285, 147–158 CrossRef CAS.
- P. Schwach, X. Pan and X. Bao, Chem. Rev., 2017, 117, 8497–8520 CrossRef CAS PubMed.
- M. Ravi, M. Ranocchiari and J. A. van Bokhoven, Angew. Chem., Int. Ed., 2017 DOI:10.1002/anie.201702550.
- R. Palkovits, C. von Malotki, M. Baumgarten, K. Müllen, C. Baltes, M. Antonietti, P. Kuhn, J. Weber, A. Thomas and F. Schüth, ChemSusChem, 2010, 3, 277–282 CrossRef CAS PubMed.
- E. Peringer, M. Salzinger, M. Hutt, A. A. Lemonidou and J. A. Lercher, Top. Catal., 2009, 52, 1220–1231 CrossRef CAS.
- M. H. Groothaert, P. J. Smeets, B. F. Sels, P. A. Jacobs and R. A. Schoonheydt, J. Am. Chem. Soc., 2005, 127, 1394–1395 CrossRef CAS PubMed.
- J. S. Woertink, P. J. Smeets, M. H. Groothaert, M. A. Vance, B. F. Sels, R. A. Schoonheydt and E. I. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 18908–18913 CrossRef CAS PubMed.
- S. Kim, J. Ståhlberg, M. Sandgren, R. S. Paton and G. T. Beckham, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 149–154 CrossRef CAS PubMed.
- K. A. Dubkov, V. I. Sobolev and G. I. Panov, Kinet. Catal., 1998, 39, 72–79 CAS.
- K. A. Dubkov, N. S. Ovanesyan, A. A. Shteinman, E. V. Starokon and G. I. Panov, J. Catal., 2002, 207, 341–352 CrossRef CAS.
- B. E. R. Snyder, P. Vanelderen, M. L. Bols, S. D. Hallaert, L. H. Böttger, L. Ungur, K. Pierloot, R. A. Schoonheydt, B. F. Sels and E. I. Solomon, Nature, 2016, 536, 317–321 CrossRef CAS PubMed.
- B. Ipek and R. F. Lobo, Chem. Commun., 2016, 52, 13401–13404 RSC.
- K. A. Dubkov, V. I. Sobolev, E. P. Talsi, M. A. Rodkin, N. H. Watkins, A. A. Shteinman and G. I. Panov, J. Mol. Catal. A: Chem., 1997, 123, 155–161 CrossRef CAS.
- G. I. Panov, V. I. Sobolev, K. A. Dubkov, V. N. Parmon, N. S. Ovanesyan, A. E. Shilov and A. A. Shteinman, React. Kinet. Catal. Lett., 1997, 61, 251–258 CrossRef CAS.
- C. Hammond, M. M. Forde, M. H. Ab Rahim, A. Thetford, Q. He, R. L. Jenkins, N. Dimitratos, J. A. Lopez-Sanchez, N. F. Dummer, D. M. Murphy, A. F. Carley, S. H. Taylor, D. J. Willock, E. E. Stangland, J. Kang, H. Hagen, C. J. Kiely and G. J. Hutchings, Angew. Chem., Int. Ed., 2012, 51, 5129–5133 CrossRef CAS PubMed.
- C. Hammond, R. L. Jenkins, N. Dimitratos, J. A. Lopez-Sanchez, M. H. ab Rahim, M. M. Forde, A. Thetford, D. M. Murphy, H. Hagen, E. E. Stangland, J. M. Moulijn, S. H. Taylor, D. J. Willock and G. J. Hutchings, Chem. – Eur. J., 2012, 18, 15735–15745 CrossRef CAS PubMed.
- C. Hammond, N. Dimitratos, R. L. Jenkins, J. A. Lopez-Sanchez, S. A. Kondrat, M. Hasbi ab Rahim, M. M. Forde, A. Thetford, S. H. Taylor, H. Hagen, E. E. Stangland, J. H. Kang, J. M. Moulijn, D. J. Willock and G. J. Hutchings, ACS Catal., 2013, 3, 689–699 CrossRef CAS.
- J. Xu, R. D. Armstrong, G. Shaw, N. F. Dummer, S. J. Freakley, S. H. Taylor and G. J. Hutchings, Catal. Today, 2016, 270, 93–100 CrossRef CAS.
- G. J. Hutchings, Top. Catal., 2016, 59, 658–662 CrossRef CAS.
- N. V. Beznis, B. M. Weckhuysen and J. H. Bitter, Catal. Lett., 2010, 138, 14–22 CrossRef CAS.
- E. M. Alayon, M. Nachtegaal, M. Ranocchiari and J. A. van Bokhoven, Chem. Commun., 2012, 48, 404–406 RSC.
- M. J. Wulfers, S. Teketel, B. Ipek and R. F. Lobo, Chem. Commun., 2015, 51, 4447–4450 RSC.
- V. L. Sushkevich, D. Palagin, M. Ranocchiari and J. A. van Bokhoven, Science, 2017, 356, 523 CrossRef CAS PubMed.
- N. V. Beznis, B. M. Weckhuysen and J. H. Bitter, Catal. Lett., 2010, 136, 52–56 CrossRef CAS.
- N. V. Beznis, A. N. C. van Laak, B. M. Weckhuysen and J. H. Bitter, Microporous Mesoporous Mater., 2011, 138, 176–183 CrossRef CAS.
- Y. K. Krisnandi, B. A. P. Putra, M. Bahtiar, Zahara, I. Abdullah and R. F. Howe, Procedia Chem., 2015, 14, 508–515 CrossRef CAS.
- J. Shan, W. Huang, L. Nguyen, Y. Yu, S. Zhang, Y. Li, A. I. Frenkel and F. Tao, Langmuir, 2014, 30, 8558–8569 CrossRef CAS PubMed.
- J. Xu, A. Zheng, X. Wang, G. Qi, J. Su, J. Du, Z. Gan, J. Wu, W. Wang and F. Deng, Chem. Sci., 2012, 3, 2932–2940 RSC.
- A. Oda, H. Torigoe, A. Itadani, T. Ohkubo, T. Yumura, H. Kobayashi and Y. Kuroda, J. Phys. Chem. C, 2013, 117, 19525–19534 CAS.
- A. A. Gabrienko, S. S. Arzumanov, M. V. Luzgin, A. G. Stepanov and V. N. Parmon, J. Phys. Chem. C, 2015, 119, 24910–24918 CAS.
- P. J. Smeets, R. G. Hadt, J. S. Woertink, P. Vanelderen, R. A. Schoonheydt, B. F. Sels and E. I. Solomon, J. Am. Chem. Soc., 2010, 132, 14736–14738 CrossRef CAS PubMed.
- P. Vanelderen, R. G. Hadt, P. J. Smeets, E. I. Solomon, R. A. Schoonheydt and B. F. Sels, J. Catal., 2011, 284, 157–164 CrossRef CAS PubMed.
- P. Vanelderen, J. Vancauwenbergh, M.-L. Tsai, R. G. Hadt, E. I. Solomon, R. A. Schoonheydt and B. F. Sels, ChemPhysChem, 2014, 15, 91–99 CrossRef CAS PubMed.
- M. L. Tsai, R. G. Hadt, P. Vanelderen, B. F. Sels, R. A. Schoonheydt and E. I. Solomon, J. Am. Chem. Soc., 2014, 136, 3522–3529 CrossRef CAS PubMed.
- P. Vanelderen, B. E. R. Snyder, M.-L. Tsai, R. G. Hadt, J. Vancauwenbergh, O. Coussens, R. A. Schoonheydt, B. F. Sels and E. I. Solomon, J. Am. Chem. Soc., 2015, 137, 6383–6392 CrossRef CAS PubMed.
- E. M. C. Alayon, M. Nachtegaal, A. Bodi and J. A. van Bokhoven, ACS Catal., 2014, 4, 16–22 CrossRef CAS.
- E. M. C. Alayon, M. Nachtegaal, A. Bodi, M. Ranocchiari and J. A. van Bokhoven, Phys. Chem. Chem. Phys., 2015, 17, 7681–7693 RSC.
- P. Tomkins, A. Mansouri, S. E. Bozbag, F. Krumeich, M. B. Park, E. M. C. Alayon, M. Ranocchiari and J. A. van Bokhoven, Angew. Chem., 2016, 128, 5557–5561 CrossRef.
- S. E. Bozbag, E. M. C. Alayon, J. Pechacek, M. Nachtegaal, M. Ranocchiari and J. A. van Bokhoven, Catal. Sci. Technol., 2016, 6, 5011–5022 CAS.
- P. Tomkins, M. Ranocchiari and J. A. van Bokhoven, Acc. Chem. Res., 2017, 50, 418–425 CrossRef CAS PubMed.
- D. Palagin, A. J. Knorpp, A. B. Pinar, M. Ranocchiari and J. A. van Bokhoven, Nanoscale, 2017, 9, 1144–1153 RSC.
- B. Ipek, M. J. Wulfers, H. Kim, F. Göltl, I. Hermans, J. P. Smith, K. S. Booksh, C. M. Brown and R. F. Lobo, ACS Catal., 2017, 7, 4291–4303 CrossRef CAS.
- K. Narsimhan, K. Iyoki, K. Dinh and Y. Román-Leshkov, ACS Cent. Sci., 2016, 2, 424–429 CrossRef CAS PubMed.
- P. J. Smeets, M. H. Groothaert and R. A. Schoonheydt, Catal. Today, 2005, 110, 303–309 CrossRef CAS.
- T. Sheppard, C. D. Hamill, A. Goguet, D. W. Rooney and J. M. Thompson, Chem. Commun., 2014, 50, 11053–11055 RSC.
- S. Grundner, M. A. C. Markovits, G. Li, M. Tromp, E. A. Pidko, E. J. M. Hensen, A. Jentys, M. Sanchez-Sanchez and J. A. Lercher, Nat. Commun., 2015, 6 DOI:10.1038/ncomms8546.
- M. A. C. Markovits, A. Jentys, M. Tromp, M. Sanchez-Sanchez and J. A. Lercher, Top. Catal., 2016, 59, 1554–1563 CrossRef CAS.
- S. Grundner, W. Luo, M. Sanchez-Sanchez and J. A. Lercher, Chem. Commun., 2016, 52, 2553–2556 RSC.
- H. V. Le, S. Parishan, A. Sagaltchik, C. Göbel, C. Schlesiger, W. Malzer, A. Trunschke, R. Schomäcker and A. Thomas, ACS Catal., 2017, 7, 1403–1412 CrossRef CAS.
- Y. Kim, T. Y. Kim, H. Lee and J. Yi, Chem. Commun., 2017, 53, 4116–4119 RSC.
- D. K. Pappas, E. Borfecchia, M. Dyballa, I. Pankin, K. A. Lomachenko, A. Martini, M. Signorile, S. Teketel, B. Arstad and G. Berlier, J. Am. Chem. Soc., 2017 DOI:10.1021/jacs.7b06472.
- E. T. C. Vogt, G. T. Whiting, A. Dutta Chowdhury and B. M. Weckhuysen, in Advances in Catalysis, ed. C. J. Friederike, Academic Press, 2015, vol. 58, pp. 143–314 Search PubMed.
- G. Li, P. Vassilev, M. Sanchez-Sanchez, J. A. Lercher, E. J. Hensen and E. A. Pidko, J. Catal., 2016, 338, 305–312 CrossRef CAS.
- E. Borfecchia, K. A. Lomachenko, F. Giordanino, H. Falsig, P. Beato, A. V. Soldatov, S. Bordiga and C. Lamberti, Chem. Sci., 2015, 6, 548–563 RSC.
- A. R. Kulkarni, Z.-J. Zhao, S. Siahrostami, J. K. Nørskov and F. Studt, ACS Catal., 2016, 6, 6531–6536 CrossRef CAS.
- E. M. C. Alayon, M. Nachtegaal, A. Bodi and J. A. van Bokhoven, ACS Catal., 2013, 4, 16–22 CrossRef.
- A. A. Arvidsson, V. P. Zhdanov, P.-A. Carlsson, H. Gronbeck and A. Hellman, Catal. Sci. Technol., 2017, 7, 1470–1477 CAS.
- T. Yumura, Y. Hirose, T. Wakasugi, Y. Kuroda and H. Kobayashi, ACS Catal., 2016, 6, 2487–2495 CrossRef CAS.
- M. H. Mahyuddin, A. Staykov, Y. Shiota, M. Miyanishi and K. Yoshizawa, ACS Catal., 2017, 7, 3741–3751 CrossRef CAS.
- Z.-J. Zhao, A. Kulkarni, L. Vilella, J. K. Nørskov and F. Studt, ACS Catal., 2016, 6, 3760–3766 CrossRef CAS.
- A. A. Latimer, A. R. Kulkarni, H. Aljama, J. H. Montoya, J. S. Yoo, C. Tsai, F. Abild-Pedersen, F. Studt and J. K. Norskov, Nat. Mater., 2017, 16, 225–229 CrossRef CAS PubMed.
- M. H. Mahyuddin, A. Staykov, Y. Shiota and K. Yoshizawa, ACS Catal., 2016, 6, 8321–8331 CrossRef CAS.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149 CrossRef.
- K. D. Vogiatzis, G. Li, E. J. M. Hensen, L. Gagliardi and E. A. Pidko, J. Phys. Chem. C, 2017, 121, 22295–22302 CAS.
- S. D. Hallaert, M. L. Bols, P. Vanelderen, R. A. Schoonheydt, B. F. Sels and K. Pierloot, Inorg. Chem., 2017, 56, 10681–10690 CrossRef CAS PubMed.
- F. Göltl, C. Michel, P. C. Andrikopoulos, A. M. Love, J. Hafner, I. Hermans and P. Sautet, ACS Catal., 2016, 6, 8404–8409 CrossRef.
- V. Fung, F. F. Tao and D.-e. Jiang, J. Phys. Chem. Lett., 2017, 2206–2211, DOI:10.1021/acs.jpclett.7b00861.
- J. Lee and J. J. Grabowski, Chem. Rev., 1992, 92, 1611–1647 CrossRef CAS.
- P. Deshlahra and E. Iglesia, J. Phys. Chem. C, 2016, 120, 16741–16760 CAS.
- L. Vilella and F. Studt, Eur. J. Inorg. Chem., 2016, 2016, 1514–1520 CrossRef CAS.
- K. Narsimhan, V. K. Michaelis, G. Mathies, W. R. Gunther, R. G. Griffin and Y. Román-Leshkov, J. Am. Chem. Soc., 2015, 137, 1825–1832 CrossRef CAS PubMed.
- M. Boronat and A. Corma, Catal. Lett., 2015, 145, 162–172 CrossRef CAS.
- G. Ertl, H. Knözinger and J. Weitkamp, Handbook of Heterogeneous Catalysis, Wiley, 1997, ISBN: 978-3-527-31241-2 Search PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Summary of experimental and computational reports for methane activation in Cu-exchanged zeolites, discussion of rates of reaction, reference states, theoretical capacity, Tables S1–S9 and Fig. S1–S7. See DOI: 10.1039/c7cy01229b |
| This journal is © The Royal Society of Chemistry 2018 |