Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The impact of tensorial temperature on equilibrium thermodynamics
Marcello
Sega
 *a and
Pál
Jedlovszky
*a and
Pál
Jedlovszky
 b
b
aUniversity of Vienna, Faculty of Physics, Boltzmangasse 5, A-1090 Vienna, Austria. E-mail: marcello.sega@univie.ac.at
bDepartment of Chemistry, Eszterházy Károly University, Lányka u. 6, H-3300 Eger, Hungary
First published on 4th June 2018
Abstract
Thermodynamic temperature is a scalar. However, the connection with the kinetic energy tensor in statistical mechanics leaves open the possibility to define a tensorial temperature. This concept has sometimes been used to simulate isothermal conditions in out-of-equilibrium systems. Here, we show, by studying a sessile water droplet, that a tensorial temperature leads to the wrong thermodynamics, or, in other words, the equilibrium isothermal ensemble generated using a tensorial temperature is not the canonical one, with interfacial free energies that can differ up to 40% from the correct ones.
Molecular dynamics simulations, by integrating Newton's equations of motion, naturally sample microcanonical ensembles, where the state of the system evolves on the constant energy hypersurface of the phase space. Often, however, it is necessary or preferable to simulate other ensembles. Modifications to the numerical integration scheme, which allow for the sampling of isothermal ensembles, go under the generic name of a “thermostat”. In the literature, one can find a large number of different thermostats, each one with its own advantages and disadvantages.1–3 Here, we focus on the consequences of considering temperature as a tensorial quantity and decoupling one or more spatial directions from a global thermostat, particularly in view of its application to out-of-equilibrium simulations.
It is worth remembering that a global thermostat is one that uses the total kinetic energy of the system to define its temperature, according to its statistical mechanical definition. Strictly speaking, all global thermostats work only at equilibrium and fail if the time-averaged velocity field is not zero (or a constant) everywhere, as in the case of an imposed shear flow. Often, the following simple modification of a global thermostat is thought to be a good enough solution. Let’s consider, for example, the shear flow mentioned before, whose stationary velocity field has the form v(x,y,z) = u(z)ŷ. In a linear regime, one could reasonably assume that the dynamics are perturbed from the equilibrium only along the direction of the flow, ŷ. One can then modify any global thermostat in such a way that only the velocity components in the two orthogonal directions, ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) and ẑ, are affected by the thermostat. Of course, the way the temperature is computed from the set of velocities has to be changed accordingly, to take into account the loss of one degree of freedom per particle.
and ẑ, are affected by the thermostat. Of course, the way the temperature is computed from the set of velocities has to be changed accordingly, to take into account the loss of one degree of freedom per particle.
This approach has often been used, including by one of the authors of this work, to simulate the flow of fluids in nanochannels,4–10 and is usually believed to be accurate enough if not too far from equilibrium.11 However, some legitimate concerns could arise when dealing with molecular fluids with rigid bonds, because the configuration space and the momentum space are no longer independent of each other, and this can have significant consequences (it is worth noting here that in atomistic models, most molecular bonds have to be modelled as rigid at room temperature, as the first available bond-stretching modes have energies several times higher than the thermal energy; in water, this is true also for the bending modes). As we have shown in our previous work,12 for example, the configurational part of the pressure (i.e., the virial part) is not enough to describe the average value of the surface tension of liquid interfaces because of the preferential orientation of the molecules at the boundaries.
Let’s assume, for simplicity, that one of the molecular axes is fixed in a macroscopic reference frame (in this case, the liquid vapor interface). In this example, it is clear that the rotational degrees of freedom do not contribute to the kinetic part of the stress in equal measure along the three Cartesian axes. The anisotropy of the kinetic energy tensor at interfaces (which, by the way, constitutes no violation of the equipartition theorem) can contribute a considerable amount to the surface tension – for example, 15% in water, modeled using the SPC/E potential.12,13
The modification of global thermostats for out-of-equilibrium flows that we mentioned before consists, in its essence, of the consideration of the temperature as a tensorial object, and the restriction of the original algorithm to two Cartesian components only. Because of the anisotropy of the kinetic energy tensor, however, it is reasonable to question the validity of this approach. In the typical setup for shear flow in a nanochannel, the fluid fills the region between two planar walls, which are sheared by imposing either constant velocity or constant force on the walls' atoms. One basic requirement for these modified thermostats is to be able to reproduce, at equilibrium, the correct free energy of the system, which in this case can be probed by computing the liquid/solid and liquid/vapor surface tensions.
As a representative system, we have chosen water in contact with a graphitic surface. Water molecules are modeled using the SPC/E potential, while the substrate is modeled using a graphite-like structure of carbon atoms, fixed in space and arranged in six layers. The interlayer distance is 0.3394 nm, and in each layer, the atoms are located on a hexagonal lattice with bond lengths of 0.142 nm. The carbon atoms interact with the oxygen atoms following a Lennard-Jones potential, i.e., U(r) = 4ε[(σ/r)12 − (σ/r)6], where σ = 0.3151 nm and ε = 0.65060 kJ mol−1. The depth of the energy well, ε, has been chosen with no other particular aim but to obtain a contact angle of about 75° using the unmodified thermostat. We included contributions to the Lennard-Jones interactions for pair distances of up to 1 nm, whereas we computed the electrostatic interaction using the smooth Particle Mesh Ewald method,14 with a short-range cutoff of 1 nm, a grid spacing of 0.12 nm, a 4th order interpolation scheme, and a relative accuracy at the cutoff of 10−5. No long-range corrections to the dispersion forces were applied in any case. The molecular structure of water was kept rigid using the SETTLE algorithm.15
As for the shape of the water droplet, we opted for a cylindrical cap that spans the periodic simulation box in one direction (y), instead of a spherical cap. This setup avoids having a size-dependent contact angle because of the presence of a nonzero line tension. The final system consists of a rectangular simulation box of edges 13.035, 4.118, and 10.0 nm along the x, y, and z axes, respectively, containing 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 243 carbon atoms and 2000 water molecules. The graphitic planes are arranged with their normal pointing along the z axis. For the calculation of the water/vapor surface tension, we simulated a free-standing slab of water with 4000 molecules in a simulation box of 5 × 5 × 15 nm, with the surface normal along the z axis. Fig. 1 presents a simulation snapshot of the sessile cylindrical droplet.
243 carbon atoms and 2000 water molecules. The graphitic planes are arranged with their normal pointing along the z axis. For the calculation of the water/vapor surface tension, we simulated a free-standing slab of water with 4000 molecules in a simulation box of 5 × 5 × 15 nm, with the surface normal along the z axis. Fig. 1 presents a simulation snapshot of the sessile cylindrical droplet.
We performed molecular dynamics simulations with an in-house modified version of GROMACS v. 5.1,16 integrating the equations of motion using a timestep of 1 fs. We used, as a reference thermostat, the Nosé–Hoover17,18 (NH) thermostat, simulating the canonical ensemble at T = 300 K, with a relaxation time of 0.5 ps. Additionally, we tested two modified coupling schemes. In the first one (T1), there is only one thermostat acting on the degrees of freedom parallel to a chosen plane, while the velocities along the normal direction are not modified. In the second one (T2), two thermostats are acting separately on two subspaces (the in-plane and normal directions). It should be noted that T1 can be thought of as a variant of T2, with an infinite relaxation time for the thermostat applied to the normal direction. For both of these thermostats, the scalar temperature fluctuates around the target value. However, as we will now show, they fail in sampling the canonical ensemble at equilibrium.
Solid/liquid surface tension can be accessed by measuring the contact angle of a water droplet on a solid substrate. The Young equation, γsg − γsl − γlv![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 0, relates the surface tensions, γ, between solid (s), gas (g), and liquid (l) to the macroscopic contact angle, θ. The surface tension γlv can be computed easily from a liquid/vapour interface using the mechanical definition
θ = 0, relates the surface tensions, γ, between solid (s), gas (g), and liquid (l) to the macroscopic contact angle, θ. The surface tension γlv can be computed easily from a liquid/vapour interface using the mechanical definition 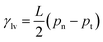 , where pn and pt are the normal and tangential components of the pressure tensor, L is the simulation box edge along the interface normal, and the factor 1/2 accounts for the presence of two interfaces.
, where pn and pt are the normal and tangential components of the pressure tensor, L is the simulation box edge along the interface normal, and the factor 1/2 accounts for the presence of two interfaces.
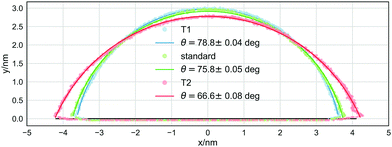
The most striking difference between the macroscopic properties sampled with the NH thermostat and those sampled with the modified thermostats is the value of the equilibrium contact angle of the sessile droplet. Fig. 2 reports one isodensity line in the x–z plane, outlining the shape of the droplet, for the same system simulated using the NH, T1, and T2 thermostats. The droplet simulated using the T2 thermostat has a remarkably different contact angle, about 10° (≃12%) smaller than that obtained with the NH thermostat. The effect of the T1 thermostat is less appreciable by visual inspection, but the value resulting from the best fit to the arc of a circle is about 3° (≃4%) larger than that obtained when using the NH thermostat. Although small (but statistically significant, as it is larger than three standard deviations), this difference has a considerable impact on the value of γsg − γsl.
The other ingredient needed is the liquid/vapor surface tension, γlv, which can be obtained directly from the sampled values of the pressure tensor in the simulation of the free-standing water slab. The two modified thermostats also have an impact on this surface free energy, which is about 3% (T1) and 6% (T2) smaller than that of the standard NH thermostat. The values of cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and γlv can be combined to obtain γsg − γsl, which is 146 ± 3, 113 ± 2, and 222 ± 4 bar nm, for NH, T1, and T2, respectively. This result implies that γsg − γsl is about 20% smaller and 40% larger than it should be when using T1 and T2, respectively. The significant difference in the T1 case could strike one as unexpected because the contact angle is close to the NH one. What matters, however, is the combined effect of the liquid/vapor surface tension and the cos
θ and γlv can be combined to obtain γsg − γsl, which is 146 ± 3, 113 ± 2, and 222 ± 4 bar nm, for NH, T1, and T2, respectively. This result implies that γsg − γsl is about 20% smaller and 40% larger than it should be when using T1 and T2, respectively. The significant difference in the T1 case could strike one as unexpected because the contact angle is close to the NH one. What matters, however, is the combined effect of the liquid/vapor surface tension and the cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ factor: the closer θ is to 90°, the more the factor changes, and it is, in fact, T1 that generates the largest contact angle (in Table 1, we report the calculated average values and the standard deviations of the liquid/vapor surface tension for the NH, T1, and T2 thermostats).
θ factor: the closer θ is to 90°, the more the factor changes, and it is, in fact, T1 that generates the largest contact angle (in Table 1, we report the calculated average values and the standard deviations of the liquid/vapor surface tension for the NH, T1, and T2 thermostats).
| Thermostat | γ lv/(bar nm) | (γsg − γsl)/(bar nm) | θ/° |
|---|---|---|---|
| NH | 596 ± 9 | 146 ± 3 | 75.8 ± 0.05 |
| T1 | 575 ± 5 | 113 ± 2 | 78.8 ± 0.04 |
| T2 | 559 ± 7 | 222 ± 4 | 66.6 ± 0.08 |
One could wonder whether this behaviour is characteristic of Nosé–Hoover-like thermostats only, or of other types of thermostats as well. We also investigated the case of the Langevin thermostat, implemented as in ref. 19. Due to the very structure of the Langevin equation, an equivalent version of the T2 thermostat is meaningless, but it is possible to realize an equivalent of T1, where the Langevin friction and forcing terms are applied only in the x–y plane. The simulations run with the full Langevin thermostat lead to a contact angle of 75.7° ± 0.1°, in accordance with the NH results, whereas those run when not applying the Langevin friction and stochastic forcing to the z direction yield a contact angle of 72.7° ± 0.2°. Perhaps more importantly, the thermostat with partial Langevin coupling also led to a wrong temperature of 296.1 ± 0.2 K (compared to the value of 300.0 ± 0.1 K obtained with all other thermostats), due to the fact that the projected constrained degrees of freedom do not satisfy the usual fluctuation–dissipation relations.
The conclusion that can be drawn from this investigation is that using a tensorial temperature and applying separate (albeit identical) thermostats to its elements, or removing one of the spatial directions from the thermostating procedure, does not allow for the sampling of canonical ensembles at equilibrium. This failure arises from the fact that the Cartesian kinetic tensor is not always isotropic everywhere, as in the case of rigid molecules in the presence of interfaces. Fully flexible molecules and monatomic liquids are not affected by this problem because the kinetic and configurational parts of the partition function are independent of each other. We showed that in a test case of water in contact with a graphite-like material, γsg − γsl is affected so much as to change by 20–40% from its “true” value obtained in the canonical ensemble. We advise refraining from using these kinds of thermostats in cases where thermodynamic consistency is a strict requirement.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
P. J. acknowledges the financial support of the Hungarian NKFH Foundation under project no. 119732.References
- P. H. Hünenberger, Adv. Polym. Sci., 2005, 173, 105–149 CrossRef.
- T. Soddemann, B. Dünweg and K. Kremer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 046702 CrossRef PubMed.
- J. E. Basconi and M. R. Shirts, J. Chem. Theory Comput., 2013, 9, 2887–2899 CrossRef PubMed.
- P. A. Thompson and M. O. Robbins, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 6830 CrossRef.
- N. V. Priezjev and S. M. Troian, Phys. Rev. Lett., 2004, 92, 018302 CrossRef PubMed.
- N. V. Priezjev, A. A. Darhuber and S. M. Troian, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 041608 CrossRef PubMed.
- D. M. Huang, C. Sendner, D. Horinek, R. R. Netz and L. Bocquet, Phys. Rev. Lett., 2008, 101, 226101 CrossRef PubMed.
- K. Falk, F. Sedlmeier, L. Joly, R. R. Netz and L. Bocquet, Nano Lett., 2010, 10, 4067–4073 CrossRef PubMed.
- M. Sega, M. Sbragaglia, L. Biferale and S. Succi, Soft Matter, 2013, 9, 8526–8531 RSC.
- M. Sega, M. Sbragaglia, L. Biferale and S. Succi, Eur. Phys. J. E: Soft Matter Biol. Phys., 2015, 38, 127 CrossRef PubMed.
- C. Pastorino, T. Kreer, M. Müller and K. Binder, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 026706 CrossRef PubMed.
- M. Sega, B. Fábián and P. Jedlovszky, J. Phys. Chem. Lett., 2017, 8, 2608–2612 CrossRef PubMed.
- H. Berendsen, J. Grigera and T. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef.
- S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962 CrossRef.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25 CrossRef.
- S. Nosé, Mol. Phys., 1984, 52, 255–268 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695 CrossRef.
- N. Goga, A. Rzepiela, A. De Vries, S. Marrink and H. Berendsen, J. Chem. Theory Comput., 2012, 8, 3637–3649 CrossRef PubMed.
| This journal is © the Owner Societies 2018 |