Experiment and theory at the convergence limit: accurate equilibrium structure of picolinic acid by gas-phase electron diffraction and coupled-cluster computations†
Abstract
The accurate molecular structure of picolinic acid has been determined from experimental data and computed at the coupled cluster level of theory. Only one conformer with the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C–N and H–O–C
C–C–N and H–O–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O fragments in antiperiplanar (ap) positions, ap–ap, has been detected under conditions of the gas-phase electron diffraction (GED) experiment (Tnozzle = 375(3) K). The semiexperimental equilibrium structure, rsee, of this conformer has been derived from the GED data taking into account the anharmonic vibrational effects estimated from the ab initio force field. The equilibrium structures of the two lowest-energy conformers, ap–ap and ap–sp (with the synperiplanar H–O–C
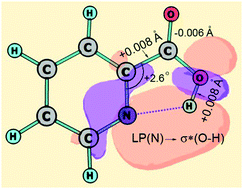
O fragments in antiperiplanar (ap) positions, ap–ap, has been detected under conditions of the gas-phase electron diffraction (GED) experiment (Tnozzle = 375(3) K). The semiexperimental equilibrium structure, rsee, of this conformer has been derived from the GED data taking into account the anharmonic vibrational effects estimated from the ab initio force field. The equilibrium structures of the two lowest-energy conformers, ap–ap and ap–sp (with the synperiplanar H–O–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O fragment), have been fully optimized at the CCSD(T)_ae level of theory in conjunction with the triple-ζ basis set (cc-pwCVTZ). The quality of the optimized structures has been improved due to extrapolation to the quadruple-ζ basis set. The high accuracy of both GED determination and CCSD(T) computations has been disclosed by a correct comparison of structures having the same physical meaning. The ap–ap conformer has been found to be stabilized by the relatively strong N⋯H–O hydrogen bond of 1.973(27) Å (GED) and predicted to be lower in energy by 16 kJ mol−1 with respect to the ap–sp conformer without a hydrogen bond. The influence of this bond on the structure of picolinic acid has been analyzed within the Natural Bond Orbital model. The possibility of the decarboxylation of picolinic acid has been considered in the GED analysis, but no significant amounts of pyridine and carbon dioxide could be detected. To reveal the structural changes reflecting the mesomeric and inductive effects due to the carboxylic substituent, the accurate structure of pyridine has been also computed at the CCSD(T)_ae level with basis sets from triple- to 5-ζ quality. The comprehensive structure computations for pyridine as well as for carbon dioxide have been used to examine the convergence with respect to the basis set size.
O fragment), have been fully optimized at the CCSD(T)_ae level of theory in conjunction with the triple-ζ basis set (cc-pwCVTZ). The quality of the optimized structures has been improved due to extrapolation to the quadruple-ζ basis set. The high accuracy of both GED determination and CCSD(T) computations has been disclosed by a correct comparison of structures having the same physical meaning. The ap–ap conformer has been found to be stabilized by the relatively strong N⋯H–O hydrogen bond of 1.973(27) Å (GED) and predicted to be lower in energy by 16 kJ mol−1 with respect to the ap–sp conformer without a hydrogen bond. The influence of this bond on the structure of picolinic acid has been analyzed within the Natural Bond Orbital model. The possibility of the decarboxylation of picolinic acid has been considered in the GED analysis, but no significant amounts of pyridine and carbon dioxide could be detected. To reveal the structural changes reflecting the mesomeric and inductive effects due to the carboxylic substituent, the accurate structure of pyridine has been also computed at the CCSD(T)_ae level with basis sets from triple- to 5-ζ quality. The comprehensive structure computations for pyridine as well as for carbon dioxide have been used to examine the convergence with respect to the basis set size.


 Please wait while we load your content...
Please wait while we load your content...