Systematic exploitation of thermotropic bicontinuous cubic phase families from 1,2-bis(aryloyl)hydrazine-based molecules

Abstract

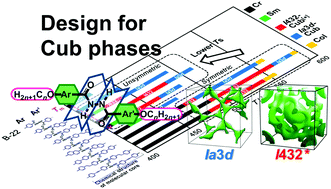
Rational design of molecules that exhibit a thermotropic bicontinuous cubic (Cub) phase has been earnestly desired. In this work, we describe the suitable selection of a molecular motif that has enabled the systematic exploitation of eight new series of Cub-phase molecules with symmetric molecular cores, N-n (1), PB-n (2), S-n (3), and PEB-n (4), and unsymmetric cores, B-N-n (5), B-PB-n (6), B-S-n (7), and B-PEB-n (8). These eight series all originate from achiral chain-core-chain type rod-like molecules that exhibit two types of Cub phases, an achiral Ia3d phase, and a chiral phase. All the Ia3d phases formed were found to be isomorphous structures, with their cell dimensions being proportional to the core size, and the same was true for the latter chiral phase. We demonstrated that the formation is mainly governed by the segregation between core and alkyl moieties of the molecules, and thus, by the weight fraction of the core portion f_core. This work also demonstrates that the central dicarbonylhydrazine linkage bearing intermolecular hydrogen bonding ability exhibits a pinning effect that prevents slippage of π-stacks of molecules, which is critical for the formation of the two Cub phases that are composed of chiral networks with twisted molecular arrangements. In each series, the emergence of spontaneous chirality formation that occurred in the chiral phase was limited to between 0.36 and 0.50 in the range of f_core. An interesting insight was that the introduced unsymmetry of the molecular core strongly influenced the phase behavior, which lowered the temperature range of Cub phases to around that of the smallest core series B-n, while the high temperature limit (T_c) was roughly proportional to the core size, as determined by the strength of intermolecular π–π interactions.