Open Access Article
Open Access ArticleOn the regioselectivity of the Diels–Alder cycloaddition to C60 in high spin states†
Ouissam
El Bakouri
a,
Marc
Garcia-Borràs
 ab,
Rosa M.
Girón
c,
Salvatore
Filippone
c,
Nazario
Martín
ab,
Rosa M.
Girón
c,
Salvatore
Filippone
c,
Nazario
Martín
 *cd and
Miquel
Solà
*cd and
Miquel
Solà
 *a
*a
aInstitut de Química Computacional i Catàlisi (IQCC) and Departament de Química, Universitat de Girona, c/Maria Aurèlia Capmany 6, 17003 Girona, Spain. E-mail: miquel.sola@udg.edu
bDepartment of Chemistry and Biochemistry, University of California, Los Angeles 607 Charles E Young Drive East, 90095 Los Angeles, CA, USA
cDepartamento de Química Orgánica, Facultad de Química, Universidad Complutense, Avda. Complutense s/n, E-28040 Madrid, Spain. E-mail: nazmar@ucm.es
dIMDEA–Nanociencia, C/Faraday, 9, Campus de Cantoblanco, E-28049 Madrid, Spain
First published on 24th January 2018
Abstract
Controlling the regioselectivity in the exohedral functionalization of fullerenes and endohedral metallofullerenes is essential to produce specific desired fullerene derivatives. In this work, using density functional theory (DFT) calculations, we show that the regioselectivity of the Diels–Alder (DA) cycloaddition of cyclopentadiene to 2S+1C60 changes from the usual [6,6] addition in the singlet ground state to the [5,6] attack in high spin states of C60. Changes in the aromaticity of the five- and six-membered rings when going from singlet to high spin C60 provide a rationale to understand this regioselectivity change. Experimentally, however, we find that the DA cycloaddition of isoindene to triplet C60 yields the usual [6,6] adduct. Further DFT calculations and computational analysis give an explanation to this unanticipated experimental result by showing the presence of an intersystem crossing close to the formed triplet biradical intermediate.
Introduction
The functionalization of fullerenes and endohedral metallofullerenes (EMFs) has attracted considerable attention in the last few decades.1–7 The derivatization of these compounds helps to modulate their electronic and physicochemical properties, generating fullerene and EMF derivatives more suitable for practical applications.2,8–12 Fullerenes undergo a variety of chemical reactions favored by their electron deficient nature, especially cycloadditions and nucleophilic additions.1,6,7,13–15 Generally, the reactions in fullerenes take place in their singlet ground states. Less often, however, the reaction can occur in high spin states. In some cases, this is because the ground state of the fullerene or EMFs is a high spin state. High spin ground states in EMFs are attributed usually to the electronic structure of the encapsulated species.16–20 Although less common, some empty fullerene cages like C68 can also have high spin ground states.21,22 The triplet ground state of C68 is attributed to the aromatic character of this electronic state as compared to the antiaromatic character of its singlet state.21,23 In other cases, fullerenes can be photoexcited to higher spin states and the reaction takes place in these excited states. The photophysical and photochemical properties of 3C60, which is the lowest-lying excited state of C60, have been studied by several groups since 1991.24–27 Their investigations proved that during the excitation of C60, the intersystem crossing (ISC) from the first singlet excited state to the first triplet excited state (S1 to T1) occurs with a high efficiency, mainly due to the small splitting between these two states as well as the large spin-orbital interaction in the spherical cage. The straightforward generation of the first triplet excited state of C60 opened the door to photochemical processes. For instance, the [2+2] photocycloadditions on fullerenes are common since the 90s.28–31 In fact, fullerenes have been able to react photochemically with, among others, alkenes, enones, styrenes, etc. The existence of a biradical intermediate was demonstrated in many of these reactions.28–35 Moreover, several studies found that it is also possible to obtain Diels–Alder (DA) adducts from the 3C60 species.36,37The multiple addition sites available in fullerenic cages makes controlling the regioselectivity in the chemical functionalization of fullerenes one of the most challenging aspects in fullerene chemistry.38,39 Fullerenes following the isolated pentagon rule (IPR)40 have two different types of C–C bonds, namely, the [6,6] bonds in hexagon–hexagon ring junctions and the [5,6] bonds in the connection between an hexagon and a pentagon. Usually, the [6,6] bonds are more reactive than the [5,6] bonds in hollow fullerenes, while [5,6] additions are more common in EMFs.41–43 In 2013, some of us studied the changes in the regioselectivity of the exohedral functionalization of C60 after successive electron additions.44 It was shown that successive reductions of C60 (C60−q, q = 0–6) dramatically modify the regioselectivity of the DA additions, from the usual [6,6] addition in neutral species to addition to the [5,6] bond when the number of electrons added to C60 was higher than four. This regioselectivity change was rationalized in terms of local aromaticity variations in the 5- and 6-membered rings (6-MRs) of the fullerene due to the reduction process. Electrons added to the cage accumulate in the 5-MRs that gain cyclopentadienyl anion character, increasing significantly their aromaticity. In this situation, addition to a [5,6] bond, which involves breaking the aromaticity of a unique 5-MR, becomes more favorable than addition to a [6,6] bond that destroys the aromaticity of two 5-MRs.
It is well known that the cyclopentadienyl cation, C5H5+, has a triplet ground state.45 The stability of this triplet state is justified by the so-called Baird rule of aromaticity.46,47 Taking this result into account, one could hypothesize that by increasing the spin of the fullerenic cage, the spin density could accumulate in the 5-MRs that may become more aromatic by getting more triplet cyclopentadienyl cation character. If this is true and from the results obtained in reduced C60, it is likely that we may observe in C60 a change in the regioselectivity of the DA cycloaddition from [6,6] to [5,6] when increasing the spin of the fullerenic cage. The present study checks this hypothesis. Our goal is to analyze the effect of changing the spin (S = 0–6) in the DA cycloaddition between C60 and two different dienes, cyclopentadiene and isoindene. We explore different spin states (S from 0 to 6, the latter having 12 unpaired electrons, i.e., one unpaired electron per 5-MR) with the aim of determining the spin state that has to be reached to change the regioselectivity of the DA reaction. We anticipate here that our computational results predict a change in the regioselectivity of the process already in the triplet state. Subsequently, we have carried out experiments to verify the calculations. Unfortunately, experiments have not confirmed our initial predictions for the triplet state. Finally, we have performed additional calculations that justify the experimental outcome in this triplet state.
Methods
(a) Computational methodology
All geometry optimizations were performed with the Gaussian 09 package48 at the B3LYP-D3/6-31G(d)49–52 level of theory that includes the Grimme dispersion corrections (D3).53 The selected basis set was successfully used in computational studies of fullerenes. Although larger basis sets are recommended for the description of high spin states,54 the size of the systems studied prevents the use of larger basis sets. Inclusion of dispersion corrections is essential to get a good theoretical description of the Diels–Alder cycloaddition to fullerenes.55 Analytical Hessians were computed to confirm that the optimized structures are indeed minima (zero imaginary frequencies) or transition states (one imaginary frequency) and to calculate unscaled zero-point energies (ZPEs) as well as thermal corrections and entropy contributions using the standard statistical-mechanics relationships for an ideal gas. These two latter terms were computed at 298.15 K and 1 atm to provide gas-phase Gibbs energies at the B3LYP-D3/6-31G(d) level of theory. Gibbs energies in toluene solution were calculated from the gas-phase Gibbs energies by adding the Gibbs solvation energies in toluene obtained with the polarizable continuum model (PCM)56 by single point energy calculations using the gas-phase geometries. It should be noted that although changes in reaction energies and energy barriers when going from gas-phase to solution obtained with the PCM model are trustworthy, the absolute solvation energies are likely overestimated.57The harmonic oscillator model of aromaticity (HOMA) index,58,59 the multicenter index (MCI),60 and the normalized version of MCI (INB)61 were used to quantify the aromatic character of the 5- and 6-MRs of C60.62 The HOMA is defined as:
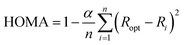 | (1) |
The MCI is an electronic index obtained from Iring values63 as follows:
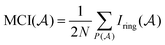 | (2) |
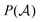 stands for a permutation operator which interchanges the atomic labels A1, A2, …, AN (see eqn (3)) to generate up to the N! permutations of the elements in the string
stands for a permutation operator which interchanges the atomic labels A1, A2, …, AN (see eqn (3)) to generate up to the N! permutations of the elements in the string 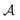 , and the Iring index is defined as:
, and the Iring index is defined as: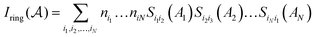 | (3) |
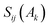 the overlap between MOs i and j within the molecular space assigned to atom Ak. Finally, INB is given by:
the overlap between MOs i and j within the molecular space assigned to atom Ak. Finally, INB is given by: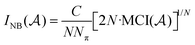 | (4) |
 . The MCI and INB were calculated with the B3LYP-D3/6-311G(d)//B3LYP-D3/6-31G(d) method. All MCI and INB calculations were performed using the ESI-3D program,64–67 using the QTAIM (Quantum Theory of Atoms in Molecules) atomic partition and the integration scheme as implemented in the AIMAll package.68
. The MCI and INB were calculated with the B3LYP-D3/6-311G(d)//B3LYP-D3/6-31G(d) method. All MCI and INB calculations were performed using the ESI-3D program,64–67 using the QTAIM (Quantum Theory of Atoms in Molecules) atomic partition and the integration scheme as implemented in the AIMAll package.68
(b) Experimental methods and materials
The commercially available reagents and solvents were used without further purification. Indene (99%), Rose Bengal (95%) and Methylene Blue were provided by Sigma Aldrich and Toluene (HPLC grade) from Fisher Chemical. [Ru(bpy)3](ClO4)2 was synthesized according to the procedure previously described.69 Reactions carried out under 420 nm and UVA light were irradiated using a Photoreactor Package LZC-ORG (Luzchem). When the irradiation was carried out with the Hg lamp, a solution of KMnO4 or CoSO4 (CoCl2 + Na2SO4) in water (4 × 10−5 M) was located between the lamp and the reaction flask acting like a filter. Reactions were monitored by HPLC column Buckyprep (Waters) (4.6 × 250 mm). All these values were monitored in a 320 nm spectrophotometer detector. For conversions, also HPLC was employed.Results and discussion
This section is divided into two subsections. First, we perform a computational study of the DA cycloaddition of cyclopentadiene to 2S+1C60 (S = 0–6). And second, we discuss the experimental and computational results of the DA cycloaddition of isoindene to 3C60.(a) The Diels–Alder cycloaddition of cyclopentadiene to 2S+1C60 (S = 0–6). A computational study
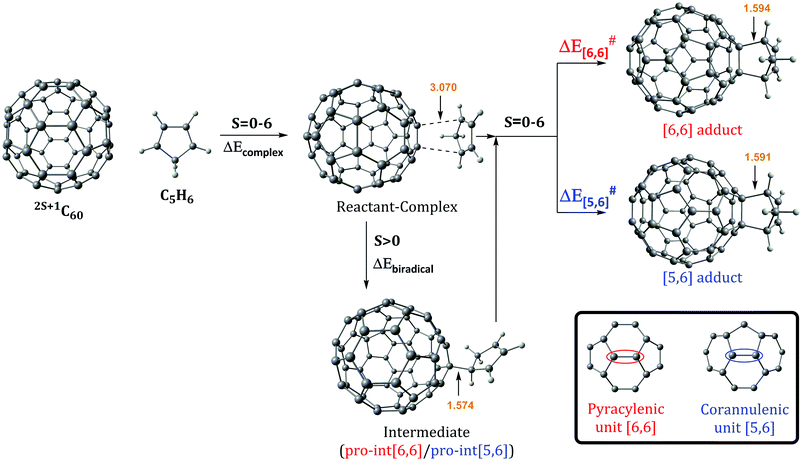
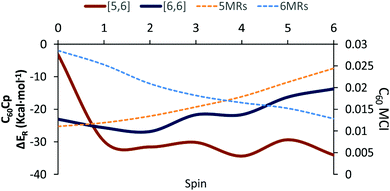
The Diels–Alder reaction between 2S+1C60 and cyclopentadiene (Cp) can occur concertedly or stepwise (see Fig. 1). Our results show that the reaction takes place concertedly only in the S0 state. From S = 1 to S = 6, the process is stepwise through the formation of a high spin radical intermediate. In this intermediate, the carbon atom of the Cp fragment that has to form the second C–C bond can be oriented to attack the C atom of a [6,6] bond and generate the pro-int[6,6] intermediate or oriented towards the C atom of a [5,6] bond and form the pro-int[5,6] intermediate. These two intermediates are almost isoenergetic (energies differences of 0.3–0.5 kcal mol−1) and the conversion from one intermediate to another takes place easily by rotation along the newly formed C–C sigma bond (ΔE‡ = 6.2–6.7 kcal mol−1, Table S6, ESI†).Table 1 collects the Gibbs and electronic energy differences in reaction energies and energy barriers for the additions to the [5,6] and [6,6] bonds of 2S+1C60. Energy differences in Table 1 are obtained from the Gibbs and electronic energy barriers for the DA cycloaddition listed in Table S5 (ESI†), which are given with respect to the most stable intermediate (the pro-int[6,6] for S = 1–6 or the van der Waals reactant complex for S = 0) for each reaction. Positive values indicate that the [5,6] attack is thermodynamically (ΔΔGR) or kinetically (ΔΔG‡) more favorable than the [6,6] addition. Comparison of Gibbs energy differences in the gas-phase and toluene solution of Table 1 shows that solvent effects are minor (less than 0.5 kcal mol−1 differences) and, in general, favor the [5,6] addition. Fig. 2 reports the gas-phase Gibbs reaction energy for the [5,6] and [6,6] additions as well as the aromaticity of the 5-MRs and 6-MRs measured in terms of the MCI for the different studied spin states. In the S0 state, our calculations indicate that the concerted [6,6] addition is thermodynamically and kinetically more favored than the [5,6] one as expected from previous theoretical studies.41,42,44 This result concurs with experimental evidence70,71 showing that the reaction takes place over the [6,6] bond with an activation energy of 6.9 kcal mol−1 (compared to our ΔH‡ of 10.2 kcal mol−1 calculated at the B3LYP-D3/6-31G(d) level of theory as the enthalpy difference between the transition state and the van der Waals reactant complex) and a reaction enthalpy of −19.8 ± 2.2 kcal mol−1 (ΔHr = −23.5 kcal mol−1 with the B3LYP-D3/6-31G(d) method). Nevertheless, the regioselectivity changes drastically once 3C60 is considered and the [5,6] addition becomes the most favored. The reaction energy and energy barrier differences between [5,6] and [6,6] attacks for the different spin states given in Table 1 show that the inversion of the regioselectivity already occurs when going from 1C60 to 3C60 and it is maintained for the rest of the high spin states (2S+1C60 with S > 0). Therefore, spin states of C60 with S = 1–6 favor the [5,6] addition both thermodynamically and kinetically even if pro-int[6,6] is formed first. The barriers involving the transformation from pro-int[6,6] to pro-int[5,6] and to the adduct [5,6] are lower than the barrier corresponding to the formation of the [6,6] adduct from pro-int[6,6].
| 2S + 1 = | 1 | 3 | 5 | 7 | 9 | 11 | 13 |
|---|---|---|---|---|---|---|---|
| a Gas-phase Gibbs energy differences. b Gibbs energy differences in toluene. | |||||||
| ΔΔER([6,6]–[5,6]) | −19.87 | 4.13 | 4.74 | 8.48 | 12.72 | 13.10 | 20.33 |
| ΔΔE‡([6,6]–[5,6]) | −15.26 | 9.56 | 9.71 | 10.47 | 15.13 | 14.57 | 17.11 |
| ΔΔGR([6,6]–[5,6])a | −19.29 | 3.14 | 3.43 | 6.85 | 10.75 | 11.79 | 17.90 |
| ΔΔG‡([6,6]–[5,6])a | −13.64 | 8.05 | 7.52 | 9.35 | 13.17 | 12.77 | 15.20 |
| ΔΔGR,solv([6,6]–[5,6])b | −19.24 | 3.21 | 3.56 | 6.96 | 10.79 | 11.82 | 17.79 |
| ΔΔG‡solv([6,6]–[5,6])b | −13.88 | 8.51 | 7.95 | 9.51 | 13.23 | 12.78 | 14.99 |
Changes in C–C bond distances and pyramidalization angles do not explain the inversion of the regioselectivity when going from singlet to high spin states. Pyramidalization angles remain more or less the same and the [5,6] C–C bond distances are for all spin states studied larger than the [6,6] ones. The regioselectivity change can only be understood by analyzing the local aromaticity of the rings involved in the DA reaction. Tables S1 and S2 (ESI†) gather the calculated HOMA, MCI, and INB for the 5-MRs and 6-MRs of different 2S+1C60 (S = 0–6) species. HOMA, which is a geometric-based indicator of aromaticity that only takes into account the C–C bond distances, shows an increase of the aromaticity of the 5-MRs when the spin state increases, whereas for the 6-MRs it does not follow a clear trend. As HOMA was developed for ground state species, it is likely that evaluation of aromaticity for the high spin systems is not accurate enough. Electronic indices are expected to be more reliable.67,72–75 MCI and INB give the same tendency for the aromatic character of 5-MRs as HOMA does. Nevertheless, employing these electronic indices, we notice that the aromaticity of the 6-MRs decreases when the spin increases. Actually, the same trends were also observed when reducing C60 by adding up to six electrons to the carbon cage.44 Interestingly, for C70 we find the same behavior, i.e., the aromatic character of the 5-MRs increases and that of the 6-MRs decreases when the spin of the fullerene increases (see Tables S3 and S4, ESI†). Our interpretation of this result is that 5-MRs become more aromatic by getting more triplet cyclopentadienyl cation character. Indeed, our results show that the spin density accumulates mainly in the 5-MRs of 2S+1C60 (S = 1–6). On the other hand, increasing the radical character of 6-MRs reduces their aromaticity.
With this information, we can rationalize the changes in the regioselectivity of the DA reaction between 2S+1C60 and cyclopentadiene. Table 2 gathers the 2S+1C60 MCIPyr, 2S+1C60 MCICor, 2S+1C60Cp MCIPyr and 2S+1C60Cp MCICor values, where the MCI is calculated summing the four rings involved in the corannulenic (MCICor) or the pyracylenic (MCIPyr) unit (see the inset of Fig. 1 for a picture of corannulenic and pyracylenic units). ΔMCI is the difference between the sum of the MCI of the rings of the pyracylenic/corannulenic unit in the product 2S+1C60Cp and the same sum in the reactant 2S+1C60. And ΔΔMCIPyr–Cor in Table 2 corresponds to the difference in the loss of aromaticity measured with the MCI between the [5,6] corannulenic addition and the [6,6] pyracylenic addition. A positive ΔΔMCIPyr–Cor value indicates that the reduction of the aromaticity due to a [5,6] attack is more important than that of the [6,6] addition and the other way round.
| 2S + 1 = | 1 | 3 | 5 | 7 | 9 | 11 | 13 |
|---|---|---|---|---|---|---|---|
| 2S+1C60 MCIPyr | 5.63 | 5.89 | 5.25 | 5.20 | 5.64 | 6.02 | 6.46 |
| 2S+1C60 MCICor | 6.25 | 5.90 | 5.39 | 4.81 | 4.78 | 4.84 | 4.89 |
| 2S+1C60Cp MCIPyr | 1.06 | 1.05 | 1.08 | 1.13 | 1.12 | 1.13 | 1.04 |
| 2S+1C60Cp MCICor | 1.13 | 0.92 | 0.94 | 0.90 | 0.89 | 0.85 | 0.78 |
| ΔMCIPyr | −4.57 | −4.84 | −4.17 | −4.07 | −4.52 | −4.89 | −5.41 |
| ΔMCICor | −5.11 | −4.99 | −4.44 | −3.91 | −3.88 | −3.99 | −4.09 |
| ΔΔMCIPyr–Cor | 0.54 | 0.15 | 0.27 | −0.16 | −0.63 | −0.90 | −1.32 |
From the results of Tables 1 and 2, we see that the [5,6] addition becomes more favorable when the ΔΔMCIPyr–Cor value decreases. Although there is not a perfect correlation (aromaticity changes are not the only factor that intervenes and, for instance, spin density accumulation may be another important aspect to take into account and, consequently, correlation coefficients are not large: for instance, r2 = 0.58 for the linear relationship between ΔΔMCIPyr–Cor and ΔΔG‡), the trend is clear: when ΔΔMCIPyr–Cor decreases, ΔΔGR and ΔΔG‡ increase. As said before, 5-MRs become more aromatic when the spin state increases. The [5,6] addition (corannulenic unit, Fig. 1) disrupts the aromaticity of one 5-MR and three 6-MRs, whereas the [6,6] attack (pyracylenic unit, Fig. 1) breaks the aromaticity of two 5-MRs and two 6-MRs. For 1C60, 6-MRs are more aromatic than 5-MRs, therefore the [6,6] addition is more favorable since it destroys the aromaticity of only two 6-MRs as compared to three in the [5,6] attack. On the other hand, for high spin states, the 5-MRs become more aromatic than the 6-MRs. In this situation, addition to a [5,6] bond becomes more favorable because it breaks the aromaticity of only a single 5-MR.
(b) The Diels–Alder cycloaddition of isoindene to 3C60
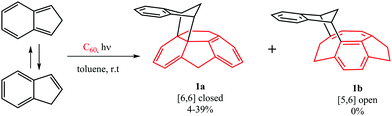
The computational results from the previous section indicate that DA cycloadditions involving 3C60 should generate [5,6] adducts. Prompted by these results, we decided to validate experimentally these theoretical predictions. To this end, we performed the photochemically induced DA cycloaddition between 3C60 and isoindene. In a previous work, Puplovskis et al. isolated the resulting [6,6] product from the Diels–Alder reaction between 1C60 and isoindene, which is prepared in situ from indene in refluxing o-dichlorobenzene (o-Cl2C6H4).76 Here, for the preparation of the [5,6] cycloadduct 1b, we used photochemical conditions and temperatures below 40 °C to avoid the thermal cycloaddition. Under these photochemical conditions, it is known that indene transforms into isoindene.77,78 Thus, [60]fullerene (10 mg, 0.014 mmol) was dissolved in toluene (50 mL) along with indene (160 μL, 100 equiv.) and the solution was degassed with argon in order to remove the oxygen. After 15 minutes, the flask was irradiated with a Hg lamp (300 W) and monitored by HPLC for 2–18 hours. [6,6] derivative 1a was the sole monoadduct obtained with 4–39% yield depending on the reaction time (see Fig. 3). On the other hand, the [5,6] adduct 1b was not observed. The reaction afforded the expected product in moderate yield together with pristine [60]fullerene, since longer reaction times lead to the formation of a mixture of regioisomeric bisadducts.Any other attempt to afford 1b by changing light wavelength, concentrations, and the molecular ratio failed (see Table S14 in the ESI†). In particular, we hypothesized that no formation of 1b could be due to a further photochemically induced rearrangement that could convert 1b into 1a. However, efforts to avoid such rearrangement by using chemical filters or sensitizers (see ESI†) gave rise to 1a or prevented the reaction, since no selective sensitization of the sole fullerene triplet affording 1b occurred. It is worth noting that this hypothetic photochemically induced rearrangement is not supported by our computational results (vide infra, Fig. 4 and Fig. S1, ESI†) showing that, in the T1 state, the [5,6] product is more stable than the [6,6] one by ΔG = 4.7 kcal mol−1. Therefore, in the case of the existence of a possible rearrangement in the T1 state, the accumulated product would be [5,6] and not [6,6] as found experimentally.
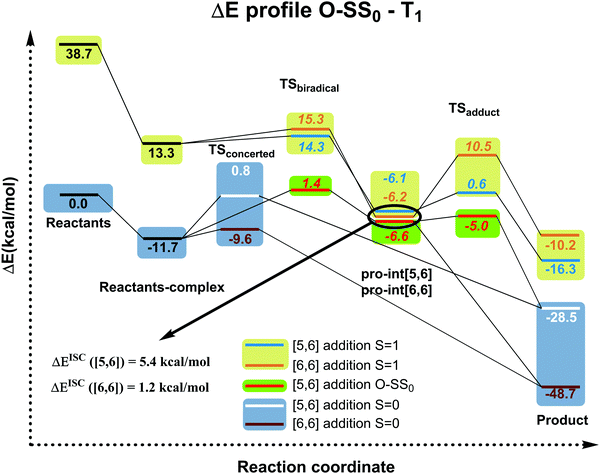 | ||
| Fig. 4 Electronic energy profiles (kcal mol−1) (see Fig. S1 (ESI†) for Gibbs energies in the gas-phase and in toluene solution) for the reaction between C60 and isoindene in the closed or open-shell (O–S) singlet and triplet states at the B3LYP-D3/6-31G(d) level (ΔEISC([5,6]) = Ecrossing([5,6]) − Epro-int([5,6]T1); ΔEISC([6,6]) = Ecrossing([6,6]) − Epro-int([6,6]T1)). Values in italics correspond to biradical open-shell singlet species. | ||
Since the experimental results did not confirm our theoretical prediction, we decided to analyze computationally in more detail the photochemical DA cycloaddition between 3C60 and isoindene. Our aim was to see whether the use of a different diene (cyclopentadiene/isoindene) could explain the mismatch between experiments and computations. As previously found for cyclopentadiene, our calculations indicate that the DA addition of isoindene to C60 is concerted in the S0 state and stepwise in the T1 state. Table S7 (ESI†) collects the gas-phase Gibbs and electronic reaction energies and energy barriers for the [5,6] and [6,6] addition when the reaction takes place with isoindene in the S0 and T1 states (we also calculated the gas-phase Gibbs and electronic reaction energies and energy barriers considering indene as diene, see Table S10, ESI†). Generally, the lower energy barriers involved in the addition of isoindene indicate that this compound is more reactive than indene. Our results (Tables S7–S9, ESI†) using isoindene as diene show that the formation of the [6,6] adduct is more exergonic and has a lower energy barrier than that of the [5,6] adduct in the S0 state, whereas the opposite is found for the T1 state. Therefore, the inversion of regioselectivity should also be occurring in this case but experimentally only the [6,6] adduct is obtained. At the first glance, the computational and experimental results did not match. Nevertheless, it has been reported that 1C60 can undergo intersystem crossing to 3C60 with very high quantum yields.24 Thus, if a crossing point between the potential energy surfaces of the S0 and T1 states along the DA reaction exists, then it is likely that T1 states can be deactivated through this intersystem crossing quite effectively. At this point, it is difficult to observe if there is a crossing point or not because the mechanism is different (concerted reaction for the S0 ground state and stepwise addition for the T1 state). So, we decide to compute the energy profile in the open-shell singlet potential energy surface (PES) for the stepwise mechanism (Fig. 4). The closed- and open-shell singlet PESs coincide except in the region of the biradical intermediate. In the open-shell singlet case (Table S7, ESI†), the predicted regioselectivity coincides with that of the closed-shell singlet state case, thus favoring the [6,6] addition although differences in energy barriers for the two additions are smaller. In the open-shell singlet PES, we have been unable to locate the transition state for the last step of the [6,6] addition. A linear-transit calculation for the transformation of pro-int[6,6] into the adduct has shown that it is a barrierless process. It is worth highlighting that the open-shell singlet character is detected only in TSbiradical, pro-int[5,6], pro-int[6,6], and TSadduct[5,6] species. If we analyze the energy profile (Fig. 4) and the molecular structures shown in Fig. 5, we observe that the pro-int[5,6] and pro-int[6,6] are the most suitable structures for being close to crossing state points. Indeed, the fact that these structures are not far from crossing points was confirmed using Harvey's method79,80 to locate spin-crossing points (Fig. 5). The intersystem crossing (ISC) energies (ΔEISC[5,6] and ΔEISC[6,6]) are calculated as the difference between the crossing point energy and the pro-int[5,6] or pro-int[6,6] energy in their T1 state. ΔEISC([5,6]) and ΔEISC([6,6]) are 5.4 and 1.2 kcal mol−1, respectively. Thus, based on our computations, when pro-int[5,6] is formed in the T1 state, it can fall to the open-shell S0 state through an ISC by surmounting a barrier of 5.4 kcal mol−1. Once pro-int[5,6] is formed in the open-shell S0 state, the [5,6] adduct can be formed (energy barrier is only ΔE‡ = 1.6 kcal mol−1) (Table S7, ESI†). The transformation of pro-int[5,6]T1 into the [5,6]S0 adduct releases 21.9 kcal mol−1. This means that this process is reversible at 40 °C. Otherwise, if pro-int[6,6]T1 is formed first or is obtained after rotation of pro-int[5,6]T1 (rotation barriers of ca. 7 kcal mol−1, see Table S6, ESI†), pro-int[6,6]T1 can be converted from T1 to S0 through an ISC with a barrier of only 1.2 kcal mol−1 to get the [6,6] adduct in a barrierless process. The transformation of pro-int[6,6]T1 into the [6,6]S0 adduct releases 43.1 kcal mol−1 and, therefore, it is an irreversible process at 40 °C. Therefore, our computational results indicate that the [6,6] adduct should be the major product formed in the DA of isoindene to 3C60, as found experimentally.
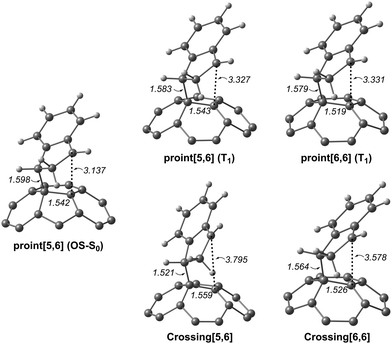 | ||
| Fig. 5 The molecular structure (distances in Å) of the biradical open-shell singlet (OS-S0) and triplet (T1) intermediates and crossing points. | ||
Conclusions
We have computationally studied the Diels–Alder reaction between C60 and cyclopentadiene in the ground and high spin excited states. In high spin states, the most favored product is the [5,6] adduct, whereas in the ground state it is the [6,6] product. The origin of this change in the regioselectivity is connected with the aromatic character of the molecular cage. Despite the fact that our computations predict a change in regioselectivity when moving from S0 to T1 energy profiles, the experimental results show that the Diels–Alder between isoindene and photoexcited 3C60 also generates the [6,6] adduct instead of the [5,6] one. Analyzing the reaction in more detail, we have computationally found that in the T1 state the reaction goes through an intersystem crossing to reach the S0 state. When this occurs, the reaction ends in the ground state giving the [6,6] product. It remains to be seen yet whether the change of regioselectivity could be effective in spin states higher than the T1 state.Author contribution
M. S. conceived the project, coordinated the research, co-wrote the paper, and coordinated the paper composition. O. E. B. and M. G.-B. carried out the quantum chemical calculations, and co-wrote the paper. N. M. and S. F. designed the reactions, interpreted the data and co-wrote the paper. R. M. G. conducted the reactions.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
We are grateful for financial support from the Spanish Ministerio de Economía y Competitividad (MINECO) for projects CTQ2014-52045-R and CTQ2017-85341-P. N. M. thanks the European Research Council (ERC-320441-Chirallcarbon) and the Comunidad Autónoma de Madrid (FOTOCARBON project S2013/MIT-2841). O. E. B., M. G.-B., and M. S. acknowledge the Catalan DIUE (project 2014SGR931 and XRQTC), and the FEDER fund (UNGI10-4E-801). M. S. is grateful to the Generalitat de Catalunya for the ICREA Academia 2014 Award. M. G.-B. thanks the Spanish MECD for a PhD grant (AP2010-2517) and the Ramón Areces Foundation for a postdoctoral fellowship. O. E. B. is grateful to the Generalitat de Catalunya (grant no. 2014FI_B 00429) and R. M. G. thanks the Spanish MECD for a FPU grant (FPU13/03677). Excellent service from computational centers CSUC and BSC-CNS is acknowledged.References
- N. Martín, B. Elliott, J. S. Hudson, A. Amirkhanian, L. Echegoyen, D. M. Guldi, E. Vázquez, M. Prato, D. Zhu, H. Imahori, S. Fukumuzi and S. Nagase, New challenges in fullerene chemistry, Chem. Commun., 2006, 2093–2104 RSC.
- N. Martín, M. Altable, S. Filippone and A. Martín-Domenech, New Reactions in Fullerene Chemistry, Synlett, 2007, 3077–3095 CrossRef.
- M. N. Chaur, F. Melin, A. L. Ortiz and L. Echegoyen, Chemical, Electrochemical, and Structural Properties of Endohedral Metallofullerenes, Angew. Chem., Int. Ed., 2009, 48, 7514–7538 CrossRef CAS PubMed.
- M. Yamada, T. Akasaka and S. Nagase, Endohedral Metal Atoms in Pristine and Functionalized Fullerene Cages, Acc. Chem. Res., 2010, 43, 92–102 CrossRef CAS PubMed.
- V. V. Chaban, E. E. Fileti and O. V. Prezhdo, Buckybomb: Reactive molecular dynamics simulation, J. Phys. Chem. Lett., 2015, 6, 913–917 CrossRef CAS PubMed.
- A. Hirsch, The chemistry of fullerenes, Top. Curr. Chem., 1999, 199, 1–65 CrossRef CAS.
- A. Hirsch and M. Brettreich, Fullerenes: Chemistry and Reactions, Wiley & Sons, Weinheim, 2005 Search PubMed.
- N. Martin, L. Sanchez, B. Illescas and I. Perez, C60-Based Electroactive Organofullerenes, Chem. Rev., 1998, 98, 2527–2547 CrossRef CAS PubMed.
- S.-J. Wang, Y. Li, Y.-F. Wang, D. Wu and Z.-R. Li, Structures and nonlinear optical properties of the endohedral metallofullerene-superhalogen compounds Li@C60-BX4 (X = F, Cl, Br), Phys. Chem. Chem. Phys., 2013, 15, 12903–12910 RSC.
- T. Miura, R. Tao, S. Shibata, T. Umeyama, T. Tachikawa, H. Imahori and Y. Kobori, Geometries, Electronic Couplings, and Hole Dissociation Dynamics of Photoinduced Electron–Hole Pairs in Polyhexylthiophene–Fullerene Dyads Rigidly Linked by Oligophenylenes, J. Am. Chem. Soc., 2016, 138, 5879–5885 CrossRef CAS PubMed.
- M. Rudolf, S. V. Kirner and D. M. Guldi, A multicomponent molecular approach to artificial photosynthesis – the role of fullerenes and endohedral metallofullerenes, Chem. Soc. Rev., 2016, 45, 612–630 RSC.
- B. C. Schroeder, Z. Li, M. A. Brady, G. C. Faria, R. S. Ashraf, C. J. Takacs, J. S. Cowart, D. T. Duong, K. H. Chiu, C.-H. Tan, J. T. Cabral, A. Salleo, M. L. Chabinyc, J. R. Durrant and I. McCulloch, Enhancing Fullerene-Based Solar Cell Lifetimes by Addition of a Fullerene Dumbbell, Angew. Chem., Int. Ed., 2014, 53, 12870–12875 CrossRef CAS PubMed.
- A. Hirsch, The Chemistry of Fullerenes, Thieme, Stuttgart, 1994 Search PubMed.
- C. Thilgen, A. Herrmann and F. Diederich, The Covalent Chemistry of Higher Fullerenes – C70 and Beyond, Angew. Chem., Int. Ed. Engl., 1997, 36, 2269–2280 CrossRef.
- F. N. Diederich, Covalent fullerene chemistry, Pure Appl. Chem., 1997, 69, 395–400 CrossRef CAS.
- E. L. Romero and L. Echegoyen, Electron spin resonance spectroscopy of empty and endohedral fullerenes, J. Phys. Org. Chem., 2016, 29, 781–792 CrossRef CAS.
- W. Fu, J. Zhang, T. Fuhrer, H. Champion, K. Furukawa, T. Kato, J. E. Mahaney, B. G. Burke, K. A. Williams, K. Walker, C. Dixon, J. Ge, C. Shu, K. Harich and H. C. Dorn, Gd2@C79N: Isolation, Characterization, and Monoadduct Formation of a Very Stable Heterofullerene with a Magnetic Spin State of S = 15/2, J. Am. Chem. Soc., 2011, 133, 9741–9750 CrossRef CAS PubMed.
- X. Dai, J. Han, Y. Gao and Z. Wang, De Novo Design of an Endohedral Heteronuclear Dimetallofullerene (U-Gd)@C60 with Exceptional Structural and Electronic Properties, ChemPhysChem, 2014, 15, 3871–3876 CrossRef CAS PubMed.
- T. Futagoishi, T. Aharen, T. Kato, A. Kato, T. Ihara, T. Tada, M. Murata, A. Wakamiya, H. Kageyama, Y. Kanemitsu and Y. Murata, A Stable, Soluble, and Crystalline Supramolecular System with a Triplet Ground State, Angew. Chem., Int. Ed., 2017, 56, 4261–4265 CrossRef CAS PubMed.
- Z. Hu, B.-W. Dong, Z. Liu, J.-J. Liu, J. Su, C. Yu, J. Xiong, D.-E. Shi, Y. Wang, B.-W. Wang, A. Ardavan, Z. Shi, S.-D. Jiang and S. Gao, Endohedral Metallofullerene as Molecular High Spin Qubit: Diverse Rabi Cycles in Gd2@C79 N, J. Am. Chem. Soc., 2018, 140, 1123–1130 CrossRef CAS PubMed.
- J.-S. Dang, J.-J. Zheng, W.-W. Wang and X. Zhao, Open-shell triplet character of (#6094)C68: spherical aromaticity, thermodynamic stability, and regioselective chlorination, Inorg. Chem., 2013, 52, 4762–4764 CrossRef CAS PubMed.
- Y.-Z. Tan, R.-T. Chen, Z.-J. Liao, J. Li, F. Zhu, X. Lu, S.-Y. Xie, J. Li, R.-B. Huang and L.-S. Zheng, Carbon arc production of heptagon-containing fullerene[68], Nat. Commun., 2011, 2, 420 CrossRef PubMed.
- K. Y. Amsharov, K. Ziegler, A. Mueller and M. Jansen, Capturing the antiaromatic (#6094)C68 carbon cage in the radio-frequency furnace, Chem. – Eur. J., 2012, 18, 9289–9293 CrossRef CAS PubMed.
- R. R. Hung and J. J. Grabowski, A precise determination of the triplet energy of carbon (C60) by photoacoustic calorimetry, J. Phys. Chem., 1991, 95, 6073–6075 CrossRef CAS.
- M. R. Wasielewski, M. P. O’Neil, K. R. Lykke, M. J. Pellin and D. M. Gruen, Triplet states of fullerenes C60 and C70. Electron paramagnetic resonance spectra, photophysics, and electronic structures, J. Am. Chem. Soc., 1991, 113, 2774–2776 CrossRef CAS.
- J. W. Arbogast, A. P. Darmanyan, C. S. Foote, F. N. Diederich, R. L. Whetten, Y. Rubin, M. M. Alvarez and S. J. Anz, Photophysical properties of sixty atom carbon molecule (C60), J. Phys. Chem., 1991, 95, 11–12 CrossRef CAS.
- Y. Wang, Photophysical properties of fullerenes and fullerene/N,N-diethylaniline charge-transfer complexes, J. Phys. Chem., 1992, 96, 764–767 CrossRef CAS.
- G. Vassilikogiannakis and M. Orfanopoulos, Stereochemistry and isotope effects of the [2+2] photocycloadditions of arylalkenes to C60. A stepwise mechanism, J. Am. Chem. Soc., 1997, 119, 7394–7395 CrossRef CAS.
- M. Hatzimarinaki, G. Vassilikogiannakis and M. Orfanopoulos, Stereochemistry and steric isotope effect on the [2+2] photocycloaddition of β,β-dimethyl-p-methoxystyrene to C60: the nature of the transition state structures, Tetrahedron Lett., 2000, 41, 4667–4670 CrossRef CAS.
- G. Vassilikogiannakis, M. Hatzimarinaki and M. Orfanopoulos, Mechanism of the [2+2] photocycloaddition of fullerene C60 with styrenes, J. Org. Chem., 2000, 65, 8180–8187 CrossRef CAS PubMed.
- S. R. Wilson, N. Kaprinidis, Y. Wu and D. I. Schuster, A new reaction of fullerenes: [2+2] photocycloaddition of enones, J. Am. Chem. Soc., 1993, 115, 8495–8496 CrossRef CAS.
- G. Vassilikogiannakis and M. Orfanopoulos, [2+2] Photocycloadditions of cis/trans-4-propenylanisole to C60. A step-wise mechanism, Tetrahedron Lett., 1997, 38, 4323–4326 CrossRef CAS.
- G. Vassilikogiannakis, N. Chronakis and M. Orfanopoulos, A new [2+2] functionalization of C60 with alkyl-substituted 1,3-butadienes: a mechanistic approach. Stereochemistry and isotope effects, J. Am. Chem. Soc., 1998, 120, 9911–9920 CrossRef CAS.
- G. Vassilikogiannakis and M. Orfanopoulos, Regio- and stereoselectivity of the [2+2] photocycloaddition of acyclic enones to C60, J. Org. Chem., 1999, 64, 3392–3393 CrossRef CAS PubMed.
- M. Hatzimarinaki, M. M. Roubelakis and M. Orfanopoulos, Biradical intermediate in the [2+2] photocycloaddition of dienes and alkenes to [60]fullerene, J. Am. Chem. Soc., 2005, 127, 14182–14183 CrossRef CAS PubMed.
- K. Mikami, S. Matsumoto, T. Tonoi, Y. Okubo, T. Suenobu and S. Fukuzumi, Solid state photochemistry for fullerene functionalization: solid state photoinduced electron transfer in the Diels–Alder reaction with anthracenes, Tetrahedron Lett., 1998, 39, 3733–3736 CrossRef CAS.
- K. Mikami, S. Matsumoto, Y. Okubo, M. Fujitsuka, O. Ito, T. Suenobu and S. Fukuzumi, Stepwise Bond Formation in Photochemical and Thermal Diels–Alder Reactions of C60 with Danishefsky's Dienes, J. Am. Chem. Soc., 2000, 122, 2236–2243 CrossRef CAS.
- S. Osuna, M. Swart and M. Solà, The Reactivity of Endohedral Fullerenes. What Can Be Learnt from Computational Studies?, Phys. Chem. Chem. Phys., 2011, 13, 3585–3603 RSC.
- A. A. Popov, S. Yang and L. Dunsch, Endohedral Fullerenes, Chem. Rev., 2013, 113, 5989–6113 CrossRef CAS PubMed.
- H. W. Kroto, The stability of the fullerenes Cn, with n = 24, 28, 32, 36, 50, 60 and 70, Nature, 1987, 329, 529–531 CrossRef CAS.
- M. Solà, J. Mestres, J. Martí and M. Duran, An AM1 Study of the Reactivity of Buckminsterfullerene (C60) in a Diels–Alder Model Reaction, Chem. Phys. Lett., 1994, 231, 325–330 CrossRef.
- I. Fernández, M. Solà and F. M. Bickelhaupt, Why Do Cycloaddition Reactions Involving C60 Prefer [6,6] over [5,6] Bonds?, Chem. – Eur. J., 2013, 19, 7416–7422 CrossRef PubMed.
- S. Osuna, R. Valencia, A. Rodríguez-Fortea, M. Swart, M. Solà and J. M. Poblet, Full Exploration of the Diels–Alder Cycloaddition on Metallofullerenes M3N@C80 (M = Sc, Lu, Gd): The D5hversus Ih Isomer and the Influence of the Metal Cluster, Chem. – Eur. J., 2012, 18, 8944–8956 CrossRef CAS PubMed.
- M. Garcia-Borràs, S. Osuna, M. Swart, J. M. Luis and M. Solà, Electrochemical control of the regioselectivity in the exohedral functionalization of C60: the role of aromaticity, Chem. Commun., 2013, 49, 1220–1222 RSC.
- M. Saunders, R. Berger, A. Jaffe, J. M. McBride, J. O’Neill, R. Breslow, J. M. Hoffmann, C. Perchonock, E. Wasserman, R. S. Hutton and V. J. Kuck, Unsubstituted cyclopentadienyl cation, a ground-state triplet, J. Am. Chem. Soc., 1973, 95, 3017–3018 CrossRef CAS.
- N. C. Baird, Quantum organic photochemistry. II. Resonance and aromaticity in the lowest 3ππ* state of cyclic hydrocarbons, J. Am. Chem. Soc., 1972, 94, 4941–4948 CrossRef CAS.
- H. Ottosson, Organic photochemistry: exciting excited-state aromaticity, Nat. Chem., 2012, 4, 969–971 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, rev E.01, Gaussian Inc., 2009 Search PubMed.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian-Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules (6-31G* basis set), J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- P. C. Hariharan and J. A. Pople, Influence of polarization functions on molecular-orbital hydrogenation energies, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- S. Grimme, J. Antony and S. Ehrlich, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. Swart, M. Güell, J. M. Luis and M. Solà, Spin-state-corrected Gaussian-type orbital basis sets, J. Phys. Chem. A, 2010, 114, 7191–7197 CrossRef CAS PubMed.
- S. Osuna, M. Swart and M. Solà, Dispersion corrections essential for the study of chemical reactivity in fullerenes, J. Phys. Chem. A, 2011, 115, 3491–3496 CrossRef CAS PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- N. A. Andreeva and V. V. Chaban, Electronic and thermodynamic properties of the amino- and carboxamido-functionalized C60-based fullerenes: towards non-volatile carbon dioxide scavengers, J. Chem. Thermodyn., 2018, 116, 1–6 CrossRef CAS.
- J. Kruszewski and T. M. Krygowski, Definition of aromaticity basing on the harmonic oscillator model, Tetrahedron Lett., 1972, 13, 3839–3842 CrossRef.
- T. M. Krygowski, Crystallographic studies of Inter- and Intra-Molecular Interactions Reflected in benzenoid Hydrocarbons. Nonequivalence of Indices of Aromaticity, J. Chem. Inf. Comput. Sci., 1993, 33, 70–78 CrossRef CAS.
- P. Bultinck, M. Rafat, R. Ponec, B. van Gheluwe, R. Carbó-Dorca and P. Popelier, Electron delocalization and aromaticity in linear polyacenes: atoms in molecules multicenter delocalization index, J. Phys. Chem. A, 2006, 110, 7642–7648 CrossRef CAS PubMed.
- J. Cioslowski, E. Matito and M. Solà, Properties of Aromaticity Indices Based on the One-Electron Density Matrix, J. Phys. Chem. A, 2007, 111, 6521–6525 CrossRef CAS PubMed.
- M. Garcia-Borràs, S. Osuna, J. M. Luis, M. Swart and M. Solà, The role of aromaticity in determining the molecular structure and reactivity of (endohedral metallo)fullerenes, Chem. Soc. Rev., 2014, 43, 5089–5105 RSC.
- M. Giambiagi, M. S. de Giambiagi, C. D. dos Santos and A. P. de Figueiredo, Multicenter bond indices as a measure of aromaticity, Phys. Chem. Chem. Phys., 2000, 2, 3381–3392 RSC.
- E. Matito, ESI-3D: Electron Sharing Indexes Program for 3D Molecular Space Partitioning, Institute of Computational Chemistry and Catalysis, Girona, Catalonia, Spain, 2006, http://iqc.udg.es/~eduard/ESI.
- E. Matito, M. Duran and M. Solà, The aromatic fluctuation index (FLU): a new aromaticity index based on electron delocalization, J. Chem. Phys., 2005, 122, 14109 CrossRef PubMed; E. Matito, M. Duran and M. Solà, J. Chem. Phys., 2006, 125, 059901 CrossRef.
- E. Matito, M. Solà, P. Salvador and M. Duran, Electron Sharing Indexes at the Correlated Level. Application to Aromaticity Measures, Faraday Discuss., 2007, 135, 325–345 RSC.
- F. Feixas, E. Matito, J. Poater and M. Solà, Quantifying aromaticity with electron delocalisation measures, Chem. Soc. Rev., 2015, 44, 6434–6451 RSC.
- T. A. Keith, AIMAll program (v. 14.11.23), TK Gristmill Software (aim.tkgristmill.com), Overland Park KS, USA, 2017 Search PubMed.
- X. Xiao, J. Sakamoto, M. Tanabe, S. Yamazaki, S. Yamabe and T. Matsumura-Inoue, Microwave synthesis and electrospectrochemical study on ruthenium(II) polypyridine complexes, J. Electroanal. Chem., 2002, 527, 33–40 CrossRef CAS.
- L. S. K. Pang and M. A. Wilson, Reactions of fullerenes C60 and C70 with cyclopentadiene, J. Phys. Chem., 1993, 97, 6761–6763 CrossRef CAS.
- L. M. Giovane, J. W. Barco, T. Yadav, A. L. Lafleur, J. A. Marr, J. B. Howard and V. M. Rotello, Kinetic stability of the fullerene C60-cyclopentadiene Diels–Alder adduct, J. Phys. Chem., 1993, 97, 8560–8561 CrossRef CAS.
- F. Feixas, E. Matito, J. Poater and M. Solà, On the performance of some aromaticity indices: a critical assessment using a test set, J. Comput. Chem., 2008, 29, 1543–1554 CrossRef CAS PubMed.
- F. Feixas, J. O. C. Jiménez-Halla, E. Matito, J. Poater and M. Solà, A Test to Evaluate the Performance of Aromaticity Descriptors in All-Metal and Semimetal Clusters. An Appraisal of Electronic and Magnetic Indicators of Aromaticity, J. Chem. Theory Comput., 2010, 6, 1118–1130 CrossRef CAS.
- M. Solà, F. Feixas, J. O. C. Jiménez-Halla, E. Matito and J. Poater, A Critical Assessment of the Performance of Magnetic and Electronic Indices of Aromaticity, Symmetry, 2010, 2, 1156–1179 CrossRef.
- L. Zhao, R. Grande-Aztatzi, C. Foroutan-Nejad, J. M. Ugalde and G. Frenking, Aromaticity, the Hückel 4
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n + 2 Rule and Magnetic Current, ChemistrySelect, 2017, 2, 863–870 CrossRef CAS.
n + 2 Rule and Magnetic Current, ChemistrySelect, 2017, 2, 863–870 CrossRef CAS. - A. Puplovskis, J. Kacens and O. Neilands, New route for [60]fullerene functionalisation in [4+2] cycloaddition reaction using indene, Tetrahedron Lett., 1997, 38, 285–288 CrossRef.
- G. W. Griffin, A. F. Marcantonio, H. Kristinsson, R. C. Petterson and C. S. Irving, Photocyclization of propenes to cyclopropanes novel phenyl and hydrogen migrations in π, π systems, Tetrahedron Lett., 1965, 6, 2951–2958 CrossRef.
- J. J. McCullough, o-Xylylenes and isoindenes as reaction intermediates, Acc. Chem. Res., 1980, 13, 270–276 CrossRef CAS.
- J. N. Harvey, M. Aschi, H. Schwarz and W. Koch, The singlet and triplet states of phenyl cation. A hybrid approach for locating minimum energy crossing points between non-interacting potential energy surfaces, Theor. Chem. Acc., 1998, 99, 95–99 CrossRef CAS.
- R. Poli, J. N. Harvey, H.-B. Kraatz, R. Poli and T. R. Cundari, Spin forbidden chemical reactions of transition metal compounds. New ideas and new computational challenges, Chem. Soc. Rev., 2003, 32, 1–8 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Cartesian coordinates and energies of all species involved, the aromaticity results (HOMA, MCI, and INB), Gibbs and electronic reaction energies and energy barriers for the reaction between 2S+1C60 (S = 0–6) and cyclopentadiene as well as for the reaction between 2S+1C60 (S = 0, 1) and isoindene/indene, and the experimental results with different reagent concentrations, type of irradiation, and conditions for the cycloaddition of indene and C60. See DOI: 10.1039/c7cp07965f |
| This journal is © the Owner Societies 2018 |