Open Access Article
Open Access Article“Where does the fluorescing moiety reside in a carbon dot?” – Investigations based on fluorescence anisotropy decay and resonance energy transfer dynamics†
Ananya
Das
a,
Debjit
Roy
a,
Chayan K.
De
a and
Prasun K.
Mandal
 *ab
*ab
aDepartment of Chemical Sciences, Indian Institute of Science Education and Research (IISER) Kolkata, Mohanpur, West-Bengal 741246, India. E-mail: prasunchem@iiserkol.ac.in
bCentre for Advanced Functional Materials, Indian Institute of Science Education and Research (IISER) Kolkata, Mohanpur, West-Bengal 741246, India
First published on 19th December 2017
Abstract
It has been shown recently that aggregated dyes are responsible for very high fluorescence in a carbon dot (CD). However, what is the location of the fluorescing moiety in CD? Is it inside the CD or attached to the CD's surface? In order to answer these intriguing questions regarding the location of the fluorescing moiety in a CD, we performed rotational anisotropy decay dynamics and resonance energy transfer (RET) dynamics. Rotational correlation time of ∼120 picoseconds nullifies the fact that the whole CD is fluorescing. Instead, we can say that the fluorescing moiety is either embedded inside the CD or attached to the surface of the CD or linked to the CD through covalent bonds. From the fluorescence anisotropy decay dynamics in solvents of different viscosities, we could show that the fluorescing moiety is not attached to the surface of the CD or for that matter, the fluorescing moiety is not in a rigid environment inside the CD. RET dynamical analysis has shown that the time for RET (from CD to acceptor Rh123) is about 5.4 ns and the RET dynamics are independent of the acceptor concentration. Using RET dynamics, we could prove that the fluorescing moiety is not outside the CD; rather, it is inside the CD, but not in a rigid environment. The geometric distance between the fluorescing moiety of the CD and the acceptor (Rh123) has been obtained to be 4.55 nm. Using Förster formulation, the distance between the fluorescing moiety inside the CD and the acceptor Rh123 has been calculated to be 4.24 nm. Thus, we could not only reveal the exact location of the fluorescing moiety in a CD, but we could also demonstrate that unlike for many other nanomaterials, Förster formulation could explain the experimental observables regarding RET involving CD reasonably well.
Introduction
The unusual photoluminescent behaviour of carbon dots (CDs) has enthralled the researchers for quite some time.1–13 However, the origin and the mechanism of photoluminescence remains to be majorly debated. Some researchers have mentioned that the quantum confinement effect is responsible for the observed PL of CDs.14,15 Different views have been expressed in literature regarding the origin of PL in CDs. For example, (a) existence of different types of functional groups,16,17 (b) radiative recombination of self trapped excitons,18 (c) assembly of different emitters within the particle core,19 (d) their charge-transfer complexes formed with polar groups on the particle surface,20 (e) exciton-hole recombination,21 (f) delocalized surface states,22 (g) specific edge states23 or (h) free molecules.24 Recently, a few reports have shown that the high photoluminescence (PL) of carbon dots originates from an aromatic dye like structure.25–31 In a comprehensive review by Demchenko et al., it was suggested that the optical properties of CDs arise due to the formation of H-aggregate type excitonic states through dye like single emitters.29However, there are contradicting reports regarding the location of the fluorescing moiety of CD. Some researchers surmise that the fluorophore is attached to the surface,14,32 while other researchers assume that the fluorescing moiety is embedded inside or in the core of the CD.26 Hence, it is quite pertinent to know the answer of an apparently naive but difficult question: “what is the location of the fluorescing moiety in CD?”.
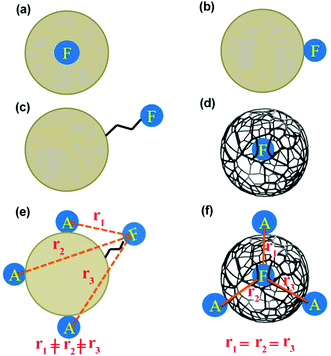
We have recently shown in two different cases that the PL of CDs is aggregation induced.30,31 This observation perhaps points to the fact that the fluorescing moiety is inside the CDs. However, CDs show pH dependent emission behaviour (for example PLQY).33 The latter observation perhaps points to the fact that the fluorescing moiety is at the surface of the CD. In this present work, we have used the same CD reported earlier.31 In order to answer the question regarding the location of fluorescing moiety in CD (Chart 1), we have performed two different fluorescence dynamic experiments: (a) fluorescence anisotropy decay dynamics and (b) resonance energy transfer (RET) dynamics.
 | ||
| Chart 1 Different possibilities regarding the location of fluorescing moiety (F) in CD. “A” means acceptor for RET. | ||
Fluorescence anisotropy measurements provide information regarding the shape, size and location of the fluorescing moiety.12 Rotational diffusion of the fluorophore significantly affects the fluorescence anisotropy. Rotational diffusion typically depends on the fluorophore's local chemical environment.
We have considered all the possible locations of the fluorescing unit of CD (see Chart 1). If the whole spherical CD is fluorescing, then we should not observe any fluorescence anisotropy decay.12 If the fluorescing moiety is attached to the CD surface through covalent bonds, then its rotational correlation time would be in the range of picoseconds (Chart 1). If the fluorescing moiety remains embedded inside the CD, then the rotation of the fluorescing moiety can lead to two different situations. If the fluorescing moiety is in a solid/rigid environment (Chart 1a), then the rotation of the fluorescing moiety means the rotation of the whole CD. In this condition, based on the size of the CD (∼8.3 nm), rotational correlation time should be in the nanosecond region. If the fluorescing moiety remains embedded inside the CD (Chart 1d) but not in a rigid matrix i.e. with ease of rotation, the rotational correlation time should be in the picosecond region. Moreover, if the fluorescing moiety can come in contact with the external solvent, then the rotational correlation time would be dependent on the viscosity of the external medium. Thus, the measurement of rotational correlation time can provide important information regarding the location of fluorescing moiety.
RET has been used as an important non-invasive technique to measure sub-nanometre to nanometre length scales.34 CDs have been used extensively for bioimaging.35 Hence, a RET based investigation is expected to provide spatial information, i.e., location of the fluorescing moiety of CD. It is quite essential to know the mechanism of RET in CDs as several applications in cellular environment using CDs are already in place.35 Based on the location of the fluorescing moiety in CD, the dynamics of RET will be different. Hence, an investigation based on dynamics of RET in CD is quite pertinent. In this study, RET experiment was performed in an aqueous medium keeping in mind the application of CD in the cellular environment.
Hence, the investigation based on RET dynamics will help us understand the location of the fluorescing moiety in CD. It has been reported in literature that numerous nanomaterials do not follow the Förster mechanism of RET.36–40 Therefore, this investigation based on RET dynamics will also verify whether the Förster mechanism can explain the experimental observations based on RET in the case of CD. Based on two rigorous fluorescence dynamic experiments, i.e., fluorescence anisotropy decay dynamics and resonance energy transfer dynamics, we would show that the fluorescing moiety resides inside the CD in a rather flexible environment. We would also demonstrate that Förster formulation could satisfactorily explain the experimental observables regarding RET involving CD.
Experimental methods
Materials
Ethanolamine and citric acid monohydrate were procured from Sigma Aldrich and were used as received. All solvents used are of HPLC grade.Synthesis and purification of carbon dot
Citric acid monohydrate and ethanolamine (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 molar ratio) were refluxed at 180 °C for 1 h (Fig. 1). A dark brown product was formed. This product was then fractionalized by column chromatography using 10
3 molar ratio) were refluxed at 180 °C for 1 h (Fig. 1). A dark brown product was formed. This product was then fractionalized by column chromatography using 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 90 MeOH
90 MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DCM. Then, the most fluorescent spot on the TLC plate was separated. Finally, the purified product was dried under high vacuum (10−3 mbar). (Thin Layer Chromatography (TLC) analysis was performed on a Merck Kieselgel 60 F254 plate using 100–200 mesh size silica gel.)
DCM. Then, the most fluorescent spot on the TLC plate was separated. Finally, the purified product was dried under high vacuum (10−3 mbar). (Thin Layer Chromatography (TLC) analysis was performed on a Merck Kieselgel 60 F254 plate using 100–200 mesh size silica gel.)
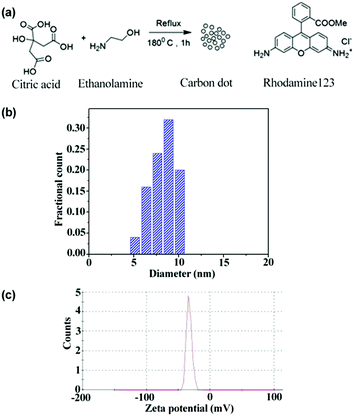 | ||
| Fig. 1 Synthesis scheme of CD and the chemical structure of Rh123 (a), size distribution from TEM (b), and zeta potential distribution of CD (c). | ||
Characterization
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, C
C, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, sp2 C–H, sp3 C–H, N–H, C–N, C–O have been confirmed.17 Proton NMR confirms the presence of amide proton (–CONH), hydroxyl proton (–OH), protons attached to sp2 (C
O, sp2 C–H, sp3 C–H, N–H, C–N, C–O have been confirmed.17 Proton NMR confirms the presence of amide proton (–CONH), hydroxyl proton (–OH), protons attached to sp2 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) carbon, protons of the methylene group (–CH2), which are attached to electronegative elements such as nitrogen and oxygen in ethanolamine, and protons (diastereotopic proton) of the methylene group of citric acid.31 In the MALDI mass spectrum, the molecular ion peak and the corresponding fragmented peaks have been detected.31 One broad peak in the Raman spectrum suggested the C
C) carbon, protons of the methylene group (–CH2), which are attached to electronegative elements such as nitrogen and oxygen in ethanolamine, and protons (diastereotopic proton) of the methylene group of citric acid.31 In the MALDI mass spectrum, the molecular ion peak and the corresponding fragmented peaks have been detected.31 One broad peak in the Raman spectrum suggested the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibration present within the CD. A broad peak at ∼22° implies the presence of (002) plane having a “d spacing” of ∼0.38 nm, which exactly matches the interplanar distance derived from HRTEM.31
C stretching vibration present within the CD. A broad peak at ∼22° implies the presence of (002) plane having a “d spacing” of ∼0.38 nm, which exactly matches the interplanar distance derived from HRTEM.31
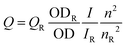 | (1) |
Time resolved measurements
Fluorescence lifetime measurement at ps–ns time domain was carried out using a time correlated single photon counting (TCSPC) spectrometer (Horiba Jobin Yvon IBH), equipped with a diode laser (λex = 377 nm) that was used as the excitation source and an MCP photomultiplier tube (PMT) (Hamamatsu R3809U-50 series) as the detector. The width (FWHM) of the instrument response function (IRF), which was limited by the FWHM of the exciting pulse, was less than 100 ps for 377 nm excitation source. IRF was recorded using a scatterer (a dilute solution of ludox in water). Nonlinear least square iterative reconvolution procedure using IBH DAS6 (Version 2.2) was employed to fit the fluorescence decay curve using a proper exponential decay equation. The quality of the fit was assessed from the χ2 values and the distribution of the residuals.Rotational anisotropy decay measurements
Time resolved rotational anisotropy data were collected via the same TCSPC setup using excitation and emission polarizers. Time-resolved fluorescence anisotropy, r(t), was calculated using the following equation: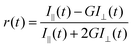 | (2) |
Results and discussion
In order to understand the dynamics of fluorescence anisotropy decay and RET, it is essential to determine the size of the CD. From the TEM measurement, the size of the CD is noted to be ∼8.5 nm (Fig. 1b). The recorded atomic force microscopy (AFM) image of CDs also suggested that the size of a CD is ∼8.1 nm (Fig. S1 in ESI†). Thus, the size of the CDs obtained from AFM and TEM are similar and is ∼8.3 nm. It is also important to know the surface charges on the CD. As can be observed from the zeta potential distribution (Fig. 1c), the surface charge on the CD is negative.Rotational anisotropy decay dynamics
Quite surprisingly, we observed a rotational anisotropy decay in the case of CD (Fig. 2). For a spherical fluorescing moiety (e.g. a spherical fluorophore or a spherical quantum dot with no particular direction of the transition dipole moment), it is expected that the fluorescence anisotropy would be absent.12,34 Observation of the rotational anisotropy decay with a correlation time of about 120 ps in ACN confirms that the whole spherical CD is not the fluorescing moiety.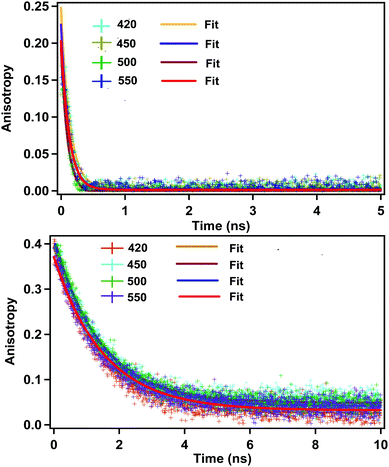 | ||
| Fig. 2 Rotational anisotropy decay in acetonitrile (above) and ethylene glycol (below) (λex = 377 nm). Monitoring wavelengths are shown in inset. Initial anisotropy in the case of ACN is around 0.25. | ||
From the classical Stokes–Einstein–Debye equation34 shown below
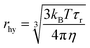 | (3) |
| Solvent | Viscosity at 25 °C (cP) | Monitoring wavelength (nm) | τ Rot (ns) | Hydrodynamic radius (nm) |
|---|---|---|---|---|
| Acetonitrile | 0.334 | 420 | 0.13 | 0.71 |
| 450 | 0.12 | |||
| 500 | 0.11 | |||
| 550 | 0.12 |
Four possibilities may arise regarding the location of the fluorescing moiety in CD as shown in Chart 1. In ‘a’ the fluorescing moiety is inside the CD in a rigid environment; in ‘b’ the fluorescing moiety is attached on to the CD surface; in ‘c’ the fluorescing moiety is attached to CD through a chemical bond; in ‘d’ the fluorescing moiety is inside the CD, but not in a rigid environment. If situation ‘a’ arises, then the rotational correlation time of the fluorescing moiety would be same as that of the CD. A similar situation would occur if situation ‘b’ arises. However, as mentioned in the previous section, experimentally determined rotational correlation time of the fluorescing moiety is much less than that for the whole CD. Thus, situations ‘a’ and ‘b’ can be nullified. If situation ‘c’ persists, then we should see a biexponential rotational anisotropy decay because of (i) rotation of only the fluorescing unit (in the range of hundreds of picoseconds) and (ii) long rotational correlation time (in several nanoseconds) for rotation of the whole system, i.e., the fluorescing unit attached to the CD. However, we have observed only one rotational correlation time in the order of hundreds of picoseconds. Thus, situation ‘c’ can also be nullified. However, there is a faint possibility that the contribution of nanosecond-domain rotation correlation time will have a lesser magnitude and hence, it may not be observed.
If situation ‘c’ arises, then we should observe two different rotational correlation times: one in the order of tens of picoseconds (only for the fluorescing unit) and the other in the order of a few nanoseconds (for the whole CD plus the fluorescing unit). However, if situation ‘d’ arises, then the rotational correlation time of the fluorescing moiety would be much less than that of the whole CD. Moreover, if situations ‘c’ and ‘d’ arise, the rotational correlation time would depend on the viscosity of the surrounding medium. This is exactly what has been observed experimentally. Rotational correlation times in acetonitrile, ethylene glycol, propylene glycol and glycerol were noted to be ∼0.12 ns, 1.32 ns, 4.10 ns and 31 ns respectively. If the fluorescing unit been a small fluorophore, we should have observed a rotational correlation time of approximately 10–50 ps. However, if the fluorescing unit is in a rigid environment, inside a CD of size ∼5–10 nm, then a rotational correlation time of greater than 15–20 ns could be expected.27 For situation ‘c’ we should have observed two different rotational correlation times: one in the order of tens of ps (arising due to the rotation of fluorescing unit only), and the other in the order of several ns (arising due to the rotation of fluorescing unit plus the CD). Nevertheless, we did not observe two different rotational correlation times. We have already reported31 that the fluorescing unit of our as-prepared CD exhibits an aggregated (through pi–pi and H-bonding) molecular dye-like (2-pyridone derivative) structure. Therefore, it is highly likely that, fluorescing unit is inside the CD and can rotate inside the CD with a rotational correlation time of ∼120 ps. Thus, based on the fluorescence anisotropy decay dynamics, out of the four possibilities/situations mentioned in Chart 1, ‘a’, ‘b’, and ‘c’ can be nullified completely; however, situation ‘d’ could be a possibility.
Resonance energy transfer dynamics
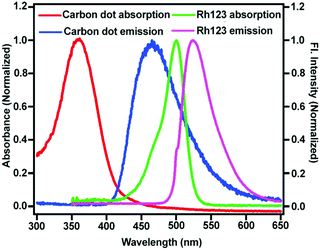
If the location of the fluorescing moiety is inside (more precisely at the centre) the CD, then the distance between the acceptor dye (Rhodamine 123 (Rh123) Fig. 1) and the fluorescing moiety will be the same (Chart 1f). Hence, the RET dynamics will be independent of acceptor concentration. However, if the fluorescing moiety is at the surface of the CD or is attached to the CD through a covalent bond, then the distance between the acceptor dye (Rh123) and the fluorescing moiety will be different in different CD-Rh123 hybrids (Chart 1e). Thus, in the latter case (Chart 1e), the energy transfer time from the fluorescing moiety to Rh123 will be different in different cases. In order to confirm that situation ‘d’ and not situation ‘c’ (Chart 1) represents the actual location of the fluorescing unit, we performed resonance energy transfer experiments.We chose Rhodamine 123 as the suitable organic dye to study the dynamics of RET (Fig. 1). The rationale behind this judicious choice are as follows: (a) Rh123 is positively charged and hence, it has a higher propensity to get attached to the negatively charged CD surface; (b) absorption spectrum of Rh123 significantly overlaps with the emission spectrum of the CD (Fig. 3), which is a necessary criterion to be fulfilled to observe RET process; (c) Rh123 is soluble in aqueous media; (d) to investigate the RET dynamics, it is necessary to choose a dye that will not be excited at the excitation wavelength of the laser diode (377 nm in our case, Fig. 1). Thus, only CD will be excited at the excitation wavelength (377 nm) and because of the spectral overlap between the emission spectrum of the CD and the absorption spectrum of the Rh123 (Fig. 3), RET phenomenon is expected to be observed from CD (donor) to Rh123 (acceptor).
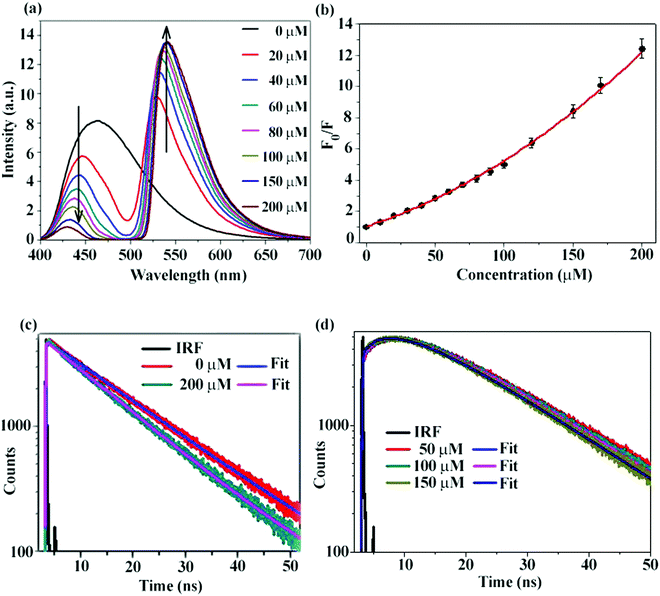
Reduction of the emission intensity of CD with increasing concentrations of Rh123 has been depicted in Fig. 4a. It is clearly noticed that with increase in acceptor concentration, donor emission is gradually decreased. We have also plotted the ratio of integrated emission of donor in the absence of acceptor (F0) to the integrated emission of donor in the presence of acceptor (F) against different concentrations of the acceptor (Fig. 4b). A non-linear plot with an intercept of one validates the Stern–Volmer (SV) relationship and hints towards the presence of both static and dynamic quenching. Validation of the SV relationship, however, does not indicate conclusively that RET is occurring. Since the CD is negatively charged and the Rh123 is positively charged, it is expected that the static quenching will be present. In order to conclusively prove that dynamic quenching is indeed present, we measured the fluorescence decay of CD in the absence and in the presence of Rh123. As shown in Fig. 4c, PL decay of the CD becomes faster in the presence of Rh123 and a gradual decrease of the fluorescence lifetime with an increase in acceptor concentration is noticed (Table 2). Thus, we can conclusively say that dynamic quenching is present in addition to static quenching. This observation, however, does not conclusively prove that RET is occurring.34,41
| Solvent | Donor amount | Acceptor concentration (μM) | τ (ns) for λem = 450 nm (donor) | χ 2 | τ (ns) for λem = 620 nm (acceptor) | χ 2 | |
|---|---|---|---|---|---|---|---|
| τ 1 (B1) | τ 2 (B2) | ||||||
| Water | 2 mg in 2.5 mL | 0 | 14.60 | 1.14 | — | — | — |
| 50 | 14.14 | 1.14 | 5.37 (−31.79) | 14.82 (131.79) | 1.05 | ||
| 100 | 13.46 | 1.20 | 5.52 (−35.79) | 14.24 (135.79) | 1.02 | ||
| 150 | 12.92 | 1.27 | 5.46 (−34.68) | 13.78 (134.68) | 0.99 | ||
| 200 | 12.51 | 1.28 | 5.37 (−32.33) | 13.44 (132.33) | 1.01 | ||
We have tried to understand the RET phenomenon using the Förster formulation.34 According to the Förster formulation, the necessary condition for RET is that there should be an overlap between the emission spectrum of the donor and the absorption spectrum of the acceptor. The magnitude of spectral overlap can be calculated using eqn (4).
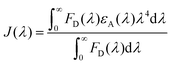 | (4) |
| R0 = 0.211[κ2η4QDJ(λ)]1/6 | (5) |
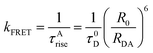 | (6) |
Furthermore, we would like to discuss the calculation of RET dynamics in detail. Let us consider that there is one acceptor per donor, i.e., the donor–acceptor stoichiometry is known and fixed (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). In the absence of the acceptor, suppose the rate constant of donor decay is k1. In the presence of the acceptor, since the RET channel is open that results in another channel of decay, let us suppose that the rate constant of RET is k2. Now, in presence of the acceptor the overall rate constant of decay of the donor will be k3 = k1 + k2. As k2 is a positive quantity, the magnitude of k3 will be higher than k1. This is why the donor decay becomes faster in the presence of an acceptor in comparison to the situation where the acceptor is not present. The acceptor, however, will not be excited directly; hence, the risetime of the acceptor will be equal to 1/k2. Hence, there will be 1
1). In the absence of the acceptor, suppose the rate constant of donor decay is k1. In the presence of the acceptor, since the RET channel is open that results in another channel of decay, let us suppose that the rate constant of RET is k2. Now, in presence of the acceptor the overall rate constant of decay of the donor will be k3 = k1 + k2. As k2 is a positive quantity, the magnitude of k3 will be higher than k1. This is why the donor decay becomes faster in the presence of an acceptor in comparison to the situation where the acceptor is not present. The acceptor, however, will not be excited directly; hence, the risetime of the acceptor will be equal to 1/k2. Hence, there will be 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 correspondence between donor-decay and acceptor-rise. This is particularly true for 1
1 correspondence between donor-decay and acceptor-rise. This is particularly true for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 donor–acceptor stoichiometry when both the donor and the acceptor are dyes. However, the situation becomes quite complicated when the donor becomes a nanoparticle or a quantum dot. It is well known in the nanoparticle/quantum dot community that the concentration of the nanoparticle/quantum dot inside a solution is very difficult to measure. In our measurements, the concentration of the dye is known. However, it is very difficult to know the concentration of CD precisely. Hence, it is even more difficult to predict the stoichiometry ratio of donor to acceptor. It could be possible for several nanoparticles/quantum dots to not have any acceptors in the vicinity. It is also possible to have more than one acceptor dye per nanoparticle/quantum dot. Thus, there is a possibility for different stoichiometric ratio of donor–acceptor to be present in the solution. Thus in this situation, the donor decay in the presence of a certain concentration of acceptor will have contributions from all these sub-ensembles. It is also quite understandable that 1
1 donor–acceptor stoichiometry when both the donor and the acceptor are dyes. However, the situation becomes quite complicated when the donor becomes a nanoparticle or a quantum dot. It is well known in the nanoparticle/quantum dot community that the concentration of the nanoparticle/quantum dot inside a solution is very difficult to measure. In our measurements, the concentration of the dye is known. However, it is very difficult to know the concentration of CD precisely. Hence, it is even more difficult to predict the stoichiometry ratio of donor to acceptor. It could be possible for several nanoparticles/quantum dots to not have any acceptors in the vicinity. It is also possible to have more than one acceptor dye per nanoparticle/quantum dot. Thus, there is a possibility for different stoichiometric ratio of donor–acceptor to be present in the solution. Thus in this situation, the donor decay in the presence of a certain concentration of acceptor will have contributions from all these sub-ensembles. It is also quite understandable that 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 correspondence of additional donor decay rate constant (1/(k3 − k1)) and acceptor rise time (1/k2) will not be observed in nanoparticle/quantum dot (donor)–dye (acceptor) hybrid, in this situation. Hence, it is quite difficult to calculate the RET dynamics in these systems from donor decay. There is a high chance that it will not be accurate. Instead, it is more straight forward and much more accurate to calculate the RET dynamics from acceptor risetime.
1 correspondence of additional donor decay rate constant (1/(k3 − k1)) and acceptor rise time (1/k2) will not be observed in nanoparticle/quantum dot (donor)–dye (acceptor) hybrid, in this situation. Hence, it is quite difficult to calculate the RET dynamics in these systems from donor decay. There is a high chance that it will not be accurate. Instead, it is more straight forward and much more accurate to calculate the RET dynamics from acceptor risetime.
In order to prove that RET is indeed occurring and to calculate the time constant of RET dynamics, we investigated the fluorescence decay of the acceptor, i.e., Rh123. Since the acceptor will not be directly excited at the excitation wavelength (377 nm), if RET occurs, then we should observe a rise in the fluorescence decay curve of Rh123, followed by the decay. If a rise could be observed, then the dynamics of the RET could also be calculated by fitting the fluorescence decay profile of Rh123. As shown in Fig. 4d, in the fluorescence decay profile of Rh123, a clear rise could be observed, which conclusively proves that RET is indeed occurring from CD (as donor) to Rh123 (as acceptor). By fitting the decay profile of Rh123, the time constant for the RET dynamics was calculated to be 5.4 ns in water. It is worth mentioning here that carbon nano-tubes/particles are known to quench fluorescence.42,43 However, in our study, we showed that CD can act as a donor in RET phenomena. Out of the four possible situations depicted in Chart 1, ‘a’ and ‘b’ were nullified using fluorescence anisotropy decay dynamics. If situation ‘c’ is occurring, then as the concentration of the positively charged acceptor (Rh123) increases, the location at which the acceptor will get attached to the negatively charged CD surface will be different (Chart 1e). Thus, as the concentration of the acceptor increases the distance between the donor and the acceptor will change (Chart 1e).
Hence, the dynamics of RET from the donor to the acceptor should change with increasing acceptor (Rh123) concentration if situation ‘c’ pertains. If the fluorescing moiety (shown as F) is at the core of the negatively charged CD (situation ‘d’), then, even on the increasing concentration of the positively charged acceptor (Rh123), the distance between the donor and the acceptor will not change (Chart 1f). Hence, with increasing concentration of Rh123, the dynamics of RET will not change.
As shown in Fig. 4d, the dynamics of RET does not change even when the concentration of Rh123 increases in several folds. Thus, RET dynamical investigation establishes that situation ‘d’ represents the actual location of the fluorescing unit and not situation ‘c’ (or for that matter, not situations ‘a’ or ‘b’). Thus, using fluorescence anisotropy decay dynamics as well as RET dynamics, we could demonstrate that situation ‘d’ represents the actual location of the fluorescing unit. Thus, we could show that the fluorescing moiety remains at the core of the CD in a rather flexible environment.
We have already reported that our CD comprises an aggregated (through pi–pi and H-bonding) molecular dye (2-pyridone derivative) as the fluorescing moiety; around this moiety exists a condensed acyclic framework with no electronic coupling between the fluorescing unit and the surrounding framework.31 This proposition is in consonance with the current proposition that the fluorescing unit is inside the CD structure.
It is expected that during the formation of CD, the outer framework will be there in equal proportions in all directions surrounding the aggregated fluorescing unit. Hence, an isotropic structure will be formed and the formation of an anisotropic structure is less likely. However, since the particle size is less than 10 nm, it would be very difficult to say whether the fluorescing unit is exactly (with a spatial precision of sub-nm length scale) at the centre. However, it is expected that the fluorescing unit will definitely be inside the CD if not exactly at the centre. Thus, the average distance between the fluorescing unit in CD (donor) and the Rh123 dye (acceptor) will be the same.
Model ‘e’ (originating from model ‘c’) cannot explain the acceptor concentration independence of RET dynamics. Moreover, for model ‘e’ (originating from model ‘c’), we should have observed two different rotational correlation times: one in the order of tens of ps (arising due to the rotation of fluorescing unit only) and the other in the order of several ns (arising due to the rotation of fluorescing unit plus the CD). However, we did not experimentally observe two different rotational correlation times. Furthermore, for model ‘e’ (originating from model ‘c’), we should have observed a donor–acceptor distance (obtained following the Förster formulation) that is different from the geometrical distance between the donor and the acceptor. Hence, model ‘e’ does not fit with our experimental observations. It is model ‘f’ (originating from model ‘d’), which can explain that the acceptor concentration is independent of RET dynamics. Model ‘f’ is also consistent with observed correlation time of ∼120 ps (for the aggregated dye structures).
Validity of the Förster model
From the physical model, the core to core distance between CD and Rh123 has been calculated to be ∼[(8.3 + 0.8)/2] nm, which is ∼4.55 nm more than the experimental parameters (for CD: from TEM and AFM, for Rh123: from geometry optimization (see ESI†)). Using the Förster model, the core to core distance (CD to Rh123) has been obtained to be about 4.24 nm (Table S2 in ESI†). Thus, the Förster model predicted value and the experimentally obtained donor to acceptor distance values are quite similar and within the experimental error limit of <10%. Thus, we could conclude that unlike for many nanomaterials,36–40 Förster formulation could successfully explain the experimental observations related to RET process involving CD with reasonable accuracy. Assuming model ‘f’ to be the valid model, the donor–acceptor distance from the Förster model and the geometrical distance between the donor and the acceptor matches quite well. We would like to mention here that a similar calculation has been performed and reported in literature for QDs.44 The fact that only RET occurs and no other process (such as exciplex formation etc.) is operating was confirmed by several control experiments (see ESI† for details of control experiments).Conclusion
In order to answer an intriguing question regarding the location of the fluorescing moiety in a CD, we performed rotational anisotropy decay dynamics and RET dynamics. Rotational correlation time of about 120 picosecond nullifies the fact that the whole CD is fluorescing. Instead, the fluorescing moiety could either be embedded inside the CD or attached to the surface of the CD or attached to the CD through covalent bonds. From the fluorescence anisotropy decay dynamics, we could nullify the situations, in which the fluorescing moiety is attached to the surface of CD or the fluorescing moiety is in a rigid environment inside the CD. RET dynamical analysis showed that the time required for RET (from CD to acceptor Rh123) is about 5.4 ns and the RET dynamics are independent of the acceptor concentration. Using fluorescence anisotropy decay dynamics and RET dynamics, and by nullifying other possibilities, we could establish that the fluorescing moiety is inside the flexible core environment of CD. The geometric distance between the fluorescing moiety of the CD and the acceptor (Rh123) has been obtained to be 4.55 nm. Using the Förster formulation, the distance between the fluorescing moiety inside the CD and the acceptor Rh123 has been calculated to be 4.24 nm. Thus, we could also show that unlike for many other nanomaterials, Förster formulation could explain the experimental observations related to CD's RET, reasonably well.Conflicts of interest
There are no conflicts to declare.Acknowledgements
PKM thanks IISER-Kolkata for financial help and instrumental facilities. Support from the CSIR India, Project No. 01(2848)/16/EMR-II is gratefully acknowledged. AD and DR thank CSIR, and CKD thanks DST-INSPIRE for respective fellowship.Notes and references
- S. N. Baker and G. A. Baker, Angew. Chem., Int. Ed., 2010, 49, 6726–6744 CrossRef CAS PubMed.
- S. Kalytchuk, K. Polakova, Y. Wang, J. P. Froning, K. Cepe, A. L. Rogach and L. R. Zboril, ACS Nano, 2017, 11, 1432–1442 CrossRef CAS PubMed.
- L. Zhao, F. Di, D. Wang, L.-H. Guo, Y. Yang, B. Wan and H. Zhang, Nanoscale, 2013, 5, 2655–2658 RSC.
- Y. Hu, M. M. A. Awak, F. Yang, S. Yan, Q. Xiong, P. Wang, Y. Tang, L. Yang, G. E. LeCroy, X. Hou, C. E. Bunker, L. Xu, N. Tomlinsona and Y.-P. Sun, J. Mater. Chem. C, 2016, 4, 10554–10561 RSC.
- Y. Liu, P. Wang, K. A. S. Fernando, G. E. LeCroy, H. Maimaiti, B. A. H. Miller, W. K. Lewis, C. E. Bunker, Z.-L. Houa and Y.-P. Sun, J. Mater. Chem. C, 2016, 4, 6967–6974 RSC.
- X. Zhang, Y. Zhang, Y. Wang, S. Kalytchuk, S. V. Kershaw, Y. Wang, P. Wang, T. Zhang, Y. Zhao, H. Zhang, T. Cui, Y. Wang, J. Zhao, W. W. Yu and A. L. Rogach, ACS Nano, 2013, 7, 11234–11241 CrossRef CAS PubMed.
- Y. Wang, S. Kalytchuk, Y. Zhang, H. C. Shi, S. V. Kershaw and A. L. Rogach, J. Phys. Chem. Lett., 2014, 5, 1412–1420 CrossRef CAS PubMed.
- W. Chung, H. Jung, C. H. Lee and S. H. Kim, J. Mater. Chem. C, 2014, 2, 4227–4232 RSC.
- B. De and N. Karak, RSC Adv., 2013, 3, 8286–8290 RSC.
- F. Wang, M. Kreiter, B. He, S. Pang and C.-Y. Liu, Chem. Commun., 2010, 46, 3309–3311 RSC.
- W. Liu, C. Li, Y. Ren, X. Sun, W. Pan, Ya. Li,J. Wang and W. Wang, J. Mater. Chem. B, 2016, 4, 5772–5788 RSC.
- M. O. Dekaliuk, O. Viagin, Y. V. Malyukin and A. P. Demchenko, Phys. Chem. Chem. Phys., 2014, 16, 16075–16084 RSC.
- T. Zhang, J. Zhu, Y. Zhai, H. Wang, X. Bai, B. Dong, H. Wang and H. Song, Nanoscale, 2017, 9, 13042–13051 RSC.
- Y.-P. Sun, B. Zhou, Y. Lin, W. Wang, K. A. Shiral Fernando, P. Pathak, M. J. Meziani, B. A. Harruff, X. Wang, H. Wang, P. G. Luo, H. Yang, M. E. Kose, B. Chen, L. M. Veca and S.-Y. Xie, J. Am. Chem. Soc., 2006, 128, 7756–7757 CrossRef CAS PubMed.
- K. Linehan and H. Doyle, J. Mater. Chem. C, 2014, 2, 6025–6031 RSC.
- R. Wang, K.-Q. Lu, Z. Tang and Y. J. Xu, J. Mater. Chem. A, 2017, 5, 3717–3734 CAS.
- X. Li, H. Wang, Y. Shimizu, A. Pyatenko, K. Kawaguchi and N. Koshizaki, Chem. Commun., 2011, 47, 932–934 RSC.
- L. Xiao, Y. Wang, Y. Huang, T. Wong and H. Sun, Nanoscale, 2017, 9, 12637–12646 RSC.
- M. Fu, F. Ehrat, Y. Wang, K. Z. Milowska, C. Reckmeier, A. L. Rogach, J. K. Stolarczyk, A. S. Urban and J. Feldmann, Nano Lett., 2015, 15, 6030–6035 CrossRef CAS PubMed.
- C. Galande, A. D. Mohite, A. V. Naumov, W. Gao, L. Ci, A. Ajayan, H. Gao, A. Srivastava, R. B. Weisman and P. M. Ajayan, Sci. Rep., 2011, 1, 85, DOI:10.1038/srep00085.
- D. Qu, M. Zheng, L. Zhang, H. Zhao, Z. Xie, X. Jing, R. E. Haddad, H. Fan and Z. Sun, Sci. Rep., 2014, 4, 5294, DOI:10.1038/srep05294.
- A. Sciortino, A. Cayuela, M. L. Soriano, F. M. Gelardi, M. Cannas, M. Valcárcel and F. Messina, Phys. Chem. Chem. Phys., 2017, 19, 22670–22677 RSC.
- L. Wang, S.-J. Zhu, H.-Y. Wang, S.-N. Qu, Y.-L. Zhang, J.-H. Zhang, Q.-D. Chen, H.-L. Xu, W. Han and B. Yang, ACS Nano, 2014, 8(3), 2541–2547 CrossRef CAS PubMed.
- M. Righetto, M. L. Curri, R. Bozio, A. Privitera, M. Corricelli, C. Ferrante, I. Fortunati, A. Moretto, D. Mosconi, S. Agnoli, M. Zerbetto and L. Franco, J. Phys. Chem. Lett., 2017, 8, 2236–2242 CrossRef CAS PubMed.
- L. Wang, S.-J. Zhu, H.-Y. Wang, Y.-F. Wang, Y.-W. Haoo, J.-H. Zhang, Q.-D. Chen, Y.-L. Zhang, W. Han, B. Yang and H.-B. Sun, Adv. Opt. Mater., 2013, 1, 264–271 CrossRef.
- S. K. Das, Y. Liu, S. Yeom, D. Y. Kim and C. I. Richards, Nano Lett., 2014, 14, 620–625 CrossRef CAS PubMed.
- S. Ghosh, A. M. Chizhik, N. Karedla, M. O. Dekaliuk, I. Gregor, H. Schuhmann, M. Seibt, K. Bodensiek, I. A. T. Schaap, O. Schulz, A. P. Demchenko, J. Enderlein and A. I. Chizhik, Nano Lett., 2014, 14, 5656–5661 CrossRef CAS PubMed.
- Y. Song, S. Zhu, S. Zhang, Y. Fu, L. Wang, X. Zhao and B. Yang, J. Mater. Chem. C, 2015, 3, 5976–5984 RSC.
- A. P. Demchenko and M. O. Dekaliuk, Nanoscale, 2016, 8, 14057–14069 RSC.
- V. Gude, A. Das, T. Chatterjee and P. K. Mandal, Phys. Chem. Chem. Phys., 2016, 18, 28274–28280 RSC.
- A. Das, V. Gude, D. Roy, T. Chatterjee, C. K. De and P. K. Mandal, J. Phys. Chem. C, 2017, 121, 9634–9641 CAS.
- S.-L. Hu, K.-Y. Niu, J. Sun, J. Yang, N.-Q. Zhao and X.-W. Du, J. Mater. Chem., 2009, 19, 484–488 RSC.
- X. F. Jia, J. Lia and E. K. Wang, Nanoscale, 2012, 4, 5572–5575 RSC.
- J. R. Lakowicz, Principles of Fluorescence Spectroscopy, Springer, New York, 3rd edn, 2006 Search PubMed.
- S. Zhu, Q. Meng, L. Wang, J. Zhang, Y. Song, H. Jin, K. Zhang, H. Sun, H. Wang and B. Yang, Angew. Chem., Int. Ed., 2013, 52, 3953–3957 CrossRef CAS PubMed.
- D. Beljonne, C. Curutchet, G. D. Scholes and R. J. Silbey, J. Phys. Chem. B, 2009, 113, 6583–6599 CrossRef CAS PubMed.
- F. Aldeek, X. Ji and H. Mattoussi, J. Phys. Chem. C, 2013, 117, 15429–15437 CAS.
- W. R. Algar, H. Kim, I. L. Medintz and N. Hildebrandt, Coord. Chem. Rev., 2014, 263, 65–85 CrossRef.
- M. H. Stewart, A. L. Huston, A. M. Scott, A. L. Efros, J. S. Melinger, K. B. Gemmill, S. A. Trammell, J. B. Blanco-Canosa, P. E. Dawson and I. L. Medintz, ACS Nano, 2012, 6, 5330–5343 CrossRef CAS PubMed.
- S. Saini, G. Srinivas and B. Bagchi, J. Phys. Chem. B, 2009, 113, 1817–1832 CrossRef CAS PubMed.
- K. Santhosh, S. Patra, S. Soumya, D. C. Khara and A. Samanta, ChemPhysChem, 2011, 12, 2735–2741 CrossRef CAS PubMed.
- C. F. Chiu, N. Dementev and E. Borguet, J. Phys. Chem. A, 2011, 115, 9579–9584 CrossRef CAS PubMed.
- P. J. Goutam, D. K. Singh and P. K. Iyer, J. Phys. Chem. C, 2012, 116, 8196–8201 CAS.
- T. Ren, P. K. Mandal, W. Erker, Z. Liu, Y. Avlasevich, L. Puhl, K. Müllen and T. Basche, J. Am. Chem. Soc., 2008, 130, 17242–17243 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp07411e |
| This journal is © the Owner Societies 2018 |