Singlet–triplet energy gaps and the degree of diradical character in binuclear copper molecular magnets characterized by spin-flip density functional theory†
Abstract
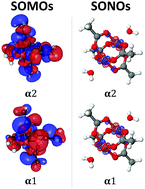
Molecular magnets, defined here as organic polyradicals, can be used as building blocks in the fabrication of novel and structurally diverse magnetic light-weight materials. We present a theoretical investigation of the lowest spin states of several binuclear copper diradicals. In contrast to previous studies, we consider not only the energetics of the low-lying states (which are related to the exchange-coupling parameter within the Heisenberg–Dirac–van-Vleck model), but also the character of the diradical states themselves. We use natural orbitals, their occupations, and the number of effectively unpaired electrons to quantify bonding patterns in these systems. We compare the performance of spin-flip time-dependent density functional theory (SF-TDDFT) using various functionals and effective core potentials against the wave function based approach, equation-of-motion spin-flip coupled-cluster method with single and double substitutions (EOM-SF-CCSD). We find that SF-TDDFT paired with the PBE50 and B5050LYP functionals performs comparably to EOM-SF-CCSD, with respect to both singlet–triplet gaps and states' characters. Visualization of frontier natural orbitals shows that the unpaired electrons are localized on copper centers, in some cases exhibiting slight through-bond interaction via copper d-orbitals and p-orbitals of neighboring ligand atoms. The analysis reveals considerable interactions between the formally unpaired electrons in the antiferromagnetic diradicaloids, meaning that they are poorly described by the Heisenberg–Dirac–van-Vleck model. Thus, for these systems the experimentally derived exchange-coupling parameters are not directly comparable with the singlet–triplet gaps. This explains systematic discrepancies between the computed singlet–triplet energy gaps and the exchange-coupling parameters extracted from experiment.


 Please wait while we load your content...
Please wait while we load your content...