The aggregation of an alkyl–C₆₀ derivative as a function of concentration, temperature and solvent type

Abstract

Contrast-variation small-angle neutron scattering (CV-SANS), small-angle X-ray scattering (SAXS), nuclear magnetic resonance (NMR) measurements of diffusion and isothermal titration calorimetry (ITC) are used to gain insight into the aggregation of an alkyl–C₆₀ derivative, molecule 1, in n-hexane, n-decane and toluene as a function of concentration and temperature. Results point to an associative mechanism of aggregation similar to other commonly associating molecules, including non-ionic surfactants or asphaltenes in non-aqueous solvents. Little aggregation is detected in toluene, but small micelle-like structures form in n-alkane solvents, which have a C₆₀-rich core and alkyl-rich shell. The greatest aggregation extent is found in n-hexane, and at 0.1 M the micelles of 1 comprise around 6 molecules at 25 °C. These micelles become smaller when the concentration is lowered, or if the solvent is changed to n-decane. The solution structure is also affected by temperature, with a slightly larger aggregation extent at 10 °C than at 25 °C. At higher concentrations, for example in solutions of 1 above 0.3 M in n-decane, a bicontinuous network becomes apparent. Overall, these findings aid our understanding of the factors driving the assembly of alkyl–π-conjugated hydrophobic amphiphiles such as 1 in solution and thereby represent a step towards the ultimate goal of exploiting this phenomenon to form materials with well-defined order.

---

Introduction

Molecular self-assembly is fundamental to the success of many natural, commercial and industrial processes. Governing it are non-covalent interactions imposed by the molecular structure. In solution, assembly is not only driven by these intermolecular interactions, but also by other parameters such as temperature, concentration and solvent type. These factors often affect larger changes in the resulting assembly than can be accounted for by the molecular structure alone. In water, for example, a typical non-ionic surfactant such as pentaethylene glycol monododecyl ether (C₁₂E₅) can form six isotropic phases with different structures – including micelles and various liquid crystalline states – when only the solution temperature and concentration are altered.¹ The solvent choice is also crucial: at 10 wt% and 25 °C, C₁₂E₅ forms large elongated normal-phase micelles in water and smaller reverse-phase micelles in n-hexane, while in 1,4-dioxane no aggregation occurs.² Significant effort goes into understanding the effect of solution parameters on assembly morphology, as obtaining the desired solution structure is often key to the use of surfactants such as C₁₂E₅ in commercial or industrial applications.

We recently demonstrated that the attachment of alkyl groups to π-conjugated molecules yields hydrophobic amphiphiles capable of forming micelles and liquid crystal-like gel phases in n-alkane solvents.³ Assembled π-conjugated molecules are of interest for their associated optoelectronic properties, the efficiency of which is directly influenced by the structural organization.^4–7 Given the variety in assembly states accessible to conventional amphiphiles (e.g. C₁₂E₅), hydrophobic amphiphiles incorporating π-conjugated units have the potential to allow significant control and tunability over their organization. However, while the (hydrophobic) driving force behind the self-assembly of surfactants is mostly understood, this is not the case for the new alkyl–π-conjugated amphiphiles. To manipulate the molecular chemistry so as to further fine-tune the assembly structure, an improved understanding of the factors driving structural formation is needed.

The assembly of alkyl–C₆₀ derivative 1 (Fig. 1a) into micellar aggregates is the focus of this study. While this system has no noteworthy optoelectronic properties, it allows the effect of solution parameters to be unambiguously elucidated, including changes resulting from solvent type, concentration and temperature. Contrast-variation small-angle neutron scattering (CV-SANS), small-angle X-ray scattering (SAXS) and nuclear magnetic resonance (NMR) measurements of diffusion were used to determine size and nanostructure, while isothermal titration calorimetry (ITC) is used to probe the aggregation mechanism. Overall, the results support an associative mechanism of aggregation that is strongly affected by solvent type and concentration, while weakly affected by temperature.

Fig. 1 (a) Structure of molecule 1. (b) CV-SANS data for 0.1 M 1 in n-hexane at 25 °C, showing the three contrast profiles highlighting the scattering contributions from the micelle core (CM-alkyl), shell (CM-C₆₀) and whole micelle (hexane-d₁₄), as described in the text. (c) SAXS data for samples of 1 in n-decane at 25 °C at concentrations as indicated in the legend. For both the SANS and SAXS results, the solid lines are fits to the data, using a model consisting of a superposition of a Schulz distribution of core–shell spheres, a Lorentzian peak function and a flat background.

Experimental

Chemicals

Molecule 1, 2-{3,5-bis[(2-decyltetradecyl)oxy]phenyl}-1-methyl-fulleropyrrolidine (Fig. 1a) was synthesised and purified by previously outlined methods.^3,8 Hydrogenated solvents n-hexane, n-decane and toluene were purchased from Sigma-Aldrich. Deuterated n-hexane-d₁₄ and n-decane-d₂₂ were purchased from Apollo Scientific, while toluene-d₈ was purchased from Goss. All solvents were used without further purification. Samples in concentrations up to 0.1 M were made up by weighing out an appropriate amount of 1, adding an appropriate amount of solvent and agitating until the sample appeared homogenous. To ensure complete mixing at concentrations of 1 above 0.1 M, samples were prepared in the same way as above but then sealed and annealed in a warm oven (50 °C) to promote dissolution. In all cases, concentrations were calculated as moles of 1 divided by total volume. In this case, the total volume in mL, V_t = g(1)/d(1) + V_s, where V_s denotes the volume of solvent added in mL, g(1) the mass of 1 in gram and d(1) the approximated density of 1 (1.17 g mL⁻¹ – see ESI†). Consideration of the volume occupied by 1 is important, in particular for higher concentrations, but comes at the cost of an increased uncertainty in the concentration due to the approximated density. This uncertainty is small, however, as changing d(1) from 1.17 to 1.0 g mL⁻¹, for example, only yields a change in calculated concentration of 2%.

Techniques

SANS measurements were carried out on the D11 beamline at Institut Laue Langevin, France. The samples were contained in 1 mm path-length Hellma cells. Sample temperature (10 °C or 25 °C) was controlled via a thermostated bath coupled to the D11 sample changer. Two sample-detector distances were used: 1.2 m and 8 m. The incident wavelength was 4.6 Å and the resulting detectable scattering vector, Q range was approximately 0.009–0.7 Å⁻¹. Absolute intensities for the scattered intensity, I(Q) (in cm⁻¹) were determined by calibrating the received signal to water and correcting for sample transmission and solvent background, giving the data shown in Fig. 1b and Fig. S1 (ESI†).

SAXS measurements were carried out on BL40B2 at SPring8, with an incident wavelength of 1.01 Å, a sample-detector distance of 1.647 m and a 3000 × 3000 pixel IP detector, giving a detectable Q range of approximately 0.03–0.51 Å⁻¹. The sample temperature was controlled by a hot/cold stage (HCS302, Instec Inc., CO). Collected data were corrected for natural background radiation, transmission, sample thickness, measurement time, primary beam flux, parasitic background, polarisation and detector solid angle coverage using in-house developed data reduction software written in Python.⁹ Sample transmission was established through comparison of the signals from two ion chambers, placed before and after the sample position, intercalibrated by a measurement with no sample in place. The average cylindrical capillary thickness (1.5 mm capillary), based on a beam width of 8 mm × 4 mm, was calculated to be 1.42 mm. The intensity was subsequently binned using 200 linear bins spanning the aforementioned Q range, and scaled to absolute units using a calibrated glassy carbon standard provided by Jan Ilavsky and coworkers.¹⁰ The result was three-column data with Q, and I(Q) in absolute units, in addition an uncertainty estimate, giving data shown in Fig. 1c.

Diffusion NMR measurements of 1 in n-hexane-d₁₄, n-decane-d₂₂ and toluene-d₈ were performed as a function of concentration at an observation time, Δ, of 20 ms, with a gradient duration, δ, of 2 ms, a maximum gradient strength, G, of 400 G cm⁻¹ and 32 gradient steps. The diffusion coefficient, D_exp, from molecule 1 was determined using the Stejskal–Tanner equation:¹¹

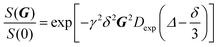where γ is the gyromagnetic ratio and (S(G))/(S(0)) the normalised signal attenuation, which was acquired by integrating the peak at 2.85 ppm in the ¹H spectrum for compound 1, which arises from the methyl group attached to the nitrogen atom.⁸

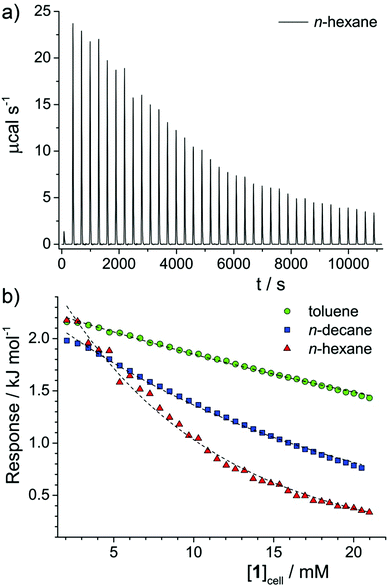
Isothermal titration calorimetry (ITC) measurements were carried out using a Microcal VP-ITC system. After thorough washing, pure solvent (i.e. n-decane, n-hexane or toluene) was entered into both reference and sample cells. The injector syringe was filled with a solution (124 mM) of molecule 1 in the same solvent. The syringe has a maximum volume of approximately 0.295 mL and the sample cell volume is 1.414 mL, so the maximum concentration that could be reached was around 21 mM. A typical run consisted of 36 injections of 8 μL, after an initial injection of 1 μL. Using the OriginPro 8.1J plugin, datasets were corrected for the baseline signal, giving the raw data plots shown in Fig. 3a. For comparison, the data in Fig. S2 (ESI†) is shown prior to background subtraction. Finally, for all solvents the peaks were integrated and corrected for concentration, resulting in a plot of response vs. [1] in the sample cell, shown in Fig. 3b.

Results and discussion

Small-angle scattering

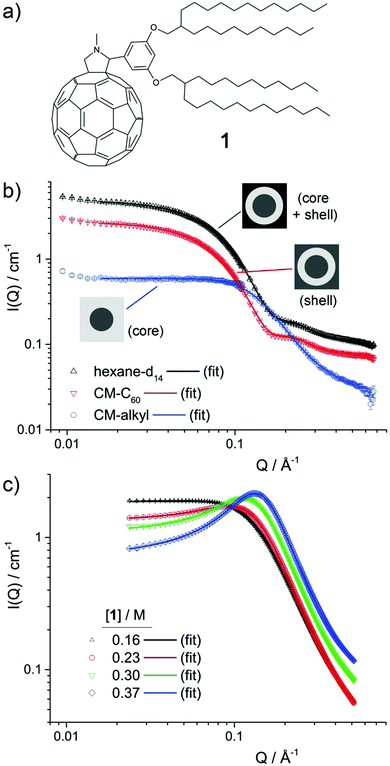
Contrast-variation SANS data was collected for samples of 1 in n-hexane, n-decane and toluene.¹²Fig. 1b shows the data for 0.1 M 1 in n-hexane at 25 °C, while the data for 0.025 M and 0.05 M in n-hexane at 25 °C, 0.1 M in n-hexane at 10 °C, and 0.1 M in n-decane and in toluene at 25 °C are shown in Fig. S1 (ESI†). In all cases, three contrast profiles were used: SANS from the whole micelle (core + shell) was obtained when a perdeuterated n-alkane solvent was used, while the shell and core were individually highlighted using blends of perdeuterated and perhydrogenated n-alkane solvents contrast-matched to the scattering length density, ρ of C₆₀, ρ_C60 (CM-C₆₀) or of the alkyl chains in 1, ρ_alkyl (CM-alkyl). Values of ρ_C60 and ρ_alkyl were estimated to be 5.0 × 10⁻⁶ Å⁻⁶ and 1.0 × 10⁻⁷ Å⁻⁶ respectively (see ESI†). Key to the use of CV-SANS here is the assumption that a switch from primarily hydrogenated to primarily deuterated solvent media will not strongly affect the structure of the primary aggregates that are formed. This assumption is reasonable as CH–π and CD–π interactions that are likely to drive aggregation are known to be almost indistinguishable.¹³

The different contrast profiles shown in Fig. 1b exhibit changes in I(Q) in line with typical CV-SANS of dispersed core–shell micelles.^14,15 This suggests that the ρ_C60 and ρ_alkyl estimates are reasonable, and indicates that clusters of 1 possess a core–shell structure, with a C₆₀-rich core and an alkyl-rich shell, in line with previously published combined SAXS and SANS results.³ All profiles exhibit a plateau region at low-mid Q where I(Q) scales proportionally to Q⁰, followed by at least one decay. The position in Q of the onset points of these decays are inversely related to the radius of gyration of the scattering objects.^14,16 For the hexane-d₁₄ and CM-C₆₀ solutions, the first decay with an onset at around Q ≈ 0.05 Å⁻¹ is related to the total micelle radius, i.e. the core radius, r_core plus the shell thickness, δ_shell. The second decay at just over Q ≈ 0.2 Å⁻¹ is related to δ_shell. For the CM-alkyl solution, conversely, a single decay with an onset at around Q ≈ 0.1 Å⁻¹ corresponds to r_core. The factor of two difference between the locations in Q of the onsets of these decays suggests that r_core and δ_shell have a similar magnitude.

To examine the effect of an increase in the concentration of 1 (henceforth referred to as [1]), several samples were prepared, ranging from 0.16 M (30 wt%) to 0.37 M (60 wt%), in n-decane and analysed by SAXS. Here, n-decane was used to lower the risk of solvent evaporation. The SAXS data is shown in Fig. 1c. SAXS highlights the electron-dense regions of a scattering object, here being the core of the micelles. At the lowest concentration, the SAXS data is very similar to the CM-alkyl SANS data, exhibiting a single decay with an onset at around Q ≈ 0.1 Å⁻¹ that is related to r_core. However, with increased [1], a broad peak appears in the scattering, similar to that observed for mixtures of ionic liquids.^17,18 There, such transitions in small-angle scattering are thought to come from the growth of continuous, non-polar sub-phase within the polar matrix, resulting in broad polar–non-polar peak (PNPP) representative of the spacial separation between polar regions. Likewise, in microemulsions at higher concentrations, a transition from a droplet structure to a bicontinuous system tends to lead to a broad peak in the scattering.^19,20 Reflecting this to the results presented here, it is therefore probable that as [1] increases, the aggregates coalesce into a bicontinuous network. The peak then arises from the spacial separation between domains within the network.²⁰

To further analyse the SANS and SAXS data, a mixed model comprising a superimposed combination of a Schultz distribution of polydisperse core–shell spheres,^21,22 a Lorentzian peak function and a flat background was used to model the contributions arising from micelle-like clusters and the developing network. Other methods to analyse the SAXS data, using the Teubner–Strey (TS) or Ornstein–Zernike (OZ) + Peak models, which are frequently applied to scattering from bicontinuous systems,²⁰ were also attempted. However, while these methods gave results that are broadly consistent with the mixed model (Fig. S2, Tables S3 and S4, ESI†), neither showed the same level of agreement with all datasets. Equations for all of the models, and further justification for their use, are given in the ESI.†

For the mixed model, fitted parameters were the scale factor N, which is related to the number density of scattering objects, the core radius r_core and its dispersity σ, the shell width δ_shell, and the peak amplitude A_peak, centre Q_peak, and half width at half maximum w_peak. An additional flat background contribution, I_bkg was allowed for all datasets, as while both the SANS and SAXS data were normalised and the background solvent scattering subtracted, some under-/over-subtraction occurred as a result of (1) the high ¹H content in 1 and (2) displaced volume effects.²³ The SASfit analysis software was used in all cases.²⁴ For the SANS data, the three different contrast profiles CM-alkyl, CM-C₆₀ and the 100% deuterated solvent were analysed simultaneously, using the “multifit” capability of SASfit. In this case, global parameters N, r_core, δ_shell, σ, Q_peak and w_peak were held constant across the three contrast profiles, apportioning greater reliability to these values and to the overall fit. As the level of solvent penetration into the micelle shell is unknown, the scattering length density of the shell, ρ_shell was additionally allowed to float for the CM-C₆₀ and 100% deuterated solvent contrast profiles (NB: not for CM-alkyl, as ρ_shell = ρ_solvent). Fitted values point to a solvent penetration into the shell of around 20%, which seem reasonable based on the molecular dimensions of 1.

Results of the data analysis are shown as solid lines on Fig. 1b, c and in Fig. S1 (ESI†). Despite its relative simplicity, the model shows excellent agreement with the data in all cases. Selected parameters for SANS and SAXS data are provided in Table 1. For all samples in n-hexane and n-decane the fitted values for r_core and δ are similar, in line with the position of the maxima as discussed above. In n-hexane, increasing [1] from 0.025 to 0.1 M leads to an increase in r_core, and a coincident decrease in σ. To understand the correlation between these two, it is important to consider the approximate mean aggregation numbers, N_agg for these two samples: using a molar volume of 780 ų per molecule for the C₆₀ part of 1 (see ESI†), N_agg = 8.2 and 3.5 for 0.1 and 0.025 M 1 in n-hexane at 25 °C respectively. Given that dispersity in either sample is likely to arise from the loss or gain of a molecule of 1 into a micelle within the population, the consequential percentage change in volume can be calculated as 1/N_agg × 100. For 0.1 M, this is 17%, while for 0.025 M it is 40% (which equates to a change in the radius of 5% and 12%, respectively). The larger dispersity σ for lower r_core values is therefore a function of the relatively small N_agg values found in these samples and is unlikely to be indicative of a significant change in micelle morphology.

Table 1 Selected parameters, including the core radius r_core and its dispersity σ, shell width δ_shell, peak amplitude A_peak, peak centre Q_peak, and peak half width at half maximum w_peak, from fitting SAXS and SANS data of samples of 1 in n-hexane and n-decane at different concentrations and temperatures

[1]/M	T/°C	Solvent	r core/Å	σ	δ shell/Å	A peak/cm^−1	Q peak/Å^−1	w peak/Å^−1
a Value for the CM-alkyl contrast profile. b During the analysis of the SAXS profiles, the dispersity parameter was unreliable and tended to adopt unrealistic values. Consequently, it was fixed at 0.46, based on the value found by analysis of the CV-SANS data. Changing this value has very little influence on the overall analysis, particularly on the peak parameters.
0.1	10	n-hexane	11.7	0.31	10.1	0.33^a	0.096	0.071
0.1	25	n-hexane	11.5	0.33	10.0	0.27^a	0.094	0.079
0.05	25	n-hexane	10.9	0.41	10.3	0.11^a	0.098	0.092
0.025	25	n-hexane	8.6	0.53	11.1	0.04^a	0.099	0.153
0.1	25	n-decane	8.6	0.46	8.8	0.13^a	0.096	0.121
0.16	25	n-decane	8.3	0.46^b	—	0.99	0.094	0.081
0.23	25	n-decane	7.7	0.46^b	—	1.23	0.106	0.070
0.30	25	n-decane	6.7	0.46^b	—	1.60	0.119	0.065
0.37	25	n-decane	5.4	0.46^b	—	1.93	0.134	0.064
0.1	25	toluene	3.5	0.58	10.6	0.06^a	0.206	0.156

---

Increasing [1] in n-hexane (0.025–0.1 M), and in n-decane (0.16–0.37 M) results in an increase in A_peak, in line with the observations of a growing second bicontinuous phase in the system. Concurrent with this, above 0.1 M in n-decane, the micelle population appears to shrink, indicating a transition from aggregate clusters of 1 to the likely bicontinuous phase. Simultaneously, Q_peak shifts to higher values and w_peak decreases indicating that the new phase is becoming more extensive and that the spacing between C₆₀ units reduces. Decreasing the temperature of the 0.1 M sample of 1 in n-hexane results in a slight increase in r_core (and commensurate decrease in σ as before), and in A_peak, suggesting that cooling tends to slightly promote aggregation in these systems. Finally, the fitted value of r_core for 0.1 M 1 in toluene is very similar to the unsolvated radius of gyration of C₆₀ (3.48 Å)²⁵ and consequently is indicative of little or no aggregation, in line with previously published SAXS data on this system.³ In that case the peak function is broader, shifted to higher Q, and is therefore more likely indicative of monomer–monomer spacing within the unstructured solution, rather than a developing bicontinuous phase.

Diffusion NMR

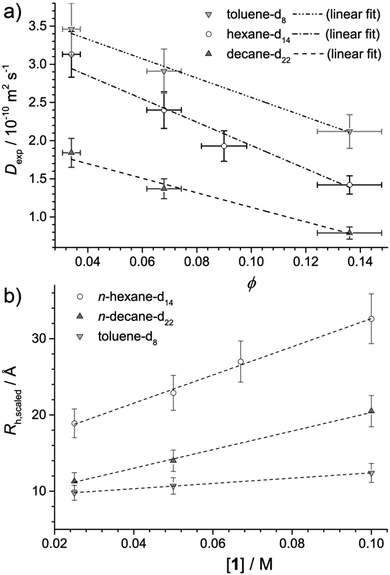
Fig. 2a plots the observed diffusion coefficient, D_exp as a function of the calculated volume fraction ϕ for 1 in n-hexane-d₁₄, n-decane-d₂₂ and toluene-d₈. For reference, the highest volume fraction ϕ = 0.145 is equal to 0.1 M while the lowest ϕ = 0.036 is equal to 0.025 M. In all solvents, D_exp is observed to decrease with ϕ. This reduction in D_exp can be explained either by (i) an increase in intermolecular collisions due a larger number of aggregates present at high ϕ, (ii) an increase in the size of the aggregate, or a combination of (i) and (ii). If the decrease were solely due to (i), the data should be modelled using D_exp = D₀(1 + αϕ), for which D₀ is the diffusion coefficient at infinite dilution and α is the viral coefficient, which should have a value of −2 if accounting for obstructions between non-interacting hard spheres.²⁶ Results are provided in Table 2 and while reasonable agreement between the data and linear model is found, values of α are all higher than −2, indicating that a change in the system, particularly in the n-alkane solvents, occurs as ϕ is increased.

Fig. 2 (a) Plot of the measured diffusion coefficient, D_exp (±10%) as a function of volume fraction, ϕ for samples of 1 in deuterated solvents as noted in the legend. Dashed lines represent fits to the data using D_exp = D₀(1 + αϕ), where D₀ and α were floated parameters. Errors in ϕ indicate ± one standard deviation based on the density of 1 ± 10%. (b) Plot of the calculated scaled radius of hydration of the aggregates of 1, R_h,scaled = (1 − 2ϕ)k_BT/6πηD_exp as a function of molar concentration, [1] in the different solvents. Dashed lines are provided to guide the eye.

Table 2 Parameters obtained from the linear fit of diffusion data shown in Fig. 2a to the equation D_exp = D₀(1 + αϕ), where D₀ is the diffusion coefficient at infinite dilution and α is the viral coefficient, which accounts for greater obstructions at higher concentrations

Solvent	D 0/10^−10 m^2 s^−1	α
Hexane-d14	3.5 ± 0.3	−4.4
Decane-d22	2.1 ± 0.2	−4.6
Toluene-d8	3.4 ± 0.4	−3.8

---

Assuming the micelles are spherical, as can be concluded from the SANS analysis, any deviation from α = −2 could be explained by an increase in aggregate size with concentration. Then, by combining the Stokes–Einstein equation R_h = k_BT/6πηD₀ with D_exp = D₀(1 + αϕ) to account for obstructions at higher volume fraction, an effective radius of hydration, R_h,scaled can be calculated from D_exp as R_h,scaled = (1 − αϕ)k_BT/6πηD_exp, where α = −2. The solvent viscosity, η of the deuterated solvents given in Table 2 was approximated using the viscosity of the hydrogenated solvents (0.295,²⁷ 0.85,²⁷ and 0.554²⁸ mPa s for n-hexane-h₁₄, n-decane-h₂₂ and toluene-h₈, respectively) multiplied by the ratio of the molar masses of the deuterated and hydrogenated solvents.²⁹

Fig. 2b plots R_h,scaled as a function of the concentration of 1, [1]. Taking into account that they are representative of the entire micelle radius (i.e. r_core + δ_shell), the R_h,scaled values obtained by diffusion NMR are mostly similar to those obtained by SANS presented in Table 1, and show similar trends in aggregate size both as a function of concentration and solvent. However, the R_h,scaled value for 0.1 M 1 in n-hexane is larger than that obtained by SANS. This may be due to a greater level of interaction between neighbouring micelles originating from the larger extent of aggregation in this sample. Such interactions would reduce the diffusion coefficient and lead to an overestimation of R_h,scaled. Network formation, implied in the SANS and SAXS analysis, would have the same effect and could also contribute to the overestimation.

Values of R_h,scaled ≈ 10 Å for all samples in toluene, and for 0.025 M 1 in n-decane suggest a predominance of non-associated monomers of 1, given that for bare C₆₀ in benzene, R_h = 6.4 Å,³⁰ in line with both the SANS data presented above and previously published SAXS data.³ The change in R_h,scaled between 0.025 and 0.05 M for 1 in n-decane suggests that the aggregation onset in that solvent system lies between those concentrations. On the other hand, 1 in n-hexane appears to be present in an aggregated state throughout the concentration range studied, in line with SANS results.

Isothermal titration calorimetry

One technique that has been widely applied to clustering and aggregation in aqueous and non-aqueous solvents is isothermal titration calorimetry (ITC). In a typical experiment, a concentrated (aggregated) solution of the amphiphile is titrated into a dilute solution in the sample cell and the calorimetric response detected. In the case of solutions that aggregate, enthalpy changes can arise from (i) aggregate dilution, (ii) aggregate disassembly (demicellisation), and (iii) dissolution of the monomeric species. Assuming all solutions are injected in an aggregated state, (i) must occur throughout the titration procedure and can be assumed to give an approximately constant signal. Therefore, any changes can only be ascribed to (iii), which should again be an approximately constant contribution, or (ii). The shape of the ITC response vs. concentration curve can therefore identify the most likely mode of aggregation. Conventional surfactants in water exhibit a large initial response, indicative of (ii) and (iii), which remains constant until the critical micelle concentration (CMC)^31,32 after which it decays abruptly to a lower constant response, indicative of mainly (i). Associating surfactants,³³ dye molecules or asphaltenes³² in non-aqueous solvents shows a similar reduction in response with concentration, but with a loss of the initial high-response plateau and a more gradual reduction in response with concentration, indicating an associative mechanism of aggregation,³⁴ with no easily identifiable CMC.²

Fig. 3a shows the raw ITC data obtained for a solution of 1 in n-hexane. Data for other solvents can be found in the ESI,† (Fig. S2). By integrating each injection peak the enthalpy response per mole of 1 injected has been determined as a function of the concentration of 1 in the sample cell, [1]_cell (Fig. 2b) for the various solvents studied. Solutions in n-hexane initially show a positive enthalpic response, of a similar order to values obtained for Rhodamine 6G in water,³² indicating that aggregation is favourable with respect to enthalpy. This response then gradually reduces with [1]_cell, which points to an associative mechanism of aggregation, with no sharp onset in the investigated concentration range. Similar behaviour is noted for solutions of 1 in n-decane and toluene, albeit with reduced rates of decay. Generally, the results indicate a greater tendency to aggregate in n-hexane than in n-decane or toluene, in line with results obtained by small-angle scattering techniques and NMR measurements of diffusion.

Given the known miscibility of the alkyl chains of 1 with n-alkanes and toluene, the ITC results support the hypothesis that the primary driving force for aggregation in this system is the solvophobicity of the C₆₀ unit. One way to quantify this uses Hansen solubility parameters, δ_H with literature values of δ_H = 14.9, 15.7, 18.2 and 20.1 J^1/2 cm^−3/2 for n-hexane, n-decane, toluene³⁵ and C₆₀,³⁶ respectively. Substances with similar solubility parameters tend to be miscible with one another. The largest aggregation extent should therefore be obtained by maximising the difference in δ_H between the C₆₀ and the solvent, Δδ_H, exemplified here by dissolving 1 in n-hexane.

Fig. 3 (a) Raw data of recorded calorimetric response from repeated injections of a concentrated solution of 1 in n-hexane ([1] = 124 mM) into pure n-hexane. After an initial injection (1 μL), each peak indicates a single injection of 8 μL. (b) Plot of enthalpy change per mole of 1 injected versus the concentration of 1 in the sample cell, [1]_cell. Dashed lines are guides to the eye.

Considering this factor alone, it is found here that larger values of Δδ_H yield a greater aggregation extent, pointing to the existence of a clear solvophobic driving force for aggregation. However, moving to a more general case of any assembling alkyl–π-conjugated molecule it is conceivable that values of Δδ_H above a certain threshold may lead to insufficient solubility and/or kinetically-trapped structures formed by fast precipitation. Likewise, the nanostructure of the assembly that forms should also be a function of the chemistry of the alkyl chains, demonstrated most clearly in previous work³ where derivitising C₆₀ with hyper-branched alkyl chains yielded an extensive structured gel in n-hexane at room temperature, instead of micelles. A systematic study of this latter effect in C₆₀ systems is underway.

Conclusion

Using results from small-angle scattering techniques and NMR measurements of diffusion, it has been demonstrated that 1 self-assembles into relatively small micelle-like clusters in n-alkane solvents. These clusters grow in size with increased concentration, in line with the associative aggregation mechanism typical for non-ionic surfactants and other self-assembling species in non-aqueous media.^32,33 A bicontinuous network develops at higher concentrations, which in n-decane is particularly apparent above 0.3 M (= 50 wt%). Overall, the extent of aggregation is only slightly affected by temperature, but is strongly affected by solvent type, as 1 forms smaller micelles in n-decane versus n-hexane and does not micellize in toluene solutions at identical temperature and concentration. Therefore, for the solvents reported, the aggregation extent is maximised when the difference in Hansen solubility parameter between the solvent and the C₆₀ unit, Δδ_H is at the maximum value. However, while it is likely that Δδ_H is one key parameter in driving structural formation, more work is required in order to generalise this principle to other systems and to take into account other factors, such as the chemistry of the alkyl part of an alkyl–π-conjugated molecule.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was partially supported by Grants-in-Aid for Scientific Research (JSPS KAKENHI Grant Number JP25104011). The SPring-8 synchrotron radiation experiment was performed on BL40B2 with the approval the Japan Synchrotron Radiation Research Institute (JASRI; proposal no. 2011B1548). The authors thank the beamline contact (N. Ohta, SPring8) for his help with performing SAXS measurements. We thank the ILL for the beam time on the D11 instrument. The neutron data set is available at DOI: http://10.5291/ILL-DATA.9-10-1422.¹² MMB and CFS thank the EPSRC (grant EP/K039245/1) and University of Birmingham for financial support. AD thanks the University of Birmingham and the EU (Marie Curie “SusNano”) for his PhD studentship. Finally, STFC is acknowledged for the allocation of beam time, consumables and travel.

References

1. C. A. Miller and K. H. Raney, Solubilization-emulsification mechanisms of detergency, Colloids Surf., A, 1993, 74, 169–215.
2. M. J. Hollamby, R. Tabor, K. J. Mutch, K. Trickett, J. Eastoe, R. K. Heenan and I. Grillo, Effect of Solvent Quality on Aggregate Structures of Common Surfactants, Langmuir, 2008, 24, 12235–12240.
3. M. J. Hollamby, M. Karny, P. H. H. Bomans, N. A. J. M. Sommerdijk, A. Saeki, S. Seki, H. Minamikawa, I. Grillo, B. R. Pauw, P. Brown, J. Eastoe, H. Möhwald and T. Nakanishi, Directed assembly of optoelectronically active alkyl–π-conjugated molecules by adding n-alkanes or π-conjugated species, Nat. Chem., 2014, 6, 690–696.
4. H. Li, B. C.-K. Tee, J. J. Cha, Y. Cui, J. W. Chung, S. Y. Lee and Z. Bao, High-Mobility Field-Effect Transistors from Large-Area Solution-Grown Aligned C₆₀ Single Crystals, J. Am. Chem. Soc., 2012, 134, 2760–2765.
5. M. Campoy-Quiles, T. Ferenczi, T. Agostinelli, P. G. Etchegoin, Y. Kim, T. D. Anthopoulos, P. N. Stavrinou, D. D. C. Bradley and J. Nelson, Morphology evolution via self-organization and lateral and vertical diffusion in polymer:fullerene solar cell blends, Nat. Mater., 2008, 7, 158–164.
6. Y. Yamamoto, T. Fukushima, Y. Suna, N. Ishii, A. Saeki, S. Seki, S. Tagawa, M. Taniguchi, T. Kawai and T. Aida, Photoconductive Coaxial Nanotubes of Molecularly Connected Electron Donor and Acceptor Layers, Science, 2006, 314, 1761–1764.
7. V. Altoe, F. Martin, A. Katan, M. Salmeron and S. Aloni, Electron Microscopy Reveals Structure and Morphology of One Molecule Thin Organic Films, Nano Lett., 2012, 12, 1295–1299.
8. H. Li, S. S. Babu, S. T. Turner, D. Neher, M. J. Hollamby, T. Seki, S. Yagai, Y. Deguchi, H. Möhwald and T. Nakanishi, Alkylated-C₆₀ based soft materials: regulation of self-assembly and optoelectronic properties by chain branching, J. Mater. Chem. C, 2013, 1, 1943–1951.
9. B. R. Pauw, J. S. Pedersen, S. Tardif, M. Takata and B. B. Iversen, Improvements and considerations for size distribution retrieval from small-angle scattering data by Monte Carlo methods, J. Appl. Crystallogr., 2013, 46, 365–371.
10. F. Zhang, J. Ilavsky, G. G. Long, J. P. G. Quintana, A. J. Allen and P. R. Jemian, Glassy Carbon as an Absolute Intensity Calibration Standard for Small-Angle Scattering, Metall. Mater. Trans. A, 2009, 41, 1151–1158.
11. E. O. Stejskal and J. E. Tanner, Spin Diffusion Measurements: Spin Echoes in the Presence of a Time-Dependent Field Gradient, J. Chem. Phys., 1965, 42, 288–292.
12. M. Hollamby, A. Danks, I. Grillo, B. R. Pauw and Z. Schnepp, 2014, Influence of alkyl chain chemistry on the self-assembly of alkyl–C₆₀ hydrophobic amphiphiles, Institut Laue-Langevin (ILL), DOI: http://10.5291/ILL-DATA.9-10-1391.
13. C. Zhao, R. M. Parrish, M. D. Smith, P. J. Pellechia, C. D. Sherrill and K. D. Shimizu, Do Deuteriums Form Stronger CH–π Interactions?, J. Am. Chem. Soc., 2012, 134, 14306–14309.
14. M. J. Hollamby, Practical applications of small-angle neutron scattering, Phys. Chem. Chem. Phys., 2013, 15, 10566–10579.
15. S. Nave, J. Eastoe, R. K. Heenan, D. C. Steytler and I. Grillo, What Is So Special about Aerosol-OT? 2. Microemulsion Systems, Langmuir, 2000, 16, 8741–8748.
16. A. Guinier, Ann. Phys., 1939, 12, 161–237.
17. D. W. Bruce, C. P. Cabry, J. N. C. Lopes, M. L. Costen, L. D’Andrea, I. Grillo, B. C. Marshall, K. G. McKendrick, T. K. Minton, S. M. Purcell, S. Rogers, J. M. Slattery, K. Shimizu, E. Smoll and M. A. Tesa-Serrate, Nanosegregation and Structuring in the Bulk and at the Surface of Ionic-Liquid Mixtures, J. Phys. Chem. B, 2017, 121, 6002–6020.
18. C. P. Cabry, L. D’Andrea, K. Shimizu, I. Grillo, P. Li, S. E. Rogers, D. W. Bruce, J. N. C. Lopes and J. M. Slattery, Exploring the bulk-phase structure of ionic liquid mixtures using small-angle neutron scattering, Faraday Discuss. 10.1039/C7FD00167C.
19. M. Teubner and R. Strey, Origin of the scattering peak in microemulsions, J. Chem. Phys., 1987, 87, 3195–3200.
20. S. Prevost, T. Lopian, M. Pleines, O. Diat and T. Zemb, Small-angle scattering and morphologies of ultra-flexible microemulsions, J. Appl. Crystallogr., 2016, 49, 2063–2072.
21. G. V. Schulz, Z. Phys. Chem., 1939, B43, 25.
22. M. Kotlarchyk, R. B. Stephens and J. S. Huang, Study of Schultz distribution to model polydispersity of microemulsion droplets, J. Phys. Chem., 1988, 92, 1533–1538.
23. B. R. Pauw, A. J. Smith, T. Snow, N. J. Terrill and A. F. Thünemann, The modular SAXS data correction sequence for solids and dispersions, 2017, arXiv:1706.06769 [physics].
24. I. Breßler, J. Kohlbrecher and A. F. Thünemann, SASfit: a tool for small-angle scattering data analysis using a library of analytical expressions, J. Appl. Crystallogr., 2015, 48, 1587–1598.
25. S. J. Henderson, Measurement of the Second Virial Coefficient of C₆₀ in CS2 Solution from Small-Angle Neutron Scattering, Langmuir, 1997, 13, 6139–6145.
26. T. Ohtsuki and K. Okano, Diffusion coefficients of interacting Brownian particles, J. Chem. Phys., 1982, 77, 1443–1450.
27. J. H. Dymond and H. A. O/ye, Viscosity of Selected Liquid n-Alkanes, J. Phys. Chem. Ref. Data, 1994, 23, 41–53.
28. F. J. V. Santos, C. A. Nieto de Castro, J. H. Dymond, N. K. Dalaouti, M. J. Assael and A. Nagashima, Standard Reference Data for the Viscosity of Toluene, J. Phys. Chem. Ref. Data, 2005, 35, 1–8.
29. R. Evans, Z. Deng, A. K. Rogerson, A. S. McLachlan, J. J. Richards, M. Nilsson and G. A. Morris, Quantitative Interpretation of Diffusion-Ordered NMR Spectra: Can We Rationalize Small Molecule Diffusion Coefficients?, Angew. Chem., Int. Ed., 2013, 52, 3199–3202.
30. Q. Ying, J. Marecek and B. Chu, Solution behavior of buckminsterfullerene (C₆₀) in benzene, J. Chem. Phys., 1994, 101, 2665–2672.
31. S. Paula, W. Sues, J. Tuchtenhagen and A. Blume, Thermodynamics of Micelle Formation as a Function of Temperature: A High Sensitivity Titration Calorimetry Study, J. Phys. Chem., 1995, 99, 11742–11751.
32. D. Merino-Garcia and S. I. Andersen, Calorimetric Evidence about the Application of the Concept of CMC to Asphaltene Self-Association, J. Dispersion Sci. Technol., 2005, 26, 217–225.
33. P. R. Majhi and S. P. Moulik, Microcalorimetric Investigation of AOT Self-Association in Oil and the State of Pool Water in Water/Oil Microemulsions, J. Phys. Chem. B, 1999, 103, 5977–5983.
34. E. Ruckenstein and R. Nagarajan, Aggregation of amphiphiles in nonaqueous media, J. Phys. Chem., 1980, 84, 1349–1358.
35. A. F. M. Barton, Solubility parameters, Chem. Rev., 1975, 75, 731–753.
36. C. M. Hansen and A. L. Smith, Using Hansen solubility parameters to correlate solubility of C₆₀ fullerene in organic solvents and in polymers, Carbon, 2004, 42, 1591–1597.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp06348b

---