Visualizing rotational wave functions of electronically excited nitric oxide molecules by using an ion imaging technique†
Abstract
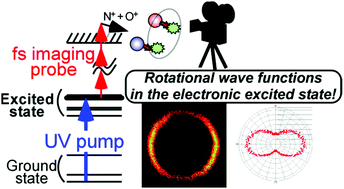
Here we report the dissociative ionization imaging of electronically excited nitric oxide (NO) molecules to visualize rotational wave functions in the electronic excited state (A 2Σ+). The NO molecules were excited to a single rotational energy eigenstate in the first electronic excited state by a resonant nanosecond ultraviolet pulse. The molecules were then irradiated by a strong, circularly polarized femtosecond imaging pulse. Spatial distribution of the ejected N+ and O+ fragment ions from the dissociative NO2+ was recorded as a direct measure of the molecular axis distribution using a high-resolution slice ion imaging apparatus. The circularly polarized probe pulse realizes the isotropic ionization and thus undistorted shapes of the functions can be visualized. Due to the higher ionization efficiency of the excited molecules relative to the ground state ones, signals from the excited NO were enhanced. We can, therefore, extract shapes of the square of rotational wave functions in the electronic excited state although the unexcited ground state molecules are the majority in an ensemble. The observed images show s-function-like and p-function-like shapes depending on the excitation wavelengths. These shapes well reflect the rotational (angular momentum) character of the prepared states. The present approach directly leads to the evaluation method of the molecular axis alignment in photo-excited ensembles, and it could also lead to a visualization method for excited state molecular dynamics.
- This article is part of the themed collection: Complex molecular systems: supramolecules, biomolecules and interfaces


 Please wait while we load your content...
Please wait while we load your content...