Excited state energy fluctuations in the Fenna–Matthews–Olson complex from molecular dynamics simulations with interpolated chromophore potentials†
Abstract
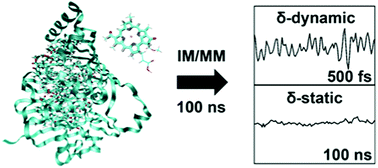
We analyze the environment-induced fluctuation of pigment excitation energies in the Fenna–Matthews–Olson (FMO) complex from various perspectives, by employing an interpolation-based all-atom potential energy model for describing realistic pigment vibrations. We conduct molecular dynamics simulations on a 100 ns timescale, which is an extent that can enclose the effect of static disorder, and demonstrate its timescale separation from fast dynamic disorder. We extract the spectral densities of the complex by considering both the site and the exciton bases. We show that exciton delocalization reduces the effective environmental fluctuation and rationalize this aspect based on a model of fluctuating molecular aggregates. We also obtained the spectral density of the lowest exciton state under low temperature conditions and show that it reasonably well reproduces the experimental result. Finally, by additionally performing non-equilibrium excited state trajectory simulations, we show that the system lies well within the linear response regime after photo-absorption and that the pigments do not visit anharmonic regions of the potential surface to a significant extent. This indicates that methodologies based on harmonic bath models are indeed reasonable approaches for describing the excited state dynamics of the FMO complex.
- This article is part of the themed collections: 2018 PCCP HOT Articles and Complex molecular systems: supramolecules, biomolecules and interfaces


 Please wait while we load your content...
Please wait while we load your content...