A general method for the inclusion of radiation chemistry in astrochemical models
Abstract
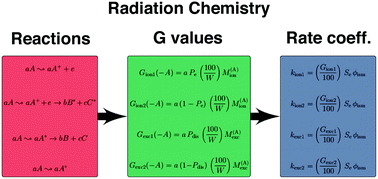
In this paper, we propose a general formalism that allows for the estimation of radiolysis decomposition pathways and rate coefficients suitable for use in astrochemical models, with a focus on solid phase chemistry. Such a theory can help increase the connection between laboratory astrophysics experiments and astrochemical models by providing a means for modelers to incorporate radiation chemistry into chemical networks. The general method proposed here is targeted particularly at the majority of species now included in chemical networks for which little radiochemical data exist; however, the method can also be used as a starting point for considering better studied species. We here apply our theory to the irradiation of H2O ice and compare the results with previous experimental data.
- This article is part of the themed collections: 2018 PCCP HOT Articles and Theory, experiment, and simulations in laboratory astrochemistry


 Please wait while we load your content...
Please wait while we load your content...