On the growth morphology and crystallography of the epitaxial Cu7Te4/CdTe interface†
Abstract
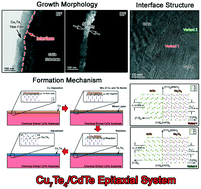
Controlling interface structures in the epitaxial growth of thin films is quite essential as it is closely related to some special physical and chemical properties. Using crystallographic calculation methods, growth behavior of the thin film as well as the interface geometry can be satisfactorily interpreted. In this study, the growth morphology and crystallography of the epitaxial Cu7Te4/CdTe interface were investigated in detail through comprehensive TEM analysis and crystallographic calculations. The results indicated that the growth interface was not smooth at the atomic level, which may be caused by chemical etching of the CdTe surface. The crystallographic orientation relationship between CdTe and Cu7Te4 was confirmed to be [101]CdTe//[11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0]Cu7Te4, (1
0]Cu7Te4, (1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )CdTe//(0001)Cu7Te4 and (
)CdTe//(0001)Cu7Te4 and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 1)CdTe//(
1)CdTe//(![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 100)Cu7Te4, which is a typical relationship in FCC/HCP system. Two variants of the Cu7Te4 phase were found to be randomly distributed across the interface region, indicating the equivalent crystallographic relationship between the 2 variants. Both the invariant line and the near coincident site lattice calculations confirmed that the observed orientation relationship between CdTe and Cu7Te4 had the lowest lattice mismatch and interface energy. The mutual rotation angles of ±54.74° and ±35.26° could be applied to obtain 2 types of coherent interfaces. Based on the TEM observation and crystallographic calculations, the possible growth process of the Cu7Te4 thin film on the CdTe substrate was discussed.
100)Cu7Te4, which is a typical relationship in FCC/HCP system. Two variants of the Cu7Te4 phase were found to be randomly distributed across the interface region, indicating the equivalent crystallographic relationship between the 2 variants. Both the invariant line and the near coincident site lattice calculations confirmed that the observed orientation relationship between CdTe and Cu7Te4 had the lowest lattice mismatch and interface energy. The mutual rotation angles of ±54.74° and ±35.26° could be applied to obtain 2 types of coherent interfaces. Based on the TEM observation and crystallographic calculations, the possible growth process of the Cu7Te4 thin film on the CdTe substrate was discussed.


 Please wait while we load your content...
Please wait while we load your content...