Thermal deformations of crystal structures formed in the systems of malic acid enantiomers and L-valine–L-isoleucine enantiomers

Abstract

The thermal behavior of discrete phases formed in the respective systems of malic acid enantiomers and L-enantiomers of the amino acids valine and isoleucine was studied using the temperature-resolved PXRD method. In the (S)-malic acid–(R)-malic acid system, thermal deformations in crystal structures of stable compounds (enantiomer S, racemates RSI and RSII, and non-equimolar compound S₃R) and polymorph transformations of metastable compounds (racemate RSIII and non-equimolar compound 3S1R) were examined. In the L-valine–L-isoleucine system, thermal deformations in crystal structures of stable compounds L-Val and L-Ile and non-equimolar compound V₂I were investigated. Thermal deformation analysis included plotting the temperature dependence of the unit cell parameters and volume, calculating thermal deformation tensors, plotting figures of thermal expansion coefficients (CTE), and estimating the extent of thermal deformation anisotropy. In all the cases studied, the maximal thermal expansion was observed in the direction of the weakest hydrogen (malic acid) or van der Waals (valine and isoleucine) intermolecular bonds, i.e. in the directions closest to that perpendicular to the dimer molecule chains (malic acid) or to molecular layers (valine and isoleucine). The strongest anisotropy of thermal deformations in monoclinic crystals was observed in the ac plane, in which the symmetrically unfixed angle β can vary.

---

1. Introduction

In the published literature, there are many works concerning studies of phase relations in organic systems by means of temperature-resolved powder X-ray diffraction (TRPXRD). Usually, reported data are limited to temperatures of solid-phase transformations (e.g., polymorphic transitions) and determination of melting points and decomposition or sublimation temperatures. With regard to thermal expansion or thermal deformations in crystal structures, such studies are predominately considered for inorganic systems, including minerals.^1–7

Examinations of thermal deformations in crystal structures of organic substances are much scarcer. This fact was mentioned by B. K. Saha⁸ in a recently published review that summarizes data on thermal expansion of organic crystals. Some years before, C. C. Sun⁹ reported statistics of such investigations based on a survey of the Cambridge Structural Database (CSD). Both reviews^8,9 revealed significant progress in studies of this type within the last few decades. However, a relatively high percentage of the works concerns thermal expansion of organometallic compounds,^10,11 solvates,¹² and organic salts,¹³ while only a minority focuses on pure organic compounds^14–25 and their various complexes, including co-crystals.^26–29 Some authors reported thermal expansion data obtained for different polymorphs,^18–24 isoskeletal compounds,²⁵ and solid solutions.^18,19 Among the papers we have found, only two works address substances formed in chiral systems, both of which published recently. An article by B. Nicolaï et al.³⁰ presents results of the thermal expansion of L-ascorbic acid, and an article by N. Taratin et al.³¹ is related to thermal deformations in the crystal structures of diastereomeric L-threonine and L-allo-threonine and two particular solid solutions in this system. Chiral organic compounds participate in a vast variety of natural and industrial processes occurring at various temperatures; therefore, discovering the causalities governing their high-temperature behavior is not only of fundamental significance but also of an applied one.

This article presents results of studying thermal deformations in crystal structures of discrete phases in two chiral systems, namely, (S)-malic acid–(R)-malic acid and L-valine–L-isoleucine, using temperature-resolved PXRD. In the first system, composed of the malic acid enantiomers, non-equimolar 1 : 3 and 3 : 1 discrete compounds as well as three racemic compound polymorphs exist. L-Valine and L-isoleucine were shown to constitute a 2 : 1 intermolecular compound. The present work is a continuation of our previous research on these chiral systems.^32–35

2. Materials and methods

2.1 Materials

(S)- and (R)-malic acid (C₄H₆O₅) and the racemate of RSI modification, all having 98% purity, were provided by Merck Schuchardt OHG, Hohebrunn, Germany. L-Valine (C₅H₁₁NO₂) and L-isoleucine (C₆H₁₃NO₂) were obtained from Alfa Aesar, Massachusetts, USA with 99% purity. The techniques for preparation of intermolecular compounds in both systems and of racemic malic acid polymorphs are described in detail elsewhere.^32–35

2.2 Experimental techniques

Powder X-ray diffraction (PXRD). Measurements for malic acid were performed using a Bruker D2 Phaser diffractometer (Germany) applying Cu_Kα radiation and collecting data in the 2θ range of 5–45° with a step size of 0.02°.^32,33 Studies in the L-valine–L-isoleucine system were carried out using an X'Pert Pro diffractometer (PANalytical GmbH, Germany) with Cu_Kα radiation and an X'Celerator detector in a 2θ range of 3–40° with a step size of 0.017°.³⁴ The diffraction patterns obtained were processed using an STOE WinXPOW software package. Unit cell parameters have been calculated via the least squares method using the UnitCell program. Germanium powder was used as the inner standard for peak position calibration. The ESI:† Tables S1–S7 include experimentally observed and calculated values of interplanar distances d, diffraction angles 2θ and hkl indices of diffraction maxima of discrete compounds formed in the (S)-malic acid–(R)-malic acid system and in the L-valine–L-isoleucine system.

Temperature-resolved powder X-ray diffraction (TRPXRD). Malic acid system: an STOE STADI-P diffractometer (Germany) (Cu_Kα radiation) equipped with a high-temperature unit was used in air atmosphere. Temperature variation took place from room temperature to the substance decomposition point with a temperature step of 2–10 °C.^36,37L-Valine–L-isoleucine system: a Rigaku Ultima IV diffractometer (Japan) (Cu_Kα radiation) provided with high-temperature equipment was applied in air atmosphere. Temperature was varied between room temperature and the substance decomposition point with a temperature step of 20 °C. Computations of X-ray diffractograms were performed using the STOE WinXPOW software package as above. Unit cell parameters at various temperatures were calculated by means of the UnitCell program. Values of the parameters at various temperatures as well as approximation equations of their temperature dependences are given for all the compounds studied in ESI:† Fig. S1–S7.

Approximated temperature dependencies of unit cell parameters were used for calculations of the crystal structure thermal expansion coefficients (CTE) α, 10⁻⁶ °C⁻¹, along the three perpendicular axes of the thermal deformation tensor (α₁₁, α₂₂, α₃₃), as well as parameters (α_a, α_b, α_c, α_α, α_β, α_γ) and volume (α_V). Calculated CTE values allowed plotting the figures of thermal expansion coefficients on the ac plane of the crystal structure for monoclinic compounds and plotting the 3D figure of CTE for the triclinic compound. μ_ij is the angle between the corresponding tensor axis α_ii and unit cell axis j. The angle determines the orientation of the CTE figure with respect to the unit cell. Calculations of the thermal expansion tensor and plotting of the CTE figures were carried out using the programs DTC³⁸ (monoclinic crystals) and RTT³⁹ (triclinic crystals).

3. Thermal deformations of discrete phase crystal structures in the system of malic acid enantiomers

The binary (S)- and (R)-malic acid system (also known as L(−)- and D(+)-malic acid) has been repeatedly studied by various authors,^40–46 as well as by the present authors,^{32,33,35–37,47} using diverse chemical, spectroscopic, diffraction, and other techniques. At present, it is stated^33,35 that the phase diversity of this system includes the following discrete phases: enantiomers (S and R), equimolar racemic compounds of three modifications (RSI, RSII, and RSIII), and non-equimolar 1 : 3 and 3 : 1 stable (SR₃ and S₃R) and metastable (1S3R and 3S1R) compounds. The crystal structures of the S-enantiomer,⁴¹ racemates RSI⁴² and RSII⁴³ and compound S₃R are known.³⁵ Detailed specifications of all the phases are given in our highlight article published recently.³⁵ Structural peculiarities of the discrete compounds in this system are reflected in the particular character of their thermal deformations that will be described and discussed below.

3.1 Enantiomer

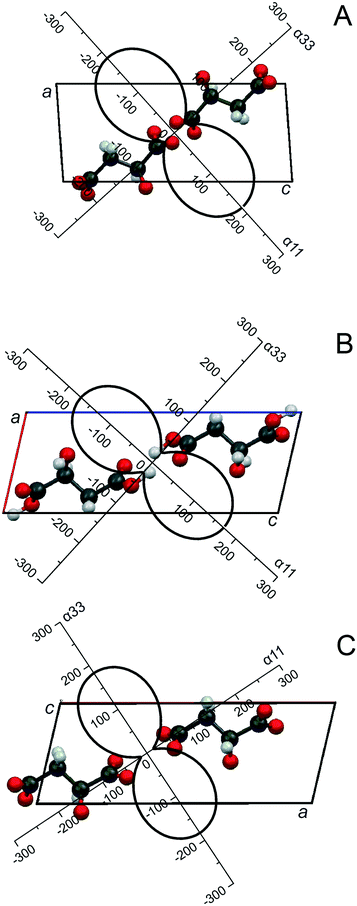
Earlier we reported that heating (S)-malic acid to its melting point (100 °C) did not cause any solid phase (polymorph) transformations.³⁶ This means that heating only induces structural (thermal) deformations in the crystal structure, which should be reflected in variations of its monoclinic cell parameters (S.G. P2₁). The unit cell parameters were calculated using 29 peak positions (ESI:† Table S1). The plotted temperature dependence of linear (a, b and c, Å) and angular (β, °) parameters and the volume (V, ų) of the unit cell of (S)-malic acid (ESI:† Fig. S1) show that all the parameters, including the volume, continuously increase with increasing temperature.

These temperature dependencies were used to calculate the coefficients of thermal expansion CTE (α, 10⁻⁶ °C⁻¹) along the three mutually perpendicular axes of the thermal deformation tensor (α₁₁, α₂₂, α₃₃), as well as the CTE of parameters (α_a, α_b, α_c, α_β) and volume (α_V) of the enantiomer monoclinic cell. The results are compiled in Table 1. In the conventional orientation of monoclinic crystals, one of the tensor axes (α₂₂) is positioned along the direction b (the 2 or 2₁ axis or the axis normal to the plane of symmetry),¹ and therefore, α₂₂ = α_b. In Fig. 1A, the projection of the CTE figure onto the ac plane, i.e. the plane that includes the symmetrically unfixed angle β of the enantiomer crystal structure, is shown. In order to plot a fragment of the crystal structure, the CSD data (COFRUK10)⁴⁸ were applied. As seen in Fig. 1A, the maximal thermal expansion (α₁₁) of the crystal structure of (S)-malic acid occurs along the direction of the bisector of the obtuse monoclinic angle a^c. This direction is close to that perpendicular to the elongation of dimer molecules' chains.

Table 1 Thermal deformation tensor parameters and thermal expansion coefficients α (10⁻⁶ °C⁻¹) of the monoclinic cell parameters in the crystal structures of (S)-malic acid and malic acid racemates RSI and RSII

Compound	α 11	α 22	α 33	1μ3c = α33^c	α a	α b	α c	α β
S	185.0	70.1	27.4	−42.0	125.0	70.1	98.0	94.4
RSI	179.0	58.5	5.88	−42.4	61.2	58.5	84.9	−92.8
RSII	14.5	59.4	183.0	−46.7	65.3	59.4	94.0	−89.6

---

Fig. 1 Projections of the figures of thermal expansion coefficients (CTE) on the ac plane of monoclinic unit cells in the crystal structures of malic acid compounds S (A), RSI (B), and RSII (C). Only dimer molecules forming the same molecular chain are shown in unit cells.

3.2 Equimolar discrete compounds

RSI and RSII are monotropic monoclinic polymorphs of the malic acid racemic compound. Racemate RSI is a stable modification (S.G. P2₁/c), while racemate RSII is metastable (S.G. Cc).^32,35,36 The thermal behavior of both compounds is in accordance with this. Heating racemate RSI up to its melting point (124 °C) only induces thermal deformations in the crystal structure. Metastable RSII in the vicinity of its melting point (∼120 °C) suffers from transformation into the stable modification, i.e. polymorphic transition RSII → RSI occurs,^32,35 so thermal deformations of racemate RSII were only studied in the range of 25–108 °C. Monoclinic cell parameters of racemates RSI and RSII at various temperatures were calculated using 30 and 27 peak positions, respectively (ESI:† Tables S2 and S3). Judging the character of their crystal structure thermal deformations, both racemates are close to each other. When the substances are being heated, linear parameters a, b, and c and the volume V of the racemates' monoclinic cells continuously increase, while the angle β decreases (ESI:† Fig. S2 and S3). The decline of angle β with increasing temperature is a distinction between thermal behaviors of the racemates and (S)-malic acid, which is caused by the different orientations of the monoclinic cell in relation to the molecular chains for the racemates and the enantiomer.

The temperature dependencies were used to calculate the parameters of the thermal deformation tensor and the CTE parameters of the monoclinic cells of both racemates, given in Table 1. On that basis and applying CSD data,⁴⁸ DLMALC11 (RSI) and DLMALC (RSII), the projection of the CTE figure onto the ac plane of the crystal structures of racemates RSI and RSII is plotted in Fig. 1B and C. Maximal thermal expansion of both compounds' crystal structures (α₁₁ and α₃₃, respectively for RSI and RSII) occurs along the direction of the bisector of the acute monoclinic angle a^c (Fig. 1B and C). This direction is close to that perpendicular to the axis of elongation of the dimer molecule chains.

Racemate RSIII was detected by the present authors^32,33 and its crystallization conditions were reported in our earlier works.^32,35 The melting point of RSIII (123 °C) is only one degree lower and three degrees higher than the melting points of RSI and RSII, respectively. It does not undergo polymorph transitions. This raises the question of which of the two modifications (RSI and RSIII) has to be considered as the more stable one.

Therefore, a sample consisting of a physical mixture of RSI and RSIII was prepared and used in heating experiments. The resulting PXRD patterns are shown in Fig. 2. For convenience, two of the characteristic peaks of each component are used for comparison. In the temperature range between 25 and 110 °C, the ratio of the peak intensities gradually shifted towards the RSI phase, at 120 °C, RSI became the predominating phase, and at 123 °C, the RSIII phase converted into RSI completely. Obviously, the solid–solid (polymorphic) phase transformation of one mixture component into the other in the presence of the latter⁴⁹ occurred. The RSIII phase transformed into RSI in the presence of RSI. The TRPXRD results are in accordance with the DSC data, as well as with results of storing and slurring experiments.³⁵ Thus, it was proven that the RSIII modification is metastable with respect to RSI.

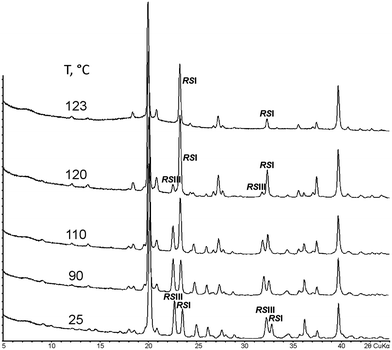Fig. 2 PXRD patterns (2θ_CuKα) of a sample containing a physical mixture of equal amounts of malic acid racemates RSI and RSIII measured at various temperatures.

3.3 Non-equimolar 1 : 3/3 : 1 discrete compounds

Compound S₃R was discovered some time ago,³³ and its crystal structure was discussed in a previous work.³⁵ It crystallizes in a triclinic cell and is the stable polymorph of the 1 : 3/3 : 1 discrete compound of malic acid. Triclinic cell parameters of compound S₃R at various temperatures were calculated using 35 peak positions (ESI:† Table S4). Heating this compound induces only thermal deformations: all the linear unit cell parameters a, b, and c, two angle parameters β and γ, and the unit cell volume V steadily increase, while the angle α undergoes continuous decrease (ESI:† Fig. S4). The melting point of the compound is 117 °C.

Table 2 contains the calculated parameters of the thermal deformation tensor and the CTEs of the triclinic cell parameters of compound S₃R, and Fig. 3 shows the resulting figure of its thermal expansion coefficients. The CTE figure is presented as a three-dimensional diagram for convenience and projected onto the triclinic cell of the S₃R crystal structure. Data of our previous work³⁵ were used to plot a fragment of the compound's crystal structure. It is revealed that the maximal thermal expansion (α₂₂) of the S₃R crystal structure occurs along the direction, which is substantially perpendicular to the elongation of its molecular chains.

Table 2 Thermal deformation tensor parameters and thermal expansion coefficients α (10⁻⁶ °C⁻¹) of the triclinic cell parameters in the crystal structure of malic acids' non-equimolar discrete compound S₃R

α 11	α 22	α 33	μ 1a = α11^a	μ 2b = α22^b	μ 3c = α33^c	α a	α b	α c	α α	α β	α γ
63.0	146.4	2.7	59.5	55.6	35.4	91.0	87.8	34.4	28.5	55.4	32.0

---

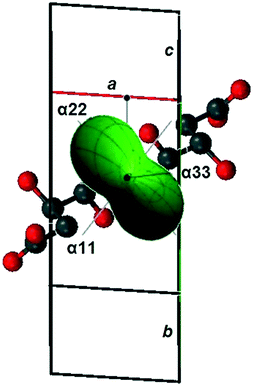Fig. 3 The CTE figure of the crystal structure of malic acids' non-equimolar discrete compound S₃R plotted as a projection onto the triclinic unit cell.

Compound 3S1R is a metastable monotropic polymorph of compound S₃R.^33,35 As shown in Fig. 4, with heating, it undergoes polymorphic phase transition into the stable S₃R phase in the temperature range of 60–80 °C. At 110 °C, only S₃R is left, which melts at 117 °C.

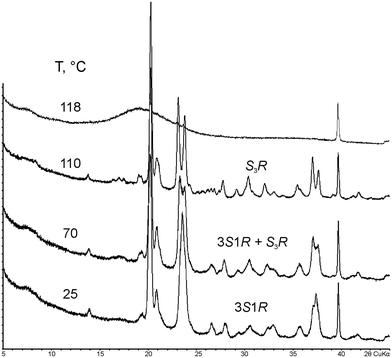Fig. 4 PXRD patterns (2θ_CuKα) of malic acids' metastable non-equimolar discrete compound 3S1R measured at various (selected) temperatures.

3.4 Discussion of main characteristics of thermal deformations

In the following, both common and different features characterizing thermal deformations of the S-enantiomer, racemates RSI and RSII, and non-equimolar compound S₃R of malic acid are discussed. Thermal deformations of the metastable compounds RSIII and 3S1R are not considered, since their crystal structures have not been deciphered yet.

The shapes of the CTE figures of compounds S, RSI, RSII (Fig. 1), and S₃R (Fig. 3) are substantially similar reflecting the anisotropic behavior of their thermal deformations. The degree of anisotropy of crystal structure deformations in the ac plane can be expressed by the following formula:¹Δ₁₃ = (α₁₁ − α₃₃)/(α₁₁ + α₃₃) providing degrees of anisotropy of 0.74, 0.94, and 0.85 for S-malic acid and racemates RSI and RSII, respectively. These values do not show considerable differences, and the least extent of thermal deformation anisotropy is observed for the enantiomer. The degrees of thermal deformation anisotropy of the S₃R crystal structure in the ac, ab and bc planes can be calculated accordingly: Δ₁₃ = (α₁₁ − α₃₃)/(α₁₁ + α₃₃) = 0.91, Δ₂₁ = (α₂₂ − α₁₁)/(α₂₂ + α₁₁) = 0.40, and Δ₂₃ = (α₂₂ − α₃₃)/(α₂₂ + α₃₃) = 0.96. Thus, the least anisotropic deformation occurs in the ab plane which can also be seen at the CTE figure of S₃R in Fig. 3.

It is obvious that thermal expansion is inversely proportional to the strength of bonding between molecules or atoms. Hydrogen bonds between the molecular chains in the crystal structures of all studied compounds are much weaker than the bonding within the chains. For example, the average distance between molecules within the chains (O…O distance) in racemate RSI is 2.675 Å, while the O…O gap between these chains is not less than 2.859 Å.⁴⁸ Consequently, when heating the substance, the space between the chains increases more intensely than that between molecules inside the chains. Therefore, the maximal thermal expansion occurs in the direction nearing the perpendicular to the elongation of the molecular chains. The deviation from the perpendicular does not exceed 17°. This deviation can also be indicative of shear deformations occuring in the crystal structure together with thermal deformations. The shear deformations cause shifting (slipping) of the dimer chains in relation to each other in the direction of their elongation. The shear deformations correlate with changes of the unit cell angle parameters, which are not symmetry-fixed.¹ In the case of monoclinic crystals, this is the angle β, and in the case of triclinic crystals, these are angles α, β, and γ.

Depending on the crystal structure orientation with respect to coordinate axes, the directions of the maximal and minimal expansion are the tensor parameters α₁₁ and α₃₃ (S and RSI), α₃₃ and α₁₁ (RSII), and α₂₂ and α₃₃ (S₃R), respectively (Tables 1 and 2). The maximal expansion direction in the monoclinic crystals of (S)-malic acid and racemates RSI and RSII lies along the bisector of the angle between the a and c(a^c) axes (Fig. 1). When the S-enantiomer is heated, the β angle increases (ESI:† Fig. S1). The bisectors corresponding to the directions of the greatest and weakest expansions divide the related obtuse angle a^c and its adjacent angle in halves (Fig. 1A). Heating racemates RSI and RSII causes the β angle to decline (ESI:† Fig. S2 and S3), while the bisectors corresponding to the directions of the maximal and minimal expansions halve the acute a^c angle and its adjacent angle, respectively (Fig. 1B and C).

The relative volume expansions, ΔV, of all the discrete compounds are rather close, being 2.1%, 2.3%, 2.2%, and 3.0% for S, RSI, RSII, and S₃R, respectively. These values, however, were defined in the individual temperature ranges confined by the existence range of each compound, i.e. from room temperature to the melting point. As the latter differ, the correct way to compare ΔV of various compounds is to define a common temperature range, e.g., from ∼25 to 100 °C. In this case, the relative volume expansions of discrete compounds S, RSI, RSII, and S₃R are 2.1% 1.8%, 1.9%, and 1.4%, respectively.

The S-enantiomer has the lowest melting point in the system. It is composed of alternating layers of molecules of the same chirality (–S–S–S–S–), has hydrogen contacts between the molecular chains, and has the least value of Δ₁₃ and the greatest ΔV. Compounds RSI, RSII and S₃R exhibit relatively high melting points. The racemates contain alternating chains of molecules of different chiralities, i.e. –S–R–S–R–, while compound S₃R is composed of alternating homochiral (–S–S–S–S–) and heterochiral (–S–R–S–R–) chains.³⁵ Racemate RSI is characterized by the presence of hydrogen bonds between the molecular chains and a relatively high ΔV value, while RSII is distinguished by the absence of such bonding and a relatively small ΔV. Compound S₃R has a triclinic cell and shows significantly lower volume expansion in comparison with the enantiomer and the racemates. The triclinic cell provides greater space for shear deformations, since it contains three non-fixed angle parameters α, β, and γ. Shear deformations can partially compensate thermal expansion. Most significant thermal deformations in the crystal structure of compound S₃R were observed in the ac and bc planes, as shown by the related Δ₁₃ and Δ₂₃ parameters.

4. Thermal deformations of discrete phase crystal structures in the system of L-valine and L-isoleucine

This enantiomeric system is composed of two different natural L-amino acids, i.e.L-valine and L-isoleucine. The two molecules differ by one additional methylene group in isoleucine, resulting in an extra chiral center. According to our data^35,37 and the literature,⁵⁰ both substances sublime when heated. Thus, DSC, commonly used for melting point and melt phase diagram determination, is not applicable. The single system components were studied in other works;^51–55 the whole binary system L-Val–L-Ile was investigated by Koolman and Rousseau,⁵⁶ Kurosawa et al.,⁵⁷ and the present authors^34,35,37 as well. A distinguishing feature of this system is the formation of a non-equimolar discrete 2 : 1 compound V₂I (with V and I for L-Val and L-Ile, respectively),^34,35 which is the only example of a non-equimolar compound known, whose crystal structure contains molecules of different amino acids of the same chirality. The crystal structures of the compounds in the system are already established (L-Val,⁵¹L-Ile,⁵² and V₂I compound³⁴).

Results of TRPXRD investigations demonstrated that L-Val, L-Ile, and V₂I do not undergo any solid phase (polymorphic) transformations,³⁷ which is supported by the temperature-resolved diffraction patterns shown in ESI:† Fig. S8A–C. Therefore, the discussion below concerns the results of studying thermal deformations of the above-mentioned discrete phases.

4.1 Valine and isoleucine enantiomers

The monoclinic cells of Val and Ile enantiomers (both S.G. P2₁) are characterized by two crystallographically independent positions of the molecules. Calculations of L-Val and L-Ile unit cell parameters at various temperatures have been performed using 20 and 16 peak position values, respectively (ESI:† Tables S5 and S6). Heating samples of L-valine and L-isoleucine causes all the linear parameters a, b, and c, as well as the volume V of the monoclinic cells to increase, while the angle parameter β decreases (ESI:† Fig. S5 and S6, respectively). Sublimation of L-Val starts at 205 °C, while sublimation of L-Ile starts at 215 °C, both of which are accompanied by the onset of partial decomposition (see ESI:† Fig. S8). The calculated parameters of the thermal deformation tensor and thermal expansion coefficients of the monoclinic cell parameters of Val and Ile are given in Table 3; the figures of the thermal expansion coefficients of the related crystal structures are shown in Fig. 5A and B, respectively. CSD data (LVALIN01 and LISLEU02)⁴⁸ were used to plot projections of the Val and Ile crystal structure fragments onto the ac plane of their monoclinic cells. As seen, the directions of maximal thermal expansion α₃₃ (Val) and α₁₁ (Ile) in the ac plane of both enantiomers' crystal structures are close to that perpendicular to the molecular layers.

Table 3 Thermal deformation tensor parameters and thermal expansion coefficients α (10⁻⁶ °C⁻¹) of the monoclinic cell parameters in crystal structures of L-Val, L-Ile and non-equimolar discrete compound V₂I

Compound	α 11	α 22	α 33	μ 3c = α33^c	α a	α b	α c	α β
L-Val	17.6	67.1	82.9	77.0	21.3	67.1	79.6	−18.9
L-Ile	53.3	54.6	12.4	−36.0	22.8	54.6	39.2	−22.3
V2I	11.6	54.6	84.0	101.5	76.6	54.6	14.5	−21.3

---

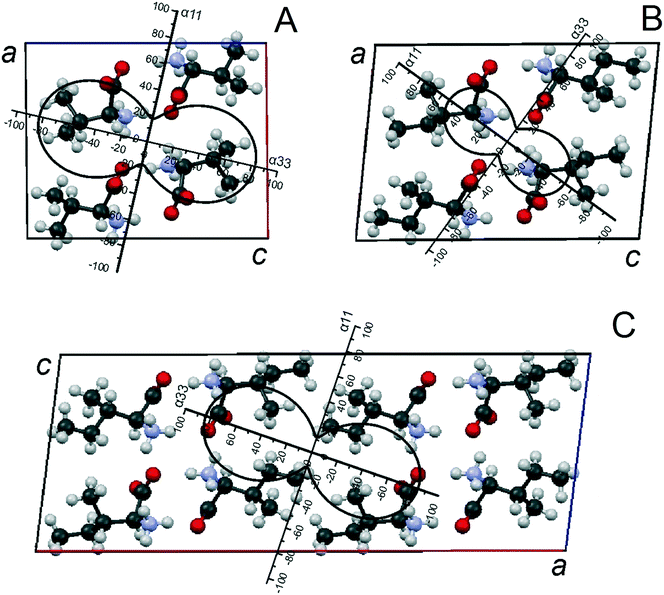Fig. 5 Projections of the CTE figures on the ac plane of monoclinic unit cells in the crystal structures of compounds Val (A) and Ile (B) and discrete compound V₂I (C) (adapted from ref. 37).

4.2 Non-equimolar discrete compound V₂I

The monoclinic cell of the V₂I compound (S.G. C2) comprises eight molecules, so it is doubled in comparison to monoclinic cells of Val and Ile.³⁴ This is because of the neighboring molecular layers, which are symmetrically non-equivalent in the compound V₂I, and the translation, which is perpendicular to them, involving two layers. Each of the two independent molecular positions is characterized by mixed population, i.e. it can be occupied either by valine or isoleucine molecules.^34,35 Calculations of unit cell parameters at various temperatures have been performed using 12 peak position values (ESI:† Table S7). At elevated temperatures, compound V₂I behaves similarly to L-valine and L-isoleucine. When heated, the crystal structure exhibits solely thermal deformations: all the linear parameters a, b, and c and the volume V of its monoclinic cell continuously increase, while the angle β decreases (ESI:† Fig. S7). The substance sublimes at 215 °C. Table 3 summarizes the calculated parameters of the thermal deformation tensor and thermal expansion coefficients of the monoclinic cell parameters, and Fig. 5C shows the corresponding CTE figure of the compounds' crystal structure. A projection of a fragment of its crystal structure onto the ac plane was plotted using the data of our previous work.³⁴ It can be derived that the direction of the maximal thermal expansion α₃₃ of the V₂I crystal structure is close to that perpendicular to the molecular layers.

4.3 Elucidation of main characteristics of thermal deformations

A very detailed analysis of molecular packing in the crystal structures of valine, isoleucine and compound V₂I is provided in our previous works.^34,35 In particular, it should be mentioned here that all three compounds' molecules form hydrogen-bonded dimer molecules which are combined in layers via identical frameworks of relatively strong hydrogen bonds. This means that differences in the thermal behavior of the crystal structures of Val, Ile, and V₂I are generally attributed to different principles of connection between the molecular layers via relatively weak van der Waals forces. Consequently, thermal deformations in the crystal structures of these discrete compounds occur mostly via elongation of the distances between the molecular layers. Peculiarities of the thermal expansion of the Val, V₂I, and Ile crystal structures are more clearly seen in the projections of their CTE figures onto the ac plane of their monoclinic cells (Fig. 5). Projections plotted for all the three compounds are similar in shape. However, considering the parameters of the thermal deformation tensor and the orientation of the CTE figure projections in relation to the monoclinic cell axes, a closer similarity is observed between the CTE figures of Val (Fig. 5A) and compound V₂I (Fig. 5C). Parameters of the thermal deformation tensor of the Ile CTE figure (Fig. 5B) have lower values, and the rotation angle of the figure with respect to the a and c axes of the monoclinic cell differs from that of the Val and V₂I CTE figures.

The calculated degrees of thermal deformation anisotropy, Δ₁₃, in the crystal structures of L-Val, L-Ile, and compound V₂I are 0.65, 0.62, and 0.76, respectively. The differences between these values are not too great; however, compound V₂I shows a slightly higher degree of deformation anisotropy than the others. The directions of the maximum thermal expansion in the three crystal structures are close to those perpendicular to the molecular layers, while the directions of the minimum thermal expansion lies on the plane of the molecular layer.

Relative volume expansions ΔV of enantiomers Val and Ile and compound V₂I are 2.6%, 2.0%, and 2.5%, correspondingly. The beginning sublimation temperatures are found at 205 °C for Val and at 215 °C for Ile and compound V₂I (±5 °C). Despite the analogous order of the molecular layer packing in the crystal structures of Val and Ile, the differences in their thermal expansions and the beginning sublimation temperatures are significant. In contrast, the extent of thermal expansion in the Val crystal structure is close to the corresponding parameters of compound V₂I despite their different arrangements of molecular layers.

These relative similarities and dissimilarities in the thermal behavior of Val, V₂I and Ile can be understood from quantitative estimation of the number of van der Waals contacts between the molecular layers in crystal structures of the compounds being studied.^34,35 The reason for the relatively lower or higher number of contacts between the related molecular layers in Val and Ile is the nature of the end group, which is a hydrogen atom in the Val molecule and a methyl group in Ile. Therefore, the V₂I compound (Val : Ile = 2 : 1) is similar to Val in terms of the number of van der Waals contacts. This explains why the volumetric thermal expansion α_V of the V₂I crystal structure is only slightly lower than that of Val, but significantly higher than that of Ile (Table 4).

Table 4 Coefficients of volumetric thermal expansion α_V (10⁻⁶ °C⁻¹) of the unit cells in crystal structures of phases in the systems of malic acid enantiomers, valine and isoleucine enantiomers, and threonine diastereomers³⁰

(S)-Malic acid–(R)-malic acid		L-Valine–L-isoleucine		L-Threonine–L-allo-threonine^30
Compound	α V	Compound	α V	Compound	α V
S	282	L-Val	168	L-Thr	109
RSI	244	L-Ile	120	(L0.34,L-a0.66)-Thr	117
RSII	257	V2I	150	(L0.90,L-a0.10)-Thr	119
S 3 R	212			L-aThr	107

---

5. Summary and conclusions

The thermal behavior of the discrete compounds formed in the system of malic acid enantiomers and in the system composed of L-enantiomers of two different amino acids, valine and isoleucine, has been studied at elevated temperatures.

In the (S)-malic acid–(R)-malic acid system, the only changes the stable discrete compounds (enantiomers, racemate RSI and non-equimolar compounds S₃R and SR₃) undergo in the temperature range up to their melting point are thermal deformations (thermal expansion). This conclusion is supported by monotonically increasing or decreasing curves in the temperature dependencies of the monoclinic (S, RSI) and triclinic (S₃R) unit cell parameters. Thermal deformation data obtained for discrete malic acid compounds as well as the figures of their thermal expansion coefficients are concordant with the peculiarities of the crystal structures of these phases. In all of these cases, maximal thermal expansion occurs in the direction which is close to that perpendicular to the plane of dimer molecule chains. In general, the shapes of thermal expansion figures of all studied crystal structures are similar and reflect the anisotropy of thermal deformations, where a noticeable part consists of shear deformations. In contrast, when heated, the metastable discrete compounds (racemates RSII and RSIII and compounds 3S1R and 1S3R) also experience thermal deformations, but in addition, in the vicinity of their melting points, they convert into stable phases as follows: RSII → RSI, RSIII → RSI, and 3S1R (1S3R) → S₃R (SR₃).

In the L-valine–L-isoleucine system, all discrete phases existing (L-Val, L-Ile and non-equimolar compound V₂I) are stable. In the temperature range up to their respective sublimation temperatures, they show only thermal deformations, and the direction of their maximal thermal expansion is close to that perpendicular to the plane of their molecular layers. The reason for the differences observed in sublimation temperatures, volumetric expansion values, degrees of thermal deformation anisotropy and orientations of projections of the CTE figures in relation to the monoclinic cell axes arises from the different proportions of hydrogen atoms and methyl groups present in the molecule and, correspondingly, from the different proportions of van der Waals contacts between molecular layers in the crystal structures of L-Val, L-Ile and V₂I.

Thermal deformations in the discrete phases discussed show certain similarities: 1) with thermal deformations of diastereomers and solid solutions in the amino acid L-threonine−L-allo-threonine system recently studied by the authors³¹ and 2) with thermal deformations of L-ascorbic acid published by B. Nicolaï et al.³⁰

The system of the levorotatory diastereomers of threonine (C₄H₉NO₃) is a representative of a rare class of chiral systems forming continuous solid solutions. When heated, both diastereomers, L-threonine (L-Thr) and L-allo-threonine (L-aThr), and the investigated solid solutions of composition (L_0.34,L-a_0.66)-Thr and (L_0.90,L-a_0.10)-Thr, experience only thermal deformations. The degree of thermal deformation anisotropy of the orthorhombic cells (S.G. P2₁2₁2₁) varies depending on the composition. The most significant manifestations of anisotropy were observed for the single diastereomers; even negative thermal expansion was obtained in the direction close to the plane of the molecular layer. Anisotropy manifestations are considerably weaker in solid solutions; the greater the concentration of the admixture molecules in the crystal structure, the weaker the anisotropy nature. Such thermal behavior is based on different numbers, lengths, and geometries of hydrogen contacts.³¹ We think that peculiarities of thermal behavior of the discrete phases in the systems discussed above have a similar basis. The values of volumetric thermal expansion of phases formed in the system of malic acid enantiomers, valine and isoleucine enantiomers and threonine diastereomers are compared in Table 4.

According to Nicolaï et al.,³⁰L-ascorbic acid (C₆H₈O₆) does not undergo polymorphic transitions when heated. Its monoclinic cell parameters (S.G. P2₁) linearly increase and the thermal expansion of its crystal structure is anisotropic in the observed temperature range (110–440 K). The maximal expansion is found along the b axis. Hydrogen bonding is practically perpendicular to this axis.³⁰ In other words, hydrogen bonding occurs mostly within molecular layers. Therefore, the maximal thermal expansion takes place in the direction of the weak intermolecular forces, i.e. in the direction which is perpendicular to the molecular layers. This interpretation agrees with our discussion of thermal deformations for discrete compounds in the three chiral systems mentioned above. Further, the volumetric thermal expansion value of α_V = 120 × 10⁻⁶ K⁻¹ for L-ascorbic acid³⁰ is comparable to the data provided for discrete compounds in Table 4.

The extent of thermal expansion of the linear unit cell parameters and volume of inorganic crystal structures¹ is usually 1.5–2 times less than the corresponding values found in organic compounds (including chiral compounds). This is caused by the presence of hydrogen and van der Waals intermolecular bonds in the crystal structures of organic substances, which are significantly weaker than covalent, ionic, and metal chemical bonding in the structures of inorganic substances. The degree of anisotropy of the crystal structure thermal expansion of organic compounds is governed by the number and direction of hydrogen bonds. Thus, the value and anisotropy of thermal expansion (or compression) are general characteristics of crystalline materials and can be used to derive correlations of the composition–structure–properties type. Ascertainment of such correlations in chiral systems is essential for crystal chemistry and technology.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The investigations were performed using equipment of the Resource Centre “Centre for X-ray Diffraction Studies” of SPSU and equipment of the MPI Magdeburg PCF Lab. The authors thank Dr. M. G. Krzhizhanovskaya, Dr. L. Yu. Kryuchkova, Dr. S. N. Bocharov, and Dr. A. A. Zolotarev Jr. for their collaboration. The authors appreciate the financial support provided by the Saint Petersburg State University Foundation (NIR 2/15, project 3.38.243.2015) and the Russian Foundation for Basic Research (Project 16-05-00837-a). Open Access funding provided by the Max Planck Society.

Notes and references

1. S. K. Filatov, High-temperature crystal chemistry, Nedra, Leningrad, 1990, p. 288.
2. S. M. Jessen and H. Kuppers, The precision of thermal-expansion tensors of triclinic and monoclinic crystals, J. Appl. Crystallogr., 1991, 24, 239–242.
3. P. Paufler and T. Weber, On the determination of linear thermal expansion coefficients of triclinic crystals using X-ray diffraction, Eur. J. Mineral., 1999, 11, 721–730.
4. J. S. O. Evans, Negative thermal expansion materials, J. Chem. Soc., Dalton Trans., 1999, 3317–3326.
5. G. D. Barrera, J. A. O. Bruno, T. H. K. Barron and N. L. Allan, Negative thermal expansion: a review, J. Phys.: Condens. Matter, 2005, 17(4), R217–R252.
6. W. Miller, C. W. Smith, D. S. Mackenzie and K. E. Evans, Negative thermal expansion: a review, J. Mater. Sci., 2009, 44(20), 5441–5451.
7. J. Chen, L. Hu, J. Deng and X. Xing, Negative thermal expansion in functional materials: controllable thermal expansion by chemical modifications, Chem. Soc. Rev., 2015, 44, 3522–3567.
8. B. K. Saha, Thermal Expansion in Organic Crystals, J. Indian Inst. Sci., 2017, 97(2), 177–191.
9. C. C. Sun, Thermal Expansion of Organic Crystals and Precision of Calculated Crystal Density: A Survey of Cambridge Crystal Database, J. Pharm. Sci., 2007, 96(5), 1043–1052.
10. C. Yang, X. Wang and M. A. Omary, Crystallographic Observation of Dynamic Gas Adsorption Sites and Thermal Expansion in a Breathable Fluorous Metal–Organic Framework, Angew. Chem., Int. Ed., 2009, 48(14), 2500–2505.
11. Y.-J. Su, K.-X. Wei, B. Huang, W.-J. Xu, W.-X. Zhang, M.-H. Zeng and X.-M. Chen, Deformable Mn(III)–Schiff-base dimer for anomalously large positive and negative anisotropic thermal expansions, CrystEngComm, 2017, 19(13), 1725–1728.
12. E. R. Engel, V. J. Smith, C. X. Bezuidenhout and L. J. Barbour, Uniaxial negative thermal expansion facilitated by weak host–guest interactions, Chem. Commun., 2014, 50(32), 4238–4241.
13. I. de Pedro, A. García-Saiz, J. Dupont, P. Migowski, O. Vallcorba, J. Junquera, J. Rius and J. Rodríguez Fernández, On the Colossal and Highly Anisotropic Thermal Expansion Exhibited by Imidazolium Salts, Cryst. Growth Des., 2015, 15(11), 5207–5212.
14. N. B. Bolotina, M. J. Hardie, R. L. Speer Jr and A. A. Pinkerton, Energetic materials: variable-temperature crystal structures of γ- and ε-HNIW polymorphs, J. Appl. Crystallogr., 2004, 37, 808–814.
15. D. Das, T. Jacobs and L. J. Barbour, Exceptionally large positive and negative anisotropic thermal expansion of an organic crystalline material, Nat. Mater., 2010, 9, 36–39.
16. S. Bhattacharya, V. G. Saraswatula and B. K. Saha, Thermal Expansion in Alkane Diacids—Another Property Showing Alternation in an Odd–Even Series, Cryst. Growth Des., 2013, 13(8), 3651–3656.
17. V. G. Saraswatula and B. K. Saha, A thermal expansion investigation of the melting point anomaly in trihalomesitylenes, Chem. Commun., 2015, 51(48), 9829–9832.
18. E. N. Kotelnikova and S. K. Filatov, Crystal Chemistry of Paraffins, St. Petersburg, Neva, 2002, p. 352.
19. S. Yu. Chazhengina, E. N. Kotelnikova, I. V. Filippova and S. K. Filatov, Phase transitions of n-alkanes as rotator crystals, J. Mol. Struct., 2003, 647, 243–257.
20. N. V. Platonova, E. N. Kotelnikova, S. K. Filatov, G. A. Puchkovskaya, I. I. Gnatyuk, J. Baran and M. Drozd, Polymorphic transformations and thermal deformations of monoclinic n-paraffins C₃₀H₆₂ and C₃₂H₆₆, J. Struct. Chem., 2012, 53(5), 973–987.
21. G. Wójcik and I. Mossakowska, Polymorphs of p-nitrophenol as studied by variable-temperature X-ray diffraction and calorimetry: comparison with m-nitrophenol, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 143–152.
22. T. Siegrist, C. Besnard, S. Haas, M. Schiltz, P. Pattison, D. Chernyshov, B. Batlogg and C. Kloc, A Polymorph Lost and Found: The High-Temperature Crystal Structure of pentacene, Adv. Mater., 2007, 19(16), 2079–2082.
23. T. N. Drebushchak, E. V. Boldyreva and M. A. Mikhailenko, Crystal structures of sulfathiazole polymorphs in the temperature range 100–295 K: A comparative analysis, J. Struct. Chem., 2008, 49(1), 84–94.
24. D. Das, T. Jacobs, A. Pietraszko and L. J. Barbour, Anomalous thermal expansion of an organic crystal—implications for elucidating the mechanism of an enantiotropic phase transformation, Chem. Commun., 2011, 47(21), 6009–6011.
25. E. R. Engel, V. J. Smith, C. X. Bezuidenhout and L. J. Barbour, Thermoresponsive Organic Inclusion Compounds: Modification of Thermal Expansion Behavior by Simple Guest Replacement, Chem. Mater., 2016, 28(14), 5073–5079.
26. K. M. Hutchins, K. A. Kummer, R. H. Groeneman, E. W. Reinheimer, M. A. Sinnwell, D. C. Swenson and L. R. MacGillivray, Thermal expansion properties of three isostructural co-crystals composed of isosteric components: interplay between halogen and hydrogen bonds, CrystEngComm, 2016, 18(43), 8354–8357.
27. S. Bhattacharya and B. K. Saha, Interaction Dependence and Similarity in Thermal Expansion of a Dimorphic 1D Hydrogen-Bonded Organic Complex, Cryst. Growth Des., 2013, 13(8), 3299–3302.
28. R. H. Jones, K. S. Knight, W. G. Marshall, J. Clews, R. J. Darton, D. Pyatt, S. J. Coles and P. N. Horton, Colossal thermal expansion and negative thermal expansion in simple halogen bonded complexes, CrystEngComm, 2014, 16(2), 237–243.
29. S. Bhattacharya, V. G. Saraswatula and B. K. Saha, Does Higher-Dimensional Hydrogen Bonding Guarantee a Smaller Thermal Expansion? A Thermal Expansion Study of an Interdigitated 1D and Interpenetrated 3D Hydrogen-Bonded Colored Dimorphic System, Cryst. Growth Des., 2016, 16(1), 277–284.
30. B. Nicolaï, M. Barrio, J.-L. Tamarit, R. Ceolin and I. B. Rietveld, Thermal expansion of L-ascorbic acid, Eur. Phys. J.: Spec. Top., 2017, 226, 906–912.
31. N. Taratin, H. Lorenz, D. Binev, A. Seidel-Morgenstern and E. Kotelnikova, Solubility Equilibria and Crystallographic Characterization of the L-Threonine/L-allo-Threonine System, Part 2: Crystallographic Characterization of Solid Solutions in the Threonine Diastereomeric System, Cryst. Growth Des., 2015, 15(1), 137–144.
32. A. I. Isakov, E. N. Kotelnikova, L. Yu. Kryuchkova and H. Lorenz, Effect of crystallization conditions on polymorphic diversity of malic acid RS-racemate, Trans. Tianjin Univ., 2013, 19(2), 86–91.
33. A. I. Isakov, E. N. Kotelnikova and H. Lorenz, Non-Equimolar Discrete Phases Formed in the System of Malic Acid Enantiomers, Chem. Eng. Technol., 2015, 38(6), 1047–1052.
34. A. I. Isakov, E. N. Kotelnikova, S. Muenzberg, S. N. Bocharov and H. Lorenz, Solid Phases in the System L-Valine – L-Isoleucine, Cryst. Growth Des., 2016, 16(5), 2653–2661.
35. E. N. Kotelnikova, A. I. Isakov and H. Lorenz, Non-equimolar discrete compounds in binary chiral systems of organic substances, CrystEngComm, 2017, 19(14), 1851–1869.
36. A. I. Isakov, E. N. Kotelnikova, L. Yu. Kryuchkova and H. Lorenz, Isomorphism and polymorphism in the system of malic acid enantiomers on the basis of X-ray and high-temperature X-ray diffractometry, in BIWIC 2013 – 20th International Workshop on Industrial Crystallization, ed. H. Qu, J. Rantanen and C. Malwade, Univ. of Southern Denmark, Odense, 2013, pp. 395–402.
37. A. I. Isakov, E. N. Kotelnikova, S. N. Bocharov, A. A. Zolotarev Jr. and H. Lorenz, Thermal deformations of the crystal structures of L-valine, L-isoleucine and discrete compound V₂I, in BIWIC 2016 – 23rd International Workshop on Industrial Crystallization, ed. H. Lorenz and H. Buchholz, Cuvillier Verlag, Göttingen, 2016, pp. 7–12.
38. R. I. Belousov and S. K. Filatov, Algorithm for calculating the thermal expansion tensor and constructing the thermal expansion diagram for crystals, Glass Phys. Chem., 2007, 33(3), 271–275.
39. V. A. Firsova, R. S. Bubnova, S. N. Volkov and S. K. Filatov, Rietveld To Tensor (RTT), Institute of Silicate Chemistry of Russ. Acad. Sci., St. Petersburg, Russia, 2015.
40. M. Andersson, A. Fredga and B. Jerslev, Anomalous Racemates of Malic Acid, Acta Chem. Scand., 1966, 20, 1060–1063.
41. P. Van der Sluis and J. Kroon, Structure of (−)-Malic Acid, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1989, 45(9), 1406–1408.
42. P. Van der Sluis and J. Kroon, The Structure of (±)-malic acid, (±)-C₄H₆O₅, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1985, 41(6), 956–959.
43. J. Van Loock, W. Van Havere and A. Lenstra, The structure of (plus or minus)-malic acid, Bull. Soc. Chim. Belg., 1981, 90, 161–166.
44. R. Ceolin, H. Szwarc and F. Lepage, On the dimorphism of DL-malic acid, Thermochim. Acta, 1990, 158(2), 347–352.
45. H. Barańska, J. Kuduk-Jaworska, R. Szostak and A. Romaniewska, Vibrational spectra of racemic and enantiomeric malic acids, J. Raman Spectrosc., 2003, 34(1), 68–76.
46. Y. Yuan, Y. Leng, H. Shao, C. Huang and K. Shan, Solubility of DL-malic acid in water, ethanol and in mixtures of ethanol + water, Fluid Phase Equilib., 2014, 377, 27–32.
47. H. Kaemmerer, H. Lorenz, S. N. Black and A. Seidel-Morgenstern, Study of System Thermodynamics and the Feasibility of Chiral Resolution of the Polymorphic System of Malic Acid Enantiomers and Its Partial Solid Solutions, Cryst. Growth Des., 2009, 9(4), 1851–1862.
48. CSD files (identifier): COFRUK10 (enantiomer S), DLMALC11 (racemate RSI), DLMALC (racemate RSII), LVALIN01 (L-valine) and LISLEU02 (L-isoleucine).
49. V. Ya. Anosov, M. I. Ozerova and Yu. Ya. Fialkov, Fundamentals of physical-chemical analysis, Nauka, Moscow, 1976, p. 503.
50. The Merck Index: An Encyclopedia of Chemicals, Drugs, and Biologicals, ed. M. J. O'Neil, 14th edn, Merck & Co, NJ, 2006, p. 2708.
51. K. Torii and Y. Iitaka, The crystal structure of L-valine, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1970, 26, 1317–1326.
52. K. Torii and Y. Iitaka, The crystal structure of L-isoleucine, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1971, 27, 2237–2246.
53. C. Zhang, B. Liu, X. Wang, H. Wang and H. Zhang, Measurement and Correlation of the Solubilities of L-Valine in Water + (Ethanol, N,N-Dimethylformamide, Acetone, Isopropyl Alcohol) from 293.15 K to 343.15 K, J. Chem. Eng. Data, 2014, 59(9), 2732–2740.
54. R. C. Zumstein and R. W. Rousseau, Solubility of L-isoleucine in and Recovery of L-isoleucine from Neutral and Acidic Aqueous Solutions, Ind. Eng. Chem. Res., 1989, 28(8), 1226–1231.
55. C. H. Görbitz and B. Dalhus, L-Isoleucine, Redetermination at 120 K, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1996, 52(6), 1464–1466.
56. H. C. Koolman and R. W. Rousseau, Effects of isomorphic compounds on the purity and morphology of L-isoleucine crystals, AIChE J., 1996, 42(1), 147–153.
57. I. Kurosawa, A. S. Teja and R. W. Rousseau, Solubility measurements in the l-Isoleucine + l-Valine + Water System at 298 K, Ind. Eng. Chem. Res., 2005, 44(9), 3284–3288.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1–S8 and Tables S1–S7. See DOI: 10.1039/c7ce02047c

---