Understanding the crystalline formation of triazene N-oxides and the role of halogen⋯π interactions†
Marcos A. P.
Martins
 *a,
Paulo R. S.
Salbego
*a,
Paulo R. S.
Salbego
 a,
Guilherme A.
de Moraes
a,
Guilherme A.
de Moraes
 b,
Caroline R.
Bender
b,
Caroline R.
Bender
 a,
Priscilla J.
Zambiazi
b,
Tainára
Orlando
a,
Priscilla J.
Zambiazi
b,
Tainára
Orlando
 a,
Anderson B.
Pagliari
a,
Clarissa P.
Frizzo
a and
Manfredo
Hörner
*b
a,
Anderson B.
Pagliari
a,
Clarissa P.
Frizzo
a and
Manfredo
Hörner
*b
aNúcleo de Química de Heterociclos (NUQUIMHE), Department of Chemistry, Federal University of Santa Maria (UFSM), 97105-900, Santa Maria, RS, Brazil. E-mail: marcos.nuquimhe@gmail.com
bNúcleo de Investigação de Triazenos e Complexos (NITRICO), Department of Chemistry, Federal University of Santa Maria (UFSM), 97105-900, Santa Maria, RS, Brazil. E-mail: hoerner.manfredo@gmail.com
First published on 22nd November 2017
Abstract
The crystallization of a series of 1-(4-halophenyl)-3-phenyltriazenide N1-oxides (1–4) and 1-(phenyl)-3-phenyltriazenide N1-oxide (5) was evaluated using the supramolecular cluster approach. This method is an efficient tool to assess the crystallization mechanism of compounds and, consequently, the steps involved in crystal formation. Compounds 1 and 4 show crystallization in two main steps while compounds 2 and 3 present three main steps, in which column formation occurs in the first step. The crystallization process for 5 occurs in 3 main steps, starting from a robust dimer formation (−16.82 kcal mol−1). Two new parameters – NCG% (topological and energetic contribution percentage) and NG/NC (energetic parameter/topological parameter ratio) – assisted in the interpretation of crystal growth. Compounds 1–4 showed NCG% = 50 in the first step while compound 5 reached only 50% of the contribution in the second step. The differences in NCG% were attributed to strong hydrogen bonds in the non-halogenated compound. The dominant parameter in each step of the crystallization process was indicated by the NG/NC parameter. The crystallization mechanism in all compounds was initially driven by an energetic process followed by a topological process. The existence of X⋯π interactions was shown and was observed to be a consequence of a topological process and without any major contributions to crystal formation. Thermal analysis and UV-vis spectral data were also discussed regarding the properties of these compounds.
Introduction
The understanding of crystalline networks requires the use of certain parameters in order to understand the interactions that form the system. The geometric parameter has been a widely used tool for describing intermolecular interactions, including halogen interactions.1,2 Recognizing interactions helps elucidate the crystallization processes of different molecules, whose final goal is to correlate characteristics of this process with the final emergent properties. However, a broad approach using topological and energetic data parameters in addition to geometric data for the study of crystals remains scarce in the literature.According to Kitaigorodskii,3 the assembly route of molecules to crystals is governed by molecules approaching each other to form the first close-pack, which are then close-packed by other layers or chains of molecules. Because of this, the crystallization process can be viewed as a stepwise progression in which molecule association increases system complexity, leading to the final 3D crystal. This progression occurs analogously to Darwinian evolution,4 where the process of self-organization blends competition, cooperation, and complementarity. The Darwinian process improves individual organization, which leads to the emergence of the crystalline arrangement.
Following this idea, our research group proposed a method in a previous study5 where crystallization mechanisms for isoxazoles were presented in order to better understand crystalline formation. This proposal was based on the observation of the energetic contributions of different dimers that formed the crystal and used the supramolecular cluster as part of the study. Our findings show that the supramolecular cluster has an energetic hierarchy related to the formation of interactions; in this case, the hydrogen bond was the strongest interaction and the first to form. The π-interactions, on the other hand, were weaker and were observed in other steps of the crystallization.
Triazene N1-oxide derivatives are an important class of molecules due to the hard basic character of the coordinating atoms O and N. This characteristic imposes electronic properties that allow molecular self-organization via intermolecular secondary interactions.6 These species have different applications in chemistry and biology, such as in sensors, electronic displays,7,8 and antileukemic and anticancer drugs.9,10 Some of these applications are a result of non-covalent intermolecular interactions and the packing behavior of these compounds.
Therefore, our aim is to assess the comprehension of the system by studying the analysis of crystal formation while considering the topological and energetic normalized data of the supramolecular cluster as a tool. In pursuance of this, a series of five N1-oxide triazenes was used in addition to the proposal of crystallization mechanisms for each system in order to observe the contrasts between different substituents. Important information regarding the contribution of each crystallization step will be provided. This will be done by observing the dominant parameter of the process in addition to observing the influence of halogen⋯π interactions on crystal formation. Geometric and QTAIM data were used to answer the questions on the role of halogen⋯π interactions in crystal formation. Additionally, thermal analyses (TGA and DSC) and UV-vis spectroscopy were carried out to determine the potential applications of these molecules.
Results and discussion
Molecular description
Crystals suitable for X-ray single crystal analysis of compounds 1–5 were obtained from the respective solutions by means of crystallization through slow evaporation of the solvent. Fig. 1 shows the molecular structures of the compounds. Crystallographic data are shown in Table 5 and additional data regarding bond lengths (Å) and angles (°) are demonstrated in Table S1 (ESI†).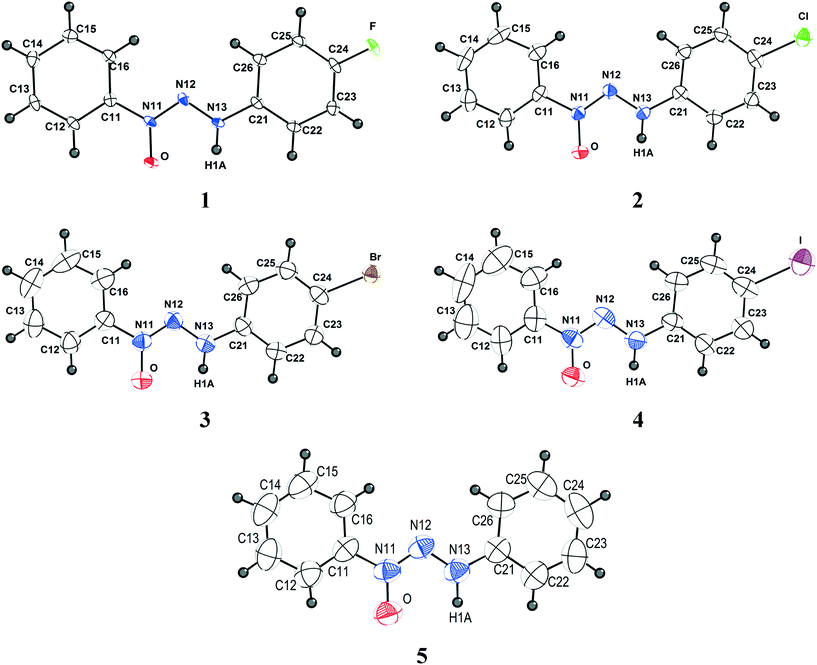 | ||
| Fig. 1 Projection of the molecular structures of compounds 1–5. H atoms are represented with arbitrary radii. Non-hydrogen atoms are represented with thermal ellipsoids at the 50% probability level. | ||
All compounds discussed in this study belong to the class of triazene N1-oxides, such as derivatives from the classical triazenes, in which the double-bonded terminal N atom in the nitrogen triad is substituted by an “oxo” group in the solid state. In solution, these compounds are in chemical equilibrium with the respective tautomer form in which the oxo group is protonated, resulting in a hydroxyl functional group. The diazo(oxide)amine [–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N(→O)–N(H)–] functional group can be stabilized by substitution of the terminal N atoms with alkyl, phenyl, or aryl substituents. In the present study, 1-phenyl-3-para-halophenyl (p-F, p-Cl, p-Br and p-I) substitution was selected in view of the comparison of its crystallographic features with that of the unsubstituted 1,3-bis(phenyl)triazene N1-oxide.
N(→O)–N(H)–] functional group can be stabilized by substitution of the terminal N atoms with alkyl, phenyl, or aryl substituents. In the present study, 1-phenyl-3-para-halophenyl (p-F, p-Cl, p-Br and p-I) substitution was selected in view of the comparison of its crystallographic features with that of the unsubstituted 1,3-bis(phenyl)triazene N1-oxide.
Compound 1 belongs to a monoclinic crystal system in a primitive three-dimensional lattice corresponding to Bravais type P and chiral space group P21 (Z = 2; Z′ = 1). Given that compound 1 does not present a heavy atom with anomalous scattering, we were unable to determine its absolute configuration. Thus, the selected molecular configuration was based on the lowest Flack value observed, which was 0.1(3). An attempt to solve the structure considering the centrosymmetric space group P21/m in comparison with the acentric space group P21 was fruitless. Compounds 2 and 3 are isostructural and belong to the centrosymmetric monoclinic space group P21/c (Z = 4; Z′ = 1). Compound 4 belongs to the orthorhombic and chiral P212121 space group (Z = 4; Z′ = 1), and its molecular configuration was selected based on the lowest Flack value observed, which was 0.048(18). Compound 5 crystallizes in the centrosymmetric monoclinic space group P21/n (Z = 4; Z′ = 1). All molecules present the expected trans stereochemistry regarding the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bond in the [–N
N double bond in the [–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N(→O)–N(H)–] diazoamine N1-oxide moiety and an almost planar shape. Molecules 1–5 deviate slightly from planarity [r.m.s. deviation from the least-squares plane through the non-hydrogen atoms: 0.0857 Å (1), 0.0353 Å (2), 0.0318 Å (3), 0.0466 Å (4), 0.0468 Å (5)]. The N13–N12–N11–O dihedral angle in the molecules {[−0.3(2)° (1)], [−0.9(4)° (2)], [−1.1(4)° (3)], [1.4(12)° (4)] and [0.5(3)° (5)]} is similar to the angle [N13–N12–N11–O1 = 0.7(5)°] found in 3-phenyl-1-methyltriazene N1-oxide and contributes to the near-planar conformation of the molecules.11 The average value of 1.295 Å for the N11–O bond distance observed in molecules 1–5 (ESI,† Table S1) is in agreement with the N11–O1 bond distance of 1.246(4) Å observed in a similar compound, 3-phenyl-1-methyltriazene N1-oxide, which indicates that the molecules adopt the N-oxide tautomeric form in the solid state.11 The angles between the planes of the rings presented values of 10.32, 3.01, 2.16, 5.93, and 3.53 for 1–5, respectively. These values are a result of the influence of the crystal packing on the different intermolecular interactions of each structure.
N(→O)–N(H)–] diazoamine N1-oxide moiety and an almost planar shape. Molecules 1–5 deviate slightly from planarity [r.m.s. deviation from the least-squares plane through the non-hydrogen atoms: 0.0857 Å (1), 0.0353 Å (2), 0.0318 Å (3), 0.0466 Å (4), 0.0468 Å (5)]. The N13–N12–N11–O dihedral angle in the molecules {[−0.3(2)° (1)], [−0.9(4)° (2)], [−1.1(4)° (3)], [1.4(12)° (4)] and [0.5(3)° (5)]} is similar to the angle [N13–N12–N11–O1 = 0.7(5)°] found in 3-phenyl-1-methyltriazene N1-oxide and contributes to the near-planar conformation of the molecules.11 The average value of 1.295 Å for the N11–O bond distance observed in molecules 1–5 (ESI,† Table S1) is in agreement with the N11–O1 bond distance of 1.246(4) Å observed in a similar compound, 3-phenyl-1-methyltriazene N1-oxide, which indicates that the molecules adopt the N-oxide tautomeric form in the solid state.11 The angles between the planes of the rings presented values of 10.32, 3.01, 2.16, 5.93, and 3.53 for 1–5, respectively. These values are a result of the influence of the crystal packing on the different intermolecular interactions of each structure.
Supramolecular cluster
The supramolecular cluster (grown from the neighboring molecules around a reference molecule (M1)) approach12 was used to obtain information on the contact surface (topologic parameter) and energy of interaction (energetic parameter) between the molecules in the crystalline arrangement of each structure (see the ESI,† Fig. S2–S7 and Tables S2–S6). The cluster was speculated since we are considering a 3D portion of the crystal that provides all the necessary information on the involved interactions in the whole crystal. This method can assess the understanding of crystal formation without neglecting molecules that are important to the system.The neighboring molecules around M1 represent the molecular coordination number (MCN). These dimers are represented by the interaction between the M1 and MN molecules (e.g., M1⋯M2, M1⋯M3, …, M1⋯M15). All molecules which share the surface contact area of the van der Waals radii with the reference molecule M1 are considered part of the cluster. The supramolecular cluster with the surface contact area of each dim was obtained using the Voronoi–Dirichlet polyhedra (VDP) method with the ToposPro 4.0 software.13 This method has already been reported5,14–16 as an efficient tool to assess crystalline understanding, especially regarding the steps involved in crystal formation, i.e. the crystallization mechanism.5
The different supramolecular clusters can be compared by the normalization12 of raw topological and energetic data in order to observe the distinct behavior of the dimers in the formation of each crystalline structure. Normalization is a tool that places all the different data in the same scale, allowing precise comparisons and interpretations of different systems. Hence, all N molecules in the cluster contribute in some way to the whole system, and it is necessary to assess the contribution of each one in relation to a standard, in our case, in relation to the number of molecules present in the cluster (around reference molecule M1).
For example, in a cluster with an MCN of 16, all dimers must have an ideal contribution of 1 for all considered parameters (e.g. energy), which leads to a 100% contribution of 16. However, this is not the reality for most molecules where distinct interactions occur, leading to different dimeric contributions. Therefore, all raw data should be reduced to the same scale using the MCN as reference for this normalization.
From normalized values, intermolecular interactions can be divided into four types.12 Type I represents a molecular dimer with a high interaction energy on a small contact surface (e.g. hydrogen bonds). Type II corresponds to a high interaction energy on a large contact surface (e.g., π⋯π interactions). Type III corresponds to both small interaction energy and contact surfaces with a maximum difference of ±0.5 between both parameters, and type IV is a contribution based on large contact surfaces with low interaction energy.
Topological and energetic normalized data of each dimer from the supramolecular cluster of compounds 1, 2, and 5 (for 3 and 4, see the ESI,† Fig. S1) with the respective dimer classification are described in Fig. 2.
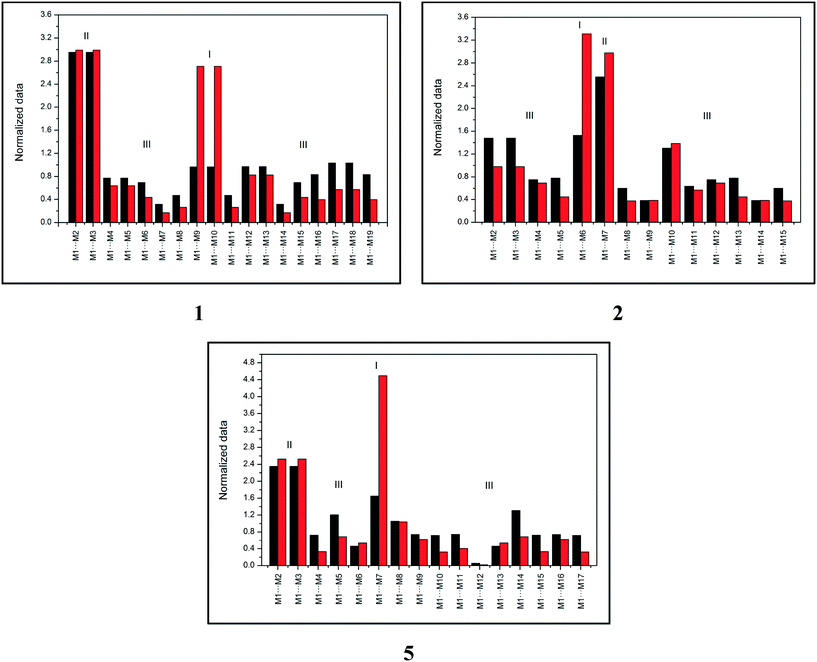 | ||
| Fig. 2 Topological (black) and energetic (red) normalized data of each dimer from the supramolecular cluster of compounds 1, 2, and 5. | ||
Fig. 2 demonstrates that compound 1 has two type I dimers and two type II dimers, which correspond to dimers involved in hydrogen interactions and stacking, respectively. The remaining dimers exhibited a type III behavior with low area and energy values. Notably, data from compound 1 are similar to data from compound 4 (see the ESI,† Fig. S1). Compound 2 (similar for compound 3, see the ESI,† Fig. S1) had only one dimer with type I behavior and one dimer with type II behavior, which is different from what was observed in compounds 1 and 4. These data provide important information on the formation of the crystalline structure, especially concerning the first dimers formed (the most energetic ones). Finally, compound 5 displayed a distinct characteristic when compared to compounds 1–4. The supramolecular cluster presented only one type I dimer of the highest energetic contribution of all systems and two type II dimers with lower contribution regarding stacking interactions when compared to 1–4. This normalized data approach provides significant data of the characteristics of the dimers and enables the understanding of the crystal formation, which is discussed in the following section.
Crystallization mechanism
Since crystallization is a stepwise process that takes into account energy hierarchies, crystallization mechanisms have been proposed for a series of compounds in order to understand crystal formation. The normalized data previously presented were used to assess the proposed crystallization mechanism5 for each structure. The main difference between these proposed mechanisms and that of the earlier study5 is that the normalized values were used in all steps and in the interpretation of the mechanisms.Firstly, individual dimer data regarding stabilization energy were used to define the highest and lowest dimer hierarchies in order to assess the steps of crystal formation. Then, the main steps were defined, where in some cases more than one hierarchy is present in the same crystallization step. The proposed crystallization mechanism for compounds 1, 2, and 5 are presented in Fig. 3, 4 and 5, respectively.
 | ||
| Fig. 3 Proposed crystallization mechanism of compound 1. NG = normalized energy. The shaded area represents the portion in the previous step. | ||
 | ||
| Fig. 4 Proposed crystallization mechanism of compound 2. NG = normalized energy. The shaded area represents the portion in the previous step. | ||
 | ||
| Fig. 5 Crystallization mechanism of compound 5. NG = normalized energy. The shaded area represents the portion in the previous step. | ||
Once the main steps were determined, we returned to the data of the normalized dimer in order to obtain two main parameters to assess the elucidation of the process:
• The topological and energetic contribution for each step of the crystal growth. The percentage of contribution (NCG%) from each given step can be found by the sum of the normalized topological and energetic data (NC + NG) of each step, in which the total NC + NG of the cluster is 100%. As a result, we are able to establish the steps with the highest contribution for both parameters, i.e. surface area and energy. The step contribution can indicate where the definitive step towards the considered crystalline structure is.
• The ratio between NG and NC to find the parameter that rules each step. The NG/NC ratio provides important information on the governing parameter in each step, in which values over 1.0 indicate a higher energetic contribution and values under 1.0 indicate a dominant topologic parameter. Values near 1.0 indicate a balance between parameters. Thus, it is possible to inform where the changes between the dominant parameters occur.
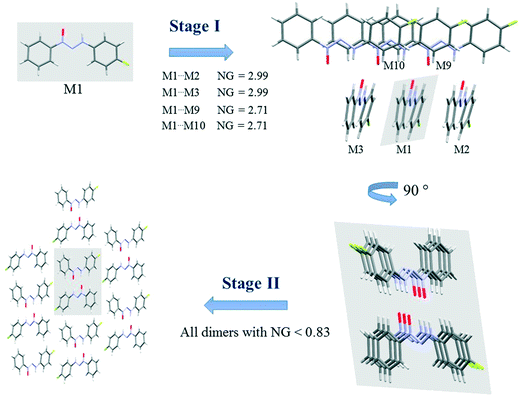
Fig. 3 presents the steps of the crystallization mechanism for compound 1. Compound 4 also presents the same general steps, and an illustration can be found in the ESI† (Fig. S8). The cluster molecules involved in the steps were depicted and their normalized energy values were highlighted.
The proposed crystallization mechanism for structures 1 and 4 shows two major steps (Fig. 3). The first step occurs with the formation of interconnected columns by hydrogen interactions with a stabilization energy of −9.78 kcal mol−1 (NG = 2.99) for each of the two dimers involved and an energy value of −8.85 kcal mol−1 (NG = 2.71) for the molecule stacking of each dimer. The dimers involved in this step present the highest portion of surface contact area and stabilization energy in relation to the whole supramolecular cluster (see Fig. 2). This step contributes 53.4% to crystal formation when both stabilization energy (NG) and surface contact area (NC) are considered, namely the topological and energetic parameters are taken into consideration in the final contribution (NCG%).
Step 2 presents the final crystal formation (3D growth) with the interaction between the columns formed in step 1. These dimer interactions occur with stabilization energy below −2.7 kcal mol−1 (NG < 0.83). All these dimers represent the remaining 46.6% of topological and energetic contribution to form the 3D network.
A value of 1.46 was found for the first step, regarding the second parameter (NG/NC), which indicates a strong impact from the energetic parameter in this step of crystal growth, i.e. almost 50% more influence than the topological factor. Moreover, a value of 0.65 was found for the second step, demonstrating a change in the dominant parameter in this step of the crystallization where topology plays a more relevant role than stabilization energy.
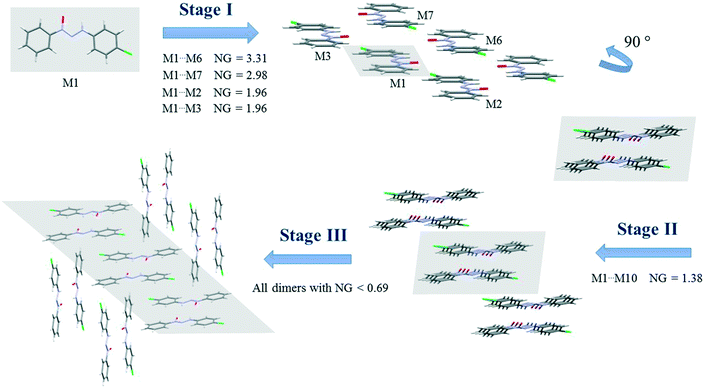
Compounds 2 and 3 present similar clusters with isostructural behavior, which leads to identical proposals of crystallization mechanism. Fig. 4 depicts the mechanism of compound 2 (for compound 3, see the ESI,† Fig. S9).
There are three main steps in the proposed crystallization mechanism for compounds 2 and 3. In the first step, the two main energetic dimers form the displaced columns: the dimer involved in a hydrogen interaction of −15.17 kcal mol−1 (NG = 3.31) and the stacking dimer of −13.65 kcal mol−1 (NG = 2.98). Two dimers from the supramolecular cluster with a stabilization energy of −4.48 kcal mol−1 (NG = 1.96) appear in this step due to the formation of the displaced columns. The dimers considered in the first step had an NCG% of 54.6%, indicating that this first step is a point of no return for the crystal since over 50% of all stabilization energy and surface contact area of the crystal rely on this first step.
The second step is the interaction between the columns (formed in step 1) with an interaction energy of −6.34 kcal mol−1, which leads to the 2D growth of the crystal. In this step, crystallization is increased by a NCG% of 9.6%. Finally, the third step is responsible for the formation of the 3D crystal network. In this final step, the 2D columns interact through dimers with a lower stabilization energy below −3.2 kcal mol−1 (NG < 0.69). This final step represents the remaining 35.8% of the topological and energetic contributions. The NG/NG parameter presented values of 1.17, 1.06, and 0.77 for the first, second, and third steps, respectively. These data demonstrate the evolution of the dominant parameter through the crystallization process with a slight dominance of the stabilization energy in the first step and the subsequent rise of topological governance in the other two steps.
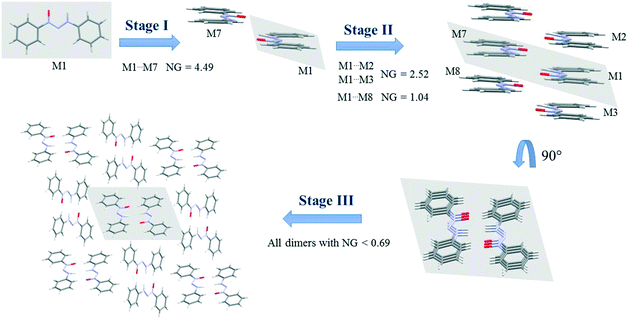
Fig. 5 demonstrates the proposed crystallization mechanism of compound 5, which differs from the other supramolecular structures.
The first step for compound 5 (Fig. 5) differs from those of the previous compounds due to the formation of a dimer with a robust stabilization energy of −16.82 kcal mol−1. The normalized data (NG = 4.49) show the magnitude of this dimer with a value four and a half times greater than expected, which represents a strong hydrogen interaction. This first step corresponds to 19.2% of the contribution of the whole crystal, even though it is only one dimer. The second step is the stacking interaction of these dimers in order to form columns with a stabilization energy of −9.44 kcal mol−1 (NG = 2.52) and −3.89 kcal mol−1 (NG = 1.04). At this moment, there is an increase of 37% in the contribution. The third step is similar to that of compounds 1 and 4, where the columns interact with each other with energies below −2.6 kcal mol−1 (NG < 0.69) in order to form the 3D crystal lattice. The last step contributes with an NCG% of 43.8. The crystallization behavior of this structure differs from that of the others in the contribution of each step, since there is a unique first step with a strong hydrogen interaction between the two molecules. The NG/NC ratio showed values of 2.72, 1.05, and 0.63 for steps 1, 2, and 3, respectively. These data clearly demonstrate the transition between the dominant parameter in each step. The first step with high energy in a smaller surface area had a value almost three times higher, thus highlighting the importance of the energetic parameter. The transition in the dominant parameters in the second step indicated a balance between the surface and energy parameters. The last step, due to the presence of lower stabilization energies in column approximation, was highly influenced by the topological parameter.
For better visualization, the three proposed mechanisms of crystallization for compounds 1–5 are summarized in Fig. 6.
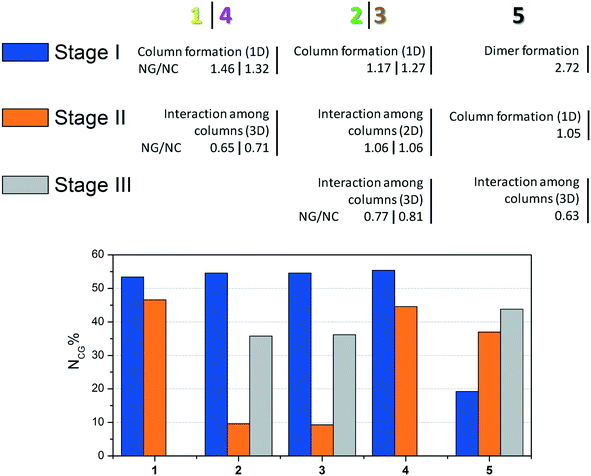 | ||
| Fig. 6 Summary of crystallization steps for compounds 1–5 with the topologic and energetic contribution (NCG%). The NG/NC parameter is also demonstrated for each stage. | ||
The data presented in Fig. 6 show the main event in each step for compounds 1–5 until 3D crystal growth. In each step, the combined contribution considering topological and energetic parameters is described in order to have a comprehensive view of the steps in all the studied supramolecular structures. Compounds 1–4 had contributions of over 50% in the first step. Compound 5, which formed a strong first dimer, reached a contribution of 50% only when the first and second stages were considered. However, it is possible to state that the first dimer is formed irreversibly, since the hydrogen interaction formed corresponds to almost 20% of the entire interaction energy of the crystal.
The NG/NC parameter allows us to observe the transition between the dominant parameters during the crystallization process. Compounds 1–5 behaved similarly during the steps, in other words, the first dominance of the stabilization energy of the interactions involved in the considered dimers, its subsequent decrease, and the increase of the topological relevance to the crystal growth. The final step of the crystallization process relies almost exclusively on a topologically dependent process.
Thus, based on such findings, differences between the angles of the rings in each structure mentioned in the molecular description section can be better understood. Compounds 1 and 4 have the highest angles, which is unexpected due to the differences between F and I. However, the influence on these torsion angles relies on crystal packing, and it was possible to observe that 1 and 4 have similar mechanisms of crystallization, achieving a similar 3D crystal network. Structures 2 and 3 are isostructural and consequently present similar torsion values. The structure without a substituent (5) has an intermediate value, which is distinct from the others and consistent with its different crystal packing.
Intermolecular interactions
The supramolecular cluster aided in comprehending the differences in the crystal packing of the studied systems. From this approach, it is possible to look even further into specific interactions to assess if the considered dimers are relevant to crystal packing. In view of studies that conventionally focus on intermolecular interactions in a geometric perspective, we will first discuss this parameter and afterwards advance to a broader view using the supramolecular cluster as the essential portion of the study.This discussion will focus mainly on halogen interactions and its importance to crystal packing. These intermolecular interactions were identified according to the standardization of the Platon program.17 The arrangements involving halogen⋯π interactions for compounds 1–4 are shown in the ESI† (Fig. S40), where a supposed prominence of these intermolecular interactions is demonstrated. Fig. 7 presents the orientation of the halogen atoms for compounds 1–4 in relation to the plane of the aromatic ring forming the halogen⋯π interactions. The geometric parameters for all halogen⋯π interactions are presented in Table 1.
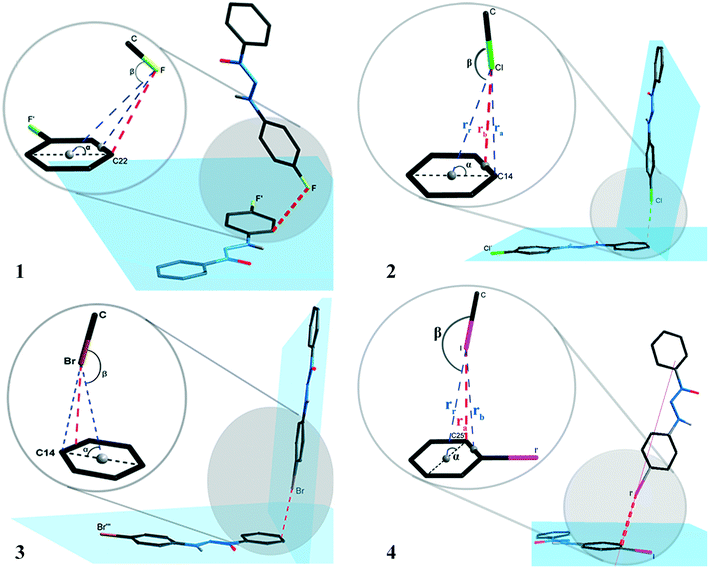 | ||
| Fig. 7 Orientation of the halogen atoms in relation to the plane of the aromatic ring forming the halogen⋯π type interactions for compounds 1–4. | ||
| Parameter | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| α = X⋯centroid–plane. β = C–X⋯centroid. | ||||
| Dist. ra (Å) | 3.2654(5) | 3.5379(4) | 3.5332(1) | 3.6053(1) |
| Dist. rb (Å) | 3.4127(5) | 3.4023(4) | 3.4054(1) | 3.9080(2) |
| Dist. rr (Å) | 4.1018(7) | 3.7591(5) | 3.7499(1) | 3.9080(2) |
| β (°) | 91.443(5) | 154.064(7) | 154.457(2) | 170.601(1) |
| α (°) | 44.757(4) | 70.169(8) | 70.344(2) | 49.518(1) |
| Symmetry operators | 2 − x, −½ + y, −z | 1 + x, −½ − y, ½ + z | 1 + x, ½ − y, ½ + z | 1 − x, −½ + y, 1½ − z |
The interactions presented in 1 and 4 are classified as localized and type (L).1,2 This is due to their parameter ra (distance from the halogen to a specific carbon) as the shortest distance when compared to the parameters rr (distance from the halogen to the centroid) and rb (distance from the halogen to the bond between two carbons of the aromatic ring). Table 4 shows ra values equal to 3.2654(5) and 3.6053(1) Å for compounds 1 and 4. The distance of the van der Waals radii for F⋯C and I⋯C are 3.17 and 3.68 Å, respectively, indicating a strong halogen⋯π interaction for compound 4, whereas values for distance ra are lower than the sum of the van der Waals I⋯C radii.
Compounds 2 and 3 are classified as semi-localized and type (SL). Their distances of lower values registered for parameter rb are 3.4023(4) and 3.4054(1) Å, respectively, where the distances of the interactions Cl⋯π and Br⋯π are 3.4023(4) and 3.4054(1) Å, respectively. In this sense, values below the sum of the van der Waals radii, which are 3.45 and 3.55 Å, respectively, for Cl⋯C and Br⋯C, indicate a significant interaction. The halogen⋯π interaction nomenclature for compounds 1–4 can also be attributed to the geometric criteria. For compound 1, the F⋯π interaction shows angle β(C–F⋯centroid) as 91.443(5)°, a value very close to the orthogonal one, thus indicating that it is a lone pair⋯π type interaction according to Mooibroek et al.18 For compounds 2–4, the halogen⋯π interactions have a β angle of 154.064(7), 154.457(2), and 170.601(1), respectively, and present values close to linearity (180°). This indicates that these are σ-hole type interactions.
In this geometric approach, it is possible to assess some magnitude of the X⋯π interactions using only the atom–atom distances, in accordance with the established literature. However, how can the existence of the X⋯π interactions be ensured only by means of raw geometric data? And what about the strength of those interactions, how can it be assessed without considering an energetic approach? How can it be properly assessed that these types of interactions are relevant to crystal formation?
QTAIM approach
The quantum theory of atoms in molecules (QTAIM)19 analysis was carried out to assess the identification and strength of the intermolecular interactions. This was done to corroborate the intermolecular interactions observed by the geometric parameter and to attempt to answer some of the earlier questions. Bond critical points (BCPs) were obtained to confirm the existence of the interactions. The intermolecular X⋯·π interactions were confirmed for structures 1–4 (Fig. 8), corroborating the observed data in the geometric discussion in addition to other interactions observed. In the case of structure 1, two different types of interactions (X⋯π and C–H⋯π) were observed, which were different from those of compounds 2–4 that presented only X⋯π interactions. Structure 5, which had no replacement in the phenyl ring, presented, in a similar dimer, two C–H⋯π interactions.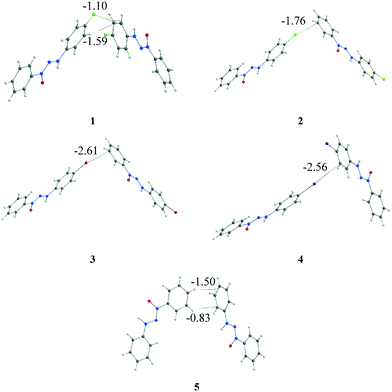 | ||
| Fig. 8 Representation of X⋯π (1–4) and C–H⋯π (1 and 5) interactions through the BCPs observed by QTAIM analysis. The energy involved in each interaction is highlighted (in kcal mol−1). | ||
The first question regarding the existence of the intermolecular interactions is then answered: each interaction involved in the considered dimer has been identified by the BCPs in the QTAIM. The second and third questions are still pendent and, thus, it is necessary to go beyond the energy calculation of the dimer and the observed interaction. A referential is necessary to assess the relevance of this dimer/interaction, and the supramolecular cluster can aid us in acquiring this information. Therefore, the energy involved in each interaction was obtained through the fragmentation of the energy from the considered dimer using a previously reported method,5,14 which is highlighted in Fig. 8.
The QTAIM data regarding the interactions involved in these dimers are presented in Table 2. These interactions observed by the BCPs, in a separate form, can induce the observer to conclude that X⋯π interactions are relevant to crystal formation. However, when considering the energy of the involved dimers that range from −1.76 to −2.69 kcal mol−1, it becomes clear that these dimers have a low energetic value when considering total crystal energy. Consequently, this information helps answer the two remaining questions.
| Comp. | Dimer | G M1⋯MN (kcal mol−1) | Interaction | ρ INT (a. u.) | G AI (x⋯Y) (kcal mol−1) | %d |
|---|---|---|---|---|---|---|
| a Stabilization energy obtained by DFT calculation. b Obtained using QTAIM. c Interaction energy involved in each interaction obtained by the fragmentation. d Interaction contribution regarding the total energy cluster. | ||||||
| 1 | M1⋯M12 | −2.69 | F⋯π | 0.004047 | −1.10 | 3.7 |
| M1⋯M13 | H⋯π | 0.005811 | −1.59 | 5.4 | ||
| 2 | M1⋯M9 | −1.76 | Cl⋯π | 0.006136 | −1.76 | 5.5 |
| M1⋯M14 | ||||||
| 3 | M1⋯M9 | −2.61 | Br⋯π | 0.007093 | −2.61 | 7.9 |
| M1⋯M14 | ||||||
| 4 | M1⋯M16 | −2.56 | I⋯π | 0.005375 | −2.56 | 7.0 |
| M1⋯M19 | ||||||
| 5 | M1⋯M9 | −2.33 | H⋯π | 0.002655 | −0.83 | 2.8 |
| M1⋯M16 | H⋯π | 0.004812 | −1.50 | 5.0 | ||
The fragmentation of the interaction energy of the dimer in the different interactions provides important additional data. The contribution of X⋯π interactions is discernible when the whole system is considered. Moreover, X⋯π interactions are responsible for less than 7.9% of the entire stabilization energy of the supramolecular cluster, contributing 3.7%, 5.5%, 7.9%, and 7.0% for compounds 1 to 4, respectively. These data provide an important insight into X⋯π interactions and allow us to answer the previous question of the importance of this kind of interaction for crystal formation. This broad analysis has shown us that in these series of crystal molecules, halogen⋯π interactions are a topological consequence of the crystallization process because they are present in the last steps of the crystallization process in the approximation of the columns. The complex approach, which is not solely dependent on geometric parameters, enabled us to confidently assess that halogen⋯π interactions do not drive the crystallization process.
Using the molecular electrostatic potential (MEP), it is possible to observe the regions with negative and positive potential in the molecules.20 In the case of compounds 2–4, it is possible to observe the positive region in the halogen atom (σ-hole) (Fig. 9), which allows the σ-hole⋯π interaction observed in the previous section to occur. Compound 1 with the fluorine atom, on the other hand, does not present the σ-hole, which leads to a lone-pair⋯π interaction.20 Additional MEPs regarding the involved dimers are presented in the ESI† (Fig. S10).
Thermal analysis
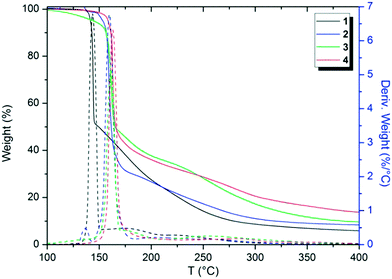
Thermal analytical techniques can provide important information on the storage and stability of different compounds. As previously reported in the literature, triazenes are compounds with excellent biological activity against tumor cells (e.g. TLX5 lymphoma and L1210 leukemia cells).9,10,21 Thus, understanding the thermal behavior of these compounds is an important and integral part of developing stable drugs.22DSC and TG analyses were carried out to elucidate the thermal performance of these structures in a broad range of temperatures. Firstly, TGA screening was carried out for compounds 1–4 at a temperature range of 25 to 900 °C in order to observe the decomposition steps and decomposition temperature of the structures as a function of the halogen p-substituted in the aromatic ring (see the ESI;† Fig. S11–S15). The decomposition percentage indicates that the decomposition of the samples is almost complete (>90%) in the evaluated temperature range. Nevertheless, Fig. 10 shows the TGA thermograms of compounds 1–4 in a range from 100 to 400 °C, in which the main changes in weight loss versus temperature were observed. For a better visualization, the TGA thermogram of 5 was omitted from Fig. 10 and depicted in the ESI.†
From Fig. 10, it is possible to note that these structures decompose in two main steps, the first from 90 to 220 °C and the second from 150 to 450 °C, approximately. Furthermore, by peak differences in the derivative weight as a function of temperature plots, it can be noted that the halogens influence the decomposition pattern of triazene N-oxides. Table 3 shows data regarding the initial decomposition temperature (Ti), final decomposition temperature (Tf), decomposition percentage (%), and temperature of maximum decomposition (Td). Ti is the temperature at which the compound starts to lose mass and indicates that no thermal degradation based on mass loss occurs at temperatures below Ti. Tf indicates the temperature in which mass loss is complete. Td corresponds to the temperature of the maximum peaks in the derivative weight (%) as a function of temperature (T) in the TGA thermogram (Fig. 10).
| Compound | Step | T i (°C) | T f (°C) | T d (°C) | %d |
|---|---|---|---|---|---|
| a Initial decomposition temperature. b Final decomposition temperature. c Temperature of maximum decomposition. d Decomposition percentage. | |||||
| 1 | 1 | 129.36 | 155.16 | 143.97 | 52.50 |
| 2 | 155.16 | 396.20 | 177.54 | 41.47 | |
| 2 | 1 | 137.24 | 173.59 | 159.96 | 67.77 |
| 2 | 173.59 | 400.05 | 241.27 | 23.68 | |
| 3 | 1 | 94.92 | 207.79 | 160.92 | 63.34 |
| 2 | 207.79 | 449.78 | 254.66 | 27.58 | |
| 4 | 1 | 121.70 | 217.35 | 162.83 | 66.61 |
| 2 | 217.35 | 455.52 | 282.40 | 20.45 | |
| 5 | 1 | 128.40 | 154.26 | 138.76 | 60.49 |
| 2 | 154.26 | 312.88 | 166.60 | 35.84 | |
Halogens, in general, tend to increase the stability of triazene compounds as observed in Table 3. An order for decomposition temperatures can be estimated for the compounds in this study, in which 5 < 1 < 2 < 3 < 4. This order in relation to compounds in which X = halogen corresponds to F < Cl < Br < I.
In the literature, halogen compounds exhibit a pattern of decomposition behavior generally related to the strengths of the carbon–halogen (C–X) bonds. The greater the C–X bond dissociation enthalpies, the more thermally stable the halogenated compounds.23 For alkyl halides, for example, the bond dissociation enthalpies are 106, 81, 69, and 54 kcal mol−1 for C–F, C–Cl, C–Br and C–I, respectively, in which the stability order is I < Br < Cl < F.24 This order represents the opposite trend found in this study. We suppose that the order found for triazene N-oxides is a result of two mutual factors: (i) halogen electronegativity and (ii) atomic radius. An increase in decomposition temperature of the compounds as the halogen atomic radius increases and electronegativity decreases can be highlighted. Unexpectedly, this indicates that triazene N-oxides substituted in the para position by hard substituents (lower atomic radius and greater electronegativity, i.e. F atom) decomposed at lower temperatures than the same compounds with soft substituents in the same position (greater atomic radius and lower electronegativity, i.e. I atom) that possess a more polarizable electronic cloud.
Compounds were submitted to DSC analysis in order to determine their thermal events (e.g. melting and crystallization temperatures). Each sample was subjected to three cycles of heating and cooling at a safe temperature range varied according to the decomposition temperature of the compounds present in the sample. This was done to avoid decomposition within the DSC equipment. However, no thermal events were observed for 1–4 in all cycles within the temperature ranges evaluated (see the ESI;† Fig. S16–S19). This leads us to believe that the melting point of the compounds is likely very close to the point at which they decompose. This assumption is in accordance with the study reported by Serebryanskaya et al.25 The authors observed thermal decompositions for 1,3-bis(2-alkyltetrazol-5-yl)triazenes and their Fe(II), Co(II), and Ni(II) complexes using DSC in addition to finding that the triazene complexes decomposed without melting at temperatures above 240 °C.
UV-vis
The absorption of electromagnetic radiation of the ultraviolet-visible light by molecules, atoms, or ions is usually associated with electronic transitions. The development of semi-conductor materials with optical properties can result in optical electronic devices, such as light-emitting diode (LED) displays, applications in optical communication, and biological labeling.7,8 Therefore, the optical behavior of compounds 1–4 in ethanol were evaluated from the spectroscopy of molecular absorption in the UV-visible region (at a range of 200 to 600 nm). All the compounds show three distinct peaks of absorbance at a range of 190 to 400 nm, which corresponds to the UV region (Fig. 11(a)). These peaks of absorbance occur when an electron is promoted from a low-energy to a high-energy electronic state by the interaction of the absorbent medium with electromagnetic radiation. Fig. 11(a) demonstrates absorbance as a function of wavelength (λ) in different concentrations of compound 1, which presents three peaks at 200, 234, and 348 nm (black arrows). From this data, an absorbance versus concentration plot can be constructed for each absorption peak. Fig. 11(b) demonstrates this plot for compound 1 at 200 nm.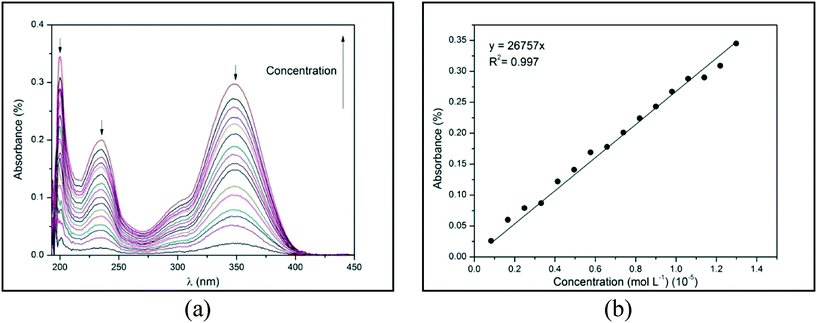 | ||
| Fig. 11 (a) Absorbance versus wavelength (λ) and (b) absorbance versus concentration for 1 at 200 nm in ethanol at 25 °C. | ||
By using the Lambert–Beer law, the angular coefficient of the straight line observed in Fig. 11(b) corresponds to the molar absorptivity (ε) of compound 1 in ethanol at 200 nm. The absorbance versus λ for 2–4 and the absorbance versus concentration plots for 1 at 234 and 348 nm and 2–4 in all λ of absorption are depicted in ESI,† Fig. S28–S31. The straight lines of all experimental data were obtained with an excellent determination coefficient. Molar absorptivity (ε) measures the ability of a mole of substance to attenuate light incident on a given wavelength. It is an intrinsic property of substances and provides an estimation of how strongly a substance absorbs radiation of a given frequency. Table 4 shows the λ1, λ2, and λ3 of absorption peaks and the molar absorptivity (ε) in each λ for compounds 1–4.
| Compound | λ 1 (nm) | λ 2 (nm) | λ 3 (nm) | ε 1 (L mol−1 cm−1) | ε 2 (L mol−1 cm−1) | ε 3 (L mol−1 cm−1) |
|---|---|---|---|---|---|---|
| a ε 1, ε2 and ε3 correspond to molar absorptivity in λ1, λ2, λ3, respectively. | ||||||
| 1 | 348 | 234 | 200 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 098 098 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 289 289 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 757 757 |
| 2 | 360 | 240 | 200 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 562 562 |
6424 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 531 531 |
| 3 | 352 | 238 | 200 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 238 238 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 257 257 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 963 963 |
| 4 | 360 | 241 | 203 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 083 083 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 874 874 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 899 899 |
From Table 4, λ1, λ2, and λ3 were assigned to n → π*, n → σ* and π → π* electron transitions, respectively. The triazene chemical groups probably involved in these transitions are N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, –N
N, –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–N, and C
N–N, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, respectively. The absorption transition of these triazene N1-oxides are in agreement with data previously reported in the literature for triazene structures without coordinated oxygen.26,27 Furthermore, the ε of 1–4 demonstrates that all compounds possess a strong absorbance capacity, which shows promising optical properties.
C, respectively. The absorption transition of these triazene N1-oxides are in agreement with data previously reported in the literature for triazene structures without coordinated oxygen.26,27 Furthermore, the ε of 1–4 demonstrates that all compounds possess a strong absorbance capacity, which shows promising optical properties.
Domingues et al.26 reported an ortho-substituted triazene with a fluorine atom possessing a greater ε value than that of the ortho-substituted analogue compound with a chlorine atom. In this study, compound 1 with an aromatic ring p-F substituted shows significantly larger ε1, ε2, and ε3 values than the p-Cl substituted analogue compound (2). Nevertheless, the ε1, ε2, and ε3 values for compounds 2 and 3 were similar to values found for compound 1. This indicates that the electron transitions associated with the absorbance phenomena in triazene N1-oxides is not highly dependent on electronic effects caused by different halogen bonds in the aromatic ring.
Conclusions
Triazene N1-oxides were successfully used as a model to contribute to the understanding of crystallization mechanisms and the importance of certain interactions, such as halogen⋯π interactions, to crystal growth. Proposals of crystallization mechanisms were presented for the series of molecules using topological and energetic data obtained from the supramolecular cluster. Two new parameters were presented to interpret the crystal formation, the NCG% and the NG/NC. It was possible to observe that compounds 1–4 (X = halogen) presented contributions of over 50% in the first step. Compound 5 (X = H), which formed a strong first dimer in the first step, reached only 50% of the contribution when considering the first and second step. The NG/NC parameter enabled us to observe the transition between the dominant parameters during the crystallization process. All compounds presented similar behavior during the steps, i.e. first a dominance of the stabilization energy of the interactions and the final step of the crystallization process relying almost exclusively on a topological process. With a broad analysis, it was possible to ensure the existence of X⋯π interactions and assess their participation in crystal formation, showing that the formation of this kind of interaction in these molecules is a consequence of a topological process. UV-vis and thermal analyses (TGA and DSC) were also carried out to observe the special properties of these molecules. In addition to halogens influencing the decomposition pattern, it was also possible to assess that these structures are stable (mass loss at T > 129 °C) and decompose in two main stages. An increase in the decomposition temperature of the compounds as the atomic radius of the halogens increases and electronegativity decreases can be highlighted. No thermal events (e.g. melting and/or crystallization temperatures) were observed for the compounds in the temperature range evaluated (below decomposition temperatures). Furthermore, the ε of the halogenated compounds showed that all compounds possess strong absorbance capacity, indicating promising optical properties.Experimental
Materials and methods
The infrared absorption spectra were recorded as KBr pellets using 3 to 5 mg of sample per 100 mg of KBr on a Bruker IR spectrophotometer. UV/visible spectra were recorded using a Shimadzu UV-2600 spectrophotometer. For this analysis, a standard solution with concentration of 0.5 mM was made for compounds 1–4. From these standard solutions, 5.00 μL volumes were extracted and diluted in a cuvette containing 3 mL of ethanol. Samples were analyzed at 25 °C. The spectra were recorded within a range of 190–600 nm at a scanning rate of 600 nm min−1 (0.1 s integration per 1.0 nm). The 1H and 13C NMR spectra were obtained on Bruker Avance III (600 MHz) spectrometer (compounds 2–4) and on a Bruker DPX (400 MHz) spectrometer (compound 1) using DMSO-d6 as solvent. Raman spectra were performed on Bruker MultiRAM devices with a laser at 1064 nm wavelength and exposure time of 3 s. Thermal analysis was performed on a TGA Q5000 analyzer (TA Instruments Inc., USA). The conditions were a heating rate of 10 °C min−1 and an inert atmosphere of N2 (50 ml min−1). Elemental analysis was performed using a Perkin-Elmer CHN 2400 analyzer. DSC experiments were performed using a MDSC Q2000 calorimeter (T-zero™ DSC Technology, TA Instruments Inc., USA). Dry high purity (99.999%) nitrogen gas was used as the purge gas (50 mL min−1). The instrument was initially calibrated in standard MDSC mode using the extrapolated onset temperature of melting indium (156.60 °C) at a heating rate of 10 °C min−1 and the heat of fusion of indium (28.71 J g−1). Heat capacity calibration was carried out by running standard sapphire (α-Al2O3) measurements at the experimental temperature. The heating rate was 5 °C min−1. The instrument was initially calibrated in standard DSC mode with indium (99.99%). The reference pots and lids and the samples weighed 51 ± 0.02 mg. The samples were enclosed in aluminum pots with lids. The samples were weighed on a Sartorius scale (M500P) with an accuracy of (±0.001 mg). Data were treated using TA Universal Analysis 2000 Software, version 4.5 (TA Instruments Inc., USA).Synthesis
Solvents and reagents were used without prior treatment. The triazene N1-oxide compounds were synthesized starting from the diazotization reaction of the respective 4-halophenylamine in acidic medium with sodium nitrite (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) at 0 °C to obtain the respective diazonium salt and subsequent coupling with β-phenylhydroxylamine, previously synthesized,28 according to the methodology described in ref. 29 (Scheme 1).
1) at 0 °C to obtain the respective diazonium salt and subsequent coupling with β-phenylhydroxylamine, previously synthesized,28 according to the methodology described in ref. 29 (Scheme 1).
Synthesis of 1-(4-fluorphenyl)-3-phenyltriazenide N1-oxide (1)
For the synthesis of 1, a solution of NaNO2 (1.25 g, 17.9 mmol) in 20 mL of water was added to a solution of 4-fluoraniline (2.0 g, 17.9 mmol) in 15 mL of a mixture of concentrated HCl and water (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) cooled to 0 °C, thus forming the diazonium salt. After 20 minutes, β-phenylhydroxylamine solution (2.2 g, 17.9 mmol) in 15 mL of concentrated acetic acid was added and the reaction mixture was stirred for 40 minutes at 0 °C. The reaction mixture was carefully pH-adjusted to about 5 and the yellow opaque precipitate was vacuum filtered and recrystallized from a fraction of ethanol/pyridine solvents, which after approximately five days of slow evaporation resulted in yellow crystals in the form of needles. Compound 1 C12H10FN3O shows a yield of 75%. Elemental analysis for C12H10FN3O (%): calculated: C 63.40; H 5.32; N 17.06; experimental: C 62.27; H 4.36; N 18.19. IR (KBr): ν(N–H) 3132.26; ν(C–H) 3055; ν(C
1) cooled to 0 °C, thus forming the diazonium salt. After 20 minutes, β-phenylhydroxylamine solution (2.2 g, 17.9 mmol) in 15 mL of concentrated acetic acid was added and the reaction mixture was stirred for 40 minutes at 0 °C. The reaction mixture was carefully pH-adjusted to about 5 and the yellow opaque precipitate was vacuum filtered and recrystallized from a fraction of ethanol/pyridine solvents, which after approximately five days of slow evaporation resulted in yellow crystals in the form of needles. Compound 1 C12H10FN3O shows a yield of 75%. Elemental analysis for C12H10FN3O (%): calculated: C 63.40; H 5.32; N 17.06; experimental: C 62.27; H 4.36; N 18.19. IR (KBr): ν(N–H) 3132.26; ν(C–H) 3055; ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) 1604.71; δ(N–H) 1515.99; ν(N
C) 1604.71; δ(N–H) 1515.99; ν(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) 1429.19; ν(N–N–N) 1332.76; ν(N → O) 1298.13; ν(Car–Halog) 1220.25; ν(N–N) 1195.40 cm−1. Raman: ν(N–H) 3080; ν(C–H) 3050; ν(C
N) 1429.19; ν(N–N–N) 1332.76; ν(N → O) 1298.13; ν(Car–Halog) 1220.25; ν(N–N) 1195.40 cm−1. Raman: ν(N–H) 3080; ν(C–H) 3050; ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) 1606; δ(N–H) 1003; ν(N
C) 1606; δ(N–H) 1003; ν(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) 1431; ν(C–C) 1401; ν(N
N) 1431; ν(C–C) 1401; ν(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–N)-ring 100; ν(Car–Halog) 381; ν(C–N) 1204 cm−1. 1H NMR (400 MHz DMSO-d6) δ = 12.04 (s, 1H, OH); δ = 8.09 (d, J = 8.8 Hz, 2H, ArH); δ = 7.60–5.53 (m, 5H, ArH); δ = 7.22 ppm (t, J = 8.1 Hz, 2H, ArH); 13C NMR (400 MHz DMSO-d6); δ = 159.9 (d, 1JC–F = 238.9 Hz, C4); δ = 142.8 (C7); δ = 137.1 (C14JC–F = 2.1 Hz,); δ = 129.5 (C10); δ = 129.1 (C9, C11); δ = 119.5 (C8, C12); δ = 116.4 (d, 3JC–F = 7.9Hz, C2, C6); δ = 115.8 ppm (d, 2JC–F = 22.7 Hz, C3, C5).
N–N)-ring 100; ν(Car–Halog) 381; ν(C–N) 1204 cm−1. 1H NMR (400 MHz DMSO-d6) δ = 12.04 (s, 1H, OH); δ = 8.09 (d, J = 8.8 Hz, 2H, ArH); δ = 7.60–5.53 (m, 5H, ArH); δ = 7.22 ppm (t, J = 8.1 Hz, 2H, ArH); 13C NMR (400 MHz DMSO-d6); δ = 159.9 (d, 1JC–F = 238.9 Hz, C4); δ = 142.8 (C7); δ = 137.1 (C14JC–F = 2.1 Hz,); δ = 129.5 (C10); δ = 129.1 (C9, C11); δ = 119.5 (C8, C12); δ = 116.4 (d, 3JC–F = 7.9Hz, C2, C6); δ = 115.8 ppm (d, 2JC–F = 22.7 Hz, C3, C5).
Synthesis of 1-(4-chlorophenyl)-3-phenyltriazenide N1-oxide (2)
Compound 2 was synthesized according to the procedure described for compound 1 but using 4-chloroaniline (2.0 g; 15.74 mmol) as the primary amine. Compound 2 (C12H10ClN3O) shows a yield of 83%. Elemental analysis for C12H10ClN3O (%): calculated: C 58.19; H 4.07; N 16.97; experimental: C 58.34; H 4.27; N 16.64. IR (KBr): ν(N–H) 3186.07; ν(C–H) 3100; ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) 1598.74; δ(N–H) 1509.44; ν(N
C) 1598.74; δ(N–H) 1509.44; ν(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) 1418.37; ν(N–N–N) 1330.07; ν(N → O) 1296.74; ν(Car–Halog) 636.90; ν(N–N) 1168.33 cm−1. Raman: ν(N–H) 3078; ν(C–H) 3070; ν(C
N) 1418.37; ν(N–N–N) 1330.07; ν(N → O) 1296.74; ν(Car–Halog) 636.90; ν(N–N) 1168.33 cm−1. Raman: ν(N–H) 3078; ν(C–H) 3070; ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) 1598; δ(N–H) 1005; ν(N
C) 1598; δ(N–H) 1005; ν(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) 1420; ν(C–C) 1396 cm−1; ν(N
N) 1420; ν(C–C) 1396 cm−1; ν(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–N)-ring 93; ν(Car–Halog) 410; ν(C–N) 1213 cm−1. 1H NMR (600 MHz DMSO-d6) δ = 12.13 (s, 1H, OH); δ = 8.09 (d, J = 7.8 Hz, 2H, ArH); δ = 7.60–7.51 (m, 5H, ArH); δ = 7.41 ppm (d, J = 8.6 Hz, 2H, ArH); 13C NMR (600 MHz DMSO-d6); δ = 142.86 (C1); δ = 139.50 (C7); δ = 129.82 (C4); δ = 129.17 (C3, C5); δ = 129.08 (C9, C11); δ = 126.13 (C10); δ = 119.65 (C2, C6); δ = 116.49 ppm (C8, C12).
N–N)-ring 93; ν(Car–Halog) 410; ν(C–N) 1213 cm−1. 1H NMR (600 MHz DMSO-d6) δ = 12.13 (s, 1H, OH); δ = 8.09 (d, J = 7.8 Hz, 2H, ArH); δ = 7.60–7.51 (m, 5H, ArH); δ = 7.41 ppm (d, J = 8.6 Hz, 2H, ArH); 13C NMR (600 MHz DMSO-d6); δ = 142.86 (C1); δ = 139.50 (C7); δ = 129.82 (C4); δ = 129.17 (C3, C5); δ = 129.08 (C9, C11); δ = 126.13 (C10); δ = 119.65 (C2, C6); δ = 116.49 ppm (C8, C12).
Synthesis of 1-(4-bromophenyl)-3-phenyltriazenide N1-oxide (3)
Compound 3 was synthesized by repeating the same preparation used for compound 1 but substituting 4-fluorophenyl for 4-bromophenyl (2 g; 11.76 mmol). Compound 3 (C12H10BrN3O) had a yield of 80%. Elemental analysis for C12H10BrN3O (%): calculated: C 49.34; H 3.45; N 14.38; experimental: C 49.58; H 3.48; N 13.98. IR (KBr): ν(N–H) 3188.96; ν(C–H) 3090; ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) 1584.85; δ(N–H) 1505.15; ν(N
C) 1584.85; δ(N–H) 1505.15; ν(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) 1414.72; ν(N–N–N) 1329.03; ν(N → O) 1296.70; ν(Car–Halog) 609.23; ν(N–N) 1169.23 cm−1. Raman: ν(N–H) 3075; ν(C–H) 3069; ν(C
N) 1414.72; ν(N–N–N) 1329.03; ν(N → O) 1296.70; ν(Car–Halog) 609.23; ν(N–N) 1169.23 cm−1. Raman: ν(N–H) 3075; ν(C–H) 3069; ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) 1596; δ(N–H) 1006; ν(N
C) 1596; δ(N–H) 1006; ν(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) 1417; ν(C–C) 1394; ν(N
N) 1417; ν(C–C) 1394; ν(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–N)-ring 92; ν(Car–Halog) 553; ν(C–N) 1212 cm−1. 1H NMR (600 MHz DMSO-d6) δ = 12.13 (s, 1H, OH); δ = 8.09 (d, J = 7.4 Hz, 2H, ArH); δ = 7.54 ppm (ddd, J = 41.4, 23.7, 7.8 Hz, 7H, ArH); 13C NMR (600 MHz DMSO-d6); δ = 142.85 (C1); δ = 139.88 (C7); δ = 131.94 (C3, C5); δ = 129.84 (C10); δ = 129.18 (C9, C11); δ = 119.65 (C2, C6); δ = 116.91 (C8, C12); δ = 114.05 ppm (C4).
N–N)-ring 92; ν(Car–Halog) 553; ν(C–N) 1212 cm−1. 1H NMR (600 MHz DMSO-d6) δ = 12.13 (s, 1H, OH); δ = 8.09 (d, J = 7.4 Hz, 2H, ArH); δ = 7.54 ppm (ddd, J = 41.4, 23.7, 7.8 Hz, 7H, ArH); 13C NMR (600 MHz DMSO-d6); δ = 142.85 (C1); δ = 139.88 (C7); δ = 131.94 (C3, C5); δ = 129.84 (C10); δ = 129.18 (C9, C11); δ = 119.65 (C2, C6); δ = 116.91 (C8, C12); δ = 114.05 ppm (C4).
Synthesis of 1-(4-iodophenyl)-3-phenyltriazenide N1-oxide (4)
Compound 4 was obtained by using 4-iodophenyl (2 g; 9.13 mmol) as the primary amine and following the same procedure used for the synthesis of compound 1. Compound 4 (C12H10IN3O) shows a yield of 68%. Elemental analysis for C12H10IN3O (%): calculated: C 42.50; H 2.97; N 12.39; experimental: C 40.71; H 3.08; N 11.51. IR (KBr): ν(N–H) 3068.15; ν(C–H) 3050; ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) 1588.52; δ(N–H) 1500.44; ν(N
C) 1588.52; δ(N–H) 1500.44; ν(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) 1417.09 cm−1; ν(N–N–N) 1331.55; ν(N → O) 1298.04; ν(Car–Halog) 611.30; ν(N–N) 1086.98 cm−1. Raman: ν(N–H) 3072; ν(C–H) 3072; ν(C
N) 1417.09 cm−1; ν(N–N–N) 1331.55; ν(N → O) 1298.04; ν(Car–Halog) 611.30; ν(N–N) 1086.98 cm−1. Raman: ν(N–H) 3072; ν(C–H) 3072; ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) 1592; δ(N–H) 1003; ν(N
C) 1592; δ(N–H) 1003; ν(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) 1420; ν(C–C) 1394; ν(N
N) 1420; ν(C–C) 1394; ν(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–N)-ring 100–77 ; ν(Car–Halog) 1060; ν(C–N) 1210 cm−1. 1H NMR (600 MHz DMSO-d6) δ = 12.10 (s, 1H, OH); δ = 8.09 (d, J = 7.5 Hz, 2H, ArH); δ = 7.68 (d, J = 8.2 Hz, 2H, ArH); δ = 7.61–7.52 (m, 3H, ArH); δ = 7.35 ppm (d, J = 8.1 Hz, 2H, ArH); 13C NMR (600 MHz DMSO-d6); δ = 142.84 (C1); δ = 140.33 (C7); δ = 137.70 (C3, C5); δ = 129.82 (C10); δ = 129.15 (C9, C11); δ = 119.64 (C2, C6); δ = 117.24 (C8, C12), δ = 85.56 ppm (C4).
N–N)-ring 100–77 ; ν(Car–Halog) 1060; ν(C–N) 1210 cm−1. 1H NMR (600 MHz DMSO-d6) δ = 12.10 (s, 1H, OH); δ = 8.09 (d, J = 7.5 Hz, 2H, ArH); δ = 7.68 (d, J = 8.2 Hz, 2H, ArH); δ = 7.61–7.52 (m, 3H, ArH); δ = 7.35 ppm (d, J = 8.1 Hz, 2H, ArH); 13C NMR (600 MHz DMSO-d6); δ = 142.84 (C1); δ = 140.33 (C7); δ = 137.70 (C3, C5); δ = 129.82 (C10); δ = 129.15 (C9, C11); δ = 119.64 (C2, C6); δ = 117.24 (C8, C12), δ = 85.56 ppm (C4).
Spectroscopic analysis
Absorptions observed in the infrared spectra of compounds 1–4 at 3132 cm−1, 3186, 3189, and 3068 cm−1, respectively, correspond to the νas(N–H) stretching of the respective diazo(oxide)amine [–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N(→O)–N(H)–] chain of each compound, which is in accordance with that found at 3140 cm−1 for compound 5.1 In addition, the bands observed at 1298, 1296, 1297, and 1298 cm−1 correspond to the characteristic stretching of the νN(→O) dative bond in accordance with that found at 1339 cm−1 in compound 5 (ref. 1) and demonstrate that the compounds show the tautomeric form of the triazene N1-oxide in the solid state. In the Raman spectra of compounds 1–4, the observed bands at 3080, 3078, 3075, and 3072 cm−1 were attributed to the characteristic νs(N–H) stretching in triazene compounds. On the other hand, the vibrations observed at 381, 410, 553, and 1060 cm−1 for compounds 1, 2, 3, and 4, respectively, were attributed to the aromatic carbon–halogen [νs(Car–X); X = F, Cl, Br, and I].30,31 In the 13C NMR spectrum, the “C4” carbons bond to the respective halogens for compounds 1, 2, 3, and 4 corresponding to the peak with a chemical shift at δ 159.9 (d, 1JC–F = 238.9 Hz), δ 129.31, δ 114.58, and δ 85.06, respectively. It is possible to highlight the decreasing disbanding effect as it decreases along group 17 in the periodic table, an expected effect due to the electronegativity (I− inductive effect) decreasing from fluorine to iodine and also because of the effect of the heavy atom that increases from fluorine to iodine. Electronic absorption spectra of compounds 1, 2, 3, and 4 were recorded in ethanol, which exhibits strong absorption at 348 nm (1) and 352 nm (2, 3, and 4) (Fig. S28–S31†). When compared with the usual electronic absorption spectra of classical triazene derivatives [RN
N(→O)–N(H)–] chain of each compound, which is in accordance with that found at 3140 cm−1 for compound 5.1 In addition, the bands observed at 1298, 1296, 1297, and 1298 cm−1 correspond to the characteristic stretching of the νN(→O) dative bond in accordance with that found at 1339 cm−1 in compound 5 (ref. 1) and demonstrate that the compounds show the tautomeric form of the triazene N1-oxide in the solid state. In the Raman spectra of compounds 1–4, the observed bands at 3080, 3078, 3075, and 3072 cm−1 were attributed to the characteristic νs(N–H) stretching in triazene compounds. On the other hand, the vibrations observed at 381, 410, 553, and 1060 cm−1 for compounds 1, 2, 3, and 4, respectively, were attributed to the aromatic carbon–halogen [νs(Car–X); X = F, Cl, Br, and I].30,31 In the 13C NMR spectrum, the “C4” carbons bond to the respective halogens for compounds 1, 2, 3, and 4 corresponding to the peak with a chemical shift at δ 159.9 (d, 1JC–F = 238.9 Hz), δ 129.31, δ 114.58, and δ 85.06, respectively. It is possible to highlight the decreasing disbanding effect as it decreases along group 17 in the periodic table, an expected effect due to the electronegativity (I− inductive effect) decreasing from fluorine to iodine and also because of the effect of the heavy atom that increases from fluorine to iodine. Electronic absorption spectra of compounds 1, 2, 3, and 4 were recorded in ethanol, which exhibits strong absorption at 348 nm (1) and 352 nm (2, 3, and 4) (Fig. S28–S31†). When compared with the usual electronic absorption spectra of classical triazene derivatives [RN![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–N(H)R], these absorptions observed at the region of 348–352 nm were assigned to the partly forbidden (n → π*) transition and attributed to the (N
N–N(H)R], these absorptions observed at the region of 348–352 nm were assigned to the partly forbidden (n → π*) transition and attributed to the (N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) chromophore group.32 Additionally, medium intensity absorptions were observed at 234 nm for 1, 240 nm for 2, 238 nm for 3, and 241 nm for 4. These absorptions at 234–241 nm were assigned to the (n → σ*) transition, also in analogy to that attributed to the (N
N) chromophore group.32 Additionally, medium intensity absorptions were observed at 234 nm for 1, 240 nm for 2, 238 nm for 3, and 241 nm for 4. These absorptions at 234–241 nm were assigned to the (n → σ*) transition, also in analogy to that attributed to the (N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) chromophore group when compared with the triazenes.32 A third strong band is observed at 200 nm for all compounds that was assigned to the expected and characteristic (π → π*) transition of the phenyl and p-halophenyl substituents.
N) chromophore group when compared with the triazenes.32 A third strong band is observed at 200 nm for all compounds that was assigned to the expected and characteristic (π → π*) transition of the phenyl and p-halophenyl substituents.
Crystal structure determination
X-ray diffraction data for 1–5 are listed in Table 5. The X-ray diffraction technique was performed using a Bruker APEXII-CCD diffractometer with an area detector, graphite monochromator, and Mo-Kα radiation source with a wavelength (λ) of 0.71073 Å.33 Data reduction and absorption correction involved the SAINT and SADABS34 software programs, respectively. The structures were solved via direct methods35 and the refinement of the data included square squares (F2) and the method of least squares including complete matrices using anisotropic thermal parameters for non-hydrogen atoms. The hydrogen atoms are set as geometric for all compounds. Crystallographic data for the structural analysis of the compounds have been deposited at the Cambridge Crystallographic Data Center with the deposition numbers 1570873 (1), 1570875 (2), 1570876 (3), 1570877 (4), and 759893 (5).| Compound | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Moiety formula | C12H10FN3O | C12H10ClN3O | C12H10BrN3O | C12H10IN3O | C12H11N3O |
| Sum formula | C12H10FN3O | C12H10ClN3O | C12H10BrN3O | C12H10IN3O | C12H11N3O |
| Mw | 231.23 | 247.68 | 292.14 | 339.13 | 213.24 |
| Crystal system | Monoclinic | Monoclinic | Monoclinic | Orthorhombic | Monoclinic |
| Space group | P21 | P21/c | P21/c | P212121 | P21/n |
| a [Å] | 9.6487(15) | 6.1680(9) | 6.2398(3) | 4.7465(3) | 5.4917(5) |
| b [Å] | 5.2866(7) | 9.5740(16) | 9.7185(5) | 9.9491(6) | 16.1419(13) |
| c [Å] | 11.1382(19) | 19.477(3) | 19.5527(10) | 26.6177(14) | 12.4976(10) |
| α [°] | 90 | 90 | 90 | 90 | 90 |
| β [°] | 110.361(5) | 96.539(9) | 96.462(2) | 90 | 100.382(7) |
| γ [°] | 90 | 90 | 90 | 90 | 90 |
| V [Å3] | 532.65(14) | 1142.7(3) | 1178.17(10) | 1256.98(13) | 1090.20(16) |
| Z | 2 | 4 | 4 | 4 | 4 |
| D calcd.[g cm−3] | 1.442 | 1.440 | 1.647 | 1.792 | 1.299 |
| μ [mm−1] | 0.108 (Mo-Kα) | 0.320 (Mo-Kα) | 3.475 (Mo-Kα) | 2.535 (Mo-Kα) | 0.087 (Mo-Kα) |
| F(000) | 240 | 512 | 584 | 656 | 448 |
| T [K] | 293(2) | 293(2) | 293(2) | 293(2) | 295(2) |
| Reflections collected | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 621 621 |
9904 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 495 495 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 579 579 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 977 977 |
| Independent reflections | 2392 | 2379 | 2602 | 2719 | 3451 |
| R int | 0.0533 | 0.0638 | 0.0475 | 0.0470 | 0.0587 |
| Observed reflections [ I > 4σ(F)] | 2125 | 1489 | 1813 | 1758 | 1177 |
| Parameters refined | 154 | 154 | 155 | 154 | 145 |
| Flack x parameter | 0.1(3) | — | — | 0.048(18) | — |
| R(|F|) reflections [ I > 4σ(F)] | 0.0351 | 0.0660 | 0.0337 | 0.0466 | 0.0687 |
| wR(F2) | 0.0870 | 0.1660 | 0.0688 | 0.1145 | 0.1464 |
| S | 1.058 | 1.015 | 1.007 | 1.037 | 0.998 |
| Δρmin [e Å−3] | +0.235 | +0.506 | +0.228 | +0.373 | +0.164 |
| Δρmax [e Å−3] | −0.248 | −0.664 | −0.220 | −0.1.031 | −0.148 |
Topological analysis
The Voronoi–Dirichlet polyhedra (VDP) method was used in the ToposPro13 software for the construction of the supramolecular cluster. The molecular coordination number (MCN) found for each cluster was 18 for compounds 1 and 4, 14 for compounds 2 and 3, and 16 for compound 5. The face of the molecular VDP was considered to be a set of atomic VDP faces corresponding to the adjacent contacts between the atoms of two molecules. Thus, it was established that the area of the face of a VDP corresponds to a molecular M1⋯MN interaction, and the considered topological parameter was the contact surface area between the dimers provided by the software.36Stabilization energy calculation
The intermolecular interaction energy of the dimers from the supramolecular clusters of compounds 1–5 were determined by single-point calculations performed with geometries obtained from X-ray diffraction. The optimization of the molecular geometry was not performed. Density functional theory (DFT) at the ωB97X-D/cc-pVDZ level of theory was used for the calculation. Calculations for compound 4 were carried out with ωB97X-D/cc-pVDZ-PP because the relativistic effects of the iodine atom needed to be corrected. All calculations were performed with the Gaussian 0937 software package. The counterpoise method of Boys and Bernardi38 was employed in order to minimize the BSSE. The stabilization energy for M1⋯MN was given by the energy values of the considered dimer minus the sum of the monomer energies of M1 and MN. Wavefunctions at the B97X-D/cc-pVDZ level of theory by single point calculations with geometries obtained from X-ray data were subsequently analyzed from the perspective of the quantum theory of atoms in molecules by AIMALL software.39 Molecular electrostatic potential were generated with a isosurface value of 0.001 in the GaussView program.40Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors are grateful to the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) and the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) for supporting this study.Notes and references
- H. R. Khavasi, A. Ghanbarpour and A. A. Tehrani, CrystEngComm, 2014, 16, 749–752 RSC.
- O. V. Shishkin, Chem. Phys. Lett., 2008, 458, 96–100 CrossRef CAS.
- A. L. Kitaigorodskii, Organic Chemical Crystallography, Consultants Bureau, New York, 1961 Search PubMed.
- A. Kurakin, Network, 2007, 1–34 Search PubMed.
- M. A. P. Martins, A. R. Meyer, A. Z. Tier, K. Longhi, L. C. Ducati, H. G. Bonacorso, N. Zanatta and C. P. Frizzo, CrystEngComm, 2015, 17, 7381–7391 RSC.
- G. Manzoni De Oliveira, M. Hörner, A. Machado, D. F. Back, J. H. S. K. Monteiro and M. R. Davolos, Inorg. Chim. Acta, 2011, 366, 203–208 CrossRef CAS.
- W. Lü, W. Lv, Q. Zhao, M. Jiao, B. Shao and H. You, Inorg. Chem., 2014, 53, 11985–11990 CrossRef PubMed.
- G. Wang, Q. Peng and Y. Li, Acc. Chem. Res., 2011, 44, 322–332 CrossRef CAS PubMed.
- M. F. G. Stevens, A. Gescher and C. P. Turnbull, Biochem. Pharmacol., 1979, 28, 769–776 CrossRef CAS PubMed.
- Z. Rachid, M. MacPhee, C. Williams, M. Todorova and B. J. Jean-Claude, Bioorg. Med. Chem. Lett., 2009, 19, 5505–5509 CrossRef CAS PubMed.
- A. J. W. A. dos Santos, R. Horner, G. L. Paraginski, F. C. Machado and M. Horner, Anal. Sci., 2007, 23, x251–x252 Search PubMed.
- M. A. P. Martins, C. P. Frizzo, A. C. L. Martins, A. Z. Tier, I. M. Gindri, A. R. Meyer, H. G. Bonacorso and N. Zanatta, RSC Adv., 2014, 4, 44337–44349 RSC.
- V. A. Blatov, A. P. Shevchenko and D. M. Proserpio, Cryst. Growth Des., 2014, 14, 3576–3586 CAS.
- M. A. P. Martins, M. Hörner, J. Beck, A. Z. Tier, A. L. Belladona, A. R. Meyer, N. Zanatta, H. G. Bonacorso and C. P. Frizzo, CrystEngComm, 2016, 18, 3866–3876 RSC.
- C. P. Frizzo, A. Z. Tier, I. M. Gindri, A. R. Meyer, G. Black, A. L. Belladona and M. A. P. Martins, CrystEngComm, 2015, 17, 4325–4333 RSC.
- C. P. Frizzo, C. R. Bender, A. Z. Tier, I. M. Gindri, P. R. S. Salbego, A. R. Meyer and M. A. P. Martins, CrystEngComm, 2015, 17, 2996–3004 RSC.
- A. L. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155 CrossRef CAS PubMed.
- T. J. Mooibroek, P. Gamez and J. Reedijk, CrystEngComm, 2008, 10, 1501 RSC.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, U.K., 1990 Search PubMed.
- L. C. Gilday, S. W. Robinson, T. A. Barendt, M. J. Langton, B. R. Mullaney and P. D. Beer, Chem. Rev., 2015, 115, 7118–7195 CrossRef CAS PubMed.
- M. N. Ramos and S. R. Pereira, J. Chem. Soc., Perkin Trans. 2, 1986, 131–133 RSC.
- M. R. Sovizi, J. Therm. Anal. Calorim., 2010, 102, 285–289 CrossRef CAS.
- E. S. Swinbourne, Compr. Chem. Kinet., 1972, 5, 149–233 CrossRef.
- J. A. Kerr, Chem. Rev., 1966, 66, 465–500 CrossRef CAS.
- T. V. Serebryanskaya, L. S. Ivashkevich, A. S. Lyakhov, P. N. Gaponik and O. A. Ivashkevich, Polyhedron, 2010, 29, 2844–2850 CrossRef CAS.
- V. O. Domingues, R. Hörner, L. G. B. Reetz, F. Kuhn, V. M. Coser, J. N. Rodrigues, R. Bauchspiess, W. V. Pereira, G. L. Paraginski, A. Locatelli, J. de O. Fank, V. F. Giglio and M. Hörner, J. Braz. Chem. Soc., 2010, 21, 2226–2237 CrossRef CAS.
- M. S. Masoud, A. E. Ali, M. A. Shaker and M. A. Ghani, Spectrochim. Acta, Part A, 2005, 61, 3102–3107 CrossRef PubMed.
- C. S. Marvel and O. Kamm, J. Am. Chem. Soc., 1919, 41, 276–282 CrossRef CAS.
- A. J. R. W. A. Dos Santos, P. Bersch, H. P. M. De Oliveira, M. Hörner and G. L. Paraginski, J. Mol. Struct., 2014, 1060, 264–271 CrossRef.
- D. L. Pavia, G. M. Lampman, G. S. Kriz and J. A. Vyvyan, Introduction to Spectroscopy, Cengage, Independence, KY, 5th edn, 2014 Search PubMed.
- R. Navarro, J. García, E. P. Urriolabeitia, C. Cativiela and M. D. Diaz-de-Villegas, J. Organomet. Chem., 1995, 490, 35–43 CrossRef CAS.
- M. S. Masoud, A. E. Ali, M. A. Shaker and M. A. Ghani, Spectrochim. Acta, Part A, 2005, 61, 3102 CrossRef PubMed.
- Bruker, SAINT+, Bruker AXS Inc., Madison, Wisconsin, USA, 2007 Search PubMed.
- G. M. Sheldrick, SADABS, University of Göttingen, Göttingen, 1997 Search PubMed.
- M. C. Burla, R. Caliandro, M. Camalli, B. Carrozzini, G. L. Cascarano, L. De Caro, C. Giacovazzo, G. Polidori and R. Spagna, J. Appl. Crystallogr., 2005, 38, 381–388 CrossRef CAS.
- V. A. Blatov, Crystallogr. Rev., 2004, 10, 249–318 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- T. A. Keith, AIMAll, 2014 Search PubMed.
- R. Dennington, T. Keith and J. Millam, GaussView, 2009 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: 759893, 1570873 and 1570875–1570877. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7ce02015e |
| This journal is © The Royal Society of Chemistry 2018 |