Crystalline packing in pentacene-like organic semiconductors†
M.
Klues
and
G.
Witte
 *
*
Fachbereich Physik, Philipps-Universität Marburg, 35032 Marburg, Germany. E-mail: gregor.witte@physik.uni-marburg.de
First published on 22nd November 2017
Abstract
Since optoelectronic properties of organic semiconductors (OSCs) are largely affected by the molecular packing in the solid phase, further advances of such materials require comprehensive structure–property interrelations beyond single molecule considerations. While single molecular electronic properties can be tailored by synthetic means and their electronic properties can be reliably predicted by quantum chemical calculations, crystal structure predictions of such van der Waals bond solids remain challenging. Here we analyze correlations between the molecular structure and the resulting packing motifs adopted in the crystalline phases of the prototypical OSC pentacene as well as various differently substituted but similarly shaped π-conjugated molecules. Based on a Hirshfeld surface analysis and related fingerprint plots, specific contact points and their distribution are identified which allows classification of different structural groups. Comparing the fingerprint plots with corresponding molecular properties such as electrostatic contour plots as well as quadrupole and polarizability tensors, which were calculated by density functional theory, allows rationalizing structure determining specific intermolecular interactions. Our analysis shows in particular that molecules with uniform electrostatic potential at their periphery favor a herringbone packing, while the highly electronegative substituents (O, N and F) enable the formation of H-bonds and prefer slip-stacking or criss-cross packing motifs. The present correlations might be useful guidelines for future strategies to synthesis new OSCs.
Introduction
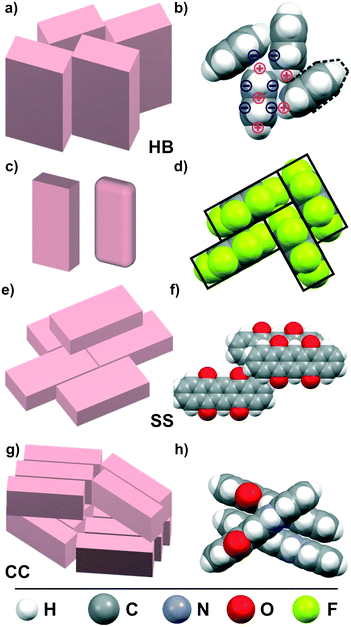
π-Conjugated organic semiconductors (OSC) have attracted widespread attention because of their promising potential for organic electronic device applications such as field effect transistors, light emitting diodes or photovoltaics.1–4 As a particular advantage of such molecular materials, the ease of tailoring their electronic levels by synthetic means is commonly named,5,6 whereas complex band engineering is required for inorganic semiconductors. However, the optoelectronic properties of molecular solids are determined not only by the molecular properties such as the frontier orbital energies and reorganization energy, but are also governed by the molecular packing motifs due to the spatial orbital overlap. As a result of the distinct shape anisotropy (typically platelet- or rod-shaped), π-conjugated molecular entities adopt anisotropic packings in their crystalline phases and accordingly reveal also anisotropic charge carrier transport or exciton dynamics.7–9 Hence, the knowledge of molecular packing motifs in OSC solids is of vital interest for the understanding and possible improvement of organic electronic devices. While nowadays the electronic energy levels of single molecules can be computed very precisely, calculations of the crystalline structure and optoelectronic properties of molecular solids still remain challenging.10–12 Especially for OSC materials, crystal structure predictions are rather ambitious since the weak, essentially van der Waals-type intermolecular interactions are difficult to compute accurately.13,14 Since dispersion interactions are not properly described by density functional theory, (DFT) various semi-empirical ‘van der Waals corrections’ have been introduced,15,16 but these approaches are still at the development and validation stage.17–19 On the other hand, ab initio methods are available that in principle permit accurate calculations of dispersion interactions.20,21 However, they are computationally very demanding which limits the examinable molecular size.21–23 Recently, detailed calculations have also been carried out for dimers of larger π-conjugated molecules,24–27 while such theoretical analyses of complete crystal structures of technologically relevant OSC are still under development and yet not generally available. Moreover, the shallow intermolecular interaction potentials in such molecular materials can lead to the existence of various energetically favored configurations with different packing motifs (i.e. polymorphs) rendering crystal structure prediction still a current research topic.28–30 For the case of unsubstituted aromatic hydrocarbons, empirical correlations between the molecular shape or the stoichiometric C/H ratio and the resulting packing motifs have been described in the pioneering work by Desiraju and Gavezzotti,31 which serves as important benchmark for refined analyses of structure–packing interrelations.32–34Fig. 1 depicts the most common packing motifs adopted in the crystalline phase of planar OSCs.Among the π-conjugated OSCs, pentacene (PEN) has become a prototypical model system, as it forms highly ordered crystalline phases, which exhibit large charge carrier mobility, and thus allows correlating optoelectronic properties with the packing motifs adopted in the individual polymorphs.11,35–38 Furthermore, acenes are versatile starting substances which allow rich chemical variations to tailor the molecular electronic properties.5,39 For example, due to its large electronegativity, fluorine forms highly polar C–F bonds, and perfluorination of acenes causes an inverted charge density distribution of the aromatic compounds yielding n-type SCs,40 while non-symmetric partial fluorination yields molecules with permanent dipole moments.40 Notably, oxidation of PEN affects not only the conjugation of the π-system but also changes the molecular arrangement from the characteristic herringbone packing into a planar slip stacking, as depicted in Fig. 1f.41,42 More recently, also N-substituted heteroacenes are considered as potential semiconductors since they are proposed as n-type SC.43–48 Interestingly, although being isoelectronic with PEN, diazapentacene (DAP) reveals a “criss cross” packing whereas dihydrodiazapentacene (DHDAP), which forms an anti-aromatic electronic system,49 adopts a herringbone packing like PEN.46,48 These examples show that seemingly small chemical variations can lead to distinctly different packing motifs in crystalline molecular solids.
A powerful method to analyze the prevalence of interactions and their spatial distribution in non-covalently bound molecular crystals is based on Hirshfeld surfaces and the related fingerprint plots.50–53 Such fingerprint plots provide a visualization containing implicit information of all intermolecular interactions as well as purely geometrical aspects like close contacts. This allows identification of prevailing interaction types such as, e.g. C⋯C or C⋯H interactions or hydrogen bonds.34,54,55 Moreover, the correlation analysis of the fingerprint plots of the various crystal structures enables a quantitative comparison of the respective distribution of all contact points. Since such contact point distributions are characteristic for the prevailing intermolecular forces, this allows detailed comparison of the various packing motifs.19
Here, we use such Hirshfeld surface and fingerprint plot analyses to compare intermolecular interactions occurring in crystalline phases of various pentacene-like molecules including the before mentioned azaacenes, fluorinated and oxidized pentacenes as well as hybrid forms of these species. Although not directly related to PEN, our analysis also covers dinaphthothienothiophene (DNTT), because of its exceptional charge carrier mobility56 as well as its geometrical resemblance. All molecules can be regarded as cuboids with dimensions similar to those of a PEN-molecule, which, in good approximation, also holds true for DNTT. The restriction to molecules without spatially extended or flexible functional side groups allows in particular excluding steric effects on the structure formation as well as entropic effects due to low energetic vibrations. Therefore, the molecules can be regarded as rigid and compact which allows dense packing. Thereby, the decisive intermolecular interactions of the partly quite different crystal structures emerge more clearly and may enable conclusions about the interrelation between the molecular structure and resulting packing motifs. In this direction, our study aims at finding correlations how chemical substitutions influence the molecular packing motifs. This complements current synthetic approaches that are usually driven by single molecular electronic considerations such as, e.g. influencing the charge distribution through mesomeric effects by substituents or functional groups as well as the addition of spacer groups.57–59 On the other hand, present developments of sophisticated ab initio based theoretical analyses are presently mostly limited to single molecules or dimers, while systematic studies are yet not available for OSC crystals.26,27 From this position, the present study provides a link between the various communities. In a long-term perspective, the presently analyzed molecular selection might even serve as meaningful benchmark collection for detailed theoretical analyses in order to quantify contributions of the different intermolecular interactions.
Methodology
The molecular ensemble
All molecules considered in this study are depicted in Fig. 2 and were selected according to the following criteria: (i) geometrical similarity to pentacene, (ii) relevance for organic electronics, and (iii) the presence of different intermolecular interactions. The first aspect limits the selection to cuboid shaped molecules with similar size and aspect ratio to PEN. Because such entities can be densely packed, deviating packing motifs can be assigned to specific interactions. Besides PEN, various other molecular materials such as perfluoropentacene (PFP),40 dihydrodiazapentacene (DHDAP),45 DNTT56 or quinacridone (QUA)66 show considerable charge carrier mobility which makes them particularly interesting for organic electronic applications. This raises the question of similarities in their respective packing motifs. In contrast, diazapentacene (DAP)47 and the two oxo-species pentacenequinone (QUI) and pentacenetetrone (TET) reveal poor mobility and are considered degradation products of the parent molecule.61 This again raises the question whether this property is only due to the modified electronic structure or if also the molecular packing is affected. Moreover, it is desirable that the various molecules of the assortment cover a wide range of possible intermolecular interactions. While the molecular arrangement of unsubstituted molecular materials is mainly determined by an interplay between quadrupolar and dispersion interactions, the packing motif of QUA is additionally governed by hydrogen bonds while hexafluorodiazapentacene (HFDP) exhibits a motif that is dominated by its static dipole moment.39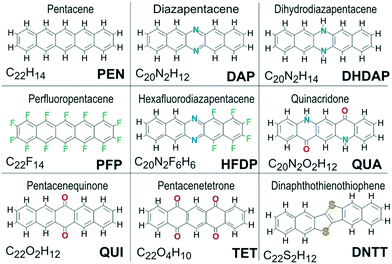 | ||
| Fig. 2 Chemical structure of all molecules whose packing motifs are analyzed in this study. Besides their names, also the sum formula and abbreviations used throughout this work are given. | ||
Many organic compounds crystallize in different polymorphs, which occur also for some of the molecules examined here. As the Hirshfeld analysis requires an exact knowledge of the crystal structure with all atomic coordinates, we have also analyzed the packing motifs for the various polymorphs of PEN, PFP and QUA, since their precise structural data are available. For PEN, both bulk-structures, the Campbell-phase62 (denoted as PEN-C) and the Siegrist-phase63 (PEN-S) as well as the thin-film phase (PEN-TF)64 are considered, the latter of which is particularly relevant for thin-film device applications. For PFP, the bulk phase (PFP-bulk)40 and a substrate induced π-stacked phase (PFP-π)65 are taken into account, while for QUA, three well known phases (QUA-α, -β and -γ)66 are analyzed. Table 1 summarizes the symmetry and packing motifs of all crystalline phases considered in this study. Additional information on the unit cell parameters as well as visualizations of the corresponding crystal structures are provided in the ESI† (cf. Table ST1, Fig. S1).
| Structure | Z | Space group | Packing motif | Ref. |
|---|---|---|---|---|
| PEN-C | 2 | P1 | HB | 62 |
| PEN-S | 2 | P1 | HB | 63 |
| PEN-TF | 2 | P1 | HB | 64 |
| PFP-bulk | 2 | P21/c | HB | 40 |
| PFP-π | 2 | P1 | SS | 65 |
| DNTT | 2 | P21 | HB | 56 |
| QUA-α | 1 | P1 | SS | 66 |
| QUA-β | 2 | P21/c | SS/CC | 66 |
| QUA-γ | 2 | P21/c | CC | 66 |
| QUI | 2 | P21/b | SS/CC | 42 |
| TET | 1 | P1 | SS | 41 |
| DHDAP | 2 | P1 | HB | 45 |
| DAP | 2 | P21/a | CC | 47/48 |
| HFDP | 4 | P21/c | CC | 39 |
Computational approach
The Hirshfeld analyses of all considered molecular crystal structures are performed using the “CrystalExplorer” package.67 For this analysis, which has been described in detail elsewhere,50–55 an effective electron density for the molecule of interest is constructed from the atomic electron densities (promolecule). By applying the so-called stockholder partitioning scheme, a specific molecular volume within the crystal structure is defined. More specifically, this molecular volume is enclosed by the Hirshfeld surface that confines a region where at least 50% of the electron distribution at every point belongs to the embedded molecule. Every surface point contains information about the relevant contact distances, namely, the distance from the surface to the nearest atom interior to the surface, di, and the distance from the surface to the nearest atom exterior to the surface, de (as depicted in Fig. S2, ESI†). Valuable information on the relation of such distances provide the fingerprint plots, where these values are first binned into discrete intervals (typical width 0.01 Å) and then the resulting (di, de)-pairs are plotted. Here, the color of each point represents the fraction of surface points in that bin ranging from blue (relatively few points) through green (moderate fraction) to red (many points). Performing this analysis for selected atoms of the molecule allows in particular identifying closest contact points (di + de) and distinguishing specific pairwise interactions, such as e.g. C⋯C, C⋯H or O⋯H as well as their contribution.Generally, all molecules within the unit cell must be considered to fully represent the crystal structure by such fingerprint plots. In the case of QUA-α and TET, this is trivial as both structures possess primitive unit cells. Although the unit cells of some of the considered phases are not primitive, their crystal structure exhibits symmetry elements (such as e.g. a screw axis) which imply a uniform molecular environment for all molecules so that a fingerprint plot of only one molecule is sufficient to account for the full structure. However, this situation is not generally fulfilled. For example, the three PEN-phases as well as the DHDAP structure and the π-stacked polymorph of PFP have P1 symmetry with two molecules in the unit cell exhibiting a slightly different local environment. Since fingerprint plots are intended to serve as a measure to compare the interactions within the different structures, it would be useful also for these cases to have only one representative plot. To account for all intermolecular interactions within the unit cell, the distribution of the (di,de)-pairs of both molecules are averaged. This fingerprint plot is then compared with the fingerprint plots of other phases.
In addition, fingerprint plots also allow a quantitative comparison of the similarity of the appearance of interaction pairs using a method introduced by Parkin et al.55 For this purpose, the (di, de)-pairs are sorted in a grid of 15 × 15 bins with distances ranging from 0 to 3 Å and calculating correlation coefficients (average of Spearman and Pearson coefficients) of the contact point distributions for the various structures by utilizing standard routines implemented in Python.68 This yields quantitative values for the correlations while the graphical representation of the individual distributions in the form of the fingerprint plots enables only a visual comparison of the similarity. Moreover, the result of this correlation analysis is shown graphically as a dendrogram using the unweighted pair-group method with arithmetic mean (UPGMA).
In addition to the Hirshfeld analyses, also electronic properties of the molecules such as their quadrupole moments and polarizabilities are computed in the frame of density functional theory (DFT) using the US-GAMESS code.69,70 The DFT-calculations are performed using the B3LYP hybrid functional and a 6311G(d,p) basis set starting with structure optimization for each molecule. To visualize the electron density, molecular electrostatic potential (MEP) plots are generated for an isovalue of 0.002 au by using Molekel,71 which yields similar molecular volumina as the Hirshfeld volume and thus are comparable.72
Results and discussion
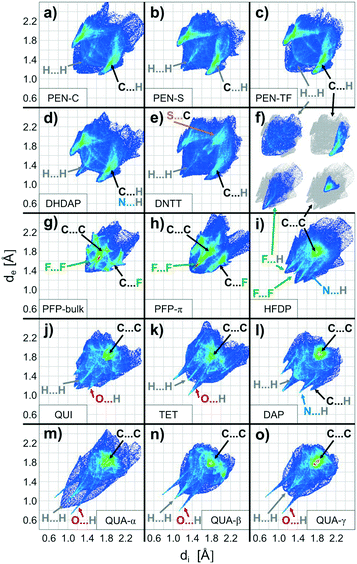
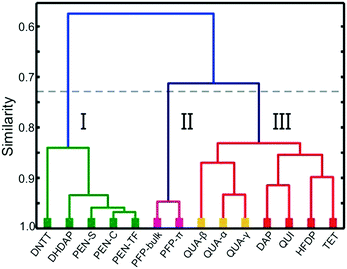
In order to compare the molecular packing motifs adopted in the crystalline phases of the considered molecules, first, fingerprint plots are calculated for all phases, which are summarized in Fig. 3. Besides an overall distribution of all contact points, the CrystalExplorer package also allows identification of interactions with specific types of atoms. They are graphically represented by coloring only those bins that form contacts to the atoms of interest,54 as shown in Fig. 3f. More details of this analysis including a table of the characteristic contact distances are provided in the ESI† (cf. Fig. S3–S6 and Table ST2).The first objective of our study is to compare the fingerprint plots of the various crystal structures and divide them into groups according to their resemblance. This corresponds to sorting them by similar intermolecular interactions. Computing correlation (as described in the previous section) allows quantification of similarity that is beyond a qualitative comparison based on their visual appearance. The matrix with the pairwise correlations for the various structures is given in the ESI† (cf. Table ST3). These correlations are also visualized in Fig. 4 by a dendrogram, which is constructed by considering at first the largest pairwise similarities. This allows identifying three main groups each with similar distributions of contact pairs that are discussed in more detail below.
Group I: Herringbone-dominated structures
The first group of interactions in the dendrogram (shown in green) consists of five molecular crystal structures comprising the different polymorphs of PEN as well as DHDAP and DNTT. Their corresponding fingerprint plots are depicted in Fig. 3a–e. Notably, the distribution of C⋯H contacts for all molecules of this group exhibits the characteristic shape of two “wings” with corresponding C⋯H distances as small as 2.7 Å. In contrast, the H⋯H contacts are rather homogeneously distributed over a large range of (di, de)-pairs (cf.Fig. 3f). In the case of DHDAP, the N⋯H contacts are also broadly distributed and resemble that of the C⋯H contacts. While similarities between the five fingerprint plots can be recognized visually, the calculated correlation coefficients provide a more accurate comparison. The least resemblance within this group shows DNTT, which is mainly attributed to the presence of C⋯S interaction pairs (with a closest contact distance of 3.3 Å) that become visible on the image diagonal of the fingerprint plot (cf. Fig. S4, ESI†). A comparison with the corresponding crystal structures shows that all these molecules adopt typical “face on edge” herringbone packing motifs as shown for PEN in Fig. 1b.Group II: Perfluorination
The second group (shown in purple) comprises only the two crystalline phases of PFP. Interestingly, both phases reveal different molecular packing motifs: PFP-bulk displays a “face on edge” motif (cf.Fig. 1d), while the molecules in the π-stacked phase are slip-stacked (cf.Fig. 1e). Despite their supposedly different arrangements, the corresponding fingerprint plots actually closely resemble each other. As depicted in Fig. 3g and h, both exhibit an aliform distribution of C⋯F contacts like the C⋯H characteristics of the hydrocarbons mentioned before with distances down to 3 Å. In addition, both phases reveal the same characteristic accumulation of C⋯C contacts at the image diagonal with the shortest contact distances of around 3.2 Å. This value can be interpreted as the molecular plane distance for parallel arrangement of planar molecules. In contrast to the broad distribution of H⋯H contacts of the first group, the F⋯F contacts reveal a characteristic localization along the diagonal of the fingerprint plots with an accumulation of (di, de)-pairs (indicated as red areas) with distances down to 2.7 Å.Group III: Directed interactions
The last seven crystalline phases are summarized in the third group (indicated red). In the associated fingerprint plots shown in Fig. 3i–o, two features are particularly noteworthy: all structures feature an accumulation of C⋯C contacts and reveal characteristic sharp, needle-like contact point distributions with comparatively short associated close contacts. Such characteristics indicate relatively strong interactions between specific atom pairs and hence are referred to as directed interactions.52,54For QUI, TET and the three QUA phases, such features show up most clearly for the O⋯H contacts, while DAP and QUA-β also exhibit an acicular distribution of H⋯H contacts with distances smaller than 2.2 Å. Since DAP and HFDP do not contain any oxygen atoms, the needle-like extensions are related to N⋯H, C⋯H and F⋯H contacts. A comparison of their crystal structures shows that QUI, TET and QUA-α adopt a slip-stack packing motif, wherein QUI is slightly different and shows a small contortion of the molecules relative to each other. We note that also for QUI, a thin film phase (QUI-TF) has been identified recently.73 In this phase, the molecules adopt a similar structural packing motif to that in the bulk phase. Accordingly, also the corresponding fingerprint plot is rather similar (cf. Fig. S7, ESI†) and, therefore, has not been analyzed separately.
The QUA-β phase reveals a layered structure of uprightly oriented and slip-stacked molecules, while the slip-stacking direction in neighboring layers is alternately tilted (cf. Fig. S1, ESI†). This results in a needle-shape distribution of H⋯H contact points in the fingerprint plots (see Fig. 3n) which belong to distances between H-atoms at the short molecular side.
DAP, HFDP and QUA-γ display a third distinct packing motif, with molecules aligned in parallel stacks, with a twisting of adjacent stacks relative to each other. In such crystal structures, molecules adjoin on another at their long side yielding only few distinct point contacts of neighboring molecules as shown in Fig. 1g. Following the previous work of Paulus et al., this arrangement is denoted as the “criss-cross” motif.66 Interestingly, such a structure is also adopted by HFDP but additionally exhibits an alternating stacking of the molecular planes (cf. Fig. S1, ESI†). This feature is attributed to the static dipole moment oriented along the long molecular axis, which is introduced by the partial fluorination and will be discussed below.
Intermolecular interactions
Next, we focus on the nature of underlying interactions that lead to the characteristic distribution of contact points. To begin with, we briefly compare the various types of intermolecular interactions occurring in the organic crystals. For a more detailed quantum chemical description of the various interactions and their computational modeling, we refer to the recent review by Sutton et al. and references therein.10Attractive interactions between π-conjugated organic molecules are generally ascribed to van der Waals forces which is actually a collective term for different electrostatic forces. These include direct interactions between permanent molecular charges or multipoles (so called Keesom interaction), Debye forces arising from interactions between permanent dipoles and induced dipoles in adjacent molecules, as well as dispersion forces (also denoted as London forces) due to interactions between fluctuating dipoles (formed by spontaneous polarization) and induced dipoles. Debye forces make up the smallest contribution to the total energy amount10,74 and seem to have only a subsidiary influence on the packing motif. In contrast, London dispersion forces constitute the main contribution whose strength scales with the dipolar polarizability of the involved molecules.26,27,75,76 Since the polarizability is a tensor, London forces generally depend not only on the static dipole polarizability, αtot, but also on the anisotropy of the tensor components. The presently considered ensemble reveals, however, rather similar relations (cf. Tab. ST4, ESI†). This results from the specific molecular selection, since the polarizability of such π-conjugated entities essentially depends on the number of valence electrons and the overall size of the molecule.26 Recent analyses of the benzene lattice energy have further shown that a precise description of dispersion forces in crystals of conjugated molecules also requires the consideration of nonadditive three-body interactions within sufficiently large distances.77,78
Although the presently considered molecules are of similar size, the oxygen containing molecules show somewhat lower polarizability, which is attributed to a loss of conjugation within the ring system. Since localization of charge at the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds causes a permanent polarization, this reduces in turn the molecular π-polarizability. As the London dispersion is weaker in these cases, direct electrostatic interactions become more decisive for the packing motifs.
O bonds causes a permanent polarization, this reduces in turn the molecular π-polarizability. As the London dispersion is weaker in these cases, direct electrostatic interactions become more decisive for the packing motifs.
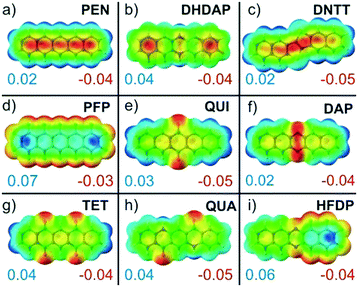
Commonly, such electrostatic interactions are described within a multipole expansion where typically only charges, dipoles and quadrupoles are considered. Except for HFDP, all molecules analyzed in this study exhibit no permanent dipole moment but differ in their quadrupole moments (cf. Tab. ST5, ESI†). Regarding multipolar electrostatic interactions, we would like to recall that in organic crystals, the molecular extension typically exceeds the intermolecular distances, so that a simple description by the far-field approximation is not valid anymore and instead other methods are required.79,80 Especially heteroatom substitutions can lead to notable charge redistribution within the π-conjugated molecular planes, resulting in strongly affected electrostatic moments. To illustrate this effect, the charge distributions within the molecules were calculated and are compared in Fig. 5 by the corresponding molecular electrostatic potential plots of the molecular planes. These MEP plots indicate characteristic differences and reveal in particular the before mentioned localized charge accumulations for the oxygen containing molecules QUI, TET and QUA. Although such MEP plots provide a vivid explanation for the occurrence of specific packing motifs, this simplified electrostatic description should be treated with some caution since polarization and screening effects due to mutual interactions are not taken into account. In contrast to fingerprint plots, which implicitly contain the information of the crystalline packing, all calculations concerning polarizability, quadrupole moments and MEPs are performed for isolated molecules without consideration of intermolecular interactions in the crystalline environment. In fact, previous studies have pointed out the importance of notable mutual polarization of π-conjugated systems at short distances. This charge penetration effect arises from a Coulomb interaction between the electron density of π-orbitals and positive core potentials of neighboring molecules due to a reduced screening of their nuclei and has to be taken into account when quantitatively analyzing the individual interactions.26,27,81,82
Besides the van der Waals forces, other attractive forces can occur which exhibit local dipolar interactions with a nearly covalent character due to hydrogen bonds. Such H-bonds appear when electron lone pairs of sufficiently small atoms (typically N, O or F) are in close contact with an electron deficient hydrogen atom of neighboring molecules.83
All previously considered forces are mainly of attractive nature and therefore counteract the Pauli exchange repulsion, which will dominate at sufficiently short intermolecular distances and hence limits the molecular packing density. Next, we analyze correlations between molecular characteristics and their packing motifs in the crystalline phases to find qualitative explanations for the various stacking patterns.
Molecules with radial-symmetric MEP
Remarkably, all molecules of the first group adopt herringbone packing motifs and invariably reveal positive electrostatic potentials at the periphery of their π-conjugated molecular plane together with corresponding antipoles located above and below this plane (cf.Fig. 5a–d). As described in a simple electrostatic model by Hunter and Sanders84 who considered a sandwich-like molecular charge distribution that is exemplarily shown for PEN in Fig. 1b, this favors the typical “face-on-edge” packing motif. This indicates that quadrupole coupling is the structure-determining factor for such molecules. In this context, we would like to mention that often a “π-stacking” is assumed for such aromatic molecules. As shown in numerous theoretical studies, this is, however, not possible due to the Coulomb repulsion between the electron rich π-orbitals.10,81,84–86 These analyses showed further that this repulsion can be lifted either by laterally shifting molecules with respect to the underlying ones such that the rim stacks above the ring center (so called slip-stacking, cf.Fig. 1e) or by adopting a face-on-edge herringbone packing, where the latter appears somewhat more stable. In this context, it should be noted that recent studies have challenged the classical picture of Hunter and Sanders, since the charge penetration effect notably influence the electrostatic interaction. For the case of acene dimers, the calculation even found that a cofacial arrangement is preferred over a HB configuration.26 This apparent deviation from the actual HB packing motifs has been attributed to the non-consideration of three-body interactions that are mandatory for a proper description of dispersion forces. At present this remains, however, challenging for larger π-conjugated molecules and in particular for their crystal structures.Herringbone packing motifs are commonly found for many unsubstituted polycyclic aromatic molecules such as acenes, thiophenes, and oligophenylenes. Interestingly, the same also applies to the case of DHDAP and DNTT. Although both species contain heteroatoms in their π-system, the electrostatic potential at the rim is rather uniform without sign change (cf.Fig. 5b and c). In the corresponding fingerprint plots, this packing motif manifests in a large fraction of C⋯H contacts distributed over a wide range of pair distances. This characteristic indicates that C⋯H contacts should not be seen as specific pair interactions but rather as π⋯H interactions mediated by the quadrupole moment. Within this approach, it becomes clear why C⋯H and N⋯H contacts are indistinguishable in the fingerprint plots of DHDAP because nitrogen is a part of the planar backbone and the π⋯H interaction does not distinguish between different ring atoms. In contrast, H⋯H interactions are repulsive which explains the generally large pair distances in the fingerprint plots (cf.Fig. 3f). The shortest H⋯H distance occurs only between the short sides of neighboring molecules. It results from the herringbone-packing motif, which appears together with a layered structure of uprightly oriented molecules and thus minimizes the region of H⋯H interaction. Notably, such crystallographic planes also have the lowest free surface energy87 and therefore form the preferred orientation of single crystals or crystalline molecular films grown on inert substrates (e.g. PEN(001) on SiO2).38
Perfluorination
While perfluorination leads to an inversion of the molecular quadrupole moment and the MEP (cf.Fig. 5d), everything discussed in the previous section fully holds true also for this case. The detailed analysis of the crystalline structure of PFP reveals, however, some notable differences to the non-fluorinated PEN, such as a somewhat different herringbone arrangement and the presence of a π-stacked polymorph.Interestingly, the fingerprint plots show some additional characteristics that do not appear for molecules of the first structural group. The most interesting feature is the distinct accumulation of F⋯F contacts (shown as green-red region in Fig. 3g and h) at an equilibrium distance of about 3.2 Å, while H⋯H contacts of PEN are homogeneously distributed (cf. inset in Fig. 3f). As the F⋯F interactions are not intrinsically attractive, this indicates a mediation of the Pauli exchange repulsion mainly via these contacts. The simple reason why this occurs for fluorine but not for hydrogen in the foregoing cases is their distinctly different atomic size. This becomes immediately evident when comparing the molecular packing motifs shown in Fig. 1b and d. The space-fill representation, using atomic van der Waals radii, shows fluorine atoms with about the same size as carbon atoms. This also yields an explanation for the orthogonal packing motif within the PFP-crystal: the PFP molecules can be considered as rectangular “bricks” (indicated by the enveloping rectangles in Fig. 1d). In contrast, molecules with a hydrogen rim appear slanted at the edge (indicated by dashed line in Fig. 1b). While this geometrical detail generally hampers a rectangular arrangement for PEN, it appears to be the best packing motif for the “PFP bricks”. This simple geometrical consideration is well supported by the corresponding molecular packing coefficients computed according to the definition of Kitaigorodskii.88 Using van der Waals radii provided by the CrystalExplorer package,89,90 typical packing coefficients of approximately 0.7 are obtained for all structures (see Table ST6, ESI†). Only the two PFP structures are more densely packed and yield values of about 0.8, while the packing coefficient of the partially fluorinated HFDP amounts to an intermediate value of 0.75.
Considering PFP molecules as cuboids also allows rationalizing the slip-stack packing motif occurring in the π-stacked phase (PFP-π) of PFP.65 As discussed in the previous section, electrostatic coupling of molecular quadrupoles favors either herringbone or slip-stack architectures. A detailed comparison of the crystal structure of both polymorphs of PFP shows that the latter arrangement is obtained from the bulk herringbone structure by turning every second molecule by 90°. This is possible since the molecules reveal already a quasi-one-dimensional slip-stack arrangement in the bulk structure (cf. Fig. S10, ESI†), hence demonstrating that both PFP packing motifs are actually very similar. Also, the C⋯F distances in both PFP phases are almost identical, again showing their intrinsic similarity. In addition, the perfluorination also results in a reduction of the π-orbital density above and below the ring plane, which reduces the mutual repulsion of π-stacked planes. Together with the attractive πδ+–Fδ− interaction due to slip stacking, this results in the smallest π-plane separation among the studied molecules of below 3.2 Å.
In contrast, such a slip-stack arrangement is not favorable for PEN. Due to its slanted molecular rim, a planar stacking would lead to the formation of voids and increased C⋯H distances that reduce the attractive intermolecular interaction. In fact, such a packing motif neither occurs in any PEN bulk phase, nor has it been observed in any substrate mediated PEN thin film.
Localized electrostatic interactions
So far, we have discussed the interaction between conjugated molecules which exhibit a rather homogeneous charge distribution (and MEP) within their π-system. This situation changes, however, when substituting heteroatoms in the aromatic ring system. A meaningful example is the case of DAP. Although the nitrogen atoms change the MEP compared to PEN only at two positions (cp. Fig. 5a and f), a completely different packing arrangement emerges. The molecules adopt a “criss-cross” packing motif as shown schematically in Fig. 1g instead of the herringbone packing motif found for PEN. This suggests that a change of sign in the electrostatic potential at the molecular periphery seems to be crucial for the absence of a face-on-edge herringbone packing, whereas moderate charge redistributions within the molecular plane appear less important. This is further evidenced by DHDAP, which adopts a herringbone packing motif although it exhibits an unequal charge distribution within the molecular plane while the potential at the periphery has a uniform sign (cf.Fig. 5b). In fact, all studied molecules that exhibit a non-uniform sign of the electrostatic potential at the rim (DAP, QUI, TET and QUA) adopt either criss-cross or slip-stack packing motifs. They are well explained by electrostatic interactions yielding attractive contacts between regions of positive and negative electrostatic potential. Notably, all these molecules have distinctly larger quadrupole moments than the herringbone stacking molecules (PEN, PFP and DHDAP) and have their largest component along the long molecular axis (cf. Tab. ST5, ESI†). The influence of nitrogen substitution in aromatic hydrocarbons on the intermolecular interaction and packing motifs has been analyzed in more detail in a previous work by Maly,91 where similar observations were made.The role of substituent effects on interaction and packing has been theoretically analyzed in great detail for small aromatic compounds such as thiophenes or substituted benzenes.86,92–95 Besides an energetically more favored slip stack-packing instead of a herringbone motif, also an alternately aligned stacking due to permanent dipoles is found. The quantitative analyses showed further that although electrostatic interaction is substantially weaker than dispersion interaction, it is highly orientational dependent and thus becomes a decisive parameter that controls the packing motif.
Among the presently studied molecules, such an alternating stacking is also found for HFDP (cf. Fig. S1, ESI†), which exhibits a permanent dipole moment of 5.2 D oriented along the long molecular axis due to partial fluorination (cf.Fig. 5i).
Remarkably, the crystalline structures of the third group exhibit an additional interaction. In all cases, atoms with lone electron pairs such as N, O or F are in close contact with hydrogen atoms of neighbor molecules, which allows the formation of hydrogen bonds. As such interactions are effective only at short “bond lengths”, their appearance manifests in the presence of characteristic needle like features in the element resolved fingerprint plots corresponding to hydrogen contacts to the N, O or F atoms.52,54 Good examples are QUI, TET and QUA (cf.Fig. 3j–o and S6, ESI†) where such needle-like features occur at O⋯H contact distances below 2.5 Å (or even <1.9 Å for QUA, cf. Tab. ST2, ESI†). In this context, it should be noted that because of the negligible X-ray cross section of H-atoms their position can only be determined approximately by means of X-ray diffraction, thus leaving some uncertainty in the exact strength of such H-bonds.96
Despite additional static electrostatic interactions, QUI shows surprisingly small lattice energy and, although having a larger mass than PEN, sublimates at lower temperature.41 This can be realized by reduced polarizability (caused by the polar C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds, cf. Tab. ST4, ESI†) and an increased distance between the molecular planes due to oxygen atoms acting as the spacer. Both effects reduce the attractive dispersion interaction, which shows that additional directed electrostatic interactions may not automatically enhance the lattice energy.
O bonds, cf. Tab. ST4, ESI†) and an increased distance between the molecular planes due to oxygen atoms acting as the spacer. Both effects reduce the attractive dispersion interaction, which shows that additional directed electrostatic interactions may not automatically enhance the lattice energy.
Within a theoretical study for various substituted benzenes, similar characteristics were reported. While in most cases substitution leads to a stabilization compared to benzene, some configurations show reduced interaction energies due to increased repulsion.22
This competition of interactions is also reflected in the crystal structure of QUI, which cannot be unambiguously assigned to one of the before mentioned packing motifs and instead shows a mixture of slip-stack and criss-cross (cf.Table 1 and Fig. S1, ESI†). Notably, by introducing an external boundary condition like a substrate interaction, a thin-film phase is formed for QUI, which features a truly parallel molecular arrangement.73
The situation is different for the other oxo-species of PEN, namely TET. Here, the O⋯H distance is 0.2 Å shorter, which yields stronger hydrogen bonds and leads to a uniform slip-stack motif. Even stronger H-bonds occur in all three QUA structures revealing H⋯O distances below 1.9 Å. Notably, the strong H-bonds even weaken the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond within the molecule, allowing the molecule to gain conjugation, which in turn affects the energy-levels as reported previously.60,97
O bond within the molecule, allowing the molecule to gain conjugation, which in turn affects the energy-levels as reported previously.60,97
The profound influence of H-bonds on the resulting packing motifs has also been demonstrated for larger aromatic systems, such as hexabenzocoronene (HBC) and its partially-fluorinated derivatives. Here, the symmetrically fluorinated hexafluoro-HBC, which has no permanent dipole moment, reveals pronounced F⋯H-bonds and a slip stack packing, whereas the non-substituted HBC adopts a herringbone packing.98
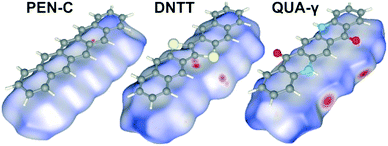
Commonly, short π–π distances are considered beneficial to achieve high charge carrier mobility. Remarkably, the best performing OSC among the assortment analyzed here, such as PEN, DHDAP and DNTT, exhibit, however, no π-stacking and instead adopt a herringbone packing motif. This indicates that also other contact points could be of great importance. To illustrate this situation, the Hirshfeld surfaces of PEN-C, DNTT and QUA-γ are compared in Fig. 6. Here, the color code denotes the comparison of di and de values relative to the van der Waals radii of the corresponding atoms. Red areas mark areas with the sum of d-values smaller than the sum of vdW-radii, while blue areas indicate the opposite. Hence, red indicates regions where neighboring molecules draw very close, thus yielding a maximal orbital overlap. A conclusive example constitutes QUA-γ where the O⋯HN contact points can be clearly seen as red regions. Comparison of the Hirshfeld surfaces of PEN and DNTT reveals particularly pronounced contact points only for DNTT. They are located at the middle of the long side of DNTT molecules and can be assigned to C⋯S contacts. Considering that overlap integrals depend on distances in a nonlinear fashion and that the sulfur atoms of DNTT are constituent of the conjugated system (in contrast to the H-atoms of PEN), this provides an efficient electronic coupling and might explain the superior charge transport properties of DNTT.
Conclusions
Since optoelectronic properties of organic semiconductor solids are determined not only by the molecular electronic properties, but also by the molecular arrangement, further advancements of such materials require guidelines for structure–property interrelations beyond simple single molecule electronic considerations. A common strategy to control molecular packing motifs is based on the use of functional side groups. For example, alkylation is frequently found to suppress herringbone packing and leads to slip-stacking.99,100 However, such flexible side chains can lead to conformational changes and are electronically insulating, which is rather unfavorable for the desired applications. To reduce this complexity and to identify structure-determining factors, we have compared in this study 9 different but geometrically similar molecules without flexible side groups. By performing Hirshfeld analyses for all 14 crystalline phases adopted by the various molecules and comparing their corresponding fingerprint plots as well as their electrostatic contour plots and calculating molecular electronic properties such as quadrupole moments and polarizability, we have obtained the following empirical correlations:• A herringbone motif is favored for molecules with a uniform sign of charge for the electrostatic potential at the periphery of the molecule.
• Conversely, disturbances of the uniform potential at the periphery cause slip-stack or criss-cross packing via introduction of strong local electrostatic interactions or even hydrogen bonds.
• In most cases, the latter interactions tend to dominate structure formation.
• The van der Waals radius of atoms at the periphery of π-conjugated molecules determines the herringbone angles and allows explaining the similarity of the seemingly different polymorphs of PFP.
• Larger heteroatomic substituents within the aromatic ring systems like, e.g. sulfur in DNTT, provide contact points with efficient electronic coupling to neighboring molecules.
These observations might be helpful guidelines for future strategies to synthesize new OSCs aiming to achieve or avoid specific packing motifs. Moreover, the present selection of molecules and the analysis of their contact points and interactions in crystals may serve as a meaningful benchmark ensemble for refined theoretical descriptions of intermolecular forces. The recent progress in the computational-based description of non-covalent interactions in molecular solids has recently also allowed detailed analyses of the individual forces between larger molecules such as acenes.26,30 It would therefore be very important to extend these studies also to the crystalline phases of the presently considered molecular ensembles of geometrically similar but chemically modified molecules, in order to quantify the influence of substitution on the balance of acting intermolecular forces. This would provide an important step towards a rational approach to tailor molecular packing motifs. In the future, similar analyses might also be performed for other geometrical classes of molecules such as e.g. phthalocyanines or coronenes to study packing motifs in crystals of four-leaf clover-shaped or discoid molecules.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the support from the Deutsche Forschungsgemeinschaft (Grant SFB 1083, TP A2) and thank Prof. Dr. Qian Miao (Chinese University Hong Kong) for providing data of the crystal structure of DAP.References
- X. J. Guo, Y. Xu, S. Ogier, N. N. Tse, M. Caironi, A. Perinot, L. Li, J. Q. Zhao, W. Tang, R. A. Sporea, A. Nejim, J. Carrabina, P. Cain and F. Yan, IEEE Trans. Electron Devices, 2017, 64, 1906–1921 CrossRef.
- A. Facchetti, Chem. Mater., 2011, 23, 733–758 CrossRef CAS.
- H. Sasabe and J. Kido, Chem. Mater., 2011, 23, 621–630 CrossRef CAS.
- Organic Electronics, ed. H. Klauk, Wiley-VCH, Weinheim, 2006 Search PubMed.
- J. E. Anthony, Angew. Chem., Int. Ed., 2008, 47, 452–483 CrossRef CAS PubMed.
- X. Guo, M. Baumgarten and K. Müllen, Prog. Polym. Sci., 2013, 38, 1832–1908 CrossRef CAS.
- N. Karl, Synth. Met., 2003, 133, 649–657 CrossRef.
- F. Ortmann, F. Bechstedt and K. Hannewald, Phys. Status Solidi B, 2011, 248, 511–525 CrossRef CAS.
- K. Kolata, T. Breuer, G. Witte and S. Chatterjee, ACS Nano, 2014, 8, 7377–7383 CrossRef CAS PubMed.
- C. Sutton, C. Risko and J.-L. Brédas, Chem. Mater., 2015, 28, 3–16 CrossRef.
- C. Ambrosch-Draxl, D. Nabok, P. Puschnig and C. Meisenbichler, New J. Phys., 2009, 11, 125010 CrossRef.
- T. Rangel, K. Berland, S. Sharifzadeh, F. Borown-Altvater, K. Lee, P. Hyldgaard, L. Kronik and J. B. Neaton, Phys. Rev. B, 2016, 93, 115206 CrossRef.
- G. M. Day, Crystallogr. Rev., 2011, 17, 3–52 CrossRef.
- K. Müller-Dethlefs and P. Hobza, Chem. Rev., 2000, 100, 143–168 CrossRef.
- J. D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- J. Antony and S. Grimme, Phys. Chem. Chem. Phys., 2006, 8, 5287–5293 RSC.
- N. Marom, A. Tkatchenko, M. Rossi, V. V. Gobre, O. Hod, M. Scheffler and L. Kronik, J. Chem. Theory Comput., 2011, 7, 3944–3951 CrossRef CAS PubMed.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1994, 100, 2975–2988 CrossRef CAS.
- M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2004, 108, 10200–10207 CrossRef CAS.
- M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2006, 110, 10656–10668 CrossRef CAS PubMed.
- D. A. Sirianni, L. A. Burn and C. D. Sherrill, J. Chem. Theory Comput., 2016, 13, 86–99 CrossRef PubMed.
- N. J. Silva, F. B. C. Machado, H. Lischka and A. J. A. Aquino, Phys. Chem. Chem. Phys., 2016, 18, 22300–22310 RSC.
- S. Tsuzuki, H. Orita and N. Sato, J. Chem. Phys., 2016, 145, 174503 CrossRef PubMed.
- S. M. Ryno, C. Risko and J.-L. Brédas, Chem. Mater., 2016, 28, 3990–4000 CrossRef CAS.
- S. M. Ryno, C. Risko and J.-L. Brédas, J. Am. Chem. Soc., 2014, 136, 6421–6427 CrossRef CAS PubMed.
- A. R. Oganov, A. O. Lyakhov and M. Valle, Acc. Chem. Res., 2011, 44, 227–237 CrossRef CAS PubMed.
- S. L. Price, Chem. Soc. Rev., 2014, 43, 2098–2111 RSC.
- J. G. Brandenburg and S. Grimme, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 502–513 CAS.
- G. R. Desiraju and A. Gavezzotti, Acta Crystallogr., Sect. B: Struct. Sci., 1989, 45, 473–482 CrossRef.
- M. Nishio, CrystEngComm, 2004, 6, 130–158 RSC.
- S. Tsuzuki and A. Fujii, Phys. Chem. Chem. Phys., 2008, 10, 2584–2594 RSC.
- B. Schatschneider, J. Phelps and S. Jezowski, CrystEngComm, 2011, 13, 7216–7223 RSC.
- A. Brillante, R. G. Della Valle, L. Farina, A. Girlando, M. Masino and E. Venuti, Chem. Phys. Lett., 2002, 357, 32–36 CrossRef CAS.
- C. C. Mattheus, G. A. de Wijs, R. A. de Groot and T. T. M. Palstra, J. Am. Chem. Soc., 2003, 125, 6323–6330 CrossRef CAS PubMed.
- A. Troisi and G. Orlandi, J. Phys. Chem. B, 2005, 109, 1849–1856 CrossRef CAS PubMed.
- I. Meyenburg, T. Breuer, A. Karthäuser, S. Chatterjee, G. Witte and W. Heimbrodt, Phys. Chem. Chem. Phys., 2016, 18, 3825–3831 RSC.
- J. Schwaben, N. Münster, M. Klues, T. Breuer, P. Hofmann, K. Harms, G. Witte and U. Koert, Chem. – Eur. J., 2015, 21, 13758–13771 CrossRef CAS PubMed.
- Y. Sakamoto, T. Suzuki, M. Kobayashi, Y. Gao, Y. Fukai, Y. Inoue, F. Sato and S. Tokito, J. Am. Chem. Soc., 2004, 126, 8138–8140 CrossRef CAS PubMed.
- D. Käfer, M. El Helou, C. Gemel and G. Witte, Cryst. Growth Des., 2008, 8, 3053–3057 Search PubMed.
- A. V. Dzyabchenko, V. E. Zavodnik and V. K. Belsky, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1979, 35, 2250–2253 Search PubMed.
- M. Winkler and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 1805–1815 CrossRef CAS PubMed.
- U. H. F. Bunz, Chem. – Eur. J., 2009, 15, 6780–6789 CrossRef CAS PubMed.
- Q. Tang, D. Q. Zhang, S. L. Wang, N. Ke, J. B. Xu, J. C. Yu and Q. Miao, Chem. Mater., 2009, 21, 1400–1405 CrossRef CAS.
- O. Tverskoy, F. Romminger, A. Peters, H.-J. Himmel and U. H. F. Bunz, Angew. Chem, Int. Ed., 2011, 15, 3557–3560 CrossRef PubMed.
- Q. Miao, Synlett, 2012, 3, 326–336 CrossRef.
- D. Liu, Z. Li, Z. He, J. Xu and Q. Miao, J. Mater. Chem., 2012, 22, 4396 RSC.
- S. Miao, S. M. Brombosz, P. von Rague Schleyer, J. I. Wu, S. Barlow, S. R. Marder, K. I. Hardcastle and U. H. F. Bunz, J. Am. Chem. Soc., 2008, 130, 7339–7344 CrossRef CAS PubMed.
- J. J. McKinnon, A. S. Mitchell and M. A. Spackman, Chem. – Eur. J., 1998, 11, 2136–2141 CrossRef.
- M. A. Spackman and J. J. McKinnon, CrystEngComm, 2002, 4, 378–392 RSC.
- M. A. Spackman and J. J. McKinnon, CrystEngComm, 2009, 11, 19–32 RSC.
- J. J. McKinnon, M. A. Spackman and A. S. Mitchell, Acta Crystallogr., Sect. B: Struct. Sci., 2004, 60, 627–668 CrossRef PubMed.
- J. J. McKinnon, D. Jayatikala and M. A. Spackman, Chem. Commun., 2007, 3814–3816 RSC.
- A. Parkin, G. Barr, W. Dong, C. J. Gilmore, D. Jayatilaka, J. J. McKinnon, M. A. Spackman and C. C. Wilson, CrystEngComm, 2007, 9, 648–652 RSC.
- S. Haas, Y. Takahashi, K. Takimiya and T. Hasegawa, Appl. Phys. Lett., 2009, 95, 22111 CrossRef.
- A. Facchetti, Mater. Today, 2007, 10, 28–37 CrossRef CAS.
- F. May, M. Al-Helwi, B. Baumeister, W. Kowalsky, E. Fuchs, C. Lennartz and D. Andrienko, J. Am. Chem. Soc., 2012, 134, 13818–13822 CrossRef CAS PubMed.
- W. Jiang, Y. Li and Z. H. Wang, Acc. Chem. Res., 2014, 47, 3135–3147 CrossRef CAS PubMed.
- E. D. Głowacki, L. Leonat, M. Irimia-Vladu, R. Schwödiauer, M. Ullah, H. Sitter, S. Bauer and N. S. Sariciftci, Appl. Phys. Lett., 2012, 101, 23305 CrossRef.
- S. H. Han, J. H. Kim, S. M. Cho, M. H. Oh, S. H. Lee, D. J. Choo and J. Jang, Appl. Phys. Lett., 2006, 88, 73519 CrossRef.
- R. B. Campbell and J. M. Robertson, Acta Crystallogr., 1962, 15, 289–290 CrossRef CAS.
- T. Siegrist, C. Kloc, J. H. Schön, B. Batlogg, R. C. Haddon, S. Berg and G. A. Thomas, Angew. Chem., Int. Ed., 2001, 40, 1732–1736 CrossRef CAS PubMed.
- S. Schiefer, M. Huth, A. Dobrinevski and B. Nickel, J. Am. Chem. Soc., 2007, 129, 10316–10317 CrossRef CAS PubMed.
- I. Salzmann, A. Moser, M. Oehzelt, T. Breuer, X. Feng, Z. Y. Juang, D. Nabok, R. G. Della Valle, S. Duhm, G. Heimel, A. Brillante, E. Venuti, I. Bilotti, C. Christodoulou, J. Frisch, P. Puschnig, C. Draxl, G. Witte, K. Müllen and N. Koch, ACS Nano, 2012, 6, 10874–10883 CrossRef CAS PubMed.
- E. F. Paulus, F. J. J. Leusen and M. U. Schmidt, CrystEngComm, 2007, 9, 131–143 RSC.
- S. K. Wolff, D. J. Grimwood, J. J. McKinnon, M. J. Turner, D. Jayatilaka and M. A. Spackman, Crystal Explorer (Version 3.1), University of Western Australia, Perth, Australia, 2013 Search PubMed.
- Python Software Foundation, Python Language Reference (Version 2.7.6.), available at: http://www.python.org Search PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- M. S. Gordon and M. W. Schmidt, in Theory and Applications of Computational Chemistry: the first forty years, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. E. Scuseria, Elsevier, Amsterdam, 2005, Advances in electronic structure theory: GAMESS a decade later, pp. 1167–1189 Search PubMed.
- U. Varetto, Molekel 5.4, Swiss National Supercomputing Centre, 2009 Search PubMed.
- R. F. W. Bader, M. T. Carroll, J. R. Cheeseman and C. Chang, J. Am. Chem. Soc., 1987, 109, 7968–7979 CrossRef CAS.
- I. Salzmann, D. Nabok, M. Oezelt, S. Duhm, A. Moser, G. Heimel, P. Puschnig, C. Ambrosch-Draxl, J. P. Rabe and N. Koch, Cryst. Growth Des., 2011, 11, 600–606 CAS.
- J. D. Dunitz and A. Gavezzotti, Chem. Soc. Rev., 2009, 38, 2622–2633 RSC.
- F. London, Trans. Faraday Soc., 1937, 33, 8–26 RSC.
- J. F. Dobson and T. Gould, J. Phys.: Condens. Matter, 2012, 24, 073201 CrossRef PubMed.
- J. Yang, W. Hu, D. Usvyat, D. Matthews, M. Schütz and G. K.-L. Chan, Science, 2014, 345, 640–643 CrossRef CAS PubMed.
- A. L. Ringer and C. D. Sherrill, Chem. – Eur. J., 2008, 14, 2542–2547 CrossRef CAS PubMed.
- A. J. Stone, Chem. Phys. Lett., 1981, 83, 233–239 CrossRef CAS.
- S. Brodersen, S. Wilke, F. J. J. Leusen and G. Engel, Phys. Chem. Chem. Phys., 2003, 5, 4923–4931 RSC.
- C. D. Sherill, Acc. Chem. Res., 2013, 46, 1020–1028 CrossRef PubMed.
- B. Wang and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 3330–3342 CrossRef CAS PubMed.
- T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76 CrossRef CAS.
- C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525–5534 CrossRef CAS.
- S. Grimme, Angew. Chem., Int. Ed., 2008, 47, 3430–3434 CrossRef CAS PubMed.
- C. R. Martinez and B. L. Iverson, Chem. Sci., 2012, 3, 2191–2201 RSC.
- D. Nabok, P. Puschnig and C. Ambrosch-Draxl, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 245316 CrossRef.
- A. I. Kitaigorodskii, Acta Crystallogr., 1965, 18, 585–590 CrossRef CAS.
- A. Bondi, J. Phys. Chem., 1964, 68, 441 CrossRef CAS.
- R. S. Rowland and R. Taylor, J. Phys. Chem., 1996, 100, 7384–7391 CrossRef CAS.
- K. E. Maly, Cryst. Growth Des., 2011, 11, 5628–5633 CAS.
- S. Tsuzuki, K. Honda, T. Uchimaru, M. Mikami and K. Tanabe, J. Am. Chem. Soc., 2002, 124, 104–112 CrossRef CAS PubMed.
- M. O. Sinnokrot and C. D. Sherill, J. Phys. Chem. A, 2003, 107, 8377–8379 CrossRef CAS.
- S. E. Wheeler, J. Am. Chem. Soc., 2011, 133, 10262–10274 CrossRef CAS PubMed.
- R. G. Huber, M. A. Margreiter, J. E. Fuchs, S. von Grafenstein, C. S. Tautermann, K. R. Liedl and T. Fox, J. Chem. Inf. Model., 2014, 54, 1371–1379 CrossRef CAS PubMed.
- Y. Nishiyama, P. Langam and H. Chanzy, J. Am. Chem. Soc., 2002, 124, 9074–9082 CrossRef CAS PubMed.
- E. D. Głowacki, M. Irimia-Vladu, M. Kaltenbrunner, J. Gąsiorowski, M. S. White, U. Monkowius, G. Romanazzi, G. P. Suranna, P. Mastrorilli, T. Sekitani, S. Bauer, T. Someya, L. Torsi and N. S. Sariciftci, Adv. Mater., 2013, 25, 1563–1569 CrossRef PubMed.
- T. Breuer, M. Klues, P. Liesfeld, A. Viertel, M. Conrad, S. Hecht and G. Witte, Phys. Chem. Chem. Phys., 2016, 18, 33344–33350 RSC.
- M. D. Curtis, J. Cao and J. W. Kampf, J. Am. Chem. Soc., 2004, 126, 4318–4328 CrossRef CAS PubMed.
- Z. Ma, H. Geng, D. Wang and Z. Shuai, J. Mater. Chem. C, 2016, 4, 4546–4555 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Details on correlation coefficients, packing coefficients, polarizabilities, quadrupole moments and close contacts, as well as the visualization of packing motifs for all structures are given. See DOI: 10.1039/c7ce01700f |
| This journal is © The Royal Society of Chemistry 2018 |