On the nature of organic and inorganic centers that bifurcate electrons, coupling exergonic and endergonic oxidation–reduction reactions
Abstract
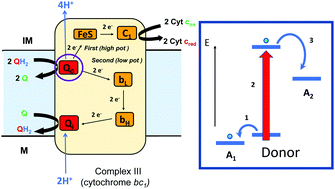
Bifurcating electrons to couple endergonic and exergonic electron-transfer reactions has been shown to have a key role in energy conserving redox enzymes. Bifurcating enzymes require a redox center that is capable of directing electron transport along two spatially separate pathways. Research into the nature of electron bifurcating sites indicates that one of the keys is the formation of a low potential oxidation state to satisfy the energetics required of the endergonic half reaction, indicating that any redox center (organic or inorganic) that can exist in multiple oxidation states with sufficiently separated redox potentials should be capable of electron bifurcation. In this Feature Article, we explore a paradigm for bifurcating electrons down independent high and low potential pathways, and describe redox cofactors that have been demonstrated or implicated in driving this unique biochemistry.


 Please wait while we load your content...
Please wait while we load your content...