Sizing sub-diffraction limit electrosprayed droplets by structured illumination microscopy†
Adam
Hollerbach
 a,
David
Logsdon
a,
Kiran
Iyer
a,
Anyin
Li
a,
David
Logsdon
a,
Kiran
Iyer
a,
Anyin
Li
 a,
J. Andy
Schaber
b and
R.
Graham Cooks
a,
J. Andy
Schaber
b and
R.
Graham Cooks
 *a
*a
aChemistry Department, Purdue University, West Lafayette, IN, USA. E-mail: cooks@purdue.edu
bBioscience Imaging Facility, Bindley Bioscience Center, Purdue University, West Lafayette, IN, USA
First published on 8th November 2017
Abstract
Electrosprayed droplets are widely studied for their role in the formation of ions at atmospheric pressure. Most droplet measurement methods used today employ light scattering to infer information about an electrosprayed droplet's size. However, these methods fail to measure droplets smaller than about 400 nm in diameter due to constraints imposed by the diffraction limit of light. To overcome this limitation, a super resolution fluorescence microscopy-based method for determining the sizes of electrosprayed droplets has been developed. Solutions containing rhodamine B and different amounts of glycerol were paper sprayed and nanoelectrosprayed onto conductive microscope coverslips using a single, high voltage pulse. Images of the deposited droplets were collected using a super resolution microscope operating in 3D structured illumination microscopy mode (3D-SIM). The sizes of droplets were measured using a modified circular Hough transformation program in Matlab. On average, the diameters of paper sprayed droplets were between 500 nm and 2 μm while almost all nanoelectrosprayed droplets were smaller than 1 μm. The center of a paper spray plume exhibited larger droplets than those at the periphery, likely due to greater Coulombic repulsive forces acting on the smaller droplets to drive them outwards. The periphery also likely contained progeny droplets in addition to smaller parent droplets. It was possible to alter the sizes of nanoelectrosprayed droplets in several ways, including by changing the solvent composition and voltage applied to the emitter. Droplets consisting of high concentrations of glycerol were larger than droplets containing high concentrations of methanol, presumably due to the high surface tension of glycerol. Correspondingly, droplets became smaller when the voltage applied to the emitter was increased, likely due to the ability to overcome the surface tension of the solvent more easily. The smallest detectable droplets confidently measured with this method were 200 nm in diameter. This method demonstrates a new way of measuring the sizes of electrosprayed droplets with half the diameter of conventional droplet size measurement methods. Through further optimization, it may be possible to measure the sizes of electrosprayed droplets as small as the theoretical resolution limit of SIM (∼100 nm).
Introduction
Electrospray ionization (ESI), also known as electrohydrodynamic (EHD) spraying, is widely used for creating charged droplets, ions, and aerosols at atmospheric pressure.1–5 Recently, much attention has been devoted to understanding the physical and chemical properties of electrosprayed droplets in mass spectrometry. It is well known that small droplets provide increased analyte ionization efficiencies6–8 and salt tolerances,9,10 which in turn have aided in the development of low flow rate ionization techniques such as nanoelectrospray11,12 and picoelectrospray ionization.13 Other experiments have used both neutral and charged droplets as microvessels to accelerate different types of chemical reactions.14–19 Possessing a fundamental understanding of droplet size is required to further explore and understand the utility of small droplets.Several different types of instruments have been developed for determining the sizes of electrosprayed droplets and aerosols,20,21 including aerodynamic particle sizers,22–24 differential mobility spectrometers,24–27 and phase-Doppler anemometers (PDA).28–34 PDA is arguably the most widely used for directly analyzing electrosprayed droplets larger than the diffraction limit of light. In PDA, a droplet travels through an interference pattern created by two lasers and scatters light at a beat frequency proportional to its velocity.35 Multiple detectors are used to detect phase differences in the beat frequency. These differences, along with spatial elements of the experimental arrangement, are used to calculate the droplet's diameter. PDA has been used to measure the sizes and velocities of both conventionally electrosprayed30 and paper sprayed droplets.32 Additionally, Beauchamp et al. used a modified PDA setup to measure the size and charge of a droplet over the droplet's lifetime.36 Their results showed that droplets shrank in size primarily due to solvent evaporation while Coulombic fission events were the primary cause of charge loss.
One of the first experiments to measure sub-diffraction limit sized electrospray droplets was performed by Chen et al.25 In this study, electrosprayed droplets containing sucrose were charge reduced and allowed to undergo complete desolvation, resulting in the formation of sucrose aggregates. A scanning mobility particle sizer was used to measure the sizes of the sucrose aggregates, which indirectly provided size measurements of the droplets which produced those aggregates. Using this method, information about droplets as small as 4 nm in diameter was inferred. Davidson et al. recently used this method to show that large droplets exhibit a much greater amount of nonspecific protein aggregation than small droplets due to the total number of protein molecules present in different sized droplets.27 Williams and coworkers10 generated very small droplets and showed that this removed deleterious effects of buffers by reducing the number of salt ions in any one droplet, even though the number of droplets containing analyte decreased sharply.
Studies performed over fifteen years ago by Ku et al. demonstrated that transmission electron microscopy (TEM) can be used to measure the sizes of electrosprayed droplets.37 The authors electrosprayed glycerol containing high concentrations of sodium iodide onto a TEM grid and subsequently froze the deposited droplets before insertion into the TEM chamber. Most of the droplets sprayed from a 100 μm I.D. fused silica capillary were between 200 and 500 nm in diameter. While their results agreed well with comparative aerodynamic particle sizer measurements performed on larger droplets, the authors noted that droplets consisting primarily of glycerol may not reflect the true size distributions of droplets consisting of more conventional organic spray solvents.
Presented here is the first super resolution fluorescence microscopy-based method for measuring sub-diffraction limit sized charged droplets. These experiments were performed to measure: (1) electrosprayed droplets smaller than the diffraction limit of light, (2) droplets with a wide range of sizes, and (3) the radial distribution of droplets in an electrospray plume. To the best of our knowledge, no current technique can simultaneously address all three of these tasks using relatively simple and easy to access instrumentation. Since super resolution fluorescence microscopy is commercially available, 3D structured illumination microscopy (3D-SIM) was selected as the technique for performing all these tasks. Droplets produced from both paper spray and nanoelectrospray ionization sources were imaged and compared. A custom algorithm in Matlab was developed and used to measure the sizes of deposited droplets down to 200 nm in diameter. The technique facilitates a deeper understanding of the droplet size distributions produced by different electrospray ionization sources while providing a simple, intuitive means to do so.
Experimental details
Microscopy
Super resolution images of droplets were acquired using a Nikon Ti-E super resolution microscope (Nikon Instruments Inc., NY, USA). The microscope was operated in 3D structured illumination microscopy (SIM) mode to obtain resolution twice that obtainable by conventional microscopes.38 Briefly, SIM is performed by placing a grid possessing a known pattern in front of a sample and illuminating both. This will cause images to contain interference patterns in the form of moiré fringes. By translating and rotating the grid, different orientations of the moiré fringes can be obtained. Each moiré fringe orientation contains high spatial frequency information about the original sample and can be deconvolved with all the other images to produce a resolution-enhanced image. In the experiments performed here, the light source was a 561 nm laser. It was possible to achieve a total magnification of 250× by combining a 100×, oil-based objective (Nikon Apo TIRF 100×/1.49, Nikon Instruments Inc., NY, USA) with a supplemental 2.5× focusing lens located between the objective and a CCD detector (Model iXon Ultra 897, Andor, Belfast, UK) (Fig. 1). The microscope's 2D motorized stage was used to image different sections of the microscope slide. The field of view of each section was 32.8 × 32.8 mm. Images of droplet residues were brought into focus using Nikon's ‘Perfect Focus’ usually followed by a small z-offset adjustment. The electron multiplier on the camera was turned off to minimize background noise. To compensate for the reduction in signal, a high concentration of fluorescent compound was used. Droplet agglomeration studies were performed on a Nikon TiS inverted confocal microscope (Nikon Instruments Inc., NY, USA) which utilized a 60× objective (Plan Apo VC 60× Oil DIC N2, Nikon Instruments Inc., NY, USA) and a CCD camera (QuantEM:512SC, Photometrics, AZ, USA) operating at 15 fps.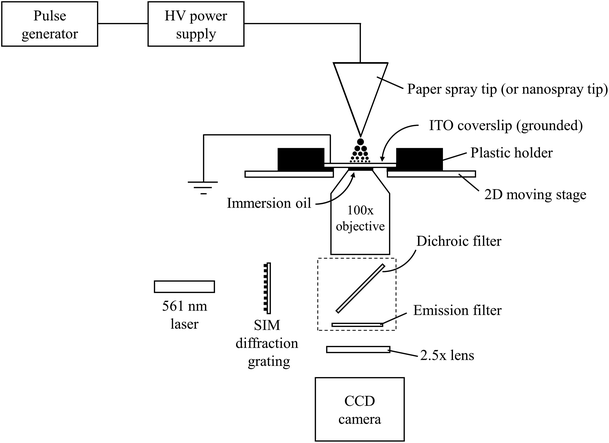 | ||
| Fig. 1 Schematic of the experimental setup used for measuring the sizes of electrosprayed droplets by 3D structured illumination microscopy. | ||
Chemicals and materials
Spray solutions consisted of 100 μM rhodamine B in glycerol and 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol
1 methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol. Rhodamine B and glycerol were purchased from Sigma (MO, USA) and methanol from Fisher Chemical (NJ, USA). Paper spray triangles were cut from Whatman #1 paper using regular scissors. Nanoelectrospray emitters with outer diameters of between 5 and 20 μm were pulled from borosilicate glass capillaries (0.86 mm i.d., Sutter Instruments, CA, USA) using a micropipette puller (Model P-97, Sutter Instruments, CA, USA). Tip outer diameters were measured by eye using a Kronos light microscope fitted with a scale bar. The error in all tip outer diameters was ±0.5 μm. In all nanoelectrospray experiments, a 0.51 mm platinum 10% iridium wire (California Fine Wire Company, CA, USA) supplied voltage to the solutions. Grounded indium-tin-oxide (ITO) microscope coverslips (∼0.16 mm thickness, NanoCS, NY, USA) were placed into contact with the objective and used as droplet deposition surfaces. Each ITO slide was sonicated in acetone and methanol to remove organic residue contaminants and stored in a dessicator prior to analysis. The fluorescent nanoparticles (Spherotech, IL, USA) used in this study possessed nominal diameters of 0.25, 0.53, and 0.84 μm. The particles were made from polystyrene and contained Nile red as the indicator dye. Each nanoparticle standard was diluted 1000× in water and stored in an amber vial to minimize degradation. Manufacturer reported distributions of the nanoparticles are described later.
glycerol. Rhodamine B and glycerol were purchased from Sigma (MO, USA) and methanol from Fisher Chemical (NJ, USA). Paper spray triangles were cut from Whatman #1 paper using regular scissors. Nanoelectrospray emitters with outer diameters of between 5 and 20 μm were pulled from borosilicate glass capillaries (0.86 mm i.d., Sutter Instruments, CA, USA) using a micropipette puller (Model P-97, Sutter Instruments, CA, USA). Tip outer diameters were measured by eye using a Kronos light microscope fitted with a scale bar. The error in all tip outer diameters was ±0.5 μm. In all nanoelectrospray experiments, a 0.51 mm platinum 10% iridium wire (California Fine Wire Company, CA, USA) supplied voltage to the solutions. Grounded indium-tin-oxide (ITO) microscope coverslips (∼0.16 mm thickness, NanoCS, NY, USA) were placed into contact with the objective and used as droplet deposition surfaces. Each ITO slide was sonicated in acetone and methanol to remove organic residue contaminants and stored in a dessicator prior to analysis. The fluorescent nanoparticles (Spherotech, IL, USA) used in this study possessed nominal diameters of 0.25, 0.53, and 0.84 μm. The particles were made from polystyrene and contained Nile red as the indicator dye. Each nanoparticle standard was diluted 1000× in water and stored in an amber vial to minimize degradation. Manufacturer reported distributions of the nanoparticles are described later.
Electrospray ionization
Both paper sprayed and nanoelectrosprayed droplets were analyzed in this study. A single electrospray pulse was used instead of continuous sprays to decrease the number of droplets produced and minimize the chances of droplet agglomeration on the surface. High voltage pulses were produced from a high voltage power supply (Model 610E-G-CE, Trek Inc., NJ, USA) connected to a waveform generator (Model AFG 3022, Tektronix, OR, USA). The voltages used for nanoelectrospray and paper spray were 3 and 5 kV, respectively. The distance between the tip of the emitter and the surface was varied between three and seven millimeters to obtain different droplet size distributions. The duration of the high voltage pulses was varied between 10 and 30 ms. Pulses longer than 30 ms were not used because significant droplet agglomeration tended to occur. A video of a 500 ms pulse was taken to showcase the extent of droplet agglomeration when using long pulses (Video 1†). The pulse in this experiment was generated using a piezoelectric discharge gun (Zerostat3, Tedpella, CA). The spray emitters were mounted on a precision stage and could be moved from the initial measurement site with sub-100 micron precision. Initial tip-to-surface distance measurements were performed by placing the tip of the spray emitter level with the top of the microscope slide holder, which was 2.8 ± 0.1 mm away from the microscope slide surface. This measurement was done by eye. The spray emitter was then moved to a desired value. Even if the initial distance measurement was slightly in error, the differences between any distances measured after the initial one were small.Results and discussion
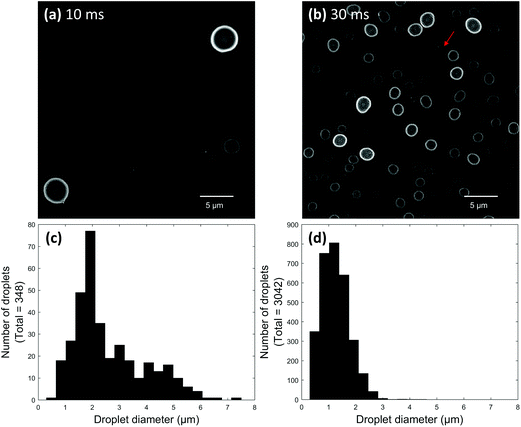
Initial electrospray experiments were performed using paper spray ionization. Fig. 2a and b show two super resolution images of droplets produced after paper spraying glycerol for 10 and 30 ms, respectively. Glycerol was used to ensure droplets did not evaporate after being deposited. Both images were acquired on the same day and represent droplets located at the center of the spray plume. The tip-to-surface distance was 3–4 mm in each experiment. For any given location on the microscope slide, the 10 ms spray pulse showed between 3 and 30 deposited droplets, while the 30 ms spray pulse showed upwards of 125 deposited droplets. Most droplets showed a high degree of circularity. Non-circular droplets or suspected agglomerates (e.g.Fig. 2b arrow) were avoided as much as possible to prevent incorrect size measurements. It is important to note that the circles in the images shown here represent the circular cross sections of the parts of the droplets directly in contact with the microscope slide. Individual droplet size distributions were generated for both pulse duration experiments by acquiring several frames at each pulse duration and added together to give a distribution for the respective pulse duration (Fig. 2c and d). For example, 55 frames were acquired for the 10 ms pulse duration experiment. These 55 frames were added together to give a distribution for the 10 ms pulse experiment. Then, in the 30 ms pulse experiment, droplets were collected on a new microscope slide and 20 frames were acquired. These 20 frames were added together to give a distribution for the 30 ms pulse experiment. The total number of frames acquired depended on the average number of droplets per image. Since each frame in the 10 ms experiment contained 6 droplets on average compared to the 159 droplets per frame in the 30 ms experiment, more frames were acquired for the 10 ms experiment to give a more representative distribution.After comparing the two paper spray pulse duration experiments, most droplets were found to possess diameters between about 500 nm and 2 μm. Some droplets greater than 5 μm in diameter were also observed for the 10 ms pulse. The sizes of the glycerol-containing droplets measured here compare reasonably well to PDA studies of droplets containing 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 water
1 water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) methanol which were paper sprayed using 3–4 mm probe distances.32 This seems to suggest that surface wetting did not cause the size measurements of droplets on the microscope slide surface to be significantly different than the corresponding air-based measurements. Interestingly, droplets produced by the 30 ms pulse seemed to be slightly smaller on average compared to droplets produced by the 10 ms pulse. This difference might be artefactual because a significantly lower overall number of droplets were produced from the 10 ms pulse, which limited the total number of droplets that could be counted for this pulse duration. Alternatively, droplets generated using shorter pulses might simply be slightly larger than droplets generated by longer pulses. This hypothesis could be extended to mean there is a difference between droplet sizes in pulsed and continuous electrosprays. This topic will be explored in detail in the future.
methanol which were paper sprayed using 3–4 mm probe distances.32 This seems to suggest that surface wetting did not cause the size measurements of droplets on the microscope slide surface to be significantly different than the corresponding air-based measurements. Interestingly, droplets produced by the 30 ms pulse seemed to be slightly smaller on average compared to droplets produced by the 10 ms pulse. This difference might be artefactual because a significantly lower overall number of droplets were produced from the 10 ms pulse, which limited the total number of droplets that could be counted for this pulse duration. Alternatively, droplets generated using shorter pulses might simply be slightly larger than droplets generated by longer pulses. This hypothesis could be extended to mean there is a difference between droplet sizes in pulsed and continuous electrosprays. This topic will be explored in detail in the future.
All super resolution images were analyzed by a modified spot detection algorithm in Matlab. The detection process is demonstrated here using an image of paper sprayed glycerol droplets (30 ms pulse). Raw intensity images obtained from the microscope (Fig. 3a) were normalized until spots were easily distinguishable from the background (Fig. 3b). The normalization values for each image were manually chosen based on the intensity distribution of the droplets in each frame. Droplets which were spherical, sufficiently bright, and within specific size ranges were detected by a circular Hough transformation (imfindcircles function) in Matlab. Circular Hough transformations essentially work by iteratively constructing circles of different diameters around a circle in an image and then using a voting procedure to determine which circle fits the best. Droplets which were either non-spherical or low in intensity were not considered. When the droplets in an image possessed a narrow range of sizes, only a single transformation was used for analysis. If an image contained droplets with a wide range of sizes, the range was subdivided into smaller size ranges and multiple Hough transformations were used (Fig. 3c). This was done to help the algorithm detect both low intensity and closely spaced droplets as well as provide the most accurate size measurements possible. An example of using a different number of transformations on an image of paper sprayed droplets is given in the ESI (Fig. S1†). The figure shows that using a larger number of transformations is required to accurately size large ranges of droplet sizes. However, when multiple transformations were employed, the transformations used to analyze small droplets routinely and incorrectly assigned small droplets to areas inside or around the peripheries of larger droplets. An overlap removal tool was used to eliminate these incorrect assignments by first determining if two or more circles overlapped by a user-defined number of pixels, which was almost always 1 pixel. If any circles did overlap, the algorithm then kept the circle possessing the most votes and deleted all the smaller ones (Fig. 3d). A few correctly identified droplets were usually discarded in the overlap removal process. It is important to note that the program was only used to detect droplets larger than 200 nanometers to prevent the detection of background noise even though the theoretical resolution limit for SIM is about 100 nm.38
To test the algorithm's accuracy, standard fluorescent nanoparticles with different nominal diameters (0.25, 0.53, and 0.84 μm) were prepared on separate microscope slides and analyzed (Fig. S2†). The algorithm measured nanoparticle diameters of 0.27 ± 0.04 μm, 0.53 ± 0.07 μm, and 0.89 ± 0.10 μm (mean ± 1 std. dev). Photographs of the manufacturer's specifications are given in the ESI† for the 0.25 and 0.53 μm nominal diameter nanoparticles (Fig. S3 and S4†). A value of 0.84 ± 0.02 μm was given by the manufacturer for the largest set of nanoparticles tested, but no distribution was provided. As can be seen from Fig. S2–S4,† the distributions of nanoparticle diameters measured using this method are well within manufacturer specifications. Additionally, most images were resized prior to analysis. This was done to improve the detection algorithm's accuracy and ability to detect small droplets. The effect of resizing an image by factors of one, two, and three is given in the ESI† using an image of 0.84 μm diameter nanoparticles (Fig. S5†). A greater number of droplets was detected in resized images compared to non-resized; however, resized images usually required longer analysis times.
As stated earlier, all images were normalized prior to analysis depending on the intensity distribution of the droplets in the image. This was done primarily to allow the user interpreting the data to visualize all the droplets present in an image and select appropriate processing parameters, such as transformation sensitivities. However, since every image required a slightly different set of normalization values, an experiment was performed to test the effect of normalizing an image on the accuracy of the program. An image containing 0.53 μm nominal diameter nanoparticles was analyzed using various normalization values (Fig. S6†). Depending on the normalization values chosen, images could be made brighter or darker by changing the higher or lower normalization value, respectively (Fig. S6a–S6e†). A single Hough transformation with an optimized sensitivity factor was used to analyze each image. As can be seen, roughly the same number of particles were detected in each image (Fig. S6f–S6j†) and the droplet size distributions acquired at each set of normalization values showed that the accuracy of the algorithm was independent of the normalization values when optimal conditions were selected (Fig. S6k–S6o†). The default normalization values outputted by the microscope software, demonstrated in Fig. S6c† in this example, were typically used for analysis.
Many electrospray solutions are prepared using some amount of organic solvent to reduce the surface tension of the spray solution and to help dissolve analytes. The effect of organic composition on droplet size was evaluated by paper spraying a 100 μM solution of rhodamine B in 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol
1 methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
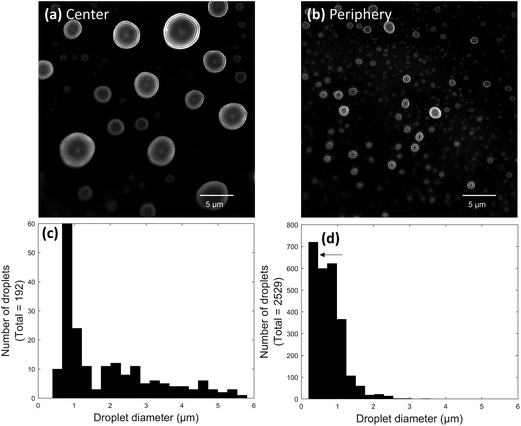
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol for 30 ms at a 3.5 ± 0.5 mm tip-to-surface distance. A low concentration of glycerol was used in the spray solvent to help droplets maintain their shape when they landed on the surface. Images of the center and periphery of a paper spray plume were acquired from different parts of the same slide (Fig. 4a and b). Clear differences could be seen in the images. The center of the spray plume contained a wide range of droplet sizes, many of which were larger than 1.5 μm in diameter (Fig. 4c). It is possible that some of the largest droplets in the paper spray plume center were agglomerated, though once again, the diameters measured here still compared well with PDA results, even though the PDA results were acquired using 1
glycerol for 30 ms at a 3.5 ± 0.5 mm tip-to-surface distance. A low concentration of glycerol was used in the spray solvent to help droplets maintain their shape when they landed on the surface. Images of the center and periphery of a paper spray plume were acquired from different parts of the same slide (Fig. 4a and b). Clear differences could be seen in the images. The center of the spray plume contained a wide range of droplet sizes, many of which were larger than 1.5 μm in diameter (Fig. 4c). It is possible that some of the largest droplets in the paper spray plume center were agglomerated, though once again, the diameters measured here still compared well with PDA results, even though the PDA results were acquired using 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 water
1 water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) methanol. In contrast, almost all the droplets at the periphery of the paper spray plume were smaller than 1.5 μm in diameter (Fig. 4d). Interestingly, the largest bin in Fig. 4d contained droplets ranging from ∼0.23 to 0.45 μm in diameter (Fig. 4d arrow). The unexpected height of this bin seems to indicate the presence of a second distribution of sub-200 nm diameter droplets. This would be consistent with PDA measurements of paper spray droplet sizes,32 however, droplets at still smaller sizes would be too small to accurately measure using this method in its current state.
methanol. In contrast, almost all the droplets at the periphery of the paper spray plume were smaller than 1.5 μm in diameter (Fig. 4d). Interestingly, the largest bin in Fig. 4d contained droplets ranging from ∼0.23 to 0.45 μm in diameter (Fig. 4d arrow). The unexpected height of this bin seems to indicate the presence of a second distribution of sub-200 nm diameter droplets. This would be consistent with PDA measurements of paper spray droplet sizes,32 however, droplets at still smaller sizes would be too small to accurately measure using this method in its current state.
3D SIM was also used to analyze droplets produced by nanoelectrospray ionization. An initial study was performed to evaluate the effect of glycerol concentration on droplet size. Experiments were performed using solutions of 1 mM rhodamine B in three different ratios of methanol and glycerol: 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 1
1, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
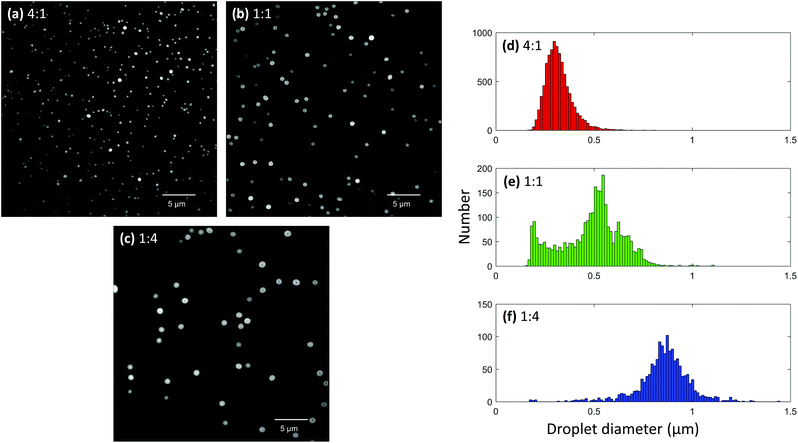
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4. Each solution was loaded into a 5 μm sized nanoelectrospray tip and deposited onto a coverslip from a 3 mm distance using a 20 ms pulse duration. After acquiring images using the different glycerol concentrations, it was possible to see clear differences in droplet sizes (Fig. 5a–c). Smaller droplets were observed with higher concentrations of methanol, and conversely, larger droplets were observed with higher concentrations of glycerol. This makes sense since glycerol has a much higher surface tension than methanol and should produce larger droplets. Droplet size distributions were generated for each solvent composition using 28, 20, and 29 frames for the 4
4. Each solution was loaded into a 5 μm sized nanoelectrospray tip and deposited onto a coverslip from a 3 mm distance using a 20 ms pulse duration. After acquiring images using the different glycerol concentrations, it was possible to see clear differences in droplet sizes (Fig. 5a–c). Smaller droplets were observed with higher concentrations of methanol, and conversely, larger droplets were observed with higher concentrations of glycerol. This makes sense since glycerol has a much higher surface tension than methanol and should produce larger droplets. Droplet size distributions were generated for each solvent composition using 28, 20, and 29 frames for the 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 1
1, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 methanol
4 methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol solvent ratios, respectively. As can be seen, the solution containing a high amount of methanol exhibited a maximum near 300 nm (Fig. 5d) while the solution containing a high glycerol content exhibited a maximum near 870 nm (Fig. 5f). Interestingly, the 1
glycerol solvent ratios, respectively. As can be seen, the solution containing a high amount of methanol exhibited a maximum near 300 nm (Fig. 5d) while the solution containing a high glycerol content exhibited a maximum near 870 nm (Fig. 5f). Interestingly, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol
1 methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol solution exhibited a bimodal distribution of droplet diameters with maxima at approximately 195 and 550 nm (Fig. 5e). It is possible that the maximum at 195 nm was the result of progeny droplets created from Coulombic explosion events. However, it should be noted that the experiment is not entirely accurate for droplets smaller than about 200 nm in diameter in its current state, and thus further optimization is needed to fully validate this bimodal effect.
glycerol solution exhibited a bimodal distribution of droplet diameters with maxima at approximately 195 and 550 nm (Fig. 5e). It is possible that the maximum at 195 nm was the result of progeny droplets created from Coulombic explosion events. However, it should be noted that the experiment is not entirely accurate for droplets smaller than about 200 nm in diameter in its current state, and thus further optimization is needed to fully validate this bimodal effect.
Glycerol was used in these experiments to minimize the effect of droplet evaporation after deposition. A study was performed to test if any significant droplet evaporation occurred over the course of an experiment. In one experiment, the sizes of nanosprayed droplets in one frame were monitored as a function of time while the laser constantly illuminated the droplets (Fig. S7,† blue trace). As can be seen, the average droplet diameter decreased when droplets were constantly exposed to the laser. However, glycerol should not evaporate at room temperature and pressure. This result likely suggests that photobleaching contributes to the degradation of sample intensity during continuous laser illumination. In a second experiment, another time study was performed for nanosprayed droplets, except this time the laser was only turned on during image acquisition (Fig. S7,† red trace). The average droplet diameter in this experiment did not seem to change significantly for 5 minutes, suggesting that the droplets were not greatly affected by photobleaching or solvent evaporation. The second experiment is more representative of how all the experiments presented herein were performed as the laser does not constantly illuminate the entire slide all at once, only a small section. It should be noted that the only data analysis parameters adjusted in these experiments were the normalization values.
Another set of nanoelectrospray ionization experiments was performed to evaluate how the voltage applied to a nanoelectrospray emitter affects droplet size. A 1 mM solution of rhodamine B in 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 methanol
1 methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycerol was loaded into a 5 μm nanoelectrospray emitter and sprayed from a 3 mm distance using a 20 ms pulse. The same emitter was used for all voltage experiments. Voltages of 1.5, 2.0, 2.5, and 3.0 kV were tested. Interestingly, the average droplet diameter shrank with increasing voltage (Fig. 6). Droplets produced from a 1.5 kV pulse showed a rather broad distribution centered at about 335 nm (Fig. 6a). As the voltage was increased to 2.0 kV, a bimodal distribution of droplets appeared with maxima a smaller at 227 and a larger maximum at 410 nm (Fig. 6b). Although the maximum at 227 nm is again likely caused by the presence of progeny droplets, the maximum at 410 nm was unexpectedly larger than the maximum obtained for the 1.5 kV experiment. When the voltage was increased to 2.5 kV, the average droplet diameter again decreased and showed maxima of relatively equal heights at 292 and 463 nm (Fig. 6c). A final voltage of 3 kV yielded droplets centered around 220 nm in diameter (Fig. 6d). These results were somewhat unexpected because higher voltages tend to deplete solution more quickly than lower voltages, meaning that flow rate is surely increased with increasing voltage. A flow rate study was conducted using 5, 10, and 20 μm o.d. nanoelectrospray tips and showed that droplet sizes do increase with increasing flow rate (Fig. S8†). However, the set of voltage data shown here seems to suggest that the decrease in droplet size due to higher voltages is more prominent than the increase in droplet size that is gained from an increase in flow rate. The decrease in droplet size can be rationalized by considering that the use of higher voltages allows the surface tension of the solution to be overcome more easily than with lower voltages, which produces smaller initial sized droplets.
glycerol was loaded into a 5 μm nanoelectrospray emitter and sprayed from a 3 mm distance using a 20 ms pulse. The same emitter was used for all voltage experiments. Voltages of 1.5, 2.0, 2.5, and 3.0 kV were tested. Interestingly, the average droplet diameter shrank with increasing voltage (Fig. 6). Droplets produced from a 1.5 kV pulse showed a rather broad distribution centered at about 335 nm (Fig. 6a). As the voltage was increased to 2.0 kV, a bimodal distribution of droplets appeared with maxima a smaller at 227 and a larger maximum at 410 nm (Fig. 6b). Although the maximum at 227 nm is again likely caused by the presence of progeny droplets, the maximum at 410 nm was unexpectedly larger than the maximum obtained for the 1.5 kV experiment. When the voltage was increased to 2.5 kV, the average droplet diameter again decreased and showed maxima of relatively equal heights at 292 and 463 nm (Fig. 6c). A final voltage of 3 kV yielded droplets centered around 220 nm in diameter (Fig. 6d). These results were somewhat unexpected because higher voltages tend to deplete solution more quickly than lower voltages, meaning that flow rate is surely increased with increasing voltage. A flow rate study was conducted using 5, 10, and 20 μm o.d. nanoelectrospray tips and showed that droplet sizes do increase with increasing flow rate (Fig. S8†). However, the set of voltage data shown here seems to suggest that the decrease in droplet size due to higher voltages is more prominent than the increase in droplet size that is gained from an increase in flow rate. The decrease in droplet size can be rationalized by considering that the use of higher voltages allows the surface tension of the solution to be overcome more easily than with lower voltages, which produces smaller initial sized droplets.
Conclusions
The experiments described here have demonstrated that super resolution fluorescence microscopy can be used to measure the sizes of electrosprayed droplets with improved resolution over conventional methods, down to 200 nm. Despite the addition of glycerol, the results measured for paper sprayed droplets, between 0.5–2 μm, matched reasonably well with the results measured without glycerol. The droplets produced by nanoelectrospray ionization were almost all smaller than 1 μm in diameter. Nanoelectrosprayed droplets increased in size with a corresponding increase in glycerol concentration due to an increase in average solution surface tension. Droplets decreased in size with an increase in applied voltage, suggesting that the decrease in droplet size due to a high voltage overcoming the surface tension of the solution is more prominent than the increase in flow rate that would otherwise cause an increase in droplet size. It should be noted that the conclusions drawn here are only valid for droplets produced from pulsed electrosprays. Although a pulsed duration study was performed to try and observe the effects of pulse duration on droplet size, more thorough study is needed to determine how the droplets produced from a continuously spraying electrospray source correlate to droplets produced from pulsed electrospray sources. It might be possible to further optimize this method by using dyes with shorter emission wavelengths than rhodamine B to probe below the 200 nm diameter cutoff used here. In the future, one application for this technique is to investigate the extent to which chemical reactions are accelerated in sub-micron sized electrospray droplets.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This material is based upon work supported by the United States Department of Energy, Office of Science, Office of Basic Energy Sciences, Separations and Analysis Program, under Award DE-FG02-06ER15807. The authors acknowledge the use of the facilities of the Bindley Bioscience Center, a core facility of the NIH-funded Indiana Clinical and Translational Sciences Institute. Adiv A. Johnson and Adriaan de Feijter from Nikon Instruments are acknowledged for their aid in operating the super resolution microscope's software. James Francis from Photometrics is acknowledged for help in optimizing the CCD camera.References
- J. Zeleny, Phys. Rev., 1914, 3, 69–91 CrossRef.
- G. Taylor, Proc. R. Soc. London, Ser. A, 1964, 280, 383 CrossRef.
- M. Wilm, Mol. Cell. Proteomics, 2011, 10, M111.009407 Search PubMed.
- S. Banerjee and S. Mazumdar, Int. J. Anal. Chem., 2012, 2012, 40 Search PubMed.
- L. Konermann, E. Ahadi, A. D. Rodriguez and S. Vahidi, Anal. Chem., 2013, 85, 2–9 CrossRef CAS PubMed.
- A. Schmidt, M. Karas and T. Dülcks, J. Am. Soc. Mass Spectrom., 2003, 14, 492–500 CrossRef CAS PubMed.
- A. El-Faramawy, K. W. M. Siu and B. A. Thomson, J. Am. Soc. Mass Spectrom., 2005, 16, 1702–1707 CrossRef CAS PubMed.
- J. T. Cox, I. Marginean, R. D. Smith and K. Tang, J. Am. Soc. Mass Spectrom., 2015, 26, 55–62 CrossRef CAS PubMed.
- R. Juraschek, T. Dülcks and M. Karas, J. Am. Soc. Mass Spectrom., 1999, 10, 300–308 CrossRef CAS PubMed.
- A. C. Susa, Z. Xia and E. R. Williams, Anal. Chem., 2017, 89, 3116–3122 CrossRef CAS PubMed.
- M. S. Wilm and M. Mann, Int. J. Mass Spectrom. Ion Processes, 1994, 136, 167–180 CrossRef CAS.
- M. Wilm and M. Mann, Anal. Chem., 1996, 68, 1–8 CrossRef CAS PubMed.
- I. Marginean, K. Tang, R. D. Smith and R. T. Kelly, J. Am. Soc. Mass Spectrom., 2014, 25, 30–36 CrossRef CAS PubMed.
- T. Müller, A. Badu-Tawiah and R. G. Cooks, Angew. Chem., Int. Ed., 2012, 51, 11832–11835 CrossRef PubMed.
- R. M. Bain, C. J. Pulliam, X. Yan, K. F. Moore, T. Muller and R. G. Cooks, J. Chem. Educ., 2014, 91, 1985–1989 CrossRef CAS.
- R. M. Bain, C. J. Pulliam and R. G. Cooks, Chem. Sci., 2015, 6, 397–401 RSC.
- R. M. Bain, C. J. Pulliam, S. T. Ayrton, K. Bain and R. G. Cooks, Rapid Commun. Mass Spectrom., 2016, 30, 1875–1878 CrossRef CAS PubMed.
- E. A. Crawford, C. Esen and D. A. Volmer, Anal. Chem., 2016, 88, 8396–8403 CrossRef CAS PubMed.
- R. M. Bain, S. T. Ayrton and R. G. Cooks, J. Am. Soc. Mass Spectrom., 2017, 28, 1359–1364 CrossRef CAS PubMed.
- D. C. Taflin, T. L. Ward and E. J. Davis, Langmuir, 1989, 5, 376–384 CrossRef CAS.
- E. J. Davis and M. A. Bridges, J. Aerosol Sci., 1994, 25, 1179–1199 CrossRef CAS.
- A. Hirabayashi and J. Fernández de la Mora, Int. J. Mass Spectrom. Ion Processes, 1998, 175, 277–282 CrossRef CAS.
- B. K. Ku and S. S. Kim, J. Aerosol Sci., 2002, 33, 1361–1378 CrossRef CAS.
- T. Musapelo and K. K. Murray, Anal. Chem., 2011, 83, 6601–6608 CrossRef CAS PubMed.
- D.-R. Chen, D. Y. H. Pui and S. L. Kaufman, J. Aerosol Sci., 1995, 26, 963–977 CrossRef CAS.
- F. Cao, F. Donnarumma and K. K. Murray, Analyst, 2016, 141, 183–190 RSC.
- K. L. Davidson, D. R. Oberreit, C. J. Hogan Jr. and M. F. Bush, Int. J. Mass Spectrom., 2017, 420, 35–42 CrossRef CAS.
- Z. Olumee, J. H. Callahan and A. Vertes, J. Phys. Chem. A, 1998, 102, 9154–9160 CrossRef CAS.
- A. Venter, P. E. Sojka and R. G. Cooks, Anal. Chem., 2006, 78, 8549–8555 CrossRef CAS PubMed.
- P. Nemes, I. Marginean and A. Vertes, Anal. Chem., 2007, 79, 3105–3116 CrossRef CAS PubMed.
- A. Wortmann, A. Kistler-Momotova, R. Zenobi, M. C. Heine, O. Wilhelm and S. E. Pratsinis, J. Am. Soc. Mass Spectrom., 2007, 18, 385–393 CrossRef CAS PubMed.
- R. D. Espy, A. R. Muliadi, Z. Ouyang and R. G. Cooks, Int. J. Mass Spectrom., 2012, 325–327, 167–171 CrossRef CAS.
- R. Wang, A. J. Gröhn, L. Zhu, R. Dietiker, K. Wegner, D. Günther and R. Zenobi, Anal. Bioanal. Chem., 2012, 402, 2633–2643 CrossRef CAS PubMed.
- J. Majewski, Electr. Rev., 2013, R. 89(3b), 300–302 Search PubMed.
- F. Onofri, T. Girasole, G. Gréhan, G. Gouesbet, G. Brenn, J. Domnick, T. H. Xu and C. Tropea, Part. Part. Syst. Charact., 1996, 13, 112–124 CrossRef CAS.
- J. N. Smith, R. C. Flagan and J. L. Beauchamp, J. Phys. Chem. A, 2002, 106, 9957–9967 CrossRef CAS.
- B. K. Ku, S. S. Kim, Y. D. Kim and S. Y. Lee, J. Aerosol Sci., 2001, 32, 1459–1477 CrossRef CAS.
- M. G. L. Gustafsson, J. Microsc., 2000, 198, 82–87 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7an01278k |
| This journal is © The Royal Society of Chemistry 2018 |