Water transport confined in graphene oxide channels through the rarefied effect†
Abstract
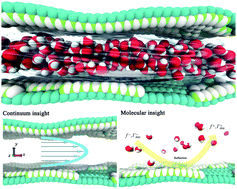
Understanding the mechanism of water transport inside an interlayer between graphene-based plates has tremendous value for theoretical studies and industrial applications. The fluid flow confined in nano-scaled spaces experiences a slip velocity near the wall, which is significantly different to that of bulk water. Here we propose a model combining classic hydrodynamics with kinetic theory to depict the dependency of the slip effect on the oxide concentration of valley plates. The influence of oxidized graphene on water flow is a comprehensive result of a slipped boundary, and depends on both the diffuse reflection coefficient of the wall, and the shrunken effective passageway caused by the electrostatic interactions between the oxidized surface and the water molecules. The former effect enhances the water flow, which reduces with increasing oxide concentration, while the latter effect inhibits water flow. We examine the diffuse reflection coefficient and the shrunken effective passageway at different oxide concentrations of the GO sheets by molecular dynamics simulations, and we quantitively predict the flux relationship at various concentrations. This work provides a molecular insight into transport processes of confined water and a useful guideline for the design of perfect graphene-derived membranes for desalination.


 Please wait while we load your content...
Please wait while we load your content...