Electron and excitation energy transfers in covalently linked donor–acceptor dyads: mechanisms and dynamics revealed using quantum chemistry†
Lorenzo
Cupellini
 *,
Samuele
Giannini‡
*,
Samuele
Giannini‡
 and
Benedetta
Mennucci
and
Benedetta
Mennucci
 *
*
Dipartimento di Chimica e Chimica Industriale, University of Pisa, Via Moruzzi 3, 56124 Pisa, Italy. E-mail: Benedetta.Mennucci@unipi.it; lorenzo.cupellini@for.unipi.it
First published on 24th November 2017
Abstract
Photoinduced electron transfer (ET), hole transfer (HT), charge recombination (CR) and energy transfer (EET) are fundamental mechanisms, which occur in both natural and artificial light harvesting systems. Here, we present a computational strategy which determines ET, HT, CR and EET rates in a consistent way and merges them in a kinetic model to reproduce the net excited state dynamics. The effects of the solvent are included in all steps of the calculations making the present strategy a useful tool for a rational design of charge and energy transfer processes in complex systems. An application to covalently linked zinc and free-base porphyrin–naphthalenediimide dyads is presented. For each of the two systems, ultrafast optical spectroscopy experiments have shown a specific photophysics with different processes taking place simultaneously. The model reveals that such a diversity is mainly due to the different relative stability of the charge-separated state, while the electronic couplings for charge and energy transfer processes are quite similar in the two dyads.
1 Introduction
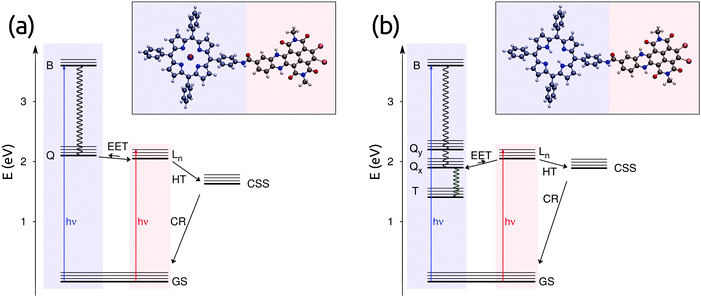
Covalently linked donor–acceptor dyads are essential model systems to understand photoinduced transport events in a controlled way. For example, model dyads can be synthesized with rigid linkers and various donor–acceptor separations, in order to study the distance dependence of energy and charge transfer.1–7 The photoinduced transport can be followed using ultrafast spectroscopic measurements, such as transient absorption (TA) spectroscopy. In many cases, the time scales of different transfer events are well separated, and the photoinduced dynamics within the dyads can be unraveled by simply analyzing the time-resolved spectroscopic measurements.6,8 However, some apparently simple dyads show very complex, excitation-dependent photophysics, where several processes occur at the same time.9–11 In all these cases, computational studies become fundamental to shed light on the photophysics by estimating the time constants of the different processes and dissecting the various possible channels.11–15Among the donor–acceptor dyads, great interest has been focused on possible materials for organic photovoltaics (OPVs),16 such as dyads based on 1,4,5,8-naphthalenediimides (NDIs). NDI compounds, also known as naphthalene carbodiimides, have attracted much attention due to their chemical characteristics, such as self-organization, and their tunable optical properties.17 NDI-based systems, bonded with different molecules, have been experimentally studied and their excited-state dynamics have been investigated.10,18–20 Yuschenko and coworkers characterized two NDI-based dyads that exhibit a rich photoinduced dynamics after excitation of either of the chromophoric units.21 These dyads are composed of zinc porphyrins (ZnP) or free-base porphyrins (FbP) as electron donors and a hydroquinoxaline-substituted bromo-NDI (HNDI) as an electron acceptor. The two moieties are connected through an essentially rigid amide bond, which allows for short interchromophore separations without altering the electronic structure of the two units (see Fig. 1).
Despite the similar structure, ZnP–HNDI and FbP–HNDI present very different excited-state photophysics, as revealed using time-resolved fluorescence and femtosecond TA experiments.21 Moreover, several processes, such as excitation energy transfer (EET), electron and hole transfers (ET and HT), as well as charge-recombination (CR), occur on similar time scales, preventing a simple interpretation of the excited-state pathways.
In this work, we established a computational protocol to describe EET, HT, ET, and CR in the two porphyrin–HNDI dyads. This protocol uses Density Functional Theory (DFT) based approaches for the calculation of the needed parameters, namely, the excitation energies, the electronic couplings and the Franck–Condon weighted density of states (FCWD), and uses a kinetic model to quantify the time scales involved in the network of charge and energy transfer processes. Diabatization schemes provide a route for computing electronic couplings taking into account the through-bond mechanism, which is a non-negligible effect in these linked systems as confirmed in this work. Marcus–Levich–Jortner's formalism is compared with the more common Marcus equation, starting from ab initio calculations of reorganization energy and driving force. Our results not only reproduce the experimental findings, but they also allow us to gain a deeper insight into the excited-state dynamics of the two investigated dyads. In particular, we highlight that both ET and HT mechanisms contribute to the charge separation in FbP–HNDI, contrary to what the authors assumed in ref. 21, i.e. charge separation occurs via ET. For the same dyad we were also able to calculate the CR rate, which, being much faster than charge separation, could not be estimated from the experiments. We found that the relative stability of the charge-separated state is of great importance, as it influences the different transfer mechanisms and the actual photophysics of the two NDI-based systems.
This paper is organized as follows. In Section 2.1, we present the computational methodologies used to obtain couplings between states participating in the transfer mechanisms. In Section 2.2 we elucidate the Frank–Condon weighted density factor accounting for the solvent effect on reorganization energy and driving force. Computational details are then reported in Section 2.3. In Section 3.1 we analyze excitation energies and coupling values and assess the influence of the covalent bond in ZnP–HNDI on the EET coupling. The rates obtained for different processes such as EET and charge transfer are reported in Sections 3.2 and 3.3 respectively. These results are used in Section 3.4 to build a kinetic model to study the effective dynamics of such systems and compare with experiments.
2 Methods
Within the weak coupling limit in the Condon approximation, all transfer processes studied in this work can be described by a second-order, nonadiabatic, perturbative treatment which gives the Fermi Golden Rule rate equation for the nonradiative transition between states |i〉 and |f〉:22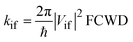 | (1) |
2.1 Excited states and electronic couplings
Excited states of the porphyrin–HNDI dyads are calculated within the TD-DFT framework in the Tamm–Dancoff approximation (TDA), including the solvent effects through the Polarizable Continuum Model (PCM).23 To describe vertical transitions, i.e. an electronic excitation or an energy/charge transfer, a non-equilibrium response is introduced in PCM, where the solvent responds only through its “fast” electronic degrees of freedom.With regard to the EET process, the electronic coupling between two moieties can be calculated, within a first-order perturbative approximation, directly from the transition densities of the noninteracting moieties. This perturbative approach was developed in the TD-DFT framework, with the assumption that the molecular orbitals can be well separated into two moieties.24 In the following we shall refer to this approach as the Direct Coupling (DC) method. Within this framework the coupling becomes:25
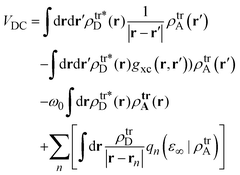 | (2) |
The DC approach needs to define separated fragments in order to compute the corresponding transition densities. As in our case the donor and acceptor are covalently bonded, we divided the dyads by cutting the single bond between the phenyl bridge and the amide nitrogen, and saturated the free valences with hydrogen atoms.26,27 This approximation is valid if the localized transitions are well separated and do not interact through the covalent bond, which cannot be excluded for this system. Finally, the DC approach can only be used for EET couplings, since the charge-transfer couplings involve states that are not localized on either the donor or the acceptor.
In order to deal with charge-transfer couplings and through-bond effects, we resort to the fragment difference diabatizaion schemes.28,29 Within this framework, an excited-state calculation on the entire system is performed to yield the adiabatic states, which are a combination of diabatic (i.e. charge- or excitation-localized) electronic states. The transformation to diabatic states is achieved through an additional operator that is diagonal for localized states. The Fragment Charge Difference (FCD)30 was introduced for the calculation of charge transfer couplings: it defines the diabatic states as those where the charge is maximally localized on either the donor or the acceptor. The operator to be used is:
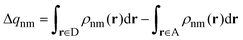 | (3) |
In analogy to the FCD method, the Fragment Excitation Difference (FED) method32 defines an operator Δx which is diagonal when the excitation is localized on either fragment. Similar to Δq, Δx is defined as:
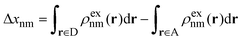 | (4) |
When degenerate or almost degenerate states are present, we report the effective coupling as the square root of the sum of all couplings involving initial and final states, that is, assuming that the degenerate states can be combined into one state maximally coupled to the final state and one uncoupled state. We assume that the uncoupled state does not participate in the observed excited-state dynamics. For example, for two degenerate initial states i1, i2 and two degenerate final states f1, f2, the effective coupling will be V2eff = V2i1,f1 + V2i1,f2 + V2i2,f1 + V2i2,f2. With this definition, the coupling Veff does not change for rotations of pairs of degenerate states.
2.2 FCWD factor and rate constants
The FCWD term of eqn (1) can assume different expressions depending on the transfer mechanism. If the nuclear degrees of freedom can be considered classical, the FCWD term reduces to the Marcus equation:22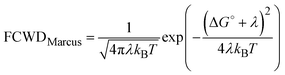 | (5) |
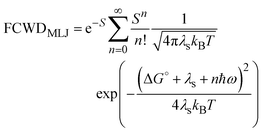 | (6) |
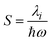 is the Huang–Rhys factor for the coupling of the charge transfer to the internal normal mode, obtained from the internal reorganization energy λi.
is the Huang–Rhys factor for the coupling of the charge transfer to the internal normal mode, obtained from the internal reorganization energy λi.
The total reorganization energy, λ = λi + λs, is usually estimated as the average of backward and forward reorganization energies (λBw and λFw,34,35 respectively). Due to the large torsion angle between the two moieties which prevents conjugation, we can safely separate the two fragments and define λBw and λFw as:34
| λBw = E(D*@D+) − E(D*@D*) + E(A@A−) − E(A@A) λFw = E(D+@D*) − E(D+@D+) + E(A−@A) − E(A−@A−) | (7) |
| −ΔGET,HT = E0–0 − (−ΔGCR) −ΔGCR = e(Eox − Ered) + ΔGS + ΔGB | (8) |
Oxidation and reduction potentials were computed as Eox(D) = E(D+@D+) − E(D@D) and Ered(A) = E(A@A) − E(A−@A−), where D is either ZnP or FbP and A is HNDI. The solvent was considered in equilibrium, as discussed in Section 2.1. Finally, the binding energy ΔGB between the two oppositely charged fragments was calculated as the electrostatic interaction between atomic charges of the D and A, scaled by the static dielectric constant ε of THF or toluene to account for the solvent screening, namely:
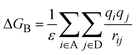 | (9) |
Moving to the EET processes, the FCWD factor is readily accessible from the experimental donor fluorescence FD(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ) and acceptor absorption AA(
) and acceptor absorption AA(![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ):
):
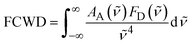 | (10) |
Once the electronic coupling and the FCWD factors for all the processes were obtained, the rates are calculated as in eqn (1) and inserted in a set of kinetic equations for the state populations Pi:
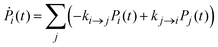 | (11) |
2.3 Computational details
All quantum chemical calculations have been performed in a locally modified version of the Gaussian 09 software.38 The two molecules ZnP–HNDI and FbP–HNDI have been modified introducing methyl instead of octyl substituents on the imide N atoms. Geometry optimizations were carried out at the B3LYP/6-31G(d) level on the entire dyads. Excited state calculations were performed on the ground-state optimized structures, employing Time Dependent DFT in the Tamm–Dancoff approximation (TDA) and using CAM-B3LYP39 as the density functional and the 6-311+G(d,p) basis set. The CAM-B3LYP functional was chosen to give a balanced description of locally excited and charge-transfer states. Other functionals (B3LYP,40 PBE0,41 and M06-2X42) and basis sets were tested, and the results are shown in the ESI.† The EET coupling values slightly decrease with increasing basis set (see Table S6 in the ESI†). For this reason, in order to reach a better convergence for the coupling values, the largest basis set was used in all the following calculations, unless otherwise stated.The two solvents, THF and toluene, included in the reference work,21 have been considered in all calculations by employing the PCM in its IEF-PCM formulation.43 The effect of the solvent has been included both in ground and excited state calculations using either an equilibrium or a non-equilibrium model as discussed in Section 2.1.
3 Results and discussion
3.1 Excitation energies and couplings
As a preliminary analysis, we computed the excitation energies of both dyads and separated fragments (see Fig. S1 and Table S1 of the ESI†). The excited states were assigned by inspecting the Natural Transition Orbitals (NTOs)44 of the transition of interest (see Section S2 in the ESI†). For both systems, the lowest transitions were assigned to the Qx and Qy bands of the porphyrins. These two states are essentially degenerate in ZnP due to the symmetry of the conjugated ring, while they split in the FbP, where the symmetry is broken by the two hydrogens replacing the Zn atom. The HNDI fragment perturbs only slightly the two structures and the Q bands remain degenerate also in ZnP–HNDI. It is worth noting that the excitation energies calculated on isolated fragments result very similar to their analogues on the entire molecules. The only difference concerns the transition assigned to the Ln excitation of the HNDI moiety, which is shifted of ca. 0.02 eV with respect to the dyads, pointing to an interaction with the corresponding fragment.We note that the CAM-B3LYP functional correctly describes the energy of the Q bands (see Table S1 in the ESI†), while the error on the Ln transition is quite large (∼0.4 eV). In order to benchmark these values, we tested different functionals and the results are reported in Table S3 of the ESI.† All tested functionals overestimate the Ln energy, with only B3LYP showing a rather good description (error of ∼0.1 eV). However, as the transition dipole magnitudes are uniform across all functionals, we can argue that the transition density of Ln is very robust despite the variability in excitation energies. As our calculations are aimed to estimating accurately electronic couplings, a good evaluation of the transition densities is the most important issue28 and we can use the CAM-B3LYP functional as a suitable method to describe these systems including their charge-transfer states.45
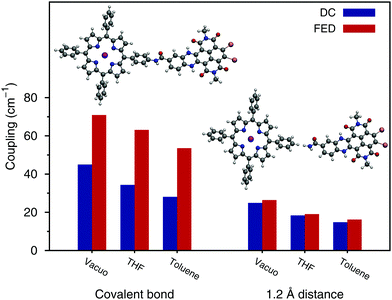
We selected the ZnP–HNDI system to assess the through-bond contribution to EET by comparing the DC and FED approaches.32 The analysis of NTOs (see Fig. S2 in the ESI†) shows that the Q states are slightly delocalized over the phenyl bridge; the cut shown in Fig. 1 was chosen so as to maximally separate the transition densities on the two chromophoric units. We considered the real covalently bonded system, as well as a model system in which the two fragments are artificially separated at a distance of 1.2 Å, cutting the covalent bond and saturating the free valences with hydrogen atoms. The resulting couplings are shown in Fig. 2, in vacuo and in solvent. Both methods predict a screening effect due to the solvent that surrounds the dyad, which decreases the EET couplings.25
When the moieties are bonded, the couplings computed with the FED are substantially larger than those computed with the DC approach. Contrary to the FED calculation, DC treats the molecular fragments separately, therefore it cannot include the effect of a covalent bond between the two moieties. The observed difference between FED and DC values could indeed arise from the presence of a covalent bond, but also from the mutual polarization of the two fragments, which is included only in the FED approach. When the two molecules are set apart at a distance of 1.2 Å, the differences between the two approaches almost completely vanish. The remaining small deviation can be ascribed to mutual polarization effects between the two fragments, whereas the large difference observed in the covalently bonded molecules can be regarded as a through-bond effect.
The through-bond contribution to the total coupling can be quantified as:
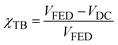 | (12) |
To gain a better understanding of the impact of through-bond effects on the coupling values in ZnP–HNDI, we analyze this contribution as a function of the dihedral angle between the chlorin ring of the ZnP and the phenyl substituent. This angle is assumed to have a quite low activation energy barrier.21 In order to avoid any spurious effect from the PCM cavity, we used in vacuo calculations for this analysis. The calculations were also performed with the smaller 6-31G+(d) basis set to reduce the computational efforts. As we want to evaluate a qualitative trend, rather than retrieving the quantitative results, those two precautions do not influence our analysis. The results are reported in Fig. 3. When the dihedral angle is more planar, the π orbitals of the phenyl become conjugated with those of the porphyrin. This increases the percentage of through-bond transfer to more than 40%. Instead, when the angle is 90 degrees, the through-bond contribution hits a minimum of 30%. At all values of the dihedral angle the Coulomb coupling remains the largest contribution, but the through-bond contribution is never negligible.
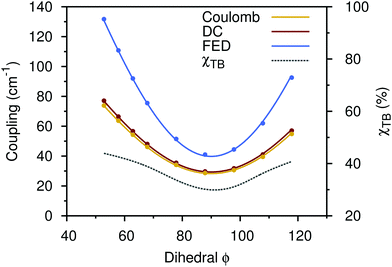 | ||
| Fig. 3 Coupling (solid lines, cm−1) and through-bond contribution (dashed line, %) with respect to the dihedral angle between the chlorin ring of ZnP–HNDI and the phenyl substituent. The FED coupling is shown (blue) along with the DC (red) and the sole Coulomb contribution (yellow). All quantities refer to in vacuo calculations (see the text). Solid colored lines represent fits of the calculated points through eqn (13). | ||
Both Coulomb and FED couplings can be fitted very well with an expression depending on the squared cosine of the dihedral angle (see Fig. 3):
V(ϕ) = V0 + β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos2(ϕ) cos2(ϕ) | (13) |
For the Coulomb coupling, this can be understood in terms of the orientational factor between transition dipoles. As the through-bond coupling depends on the extent of π-conjugation, we can expect a similar dependence on the dihedral angle. Indeed, the cos2(ϕ) dependence was found to hold experimentally for electron transfer couplings,46 singlet exciton coupling,47 and triplet transfer coupling.48 The latter case is particularly interesting since in triplet transfer the Coulomb contribution is zero.29 The triplet transfer coupling is thus a measure of the through-bond contribution, which is found to have the same torsional dependence.
3.2 EET rates
In Table 1 we report the EET couplings for both ZnP–HNDI and FbP–HNDI, calculated with FED. The excited states involved in this mechanism are the Q degenerate bands localized on the ZnP and the lower energy Qx on the FbP, as well as the Ln state of HNDI. The two dyads show quite different EET couplings, despite their structural similarity. Using the spectral overlaps obtained by Yushchenko et al. from the experimental spectra,21 we estimated the rates for the EET reactions. We report in Table 1 the transfer rates for the Q → Ln and Ln → Qx processes. These rates are in good agreement with the experiments. It is worth noting that, in spite of the smaller electronic coupling, the larger spectral overlap of the FbP–HNDI dyad compared to the ZnP–HNDI results in a similar rate to the latter. However, the FbP–HNDI spectral overlap includes both Q bands of FbP, and for this reason it could be overestimated. This might explain why the rate Ln → Qx is faster in comparison with the experiment on FbP–HNDI.| Dyad | States | THF | Toluene | ||
|---|---|---|---|---|---|
| V | τ | V | τ | ||
| ZnP–HNDI | Q → Ln | 63 | 1.4 (0.5) | 54 | 1.9 (0.5) |
| FbP–HNDI | Ln → Qx | 46 | 1.6 (2.7) | 39 | 2.2 (2.7) |
The EET processes reported in Table 1 are in equilibrium with the relative backward reactions. Considering the experimental spectral overlaps for Ln → Q and Q → Ln, of ZnP–HNDI and FbP–HNDI, respectively, the equilibrium constants are 7.4 and 86.7 in favour of Ln and Qx, respectively, for ZnP–HNDI and FbP–HNDI.
3.3 ET, HT, CR rates
As a first step for determining the rates of the charge transfer processes, we have calculated the reorganization energies λ and driving forces ΔG in both dyads as detailed in Section 2.2. The results are presented in Table 2. A realistic description of the shape of the solvent cavity and the incorporation of polarization effects allowed us to obtain a much better estimation of this parameter in comparison with the two-sphere model proposed by Marcus and based on point charges.49 Indeed, the latter model underestimates by about 30% and 20% λs in THF and in toluene respectively.| ET | HT | CR | ||||
|---|---|---|---|---|---|---|
| THF | Toluene | THF | Toluene | THF | Toluene | |
| ZnP–HNDI | ||||||
| λ i | 0.28 | 0.28 | 0.26 | 0.26 | 0.36 | 0.36 |
| λ s | 1.01 | 0.06 | 0.97 | 0.01 | 0.97 | 0.01 |
| ΔG | −0.35 | 0.13 | −0.30 | 0.18 | −1.75 | −2.23 |
| FbP–HNDI | ||||||
| λ i | 0.29 | 0.29 | 0.21 | 0.21 | 0.31 | 0.31 |
| λ s | 1.02 | 0.06 | 1.02 | 0.06 | 1.02 | 0.06 |
| ΔG | −0.08 | 0.33 | −0.23 | 0.18 | −1.82 | −2.23 |
As expected from the larger polarity, in THF, the solvent represents the main contribution to the reorganization energy, even though the internal reorganization is not negligible for these systems. By contrast, toluene gives only a small contribution. In both systems the charge-separated state in toluene is energetically much higher than the one in THF. The driving force for charge separation in toluene is positive in all cases, making the charge-separated state thermodynamically unreachable, in agreement with experimental findings.21 In addition, we observe that in THF ΔGCR < −λ, meaning that charge recombination occurs in the Marcus inverted region, whereas ET and HT occur in the direct region.
The Marcus rates for ET, HT and CR processes were calculated with eqn (5), while the Marcus–Levich–Jortner results were obtained with eqn (6). In the latter case the effective frequency of the mode coupled with the transfer was estimated from a fitting of the absorption spectra of the HNDI molecule as described in the ESI,† obtaining a frequency of 1210 cm−1.
The electronic couplings are reported in Table 3. In order to retrieve completely localized states from this approach and obtain meaningful couplings, we included more than two states in the diabatization procedure, as described in Section S5 of the ESI.†
| Dyad | Process | V | τ (Marcus) | τ (MLJ) | |
|---|---|---|---|---|---|
| ZnP–HNDI | ET | Q → CSS | 119 | 247 | 98 |
| HT | Ln → CSS | 225 | 79 | 32 | |
| CR | CSS → GS | 73 | 3.2 | 2.7 | |
| FbP–HNDI | ET | Qx → CSS | 82 | 43 × 103 | 15 × 103 |
| HT | Ln → CSS | 196 | 279 | 131 | |
| CR | CSS → GS | 68 | 5.6 | 4.1 | |
In ZnP–HNDI the charge-separated state is experimentally observed,21 rising with a time constant of 18 ps and decaying with a time constant of 7.7 ps. Our computed charge separation rates are close to the experiment but slightly slower, with the HT rate being faster than the ET rate. As the Q → Ln EET is faster than both of these rates, the charge separation starts from the Ln state of HNDI and proceeds through hole transfer. Finally, the calculated charge recombination rate is slightly overestimated with respect to the experiment. Nonetheless, the overall time scales of EET, charge separation and recombination are well reproduced by our calculation.
The charge-separated state of FbP–HNDI was only indirectly observed in transient absorption experiments.21 However, the lifetime of the FbP's Qx state shortens in THF compared to toluene. This was explained by the authors with the appearance of a new decay pathway involving the charge-separated state, which recombines much faster to the ground state.21 The charge-separation time constant was estimated to be around 10 ns by comparing the decay rates in toluene and THF. Our calculated ET time constant of ∼15 ns is in agreement with this experimental finding; however, we observe a much faster rate for the HT process. The Ln and Qx states are in equilibrium (see above), as also seen from transient absorption,21 therefore the HT pathway could contribute to the charge separation. In order to obtain a clear picture of the excited-state dynamics in this dyad, a kinetic model is discussed in the following section.
On a final note, we point out that Marcus eqn (5) always gives smaller rates than the MLJ equation, eqn (6). However, the MLJ rates are no more than three times larger than the Marcus rates. As regards the internal, discrete modes of the molecule, Marcus and MLJ equations describe two opposite temperature limits, that is, the high-temperature limit for the Marcus equation, and the zero-temperature limit for the MLJ equation. The similar order of magnitude given by the two theories indicates that the calculated rates are robust with respect to the choice of the approximation, and also to the frequency of the effective internal mode.
3.4 Time evolution of the electronic populations and comparison with the experiment
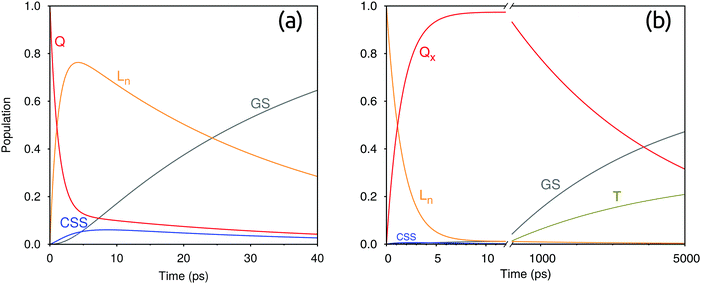
To obtain further insight into the effective excited state dynamics in the two dyads, we employed a kinetic model in the form of eqn (11) with our calculated rate constants. For this model we used the EET rates of Table 1 and the charge-transfer rates of Table 3. In the case of FbP–HNDI, we considered also the intersystem crossing (ISC) to the triplet state T, with a time constant of 14 ns as determined in ref. 21. The effective time constants obtained by solving the first order differential equations should correspond to the time constants obtained by fitting experiments with multiple exponentials. As shown in Table 4, three effective rates are found for both dyads. These rates reflect population rise and decay for the excited states considered.To assign these rates, we follow the population evolution of the two dyads reported in Fig. 4. In particular, looking at the excited-state dynamics of ZnP–HNDI in Fig. 4a, we notice that the Q states, initially populated upon excitation, transfer electronic population to the Ln state of HNDI with a time constant of 1.2 ps. The electronic population of the CSS starts rising after a few picoseconds and decays to the ground state following charge recombination. In the meantime, the electronic population of Ln decays with a time constant of 35 ps. Globally, the excited state dynamics for ZnP–HNDI is considerably fast and occurs on a picosecond time scale. The calculated effective rates are fairly close to the experiment, the largest error being on the charge recombination, whose rate is slightly overestimated by our calculations.
The excited-state dynamics of FbP–HNDI takes place on two different time scales (see Fig. 4b). The faster time scale sees the growth of the Qx state following EET from the initially excited Ln state (1.6 ps). On the slower time scale, the CSS begins to rise, but the ultrafast charge recombination consumes its population. Indeed, throughout the kinetic evolution, the CSS population remains always less than 1% of the population of the Qx/Ln states, explaining why the CSS state could not be detected from transient absorption measurements. At longer times Qx decays with a time constant of 4.4 ns, matching the rising time of the GS and the triplet state. The Qx decay rate contains both ET and HT processes, as well as the ISC. Interestingly, in FbP–HNDI, even though the first EET equilibrium is mainly towards the Qx state, the charge separation also proceeds mainly through HT from the Ln state, contrary to what was assumed in the experimental work.21
On the whole, the photophysics of FbP–HNDI in THF is captured by the kinetic model with the charge-separation decay pathway through both ET and HT. The decay rate of the Qx state only depends on the rates of the elementary ET and HT processes, as well as the Qx/Ln equilibrium constant. As long as the CR rate remains much larger than charge separation rates, the population evolution of the Qx and Ln states does not depend on the CR rate. As a consequence, this rate cannot be estimated from experiment only, unless the system is prepared in the charge-separated state. Based on our calculations, the CR rate is on the same order as in ZnP–HNDI, but slightly lower due to the larger driving force, which puts this process further into the inverted Marcus region. Moreover, as both ET and HT contribute to the charge separation, the estimated charge-separation rate cannot be directly assigned to either of these processes.
The diverse photophysics presented by the two dyads, quantitatively reproduced by the model, can be ascribed mainly to energetic factors. The electronic couplings for charge transfer processes are quite similar in the two dyads (Table 3), as can be expected from the structural similarity. However, the higher energy of the charge-separated state determines a completely different dynamics in FbP–HNDI. This suggests that the photophysics of these dyads can be drastically changed just by tuning the energy of the charge-separated state.
4 Conclusion
In this work, we have devised a computational strategy to treat the multiple transfer processes in covalently linked dyads using a consistent description allowing for a deeper understanding of the excited-state dynamics. Through this analysis, the importance of through-bond effects in the EET couplings was clearly revealed by comparing a fragment-based model (i.e. Direct Coupling) with diabatization schemes (FED and FCD models). The latter have been proven to be reliable to compute EET and charge-transfer couplings, respectively. The inclusion of the solvent through the PCM allowed us to properly account for the reorganization energy and the driving force of charge transfer. The calculated elementary transfer rates have been finally combined in a kinetic model, to retrieve effective constants, which are directly comparable with experiments.We have investigated the photoinduced energy and charge transfers characterizing the excited state dynamics of the ZnP–HNDI and FbP–HNDI dyads for which previous studies based on ultrafast spectroscopic techniques and global analysis of transient absorption21 showed the simultaneous presence of different charge and electron transfer pathways.
In agreement with the conclusions based on the experimental evidence, we have found that the excited state dynamics of ZnP–HNDI occurs on a picosecond time scale and after an EET between ZnP and HNDI, the HT from the latter fragment is the main cause for the considerable fast charge separation in such a system. In the case of FbP–HNDI, we have confirmed that the charge separation is very slow, and the following (fast) charge recombination immediately consumes the population of the charge-separated state, which cannot be detected experimentally. Notably, despite the EET equilibrium is mainly shifted towards the FbP moiety, we have found that the HT pathway from the HNDI still operates as a fast quenching mechanism for the FbP excited state. Such mechanisms contribute, along with the direct ET, to the charge separation rate. In both these donor–acceptor systems, the energetic position of the CSS state is a key component in determining their photophysics. We can therefore expect that, upon varying the oxidation and reduction potentials of the two moieties and/or the polarity of the solvent, a drastic change in their excited state dynamics will be obtained.
The results reported in this work demonstrate that a complete description of photoinduced transfer processes is possible by using an ab initio description of the single processes which are finally integrated in a kinetic model giving the full evolution of the electronic populations. We stress that our rate calculations only needed experimental absorption and fluorescence spectra, while all the other parameters are computed from quantum mechanical calculations. As a matter of fact, the same strategy can be extended to quantum chemical methods which are more accurate than TDDFT for the simulation of the optical spectra, thereby enhancing its independence of the experiments and the predictive potential.
Conflicts of interest
There are no conflicts to declare.References
- B. Albinsson and J. Mårtensson, Phys. Chem. Chem. Phys., 2010, 12, 7338–7351 RSC.
- M. Gilbert and B. Albinsson, Chem. Soc. Rev., 2015, 44, 845–862 RSC.
- G. L. Closs and J. R. Miller, Science, 1988, 240, 440–447 CAS.
- G. L. Closs, M. D. Johnson, J. R. Miller and P. Piotrowiak, J. Am. Chem. Soc., 1989, 111, 3751–3753 CrossRef CAS.
- N. Martn, L. Sánchez, M. A. Herranz and D. M. Guldi, J. Phys. Chem. A, 2000, 104, 4648–4657 CrossRef.
- M. Kuss-Petermann and O. S. Wenger, Angew. Chem., Int. Ed., 2016, 55, 815–819 CrossRef CAS PubMed.
- C. Schubert, J. T. Margraf, T. Clark and D. M. Guldi, Chem. Soc. Rev., 2015, 44, 988–998 RSC.
- S. Pla, M. Niemi, L. Martn-Gomis, F. Fernández-Lázaro, H. Lemmetyinen, N. V. Tkachenko and Á. Sastre-Santos, Phys. Chem. Chem. Phys., 2016, 18, 3598–3605 RSC.
- H. Imahori, K. Tamaki, D. M. Guldi, C. Luo, M. Fujitsuka, O. Ito, Y. Sakata and S. Fukuzumi, J. Am. Chem. Soc., 2001, 123, 2607–2617 CrossRef CAS PubMed.
- D. Villamaina, M. M. a. Kelson, S. V. Bhosale and E. Vauthey, Phys. Chem. Chem. Phys., 2014, 16, 5188–5200 RSC.
- A. Iagatti, L. Cupellini, G. Biagiotti, S. Caprasecca, S. Fedeli, A. Lapini, E. Ussano, S. Cicchi, P. Foggi, M. Marcaccio, B. Mennucci and M. Di Donato, J. Phys. Chem. C, 2016, 120, 16526–16536 CAS.
- S. Athanasopoulos, L. Alfonso Hernandez, D. Beljonne, S. Fernandez-Alberti and S. Tretiak, J. Phys. Chem. Lett., 2017, 8, 1688–1694 CrossRef CAS PubMed.
- A. K. Manna and B. D. Dunietz, J. Chem. Phys., 2014, 141, 121102 CrossRef PubMed.
- T. Nelson, S. Fernandez-Alberti, A. E. Roitberg and S. Tretiak, Acc. Chem. Res., 2014, 47, 1155–1164 CrossRef CAS PubMed.
- M. H. Lee, B. D. Dunietz and E. Geva, J. Phys. Chem. C, 2013, 117, 23391–23401 CAS.
- Y. Liu, L. Zhang, H. Lee, H. W. Wang, A. Santala, F. Liu, Y. Diao, A. L. Briseno and T. P. Russell, Adv. Energy Mater., 2015, 5, 2–9 Search PubMed.
- S. V. Bhosale, C. H. Jani and S. J. Langford, Chem. Soc. Rev., 2008, 37, 331–342 RSC.
- D. Villamaina, S. V. Bhosale, S. J. Langford and E. Vauthey, Phys. Chem. Chem. Phys., 2013, 15, 1177–1187 RSC.
- N. Banerji, S. V. Bhosale, I. Petkova, S. J. Langford and E. Vauthey, Phys. Chem. Chem. Phys., 2011, 13, 1019–1029 RSC.
- B. Robotham, K. a. Lastman, S. J. Langford and K. P. Ghiggino, J. Photochem. Photobiol., A, 2013, 251, 167–174 CrossRef CAS.
- O. Yushchenko, R. V. Hangarge, S. Mosquera-Vazquez, S. V. Boshale and E. Vauthey, J. Phys. Chem. B, 2015, 119, 7308–7320 CrossRef CAS PubMed.
- V. May and O. Kühn, Charge and Energy Transfer Dynamics in Molecular Systems, Wiley-VCH Verlag GmbH, Weinheim, Germany, 3rd edn, 2003 Search PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- C.-P. Hsu, G. R. Fleming, M. Head-Gordon and T. Head-Gordon, J. Chem. Phys., 2001, 114, 3065 CrossRef CAS.
- M. F. Iozzi, B. Mennucci, J. Tomasi and R. Cammi, J. Chem. Phys., 2004, 120, 7029–7040 CrossRef CAS PubMed.
- S. Caprasecca, C. Curutchet and B. Mennucci, J. Chem. Theory Comput., 2012, 8, 4462–4473 CrossRef CAS PubMed.
- S. Caprasecca, C. Curutchet and B. Mennucci, J. Phys. Chem. C, 2013, 117, 12423–12431 CAS.
- C.-P. Hsu, Acc. Chem. Res., 2009, 42, 509–518 CrossRef CAS PubMed.
- Z.-Q. You and C.-P. Hsu, Int. J. Quantum Chem., 2014, 114, 102–115 CrossRef CAS.
- A. A. Voityuk and N. Rösch, J. Chem. Phys., 2002, 117, 5607 CrossRef CAS.
- C.-H. Yang and C.-P. Hsu, J. Chem. Phys., 2013, 139, 154104 CrossRef PubMed.
- C.-p. Hsu, Z.-Q. You and H.-C. Chen, J. Phys. Chem. C, 2008, 112, 1204–1212 CAS.
- J. Jortner, J. Chem. Phys., 1976, 64, 4860 CrossRef CAS.
- S.-J. Lee, H.-C. Chen, Z.-Q. You, K.-L. Liu, T. J. Chow, I.-C. Chen and C.-P. Hsu, Mol. Phys., 2010, 108, 2775–2789 CrossRef CAS.
- G. Pourtois, D. Beljonne, J. Cornil, M. a. Ratner and J. L. Brédas, J. Am. Chem. Soc., 2002, 124, 4436–4447 CrossRef CAS PubMed.
- V. Vaissier, P. Barnes, J. Kirkpatrick and J. Nelson, Phys. Chem. Chem. Phys., 2013, 15, 4804–4814 RSC.
- D. Rehm and A. Weller, Isr. J. Chem., 1970, 8, 259–271 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian Inc., Wallingford CT, 2009 Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- E. Cances, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041 CrossRef CAS.
- R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777 CrossRef CAS.
- Z.-Q. You, Y.-C. Hung and C.-P. Hsu, J. Phys. Chem. B, 2015, 119, 7480–7490 CrossRef CAS PubMed.
- A. C. Benniston and A. Harriman, Chem. Soc. Rev., 2006, 35, 169–179 RSC.
- P. Stachelek and A. Harriman, J. Phys. Chem. A, 2016, 120, 8104–8113 CrossRef CAS PubMed.
- A. C. Benniston, A. Harriman, P. Li, P. V. Patel and C. A. Sams, Phys. Chem. Chem. Phys., 2005, 7, 3677 RSC.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Structure and fragment definition; natural transition orbitals of the molecules considered in this work; excitation energies and functional dependence; basis set dependence; benchmark of FCD couplings; calculation of charge transfer driving force; details of the fitting of spectra; details of the kinetic modelling. See DOI: 10.1039/c7cp07002k |
| ‡ Current affiliation: Department of Physics and Astronomy, University College London, Gower Street, London WC1E 6BT, UK |
| This journal is © the Owner Societies 2018 |

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)