Open Access Article
Open Access ArticleOn the relations between the bandgap, structure and composition of the M–Si–N (M = alkali, alkaline earth or rare-earth metal) nitridosilicates†
Otmar M.
ten Kate
 *a,
Zhijun
Zhang
b and
H. T. (Bert)
Hintzen
c
*a,
Zhijun
Zhang
b and
H. T. (Bert)
Hintzen
c
aProduct and Process Engineering, Chemical Engineering, Applied Sciences, Delft University of Technology, Van der Maasweg 9, 2629 HZ, Delft, The Netherlands. E-mail: o.m.tenkate@tudelft.nl
bSchool of Materials Science and Technology, Shanghai University, Shanghai, 200444, China
cLuminescent Materials Group, Radiation Science and Technology, Applied Sciences, Delft University of Technology, Mekelweg 15, 2629 JB, Delft, The Netherlands
First published on 17th October 2017
Abstract
Relations between the bandgap and structural properties and composition of the M–Si–N nitridosilicates (M = alkali, alkaline earth or rare earth metal) have been obtained, using experimental data collected from literature; and qualitative models are presented to explain the observed trends. Compounds with a higher degree of condensation, i.e. a higher Si/N ratio, generally have longer M–N bonds and shorter Si–N bonds. The observations can be explained based on the effective charge of N, dependent on its coordination with Si (NSix). With increasing Si/N ratio the coordination number of N by Si increases, making the effective charge of the nitrogen atom less negative, resulting in a longer and less covalent M–N bond. This also shifts the N 2p levels down in energy, lowering the top of the valence band (mainly composed of N orbitals); while decreasing the Si–N distance shifts the bottom of the conduction band (mainly composed of Si and M orbitals) upward. Some nitridosilicates show deviations to the general trends, such as γ-Si3N4 and several Li-containing compounds. These deviations have been discussed and possible explanations have been given based on peculiarities in their structural characteristics.
1. Introduction
Nitridosilicates have gained a lot of attention over the last years, especially in luminescence research, owing to their large structural diversity and chemical and optical properties.1,2 When doped with lanthanide ions such as Eu2+ or Ce3+, these compounds can show strong emission bands upon excitation with UV or blue light, with emission ranging from the blue to the red region.1,3 Some of these phosphors have shown high luminescence efficiency in combination with a good thermal and chemical stability, making them highly attractive for luminescence applications. Especially the Eu2+ doped nitridosilicates such as Sr2Si5N8:Eu2+ have shown to be very promising and have been applied as conversion phosphors for phosphor-converted white LEDs (pc-wLEDs).4–7 Here, a UV or blue LED chip is combined with red- and green-emitting phosphors, and in the case of a UV LED also blue-emitting phosphors, in order to produce white light with a high colour rendering index. Besides the use in white LEDs, nitridosilicate phosphors are also considered for other applications: as spectral conversion phosphors to enhance solar cell efficiency,8 as afterglow phosphors,9 and for LCD backlighting.10 In addition, the nitridosilicates have also attracted great interest outside the field of luminescence, mainly as ceramic materials11 due to their chemical resistance, excellent mechanical properties at high temperature and low thermal expansion. It is noteworthy to mention that the nitridosilicates can be modified by replacing some of the Si by Al and N by O, forming silicon aluminium oxy-nitridosilicates, or sialons,12,13 greatly enhancing the structural diversity. Examples of oxygen and/or aluminium containing nitridosilicate phosphors promising for white LED applications are Eu2+ doped Ca-α-sialon,14,15 CaAlSiN3,16 β-sialon,17 and SrSi2O2N2.18,19The nitridosilicates are compounds with the overall composition of MxSiyNz where M is an alkali (1+), alkaline earth (2+) or rare-earth (3+) metal ion or combination thereof. The structures generally consist of a framework of interconnected SiN4 tetrahedra with the metal ions located in the cavities of the framework. This makes the nitridosilicates comparable to the oxosilicates, which consist of interconnected SiO4 tetrahedra. However, in the oxosilicates the O atoms are usually one-fold or twofold coordinated by Si, with only a few compounds showing threefold coordination, as occurs in high-pressure phase stishovite (SiO2).20 In the nitridosilicates on the other hand, in addition to terminal (NSi1) and bridging (NSi2) nitrogen, the threefold coordination of N by Si (NSi3) is much more common, and N can even be fourfold coordinated by Si (NSi4). This allows for a much wider range of structures ranging from highly condensed Si3N4 with low M/Si ratio and high degree of condensation (Si/N ratio is 0.75), to Ca4SiN4 with a very low degree of condensation (Si/N ratio is 0.25) as a consequence of a high M/Si ratio. Such structural features strongly determine the chemical stability of the materials, showing a lower stability for compounds with a lower degree of cross-linking between SiN4 tetrahedra.21 Nitridosilicates such as Ca4SiN422,23 and Eu2SiN324 with a low degree of cross-linking are highly sensitive to water, while BaSi7N1025 with a high degree of cross-linking is very stable against oxidation and not corroded by water.
In addition to stability variations among the nitridosilicate structures, there is also a large variation in their optical properties depending on the chemical composition (i.e. M/Si ratio). The bandgap of the MxSiyNz compounds can vary greatly from as small as 2.7 eV in Li8SiN426 to as large as 6.9 eV in LiSi2N3.27,28 This has its influence on the performance as a luminescent material when the nitridosilicate host lattice is doped with lanthanide ions. For example, the position of the lowest 5d level of Eu2+ with respect to the bottom of the conduction band strongly influences the efficiency and thermal stability of the Eu2+ 5d–4f emission. When positioned inside or close to the conduction band, auto-ionization or thermal ionization of the 5d electron to the conduction band may occur and the 5d–4f emission will be quenched.29 Other examples are the position of the valence band with respect to the lanthanide 4f ground states that determines the energy of charge transfer transitions,30 and the position of the 4f ground state of the divalent ion with respect to the valence and conduction band that determines the valence stability of a divalent ion.31 These examples demonstrate the importance for the development of luminescent materials to know how the positions of the valence and conduction band of the phosphor host lattice are influenced by its composition and can be tuned.
This work presents the relations between the composition, structural properties and bandgap of the nitridosilicates and presents qualitative models that can explain the observed trends. For this we collect and analyse experimental data presented in literature on all MxSiyNz nitridosilicates where M is an alkali (1+), alkaline earth (2+) or rare earth (3+) metal or combination thereof. In the first part of the manuscript we discuss the structural characteristics of the nitridosilicates, such as bond lengths and coordination numbers, and relate it to the chemical compositions of the materials. A qualitative model is then developed to explain the influence that the Si/N ratio has on the bond lengths and coordination numbers. In the final part of the manuscript the relation between the bandgap and the structure and composition of the nitridosilicates is discussed. A second model is then developed to explain the influence of the Si/N ratio on the positions of the valence and conduction band.
2. The influence of chemical composition on crystal structure, bond lengths and bandgap
The nitridosilicates considered in this work (see Table 1) are all compounds with the general composition MxSiyNz where M is a monovalent alkali (A = Li+), divalent alkaline earth (AE = Mg2+, Ca2+, Sr2+, Ba2+), or trivalent rare-earth (RE = Sc3+, Y3+, La3+, or other trivalent lanthanide) metal ion, or combination thereof. M may also be a divalent rare earth (e.g. Eu2+). Also included in this work is Ca0.8Y1.2Si4N6.8C0.2,32 because it only contains a small amount of carbon and is closely related to the other nitridosilicates. The structure is very similar to the pure nitride (AE)(RE)Si4N7 (AE = Ca, Sr, Ba; RE = Sc, Y, Lu, Yb) compounds,33 but is a disordered variant where nitrogen is partly replaced by carbon for charge compensation and a part of the Y3+ ions is present on the Ca2+ sites.32 The lithium and magnesium containing nitridosilicates such as Li5SiN3, Li4Ca3Si2N6, Li4CaMg2Si2N6, MgSiN2 and SrMg3SiN4 have also been included, for the sake of comparison, even though it may be argued that some these compounds are not really nitridosilicates but nitrido-lithosilicates or nitrido-magnesosilicates because Li and Mg can be considered part of the nitridosilicate framework. This issue will be further discussed in this manuscript. The structural characteristics of all the nitridosilicates have been collected from experimental data from literature and are summarized in Table 1.| Compound | Space group | ICSD | Si–N network (CS = corner sharing, ES = edge sharing, 3D = 3-dimensional) | N by Si coordination N[x] | Average M–N distance (Å) | Shortest Si–N distancea (Å) | Ref. |
|---|---|---|---|---|---|---|---|
| a If there are multiple Si sites with different Si–N distances in a structure, the average is taken of the shortest Si–N distance of each site. b Li21Si3N11 and Li5SiN3 both crystallize in an anti-fluorite (Li,Si)2N structure with N 8-fold coordinated by Si and Li. c Ca16Si17N34 is also known as cubic-CaSiN2. d Structures may also be considered a 3D network of corner-sharing and edge-sharing SiN4 and LiN4 and/or MgN4 tetrahedra. e Compound contains mixed Sr/Ba, Ca/Sm, Ca/Yb or Ca/Y sites. f Distances based on a structure doped with 5% Eu. g CaYSi4N7 is actually Ca0.8Y1.2Si4N6.8C0.2. | |||||||
| α-Si3N4 | (159) | 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 797 797 |
3D CS SiN4 network | N[3] | — | 1.673 | 34 |
| β-Si3N4 | (173) | 8263 | 3D CS SiN4 network | N[3] | — | 1.704 | 35 |
| γ-Si3N4 | (227) | 97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 566 566 |
3D ES/CS SiN4/SiN6 network | N[4] | — | 1.853 | 36 |
| Li21Si3N11 | (79) | 191![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 135 135 |
2.111 | 1.656 | 37 | ||
| Li5SiN3 | (206) | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 582 582 |
2.084 | 1.910 | 38 | ||
| Li2SiN2 | (61) | 420![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 126 126 |
3D CS SiN4 network | N[2] | 2.160 | 1.728 | 39 |
| LiSi2N3 | (36) | 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 524 524 |
3D CS SiN4 network | 1N[2]:2N[3] | 2.263 | 1.681 | 40 |
| MgSiN2 | (33) | 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 731 731 |
3D CS SiN4 network | N[2] | 2.249 | 1.732 | 41 |
| Mg2Si5N8 | (9) | 3D CS SiN4 network | 1N[2]:1N[3] | 2.305 | 1.660 | 42 | |
| Ca4SiN4 | (14) | 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 872 872 |
Isolated SiN4 tetrahedrons | N[1] | 2.522 | 1.767 | 23 |
| α-Ca5Si2N6 | (15) | 414![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 462 462 |
Isolated pairs of ES SiN4 | 2N[1]:1N[2] | 2.575 | 1.713 | 43 |
| β-Ca5Si2N6 | (12) | 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 873 873 |
Isolated pairs of ES SiN4 | 2N[1]:1N[2] | 2.578 | 1.735 | 23 |
| α-CaSiN2 | (61) | 170![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 267 267 |
3D CS SiN4 network | N[2] | 2.583 | 1.729 | 44 |
| Ca16Si17N34c | (216) | 248![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 945 945 |
3D CS SiN4 network | 2N[1]:14N[2]:1N[4] | 2.536 | 1.645 | 45 |
| Ca2Si5N8 | (9) | 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 070 070 |
3D CS SiN4 network | 1N[2]:1N[3] | 2.646 | 1.671 | 46 |
| β-Ca2Si5N8 | (4) | 3D CS SiN4 network | 1N[2]:1N[3] | 2.730 | 1.618 | 42 | |
| HP-Ca2Si5N8 | (61) | 419![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 318 318 |
3D CS SiN4 network | 1N[2]:1N[3] | 2.577 | 1.664 | 47 |
| SrSiN2 | (14) | 170![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 270 270 |
3D CS/ES SiN4 network | N[2] | 2.859 | 1.711 | 44 |
| Sr2Si5N8 | (31) | 401![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
3D CS SiN4 network | 1N[2]:1N[3] | 2.949 | 1.675 | 48 |
| SrSi7N10 | (7) | 154![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 166 166 |
3D CS and ES SiN4 network | 1N[2]:4N[3] | 3.069 | 1.683 | 49 |
| SrSi6N8 | (44) | 319![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 265 265 |
3D CS SiN4 network (Si–Si bonds) | 1N[2]:3N[3] | 3.028 | 1.691 | 50 |
| Ba5Si2N6 | (19) | 81![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 570 |
Isolated pairs of ES SiN4 | 2N[1]:1N[2] | 2.862 | 1.747 | 51 |
| BaSiN2 | (64) | 170![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 268 268 |
3D CS/ES SiN4 network | N[2] | 2.991 | 1.719 | 44 |
| Ba2Si5N8 | (31) | 401![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 501 501 |
3D CS SiN4 network | 1N[2]:1N[3] | 2.999 | 1.686 | 48 |
| BaSi7N10 | (7) | 405![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 772 772 |
3D CS and ES SiN4 network | 1N[2]:4N[3] | 3.269 | 1.683 | 25 |
| BaSi6N8 | (44) | 417![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 444 444 |
3D CS SiN4 network (Si–Si bonds) | 1N[2]:3N[3] | 3.062 | 1.667 | 52 |
| Eu2Si5N8 | (31) | 59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 257 257 |
3D CS SiN4 network | 1N[2]:1N[3] | 2.894 | 1.681 | 53 |
| La5Si3N9 | (64) | 419![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 064 064 |
Branched chains of CS SiN4 | 2N[1]:1N[2] | 2.711 | 1.564 | 54 |
| La3Si6N11 | (100) | 248![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 709 709 |
3D CS SiN4 network | 9N[2]:2N[3] | 2.676 | 1.711 | 55 |
| LaSi3N5 | (19) | 130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 022 022 |
3D CS SiN4 network | 3N[2]:2N[3] | 2.802 | 1.690 | 56 |
| Ce5Si3N9 | (64) | 419![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 063 063 |
Branched chains of CS SiN4 | 2N[1]:1N[2] | 2.685 | 1.725 | 54 |
| Ce7Si6N15 (tricl.) | (2) | 420![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 199 199 |
3D CS SiN4 network | 2N[1]:5N[2] | 2.772 | 1.705 | 57 |
| Ce7Si6N15 (trig.) | (148) | 420![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
3D CS SiN4 network | 2N[1]:5N[2] | 2.770 | 1.625 | 57 |
| Ce3Si6N11 | (100) | 237![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 444 444 |
3D CS SiN4 network | 9N[2]:2N[3] | 2.661 | 1.725 | 58 |
| CeSi3N5 | (19) | 402![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 910 910 |
3D CS SiN4 network | 3N[2]:2N[3] | 2.783 | 1.686 | 56 |
| Pr5Si3N9 | (64) | 260![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 288 288 |
Branched chains of CS SiN4 | 2N[1]:1N[2] | 2.672 | 1.719 | 59 |
| Pr7Si6N15 | (2) | 420![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 201 201 |
3D CS SiN4 network | 2N[1]:5N[2] | 2.762 | 1.693 | 57 |
| Pr3Si6N11 | (100) | 402![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 178 178 |
3D CS SiN4 network | 9N[2]:2N[3] | 2.646 | 1.703 | 60 |
| Sm3Si6N11 | (100) | 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 183 183 |
3D CS SiN4 network | 9N[2]:2N[3] | 2.618 | 1.697 | 56 |
| Li4Ca3Si2N6 | (12) | 420![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 675 675 |
Isolated pairs of ES SiN4d | 2N[1]:1N[2] | 2.596 (Ca) | 1.711 | 61 |
| Li4Sr3Si2N6 | (12) | 421![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 259 259 |
Isolated pairs of ES SiN4d | 2N[1]:1N[2] | 2.735 (Sr) | 1.735 | 61 |
| Li4Ca2MgSi2N6 | (12) | 427![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 077 077 |
Isolated pairs of ES SiN4d | 2N[1]:1N[2] | 2.482 (Ca) | 1.743 | 62 |
| Li2Ca2Mg2Si2N6 | (12) | 427![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 078 078 |
Isolated pairs of ES SiN4d | 2N[1]:1N[2] | 2.588 (Ca) | 1.720 | 62 |
| Li2Ca3MgSi2N6 | (12) | Isolated pairs of ES SiN4d | 2N[1]:1N[2] | 2.554 (Ca) | 1.720 | 63 | |
| Li2Sr4[Si2N5]N | (119) | 422![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 596 596 |
Layered CS SiN4 network | 1N[0]:2N[1]:3N[2] | 2.694 (Sr) | 1.751 | 64 |
| LiCa3Si2N5 | (15) | 420![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 676 676 |
Double chain of ES/CS SiN4 | 2N[1]:1N[2] | 2.540 (Ca) | 1.726 | 65 |
| Li2CaSi2N4 | (205) | 421![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 548 548 |
3D CS SiN4 network | N[2] | 2.528 (Ca) | 1.714 | 66 |
| Li2SrSi2N4 | (205) | 421![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 549 549 |
3D CS SiN4 network | N[2] | 2.699 (Sr) | 1.738 | 66 |
| Li5La5Si4N12 | (117) | 421![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 528 528 |
Non-br. chains CS SiN4 | 2N[1]:1N[2] | 2.609 (La) | 1.740 | 67 |
| Li5Ce5Si4N12 | (117) | 421![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 527 527 |
Non-br. chains CS SiN4 | 2N[1]:1N[2] | 2.605 (Ce) | 1.709 | 67 |
| CaMg3SiN4 | (88) | 427![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 074 074 |
Isolated SiN4 tetrahedronsd | N[1] | 2.638 (Ca) | 1.763 | 68 |
| SrMg3SiN4 | (88) | 427![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 076 076 |
Isolated SiN4 tetrahedronsd | N[1] | 2.802 (Sr) | 1.791 | 68 |
| EuMg3SiN4 | (88) | 427![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 075 075 |
Isolated SiN4 tetrahedronsd | N[1] | 2.680 (Eu) | 1.757 | 68 |
| BaMg3SiN4 | (2) | 428![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 510 510 |
3D CS (Si,Mg)N4 network | — | 2.953 (Ba) | 1.892 | 69 |
| Ba4MgSi2N6 | (70−2) | 187![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 335 335 |
Isolated pairs of ES SiN4 | 2N[1]:1N[2] | 2.953 (Ba) | 1.739 | 70 |
| Ba3Ca2Si2N6 | (15) | 187![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 336 336 |
Isolated pairs of ES SiN4 | 2N[1]:1N[2] | 2.910 (Ba) | 1.730 | 70 |
| Ba1.6Sr3.4Si2N6 | (15) | 187![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 337 337 |
Isolated pairs of ES SiN4 | 2N[1]:1N[2] | 1.718 | 70 | |
| CaLaSiN3 | (64) | Non-branched chains CS SiN4 | 2N[1]:1N[2] | 71 | |||
| Eu2SiN3 | (64) | 420![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 679 679 |
Non-branched chains CS SiN4 | 2N[1]:1N[2] | 2.764 (Eu2+) | 1.731 | 24 |
| Ba2Nd7Si11N23 | (65) | 407![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 202 202 |
3D CS SiN4 zeolite network | 2N[1]:21N[2] | 3.164 (Ba) | 1.685 | 72 |
| Ca3Sm3Si9N17 | (215) | 421![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 644 644 |
3D CS SiN4 network | 16N[2]:1N[4] | 1.696 | 73 | |
| Ca3Yb3Si9N17 | (215) | 421![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 645 645 |
3D CS SiN4 network | 16N[2]:1N[4] | 1.687 | 73 | |
| Ba1.5Eu1.5YbSi6N11 | (198) | 407![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
3D CS SiN4 network | 9N[2]:2N[3] | 3.012 (Ba) | 1.701 | 74 |
| SrScSi4N7 | (186) | 189![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 117 117 |
3D CS SiN4 network | 6N[2]:1N[4] | 2.957 (Sr)f | 1.688f | 75 |
| CaYSi4N7g | (186) | 152![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 975 975 |
3D CS SiN4 network | 6N[2]:1N[4] | 1.709 | 32 | |
| SrYSi4N7 | (186) | 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 459 459 |
3D CS SiN4 network | 6N[2]:1N[4] | 3.012 (Sr) | 1.699 | 76 |
| BaYSi4N7 | (186) | 98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 276 276 |
3D CS SiN4 network | 6N[2]:1N[4] | 3.014 (Ba) | 1.701 | 77 |
| EuYSi4N7 | (186) | 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 460 460 |
3D CS SiN4 network | 6N[2]:1N[4] | 3.019 (Eu) | 1.668 | 76 |
| SrYbSi4N7 | (186) | 405![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 625 625 |
3D CS SiN4 network | 6N[2]:1N[4] | 2.996 (Sr) | 1.708 | 78 |
| EuYbSi4N7 | (186) | 592![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 58 |
3D CS SiN4 network | 6N[2]:1N[4] | 2.993 (Eu) | 1.713 | 53 |
| BaYbSi4N7 | (186) | 405![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 194 194 |
3D CS SiN4 network | 6N[2]:1N[4] | 3.017 (Ba) | 1.717 | 78 |
2.1 Crystal structure
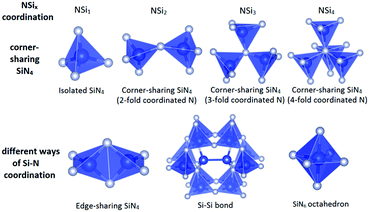
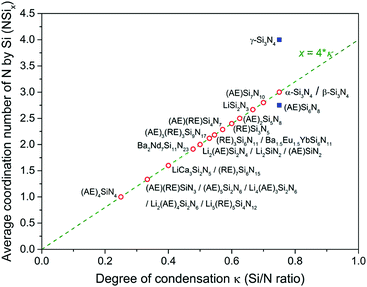
Depending on the M/Si ratio of the nitridosilicates, different ways of N by Si coordination exist, as illustrated in Fig. 1. The non-metal silicon nitrides α-Si3N434,79 and β-Si3N435,80 both consist of a three-dimensional network of corner-sharing SiN4 tetrahedra. All N atoms are coordinated by three Si atoms. As a result of its high degree of cross-linking between SiN4 tetrahedra, Si3N4 exhibits an outstanding chemical, thermal and mechanical stability. When introducing metals into the structure, Si–NSi2 bonds will be broken, reducing the degree of cross-linking between SiN4 tetrahedra. As a result, compounds such as (AE)Si7N10 (AE = Sr, Ba),25,49 (AE)2Si5N8 (AE = Ca, Sr, Ba),46,48 LaSi3N556,81 and La3Si6N1156 have N atoms both threefold and twofold coordinated by Si. However, the SiN4 tetrahedra still form a three-dimensional network of corner-sharing or, as is the case for (AE)Si7N10, also edge-sharing tetrahedra. In compounds such as BaYbSi4N782 and Ca3Sm3Si9N1773 there is no threefold coordination, but unusual fourfold coordination of N by Si exists in addition to the twofold coordination. All N atoms are twofold coordinated by Si in α-CaSiN2, SrSiN2 and BaSiN2.44 In compounds with quite high M/Si ratios resulting in low Si/N ratios, N atoms can also be singly bonded by Si, as occurs partly in Eu2SiN324 and La5Si3N9.54 In these compounds the SiN4 tetrahedra form non-branched (in Eu2SiN3) or branched (in La5Si3N9) linear chains. In (AE)5Si2N6 (AE = Ca, Ba)23,43,51 and Ca4SiN423 the SiN4 tetrahedra do not form interconnected networks anymore, but are isolated units (in Ca4SiN4) or form isolated Si2N6 pairs consisting of two edge-sharing tetrahedra (in (AE)5Si2N6).In all the previously mentioned cases, the Si and N atoms are present in SiN4 tetrahedra. As a consequence, there is a direct relation between the degree of condensation κ (here defined as the Si/N ratio) and the average coordination number x of nitrogen by silicon (NSix), with x = 4 × κ, as is shown in Fig. 2. There are a just few nitridosilicates in which not all Si and N atoms are present in SiN4 tetrahedra and the relation x = 4 × κ is not followed: γ-Si3N4 and (AE)Si6N8 (AE = Sr, Ba), which are indicated with blue squares in Fig. 2. In γ-Si3N4 with cubic spinel structure83 all N atoms are fourfold coordinated by Si and SiN6 octahedra exist in addition to SiN4 tetrahedra. In (AE)Si6N8 (AE = Sr, Ba)50,52 N3Si–SiN3 entities are present in which two Si atoms are directly bonded to each other.
The M cations are the positive counterions of the negative nitridosilicate framework and are located in the cavities of the network. They are usually coordinated by six or more N atoms. However, if the metal ion is relatively small, as is the case for Mg2+ and Li+, they can also form TN4 (T = Mg, Li) tetrahedrons similar to the SiN4 tetrahedrons. It may then be more appropriate to consider them part of the framework instead of as counterions. This is for example the case in Li5SiN3 with antifluorite structure where Si and Li are located on mixed sites forming (Si,Li)N4 tetrahedrons.37,38 In several other Li and Mg containing nitridosilicates the situation is however less obvious. Li4Ca3Si2N6 consists of SiN4 and LiN4 tetrahedra with octahedrally coordinated Ca2+ ions in between, so Si and Li can be considered part of the 3D framework and the compound could be written as Ca3[Li4Si2N6].61,62 However, for the same structure one of the Ca2+ ions can be replaced by two Li+ ions, while at the same time 4 Li+ ions are replaced by 2 Mg2+ ions resulting in Li2Ca2[Mg2Si2N6] in which tetrahedrally coordinated Mg is now part of the framework and Li+ is now a counterion forming [Li2]N6 octahedra.62 Starting form Ca3[Li4Si2N6] the Mg can also be positioned on a Ca site, while the remaining Ca2+ ions switch positions with the Li+ ions on the [Li2]N6 positions, forming Ca2Mg[Li4Si2N6] in which now Li is part of the framework in a tetrahedral coordination and Mg2+ is a counterion in a fourfold planar rectangular coordination.62
However, because Li+ and Mg2+ have a larger ionic radius, a lower electronegativity, and a lower oxidation number than Si4+, the influence of Li+ and Mg2+ on parameters like bond lengths and bandgap will be different. Consequently, it is not appropriate to simply add up the Si, Li and Mg atoms and use the (Si + Mg + Li)/N ratio as the principal parameter. Therefore, the Si/N ratio is used as the principal parameter in this manuscript, even when Mg and/or Li may be considered part of the cross-linking framework. As a result, a compound like Ba[Mg3SiN4] that is reported69 to have a degree of condensation of 1 based on its (Mg + Si)/N ratio, is listed as a compound with a Si/N ratio of 0.25 in this work.
2.2 Bond lengths
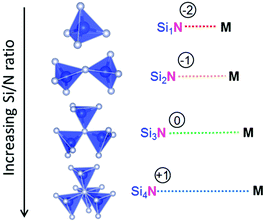
Since N is in the −III oxidation state and Si in the +IV oxidation state, the effective charge of the N atom will be zero if it is threefold coordinated by tetrahedrally coordinated Si atoms (NSi3). In twofold coordination (NSi2), the N atom is under-bonded, causing it to be effectively −1 negatively charged. This will therefore result in a stronger, more covalent interaction between N and the positively charged metal ion M in the structure. It can therefore be expected that the M–N bond will be shorter when N is in NSi2 coordination than when N is in the ideal NSi3 coordination. If the N atom is only terminally coordinated by Si (NSi1) this effect will become more pronounced. Vice versa, a less covalent interaction and longer M–N bond can be expected if the N atom is over-bonded in a fourfold coordination by Si. This means that one may expect an increase of the average M–N distance with increasing Si/N ratio, as schematically illustrated in Fig. 3.As expected, a larger M–N distance with increasing Si/N ratio is indeed the trend that can be qualitatively observed from the experimental data collected from literature (Table 1), and shown in Fig. 4. For the Ca, Sr, Ba and La sites the average distance to nitrogen tends to increase with increasing Si/N ratio in correspondence with a more positive effective charge for N. It should be noted here that, even though a linear fit through the data is presented, this does not imply that the relation between Si/N ratio and M–N distance should be linear. The purpose of the linear fit is to show that there seems to be a general trend showing an increase of M–N distance with increasing Si/N ratio, but several secondary effects might be present that cause an increased scattering of the data. Nevertheless, the deviation from the general trend is in most compounds less than 0.05 Å. The strongest increase of M–N distance with increasing Si/N ratio is observed for M = Sr, while the increase is weakest for M = Ca. The reason for the surprising order Sr–N > Ba–N > Ca–N (while in terms of size and atomic number Ba > Sr > Ca) is unclear and further studies would be necessary to clarify its cause. It might be a consequence of scattering of the data due to secondary effects as some data points have a relatively strong influence on the steepness of the slope.
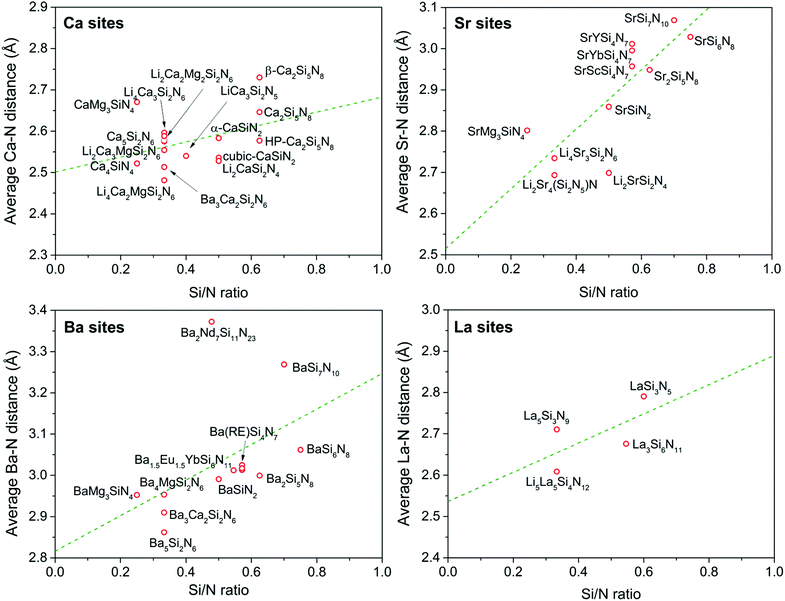 | ||
| Fig. 4 Average M–N distance (M = Ca, Sr, Ba or La) in the nitridosilicates versus the Si/N ratio. The green dashed line represents a trend line obtained by a linear fit through the data points. | ||
For the Ca sites, the increase of the Ca–N distance with increasing Si/N ratio is rather limited with only about 0.1 Å difference between Ca4SiN4 and Ca2Si5N8. This makes the increase smaller than the scattering of the data. For example, among the compounds with a Si/N ratio of 1/3, Li4Ca3Si2N6 has an almost 0.2 Å larger average Ca–N bond length than Li4Ca2MgSi2N6. As was discussed above Li4Ca2MgSi2N6 is homeotypic to Li4Ca3Si2N6 but Ca2+ ions have been partly replaced by Mg2+ ions and the remaining Ca2+ ions have switched places with the Li+ ions, which can explain the relatively short Ca–N bond length in Li4Ca2MgSi2N6. For the Sr sites the absolute scattering of the data is similar as for the Ca sites. However, among the Sr sites there is a large increase of the Sr–N distance with increasing degree of condensation, making the scattering relatively small. For the Ba sites the observed dependence on Si/N ratio is also strong, but the deviation from the general trend is quite large for BaSi7N10 and Ba2Nd7Si11N23, having relatively large Ba–N distances. This may be due to the large coordination numbers for Ba in these compounds. In BaSi7N10 the coordination number is 13,25 while in Ba2Nd7Si11N23, which has an unusual zeolite-analogous structure,72 the coordination number of some of the Ba atoms goes up to even 16.
Some scattering in the data of Fig. 4 may also be due to the fact that the Si/N ratio, which basically is a measure for the average N coordination number (see Fig. 2), may not exactly represent the actual N by Si coordination number of the N atoms surrounding the metal ion. In BaYSi4N7 for example, the N atoms have an average coordination number of 2.29 because the ratio of twofold/fourfold coordinated N atoms is 6/1. However, the N atoms surrounding Ba have an average coordination number of 2 as the fourfold coordinated N atoms are far away from and not coordinated to Ba. In addition, the scattering of the data in Fig. 4 may be enhanced due to the presence of different types of metal ions M within one compound.
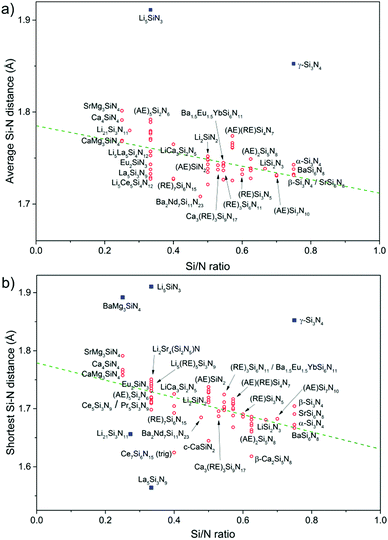
While the M–N bond lengths increase with increasing degree of condensation, the Si–N bond lengths tend to decrease with increasing degree of condensation, as has previously been observed by Schnick et al.12,84 This can also be observed from the data shown in Fig. 5a: the average Si–N distance is relatively large in for example Ca4SiN4 (1.791 Å) with very low degree of condensation, while relatively small in SrSi7N10 (1.731 Å) with a very high degree of condensation.
If the shortest Si–N distance is plotted versus the Si/N ratio (Fig. 5b) instead of the average Si–N distance (Fig. 5a), a similar trend is observed. The correlation of the data is then somewhat stronger, considering that the Pearson correlation coefficient changes from −0.53 for the fit of the average Si–N distance versus Si/N ratio to −0.67 for fit of the shortest Si–N distance versus Si/N ratio. Note that the slope of the trend line in Fig. 5b (shortest Si–N distance) is also steeper than in Fig. 5a (average Si–N distance).
A few compounds do not follow the general trend in Fig. 5a and b and have either a relatively large or relatively small shortest Si–N bond. Among them is γ-Si3N4 with a relatively large Si–N distance of 1.853 Å. Note that this is the only compound listed in which SiN6 octahedra are present in addition to SiN4 tetrahedra. Two Li compounds also deviate with Li5SiN3 having a much larger Si–N distance and Li21Si3N11 having a relatively small distance. Both compounds crystallize in distorted antifluorite structures and both are very Li rich, with the Li and Si atoms present in TN4 (T = Li, Si) tetrahedra. So, based on their crystal structures both Li5SiN3 and Li21Si3N11 are not really nitridosilicates composed of cross-linked tetrahedra such as the other compounds. It has been reported37 that in Li21Si3N11 the Si is mainly present on the smallest TN4 site (because Si4+ is smaller than Li+), resulting in a small Si–N bond length. In Li5SiN3 on the other hand, Si occupies a mixed Si/Li site making the Si–N distance actually a significantly larger (Si,Li)–N distance. Something similar also happens in BaMg3SiN4 with mixed Mg/Si sites and thus a large shortest (Mg,Si)–N distance (1.892 Å) since Mg2+ is larger than Si4+. The average (Mg,Si)–N distance in BaMg3SiN4 is also very large (2.030 Å) and falls outside the plotted range of Fig. 5a. In the other (AE)Mg3SiN4 compounds (AE = Ca, Sr, Eu) the Mg and Si sites are not mixed and the Si–N bond lengths are as expected for compounds with low Si/N ratio and in the same range as in Ca4SiN4. The very small shortest Si–N distance of 1.564 Å reported54 for La5Si3N9 seems to be not reliable, because for Ce5Si3N9 and Pr5Si3N9, that both crystallize in the same crystal structure as La5Si3N9, the reported54,59 shortest Si–N distances are much larger (1.725 Å for Ce5Si3N9 and 1.719 Å for Pr5Si3N9) and fall in line with the trend observed in Fig. 5b. Hence that the La3+ ion is similar in size as the Ce3+ and Pr3+ ions. Note that the average Si–N distance in La5Si3N9 is not an exception, but in range with the other compounds.
2.3 Bandgap
The bandgaps of the MxSiyNz compounds, listed in Table 2, have been derived from experimental data from literature. In cases the electrical bandgap EVC, i.e. the energy between the top of the valence band and the bottom of the conduction band, has not been reported, EVC is estimated from the exciton creation energy Eex85,86 or the optical bandgap Eopt. For this, absorption or reflectance spectra from undoped compounds and photoluminescence excitation spectra of low concentrated Eu2+ or Ce3+ doped compounds have been used. For several compounds, the bandgap has been calculated in literature using DFT calculations. These computationally determined bandgaps have not been taken into account as these calculations often tend to underestimate the real value of the bandgap, making comparison with experimentally determined values of other compounds not reliable. More information on the derivation of the bandgap from literature data can be found in the ESI.†| Compound | E VC (eV) | Ref. |
|---|---|---|
| a Ca16Si17N34 is also known as cubic-CaSiN2. b CaYSi4N7 is actually Ca0.8Y1.2Si4N6.8C0.2. | ||
| α-Si3N4 | 5.9 | DR87 |
| γ-Si3N4 | 5.1 | X-rays,88 PLE89 |
| Li8SiN4 | 2.7 | ABS26 |
| Li5SiN3 | 2.8 | ABS90 |
| LiSi2N3 | 6.9 | DR,28 PLE27 |
| Li2SiN2 | >6.9 | DR91 |
| MgSiN2 | 5.5 | DR,92,93 X-rays94 |
| α-CaSiN2 | 5.0 | DR,95,96 PLE95 |
| Ca16Si17N34a | 4.7 | ABS,97 DR97,98 |
| Ca2Si5N8 | 5.2 | DR,99 PLE99,100 |
| SrSiN2 | 5.0 | ABS,93 DR,93,101 PLE93,101 |
| Sr2Si5N8 | 5.1 | DR,99,102 PLE99,100 |
| SrSi6N8 | 3.7 | DR,103 PLE104 |
| BaSiN2 | 4.9 | ABS,93 DR,93 PLE93 |
| Ba2Si5N8 | 5.1 | ABS,105 DR,99 PLE99,100 |
| BaSi7N10 | 5.8 | DR,106 PLE107 |
| LaSi3N5 | 5.0 | ABS,108 DR,109 PLE109,110 |
| CaMg3SiN4 | 4.1 | PLE68 |
| SrMg3SiN4 | 4.1 | DR68 |
| BaMg3SiN4 | 4.1 | DR69 |
| Li2Ca2Mg2Si2N6 | 4.8 | DR111 |
| Li4Ca3Si2N6 | 4.1 | ABS,112 DR,112 PLE112 |
| CaLaSiN3 | 3.1 | DR113 |
| CaYSi4N7b | 5.2 | DR114 |
| SrYSi4N7 | 5.2 | DR,76,77,114 PLE76 |
| BaYSi4N7 | 5.2 | DR77,114,115 |
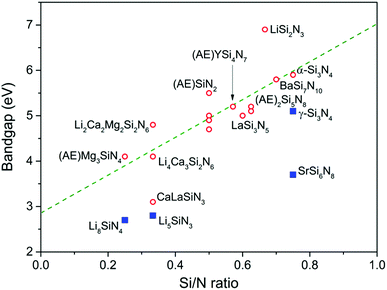
Among the nitridosilicates listed in Table 2, Li2SiN2 has the largest bandgap (>6.9 eV) and Li8SiN4 has the smallest bandgap (2.7 eV). In general the bandgap increases with increasing Si/N ratio, as shown in Fig. 6. This is in accordance with what was previously predicted by Fang et al.116 using first principle calculations for the barium nitridosilicates: the bandgap increases with increasing degree of cross-linking between SiN4 tetrahedra in the order Ba5Si2N6 < Ba2Si5N8 < BaSi7N10 < β-Si3N4. In the previous section it was explained that with increasing degree of condensation (Si/N ratio) the N atom will get a less negative effective charge. This less negative effective charge will result in a downward shift in energy of the N 2p levels, and because the top of the valence band consists mainly of N 2p levels, this will make the bandgap larger. This is also in line with the calculation by Fang et al.,116 showing a downward shift of the N 2p levels when going from singly coordinated N atoms towards N atoms coordinated by 4 Si atoms.
The increase of the bandgap with increasing degree of condensation is not only caused by a shift of the top of the valence band to lower energy, but should also be partly due to a shift of the bottom of the conduction band to higher energy (with respect to the vacuum level). As was discussed above, the Si–N bond length decreases with increasing Si/N ratio (Fig. 5). The shorter, and therefore stronger bond will give a larger splitting between the bonding orbitals at the top of the valence band (mainly N orbitals) and antibonding orbitals at the bottom of the conduction band (Si orbitals). This will result in a shift of the bottom of the conduction band to higher energy, next to a shift of the top of the valence band to lower energy. Based on analysis of the thermal quenching behaviour of the Eu2+ and Ce3+ 5d–4f emission in doped nitridosilicates it can be argued that the bottom of the conduction band should indeed shift upwards in energy with increasing degree of condensation, as will be explained in more detail in our next paper. So the increasing bandgap of the nitridosilicates with increasing degree of condensation (increasing Si/N ratio) is the consequence of the combined effect of the downward shift of the valence band and the upward shift of the conduction band as illustrated in Fig. 7. It should be noted here that this model does not take into account that the bottom of the conduction band may not only consist of Si orbitals but may also consist of M orbitals. For example, calculations on the electronic structure of LaSi3N5 and La3Si6N11 show that the bottom of the conduction band of these compounds contains La 4f and 5d states.117 Nevertheless, the calculations still show that La3Si6N11, which has a lower Si/N ratio, has a smaller bandgap than LaSi3N5 and a conduction band minimum at lower energy. The smaller bandgap may seem contradictory to the shorter La–N distance in La3Si6N11, but could be explained by the larger crystal field splitting and centroid shift of the 5d levels in La3Si6N11 as compared to LaSi3N5, lowering the bottom of the conduction band.
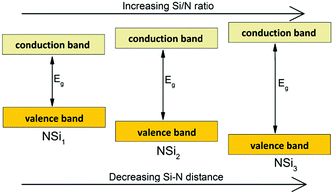 | ||
| Fig. 7 Schematic diagram, showing the influence of the degree of condensation (Si/N ratio) on the positions of the valence and conduction bands and the size of the bandgap Eg. | ||
The bandgaps of SrSi6N8 (about 3.7 eV) and γ-Si3N4 (about 5.1 eV) are small considering their high Si/N ratios and deviate from the trend established for the other nitridosilicates. As already mentioned, in γ-Si3N4 not all Si atoms are tetrahedrally coordinated by N. The presence of SiN6 octahedra causes a lowering of the Si 3s states at the bottom of the conduction band.116 The smaller bandgap is also in line with the larger Si–N bond length in γ-Si3N4 as compared to those bonds in α-Si3N4 and β-Si3N4 (Fig. 5). In SrSi6N8 as another exception not all Si atoms are tetrahedrally coordinated by N, as part of the Si atoms form Si–Si bonds. The Si–Si bonds create an empty σ* anti-bonding state forming the bottom of the conduction band, resulting in the smaller bandgap.118 Therefore it is likely that BaSi6N8, in which also Si–Si bonds are present, has a relatively small bandgap as well, but to our knowledge its bandgap has not yet been experimentally determined.
For Li2SiN2 the exact value of the bandgap is unknown, but it should be larger than 6.9 eV since it has a high reflectivity down to 200 nm radiation.91 The bandgap is thus very large considering that the Si/N ratio is only 0.5 and in the same range with that of LiSi2N3, which also has a relatively large bandgap. Such large bandgaps can be attributed to the presence of Li. As Li+ ions are relatively small, the Li–N bond is short compared to the M–N bond in other nitridosilicates. Instead of considering the coordination number of N based on the number of Si atoms around it, also the coordinating Li atoms should therefore be taken into account. This increases the N(Si,Li)x coordination number to about 4 in LiSi2N3 and even to 6 in Li2SiN2, meaning that the effective charge around N becomes more positive, the top of the valence band shifts downwards and the bandgap becomes large. Note that the same reasoning does not apply for Li5SiN3 which has a very small bandgap. The Si atoms are here located on the large Li sites, making the (Si,Li)–N bonds much longer (see Fig. 5) and weaker than in LiSi2N3 and Li2SiN2, making it more ionic with a more negative effective charge for N. Something similar may also apply for Li8SiN4 as it also has a small bandgap, but the crystal structure of Li8SiN4 has not fully been resolved in order to clarify this.
3. Conclusions
With increasing degree of condensation (Si/N ratio) in the nitridosilicates, the coordination number of N by Si increases, the Si–N bond lengths decrease, the M–N bond lengths increase and the bandgap increases as well. This can be understood by considering the changes in effective charge of N and Si–N bond lengths. With a low degree of condensation between the SiN4 tetrahedra the N atom is under-bonded, giving it an effective negative charge. This effective charge becomes less negative with a higher degree of cross-linking between the SiN4 tetrahedra, making the M–N bonds weaker and longer. As a result of the less negative effective charge of N, the N 2p levels, and thus the top of the valence band, shift downwards and the bandgap becomes larger. The bandgap is also increased with increasing degree of condensation because the Si–N distance decreases, resulting in a larger splitting between the bonding (N) and antibonding (Si) orbitals. Some compounds, such as γ-Si3N4, SrSi6N8 and several Li containing compounds, show deviations to the general trends, which can be understood based on their differences in structure as compared to the other nitridosilicates, as their framework does not solely consist of cross-linking SiN4 tetrahedra.The obtained insights on the relations between bandgap, structure and composition can be used when developing new materials with certain structural or optical properties. For example for the development of novel luminescent materials, for which the positions of the valence and conduction band are of direct influence on the photoluminescence properties.
Although we have focused ourselves in this manuscript on the nitridosilicates, the observed trends are expected to be more general and hold also for other series of compounds whose structure consists of a framework of cross-linked tetrahedra with larger counterions located in the cavities, such as the oxosilicates, oxoaluminates, nitridoaluminates and phosphates. Indeed, a decrease of the Si–O bond length with increasing Si/O ratio has been previously observed for the oxosilicates.119–121 One can therefore expect that there might also be an increase of the bandgap and increase of the M–O bond length with increasing Si/O ratio. The smaller variation in Si/O ratio among the oxosilicates versus the variation in Si/N ratio among the nitridosilicates may have hampered the establishment of such a relationship so far.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the valuable input given by Prof. Dr J. Ruud van Ommen and Prof. Dr Pieter Dorenbos during the preparation of this manuscript. This research has received funding from the Netherlands Organisation for Scientific Research (NWO) as part of the Joint Research Project on Advanced Materials with the National Natural Science Foundation of China (NSFC).Notes and references
- R. J. Xie and H. T. Hintzen, J. Am. Ceram. Soc., 2013, 96, 665–687 CrossRef CAS.
- R. J. Xie and N. Hirosaki, Sci. Technol. Adv. Mater., 2007, 8, 588–600 CrossRef CAS.
- R. J. Xie, N. Hirosaki, Y. Q. Li and T. Takeda, Materials, 2010, 3, 3777–3793 CrossRef CAS.
- R. Mueller-Mach, G. Mueller, M. R. Krames, H. A. Höppe, F. Stadler, W. Schnick, T. Juestel and P. Schmidt, Phys. Status Solidi A, 2005, 202, 1727–1732 CrossRef CAS.
- R. J. Xie, N. Hirosaki, N. Kimura, K. Sakuma and M. Mitomo, Appl. Phys. Lett., 2007, 90, 191101 CrossRef.
- S. E. Brinkley, N. Pfaff, K. A. Denault, Z. J. Zhang, H. T. Hintzen, R. Seshadri, S. Nakamura and S. P. DenBaars, Appl. Phys. Lett., 2011, 99, 241106 CrossRef.
- H. T. J. M. Hintzen and M. C. M. Van de Sanden, U.S. Pat., 12/282524, 2007 Search PubMed.
- O. M. ten Kate, M. de Jong, H. T. Hintzen and E. van der Kolk, J. Appl. Phys., 2013, 114, 084502 CrossRef.
- K. Van den Eeckhout, P. F. Smet and D. Poelman, Materials, 2011, 4, 980–990 CrossRef CAS PubMed.
- R. Withnall, J. Silver, G. R. Fern, T. G. Ireland, A. L. Lipman and B. Patel, J. Soc. Inf. Disp., 2008, 16, 359–366 CrossRef CAS.
- S. Hampshire, Mater. Sci. Forum, 2009, 606, 27–41 CrossRef CAS.
- M. Zeuner, S. Pagano and W. Schnick, Angew. Chem., Int. Ed., 2011, 50, 7754–7775 CrossRef CAS PubMed.
- S. Hampshire, H. K. Park, D. P. Thompson and K. H. Jack, Nature, 1978, 274, 880–882 CrossRef CAS.
- R. J. Xie, N. Hirosaki, M. Mitomo, Y. Yamamoto, T. Suehiro and K. Sakuma, J. Phys. Chem. B, 2004, 108, 12027–12031 CrossRef CAS.
- J. W. H. van Krevel, J. W. T. van Rutten, H. Mandal, H. T. Hintzen and R. Metselaar, J. Solid State Chem., 2002, 165, 19–24 CrossRef CAS.
- K. Uheda, N. Hirosaki, Y. Yamamoto, A. Naito, T. Nakajima and H. Yamamoto, Electrochem. Solid-State Lett., 2006, 9, H22–H25 CrossRef CAS.
- R. J. Xie, N. Hirosaki, H. L. Li, Y. Q. Li and M. Mitomo, J. Electrochem. Soc., 2007, 154, J314–J319 CrossRef CAS.
- Y. Q. Li, A. C. A. Delsing, G. de With and H. T. Hintzen, Chem. Mater., 2005, 17, 3242–3248 CrossRef CAS.
- V. Bachmann, T. Justel, A. Meijerink, C. Ronda and P. J. Schmidt, J. Lumin., 2006, 121, 441–449 CrossRef CAS.
- W. Sinclair and A. E. Ringwood, Nature, 1978, 272, 714–715 CrossRef CAS.
- J. W. H. van Krevel, H. T. Hintzen, R. Metselaar, L. Le Gendre and R. Marchand, Solid State Sci., 2001, 3, 49–56 CrossRef CAS.
- Y. Laurent and J. Lang, C. R. Seances Acad. Sci., Ser. C, 1966, 262, 103–106 CAS.
- H. Yamane and H. Morito, Inorg. Chem., 2013, 52, 5559–5563 CrossRef CAS PubMed.
- M. Zeuner, S. Pagano, P. Matthes, D. Bichler, D. Johrendt, T. Harmening, R. Pöttgen and W. Schnick, J. Am. Chem. Soc., 2009, 131, 11242–11248 CrossRef CAS PubMed.
- H. Huppertz and W. Schnick, Chem. – Eur. J., 1997, 3, 249–252 CrossRef CAS PubMed.
- T. Yamashita, S. Kuwano, K. Kuriyama and K. Kushida, Phys. Status Solidi C, 2015, 12, 845–848 CrossRef CAS.
- J. Y. Ding, Q. S. Wu, Y. Y. Li, Q. Long, C. Wang and Y. H. Wang, J. Am. Ceram. Soc., 2015, 98, 2523–2527 CrossRef CAS.
- Y. Q. Li, N. Hirosaki, R. J. Xie, T. Takeka and M. Mitomo, J. Solid State Chem., 2009, 182, 301–311 CrossRef CAS.
- P. Dorenbos, J. Phys.: Condens. Matter, 2005, 17, 8103–8111 CrossRef CAS.
- P. Dorenbos, J. Phys.: Condens. Matter, 2003, 15, 8417–8434 CrossRef CAS.
- P. Dorenbos, Chem. Mater., 2005, 17, 6452–6456 CrossRef CAS.
- K. Liddell, D. P. Thompson and S. J. Teat, J. Eur. Ceram. Soc., 2005, 25, 49–54 CrossRef CAS.
- K. Liddell, D. P. Thompson, T. Brauniger and R. K. Harris, J. Eur. Ceram. Soc., 2005, 25, 37–47 CrossRef CAS.
- P. Yang, H.-K. Fun, I. A. Rahman and M. I. Saleh, Ceram. Int., 1995, 21, 137–142 CrossRef CAS.
- J. Schneider, F. Frey, N. Johnson and K. Laschke, Z. Kristallogr., 1994, 209, 328–333 CAS.
- J. Z. Jiang, K. Ståhl, R. W. Berg, D. J. Frost, T. J. Zhou and P. X. Shi, Europhys. Lett., 2000, 51, 62–67 CrossRef CAS.
- M. Casas-Cabanas, H. Santner and M. R. Palacin, J. Solid State Chem., 2014, 213, 152–157 CrossRef CAS.
- R. Juza, H. H. Weber and E. Meyersimon, Z. Anorg. Allg. Chem., 1953, 273, 48–64 CrossRef CAS.
- S. Pagano, M. Zeuner, S. Hug and W. Schnick, Eur. J. Inorg. Chem., 2009, 1579–1584 CrossRef CAS.
- M. Orth and W. Schnick, Z. Anorg. Allg. Chem., 1999, 625, 1426–1428 CrossRef CAS.
- R. J. Bruls, H. T. Hintzen, R. Metselaar and C. K. Loong, J. Phys. Chem. Solids, 2000, 61, 1285–1293 CrossRef CAS.
- P. Bielec and W. Schnick, Angew. Chem., 2017, 129, 4888–4891 CrossRef.
- F. Ottinger and R. Nesper, Z. Anorg. Allg. Chem., 2005, 631, 1597–1602 CrossRef CAS.
- Z. A. Gál, P. M. Mallinson, H. J. Orchard and S. J. Clarke, Inorg. Chem., 2004, 43, 3998–4006 CrossRef PubMed.
- S. M. Hick, M. I. Miller, R. B. Kaner and R. G. Blair, Inorg. Chem., 2012, 51, 12626–12629 CrossRef CAS PubMed.
- T. Schlieper and W. Schnick, Z. Anorg. Allg. Chem., 1995, 621, 1037–1041 CrossRef CAS.
- S. R. Römer, C. Braun, O. Oeckler, P. J. Schmidt, P. Kroll and W. Schnick, Chem. – Eur. J, 2008, 14, 7892–7902 CrossRef PubMed.
- T. Schlieper, W. Milius and W. Schnick, Z. Anorg. Allg. Chem., 1995, 621, 1380–1384 CrossRef CAS.
- G. Pilet, H. A. Höppe, W. Schnick and S. Esmaeilzadeh, Solid State Sci., 2005, 7, 391–396 CrossRef CAS.
- F. Stadler, O. Oeckler, J. Senker, H. A. Höppe, P. Kroll and W. Schnick, Angew. Chem., Int. Ed., 2005, 44, 567–570 CrossRef CAS PubMed.
- H. Yamane and F. J. DiSalvo, J. Alloys Compd., 1996, 240, 33–36 CrossRef CAS.
- F. Stadler and W. Schnick, Z. Anorg. Allg. Chem., 2007, 633, 589–592 CrossRef CAS.
- H. Huppertz and W. Schnick, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1997, 53, 1751–1753 Search PubMed.
- C. Schmolke, D. Bichler, D. Johrendt and W. Schnick, Solid State Sci., 2009, 11, 389–394 CrossRef CAS.
- H. Yamane, T. Nagura and T. Miyazaki, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2014, 70, i23–i24 CAS.
- M. Woike and W. Jeitschko, Inorg. Chem., 1995, 34, 5105–5108 CrossRef CAS.
- C. Schmolke, O. Oeckler, D. Bichler, D. Johrendt and W. Schnick, Chem. – Eur. J., 2009, 15, 9215–9222 CrossRef CAS PubMed.
- T. Schlieper and W. Schnick, Z. Anorg. Allg. Chem., 1995, 621, 1535–1538 CrossRef CAS.
- S. Lupart and W. Schnick, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2009, 65, i43 CAS.
- T. Schlieper and W. Schnick, Z. Kristallogr., 1996, 211, 254 CAS.
- S. Pagano, S. Lupart, S. Schmiechen and W. Schnick, Z. Anorg. Allg. Chem., 2010, 636, 1907–1909 CrossRef CAS.
- S. Schmiechen, F. Nietschke and W. Schnick, Eur. J. Inorg. Chem., 2015, 1592–1597, DOI:10.1002/ejic.201403178.
- C. Poesl and W. Schnick, Chem. Mater., 2017, 29, 3778–3784 CrossRef CAS.
- S. Lupart, S. Pagano, O. Oeckler and W. Schnick, Eur. J. Inorg. Chem., 2011, 2118–2123, DOI:10.1002/ejic.201100115.
- S. Lupart and W. Schnick, Z. Anorg. Allg. Chem., 2012, 638, 2015–2019 CrossRef CAS.
- M. Zeuner, S. Pagano, S. Hug, P. Pust, S. Schmiechen, C. Scheu and W. Schnick, Eur. J. Inorg. Chem., 2010, 4945–4951 CrossRef CAS.
- S. Lupart, M. Zeuner, S. Pagano and W. Schnick, Eur. J. Inorg. Chem., 2010, 2636–2641 CrossRef CAS.
- S. Schmiechen, H. Schneider, P. Wagatha, C. Hecht, P. J. Schmidt and W. Schnick, Chem. Mater., 2014, 26, 2712–2719 CrossRef CAS.
- S. Schmiechen, P. Strobel, C. Hecht, T. Reith, M. Siegert, P. J. Schmidt, P. Huppertz, D. Wiechert and W. Schnick, Chem. Mater., 2015, 27, 1780–1785 CrossRef CAS.
- H. Yamane and H. Morito, J. Alloys Compd., 2013, 555, 320–324 CrossRef CAS.
- O. M. ten Kate, T. Vranken, E. van der Kolk, A. P. J. Jansen and H. T. Hintzen, J. Solid State Chem., 2014, 213, 126–131 CrossRef CAS.
- H. Huppertz and W. Schnick, Angew. Chem., Int. Ed. Engl., 1997, 36, 2651–2652 CrossRef CAS.
- H. Huppertz, O. Oeckler, A. Lieb, R. Glaum, D. Johrendt, M. Tegel, R. Kaindl and W. Schnick, Chem. – Eur. J., 2012, 18, 10857–10864 CrossRef CAS PubMed.
- H. Huppertz and W. Schnick, Z. Anorg. Allg. Chem., 1998, 624, 371–374 CrossRef CAS.
- D. Porob, N. Karkada, N. P. Kumar and A. Setlur, ECS Trans., 2012, 41, 27–38 CAS.
- Y. Q. Li, C. M. Fang, G. de With and H. T. Hintzen, J. Solid State Chem., 2004, 177, 4687–4694 CrossRef CAS.
- C. M. Fang, Y. Q. Li, H. T. Hintzen and G. de With, J. Mater. Chem., 2003, 13, 1480–1483 RSC.
- H. Huppertz and W. Schnick, Z. Anorg. Allg. Chem., 1997, 623, 212–217 CrossRef CAS.
- R. Marchand, Y. Laurent, J. Lang and M. T. Le Bihan, Acta Crystallogr., Sect. B: Struct. Sci., 1969, 25, 2157–2160 CrossRef.
- R. Grün, Acta Crystallogr., Sect. B: Struct. Sci., 1979, 35, 800–804 CrossRef.
- Z. Inoue, M. Mitomo and N. Ii, J. Mater. Sci., 1980, 15, 2915–2920 CrossRef CAS.
- H. Huppertz and W. Schnick, Angew. Chem., Int. Ed. Engl., 1996, 35, 1983–1984 CrossRef CAS.
- A. Zerr, G. Miehe, G. Serghiou, M. Schwarz, E. Kroke, R. Riedel, H. Fueß, P. Kroll and R. Boehler, Nature, 1999, 400, 340–342 CrossRef CAS.
- W. Schnick and H. Huppertz, Chem. – Eur. J., 1997, 3, 679–683 CrossRef CAS.
- P. Dorenbos, J. Lumin., 2005, 111, 89–104 CrossRef CAS.
- P. Dorenbos, Opt. Mater., 2017, 69, 8–22 CrossRef CAS.
- Y. Q. Li, N. Hirosaki, R. J. Xie, T. Takeda and M. Mitomo, J. Lumin., 2010, 130, 1147–1153 CrossRef CAS.
- T. Boyko, A. Hunt, A. Zerr and A. Moewes, Phys. Rev. Lett., 2013, 111, 097402 CrossRef CAS PubMed.
- L. Museur, A. Zerr and A. Kanaev, Sci. Rep., 2016, 6, 18523 CrossRef CAS PubMed.
- Y. Takeuchi, T. Yamashita, K. Kuriyama and K. Kushida, J. Solid State Electrochem., 2016, 20, 1885–1888 CrossRef CAS.
- J. Y. Ding, Y. Y. Li, Q. S. Wu, Q. Long, C. Wang and Y. H. Wang, J. Mater. Chem. C, 2015, 3, 8542–8549 RSC.
- G. P. Dubrovskii, A. M. Zykov and B. V. Chernovets, Inorg. Mater., 1981, 17, 1059–1063 Search PubMed.
- C. J. Duan, X. J. Wang, W. M. Otten, A. C. A. Delsing, J. T. Zhao and H. T. Hintzen, Chem. Mater., 2008, 20, 1597–1605 CrossRef CAS.
- T. de Boer, T. D. Boyko, C. Braun, W. Schnick and A. Moewes, Phys. Status Solidi RRL, 2015, 9, 250–254 CrossRef CAS.
- Y. Q. Li, N. Hirosaki, R. J. Xie, T. Takada, Y. Yamamoto, M. Mitomo and K. Shioi, Int. J. Appl. Ceram. Technol., 2010, 7, 787–802 CrossRef CAS.
- X. M. Wang, X. Zhang, S. Ye and X. P. Jing, Dalton Trans., 2013, 42, 5167–5173 RSC.
- H. Chen, J. Ding, X. Ding, X. Wang, Y. Cao, Z. Zhao and Y. Wang, Inorg. Chem., 2017, 56, 10904–10913 CrossRef CAS PubMed.
- W. A. Groen, M. J. Kraan and G. Dewith, J. Mater. Sci., 1994, 29, 3161–3166 CrossRef CAS.
- Y. Q. Li, J. E. J. van Steen, J. W. H. van Krevel, G. Botty, A. C. A. Delsing, F. J. DiSalvo, G. de With and H. T. Hintzen, J. Alloys Compd., 2006, 417, 273–279 CrossRef CAS.
- Y. Q. Li, G. de With and H. T. Hintzen, J. Lumin., 2006, 116, 107–116 CrossRef CAS.
- L. Chen, R. H. Liu, W. D. Zhuang, Y. H. Liu, Y. S. Hu, X. L. Ma and B. Hu, J. Rare Earths, 2016, 34, 30–35 CrossRef CAS.
- X. Q. Piao, T. Horikawa, H. Hanzawa and K. Machida, Appl. Phys. Lett., 2006, 88, 161908 CrossRef.
- K. Shioi, N. Hirosaki, R. J. Xie, T. Takeda and Y. Q. Li, J. Mater. Sci., 2008, 43, 5659–5661 CrossRef CAS.
- C.-W. Yeh, Y.-P. Liu, Z. R. Xiao, Y.-K. Wang, S.-F. Hu and R.-S. Liu, J. Mater. Chem., 2012, 22, 5828–5834 RSC.
- X. Piao, K. I. Machida, T. Horikawa and H. Hanzawa, Appl. Phys. Lett., 2007, 91, 041908 CrossRef.
- Y. Q. Li, A. C. A. Delsing, R. Metslaar, G. de With and H. T. Hintzen, J. Alloys Compd., 2009, 487, 28–33 CrossRef CAS.
- J. L. Qin, H. R. Zhang, B. F. Lei, H. W. Dong, Y. L. Liu, J. X. Meng, M. T. Zheng and Y. Xiao, J. Lumin., 2014, 152, 230–233 CrossRef CAS.
- O. M. ten Kate, H. T. Hintzen, P. Dorenbos and E. van der Kolk, J. Mater. Chem., 2011, 21, 18289–18294 RSC.
- T. Suehiro, N. Hirosaki, R. J. Xie and T. Sato, Appl. Phys. Lett., 2009, 95, 051903 CrossRef.
- Y. Zhou, Y. I. Yoshizawa, K. Hirao, Z. Lenčéš and P. Šajgalík, J. Eur. Ceram. Soc., 2011, 31, 151–157 CrossRef CAS.
- P. Strobel, V. Weiler, C. Hecht, P. J. Schmidt and W. Schnick, Chem. Mater., 2017, 29, 1377–1383 CrossRef CAS.
- Q. Wu, J. Ding, Y. Li, X. Wang and Y. Wang, J. Lumin., 2017, 186, 144–151 CrossRef CAS.
- O. M. ten Kate, H. T. Hintzen and E. van der Kolk, J. Phys.: Condens. Matter, 2014, 26, 385502 CrossRef CAS PubMed.
- T. Kurushima, G. Gundiah, Y. Shimomura, M. Mikami, N. Kijima and A. K. Cheetham, J. Electrochem. Soc., 2010, 157, J64–J68 CrossRef CAS.
- Y. Q. Li, G. de With and H. T. Hintzen, J. Alloys Compd., 2004, 385, 1–11 CrossRef CAS.
- C. M. Fang, H. T. Hintzen and G. De With, Recent Res. Dev. Mater. Sci., 2003, 4, 283–291 CAS.
- Y. Jia, A. Miglio, S. Poncé, X. Gonze and M. Mikami, Phys. Rev. B, 2016, 93, 155111 CrossRef.
- Z. Huang, F. Chen, J. Zhang, Q. Shen and L. Zhang, RSC Adv., 2017, 7, 8779–8785 RSC.
- W. H. Baur, Acta Crystallogr., Sect. B: Struct. Sci., 1978, 34, 1751–1756 Search PubMed.
- G. E. Brown and G. V. Gibbs, Am. Mineral., 1969, 54, 1528–1539 CAS.
- J. V. Smith and S. W. Bailey, Acta Crystallogr., 1963, 16, 801–811 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7tc04259k |
| This journal is © The Royal Society of Chemistry 2017 |