Effects of line defects on the electronic and optical properties of strain-engineered WO3 thin films†
Abstract
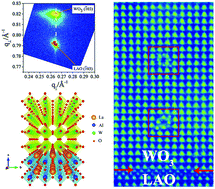
Tungsten oxide (WO3) is a promising material with a wide spectrum of important applications including smart windows, clean energy, and gas sensing. A variety of ionic defects in WO3 have attracted much attention due to their ability to greatly enhance these functionalities. In this work, we report the discovery of a new line defect in WO3 epitaxial thin films obtained via a strain engineering approach, and the modification of electronic structures in strain engineered WO3 films. This unique line defect observed by scanning transmission electron microscopy (STEM) can be regarded as an A-site deficient pseudo-perovskite cell, rotated by 45 degrees. By analyzing the distinct electronic and optical properties of these strain-engineered line defect phases, we show the emergence of an intriguing local hole channel along the line defects and highly tunable band structures, which can be harnessed in photocatalysis and electrochromism. Such defect effects induced by strain can lead to novel functionalities in artificially designed oxide heterostructures.


 Please wait while we load your content...
Please wait while we load your content...