Open Access Article
Open Access ArticleFunctionally graded ferroelectric polyetherimide composites for high temperature sensing
H.
Khanbareh
 *abc,
M.
Hegde
d,
J. C.
Bijleveld
b,
S.
van der Zwaag
b and
P.
Groen
be
*abc,
M.
Hegde
d,
J. C.
Bijleveld
b,
S.
van der Zwaag
b and
P.
Groen
be
aMaterials and Structures Research Center (MAST), Department of Mechanical Engineering, University of Bath, Claverton Down, Bath, UK. E-mail: h.khanbareh@bath.ac.uk
bNovel Aerospace Materials Group, Faculty of Aerospace Engineering, Delft University of Technology, Kluyverweg 1, Delft, The Netherlands
cMaterials Innovation Institute (M2i), Elektronicaweg 25, Delft, The Netherlands
dVirginia Tech, Department of Chemistry, Hahn Hall South, 3007, Blacksburg, VA 24061, USA
eHolst Center, TNO, High Tech Campus 31, Eindoven, The Netherlands
First published on 4th September 2017
Abstract
High temperature ferroelectrics for thermally stable devices that can detect pressure and temperature are of great industrial interest. Here we describe composites of lead titanate (PT) particle-polyetherimide (PEI) polymers with stable dielectric and piezoelectric properties over a broad range of temperature and frequency. The reported materials have a low dielectric loss (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ ∼ 0.001 at 1 kHz) and a high piezoelectric voltage coefficient of 100 mV m N−1 at record temperatures of 175 °C. We demonstrate that a small ceramic loading leads to a significant change in thermally stable piezoelectric behavior, while the processability as well as mechanical properties remain comparable to those of the neat polymer. Careful design of the microstructure is performed by dielectrophoretic assembly of ferroelectric PT micro-particles to induce micro-wire configurations, which is shown to be a key element in attaining high functionality at low ceramic loading. Thermal imidization of the composites is performed in two steps, first partial imidization at 60 °C to form free standing films containing polyamic acid, followed by full imidization at 200 °C and 300 °C. The presence of highly polar polyamic acid results in higher dielectric permittivity and electrical conductivity that facilitate efficient poling. Upon complete imidization of the films at 300 °C the dielectric and piezoelectric properties are tested at elevated temperatures. A fully imidized composite contains completely closed imide groups, resulting in a thermally stable material with a very low dielectric loss that maintains more than 85% of its room temperature piezoelectric sensitivity up to 175 °C. The room temperature piezoelectric voltage coefficient shows more than 400% improvement over that of PT ceramics.
δ ∼ 0.001 at 1 kHz) and a high piezoelectric voltage coefficient of 100 mV m N−1 at record temperatures of 175 °C. We demonstrate that a small ceramic loading leads to a significant change in thermally stable piezoelectric behavior, while the processability as well as mechanical properties remain comparable to those of the neat polymer. Careful design of the microstructure is performed by dielectrophoretic assembly of ferroelectric PT micro-particles to induce micro-wire configurations, which is shown to be a key element in attaining high functionality at low ceramic loading. Thermal imidization of the composites is performed in two steps, first partial imidization at 60 °C to form free standing films containing polyamic acid, followed by full imidization at 200 °C and 300 °C. The presence of highly polar polyamic acid results in higher dielectric permittivity and electrical conductivity that facilitate efficient poling. Upon complete imidization of the films at 300 °C the dielectric and piezoelectric properties are tested at elevated temperatures. A fully imidized composite contains completely closed imide groups, resulting in a thermally stable material with a very low dielectric loss that maintains more than 85% of its room temperature piezoelectric sensitivity up to 175 °C. The room temperature piezoelectric voltage coefficient shows more than 400% improvement over that of PT ceramics.
1 Introduction
High temperature piezoelectric materials for application in automotive, aerospace and energy production have been a growing area of research.1–3 In automotive electronics, repeated thermal cycles up to 150 °C and temperatures as high as 500 °C are reported.4 In the aerospace industry, structural health monitoring of the engines requires sensors to be as close as possible to the engine, leading to exposure to high temperatures.5,6 Moreover, exploration of new sources for clean energy, such as nuclear and wind power, as well as geothermal and electrical energy, has significantly motivated the development of high temperature electronic materials.7 High temperature sensors for structure health monitoring can ensure enhanced lifetime and reliability, less maintenance and downtime, and can thus reduce the overall cost of renewable energy sources.8,9 Piezoelectric materials can also be used to harvest mechanical energy from mechanical strain or vibrations present in the environment. An example of energy harvesting under extreme conditions is in oil producing wells, where the ambient pressures may reach 200 MPa, and the temperature reaches 200 °C. In this case local power production is crucial, since transmitting power from the surface is complicated, due to the difficulty in making reliable electrical connections in harsh environments.10The use of piezopolymers in those applications is limited by their low operating temperatures. Polymer composites, however, have broader potential applications due to their excellent property tunability. Piezocomposites have been reported to be excellent sensing devices at room temperature offering a wide range of properties. However their usage in high temperature applications has been limited, due to the reduced sensing capability of piezoceramics at elevated temperatures, increased conductivity and mechanical attenuation, as well as variation of the piezoelectric properties of the ceramic phase with temperature.11,12 Ferroelectric materials get depolarized and lose piezoelectricity above their respective Curie temperatures (Tc). Moreover the low glass transition temperature and high thermal expansion of the polymer matrix limit the operational temperature range of piezocomposites.13,14 To overcome this problem piezoceramics with a high Curie temperature can be embedded in high temperature polymers. In practice, the operating temperature must be substantially below the Curie temperature of the piezoceramic phase, in order to minimize thermal aging and property degradation.
Amorphous aromatic polyimides, as a class of high-performance polymers, are interesting candidates for the applications mentioned above.15–19 Growing interest in viable, multifunctional and lightweight materials for demanding space applications has led to the development of a new series of such polymers15,17,20 with superior mechanical, chemical and electrical properties. Some of the polymer systems in this family have been reported to show insignificant piezoelectric properties.15,16 One of the most widely reported piezo polyimides is a polymer containing a single nitrile group, (β-CN)APB/ODPA. As opposed to the well-known semicrystalline PVDF polymer family, the high temperature performance of this polyimide allows these films to retain 50% of the room temperature remnant polarization at temperatures up to 150 °C.16 However, the remnant polarization of this system is very low, 14 mC m−2, when poled at 100 kV mm−1, for 1 h above Tg. Therefore, the piezoelectric charge coefficient of this polyimide is much lower than that of PVDF.15,16 Limited chain mobility in the imidized film restricts the preferential alignment of the dipoles upon application of an electric field. To solve this problem, new polymers have been synthesized, with different types and concentrations of the polar groups.18 Despite the interesting research outcomes, the polyimide systems exhibit very low piezoelectric responses that are not high enough to attract commercial interest.15,17,18,21
The effect of processing parameters such as curing and poling conditions has also been investigated. The partially cured, corona poled polymers exhibited improved remanent polarization.21 In a more recent work in situ poling and imidization of partially cured (β-CN)APB/ODPA were investigated to maximize the degree of dipolar orientation.15 It has been shown that polyamic acid exhibits higher net dipole moment than the fully imidized polymer.15,17,18
To overcome these limitations, and to achieve adequate combinations of mechanical, thermal and functional properties ferroelectric ceramic particles are embedded within a polyimide polymer. Structuring the ceramic particles into a chain form configuration, by means of dielectrophoresis (DEP), has been previously reported to improve the dielectric and piezoelectric properties of piezocomposites in various polymer systems.13,22,23 In this work, processing of high temperature lead titanate–polyetherimide composites is presented. Among various kinds of commercially available ferroelectric ceramics for sensing, lead titanate (PT) is chosen based on the high Curie temperature of 490 °C, large spontaneous polarization and a small relative dielectric constant.2,24,25 Therefore, it serves as a viable candidate for integration within high temperature polyimide films. Amongst high performance thermoplastics, PEI polymers composed of all rigid aromatic and heterocyclic monomers show high decomposition temperatures in excess of 450 °C, high glass transition temperatures of above 200 °C, and outstanding mechanical properties (E of 3–4 GPa).26,27 The flexible ether bridge in the ODPA molecule can favorably influence the flexibility of the final polymer film.28 Here we present a detailed study of the manufacturing procedure, microstructural analysis and functional properties of high temperature piezocomposites with DEP assembled PT particles in a 4,4′-oxydiphthalic anhydride (ODPA)/3,4′-oxydianiline diamine (ODA) polymer matrix. By combining experiment and simulations an understanding of the macroscopic properties and tuning strategies is provided.
2 Experimental procedure
2.1 Composite manufacturing
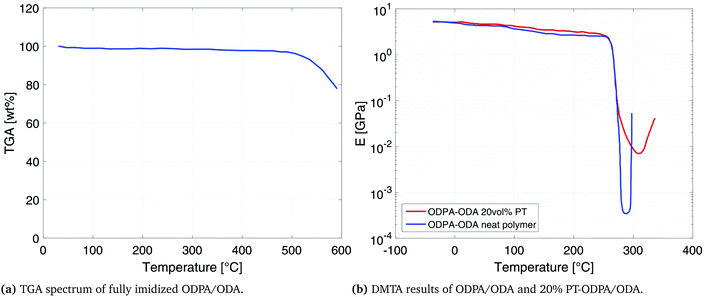
Polyetherimide polymers (PEI) are conventionally synthesized in two steps including precursor (polyamic acid (PAA)) formation followed by thermal imidization. The first step of preparation of PAA comprises the reaction of an aromatic diamine with an aromatic dianhydride in aprotic polar solvents. The scheme is shown in Fig. 1a. The PAA precursor in the current work was prepared via a solution of 4,4′-oxydiphthalic anhydride (ODPA)/3,4′-oxydianiline diamine (ODA) in N-methyl-2-pyrrolidone (NMP). The thermal properties of the films were determined by Thermogravimetric Analysis (TGA), using a Perkin Elmer Pyris Diamond, as well as Differential Scanning Calorimetry (DSC), using a Perkin Elmer Sapphire DSC. Samples were heated at a rate of 20 °C min−1 under a nitrogen atmosphere to 550 °C. Dynamic Mechanical Thermal Analysis (DMTA) was performed in the tensile mode, at a frequency of 1 Hz and a heating rate of 2.0 °C min−1, using films of approximate dimensions of 20 × 3 × 0.005 mm.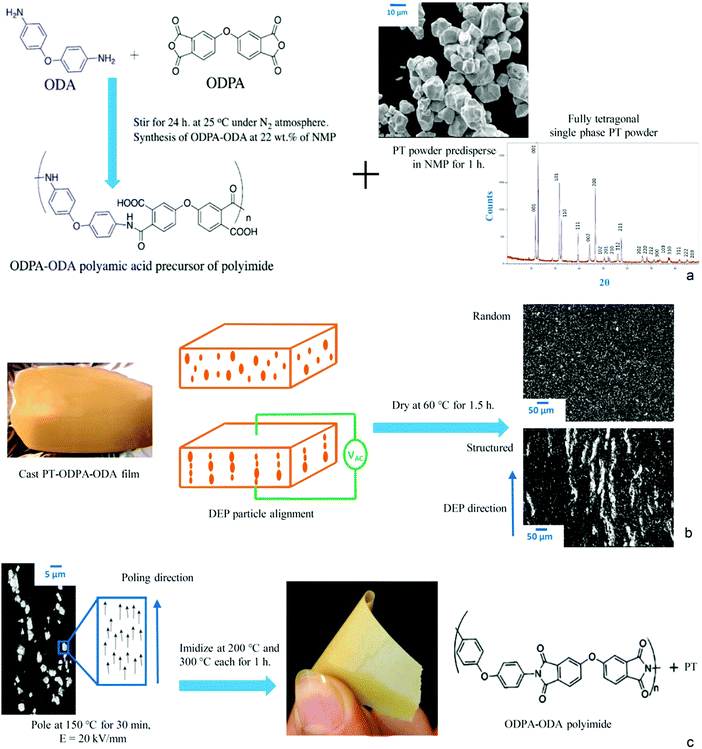 | ||
| Fig. 1 Production route of PT-ODPA–ODA composites. (a) Scheme of ODPA–ODA polymerization. (b) Dielectrophoresis structuring of particles. (c) Poling and imidization. | ||
Lead titanate (PT) ceramic powder, purchased from Sigma Aldrich, was calcined at 800 °C for 2 h to develop single phase tetragonal PbTiO3 as shown in Fig. 1a. The agglomerated powder was then dry-milled, using 5 mm zirconium balls for 2 h in a single G90 jar mill. The particle size distribution of milled powder in an aqueous solution with 10% isopropyl alcohol, measured using a Beckman Coulter LS230 laser diffraction analyzer was found to be d(50) = 3 mm. The powder was stored in a vacuum drying oven at 120 °C for 24 h prior to the experiment to avoid moisture absorption. The dried PT powder was predispered in NMP (Fig. 1a), stirred for 1 h, and added to polyamic-acid. The mixture was cast on an aluminum foil using a doctor blade, with an initial film thickness of 600 mm (Fig. 1b). Structuring of the particles in the polyamic-acid polymer was realized by a dielectrophoresis process, in which an electric field of 2 kV mm−1 and a frequency of 2 kHz was applied to the composite medium of particles dispersed in PAA, using a function generator (Agilent, 33210A) coupled to a high voltage amplifier (Radiant Technologies Inc., T6000HVA-2) at room temperature (RT) for 1 h in an Argon purged oven as shown in Fig. 1b. Once the structuring of the particles was realized, as shown in Fig. 1b, the film was dried at 60 °C for 1.5 h under the same atmosphere and electric field. The randomly dispersed samples were obtained by the process described above, only without applying an electric field by oven curing at 60 °C for 1.5 h, using inert Argon gas as the surrounding medium. The free standing films were then removed and cut into discs of 7 mm diameter. Au electrodes were sputtered on the samples, and they were poled at 150 °C for 30 min with an electric field of 20 kV mm−1. The poled films were then imidized in a vacuum oven at 200 °C and 300 °C, each for 1 h. The resulting flexible films have a fully imidized chemical structure as shown in Fig. 1c.
2.2 Measurement procedure
Novocontrol Broadband Dielectric Spectroscopy (BDS) is used in conjunction with a Cryostat high temperature sample cell and and an Aginlent E4991A impedance analyzer at 1 V and 1 kHz to measure the dielectric properties as well as electrical conductivity of the polymer films. The dielectric constant of the composites was determined by the parallel plate capacitor method using an Agilent 4263B LCR meter at 1 V and 1 kHz. The piezoelectric coefficient, d33, measurements were done using a Berlincourt type M3001 d33 meter, KCF technologies (State College, PA) at 110 Hz. Before performing the d33 measurements, the samples were grounded with their electrodes shorted at 100 °C for 24 h to remove any remaining space charges. To test the d33 values of the composites at elevated temperatures, a modified sample holder was manufactured and connected to the CF technologies PM3001 d33 meter, as shown in Fig. 2. The sample was placed on a copper electrode and heated uniformly using two integrated programmable heaters. The fixture was thermally insulated using Kapton foils, and the set-up was calibrated using reference PZT ceramics with known properties. It has to be noted that the maximum test temperature is above the advised operating temperature of the set-up. Static uniaxial tensile tests were performed using an Instron 3369 tensile testing machine with a 50 N static load cell (62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 291) with a speed of 0.1 mm min−1 at 20 °C. Five samples having approximate dimensions of 40 × 6 × 0.045 were tested and their average properties were calculated.
291) with a speed of 0.1 mm min−1 at 20 °C. Five samples having approximate dimensions of 40 × 6 × 0.045 were tested and their average properties were calculated.
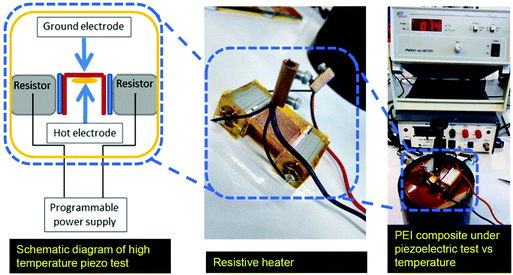 | ||
| Fig. 2 The set-up platform for high temperature piezoelectric test showing the sample holder used in conjunction with Berlincourt M3001 for d33 measurements at elevated temperatures. | ||
3 Results and discussion
3.1 Microstructure analysis
The effect of DEP structuring on the SEM microstructures of the 20% PT-ODPA/ODA composite samples is shown in Fig. 1b and c. PT particles are homogeneously dispersed in the random composite, and no sign of sedimentation is observed. It can be seen that during dielectrophoresis, ceramic particles form chain-like structures along the applied electric field direction. The chain-like particle assembly takes place as a result of attractive forces in the regions of the highest electric field gradient, as we have shown before computationally.29 The degree of alignment which affects the final dielectric and electroactive properties of the composites depends on the force acting on the particles, as a consequence of the imposed electric field.3.2 Thermo-mechanical analysis
Fig. 3a shows the thermogravimetric behavior of the obtained PEI material. An excellent thermal stability is observed and 2% weight loss is recorded at 520 °C. The DMTA results, presented in Fig. 3b, show a storage modulus of 4.0 GPa and 5.0 GPa, at room temperature for neat ODPA/ODA and ODPA/ODA with 20 vol% PT, respectively. The Tg remains unchanged at 265 °C which is in good agreement with the Tg of similarly reported compositions.30,31 The increase in high temperature storage modulus of the composite can be attributed to the enhancement of interaction between the polyetherimide matrix and the PT particles, which limits the segmental movement of the polymer.323.3 Dielectric and piezoelectric analysis
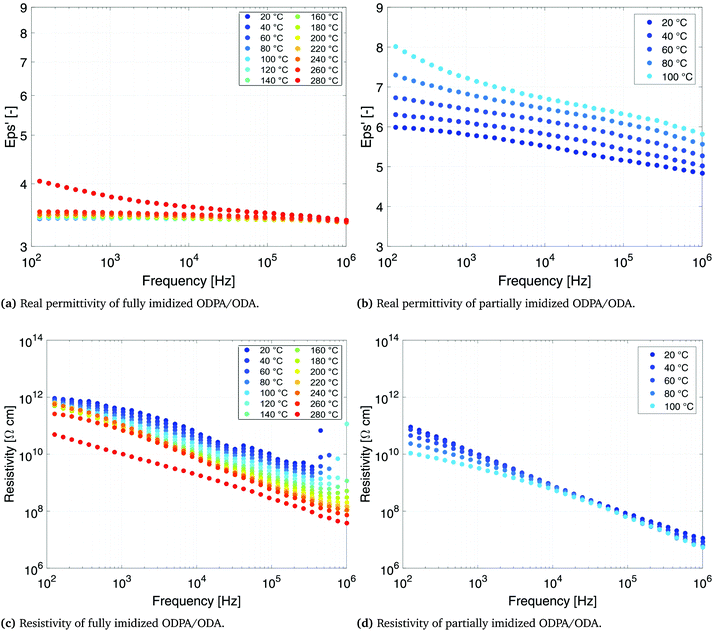
The dependence of dielectric permittivity and electrical resistivity of fully imidized ODPA/ODA (PEI), as well as partially imidized ODPA/ODA (PAA) on frequency and temperatures is presented in Fig. 4. The permittivity of all the samples decreases with frequency (Fig. 4a and b), but the decreasing degree of the partially imidized ODPA/ODA is much higher than that of the fully imidized ODPA/ODA as shown by Ding et al.33For the fully imidized polymer at temperatures below Tg the polymer shows a stable dielectric behavior34 with dielectric permittivity values ranging from 3.3 to 3.4 (Fig. 4a). Increasing the frequency from 1 MHz to 100 Hz results in a slight decrease in permittivity, which can be attributed to the dipolar dispersion. In other words dipoles gradually cannot follow the applied external field as the frequency increases.30,35,36 As the temperature approaches the glass transition temperature of fully imidized ODPA/ODA (260 °C) the dielectric permittivity increases due to the enhanced dipole motion.37,38 At low temperatures mainly electronic and atomic polarizations contribute to the permittivity.36 Similar behavior has been reported for (β-CN) APB/ODPA polyimides.20
The partially imidized ODPA/ODA film shows a higher dielectric permittivity than the fully imidized ODPA/ODA film, as PAA possesses more polar groups (–COOH) than PEI, as shown in Fig. 1a. Furthermore a more significant frequency dependent permittivity behavior is observed for partially imidized ODPA/ODA (Fig. 4b). The increase of dielectric permittivity at low frequencies can be contributed to higher interface polarization.39 The structures of dianhydrides have been shown to influence the dielectric properties, since ketone (benzophenone) groups are easily polarized in the electric field.40
The resistivity plots (Fig. 4c and d) show that the electrical conductivity of partially imidized ODPA/ODA at 100 °C is more than two orders of magnitude higher than that of fully imidized ODPA/ODA at this temperature. This is in agreement with the results of Park et al., who investigated the effect of processing parameters such as curing conditions on (β-CN) APB/ODPA systems.15 It has been shown that the partially cured (β-CN)APB/ODPA, in other words polyamic acid, exhibits a higher net dipole moment than the fully imidized polymer.15,17,18
The lower resistivity of the partially imidized ODPA/ODA (Fig. 4d) facilitates efficient poling of the embedded ferroelectric PT particles. During poling, the mobility of charges in the polymer matrix is a key parameter in defining the final poling efficiency. As the dielectric permittivity of PT is much higher than that of the polymer matrix41 the charge relaxation time is mainly governed by the electrical conductivity of the matrix. The higher conductivity of the partially imidized ODPA/ODA shortens the time required for the electric field acting on the ceramic inclusion to reach saturation, thereby making the poling of the ceramic phase more efficient.42,43 Moreover it eliminates the need to use conductive fillers such as single-wall carbon nanotubes (SWNTs) that have been reported to enhance the poling efficiency of (β-CN) APB/ODPA polyimides due to better dipolar alignment with the poling field.20 tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, as an indication of dielectric loss angle, is 0.001 and 0.02 for fully imidized and partially imidized ODPA/ODA films at 20 °C and 1 kHz, respectively. Increasing either temperature or frequency would increase the dielectric loss, as expected and reported.34 High electrical resistivity of fully imidized ODPA/ODA shows the good insulation performance of these materials.
δ, as an indication of dielectric loss angle, is 0.001 and 0.02 for fully imidized and partially imidized ODPA/ODA films at 20 °C and 1 kHz, respectively. Increasing either temperature or frequency would increase the dielectric loss, as expected and reported.34 High electrical resistivity of fully imidized ODPA/ODA shows the good insulation performance of these materials.
The effect of DEP structuring on the dielectric constant of 10%, 20% and 30% PT-ODPA/ODA composites is shown in Fig. 5a. The experimental data for random composites are fitted to Yamada's model, using an n value of 5.44 The composite is assumed to be a uniform distribution of ellipsoidal particles in an isotropic polymer matrix. The dielectric constant of the composite in the poling direction is given by
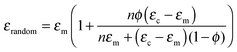 | (1) |
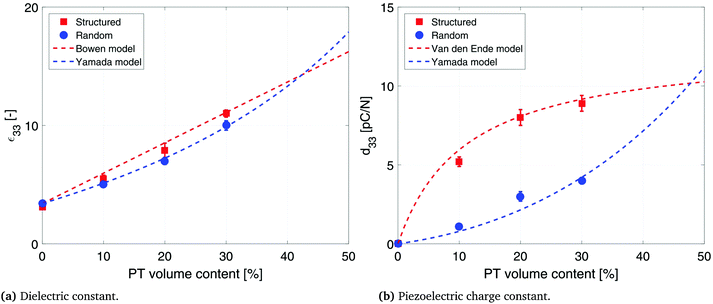 | ||
| Fig. 5 Dielectric and piezoelectric properties of structured and random 10%, 20% and 30% PT-ODPA/ODA composites with their associated models. | ||
Dielectric properties of the structured composites are fitted to Bowen's model22 as shown in Fig. 5a. According to this model, the composite is considered as a collection of particles aligned as chain-like structures along a specific direction separated by polymer gaps. The equation for the dielectric permittivity for such a composite is as follows:
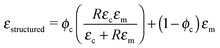 | (2) |
The influence of DEP structuring on piezoelectric charge constant, d33, of the composites is shown in Fig. 5b, where the experimental d33 values of random and structured 10%, 20% and 30% PT-ODPA/ODA composites are compared with the predictions of Yamada's and van den Ende's models.13 According to Yamada the piezoelectric charge constant, d33, of the composite in the poling direction is given by
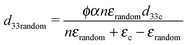 | (3) |
The model proposed by van den Ende et al.23 is applied to the structured composites. This model is an extension of Bowen's model,22 in which the d33 values of composites are obtained by modeling the particle-matrix sequences in the chains as two capacitors in series in the electrical domain, and two springs in series in the mechanical domain. The equation for the d33 values of the 1–3 composite is given by
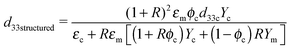 | (4) |
The interfacial interaction between the ceramic particles and the polymer influences the final dielectric and piezoelectric properties of the composite materials.45 The dielectric constant and piezoelectric charge constant of a composite are determined for understanding the nature of the interactions between the constituents of the composite. Lack of interfacial adhesion between the ceramic particles and the polymeric matrix would result in a decrease in the dielectric constant and piezoelectric coefficients of the composite materials.46,47 Analytical models used in this work account for ceramic–polymer interaction as well as size and shape of the constituent particles. The good agreement between the experimental data and predictions of the model is an indication of good interfacial adhesion and pore free interfaces, which is confirmed by SEM microstructures (as shown in Fig. 1c). It is observed that PT particles are fully encapsulated by the polymer, while aligning in the direction of the applied electric field in structured composites. Thus interface porosity has not been observed in either of the random and structured composites.
The d33 values of 20% and 30% PT-ODPA/ODA composites are tested as a function of temperature, as shown in Fig. 6. A remarkably stable behavior is observed over the temperature range from room temperature to 175 °C. Furthermore, the room temperature d33 value can be retained upon cooling back. This stability is caused by the thermally stable dielectric and piezoelectric properties of the high Tc lead titanate,48 as well as stable dielectric properties of the ODPA/ODA composites in this temperature range, as shown in Fig. 6. Similar behavior has been reported for other PEI polymers.34,49
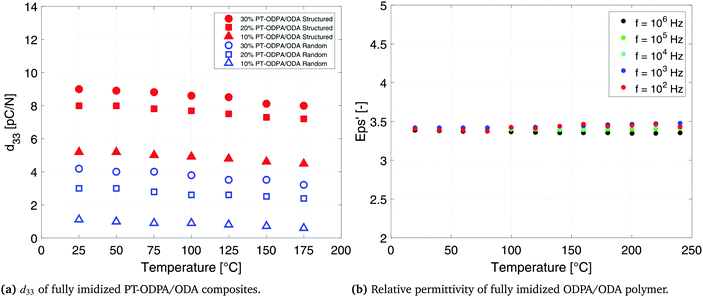 | ||
| Fig. 6 Temperature dependent behavior of the ODPA/ODA polymer and 10%, 20% and 30% random and structured PT-ODPA/ODA composites. | ||
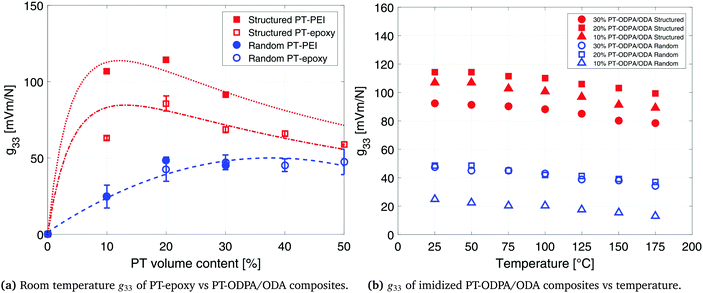
The piezoelectric voltage coefficient values, g33, at room temperature which were calculated by dividing the d33 values of the composites by their dielectric constant, are 48 mV m N−1 and 114 mV m N−1 for random and structured 20% PT-ODPA/ODA composites, respectively. The g33 values for random and structured 30% PT-ODPA/ODA composites are 45 mV m N−1 and 90 mV m N−1, respectively. The room temperature g33 values for the PT-ODPA/ODA composites are compared to those of PT-epoxy reference composites, as presented in our previous paper,13 in Fig. 7a. The DEP structured 20% PT-ODPA/ODA composites show 30% improvement in g33 compared to the structured 20% PT-epoxy composites, which is mainly due to their lower dielectric constant. The 20% PT-ODPA/ODA composites, with the highest g33, show a tensile strength of 50 MPa and a strain at a break of 2.6%. An elastic modulus of 4.7 GPa is measured, which is in good agreement with the DMTA results. The 20% PT-ODPA/ODA flexible composite films can be folded into a bending radius as small as 2 mm without any damage.
The g33 values of 10%, 20% and 30% PT-ODPA/ODA composites are calculated as a function of temperature and are shown in Fig. 7b. Structured 20% PT-ODPA/ODA composites maintain their high g33 values of over 100 mV m N−1 over the temperature range from room temperature to 175 °C. The stable g33 behavior of all composites over the mentioned temperature range is attributed to the thermally stable piezoelectric properties of the high Tc lead titanate,48 as well as stable dielectric properties of ODPA/ODA, which remain nearly independent of frequency in this temperature range, as shown in Fig. 6b. Piezopolymers such as poly(vinylidene fluoride) and poly(vinylidene fluoride-co-trifluoroethylene) (P(VDF-TrFE)) show a rapid decrease above 100 °C operating temperatures.50
4 Conclusions
This paper demonstrated the synthesis and characterization of novel high temperature piezoelectric composites by means of dielectrophoresis structuring. Fully imidized PT-ODPA/ODA composites, prepared by solution casting, show thermally stable dielectric and piezoelectric properties in the temperature range from 25 °C to 175 °C. Thermally stable functional properties of the high Tc lead titanate,48 as well as stable dielectric properties of the fully imidized polyetherimide polymer matrix result in an improved temperature functionality of these high performance composites. The uniqueness of the presented composite manufacturing technique lies in the process design based on the molecular structure of the polymer matrix. Firstly the ODPA/ODA polymer matrix is only partially imidized to maintain relatively high dielectric permittivity and electrical conductivity, due to the polar structure, to achieve high poling efficiency. Once the composites are fully poled, the matrix is fully imidized 300 °C. Upon full imidization the imide rings completely close, resulting in a thermally stable polymer with a very low dielectric loss. Therefore, composites of PT–PEI are shown to maintain more than 85% of room temperature piezoelectric sensitivity up to 175 °C, showing great potential for high temperature sensing and mechanical energy harvesting.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was carried out under project number M62.3.11438 in the framework of the Research Program of the Materials innovation institute M2i (http://www.m2i.nl).References
- L. Li, S. Zhang, Z. Xu, F. Wen, X. Geng, H. J. Lee and T. R. Shrout, J. Phys. D: Appl. Phys., 2013, 46, 165306 CrossRef PubMed.
- T. Stevenson, D. G. Martin, P. I. Cowin, A. Blumfield, A. J. Bell, T. P. Comyn and P. M. Weaver, J. Mater. Sci.: Mater. Electron., 2015, 26, 9256–9267 CrossRef CAS.
- X. Jiang, K. Kim, S. Zhang, J. Johnson and G. Salazar, Sensors, 2014, 14, 144–169 CrossRef CAS PubMed.
- S. Zhang and F. Yu, J. Am. Ceram. Soc., 2011, 94, 3153–3170 CrossRef CAS.
- I. Tumer and A. Bajwa, 35th Joint Propulsion Conference and Exhibit, Joint Propulsion Conferences, 1999.
- C. Boller, Int. J. Syst. Sci., 2000, 31, 1333–1349 CrossRef.
- Y. Sheiretov, D. Grundy, V. Zilberstein, N. Goldfine and S. Maley, IEEE Sens. J., 2009, 9, 1527–1536 CrossRef.
- H. J. Lee, S. Zhang, Y. Bar-Cohen and S. Sherrit, Sensors, 2014, 14, 14526–14552 CrossRef PubMed.
- Q. Xue, M. Stanton and G. Elfbaum, Proceedings of the IEEE Ultrasonics Symposium, 2003, pp. 1372–1375.
- H. J. Lee, S. Zhang, Y. Bar-Cohen and S. Sherrit, Sensors, 2014, 14, 14526–14552 CrossRef PubMed.
- F. Yu, Q. Lu, S. Zhang, H. Wang, X. Cheng and X. Zhao, J. Mater. Chem. C, 2015, 3, 329–338 RSC.
- D. Damjanovic, Rep. Prog. Phys., 1998, 61, 1267–1324 CrossRef CAS.
- H. Khanbareh, S. van der Zwaag and W. Groen, Smart Mater. Struct., 2014, 23, 105030 CrossRef.
- H. Khanbareh, S. van der Zwaag and W. A. Groen, J. Intell. Mater. Syst. Struct., 2017 DOI:10.1177/1045389X17689928.
- C. Park, Z. Ounaies, K. E. Wise and J. S. Harrison, Polymer, 2004, 45, 5417–5425 CrossRef CAS.
- G. M. Atkinson, R. E. Pearson, Z. Ounaies, C. Park, J. S. Harrison, S. Dogan and J. A. Midkiff, TRANSDUCERS 2003 – 12th International Conference on Solid-State Sensors, Actuators and Microsystems, Digest of Technical Papers, 2003, pp. 782–785.
- Z. Ounaies, C. Park, J. S. Harrison, J. G. Smith and J. Hinkley, Proc. SPIE-Int. Soc. Opt. Eng., 1999, 3669, 171–178 CrossRef CAS.
- Z. Ounaies, C. Park, J. S. Harrison, J. G. Smith and J. Hinkley, Proc. SPIE-Int. Soc. Opt. Eng., 1999, 3669, 171–178 CrossRef CAS.
- J. Simpson, Z. Ounaies and C. Fay, Materials Research Society Symposium-Proceedings, 1997, pp. 59–64.
- Z. Ounaies, C. Park, J. Harrison and P. Lillehei, J. Thermoplast. Compos. Mater., 2008, 21, 393–409 CrossRef CAS.
- C. Park, P. O. Su, J. Su, J. G. Smith Jr. and J. S. Harrison, Polarization Stability Of Amorphous Piezoelectric Polyimides, 1999 Search PubMed.
- C. P. Bowen, R. E. Newnham and C. A. Randall, J. Mater. Res., 1998, 13, 205–210 CrossRef CAS.
- D. van den Ende, B. Bory, W. Groen and S. van der Zwaag, J. Appl. Phys., 2010, 107, 024107 CrossRef.
- B. Jaffe, R. S. Roth and S. Marzullo, J. Appl. Phys., 1954, 25, 809–810 CrossRef CAS.
- R. N. R. C. Turner, P. A. Fuierer and T. Shrout, Appl. Acoust., 1994, 41, 299–324 CrossRef.
- X. Liu, M. Zhan, Y. Shen and K. Wang, J. Appl. Polym. Sci., 2011, 119, 3253–3263 CrossRef CAS.
- M. Hegde, U. Lafont, B. Norder, S. J. Picken, E. T. Samulski, M. Rubinstein and T. Dingemans, Macromolecules, 2013, 46, 1492–1503 CrossRef CAS.
- X. Zhang, B. Zhang, Y. Wu, D. Wang and T. Wang, J. Appl. Polym. Sci., 2017, 134 DOI:10.1002/app.44889.
- M. Gutiérrez, H. Khanbareh and S. van der Zwaag, Comput. Mater. Sci., 2016, 112(part A), 139–146 CrossRef.
- B. S. Kim, S. H. Bae, Y.-H. Park and J.-H. Kim, Macromol. Res., 2007, 15, 357–362 CrossRef CAS.
- N. G. Devaraju, E. S. Kim and B. I. Lee, Microelectron. Eng., 2005, 82, 71–83 CrossRef CAS.
- S.-H. Xie, B.-K. Zhu, X.-Z. Wei, Z.-K. Xu and Y.-Y. Xu, Composites, Part A, 2005, 36, 1152–1157 CrossRef.
- L. Ding, Y. Zhang, L. Liu, J. Hu and F. Lv, RSC Adv., 2016, 6, 56812–56818 RSC.
- Q. Chi, J. Sun, C. Zhang, G. Liu, J. Lin, Y. Wang, X. Wang and Q. Lei, J. Mater. Chem. C, 2014, 2, 172–177 RSC.
- W. Jang, D. Shin, S. Choi, S. Park and H. Han, Polymer, 2007, 48, 2130–2143 CrossRef CAS.
- D. Wang, B. Kurish, I. Treufeld, L. Zhu and L.-S. Tan, J. Polym. Sci., Part A: Polym. Chem., 2015, 53, 422–436 CrossRef CAS.
- C. P. Wong, Polymers for Electronic and Photonic Application, Elsevier, 2013 Search PubMed.
- I. Treufeld, D. Wang, B. Kurish, L.-S. Tan and L. Zhu, J. Mater. Chem. A, 2014, 2, 20683–20696 CAS.
- Broadband Dielectric Spectroscopy, ed. F. Kremer and A. Schonhals, Springer, 2004 Search PubMed.
- D. H. Wang, J. K. Riley, S. P. Fillery, M. F. Durstock, R. A. Vaia and L.-S. Tan, J. Polym. Sci., Part A: Polym. Chem., 2013, 51, 4998–5011 CrossRef CAS.
- H. Khanbareh, S. van der Zwaag and W. Groen, Smart Mater. Struct., 2015, 24, 5020 CrossRef.
- Y. T. Or, C. K. Wong, B. Ploss and F. G. Shin, J. Appl. Phys., 2003, 94, 3319–3325 CrossRef CAS.
- K. W. Kwok, S. T. Lau, C. K. Wong and F. G. Shin, J. Phys. D: Appl. Phys., 2007, 40, 6818–6823 CrossRef CAS.
- T. Yamada, T. Ueda and T. Kitayama, J. Appl. Phys., 1982, 53, 4328 CrossRef CAS.
- Y. Shen, Y. Lin and C.-W. Nan, Adv. Funct. Mater., 2007, 17, 2405–2410 CrossRef CAS.
- M. C. Araújo, C. Costa and S. Lanceros-Méndez, J. Non-Cryst. Solids, 2014, 387, 6–15 CrossRef.
- J. Yao, C. Xiong, L. Dong, C. Chen, Y. Lei, L. Chen, R. Li, Q. Zhu and X. Liu, J. Mater. Chem., 2009, 19, 2817–2821 RSC.
- B. Jaffe, W. Cook Jr. and H. Jaffe, Piezoelectric Ceramics, Academic Press Inc., London & New York, 3rd edn, 1971 Search PubMed.
- X. Fang, X. Liu, Z.-K. Cui, J. Qian, J. Pan, X. Li and Q. Zhuang, J. Mater. Chem. A, 2015, 3, 10005–10012 CAS.
- C. Baur, Y. Zhou, J. Sipes, S. Priya and W. Voit, Energy Harvesting and Systems Materials, Mechanisms, Circuits and Storage, 2014, 1, 167–177 Search PubMed.
| This journal is © The Royal Society of Chemistry 2017 |