Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Charge carrier trapping controlled by polymer blend phase dynamics
A.
Kunz
,
P. W. M.
Blom
and
J. J.
Michels
 *
*
Max Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: michels@mpip-mainz.mpg.de
First published on 21st February 2017
Abstract
It has recently been shown that diluting a semiconducting polymer with an insulating or large band gap host material can lead to elimination of charge trapping in the former. In this work we systematically study the role of the phase thermodynamics of such blends via tuning the miscibility between the semiconductor (here: MEH-PPV) and host (here: polystyrene or polyvinyl carbazole), by varying the molecular weight of the latter. We show that calculation of the ternary phase diagram of semiconductor, insulator and solvent can predict whether charge transport in the dry blend film will be trap-free or not. Blending MEH-PPV with 35 kg mol−1 polystyrene does not lead to alleviation of the trap-limited nature of the electron current due to strong segregation of the polymers and the formation of pure coexisting phases. In contrast, the electron current in miscible (1 kg mol−1 polystyrene) or partially miscible (30 kg mol−1 polyvinyl carbazole) blends increases by up to four orders of magnitude compared to the pristine semiconductor, together with a doubling in luminous efficiency of the corresponding light-emitting diode.
Introduction
Over half a decade ago Mark and Helfrich proposed a theory describing trap-limited electron transport in crystalline organic semiconductors in the space-charge-limited regime.1 They derived an expression that relates the current density in the material (J) at given voltage, permittivity and charge mobility to the densities of charge transport- and trapping-sites (Nc and Nt) according to: J ∼ Nc/Nrt. Here, r is at a temperature T given by: r = Tt/T with Tt the trap temperature, which characterizes the width of the energetic distribution of trap states. An important novelty at the time was that the theory was capable of accounting for a trap level that is distributed in energy rather than discrete. In case of an energetically distributed trap level the exponent r adopts a value larger than unity. Already two decades ago it was demonstrated that the electron transport in a poly(p-phenylene vinylene) (PPV) derivative is trap-limited and can be described using the Mark–Helfrich theory.2 To describe the electron current the energy level of these traps were considered to be exponentially distributed in energy,2 with r taking values in the range 4–5. In later studies it was found that the electron current in many conjugated polymers is trap limited, and can also be described by assuming a Gaussian density of trap states.3 Remarkably, it was found that the trap density is nearly equal for a large range of polymers, in the range 1017–1018 cm−3, with a mean energy level of around −3.6 eV.Only recently it has been realized that the above given scaling relation predicts that when both Nc and Nt are reduced by the same factor, for instance by diluting the semiconductor with a “host” material that does not contribute to the charge transport, the effect of charge trapping can be drastically reduced, leading to an increased electron current as long as electrical percolation is retained.4 The host material may either be a large bandgap semiconductor or an insulator. To all intents and purposes we will in the remainder of this paper refer to it as “insulator”.
Conjugated polymers are ideal model systems for testing this hypothesis since they can be dissolved in a solvent and hence easily be mixed with an insulating host. By separately measuring the hole- and electron current densities in single (charge) carrier devices, we experimentally demonstrated that diluting the light emitting polymer poly[2-methoxy-5-(2′-ethylhexyloxy)-p-phenylene vinylene] (MEH-PPV) in a nine-fold excess of the large bandgap material polyvinylcarbazole (PVK), fully alleviates the trap-limited nature of the electron current, which as a result becomes of similar magnitude as the hole current. In comparison, in pristine MEH-PPV the electron current is strongly trap-limited and 3–4 orders of magnitude lower than the hole current density. The balance in hole and electron currents led to a doubling in the luminous efficiency of organic light-emitting diodes (OLEDs) based on the MEH-PPV:PVK blend as active layer.
Notably, we observed reduced electron trapping despite the fact that the MEH-PPV:PVK blend exhibited pronounced macro-phase separation during solution casting. This is surprising at first glance, as it is understood that the necessary spatial separation for the dilution of adjacent trapping sites should rely on intimate mixing of semiconductor and host at the segmental level, rather than dispersion on macroscopic length scales. We explained the fact that the electron current increased nonetheless, by assuming that for the MEH-PPV:PVK blend under consideration demixing occurred in the limit of weak segregation. This implies that under thermodynamic control the phase domains comprise mixed phases containing both polymers, be it one in excess to the other. The occurrence of macro-phase separation itself was demonstrated by microscopy analysis, where the typical drop-like shapes convincingly showed phase separation to have occurred via liquid–liquid demixing. In this respect the choice of PVK as polymeric host material to dilute a polymeric semiconductor was a little unfortunate, as polymers are usually difficult to mix due to the low mixing entropy.5
In this work we elaborate on the miscibility of insulating host and semiconducting guest and demonstrate that we can actually control the dilution of the electron traps once the thermodynamics of the ternary blend of semiconductor, host and solvent is properly understood. Using Flory–Huggins theory we show that the blend's calculated phase diagram represents a qualitative but effective means to predict whether the electron current in the dry blend material would increase upon mixing due to dilution. For the present study we choose polystyrene (PS) as insulator, not only owing to its availability in a range of molecular weights, but also to prove the generality of our method of increasing OLED device performance by dilution. By comparing the present results with the mentioned recent findings on MEH-PPV:PVK blends,4 we show that the phase composition, rather than the question whether or not macro-phase separation occurs during solution casting, provides for the deciding argument governing the elimination of electron trapping.
Experimental
Poly[2-methoxy-5-(2-ethylhexyloxy)-1,4-phenylenevinylene] (MEH-PPV) with a weight-average molecular weight of![[M with combining overline]](https://www.rsc.org/images/entities/i_char_004d_0305.gif) w = 354 kg mol−1 and a polydispersity index (PDI) of 4 was synthesized according to the Gilch route.6 Polystyrene (PS) samples (
w = 354 kg mol−1 and a polydispersity index (PDI) of 4 was synthesized according to the Gilch route.6 Polystyrene (PS) samples (![[M with combining overline]](https://www.rsc.org/images/entities/i_char_004d_0305.gif) w = 35 kg mol−1, PDI = 1.09 and
w = 35 kg mol−1, PDI = 1.09 and ![[M with combining overline]](https://www.rsc.org/images/entities/i_char_004d_0305.gif) w = 1.1 kg mol−1, PDI = 1.15) were synthesized in house via anionic polymerization of styrene. In this work these PS samples are respectively named “PS35” and “PS1”, the number index referring to their weight-average molecular weight. MEH-PPV:PS blend solutions were prepared simply by dissolving weighed amounts of the polymers in chlorobenzene. Semiconductor-to-polystyrene weight ratios of 1
w = 1.1 kg mol−1, PDI = 1.15) were synthesized in house via anionic polymerization of styrene. In this work these PS samples are respectively named “PS35” and “PS1”, the number index referring to their weight-average molecular weight. MEH-PPV:PS blend solutions were prepared simply by dissolving weighed amounts of the polymers in chlorobenzene. Semiconductor-to-polystyrene weight ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, 1
0, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 1
3 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 were used. Polymer concentrations were tuned so as to obtain a final dry film thickness of ∼200 nm.
9 were used. Polymer concentrations were tuned so as to obtain a final dry film thickness of ∼200 nm.
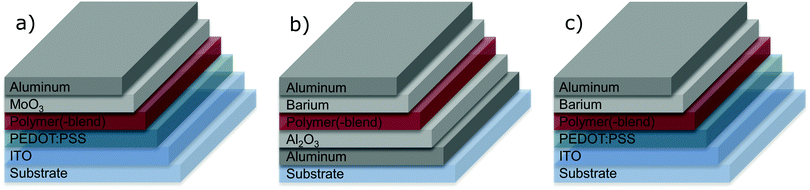
For the fabrication of hole-only (single carrier) devices (HODs, Fig. 1a) and polymer light-emitting diodes (PLEDs, Fig. 1c), glass–ITO substrates were cleaned using neutral soap and successively rinsed with de-ionized water, acetone, and 2-propanol. Each cleaning or rinsing step was performed for 10 min in an ultrasonic bath. Cleaned substrates were activated in UV-Ozone for 20 minutes for better wettability as well as removal of organic contaminants. A 55 nm thick film of poly(3,4-ethylenedioxythiophene) polystyrene sulfonate (PEDOT:PSS) (Heraeus Clevios 4083) was applied on top of the ITO layer by spin-coating from aqueous dispersion and subsequent annealing at 140 °C for ten minutes.
The substrates for electron-only (single carrier) devices (EODs, Fig. 1b) were fabricated using a slightly oxidized aluminum electrode as bottom contact, which was deposited onto the glass slide through a shadow mask by thermal evaporation. A ∼200 nm thick layer of the light-emitting polymer (LEP) or polymer blend was spin-coated on top of the PEDOT:PSS (HODs and PLEDs) or aluminum oxide (EODs). For the PLEDs and the EODs a top electrode of barium (nominally 5 nm) covered with 100 nm aluminum was evaporated through a shadow mask. Top electrodes for the HODs were fabricated by evaporating 10 nm MoO3, followed by a 100 nm Al capping layer.
Results and discussion
Many examples exist in literature where details on phase dynamics and morphology of semiconducting and electroactive blends provide for an a posteriori explanation of electronic phenomena observed on the device level.7–12 Here, we take the inverse approach and show that a priori estimation of a blend's phase behavior based on thermodynamic considerations can be used to predict optoelectronic behavior. We hence commence with calculating the ternary phase diagrams for the MEH-PPV:PS:chlorobenzene blends using Flory–Huggins theory.5 In order to tune the miscibility between semiconductor and insulator, two different PS samples are considered (see Experimental section), one with a ‘high’ molecular weight,![[M with combining overline]](https://www.rsc.org/images/entities/i_char_004d_0305.gif) w = 35 kg mol−1 (denoted PS35), and one with a low molecular weight,
w = 35 kg mol−1 (denoted PS35), and one with a low molecular weight, ![[M with combining overline]](https://www.rsc.org/images/entities/i_char_004d_0305.gif) w = 1.1 kg mol−1 (denoted PS1). Analogously, we here name the previously reported PVK-based sample “PVK30”, the number index referring to:
w = 1.1 kg mol−1 (denoted PS1). Analogously, we here name the previously reported PVK-based sample “PVK30”, the number index referring to: ![[M with combining overline]](https://www.rsc.org/images/entities/i_char_004d_0305.gif) w (PVK) = 30 kg mol−1.4 Details on the calculations of the ternary phase diagrams can be found in the Appendix.
w (PVK) = 30 kg mol−1.4 Details on the calculations of the ternary phase diagrams can be found in the Appendix.
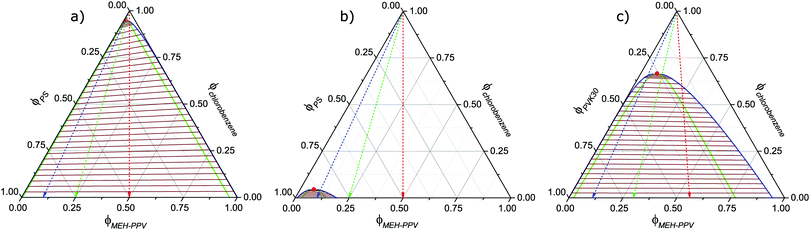
The phase diagrams calculated for the corresponding ternary blends are presented in Fig. 2a and b, together with the one for the recently studied MEH-PPV:PVK30:chlorobenzene blend (Fig. 2c). The limit of full miscibility is indicated by the binodal curve (solid blue line) above which a stable, single phase exists. In the region below the binodal, the miscibility gap, a driving force for demixing is present. For mean blend compositions beneath the green line, i.e., the spinodal, demixing is spontaneous. The positive tilt in the lines connecting the compositions of coexisting phases (“tie-lines”, brown), observed in Fig. 2a, is a consequence of MEH-PPV having a more favorable interaction with the solvent than polystyrene has (see Appendix). In contrast, Fig. 2c reveals hardly any solvent partitioning when using PVK instead of PS.
Comparing the phase diagrams in Fig. 2a and b shows that the size of the miscibility gap strongly depends on polystyrene molecular weight:† whereas it covers almost the phase diagram in case of PS35, it is (nearly) absent for PS1. The difference is explained by the increase in statistical entropy upon decreasing molecular size. Fig. 2c shows that the MEH-PPV:PVK30:chlorobenzene blend has a miscibility gap of intermediate size.‡ The fact that it is smaller than the one for MEH-PPV:PS35:chlorobenzene, despite the similar insulator molecular weight, is mainly a result of the less repulsive interaction between semiconductor and insulator (see Appendix).
During solution-casting of the blend, the mean polymer concentrations continuously increase due to on-going solvent evaporation. The mean composition-trajectory followed as a consequence of solvent evaporation is indicated in each phase diagram by the dashed arrows. The color of the arrows corresponds to different semiconductor![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) insulator weight ratios: 1
insulator weight ratios: 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (red), 1
1 (red), 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (green) and 1
3 (green) and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 (blue). Initially, all compositions lie in the single phase region above the binodal. Once evaporation pushes the composition into the miscibility gap phase separation may occur if the solvent fraction remains high enough to allow for sufficient molecular mobility. During evaporation the viscosity of the solution rises steeply as the polymer concentration increases. Eventually, mass transport completely arrests upon which the blend film solidifies, irrespective of phase separation to have occurred or not. This implies that the smaller the miscibility gap, the lower the probability of significant demixing to occur prior to solidification.
9 (blue). Initially, all compositions lie in the single phase region above the binodal. Once evaporation pushes the composition into the miscibility gap phase separation may occur if the solvent fraction remains high enough to allow for sufficient molecular mobility. During evaporation the viscosity of the solution rises steeply as the polymer concentration increases. Eventually, mass transport completely arrests upon which the blend film solidifies, irrespective of phase separation to have occurred or not. This implies that the smaller the miscibility gap, the lower the probability of significant demixing to occur prior to solidification.
Considering the above, for the MEH-PPV:PS1:chlorobenzene blend thermodynamic as well as kinetic arguments can be given for the polymers to remain mixed during film formation. In contrast, in case of MEH-PPV:PS35:chlorobenzene demixing is highly likely considering the very large miscibility gap. In this case even at high solvent concentrations a strong driving force for spontaneous demixing exists, irrespective of the polymer![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) polymer ratio. Furthermore, the fact that the binodal branches largely coincide with the axes of the composition domain suggests phase separation to result in virtually pure phases of MEH-PPV and PS35. Admittedly, due to the, at best, semi-quantitative nature of the Flory–Huggins model we cannot calculate the exact phase compositions. The important thing however is that the model predicts that should demixing result in a PS35-rich phase containing a residual amount of MEH-PPV, it is likely too little to overcome the percolation threshold for charge conduction. Vice versa, a possible residual fraction of PS35 in the MEH-PPV-rich phase is probably too small to cause noticeable trap dilution.
polymer ratio. Furthermore, the fact that the binodal branches largely coincide with the axes of the composition domain suggests phase separation to result in virtually pure phases of MEH-PPV and PS35. Admittedly, due to the, at best, semi-quantitative nature of the Flory–Huggins model we cannot calculate the exact phase compositions. The important thing however is that the model predicts that should demixing result in a PS35-rich phase containing a residual amount of MEH-PPV, it is likely too little to overcome the percolation threshold for charge conduction. Vice versa, a possible residual fraction of PS35 in the MEH-PPV-rich phase is probably too small to cause noticeable trap dilution.
Again, also with respect to phase composition the PVK30-based blend represents an intermediate case: although its miscibility gap is still rather substantial, the binodal curve is to a large extent remote from the axes of the composition domain. The latter feature is especially true for the branch representing the MEH-PPV-rich phase. For this blend the model hence predicts formation of coexisting phases having a mixed composition rather than comprising only one constituent each. Indeed, as we have recently shown,4 for this blend trap dilution and concomitant rise in electron current does occur, despite large scale demixing. Concerning the polystyrene-based blends, the above given analysis shows that without performing any prior measurements or morphological investigation, the calculated ternary phase diagrams predict electron trap dilution to be likely when blending MEH-PPV with PS1 and not if PS35 is used as host material.
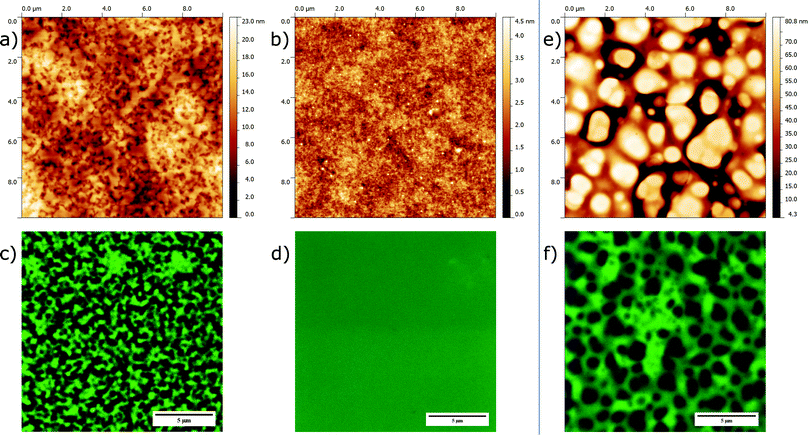
Before verifying this prediction with electrical measurements on actual thin film devices, we first present the morphological characterization of the spin-coated blend layers. To this end we chose a combination of atomic force microscopy (AFM) and confocal laser scanning microscopy (CLSM) as complementary techniques to reveal both the surface and bulk characteristics of the films. AFM guarantees a high lateral resolution but probing is limited to the top surface of the film. In contrast, CLSM, which visualizes regions rich in photoluminescent material (here: MEH-PPV) via local excitation with laser light, has a lower lateral resolution but provides for morphological information associated with the bulk of the layer. Fig. 3 shows the AFM (topology) and CLSM images obtained for the PS-based blends (panels a–d). Again, for comparison we have included the images for the MEH-PPV:PVK30 blend (panels e and f). For reasons of space we limit ourselves to presenting the data corresponding to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 blend ratio.
3 blend ratio.
Before expanding on structural details, comparison between the images corresponding to a high and low insulator molecular weight immediately reveals pronounced morphological differences. Whereas the MEH-PPV:PS35 and MEH-PPV:PVK30 blend films are rough and strongly corrugated (panels a, c, e, f), the film based on MEH-PPV:PS1 (panels b and d) is featureless and smooth. In line with the predictions based on the ternary phase diagrams, we explain this difference by macro-phase separation only to occur for the former blends and not for MEH-PPV:PS1.§
As mentioned in the introduction, the drop-like features characterizing the morphology of the MEH-PPV:PS35 and MEH-PPV:PVK30 films strongly suggest phase separation to occur via liquid–liquid demixing. Close inspection of corresponding AFM and CLSM images reveals that for both demixed blend films (i) the topologically elevated regions represent the non-photoluminescent, and hence dark, insulator-rich phase and (ii) that the surface topology matches the structure in the bulk. We further emphasize that the typical width of the phase domains significantly exceeds the film's average thickness (∼200 nm), from which we conclude that both morphologies are effectively two-dimensional.
It is noted that for MEH-PPV:PS35 demixing results in a bicontinuous morphology, whereas for MEH-PPV:PVK30 a structure is obtained in which the insulator-rich phase is dispersed in a PPV-rich matrix. The fact that for a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 blend ratio mass conservation alone would suggest the semiconductor-rich phase to be dispersed and the insulator to be continuous, i.e., opposite to what is observed, indicates the presence of dynamic asymmetry during demixing. Expanding on this would go beyond the scope of this paper, but it has been shown that a difference in (instantaneous) elastic modulus between the two phases,13e.g., due to transient network formation or difference in glass transition temperature, can give rise to the observed morphological characteristics.14
3 blend ratio mass conservation alone would suggest the semiconductor-rich phase to be dispersed and the insulator to be continuous, i.e., opposite to what is observed, indicates the presence of dynamic asymmetry during demixing. Expanding on this would go beyond the scope of this paper, but it has been shown that a difference in (instantaneous) elastic modulus between the two phases,13e.g., due to transient network formation or difference in glass transition temperature, can give rise to the observed morphological characteristics.14
As shown above, the morphologies of the MEH-PPV:PS blend films are in good qualitative agreement with the predictions based on the calculated ternary phase diagrams. Nevertheless, the morphological analysis does not teach us whether the MEH-PPV:PS35 blend indeed demixes into phases that are too pure to allow for a reduction in the trap- and transport site density with concomitant rise in electron current. Conversely, although the above given analysis demonstrates large scale phase separation to be unlikely for MEH-PPV:PS1, it does not answer the question whether mixing of the two polymers is sufficiently intimate to achieve trap dilution.
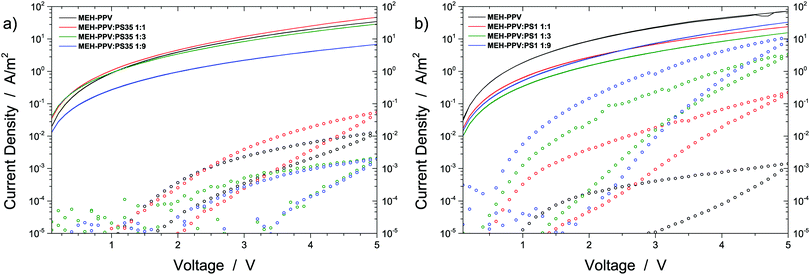
In order to resolve these matters and to complete the validation of our predictions, we proceed with discussing electrical measurements on single charge carrier devices based on the above discussed MEH-PPV:insulator blends. Details on the architecture and fabrication of these devices are given in the Experimental section. Fig. 4 presents the current densities of holes (lines) and electrons (symbols) as a function of voltage (V). As a reference, the single carrier JV-curves measured for pristine MEH-PPV (black) are included as well. As expected, the electron current density in pristine MEH-PPV is about three orders of magnitude lower than the hole current density due to the trap-limited nature of the former. Besides, the electron current exhibits a significant hysteresis due to permanent capture of electrons by deep trap states.
Fig. 4a shows that in contrast to what we observed earlier for PVK30, no rising trend in electron current is obtained when blending MEH-PPV with an increasing fraction of PS35. In case of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and 1
3 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 blend ratios the electron current density even drops below that of the pure semiconductor. Hence, for MEH-PPV:PS35 a more or less opposite behavior is observed compared to MEH-PPV:PVK30, for which the electron current density consistently increases with the insulator content (see Fig. 2 in ref. 4). The absence of a rise in electron current density with increasing polystyrene fraction shows that indeed no trap dilution occurs when blending MEH-PPV with 35 kg mol−1 polystyrene. This observation is in excellent agreement with the above given prediction that for this particular blend liquid–liquid demixing likely results in coexisting phases consisting of virtually pure semiconductor and insulator.
9 blend ratios the electron current density even drops below that of the pure semiconductor. Hence, for MEH-PPV:PS35 a more or less opposite behavior is observed compared to MEH-PPV:PVK30, for which the electron current density consistently increases with the insulator content (see Fig. 2 in ref. 4). The absence of a rise in electron current density with increasing polystyrene fraction shows that indeed no trap dilution occurs when blending MEH-PPV with 35 kg mol−1 polystyrene. This observation is in excellent agreement with the above given prediction that for this particular blend liquid–liquid demixing likely results in coexisting phases consisting of virtually pure semiconductor and insulator.
In contrast to what we observe for MEH-PPV:PS35 and in further agreement with our predictions, a consistent increase in electron current is obtained when blending MEH-PPV with the low molecular weight polystyrene sample PS1 (Fig. 4b). In case of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 blend ratio the electron current density approaches the hole current density even within an order of magnitude. The removal of the trap-limited nature of the electron current shows that mixing between MEH-PPV and PS1 is indeed sufficiently intimate to allow for spatial separation of transport- and trap sites within the semiconductor, without violating electrical percolation. These measurements demonstrate that electrically the MEH-PPV:PS1 blend behaves very similar to the earlier studied MEH-PPV:PVK30 blend, despite the fact that the latter exhibits pronounced demixing whereas the former does not.
9 blend ratio the electron current density approaches the hole current density even within an order of magnitude. The removal of the trap-limited nature of the electron current shows that mixing between MEH-PPV and PS1 is indeed sufficiently intimate to allow for spatial separation of transport- and trap sites within the semiconductor, without violating electrical percolation. These measurements demonstrate that electrically the MEH-PPV:PS1 blend behaves very similar to the earlier studied MEH-PPV:PVK30 blend, despite the fact that the latter exhibits pronounced demixing whereas the former does not.
Fig. 4b shows that blending MEH-PPV with PS1 results in a balanced transport of positive and negative charges. To demonstrate that this is beneficial to the performance of the actual OLED, we plot the luminous efficiency of dual carrier devices (see Experimental section) as a function of voltage and blend ratio (Fig. 5). Just as we observed before for the MEH-PPV:PVK30 blends and in line with theoretical predictions,15 the device based on the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 blend of MEH-PPV and PS1 (blue curve) exhibits a roughly doubled efficiency compared to the one comprising pristine MEH-PPV. The inclination of the green and blue curves at voltages exceeding 3 V is consistent with charge recombination occurring closer to the anode due to the strongly increased electron current. As a result, at high voltages the efficiency reduces somewhat due to exciton quenching by the anode.16
9 blend of MEH-PPV and PS1 (blue curve) exhibits a roughly doubled efficiency compared to the one comprising pristine MEH-PPV. The inclination of the green and blue curves at voltages exceeding 3 V is consistent with charge recombination occurring closer to the anode due to the strongly increased electron current. As a result, at high voltages the efficiency reduces somewhat due to exciton quenching by the anode.16
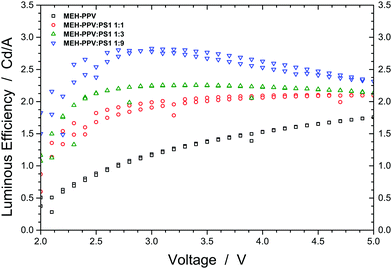 | ||
Fig. 5 Luminous efficiency plotted as a function of voltage (V) for OLED devices based on pristine MEH-PPV (black) and MEH-PPV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PS1 with a 1 PS1 with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (red), 1 1 (red), 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (green) and 1 3 (green) and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 (blue) w/w blend ratio. 9 (blue) w/w blend ratio. | ||
Conclusions
This work underlines the importance of the relation between the phase dynamics during solution-casting and thin-film device performance. We show that electron trapping in OLEDs based on disordered luminescent semiconductors such as MEH-PPV, can be eliminated by blending with low molecular weight polystyrene as insulating host. As this effect, which we have recently demonstrated using PVK as insulator, relies on spatial separation of transport and trap sites on a (near) monomeric or segmental level, mixing between semiconductor and host should be sufficiently intimate. The effect is not observed if high molecular weight polystyrene is used as host, in which case the blend shows pronounced liquid–liquid demixing during solution casting. We show that with this respect the calculated phase diagram provides for a means to predict whether the mixture of semiconductor, insulator and solvent is likely to exhibit the appropriate phase dynamics to ultimately give trap dilution and concomitant increase in OLED performance. Morphological and electrical characterization of MEH-PPV:insulator films not only validates our predictions, but also reveals that not the occurrence of demixing itself, but rather the (co)existence of (a) mixed phase(s) in the dry film determines whether electron trapping is reduced upon blending.Appendix
The ternary phase diagrams in Fig. 1 were obtained via calculation of the mixing free energy, as defined by the Flory–Huggins model.5 This model takes as input molecular size and interaction, which respectively determine the entropic and enthalpic contributions to the mixing free energy. Molecular size is represented by a relative degree of polymerization in terms of the number sites occupied per molecule on an imaginary molecular lattice. Interaction between monomers (sites) is captured by the dimensionless Flory–Huggins (binary) interaction parameters. Formulated per lattice site and given in units of kT, the mixing free energy is expressed as: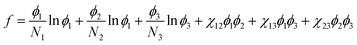 | (A1) |
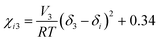 | (A2) |
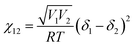 | (A3) |
| N | V i (cm3 mol−1) | δ (MPa1/2) | |
|---|---|---|---|
| a See ref. 21. b Taken from ref. 22. c Taken from ref. 23. d Taken similar to chloroform (see ref. 24). e Taken from ref. 25. | |||
| MEH-PPV | 3000 | 250.1a | 18.6b |
| Polystyrene (35 kg mol−1) | 350 | 97.9a | 17.9c |
| Polystyrene (1 kg mol−1) | 15 | 97.9a | 17.9c |
| PVK (30 kg mol−1) | 225 | 154.9a | 19.0d |
| Chlorobenzene | 1 | 101a | 19.6e |
| MEH-PPV | Polystyrene | PVK | Chlorobenzene | |
|---|---|---|---|---|
| MEH-PPV | χ 11 = 0 | χ 12 = 0.04 | χ 12 = 0.01 | χ 13 = 0.38 |
| Polystyrene | — | χ 22 = 0 | — | χ 23 = 0.47 |
| PVK | — | — | χ 22 = 0 | χ 23 = 0.35 |
| Chlorobenzene | — | — | — | χ 33 = 0 |
It should be realized that different authors have reported different values for the solubility parameter of polystyrene (see ref. 23 for more discussion on this). We have adopted the one recently obtained by Emerson et al.23 This choice is supported by the fact that the resulting value for χ23 is consistent with the one reported earlier26 by Kubo et al. (χ23 = 0.454, at T = 303 K).
The ternary phase diagrams were calculated the usual way.5,11 The spinodal is obtained by applying the condition:
| det(H) = 0, | (A4) |
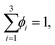 so that: ϕ3 = 1 − ϕ1 − ϕ2. The binodal is obtained using a common tangent construction following an iterative procedure that converges to satisfy the following constraints for the exchange chemical potential and osmotic pressure of coexisting phases I and II:
so that: ϕ3 = 1 − ϕ1 − ϕ2. The binodal is obtained using a common tangent construction following an iterative procedure that converges to satisfy the following constraints for the exchange chemical potential and osmotic pressure of coexisting phases I and II: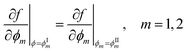 | (A5) |
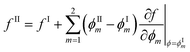 | (A6) |
Acknowledgements
Dr Charley Schaefer is kindly acknowledged for providing the software used for calculating the ternary phase diagrams. Dr Kaloian Koynov is kindly acknowledged for performing confocal laser scanning microscopy analysis on the blend films. Open Access funding provided by the Max Planck Society.Notes and references
- P. Mark and W. Helfrich, J. Appl. Phys., 1962, 33, 205 CrossRef CAS.
- P. W. M. Blom, M. J. M. de Jong and J. J. M. Vleggaar, Appl. Phys. Lett., 1996, 68, 3308 CrossRef CAS.
- H. T. Nicolai, M. Kuik, G. A. H. Wetzelaer, B. de Boer, C. Campbell, C. Risko, J. L. Brédas and P. W. M. Blom, Nat. Mater., 2012, 11, 882 CrossRef CAS PubMed.
- D. Abbaszadeh, A. Kunz, G. A. H. Wetzelaer, J. J. Michels, N. I. Craciun, K. Koynov, I. Lieberwirth and P. W. M. Blom, Nat. Mater., 2016, 15, 628 CrossRef CAS PubMed.
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, Ithaca, USA, 1953 Search PubMed.
- H. G. Gilch, J. Polym. Sci., Part A-1: Polym. Chem., 1966, 4, 1337 CrossRef CAS.
- L. Lu, T. Zheng, Q. Wu, A. M. Schneider, D. Zhao and L. Yu, Chem. Rev., 2015, 115, 12666 CrossRef CAS PubMed and references cited therein.
- S. Kouijzer, J. J. Michels, M. van den Berg, V. S. Gevaerts, M. Turbiez, M. M. Wienk and R. A. J. Janssen, J. Am. Chem. Soc., 2013, 135, 12057 CrossRef CAS PubMed.
- J. J. Michels and E. Moons, Macromolecules, 2013, 46, 8693 CrossRef CAS.
- J. J. van Franeker, D. Westhoff, M. Turbiez, M. M. Wienk, V. Schmidt and R. A. J. Janssen, Adv. Funct. Mater., 2015, 25, 855 CrossRef CAS.
- C. Schaefer, J. J. Michels and P. van der Schoot, Macromolecules, 2016, 49, 6858 CrossRef CAS.
- A. van Breemen, T. Zaba, V. Khikhlovskyi, J. J. Michels, R. Janssen, M. Kemerink and G. Gelinck, Adv. Funct. Mater., 2015, 25, 278 CrossRef CAS.
- A. Onuki and H. Nishimori, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 13649 CrossRef.
- H. Tanaka, J. Phys.: Condens. Matter, 2000, 12, R207 CrossRef CAS.
- M. Kuik, L. J. A. Koster, A. G. Dijkstra, G. A. H. Wetzelaer and P. W. M. Blom, Org. Electron., 2012, 13, 969 CrossRef CAS.
- We are aware of the fact that anode quenching can be avoided by making use of an electron blocking layer (see: D. Abbaszadeh, G. A. H. Wetzelaer, H. T. Nicolai and P. W. M. Blom, J. Appl. Phys., 2014, 116, 224508 CrossRef ), but this is outside the scope of this work.
- E. A. Grulke, Solubility Parameter Values, in Polymer Handbook, Part VII, ed. J. Brandrup, E. H. Immergut and E. A. Grulke, Wiley, New York, 4th edn, 1999, p. 675 Search PubMed.
- W. W. Greassley, R. Krishnamoorti, G. C. Reichart, N. P. Balsara, L. J. Fetters and D. J. Lohse, Macromolecules, 1995, 28, 1260 CrossRef.
- J. K. Maranas, M. Mondello, G. S. Grest, S. K. Kumar, P. G. Debenedetti and W. W. Greassley, Macromolecules, 1998, 31, 6991 CrossRef CAS.
- M. Müller, Macromol. Theory Simul., 1999, 8, 343 CrossRef.
- Calculated using ACD ChemLabs Freeware.
- R. F. Cossiello, L. Akcelrud and T. D. Z. Atvars, J. Braz. Chem. Soc., 2005, 16, 74 CrossRef CAS.
- J. A. Emerson, D. T. W. Toolan, J. R. Howse, E. M. Furst and T. H. Epps, Macromolecules, 2013, 46, 6533 CrossRef CAS.
- U. Paik, S. Lee and J.-G. Park, J. Semicond. Technol. Sci., 2008, 8, 46 CrossRef.
- C. M. Hansen, Hansen Solubility Parameters, a User's Handbook, CRC Press, New York, 1999 Search PubMed.
- K. Kubo and K. Ogino, Bull. Chem. Soc. Jpn., 1971, 44, 997 CrossRef CAS.
Footnotes |
| † The molecular weight of the MEH-PPV is not varied throughout this study. |
| ‡ The miscibility gap of the MEH-PPV:PVK:chlorobenzene blend is somewhat larger than reported earlier (see ref. 4), as in the present study the input parameters for the Flory–Huggins model were calculated in a slightly different, however more consistent, manner. |
| § Hypothetically, featureless AFM and CLSM images would also be obtained if phase separation were to occur exclusively in the vertical direction. However, as we shall see below, such stratified phase morphology can be ruled out based on the observed electrical characteristics of the blend. |
| This journal is © The Royal Society of Chemistry 2017 |