Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tuning the properties of F:SnO2 (FTO) nanocomposites with S:TiO2 nanoparticles – promising hazy transparent electrodes for photovoltaics applications†
Shan-Ting
Zhang
*ab,
Martin
Foldyna
c,
Hervé
Roussel
a,
Vincent
Consonni
a,
Etienne
Pernot
a,
Lukas
Schmidt-Mende
d,
Laetitia
Rapenne
a,
Carmen
Jiménez
a,
Jean-Luc
Deschanvres
a,
David
Muñoz-Rojas
a and
Daniel
Bellet
*a
aUniversity Grenoble Alpes, CNRS, LMGP, 3 parvis Louis Néel, 38016 Grenoble, France. E-mail: shanting.zhang@gmail.com; daniel.bellet@grenoble-inp.fr
bTechnische Universität Darmstadt, Jovanka-Bontschits-Strasse 2, 64287 Darmstadt, Germany
cLPICM-CNRS, Ecole Polytechnique, Université Paris-Saclay, 91128 Palaiseau, France
dUniversity of Konstanz, Universitaetsstr. 10, 78457 Konstanz, Germany
First published on 29th November 2016
Abstract
The appropriate choice of nanoparticles is proved to be essential in tuning the properties of F:SnO2 (FTO) nanocomposites. With the use of more conductive sulphur-doped TiO2 (S:TiO2) nanoparticles, the sheet resistance of S:TiO2–FTO nanocomposites is successfully reduced down to 38% as compared to the standard flat FTO (11.7 Ω sq−1), while the haze factor of the S:TiO2–FTO nanocomposites can be varied from almost zero (reference flat FTO) up to 60%; moreover the majority of 〈110〉 oriented S:TiO2 nanoparticles leads to a strong (110) texture in the resulting S:TiO2–FTO nanocomposites by local epitaxy. Careful morphology analyses and angle-resolved measurements reveal that the haze factor is proportional to the total surface coverage of the S:TiO2 nanoparticle agglomerates, while the feature size of the agglomerates determines the angular distribution of the scattered light – this is confirmed by an angle-resolved Mueller matrix polarimeter which allows obtaining the optical microscopic and angle-resolved images of the exact same textured region. Our work establishes the guidelines to fabricate FTO and other transparent conductive oxide (TCO) nanocomposites as promising electrodes in solar cells with tunable structural, electrical, and optical properties.
1 Introduction
Transparent conductive oxides (TCOs) have widely been used as front/back electrode materials in thin film photovoltaics (PV).1 The basis for thin film PV techniques lies in the utilization of thin absorbers ranging from hundreds of nanometres to several micrometres, which can result in a weak absorption. Light management structures thus become essential in the solar device design to improve absorption. Employing optically textured TCOs turns out to be the most studied and most widely used approach.2 For example, a world-record efficiency of 13.44% was obtained for a triple junction (a-Si:H/μc-Si:H/μc-Si:H) thin film Si solar cell made on a textured aluminum-doped zinc oxide (Al:ZnO) electrode.3 Optically textured TCOs often have high haze factors, i.e. the ratio of the scattered light intensity divided by the incident light intensity. High haze factors enable more light to be scattered and potentially to higher angles, leading to longer optical paths and improved absorption in a solar cell device. The optical texture of TCOs can intrinsically be developed during deposition, as for columnar bulk structured fluorine-doped tin oxide (F:SnO2 or FTO), or after deposition, as for crater-like textured Al:ZnO made by etching films deposited by magnetron sputtering with HCl acid.4,5 However, tuning deposition/etching parameters involves comprehensive studies requiring substantial efforts and time, and increases the cost. Alternatively, using techniques enabling uniform and conformal deposition of TCO films, the optical texture of TCOs can be defined by patterning glass substrates using chemical/physical etching, nano-imprinting etc.6–9 These processes can nevertheless become complicated to handle due to the large number of steps involved, while the masters used for nano-imprinting can be expensive. New simple and cheap strategies to control the texture of TCOs are thus being pursued.In the past, we have shown that the optical texture of TCOs can easily be controlled by spin coating nanoparticle suspensions prior to the deposition of the TCO film, which were prepared by simply dissolving nanoparticles in isopropanol.10 It is a cost-effective approach to pattern glass substrates to yield FTO nanocomposites showing controllably high haze factors as a function of the nanoparticle suspension concentration. Previously, commercial ZnO nanoparticles were used to produce hazy ZnO–FTO nanocomposites. However, in that case the increased haze factor was associated with a significant increase in sheet resistance (Rs). This poses limitations in view of using the ZnO–FTO nanocomposites as efficient electrodes in solar cells.
Being one of the most studied and most synthesized nanoparticles, TiO2 nanoparticles combined with the FTO film to prepare hazy FTO nanocomposites can be of great interest. Instead of non-doped TiO2 nanoparticles which are electrically comparable to non-doped ZnO nanoparticles, we have used sulphur-doped TiO2 (S:TiO2) nanoparticles which have been reported in the literature to be more conductive than non-doped TiO2 nanoparticles based on dielectric studies.11 The resulting S:TiO2–FTO nanocomposites show significantly reduced Rs of 7–8 Ω sq−1, which is up to 38% lower with respect to the standard flat FTO. Other than that, both the structural and optical properties of S:TiO2–FTO nanocomposites are strongly affected by the S:TiO2 nanoparticles. Furthermore, the angle resolved scattering (ARS) of this type of nanocomposites is studied in detail for the first time. With the help of an innovative angle-resolved Mueller matrix polarimeter (ARMMP), the optical microscopic and angle-resolved images of the exact same textured region can be obtained enabling a direct link between the optical properties and surface morphologies of S:TiO2–FTO nanocomposites.
2 Results and discussions
2.1 Morphology and structure of S:TiO2 nanoparticles/substrates
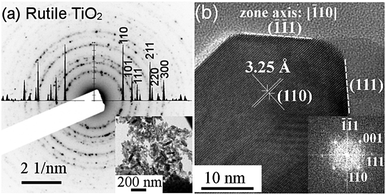
Rutile S:TiO2 nanoparticles were synthesized by a hydrothermal method and are shown in Fig. 1. The S:TiO2 nanoparticles show a non-spherical but shuttle-like shape.12,13 Each individual S:TiO2 nanoparticle is a single crystal as seen in Fig. 1b, where the edge of a nanoparticle is shown and the {110} and {111} planes can be identified as indicated. Despite their small size, the 3D form of the nanoparticles is still discernible in the scanning electron microscopy (SEM) image in Fig. S1 (ESI†). Owing to the fact that the {110} planes are thermodynamically most stable in rutile structures,14,15 a single rutile S:TiO2 nanoparticle is composed of a cuboid body whose large lateral faces correspond to the {110} planes and a short pyramid cap corresponding to the {111} planes.S:TiO2 nanoparticles were then suspended in isopropanol with 6 weight concentrations, namely, 0.2, 0.5, 0.75, 1, 1.5, and 2 wt%. The suspensions were ultrasonicated for 5 min which helped to separate the large nanoparticle aggregates, and then spin coated on glass substrates, forming the so-called rough S:TiO2 nanoparticle substrates, on which a FTO film was then deposited by ultrasonic spray pyrolysis.
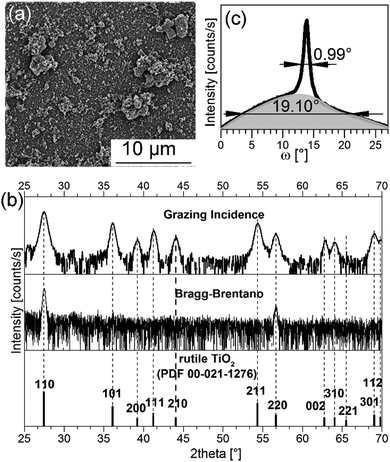
A SEM image of the surface of a 2 wt% S:TiO2 nanoparticle substrate is presented in Fig. 2a and compared to those of 0.2 wt% and 0.75 wt% S:TiO2 nanoparticle substrates in Fig. S2 (ESI†). The S:TiO2 nanoparticles are seen to form agglomerates with random sizes and they do not completely cover the glass surface. Due to the larger {110} facets, the S:TiO2 nanoparticle substrate shows interesting structural features as exemplified by the same 2 wt% nanoparticle substrate whose Bragg–Brentano and grazing incidence X-ray diffraction (XRD) patterns are presented in Fig. 2b.
The simultaneous appearance of the {110} planes in both Bragg–Brentano and grazing incidence XRD patterns reveals that not all S:TiO2 nanoparticles orient their (110) planes parallel to the glass surface. But the majority of nanoparticles should be 〈110〉 oriented thus give rise to the intense {110} diffraction peaks in the Bragg–Brentano XRD pattern. However, the portion of non-〈110〉 oriented nanoparticles is too small to contribute significant signals in the Bragg–Brentano XRD pattern; instead they are visible only in the grazing incidence XRD pattern. The same feature appears in the (110) rocking curve (or ω-scan) in Fig. 2c measured on the same nanoparticle substrate.
Two different components are clearly distinguished: a bottom background contributed by the non-〈110〉 oriented S:TiO2 nanoparticles with a broad full-width-half-maximum (FWHM) of 19.10°, and a top peak contributed by the 〈110〉 oriented S:TiO2 nanoparticles with a sharp FWHM of 0.99°, as obtained by Lorentzian fitting. The intensity of the bottom background is weak due to the small quantity of non-〈110〉 oriented S:TiO2 nanoparticles, while the top peak is intense because the majority of S:TiO2 nanoparticles are 〈110〉 oriented. With {110} being the largest facets, the S:TiO2 nanoparticles would naturally tend to lie with the {110} planes parallel to the glass surface. Therefore, the majority of the S:TiO2 nanoparticles are 〈110〉 oriented. However, due to the formation of nanoparticle agglomerates, some nanoparticles may be positioned such that crystal planes other than the {110} planes are exposed parallel to the glass surface; these nanoparticles nevertheless occupy only a very small portion. The X-ray pole figures of the same nanoparticle substrate collected on the rutile TiO2 (110) and (211) diffraction peaks in Fig. S3 (ESI†) confirm the preferential 〈110〉 orientation of the S:TiO2 nanoparticles where an intense central peak appears in the (110) pole figure; while weak intensities appearing at all radial (Chi) and azimuthal (Phi) angles in the (211) pole figure suggest random in-plane orientations.
2.2 Morphology and structure of S:TiO2–FTO nanocomposites
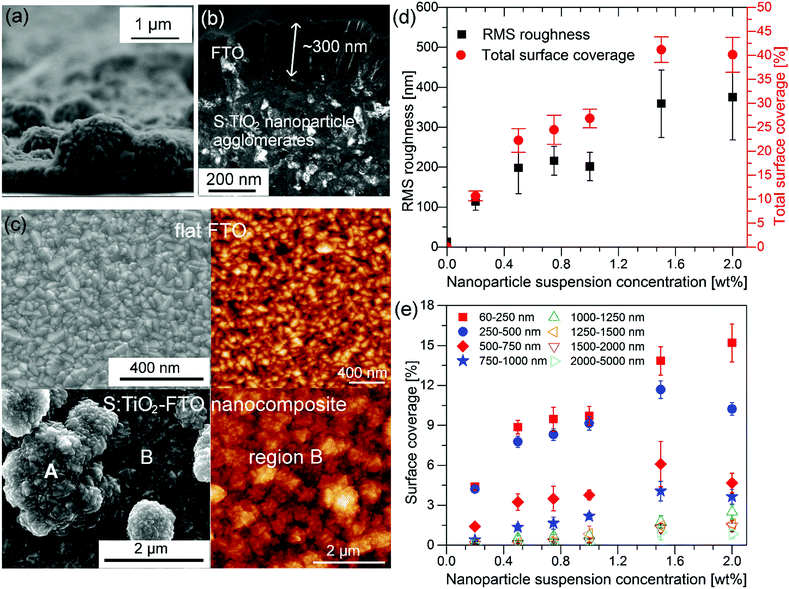
To prepare the S:TiO2–FTO nanocomposites, a thin layer of FTO was eventually deposited by ultrasonic spray pyrolysis on rough S:TiO2 nanoparticle substrates, as shown in Fig. 3a. It can be seen that the FTO film conformally covers both the bare glass regions and the S:TiO2 nanoparticle agglomerates. The FTO film grows with the usual columnar grain structure16–19 with an average thickness of around 300 nm, as seen in Fig. 3b.The so-called flat FTO refers to the FTO film deposited directly on a bare glass substrate (without any nanoparticles), thus acting as the reference to the S:TiO2–FTO nanocomposites. The flat FTO surface is very smooth as seen in both left SEM and right atomic force microscopy (AFM) images in Fig. 3c; on the contrary, the surface of S:TiO2–FTO nanocomposites is much rougher. A large-scale comparison of the surface morphology of the 0.2 wt%, 0.75 wt%, and 2 wt% S:TiO2–FTO nanocomposites is summarized in Fig. S4 (ESI†). Two regions marked as A and B are discerned on the nanocomposite surface: region A is very rough since the FTO film is deposited on large nanoparticle agglomerates, while in region B the FTO film seems to be deposited on the bare glass surface and thus appears flat.
However, if region B is zoomed in as shown in the right AFM image, it does not resemble the surface of the flat FTO. Instead, nanoparticle agglomerates are also present, but with much smaller sizes. Thus, region B is only semi-flat with its RMS roughness (calculated on the AFM image in Fig. 3c) being 58 nm, which is higher than the RMS roughness of the reference flat FTO of 13 nm. The random size distribution of the S:TiO2 nanoparticle agglomerates poses difficulties in calculating the RMS roughness of the nanocomposites, which depends largely on the chosen area. As a compromise between statistical relevance and image resolution, AFM images of 40 × 40 μm2 with a resolution of 40 nm per pixel were recorded at five or more different areas on each sample and were used to estimate the RMS roughness and corresponding error bars. The results are summarized in Fig. 3d where the RMS roughness is plotted as a function of the nanoparticle suspension concentration. Despite larger error bars for certain samples, it is safe to conclude that the roughness generally increases with the increasing nanoparticle suspension concentration. In the AFM images, if a certain height threshold is defined, the nanoparticle agglomerates can be counted as “grains” using Gwyddion software.20 Thus, the total surface area occupied by all the nanoparticle agglomerates can then be calculated and termed as the total surface coverage, which is plotted in Fig. 3d. It is clear that the total surface coverage of the nanoparticle agglomerates increases accordingly by increasing the nanoparticle suspension concentration.
Furthermore, the S:TiO2 nanoparticle agglomerates can be categorized into 8 groups according to their equivalent radius (Req) defined as the effective radius of a circle whose area is equivalent to the projected area of the grain: 60–250 nm, 250–500 nm, 500–750 nm, 750–1000 nm, 1000–1250 nm, 1250–1500 nm, 1500–2000 nm, and 2000–5000 nm. Similarly, the surface coverage of each group can be obtained as plotted in Fig. 3e as a function of the nanoparticle suspension concentration. When the concentration is increased, the nanoparticles tend to form small agglomerates with Req less than 500 nm followed by those with Req ranging 500–1000 nm. There is little chance that the nanoparticles form larger agglomerates with Req exceeding 1000 nm (especially at lower nanoparticle suspension concentration), which happens to be advantageous for solar cell applications since large feature sizes often pose technical difficulties in cell processing.21,22 The relative fractions for the 8 nanoparticle agglomerate groups are complemented in Fig. S5 (ESI†). Detailed examination reveals that for S:TiO2–FTO nanocomposites of all concentrations, more than 80% of the agglomerates have Req inferior to 1000 nm, whereas larger agglomerates with Req > 1000 nm represent only a small amount. Despite their different surface coverage values, the agglomerates present on all the S:TiO2–FTO nanocomposites share a similar feature size.
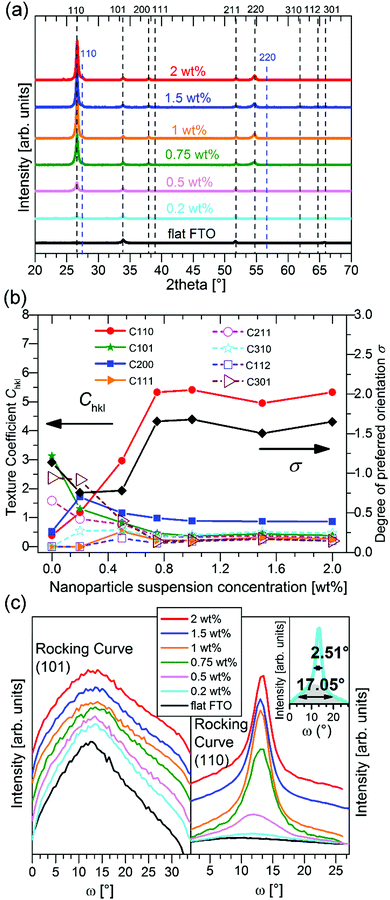
The XRD patterns in the Bragg–Brentano configuration of all S:TiO2–FTO nanocomposites with 6 weight concentrations are summarized in Fig. 4a, together with the XRD pattern of the flat FTO for reference. Accordingly, the texture coefficient Chkl for each (hkl) crystal plane and the corresponding degree of preferred orientation σ are calculated following Harris's method:23
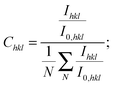 | (1) |
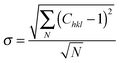 | (2) |
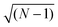 , i.e.
, i.e.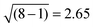 in our case.
in our case.
The Chkl and σ are plotted in Fig. 4b as a function of the nanoparticle suspension concentration. Unlike the flat FTO which has the dominant (101) texture, the S:TiO2–FTO nanocomposites instead show the prevalent (110) texture, which is strongly increased by increasing the nanoparticle suspension concentration. In other words, the FTO film deposited on S:TiO2 nanoparticles tends to grow preferentially along the 〈110〉 orientation. Consequently, the σ rises with the increasing nanoparticle suspension concentration and finally saturates at around 1.7.
A similar structural feature is thus observed for the S:TiO2–FTO nanocomposites and the S:TiO2 nanoparticle substrates: both show the preferential 〈110〉 orientation. In a similar way, the (110) rocking curves of the flat FTO and S:TiO2–FTO nanocomposites are examined in Fig. 4c with comparison to their (101) rocking curves. Although the flat FTO film has the dominant (101) texture, the grains show broad distribution as that of the (110) rocking curve, both being comparable to powder samples (see Table 1 for details). For S:TiO2–FTO nanocomposites, all (101) rocking curves are broad as expected; but for (110) rocking curves, two components are discernible as exemplified by the rocking curve of the 2 wt% S:TiO2–FTO nanocomposite in the inset, which is again similar to the S:TiO2 nanoparticle substrate. On the one hand, the bottom backgrounds in all S:TiO2–FTO nanocomposites have an FWHM as broad as powder samples; and they show weak intensities suggesting that the portion of non-〈110〉 oriented FTO grains is small. The top peak, on the other hand, becomes more intense with a narrower FWHM when the nanoparticle suspension concentration increases – the narrowest FWHM of 2.51° for the 2 wt% S:TiO2–FTO nanocomposite approaches that of 0.99° for the S:TiO2 nanoparticle substrate of the same concentration. As in the S:TiO2 nanoparticle substrate, the majority of FTO grains in the S:TiO2–FTO nanocomposites show the 〈110〉 orientation, which is confirmed by the X-ray pole figure of the 2 wt% S:TiO2–FTO nanocomposite collected on the SnO2 (110) diffraction peak (Fig. S6, ESI†) where an intense central peak appears. Similarly, the (211) pole figure (Fig. S6, ESI†) shows equally weak intensities at all angles suggesting random in-plane orientations. The S:TiO2–FTO nanocomposite is thus seen to reproduce the structural features of the S:TiO2 nanoparticle substrate.
| S:TiO2 nanoparticle suspension concentration | FWHM [°] | ||
|---|---|---|---|
| (101) | (110) bottom | (110) top | |
| 0 wt% (flat FTO) | 27.2 | 21.1 | — |
| 0.2 wt% | 27.3 | 31.4 | 7.4 |
| 0.5 wt% | 26.8 | 31.9 | 6.0 |
| 0.75 wt% | 28.5 | 21.5 | 3.7 |
| 1 wt% | 28.0 | 25.0 | 3.2 |
| 1.5 wt% | 27.7 | 21.9 | 2.9 |
| 2 wt% | 27.6 | 17.1 | 2.5 |
It means that the (110) texture of the nanocomposites is intimately related to the preferential 〈110〉 orientation of the S:TiO2 nanoparticles on the glass substrate. This implies that local epitaxy takes place, in which the (110) textured FTO grains epitaxially grow on the 〈110〉 oriented rutile S:TiO2 nanoparticles. While the structural complexity of the S:TiO2–FTO nanocomposites has not allowed a direct cross-sectional TEM observation to visualize the epitaxial relationship, we have observed that epitaxial FTO films can grow on the (110) rutile TiO2 single crystals (see Fig. S7, ESI†). A 300 nm FTO film deposited by the same ultrasonic spray pyrolysis on a commercial (110) rutile TiO2 single crystal shows only the (110) and (220) diffraction peaks suggesting a strong out-of-plane 〈110〉 orientation. The 2D X-ray pole figure collected on the (101) diffraction peak confirms the epitaxial in-plane orientation.
We thus conclude that the strong (110) texture observed in S:TiO2–FTO nanocomposites is an outcome of the epitaxial growth of FTO grains on the 〈110〉 oriented S:TiO2 nanoparticles, while FTO grains grown over bare glass regions in S:TiO2–FTO nanocomposites are expected to develop the (101) texture as in flat FTO owing to the minimization of free energy per unit volume, in accordance with ref. 16 and 17. The properties of thin film materials are well known to be crystallographic texture dependent. For FTO, Wang et al. have reported that the mobility is closely associated with the crystallographic texture development.24 The possibility to tune the FTO crystallographic texture by playing with the nanoparticle orientation thus opens up a new strategy to develop other properties in addition to the high optical haze factors of the nanocomposites.
2.3 Electrical properties of S:TiO2–FTO nanocomposites
The sheet resistance (Rs) of S:TiO2–FTO nanocomposites is plotted as a function of the nanoparticle suspension concentration in Fig. 5 and compared to the Rs of ZnO–FTO nanocomposites reported by Giusti et al.10 The error bars of the S:TiO2–FTO nanocomposites were obtained as statistical errors from five Rs measurements at different locations on each sample. The Rs of the respective flat FTO for the two nanocomposite series are also plotted as references, in both cases being around 10 Ω sq−1 (which is ideal for PV applications). The difference in the two flat FTOs is a batch-to-batch difference, originating from the variability of our laboratory process (the two depositions were made in a time gap of two years). Each reference flat FTO was deposited under exactly the same conditions as the whole nanocomposite series. Therefore, for each nanocomposite series, the comparison of Rs should be restricted to the respective reference flat FTO as in the following discussion.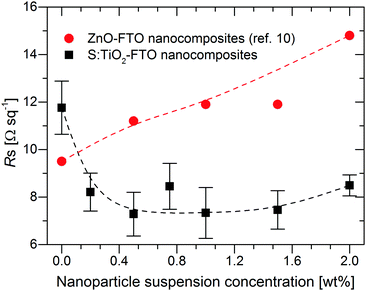 | ||
| Fig. 5 Sheet resistance (Rs) as a function of the nanoparticle suspension concentration for S:TiO2–FTO nanocomposites as well as for ZnO–FTO nanocomposites reported in ref. 10. Dashed lines are drawn to guide the eye. | ||
For ZnO–FTO nanocomposites, the Rs gradually increases from 9.5 Ω sq−1 (flat FTO) to 14.8 Ω sq−1 resulting in a 56% increase in the nanocomposite with respect to the flat FTO. However, with the inclusion of S:TiO2 nanoparticles, the Rs of S:TiO2–FTO nanocomposites drops immediately from 11.7 Ω sq−1 (flat FTO) and remains at around 7–8 Ω sq−1. A maximum 38% decrease in Rs with respect to the flat FTO is observed in the 0.5 wt% S:TiO2–FTO nanocomposite.
It is clear that the S:TiO2 nanoparticles are advantageous over ZnO nanoparticles in terms of the obtained Rs, at least under the experimental conditions used here. This can be interpreted as follows. If the nanoparticles used are very resistive, then the current will tend to flow only through the FTO film. But due to the rougher nature of the nanocomposites, charges have to travel through a longer path (thus larger resistance). As a consequence, the Rs of the resulting nanocomposites would be higher than that of the flat FTO, and increases further when the nanoparticle suspension concentration increases, as is the case of ZnO–FTO nanocomposites. However, for S:TiO2–FTO nanocomposites, with the more conductive S:TiO2 nanoparticles used, we expect the current to flow also through the S:TiO2 nanoparticle agglomerates whose resistance can become comparable with that of FTO. According to the classical resistance law, the resistance of the nanoparticle agglomerates is closely related to their size: smaller ones should be more resistant. But if the agglomerates are too small, they bring only a minor influence compared to the FTO. When the nanoparticle suspension concentration increases, both small and large agglomerates increase. Differently sized nanoparticle agglomerates seem to compensate for each other; the overall effect is that the Rs of S:TiO2–FTO nanocomposites stays relatively constant at about 7–8 Ω sq−1.
In addition, the band alignment at the interface between FTO and the nanoparticles should be taken into consideration. Rutile TiO2 was recently found to have both conduction and valence band edges higher than anatase TiO2.25,26 As a result, if only intrinsic band alignment is considered, the conduction band edge of rutile TiO2 would be higher than that of FTO by 0.2 eV as schematically drawn in Fig. S8 (ESI†).27 Since FTO is a degenerate semiconductor with its Fermi level higher than the conduction band edge of rutile TiO2, the charges can thus flow between FTO and rutile TiO2 without any problem. This should also hold true for the rutile S:TiO2 nanoparticles used in this study. Indeed, S-doping is widely employed in the field of photocatalysis as an effective approach to enable visible light absorption by reducing the bandgap of TiO2 to about 2.8 eV.28,29 This bandgap narrowing is attributed either to a rigid shift of the valence band upon mixing the sulphur states without affecting the conduction band level,30 or to the formation of impurity states just above the valence band.31 In both situations, the position of the conduction band edge of S:TiO2 is expected to be very close to that of non-doped rutile TiO2, thus maintaining the optimum band alignment with FTO. In addition, local sintering between the nanoparticles may take place during the FTO deposition with the growth temperature as high as 420 °C; as a result, less boundaries present inside the nanoparticle agglomerates may improve the charge mobility therein.
2.4 Optical properties of S:TiO2–FTO nanocomposites
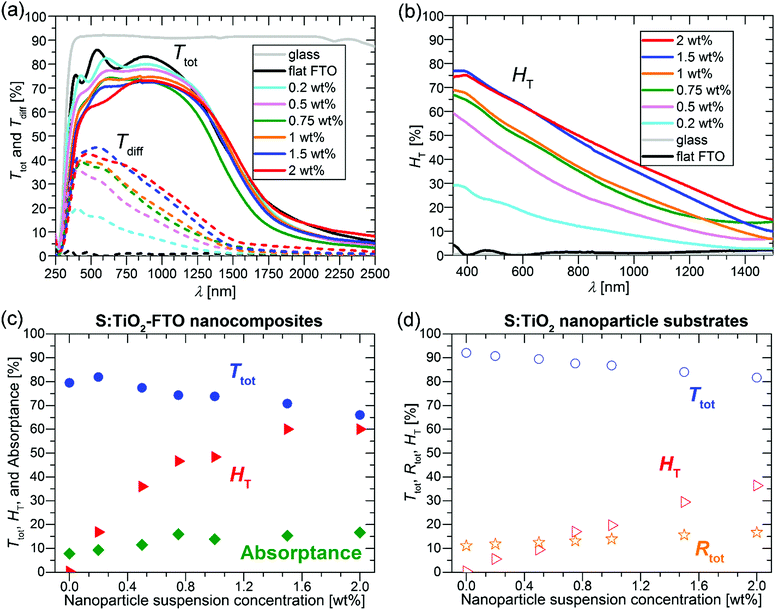
The Ttot and diffuse transmittance (Tdiff) in the 250–2500 nm range and the haze factor in transmission (HT) in the 350–1500 nm range for S:TiO2–FTO nanocomposites (and for the bare glass substrate and flat FTO) are summarized in Fig. 6a and b, respectively. For transmitted light, the HT is defined as follows: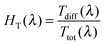 | (3) |
For bare glass and flat FTO, the HT is essentially zero at all wavelengths; while for S:TiO2–FTO nanocomposites, the HT is highest at 350 nm then decreases monotonically until 1500 nm. This behaviour is typical for fixed size scattering centres which usually diffuse more effectively at shorter wavelengths, where the ratios between the scatter size and the wavelength are larger. Nevertheless, the relatively high haze factors of S:TiO2–FTO nanocomposites in the red and near infrared region could be used to improve the performance of Si-based thin film solar cells.5
To show a more detailed comparison, the Ttot, HT and absorptance at 635 nm are plotted as a function of the nanoparticle suspension concentration in Fig. 6c. By varying the nanoparticle suspension concentration, the HT can be increased from almost zero (reference flat FTO) up to 60% accompanied nevertheless by a significant drop in Ttot from 79.5% (reference flat FTO) down to 66.0%. The simultaneous increase in absorptance suggests that the loss in Ttot is partly due to improved absorption likely in the FTO film where the optical path increases with the increased nanoparticle suspension concentration. In addition, even though the wavelength of 635 nm is below the bandgap energy of S:TiO2 nanoparticles, absorption by the nanoparticles is also observed. This is shown in Fig. 6d, where the Ttot, HT and total reflectance (Rtot) are plotted as a function of the nanoparticle suspension concentration for the S:TiO2 nanoparticle substrates (without FTO film). By increasing the nanoparticle suspension concentration, the Ttot decreases accordingly, while the Rtot increases slightly. This suggests that for the nanoparticle substrates, the absorption by the S:TiO2 nanoparticles mainly contributes to the loss in Ttot. Therefore, in S:TiO2–FTO nanocomposites the absorption by the S:TiO2 nanoparticles should also contribute to the loss in Ttot.
The reason why the S:TiO2 nanoparticles absorb visible light below their bandgap is likely due to the presence of defect levels within the gap.32 For rutile TiO2, it has been recently reported that interstitial sulphur, which is easy to form, exhibits a higher absorption coefficient in the visible range than substitutional sulphur at oxygen and titanium sites.33 Thus, absorption by S:TiO2 nanoparticles is probably contributed by the defect levels induced by interstitial sulphur. For the S:TiO2–FTO nanocomposites, although S-doping makes the TiO2 nanoparticles more conductive, it nevertheless introduces defect levels within the bandgap leading to unwanted absorption in the visible range.
The choice of the nanoparticle is thus critical in maintaining a compromise between HT, Ttot and Rs in this type of nanocomposites. At the same time, this interdependence of properties offers flexibility of design where the electrical and optical properties of TCO nanocomposites may be tuned for specific applications.
It is interesting to point out that the S:TiO2 nanoparticle substrates already show non-zero haze factors even though the values are systematically lower than those of their nanocomposite counterparts. This supports the idea that light scattering in S:TiO2–FTO nanocomposites is intimately related to the rough surface morphologies. Generally, the surface modulated TCOs developed are homogeneous media, thus the common approach to study their light scattering is by surface scattering treatment involving the surface RMS roughness, such as the Asahi type-U or W-textured FTO.34–36
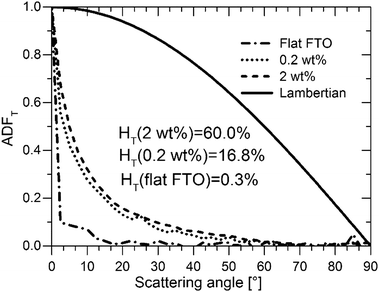
However, for the S:TiO2–FTO nanocomposites studied here, the S:TiO2 nanoparticle agglomerates show a very broad size distribution, some of which have dimensionalities much higher than the FTO film thickness. It is thus less appropriate to treat S:TiO2–FTO nanocomposites as “homogenous media”. Instead, as analysed in Section 2.2, the nanoparticle agglomerates appear as “grains” in the AFM images, which optically act as individual scattering centres. The optical scattering of S:TiO2–FTO nanocomposites can thus be modelled as collective scattering by all the nanoparticle agglomerates present. Therefore, the HT is expected to be closely associated with the total surface coverage of the nanoparticle agglomerates, as confirmed in Fig. 7 where a fairly linear dependence between the HT at 635 nm and the total surface coverage is observed.
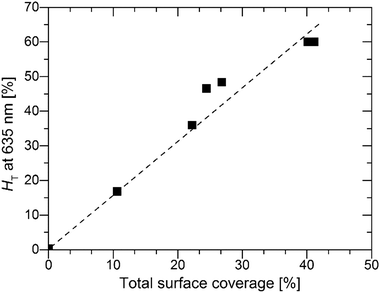 | ||
| Fig. 7 H T at 635 nm plotted as a function of the total surface coverage of the nanoparticle agglomerates. | ||
As important as it is, the HT alone does not suffice to assess S:TiO2–FTO nanocomposites as good light diffusers in solar cells. In addition to a high HT, the angles at which light scattering takes place are also of great interest. For example, to effectively improve Si absorption, the optical texture should scatter light to higher transmitted angles.36 In this context, a Lambertian diffuser following the cosine law for angular dependence of light intensity is generally taken as the ideal random texture scatterer. The angle resolved scattering (ARS) of our S:TiO2–FTO nanocomposites was measured for flat FTO (almost zero HT), the 0.2 wt% S:TiO2–FTO nanocomposite (with weak HT) and the 2 wt% S:TiO2–FTO nanocomposite (with high HT). The measurements were performed in a UV-Vis-NIR spectrophotometry implemented with a commercial automated reflectance/transmittance analyser (ARTA) module. Monochromatic light of λ = 633 nm was used as incident light. By rotating the detector with a 2.5° per step, the intensities of the scattered transmitted light were measured at discrete angles. The measured intensities are normalized to give the angular distribution function in transmittance (ADFT) in order to extract the relative angular dependence of the scattered light.37 The results are presented in Fig. 8 where the Lambertian distribution is also plotted for comparison. Attention should be paid to how fast the ADFT drops towards higher scattering angles.
For flat FTO, the intensity is most intense in the specular direction (i.e. 0° scattering angle) and then immediately drops to almost zero at larger scattering angles, consistent with its HT being almost zero. Unlike flat FTO, for the 0.2 wt% S:TiO2–FTO nanocomposite with HT = 16.8% at λ = 635 nm, the scattered light extends to non-specular directions but becomes negligible at scattering angles higher than 50°; compared to the ideal Lambertian distribution, the shape of its ADFT narrows towards the specular direction meaning that scattering is pronounced only at angles close to the specular direction. The 2 wt% S:TiO2–FTO nanocomposite shows a similar ADFT after normalization, despite its much higher HT (60.0% at λ = 635 nm). The fact that the two S:TiO2–FTO nanocomposites with different HT scatter at similar angles suggests that similar feature sizes are present on the surface of both samples: both having more than 80% of the nanoparticle agglomerates showing Req less than 1000 nm, as discussed previously.
We then conclude that the nanoparticle agglomerates are mainly responsible for the optical scattering in S:TiO2–FTO nanocomposites via a collective scattering model. The haze factor is mostly affected by the density of scattering centres, i.e. the total surface coverage. Conversely, the angular scattering depends on the feature size of the agglomerates. These findings are essential for the future development to design improved optical scattering properties of FTO and other TCO nanocomposites tailored for PV and also other optoelectronic applications using our simple preparation method.
2.5 Direct correlation between morphology and optical properties
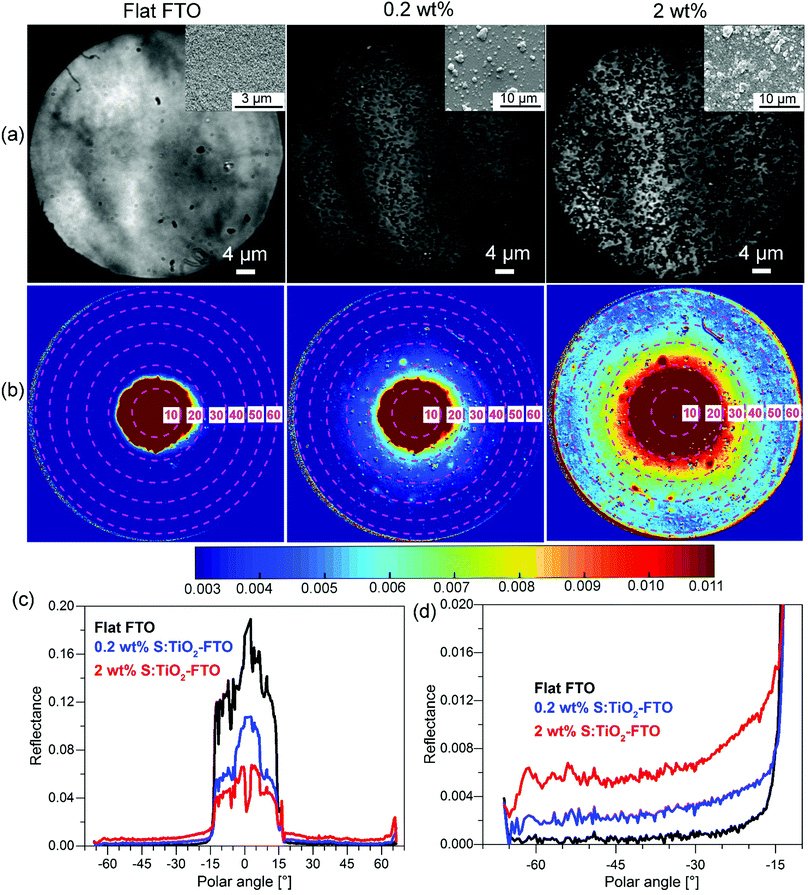
So far, we have shown the optical characterization of samples by methods which correlate the optical properties with morphological information, but measurements were not taken exactly in the same region or at the same scale. Therefore, we have also used an angle-resolved Mueller matrix polarimeter (ARMMP) developed at Ecole Polytechnique (Paris, France) to obtain the optical microscopic and angle-resolved images of the exact same textured region.38,39 Using this technique, obtaining a direct link between the optical behaviour and the surface morphology is possible, allowing us to validate our conclusions. The Mueller matrix polarimeter is coupled with a high numerical aperture reflection microscope that operates in both real (imaging) and angular (conoscopic) modes and it allows measuring the complete Mueller matrices of the sample surfaces and the angle-resolved emerging light. For our purpose, the M11 element representing the unpolarized reflected light intensity is chosen for the analysis of the angular scattering as shown in Fig. 9 for flat FTO, 0.2 wt% and 2 wt% S:TiO2–FTO nanocomposites.In Fig. 9a, the corresponding SEM images are placed in the inset which show surface morphologies consistent with the optical images obtained using the polarimeter. The total surface coverage of the nanoparticle agglomerates is seen to increase accordingly with the nanoparticle suspension concentration. By appropriate calibration on a known polished Si wafer, we can obtain the angle-resolved images in Fig. 9b showing the reflectance of the sample at all azimuths angles and up to 63° polar angles (limited by the numerical aperture of the objective). Note that the angle-resolved images were measured in k-vector space instead of a direct angular space as is common for microscope objectives. The polar angles are marked with central dashed circles with the corresponding values indicated. The reflectance intensities are scaled in colours with higher intensities appearing in shades of red and lower intensities appearing in shades of blue.
All three images have a red central spot which represents the intense specular reflection of incident light with polar angles ranging from 0° to roughly 15°. The horizontal cross sections plotted in Fig. 9c reveal the specular reflectance (plateau) for the three samples, where the flat FTO has the highest specular reflectance and the 2 wt% S:TiO2–FTO nanocomposite has the lowest specular reflectance, as expected from previous discussions. As for the light scattered at higher angles (>15°), one sees an obvious red shift in colour from flat FTO to the 0.2 wt% S:TiO2–FTO nanocomposite and then to the 2 wt% S:TiO2–FTO nanocomposite suggesting that an increased portion of light gets scattered, the absolute values of which are detailed in Fig. 9d, consistent with their increasing haze factors.
Comparing the optical images with angle-resolved images taken in the exact same region, the higher light scattering of the S:TiO2–FTO nanocomposites is clearly seen to be correlated to the higher total surface coverage of the nanoparticle agglomerates, in agreement with the results discussed above.
Similar normalization is performed on the cross section curves to obtain ADFR (R for reflectance), as shown in Fig. S9 (ESI†). The similar shape of ADFR curves of 0.2 wt% and 2 wt% S:TiO2–FTO nanocomposites evidences the similar feature size present in both samples, again consistent with the conclusion drawn from the previous ARTA measurement.
3 Conclusions
We have demonstrated that the structural, electrical and optical properties of S:TiO2–FTO nanocomposites are greatly influenced by the S:TiO2 nanoparticles.The orientation of the underlying S:TiO2 nanoparticles strongly affects the crystallographic texture of the resulting S:TiO2–FTO nanocomposites. The FTO grains epitaxially grow upon the 〈110〉 oriented S:TiO2 nanoparticles, thus the resulting S:TiO2–FTO nanocomposites show a very strong (110) texture. This signifies the importance of adjusting the orientation of the underlying nanoparticles to engineer the crystallographic texture of the nanocomposites, which can potentially introduce additional new properties.
By using more conductive S:TiO2 nanoparticles, the sheet resistance Rs of S:TiO2–FTO nanocomposites has been successfully decreased to 7–8 Ω sq−1. Compared to the reference flat FTO (11.7 Ω sq−1), a significant decrease down to 38% is achieved in the resulting S:TiO2–FTO nanocomposites. We believe that the appropriate intrinsic band alignment at the FTO and rutile TiO2 interface as well as local sintering among nanoparticles also contribute positively to the observed decrease in Rs.
By varying the S:TiO2 nanoparticle suspension concentration, the haze factor HT of the resulting S:TiO2–FTO nanocomposites can be controllably varied from almost zero up to 60%. The absorption by S:TiO2 nanoparticles due to defect levels inside the bandgap and by the FTO film has however led to a significant drop in the total transmittance Ttot from 79.5% to 66.0%. Therefore, attention should be paid to choosing S:TiO2–FTO nanocomposites with appropriate concentrations to ensure a balanced combination of Ttot and HT for each particular PV technology. For example, Chih-Hung et al. have reported that the efficiency of dye-sensitized solar cells (DSSCs) increased from 8.18% to 10.1% upon increasing the haze factor of the FTO electrode from 2% to 17% with the Ttot remaining at about 80%.40 Therefore, the 0.5 wt% S:TiO2–FTO nanocomposite with 35.9% HT and 77.3% Ttot developed in this study serves as a promising electrode to be used in DSSCs.
Due to the high surface roughness, however, the S:TiO2–FTO nanocomposites presented here would be more suitable for solar cells which are less sensitive to TCO roughness. For example, in CdTe-based solar cells, in which the absorber thickness ranges from 2 μm to 10 μm, or DSSCs (with meso-porous nc-TiO2 layer thickness usually >10 μm), the S:TiO2–FTO nanocomposites with high haze factors are expected to have great potential to improve optical absorption and cell performance. In addition to the ultrasonication required to reduce the density of large nanoparticle agglomerates, which may locally induce shorting of ultra-thin devices, additional efforts are currently being made in order to fully control the size distribution of the nanoparticle agglomerates by using chemical additives for instance.
Furthermore, the scattering behaviour of S:TiO2–FTO nanocomposites is found to be intimately related to the density and size distribution of the nanoparticle agglomerates. With the help of the innovative angle-resolved Mueller matrix polarimeter (ARMMP), the direct interplay between surface morphologies and optical properties is revealed for S:TiO2–FTO nanocomposites. We have thus concluded that the haze factor is proportional to the total surface coverage of the S:TiO2 nanoparticle agglomerates, while the angle-resolved scattering is a function of the feature size of the S:TiO2 nanoparticle agglomerates.
These findings emphasize that there exists a large room to design the properties of FTO and as well other TCO nanocomposites by tuning the underlying nanoparticle properties in order to meet specific requirements as electrodes in various types of thin film solar cells and other optoelectronic applications. Our versatile concept of preparing hazy electrodes by combining transparent conductive oxides and nanoparticles serves as an important economic general guideline to design light management structures in solar cells.
4 Experiments details
4.1 Preparation of S:TiO2–FTO nanocomposites
Rutile S:TiO2 nanoparticles were synthesized using the hydrothermal method as described in ref. 29. The as-synthesized S:TiO2 nanoparticles showed bimodal distributions with smaller nanoparticles being anatase, while bigger ones being rutile. The large rutile S:TiO2 nanoparticles were separated from small anatase nanoparticles by centrifugation. The average sizes of S:TiO2 nanoparticles are 150–300 nm in length and 20–40 nm in width. The S:TiO2 nanoparticles were weighted and dispersed in isopropanol forming 6 suspensions: 0.2, 0.5, 0.75, 1, 1.5 and 2 wt%. The suspensions were ultrasonicated for 5 min before being spin-coated on glass substrates (Corning 1737). A single-step spin coating programme was used: velocity 1500 rpm, acceleration 1500 rpm s−1 and time 200 seconds. The suspension volume used for spin-coating was fixed as 0.4 mL in total, which was injected separately two times, 0.2 mL each time. The S:TiO2 nanoparticle substrates were then coated with a conformal FTO film by ultrasonic spray pyrolysis.19 The precursor solution for FTO deposition was prepared by dissolving 0.16 M of SnCl4·5H2O and 0.04 M of NH4F in methanol. The growth temperature was 420 °C and the resulting FTO thin film thickness was around 300 nm. A bare glass substrate was positioned in the same deposition batch of nanocomposites resulting in the reference flat FTO.4.2 Characterization techniques
The as-synthesized S:TiO2 nanoparticles were examined using TEM on a JEOL-2010 LaB6 instrument operated at 200 keV. The Bragg–Brentano XRD patterns presented were measured on a Bruker D8 Advance Series II diffractometer in the 2theta range of 20°–70°; the grazing incidence XRD pattern (incidence angle 0.5°) was collected on a RIGAKU SmartLab diffractometer. All XRD rocking curves and pole figures were obtained on a SIEMENS D5000 diffractometer equipped with a 4-circle goniometer (Schultz geometry). The TEM cross section of the 0.75 wt% S:TiO2–FTO nanocomposite was prepared by focused ion beam (FIB) on a Zeiss NVision40 SEM-FIB microscope. The surface morphologies of S:TiO2–FTO nanocomposites were examined using a field-emission SEM (FEI QUANTA FEG250) and an AFM (Digital Instrument D3100 Nanoscope). The sample sheet resistance was measured using an in-line four-point probe (LucasLab Probe 4 apparatus).The optical transmittance, reflectance and absorptance were recorded on a UV-Vis-NIR spectrophotometer (PerkinElmer Lambda 950) equipped with an integrating sphere. For the angle-resolved total transmittance measurements, a commercial automated reflectance/transmittance analyser (ARTA) module was used with monochromatic incidence light of λ = 633 nm. For the angle-resolved Mueller matrix data, an in-house built polarimeter with the light source (λ = 633 nm) coupled into an optical fibre bundle was used, which illuminates the lenses in the telescopic configuration,39 providing direct access to the Fourier and real planes. The light reflected from the surface was collected by a microscope objective (NA = 0.95, mag 100× and 0.3 mm working distance) and imaged using additional lenses employing a CCD camera. The different optical states of the complete Mueller matrix were generated by combining polarizers and nematic liquid crystals before and after the microscope objective. The setup used a patented calibration method allowing the elimination of all first-order errors or imperfections of the optical components.41,42 A schematic drawing of the polarimeter is presented in Fig. S10 (ESI†).
Author contributions
Shan-Ting Zhang prepared the FTO nanocomposites, performed/participated in all the characterization techniques, conducted the data analyses and wrote the first draft of the manuscript. Lukas Schmidt-Mende guided the synthesis of S:TiO2 nanoparticles. Martin Foldyna performed the ARTA and ARMMP measurements and related analysis. Hervé Roussel performed the X-ray measurements and analysis. Etienne Pernot performed the AFM observations and related analysis. Laetitia Rapenne performed the TEM observations and analysis. Carmen Jiménez and Jean-Luc Deschanvres guided the optimization of the FTO film deposition. Vincent Consonni, David Muñoz-Rojas and Daniel Bellet directed and guided throughout the work. All the authors revised and approved the manuscript.Acknowledgements
We would like to thank especially Martin Putnik for synthesizing the S:TiO2 nanoparticles, Isabelle Gélard for the SEM observations on the S:TiO2 nanoparticles, and Florence Robaut for the preparation of the TEM cross section by focused ion beam. We thank also Stéphane Brochen and Matthieu Jouvert for fruitful discussions. The funding was supported by the European Doctoral Program “IDS-FunMat” and Agence Nationale de Recherche (ANR, France) via the programme CE05 INDEED. DMR acknowledges funding through the Marie Curie Actions (FP7/2007–2013, Grant Agreement No. 631111).References
- E. Fortunato, D. Ginley, H. Hosono and D. C. Paine, MRS Bull., 2007, 32, 242–247 CrossRef CAS.
- F.-J. Haug and C. Ballif, Energy Environ. Sci., 2015, 8, 824–837 CAS.
- S. Kim, J.-W. Chung, H. Lee, J. Park, Y. Heo and H.-M. Lee, Sol. Energy Mater. Sol. Cells, 2013, 119, 26–35 CrossRef CAS.
- H. Iida, T. Mishuku, A. Ito, Y. Hayashi and Y. Hayashi, IEEE Trans. Electron Devices, 1987, 34, 271–276 CrossRef.
- J. Müller, B. Rech, J. Springer and M. Vanecek, Sol. Energy, 2004, 77, 917–930 CrossRef.
- W. Zhang, U. W. Paetzold, M. Meier, A. Gordijn, J. Hüpkes and T. Merdzhanova, Energy Procedia, 2014, 44, 151–159 CrossRef CAS.
- M. Meier, U. W. Paetzold, M. Ghosh, W. Zhang, T. Merdzhanova, G. Jost, N. Sommer, S. Michard and A. Gordijn, IEEE J. Photovolt., 2014, 4, 772–777 CrossRef.
- J. Escarré, C. Battaglia, K. Söderström, C. Pahud, R. Biron, O. Cubero, F.-J. Haug and C. Ballif, J. Opt., 2012, 14, 24009 CrossRef.
- G. Yang, R. A. C. M. M. van Swaaij, O. Isabella and M. Zeman, Prog. Photovoltaics, 2015, 23, 1283–1290 CAS.
- G. Giusti, V. Consonni, E. Puyoo and D. Bellet, ACS Appl. Mater. Interfaces, 2014, 6, 14096–14107 CAS.
- M. Jalalah, M. Faisal, H. Bouzid, A. A. Ismail and S. A. Al-Sayari, Mater. Res. Bull., 2013, 48, 3351–3356 CrossRef CAS.
- W. Jiao, Y. Xie, R. Chen, C. Zhen, G. Liu, X. Ma and H.-M. Cheng, Chem. Commun., 2013, 49, 11770 RSC.
- J. Lin, Y.-U. Heo, A. Nattestad, Z. Sun, L. Wang, J. H. Kim and S. X. Dou, Sci. Rep., 2014, 4, 5769 CrossRef PubMed.
- G. W. Watson, P. M. Oliver and S. C. Parker, Phys. Chem. Miner., 1997, 25, 70–78 CrossRef CAS.
- P. A. Mulheran and J. H. Harding, Modell. Simul. Mater. Sci. Eng., 1992, 1, 39–43 CrossRef CAS.
- V. Consonni, G. Rey, H. Roussel and D. Bellet, J. Appl. Phys., 2012, 111, 33523 CrossRef.
- V. Consonni, G. Rey, H. Roussel, B. Doisneau, E. Blanquet and D. Bellet, Acta Mater., 2013, 61, 22–31 CrossRef CAS.
- G. Rey, C. Ternon, M. Modreanu, X. Mescot, V. Consonni and D. Bellet, J. Appl. Phys., 2013, 114, 183713 CrossRef.
- G. Rey, PhD thesis, Université de Grenoble, 2012.
- D. Nečas and P. Klapetek, Open Phys., 2012, 10, 181–188 Search PubMed.
- H. Sakai, T. Yoshida, T. Hama and Y. Ichikawa, Jpn. J. Appl. Phys., 1990, 29, 630–635 CrossRef CAS.
- C.-M. Hsu, C. Battaglia, C. Pahud, Z. Ruan, F.-J. Haug, S. Fan, C. Ballif and Y. Cui, Adv. Energy Mater., 2012, 2, 628–633 CrossRef CAS.
- G. B. Harris, London, Edinburgh Dublin Philos. Mag. J. Sci., 1952, 43, 113–123 CrossRef.
- J. T. Wang, X. L. Shi, W. W. Liu, X. H. Zhong, J. N. Wang, L. Pyrah, K. D. Sanderson, P. M. Ramsey, M. Hirata and K. Tsuri, Sci. Rep., 2014, 4, 3679 Search PubMed.
- V. Pfeifer, P. Erhart, S. Li, K. Rachut, J. Morasch, J. Brötz, P. Reckers, T. Mayer, S. Rühle, A. Zaban, I. Mora Seró, J. Bisquert, W. Jaegermann and A. Klein, J. Phys. Chem. Lett., 2013, 4, 4182–4187 CrossRef CAS.
- D. O. Scanlon, C. W. Dunnill, J. Buckeridge, S. A. Shevlin, A. J. Logsdail, S. M. Woodley, C. R. A. Catlow, M. J. Powell, R. G. Palgrave, I. P. Parkin, G. W. Watson, T. W. Keal, P. Sherwood, A. Walsh and A. A. Sokol, Nat. Mater., 2013, 12, 798–801 CrossRef CAS PubMed.
- S. Li, F. Chen, R. Schafranek, T. J. M. Bayer, K. Rachut, A. Fuchs, S. Siol, M. Weidner, M. Hohmann, V. Pfeifer, J. Morasch, C. Ghinea, E. Arveux, R. Günzler, J. Gassmann, C. Körber, Y. Gassenbauer, F. Säuberlich, G. V. Rao, S. Payan, M. Maglione, C. Chirila, L. Pintilie, L. Jia, K. Ellmer, M. Naderer, K. Reichmann, U. Böttger, S. Schmelzer, R. C. Frunza, H. Uršič, B. Malič, W.-B. Wu, P. Erhart and A. Klein, Phys. Status Solidi RRL, 2014, 8, 571–576 CrossRef CAS.
- T. Umebayashi, T. Yamaki, S. Yamamoto, A. Miyashita, S. Tanaka, T. Sumita and K. Asai, J. Appl. Phys., 2003, 93, 5156–5160 CrossRef CAS.
- W. Ho, J. C. Yu and S. Lee, J. Solid State Chem., 2006, 179, 1171–1176 CrossRef CAS.
- R. Asahi, Science, 2001, 293, 269–271 CrossRef CAS PubMed.
- M. Harb, P. Sautet and P. Raybaud, J. Phys. Chem. C, 2013, 117, 8892–8902 CAS.
- X. Chen and C. Burda, J. Am. Chem. Soc., 2008, 130, 5018–5019 CrossRef CAS PubMed.
- Q.-L. Liu, Z.-Y. Zhao and Q.-J. Liu, RSC Adv., 2014, 4, 32100 RSC.
- E. Hecht, Optics, Addison-Wesley, San Francisco, 2010 Search PubMed.
- T. Oyama, M. Kambe, N. Taneda and K. Masumo, MRS Online Proc. Libr., 2008, 1101, 1101-KK02-01 CrossRef.
- J. Krc, B. Lipovsek, M. Bokalic, A. Campa, T. Oyama, M. Kambe, T. Matsui, H. Sai, M. Kondo and M. Topic, Thin Solid Films, 2010, 518, 3054–3058 CrossRef CAS.
- J. Krč, M. Zeman, O. Kluth, F. Smole and M. Topič, Thin Solid Films, 2003, 426, 296–304 CrossRef.
- A. De Martino, S. Ben Hatit and M. Foldyna, in Proc. SPIE, ed. C. N. Archie, 2007, vol. 6518, p. 65180 Search PubMed.
- S. Ben Hatit, M. Foldyna, A. De Martino and B. Drévillon, Phys. Status Solidi A, 2008, 205, 743–747 CrossRef CAS.
- T. Chih-Hung, H. Sui-Ying, H. Tsung-Wei, T. Yu-Tang, C. Yan-Fang, Y. H. Jhang, L. Hsieh, W. Chung-Chih, C. Yen-Shan, C. Chieh-Wei and L. Chung-Chun, Org. Electron., 2011, 12, 2003–2011 CrossRef.
- E. Compain, S. Poirier and B. Drevillon, Appl. Opt., 1999, 38, 3490 CrossRef CAS PubMed.
- E. Garcia-Caurel, A. De Martino and B. Drévillon, Thin Solid Films, 2004, 455–456, 120–123 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6tc04153a |
| This journal is © The Royal Society of Chemistry 2017 |