Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Optimisation of oxide-ion conductivity in acceptor-doped Na0.5Bi0.5TiO3 perovskite: approaching the limit?†
F.
Yang
 *a,
M.
Li
*a,
M.
Li
 b,
L.
Li
b,
L.
Li
 a,
P.
Wu
a,
E.
Pradal-Velázque
a and
D. C.
Sinclair
a,
P.
Wu
a,
E.
Pradal-Velázque
a and
D. C.
Sinclair
 *a
*a
aDepartment of Materials Science & Engineering, University of Sheffield, Mappin Street, Sheffield, S1 3JD, UK. E-mail: fan.yang@sheffield.ac.uk; d.c.sinclair@sheffield.ac.uk
bDepartment of Mechanical, Materials and Manufacturing Engineering, University of Nottingham, NG7 2RD, UK
First published on 9th October 2017
Abstract
Na0.5Bi0.5TiO3 (NBT) perovskite is often considered as a potential lead-free piezoelectric material but it can also be an excellent oxide-ion conductor (M. Li et al., Nature Materials, 13, 2014, 31–35). Here we report the non-stoichiometry and oxide-ion conductivity of undoped and acceptor-doped NBT. A range of acceptor-type ions with varying doping levels are selected to incorporate into NBT or Bi-deficient NBT (nominal Na0.5Bi0.49TiO2.985; NB0.49T). Low levels of acceptors (typically < 2 at%) can be doped on both cation sites of NBT by an ionic compensation mechanism to create oxygen vacancies and are therefore effective in enhancing the bulk oxide-ion conductivity to values of ∼2 mS cm−1 at 400 °C. A maximum enhancement of less than 1 order of magnitude is achieved using either A-site Sr (or Ca) or B-site Mg doping in NB0.49T. This conductivity maximum is in good agreement with an oxygen-vacancy diffusivity limit model in a perovskite lattice proposed by R. A. De Souza (Advanced Functional Materials, 25, 2015, 6326–6342) and suggests that optimisation of the ionic conductivity in NBT has been achieved. Our findings on NBT illustrate that this approach should be applicable to other acceptor-doped perovskite oxides to determine their electrolyte (oxide-ion) conductivity limit.
Solid oxide fuel cells (SOFCs) are electrochemical devices that offer an efficient source of electrical power via oxidation of a fuel source. In attempts to drive down the operating temperatures of SOFCs from 800 to below 600 °C to reduce start-up times and to improve device lifetime there is a need to develop new oxide-ion solid electrolytes with higher conductivity at these lower temperatures. Acceptor-doped perovskites-based materials such as (La1−xSrx)(Ga1−yMgy)O3−x/2−y/2 (LSGM) and more recently Na0.5Bi0.5Ti1−xMgxO3−x are two candidate materials that have been investigated as electrolytes for Intermediate Temperature SOFCs (IT-SOFCs). De Souza recently reviewed oxygen vacancy diffusion in a wide variety of ABO3-type perovskites ranging from ferroelectric dielectrics such as BaTiO3 and mixed ionic-electronic conductors such as (Ba0.5Sr0.5)(Co0.8Fe0.2)O3−δ to electrolytes such as (La0.9Sr0.1)(Ga0.8Mg0.2)O2.85. He reported a surprising result that regardless of the level of oxygen vacancies in these materials, the oxygen vacancy diffusivity is very similar and considered the possibility of a fundamental limit to oxygen-vacancy diffusivity in the ABO3 perovskite lattice. Although unable to conclude a definitive answer to this question, De Souza estimated a plausible limit and reasoned that if the activation entropy of vacancy migration was not higher than −kB (where kB is the Boltzmann constant and for a Debye frequency of 1013 Hz) then we may be close to the physical limit for the oxygen diffusion coefficient in acceptor-doped cubic perovskites. Here we have attempted to optimise the oxide-ion conductivity in the recently reported Na0.5Bi0.5TiO3 (NBT) oxide-ion conductors by acceptor doping and found that the highest bulk conductivity obtained is consistent with the value calculated from this upper limit, therefore suggesting optimisation of oxide-ion conductivity in this lattice may have been achieved. This approach may be beneficial in trying to establish the optimisation of electrolyte conductivity in a variety of acceptor-doped perovskites and therefore help in the design and development of oxide-ion conductors based on this important class of solids for applications in electrochemical devices such as IT-SOFCs.
The ferroelectric perovskite sodium bismuth titanate, NBT has long been considered as one of the more favoured lead-free piezoelectric materials to replace lead zirconate titanate (PZT).1–3 It is also a recently discovered oxide-ion conductor with the bulk conductivity (σb) of undoped nominally stoichiometric NBT approaching 1.0 × 10−3 S cm−1 at 600 °C, which is more than three orders of magnitude higher than that of undoped LaGaO3 at the same temperature.4–6 It is therefore a promising material to achieve higher oxide-ion conductivity and to develop a family of oxide-ion conductors based on NBT.
The level of non-stoichiometry that can give rise to the high oxide-ion conductivity is low and the defect chemistry and conduction mechanism(s) remain a challenging topic, especially given the complex polymorphism that exists in NBT. The oxide-ion conductivity in nominally stoichiometric NBT, i.e. Na0.5Bi0.5TiO3, is attributed to oxygen vacancies generated by low levels of Bi2O3 loss during ceramic processing according to
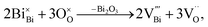 | (1) |
Our previous research showed that enhancement of σb can be achieved by inducing a low level of Bi-deficiency in NBT (e.g., nominal Na0.5Bi0.49TiO3; NB0.49T) and/or by altering the Na/Bi nominal ratio in the starting compositions prior to processing. NB0.49T has σb of ∼half an order of magnitude higher than NBT with tion > 0.9 at 600–700 °C.4 The enhanced σb is due to creation of additional oxygen vacancies, as described by eqn (1). At 500 °C, σb of NB0.49T is ∼1.1 × 10−3 S cm−1, which is above the minimum conductivity requirement for a 1 μm electrolyte in SOFCs.8 A small amount of Na, Ti-rich secondary phase can be detected in NB0.49T under SEM.4,9 Further Bi-deficiency (i.e. nominal Na0.5Bi0.48TiO3; NB0.48T) yields slightly higher σb but with a greater proportion of secondary phases. Instead of further increasing the Bi-deficiency level from NB0.49T to NB0.48T with the introduction of significant secondary phases, alternative approaches are required to enhance the oxide-ion conductivity of NBT. It should be stressed the level of A-site non-stoichiometry in undoped NBT is low and under our conditions of ceramic processing undoped compositions with Na/Bi starting ratios ≥ 1 are required to obtain high levels of oxide-ion conductivity.
Acceptor doping is a commonly employed strategy to enhance ionic conductivity in fluorite-type (i.e., Y-doped ZrO2 and Gd-doped CeO2) and perovskite-type (i.e., Sr, Mg-co-doped LaGaO3) oxide-ion conductors by creating oxygen vacancies. However, the influence of acceptor-doping on the electrical properties in many perovskite titanates, e.g., BaTiO3 (BT) and SrTiO3 (ST) is often more complex with either n-type, p-type or oxide-ion conductivity being dominant depending on a combination of the oxygen-partial-pressure, annealing temperature and cooling rate conditions employed.10–12 Furnace cooled, acceptor-doped BT and ST ceramics processed in air usually exhibit p-type hole conduction (h˙) based on the uptake of oxygen (on cooling) as given by the following mechanism
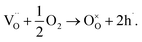 | (2) |
Here we report the oxide-ion conductivity of acceptor-doped NBT and NB0.49T based on various acceptor-type ions (with varying doping levels), i.e., Na+, K+, Ca2+, Sr2+, Ba2+ (to replace Bi3+ on A-site) and Mg2+, Zn2+, Sc3+, Al3+ and Ga3+ (to replace Ti4+ on B-site). Transition metal ions such as Fe3+, Co3+ and Ni2+ may introduce electronic conduction into NBT and are therefore not included in this study. Possible compensation mechanisms and the effect of acceptor-doping on the electrical conductivity of NBT are discussed. The results are consistent with the De Souza suggestion that we may be approaching a physical limit of oxygen-diffusion (at least for these acceptor-doped NBT-based perovskites) and the σb values reported herein represent close to optimised levels.
NBT has an ABO3 perovskite structure where the A-site is shared by randomly distributed Na+ and Bi3+ ions and the B-site is occupied by Ti4+ ions. Depending on the ionic size, acceptor-type dopants can be doped either on the A-site to replace Bi3+ (larger dopant ions) or on the B-site to replace Ti4+ (smaller dopant ions). In each case, doping may occur by either an ionic or electronic compensation mechanism. In the case of the former, acceptor doping would create oxygen vacancies. A summary of the defect reactions investigated for a range of A- and B-site acceptor dopants in this study (given in brackets) are described by the following Kroger–Vink equations:
A-site:
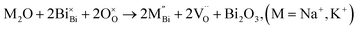 | (3a) |
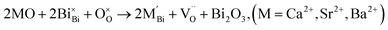 | (3b) |
B-site:
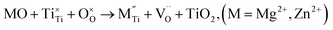 | (3c) |
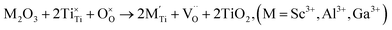 | (3d) |
Although electronic doping may occur due to eqn (2) as observed for many other titanate-based perovskites, impedance spectroscopy and EMF measurements on Sr-doped and Mg-doped NB0.49T in various atmospheres have shown an enhanced pO2-independent σb and a higher tion compared to NB0.49T (Table S1†). These electrical properties prove that acceptor-doping of NB0.49T on both sites is predominantly by an ionic compensation mechanism to create oxygen vacancies (eqn (3)). Acceptor-doping is therefore effective to enhance oxide-ion conduction of NB0.49T without introducing any significant electronic contribution.
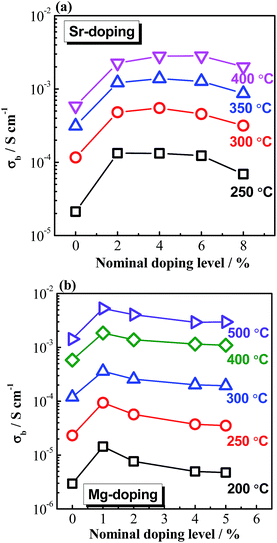
Based on the above understanding, various acceptor-type dopants have been selected to dope NBT and NB0.49T in an attempt to optimise the oxide-ion conductivity in this perovskite. Among all the dopants and doping levels investigated in this work, 2% Sr doping on the A-site (nominal Na0.5Bi0.47Sr0.02TiO2.975) and 1% Mg doping on the B-site (Na0.5Bi0.49Ti0.99Mg0.01O2.975) show a maximum enhancement of σb less than 1 order of magnitude compared to NB0.49T, Fig. 1. General features are that higher σb is obtained for equivalent doping of NB0.49T (Bi-deficient) compared to NBT (stoichiometric) compositions and that A-site doping can promote higher levels of σb compared to B-site doping. Bulk conductivity, σb, of NB0.49T with other dopants are all within the shaded region of Fig. 1. Values of σb at selected temperatures and activation energies of each composition are listed in Table S2.†
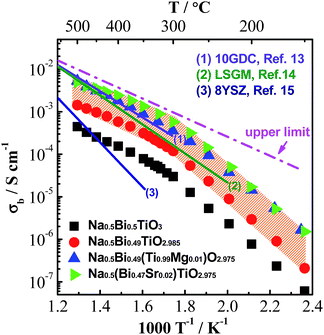 | ||
| Fig. 1 An Arrhenius plot of bulk conductivity, σb, for undoped and acceptor-doped NBT ceramics. The dash-dot line represents the upper limit of σb based on the oxygen-vacancy diffusion coefficient predicted in ref. 11, see text. σb for some of the best-known oxide-ion conductors are plotted for comparison: (1) Ce0.9Gd0.1O1.95, 10GDC;13 (2) La0.9Sr0.1Ga0.9Mg0.1 O2.9, LSGM;14 (3) Zr0.852Y0.148O1.926, 8YSZ.15σb for NB0.49T with other dopants studied in this work lie within the shaded area. | ||
There are several reasons for the limited enhancement of σb by acceptor doping. First, the solid solution limit of these dopants in NB0.49T is very low (typically < 2 at%). For example, Na2Ti6O13 and MgTiO3 secondary phases were detected by SEM for 2% Sr-doped NB0.49T and 2% Mg-doped NB0.49T, respectively (Fig. S1†). Second, although acceptor doping increases the oxygen vacancy concentration, it decreases the mobility of charge carriers by increasing the oxygen migration barriers. First-principle calculations have shown that B-site doping, such as Mg2+ for Ti4+, significantly increases the oxygen migration barriers by binding with oxygen vacancies.16 For A-site doping, such as Sr2+ for Bi3+, the mobility of oxygen ions is restricted by the lower polarisability and higher bonding strength with oxygen of Sr2+ as compared to Bi3+.9 Third, using the oxygen-vacancy diffusivity limit in a cubic ABO3 perovskite lattice proposed by R. A. De Souza,11 an upper limit for σb of NBT with oxygen deficiency of 0.025, calculated from Nernst–Einstein equation, is predicted, as shown by the dash line in Fig. 1. At >300 °C, the highest σb obtained by A-site Sr-doping and B-site Mg-doping is very close to the upper limit. As a consequence of the reasons given above, it is questionable that further enhancement of σb can be achieved by increasing the doping level, either on the A-site or the B-site, as shown in Fig. 2.
It is worth mentioning that the log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σb − 1/T relationship of undoped and acceptor-doped NB0.49T shows a change in activation energy, Ea from ∼0.4 eV above 300 °C to ∼0.9 eV below 300 °C (Fig. 1 and Table S2†). The reason(s) for a change of Ea around this temperature has not been fully established but the possibility of a change in charge carrier from oxygen ions to electrons, holes or protons has been excluded. First, impedance spectroscopy measurements in flowing N2, air and O2 show a pO2-independent bulk response, indicating the absence of any significant electronic conduction (Fig. S2†). Second, impedance measurements performed in wet and dry atmospheres, as well as on heating and cooling, show there is no change to σb, indicating there is no significant level of protonic conduction (Fig. S3†). Sodium ions are not likely to be charge carriers as there is no open framework (as in NASICON17) or Na-layers (as in P2-type NaxCoO2 (ref. 18)) in the NBT structure to provide pathways for Na+. Therefore, it is reasonable to propose the electrical conduction is still dominated by oxygen ions at temperatures below 300 °C. A plausible explanation for the change of Ea is the coexistence of rhombohedral (R) and tetragonal (T) phases in the temperature range from 250 to 400 °C, which was revealed by variable temperature neutron diffraction studies (Fig. S4†). An estimation of σb from the Maxwell model for a two-phase composite showed good agreement with the experimental data of σb, suggesting coexistence of R and T phases may be a plausible explanation for the change in Ea at ∼300 °C.19 Other possible reasons for the change of Ea are dissociation of defect clusters and/or changing of conduction paths as recently proposed by Meyer and Albe.20
σb − 1/T relationship of undoped and acceptor-doped NB0.49T shows a change in activation energy, Ea from ∼0.4 eV above 300 °C to ∼0.9 eV below 300 °C (Fig. 1 and Table S2†). The reason(s) for a change of Ea around this temperature has not been fully established but the possibility of a change in charge carrier from oxygen ions to electrons, holes or protons has been excluded. First, impedance spectroscopy measurements in flowing N2, air and O2 show a pO2-independent bulk response, indicating the absence of any significant electronic conduction (Fig. S2†). Second, impedance measurements performed in wet and dry atmospheres, as well as on heating and cooling, show there is no change to σb, indicating there is no significant level of protonic conduction (Fig. S3†). Sodium ions are not likely to be charge carriers as there is no open framework (as in NASICON17) or Na-layers (as in P2-type NaxCoO2 (ref. 18)) in the NBT structure to provide pathways for Na+. Therefore, it is reasonable to propose the electrical conduction is still dominated by oxygen ions at temperatures below 300 °C. A plausible explanation for the change of Ea is the coexistence of rhombohedral (R) and tetragonal (T) phases in the temperature range from 250 to 400 °C, which was revealed by variable temperature neutron diffraction studies (Fig. S4†). An estimation of σb from the Maxwell model for a two-phase composite showed good agreement with the experimental data of σb, suggesting coexistence of R and T phases may be a plausible explanation for the change in Ea at ∼300 °C.19 Other possible reasons for the change of Ea are dissociation of defect clusters and/or changing of conduction paths as recently proposed by Meyer and Albe.20
Nevertheless, acceptor-doped NB0.49T still shows attractive bulk conductivity. At 500 °C, σb of 2% Sr-doped or 1% Mg-doped NB0.49T is ∼5.0 × 10−3 S cm−1, which is comparable to LSMG and GDC. Comparing with the two best known δ-Bi2O3 oxide-ion conductors, (BiO1.5)0.8(ErO1.5)0.2, 20ESB and (BiO1.5)0.88 (DyO1.5)0.08(WO3)0.04, 8D4WSB, although σb of doped NB0.49T is initially lower than 20ESB and 8D4WSB, it shows no appreciable degradation with time contrary to the rapid conductivity degradation of 20ESB and 8D4WSB.19 After 50 hours, σb of Sr-doped NB0.49T is 3 times higher than that of 20ESB and 8D4WSB (Table S3†).
As σb appears to be approaching an upper limit, further improvement of electrical conductivity of doped NBT ceramics should be focused on the contributions from grain boundaries (GB's). A typical Z* plot for conducting NBT is shown in Fig. 3a and displays three (or more, depending on temperature and frequency range) arcs, from left to right (high frequency to low frequency), corresponding to the responses from the bulk, GB and electrodes, respectively. The GB's have a significant contribution to (and sometimes dominate) the overall ceramic membrane resistance. Using an equivalent circuit of three resistor-constant phase elements (R-CPE) connected in series to fit the impedance data, resistance and capacitance of the GB's can be obtained. Assuming the permittivity of the GB's is approximately the same as that of the bulk,21 a specific GB conductivity (σGB) can be calculated according to22
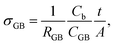 | (4) |
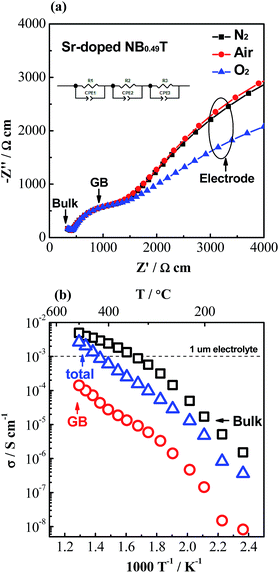 | ||
| Fig. 3 (a) Complex impedance, Z*, plots for 2% Sr-doped NB0.49T with Pt electrodes under different atmospheres at 400 °C; the inset figure is the equivalent circuit used to fit the impedance data. (b) Arrhenius plots for σb, σGB and σtot for 2% Sr-doped NB0.49T. The horizontal dash line indicates the minimum conductivity requirement for a 1 μm electrolyte for SOFCs.8 | ||
The total conductivity of 2% Sr-doped NB0.49T is higher than 1.0 × 10−3 S cm−1 at temperatures > 450 °C, as shown in Fig. 3b. Our previous studies have shown that Sr-doped NB0.49T can withstand 5% H2/95% N2 at 550 °C without decomposition.8,18 Similar behaviour has been observed in Ca-doped NB0.49T (not shown). Mg-doped NBT showed even better stability in reducing atmospheres. Impedance measurements showed no change in the bulk response at 600 °C in 5% H2/95% N2 for 45 h with 1% Mg-doped NBT in contrast to a significant reduction of the bulk response for undoped NBT under the same conditions.4 These doped NBT materials are therefore very promising to be used as an electrolyte in SOFCs working in the temperature range of 450–550 °C.
In conclusion, low levels of acceptor-type dopants either on the A-site to replace Bi3+ or on the B-site to replace Ti4+ can be used to create additional oxygen vacancies and therefore enhance the ionic conductivity of NBT (or NB0.49T). Among all the doping elements investigated in this work, Sr- or Ca-doping on A-site and Mg-doping on B-site are the most effective dopants to enhance σb; however, it does appear to be reaching a limit consistent with that proposed by De Souza. These acceptor-doped NB0.49T show excellent ionic conductivity with extremely low levels of degradation and reasonable stability in reducing atmosphere. They also have an advantage over δ-Bi2O3 oxide-ion conductors as being more sustainable (rare-earth free) materials with lower Bi-contents. Further work will be focused on understanding the grain boundary conductivity and conduction mechanism to minimise their contribution to the total conductivity of NBT-based oxide-ion conducting ceramics. The significance of this work is not only understanding the defect chemistry by acceptor doping of NBT and optimising its oxide-ion conductivity, but also trying to establish the upper limit of electrolyte conductivity in a variety of acceptor-doped perovskites from the oxygen vacancy diffusivity limit, which is determined mainly by the structural parameters of the host. The upper limit of conductivity is the highest value that can be achieved by acceptor doping, which can give a guideline whether optimisation of conductivity is achieved and will therefore help in the design and development of oxide ion conductors.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the EPSRC for funding (EP/L027348/1). Variable Temperature powder Neutron Diffraction Experiments at the ISIS Pulsed Neutron and Muon Source were supported by beamtime allocations (grant number 1620186) from the Science and Technology Facilities Council and we thank Dr Ivan da Silva for assistance with the collection of data. E. Pradal-Velázquez thanks CONACYT for his scholarship under “Becas CONACYT al extranjero (registro 327115)”.References
- E. Aksel and J. L. Jones, Sensors, 2010, 10, 1935 CrossRef CAS PubMed.
- D. Damjanovic, N. Klein, J. Lin and V. Porokhonskky, Funct. Mater. Lett., 2010, 3, 5 CrossRef CAS.
- K. Reichmann, A. Feteira and M. Li, Materials, 2015, 8, 8467 CrossRef PubMed.
- M. Li, M. J. Pietrowski, R. A. De Souza, H. Zhang, I. M. Reaney, S. N. Cook, J. A. Kilner and D. C. Sinclair, Nat. Mater., 2014, 13, 31 CrossRef CAS PubMed.
- M. Li, H. Zhang, S. N. Cook, L. Li, J. A. Kilner, I. M. Reaney and D. C. Sinclair, Chem. Mater., 2015, 27, 629 CrossRef CAS.
- T. Ishihara, H. Matsuda, M. A. bin Bustam and Y. Takita, Solid State Ionics, 1996, 86–88, 197 CrossRef.
- D. Schütz, M. Deluca, W. Krauss, A. Feteira, T. Jackson and K. Reichmann, Adv. Funct. Mater., 2010, 22, 2285 CrossRef.
- Z. Gao, L. V. Moqni, E. C. Miller, J. G. Railsback and S. A. Barnett, Energy Environ. Sci., 2016, 9, 1602 CAS.
- F. Yang, P. Wu and D. C. Sinclair, Solid State Ionics, 2017, 299, 38 CrossRef CAS.
- S. Li, J. Morasch, A. Klein, C. Chirila, L. Pintilie, L. Jia, K. Ellmer, M. Naderer, K. Reichmann, M. Gröting and K. Albe, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 045428 CrossRef.
- R. A. De Souza, Adv. Funct. Mater., 2015, 25, 6326 CrossRef CAS.
- D. M. Symth, J. Electroceram., 2003, 11, 89 CrossRef.
- T. Zhang, P. Hing, H. Huang and J. A. Kilner, Solid State Ionics, 2002, 148, 567 CrossRef CAS.
- C. Haavik, E. M. Ottesen, K. Nomura, J. A. Kilner and T. Norby, Solid State Ionics, 2004, 174, 233 CrossRef CAS.
- Y. Arachi, H. Sakai, O. Yamamoto, Y. Takeda and N. Imanishai, Solid State Ionics, 1999, 121, 133 CrossRef CAS.
- X. He and Y. Mo, Phys. Chem. Chem. Phys., 2015, 17, 18035 RSC.
- N. Anantharamulu, K. Koteswara Rao, G. Rambabu, B. Vijaya Kumar, V. Radha and M. Vithal, J. Mater. Sci., 2011, 46, 2821 CrossRef CAS.
- R. Berthelot, D. Carlier and C. Delmas, Nat. Mater., 2011, 10, 74 CrossRef CAS PubMed.
- F. Yang, H. Zhang, L. Li, I. M. Reaney and D. C. Sinclair, Chem. Mater., 2016, 28, 5269 CrossRef CAS.
- K.-C. Meyer and K. Albe, J. Mater. Chem. A, 2017, 5, 4368 CAS.
- X. Guo and J. Maier, J. Electrochem. Soc., 2011, 148, 121 CrossRef.
- X. Guo and R. Waser, Prog. Mater. Sci., 2006, 51, 151 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ta07667c |
| This journal is © The Royal Society of Chemistry 2017 |