Open Access Article
Open Access ArticleA structural study of Ruddlesden–Popper phases Sr3−xYx(Fe1.25Ni0.75)O7−δ with x ≤ 0.75 by neutron powder diffraction and EXAFS/XANES spectroscopy†
Jekabs
Grins
a,
Dariusz
Wardecki
abc,
Kjell
Jansson
a,
Stefan
Carlson
d,
Jordi J.
Biendicho
ae and
Gunnar
Svensson
 *a
*a
aDepartment of Materials and Environmental Chemistry, Stockholm University, S-106 91 Stockholm, Sweden. E-mail: gunnar.svensson@mmk.su.se
bInstitute of Experimental Physics, Faculty of Physics, University of Warsaw, Pasteura 5, 02-093 Warsaw, Poland
cDepartment of Chemistry and Chemical Engineering, Chalmers University of Technology, Gothenburg, SE-41296, Sweden
dMAX IV Laboratory, Lund University, P. O. Box 118, 221 00 Lund, Sweden
eIREC, Catalonia Institute for Energy Research, Jardins de les Dones de Negre 1, 08930, Sant Adrià de Besòs, Spain
First published on 17th October 2017
Abstract
The structures of Ruddlesden–Popper n = 2 member phases Sr3−xYxFe1.25Ni0.75O7−δ with 0 ≤ x ≤ 0.75 have been investigated using neutron powder diffraction and K-edge Fe and Ni EXAFS/XANES spectroscopy in order to gain information about the evolution of the oxygen vacancy distribution and Fe/Ni oxidation state with x. Both samples prepared at 1300 °C under a flow of N2(g), with δ = 1.41–1.00, and samples subsequently annealed in air at 900 °C, with δ = 0.44–0.59, were characterized. The as-prepared x = 0.75 phase has δ = 1, the O1 atom site is vacant, and the Fe3+/Ni2+ ions have a square pyramidal coordination. With decreasing x the O3 occupancy decreases nearly linearly to 81% for x = 0, while the O1 occupancy increases from 0 for x = 0.4 to 33% for x = 0. The air-annealed x = 0.75 sample has a δ value of 0.59 and the Fe3+/Fe4+/Ni2+/Ni3+ ions have both square pyramidal and octahedral coordination. With decreasing x, the δ value decreases to 0.45 for x = 0, implying an increase in the oxidation states of Fe/Ni ions. EXAFS/XANES data show that for the as-prepared samples the coordination changes are predominantly for Ni2+ ions and that the air-annealed samples contain both Fe3+/Fe4+ and Ni2+/Ni3+ ions.
Introduction
Ruddlesden–Popper (RP) phases are considered as promising candidates for cathode materials in intermediate temperature solid oxide fuel cells (IT-SOFCs) as they can exhibit high mixed oxide-ion and electronic conductivities.1–4 They have a layered inter-growth structure with alternating layers of perovskite and rock-salt type blocks. A high electronic conductivity may be provided by the perovskite layers and a high oxygen ion mobility by vacancies or interstitials in the rock-salt layers. Phases like Sr3Fe2O7−δ have also been studied with respect to their magnetic properties5 and how they vary with the tuneable parameter of the oxygen content. In a previous study, we investigated RP n = 2 member phases Sr3−xYxFe1.25Ni0.75O7−δ, 0 ≤ x ≤ 0.75.6 The ideal stoichiometry of an n = 2 RP phase is A3B2O7, where A is an alkaline-earth or rare-earth element, B is a transition metal element, and the structure contains two ABO3 perovskite layers that alternate with single AO rock-salt layers,7Fig. 1. The B atom is coordinated by one O1 atom, one O2 atom and 4 O3 atoms.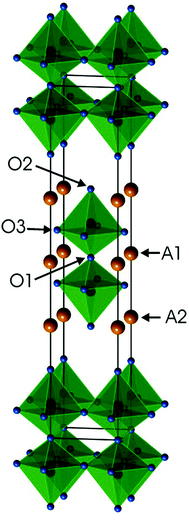 | ||
| Fig. 1 Crystal structure of the ideal A3B2O7n = 2 RP phase. Atom coordinates used are for air-annealed x = 0.75. | ||
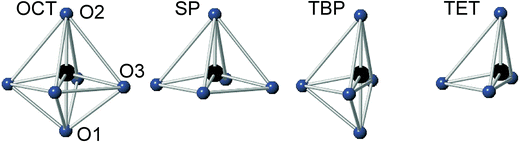
For real n = 2 RP phases, the O1 site may be partially or totally vacant and the O3 site may also be partially vacant, while no evidence for O2 vacancies has been found.8–13 The O content per formula unit, 7 − δ, may be as low as 5.45.9 For oxygen-deficient phases the probable B atom coordination polyhedra are, in varying proportions, octahedra, square pyramids, trigonal bi-pyramids and tetrahedra, Fig. 2.10 Further types of coordination polyhedra are certainly theoretically possible but we hold them less likely to be present in significant proportions. For instance, two O3 missing would correspond to a IV-coordination similar to that found for Fe atoms in brownmillerite, although very distorted. The results from XANES suggest, however, that the Fe atoms are predominantly V-coordinated for all x-values.
In this study, the structures for fifteen different compositions of Sr3−xYxFe1.25Ni0.75O7−δ have been studied, primarily by neutron powder diffraction (NPD), in order to characterise the evolution of the vacancy ordering and oxidation states of Fe and Ni with x, i.e., Y content, and oxygen content. The motivation for the study is partly to provide a part of the basis for a better understanding of how RP n = 2 phases can be tailored for IT-SOFC applications and partly to characterize the disorder in the structures from a fundamental point of view. Structural information gained from the NPD data has been supplemented by information from Ni and Fe K-edge EXAFS and XANES spectra.
Experimental section
Sample preparation
The phases Sr3−xYxFe1.25Ni0.75O7−δ were prepared by a solid-state reaction, using SrCO3, Y2O3, Fe2O3 and NiO as the starting materials.6 Pelletized samples were heated under a N2(g) flow at 1300 °C for 4 × 17 h, with intermediate grindings. Some of the as-prepared samples were subsequently heat-treated in air at 900 °C for 12 h, using a heating rate of 300 °C h−1 and a cooling rate of 50 °C h−1. The samples were stored in desiccators in order to avoid compositional and structural changes due to moisture uptake, observed to take place in similar phases, especially for low x values.9Methods
Time-of-flight (TOF) NPD patterns were collected at room temperature for some of the samples with the POLARIS instrument at ISIS, Rutherford Appleton Laboratory, England, and for the rest with the POWGEN instrument at the Oak Ridge National Laboratory, Tennessee, USA. The structural parameters were refined using the Rietveld method and the Topas software.14 The space group I4/mmm was used in all refinements.Cation compositions were determined by energy dispersive spectroscopy (EDS) micro-analysis with a JEOL 7000F SEM equipped with an Oxford Inca EDS system.
Iron and nickel K-edge EXAFS and XANES spectra were measured at the I811 beamline at the MAXlab facility, Lund, Sweden. Metal Fe/Ni foils were used for energy scale calibration. The EXAFS spectra were analyzed using the EXAFSPAK program.15 All single and multiple scattering paths were calculated with the FEFF6 package.16 XANES pre-edge peaks were fitted using the program Fityk.17
Results
Structure refinements using NPD data
For data recorded at ISIS, the 147°, 90° and 56° detector banks were used and for data recorded at the ORNL banks 2 and 5 which were by default set to 90° were used. On average, data down to d = 0.3 Å and ∼350 theoretical reflections were used. A representative TOF diffraction pattern with a fit is shown in Fig. 3.The samples contained small amounts of NiO, ≤0.5 wt%, and for the as-prepared samples also metallic Ni ≤0.2 wt%, with the exception of phase pure x = 0.75 samples, which were included in the refinements. The as-prepared samples with x = 0.6 and x = 0.75 showed additional magnetic peaks which were accounted for by adding the magnetic phase.6 The obtained χ2 values ranged between 2 and 11 and RI values between 0.8 and 5.4%. The details of the refinements and tables of refined parameter values and derived structure related parameters are given in the ESI.†
hkl dependent peak broadenings in powder diffraction data
An encountered difficulty in the structure refinements was the presence of an hkl dependent sample peak broadening, in particular revealed by 00l reflections as an asymmetric high-d tail. The broadening was clearly seen in the collected synchrotron high-resolution XRPD data, not treated further here, and less so in the lower resolution NPD data. Three causes were considered: (i) a symmetry lowering, with an orthorhombic super-cell with a ≈ b and space-group symmetry Cmcm or Cmc21,18 (ii) the presence of two RP n = 2 phases with very similar unit cell parameters,19–21 and (iii) stacking faults along [001].22Using a larger orthorhombic unit cell did not result in better fits and no super-structure reflections could be observed in NPD or XRPD patterns, nor in selected area electron diffraction patterns recorded for selected samples.
Asymmetric peak broadenings observed in synchrotron XRPD patterns of La2−2xSr1+2xMn2O7 manganites have been explained and modelled by two RP phases with very similar compositions and unit cell parameters.19–21 For the present phases, e.g., an x = 0.75 composition Sr2.25Y0.75Fe1.25Ni0.75O7−δ could accordingly ultimately phase-separate into two phases with compositions Sr2YFeNiO7−δ and Sr3Fe2O7−δ. Cation compositions in different crystallites of the as-prepared x = 0.75 were therefore determined by EDS in a SEM on cross-section polished samples containing crystal agglomerates. The observed channelling contrast made it easy to see the locations of individual grains and an accelerating voltage of 4.0 kV was used to decrease the electron-sample interaction volume. No difference in cation compositions within and between grains was, however, found.
A third possible cause for an hkl dependent peak broadening is stacking faults, frequently observed for RP phases, i.e., insertion of perovskite layers with a different n.22 Simulations using the program DISCUS23 showed that for the present phases the broadening for 00l reflections is consistent with a random replacement of about one out of twenty of the perovskite layers with an n = 1 perovskite block.
These findings make us conclude that stacking faults are the probable cause of the hkl dependent peak broadenings. For the refinements from the NPD data, they could be adequately modelled by using spherical harmonics, as implemented in the TOPAS program,14 whereas for the higher-resolution synchrotron data it was also necessary to include an anisotropic asymmetry of the peak shape.
Site occupancy factors
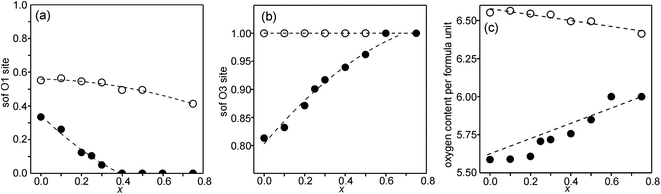
Refined site occupancy factors (sofs) for O1 and O3 atoms are shown in Fig. 4, together with the derived total O contents per formula unit. No evidence was found for vacancies on the O2 atom site. The Topas software gave errors in the O content of ≤0.01, but the true errors were certainly larger.The as-prepared samples show no occupancy of the O1 site for x ≥ 0.4, implying that there are no trigonal bipyramids. For x < 0.4, the sof for O1 increases with decreasing x to 33% for x = 0 and all four possible coordination polyhedra may coexist. The sof for O3 decreases with decreasing x continuously from 100% for x = 0.75 to 81% for x = 0. The fractions of different coordination polyhedra cannot be derived from the determined sofs for O1 and O3 alone. However, if it can be assumed that there are no octahedra, or only a small number of them, the fractions of square pyramids, trigonal bipyramids and tetrahedra can be estimated, as further considered in the Discussion section.
For the as-prepared samples the O content decreases nominally linearly with decreasing x from 6.0 for x = 0.75 to 5.63 for x = 0 if they contain only Fe3+ and Ni2+, as shown by the dashed line in Fig. 4c. For x-values ≤0.4 the observed O contents lie significantly below this line, implying that the samples contain some Fe2+. The deviation of the experimental values from this line towards lower oxygen contents is largest for x = 0.2, which indicates that the content of Fe2+ has a maximum near x = 0.2, amounting to 0.25 Fe2+ per formula unit or 20% of the total content of Fe.
For the air-annealed samples, the O1 sof is relatively constant, increasing from 41% for x = 0.75 to 55% for x = 0. No indications were found for vacancies on the O3 sites and the total O content per formula unit, Fig. 4c, varies in proportion to the O1 site occupancy.
The refinements showed that the Y atoms occupy predominantly the A1 site in the perovskite layer. This conclusion is validated by the bond valence calculations, see below. Although it cannot be ruled out that Y may also occupy the A2 site to a very small extent, the Y atoms were in the final refinements put only on the A1 site according to their nominal contents.
Atomic coordinates and bond distances
In the space-group I4/mmm the only variable coordinates are the z-coordinates for atoms A2, B, O2 and O3, while atom positions for A1 and O1 are fixed. The compositional dependences of the z-coordinates are shown in Fig. 5.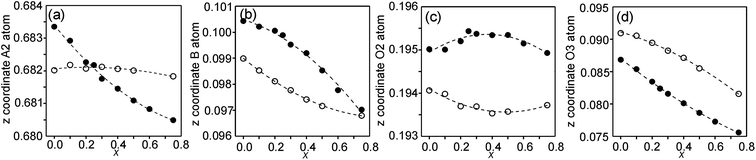 | ||
| Fig. 5 Compositional dependences of z-coordinates for (a) A2, (b) B, (c) O2 and (d) O3. Filled circles show coordinates for the as-prepared samples and open circles for the air-annealed samples. | ||
The observed over-all variation in the z-coordinate is 0.0023 for A2, 0.0036 for B, 0.0011 for O2 and 0.0137 for O3. The by far largest variation is thus observed for the O3 atom.
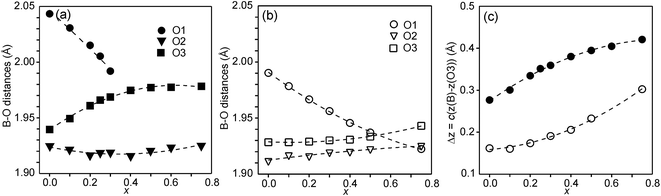
In Fig. 6, the observed B–O distances are shown, together with the observed distance Δz between the O atom and the basal plane of the O3 atoms in the z direction, i.e., c(z(B) − z(O3)).
The compositional variation of coordinates and B–O distances can largely be rationalized as follows. The O2 coordinate varies little overall and remains constant with x, see Fig. 5c. With increasing x, Y3+, which has a higher charge and smaller ionic radius than Sr2+, substitutes for Sr2+ on the A1 site in the perovskite layer. This shortens the A1–O3 bond length and causes large coordinate shifts of the O3 atoms, see Fig. 5d. The A1–O3 bond length also decreases with the fraction of vacancies on the O1 site, which accounts for the lower O3 coordinates for the as-prepared samples. The BO6 octahedra in the perovskite layer are irregular, in general with a short B–O2 distance and a long B–O1 distance (when present), with the B atoms displaced from the basal plane of the O3 atoms by Δz Å towards O2, c.f., Fig. 6c. The shift from the basal plane averts too short B–O3 distances and increases with increasing number of vacancies on the O1 atom site and decreases with increasing number of vacancies on the O3 atom site. It is accordingly larger for the as-prepared samples, which contain B cations with lower oxidation states, and thus larger ionic radii and also more O1 vacancies. The shift increases for the air-annealed samples with increasing x due to an increasing attraction of O3 atoms by the introduced Y at A1 sites.
The short B–O2 distance shows no significant variation with x or between series, see Fig. 6a and b. With decreasing x, the B–O3 distance decreases significantly for the as-prepared samples due to an increasing number of vacancies on the O3 sites.
Unit cell parameters
The compositional dependence of the unit-cell parameters is shown in Fig. 7.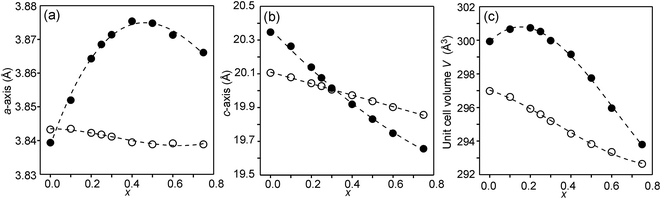 | ||
| Fig. 7 Unit-cell parameters a and c in Å and unit cell volume of the as-prepared (solid circles) and air-annealed (open circles) Sr3−xYxFe1.25Ni0.75O7−δ. | ||
The unit-cell volumes are larger for the as-prepared samples, primarily because of the lower oxidation states, and hence larger radii, of the B atoms. The maximum at x ∼ 0.2 can be ascribed to the formation of Fe2+ at low x-values. The maximum for the a-axis may be attributed to the fact that it contracts at lower x due to a large number of O3 vacancies, whereas at high x it contracts due to increasing number of Y3+ ions in the perovskite layer. For the air-annealed samples a, c and V decrease with increasing x due to the substitution of Sr2+ ions by smaller Y3+ ions. The relative constancy of the a-axis accords with the nearly constant B–O3 distances in the perovskite layer.
Atom displacement parameters
In Fig. 8, the anisotropic displacement parameters (ADPs) for atoms surrounding the B atom are shown for the as-prepared and air-annealed samples with x = 0 and 0.75. The ADPs for compositions in between show smooth progressions with x between those of these end-members, see the ESI.† One might expect that the B atoms would show ADPs that are large and reflect the proportions of different coordination polyhedra, c.f., Fig. 2. In fact, they are small and show, for some x, only a minor elongation along the c-axis. This is because the B atom has no freedom to move. The proportions of different coordination polyhedra are instead reflected by the ADPs of the O atoms, in particular O3. The as-prepared x = 0 has high proportions of the O3 and O1 sites vacant and expected coordination polyhedra are square pyramids, trigonal bipyramids, tetrahedra and, less likely, octahedra. Accordingly, the ADPs are large for the O atoms. With increasing x they decrease and for x = 0.75 the only coordination polyhedra are square pyramids. For x = 0.75, the elongation of the ADP for O3 then reflects the difference in the ionic radius of Ni2+ and Fe3+. For the air-annealed samples the O3 site is fully occupied, while the sof for O1 is roughly independent of x, and the coordination polyhedra are mainly square pyramids and octahedra. The shapes of the ADPs for x = 0.0 and 0.75 are thus similar, with the difference that they are larger for x = 0.75, most probably due to larger differences in the ionic radii of the B ions. | ||
| Fig. 8 ADPs, at 80% probability, of B and O atoms for the as-prepared (a) x = 0.0 and (b) x = 0.75 and the air-annealed (c) x = 0.0 and (d) x = 0.75. | ||
Bond valence sums
The structures of RP n = 1 phases, like La2NiO4, are known to show bond valence sums (BVSs) that deviate markedly from the valence sum rule, due to the mismatch in size requirements for the perovskite and rock-salt type layers, which leads to a compression of the former and elongation of the latter in the ab-plane.24,25 For RP n = 2 phases Sr3M2O7 with M = Ti, Ru, Mn, Ir, V structural data from the ICDD data base give average BVSs of A1 = 2.21, A2 = 2.06, B = 4.13, O1 = 2.03, O2 = 1.79 and O3 = 2.24, showing that the same type of internal strain is present for the n = 2 phases as for n = 1 phases, although to a smaller degree, which can be attributed to the small freedom for the B atom to move away from the basal plane of the O3 atoms.In Fig. 9, the calculated BVSs are shown for the present phases. In accordance with that found for other n = 2 RP phases, O3 is over-bonded with a BVS of ∼2.25 and O2 under-bonded with a BVS of ∼1.8. A large deviation from a value of 2 is found for the O1 atom in the as-prepared phases. The sof for this site is, however, less than 33%. While the BVSs for A2 vary relatively little with x, they increase for A1 from ∼2.2 for x = 0.0 to ∼3.3 for x = 0.75, demonstrating that Y substitutes for Sr on this site. The higher BVS values for A atoms, in particular A2, for the air-annealed samples can be attributed to a smaller a-axis, in turn caused by higher oxidation states of the B atoms leading to shorter B–O bonds. The BVSs for the B atom, calculated using a bond valence parameter of r0 = 1.759 for Fe3+, are shown in Fig. 9c. For the as-prepared samples the BVS remains as expected fairly constant. The fraction of Fe2+ deduced from the O content at lower x-values is too small to significantly influence the BVS. For the air-annealed samples the BVSs are expectedly much higher because of the high oxidation states of the B atoms. They increase slightly with decreasing x, from ∼3.34 for x = 0.75 to ∼3.49 for x = 0. This increase is small, and in view of this the determined total O content implies an increase in the oxidation state of the B atoms of ∼0.5. It is possible that the expected decrease in BVSs with increasing x due to the lower oxidation states of the B ions, and hence larger ionic radii, is counteracted by a simultaneous transition of the B ions to lower spin states, which have relatively smaller ionic radii.
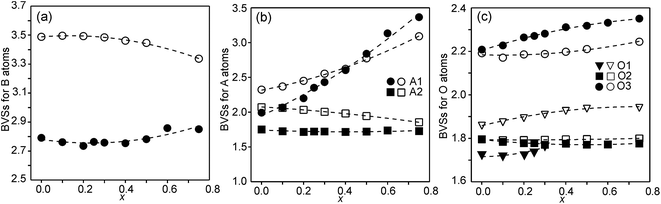 | ||
| Fig. 9 (a) BVSs for B atoms, (b) A atoms, and (c) O atoms. Data for the as-prepared samples are shown by filled symbols and data for the air-annealed samples by open symbols. | ||
EXAFS
Fe and Ni K edge EXAFS spectra were recorded for both the as-prepared and the air-annealed samples and x values are 0.1, 0.25, 0.5 and 0.75. The model used for data analysis contained interactions within one perovskite double layer and included 6 single and 2 multiple scattering paths. All spectra with corresponding fits are given in the ESI.† The spectra of the air-annealed samples are found to be quite similar and simpler to interpret than those of the as-prepared samples and they will, for this reason, be described first. The similarity indicates that the coordination around Ni/Fe atoms varies little with x. This can be expected, considering that oxygen vacancies only exist on the O1 sites and that the oxygen content is nearly independent of x and ∼6.4–6.5. The spectra of the air-annealed x = 0.75 are shown in Fig. 10. Refined B–O distances for different x are tabulated in Table 1.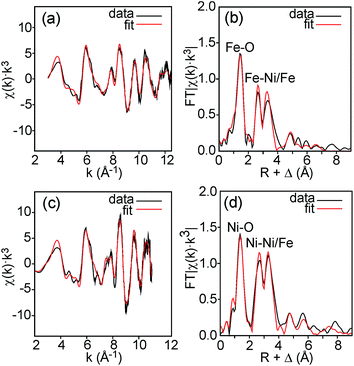 | ||
| Fig. 10 EXAFS spectra with fits and their Fourier transforms for the air-annealed x = 0.75 and (a and b) Fe and (c and d) Ni. | ||
| x | 0.10 | 0.25 | 0.50 | 0.75 |
| Air-annealed Fe | 1.892(2) | 1.905(2) | 1.912(2) | 1.920(2) |
| Air-annealed Ni | 1.945(2) | 1.940(2) | 1.954(3) | 1.941(3) |
| As-prepared Fe | 1.898(2) | 1.892(2) | 1.927(2) | 1.935(1) |
| As-prepared Ni | 1.932(3) | 1.969(3) | 2.002(1) | 2.018(1) |
The highest peaks around 1.5 Å in the Fourier transforms are from Fe/Ni interactions with the O atoms in the first coordination shell. The refined Fe–O distances show a very slight decrease with decreasing x, from 1.920(2) Å for x = 0.75 to 1.892(2) Å for x = 0.10, having a mean value of 1.907 Å, whereas the refined Ni–O distances show no systematic variation with x and have a mean value of 1.945(6) Å. These distances can be compared with the B–O distances obtained from the NPD data. For comparison, an equivalent single distance, deq, was calculated for the latter, using the formula 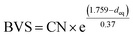 , where BVS is the calculated bond valence sum for the B atom using r0 = 1.759 Å for Fe3+ and CN is the coordination number of the B atom. The deq values are found to be constant at 1.93 Å for 0.0 ≤ x < 0.50 and only marginally higher for x = 0.75, 1.94 Å. The deq values are in fair agreement with a B atom weighted B–O mean value from EXAFS which shows a small decrease from 1.93 Å for x = 0.75 to 1.91 Å for x = 0.1.
, where BVS is the calculated bond valence sum for the B atom using r0 = 1.759 Å for Fe3+ and CN is the coordination number of the B atom. The deq values are found to be constant at 1.93 Å for 0.0 ≤ x < 0.50 and only marginally higher for x = 0.75, 1.94 Å. The deq values are in fair agreement with a B atom weighted B–O mean value from EXAFS which shows a small decrease from 1.93 Å for x = 0.75 to 1.91 Å for x = 0.1.
The next higher-lying peaks in the Fourier transforms, around 2.8 Å and 3.5 Å, originate from B atom interactions with Sr/Y and Fe/Ni atoms, respectively. The second of them has a higher intensity for Ni than for Fe. This can be explained by a higher CN for Ni. An increased number of O1 atoms will strengthen B–B interactions significantly due to the focusing effect.26 A higher CN of Ni also explains stronger peaks for Ni around 6 Å and 8 Å from outer coordination shells.
We find that further deductions for the air-annealed samples with regard to oxidation states, CNs and spin states from the obtained average distances of 1.91 Å for Fe–O and 1.95 Å for Ni–O are both difficult and uncertain.27 Both distances are fairly short.
The EXAFS spectra of the as-prepared samples were found to differ from those of the air-annealed ones, as expected considering the significantly different O contents and O vacancy distributions, c.f. the section on site occupancy factors. Peaks from higher coordination shells were in general much weaker, indicative of a higher degree of disorder, and became broader or disappeared with decreasing x. A most prominent variation with x is found for the Ni–O distance, which decreases by ∼0.09 Å from 2.018(1) Å for x = 0.75 to 1.932(3) Å for x = 0.10. These end values agree very well with the expected values of 2.014 and 1.931 Å for V- and IV-coordinated Ni2+, calculated from a bond valence sum of 2 and using r0 = 1.675 Å for Ni2+. The EXAFS data thus strongly imply that the decrease in the CN that takes place with decreasing x is predominantly associated with Ni. This in turn implies that the CN for Fe is predominantly V and mainly independent of x. Although the Fe–O distance is not, as would then be expected, found to be constant, it shows only a comparatively smaller decrease with decreasing x from ∼1.94 Å for x = 0.75 to ∼1.90 Å for x = 0.1. The B atom weighted B–O mean value from EXAFS decreases from ∼1.97 Å for x = 0.75 to ∼1.91 Å for x += 0.10, to be compared with deq values from the NPD data, which show a corresponding smaller variation from ∼1.97 Å to ∼1.94 Å. This may indicate that the Fe–O distances from EXAFS are underestimated for lower x values.
XANES
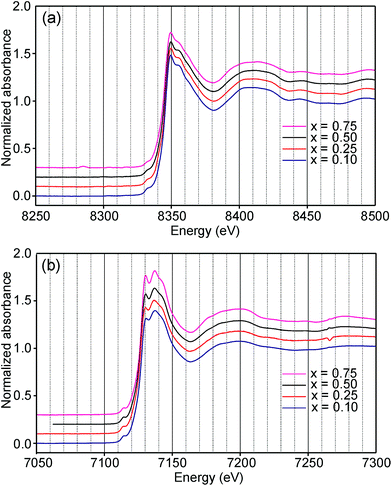
Information about the oxidation states and coordination of the Fe/Ni ions is, in general, to be found in the positions and intensities of features of the XANES pre-edge and/or main edge. We find that a consistent view of the present system is provided by the XANES data, but there are also aspects of the latter for which we have no explanation.The Ni and Fe K-edge XANES spectra of the as-prepared samples are shown in Fig. 11 and x-values are 0.1, 0.25, 0.5 and 0.75. The spectra show only small variations with x, most notably in the pre-edge region for Ni. The spectra of the air-annealed samples were found to show even less variation with x and to be similar to those of the as-prepared samples, see the ESI.†
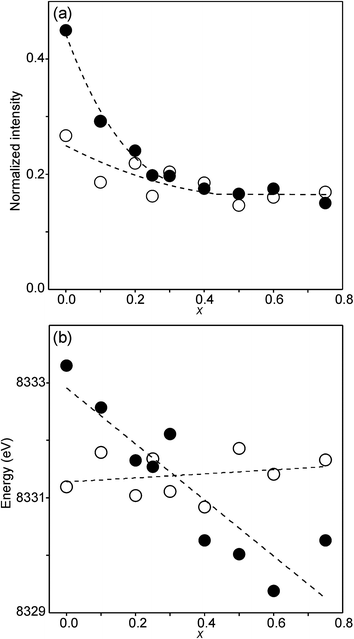
The compositional variation of the area intensity and centroid position of the Ni K pre-edge is shown in Fig. 12, and that of the peak intensity and maximum position of the main edge in Fig. 13.
 | ||
| Fig. 12 (a) Normalized area intensity and (b) centroid position of the Ni pre-edge peak in the XANES spectra of the as-prepared samples (filled circles) and air-annealed samples (open circles). | ||
 | ||
| Fig. 13 (a) Peak intensity and (b) maximum position of the normalized Ni main edge in the XANES spectra of the as-prepared samples (filled circles) and air-annealed samples (open circles). The peak intensities deduced for IV, V- and VI-coordinated Ni2+ in ref. 28 are indicated in (a). | ||
For Ni2+, the intensities of both the pre-edge and the main edge are both sensitive indicators of the Ni CN.28,29 The intensity of the pre-edge increases and that of the main edge decreases with decreasing CN. The as-prepared samples are expected to contain Ni2+ and the observed intensities accord with an increase of the CN with increasing x, from ∼4 for x = 0 to ∼5 for x = 0.75. The variation with x is significantly less for the air-annealed samples, with the intensities of both the pre-edge and the main edge decreasing slightly with increasing x. However, for them, the intensities can also be expected to depend on variations in the oxidation state of Ni.
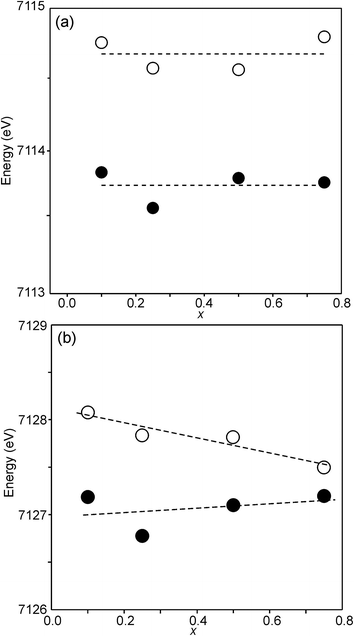
The position of the main edge has been used to determine the oxidation state of Ni in RP phases La2NiO4+δ and La4Ni3O10−δ by Wooley et al.30 For the as-prepared samples, the position shows no significant variation with x and the mean, 8345.7 eV, is in fair agreement with the value given by Wooley et al. for Ni2+ in NiO, 8345.2 eV.30 For the air-annealed samples, the edge is at considerably higher energies, implying an increase of the oxidation state. For x = 0.75, the increase is ∼1.5 eV, indicating an oxidation state of ∼2.5.30 The data also suggest that there is a smaller increase in the oxidation state of Ni with decreasing x. The centroid position of the pre-edge can be expected to depend on both the oxidation state and the CN. It is within error found to be constant for the air-annealed samples and increase with decreasing x for the as-prepared ones.
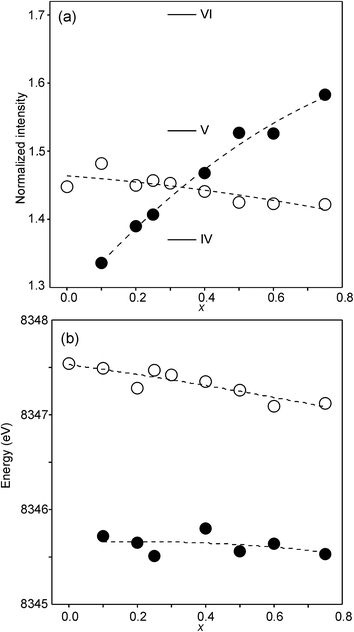
For Fe in oxidation states +2 and +3, the most useful characteristics for the determination of the oxidation state and CN are the centroid position of the pre-edge peak and its integrated intensity, respectively.31,32 The energy difference in the position between Fe2+ and Fe3+ is determined to be 1.4(1) eV and the lowest normalized integrated intensities are observed for the most centrosymmetric Fe sites. The determined centroid positions of the present samples are shown in Fig. 14a. For the as-prepared samples, the average position, 7113.8 eV, is close to the average value given by Wilke et al. for Fe3+, 7113.5 eV.31 The position for x = 0.25 is shifted to lower energies relative to the positions of the other x values. This can be attributed to the fact that the samples with x around 0.25 contain some Fe2+. For the air-annealed samples, the average position is significantly higher by 0.63 eV. Albeit the variation of the centroid position for Fe in oxidation states between +3 and +4 is not known to us, this indicates that some Fe3+ is oxidized upon annealing in air, in contrast to the conclusion in our previous study,6 where the whole oxygen uptake was attributed to an oxidation of all Ni2+ to Ni3+. For the as-prepared samples, the integrated intensity was found to vary insignificantly, between 0.19 and 0.22. The average value of 0.21 agrees well with the value of ∼0.20 deduced by Wilke et al. for V-coordinated Fe.31 This indicates that most Fe is 5-coordinated for the as-prepared samples with 0.10 ≤ x ≤ 0.75. For the air-annealed samples, the average intensity is found to be slightly higher, 0.24. The positions of the main Fe K edge are shown in Fig. 14b. The edge position was taken at the maximum of the 1st derivative, occurring at a normalized height of about one. Normalized peak intensities for the main edge are given in the ESI.† Haas et al.33 studied the Fe K-edge characteristics of La1−xSrxFeO3−δ perovskites for which the oxidation state of Fe increases formally from +3 for x = 0 to +4 for x = 1 (δ is small). They observed a positive shift of about 0.7 eV of the main edge at half height and about 1 eV at the maximum when going from Fe3+ to Fe4+. For the present samples, the difference in the peak position between the air-annealed and as-prepared x = 0.75 is ∼0.3 eV, suggesting that about 30–40% of Fe is oxidized from Fe3+ to Fe4+ upon annealing in air. For the air-annealed samples there is a positive shift of ∼0.5 eV as x decreases from 0.75 to 0.10, indicating a further oxidation of ∼50–70% of the Fe.
The half-widths of the Fe pre-edge peaks were found to be ∼3.2–4.0 eV, i.e., significantly larger than those in the study of Wilke et al., ∼1.4 eV.31 The peak for the air-annealed x = 0.1 is shown in Fig. 15a. It could be fitted by two components, using pseudo-Voigt peak functions with equal shape parameters and half-widths. The smaller component, with a relative intensity of ∼10%, is at an ∼1.4 eV higher energy than the main peak. The Fe peaks for other x values, as well as peaks for the as-prepared samples, were found to be similar, some containing a minor second component and some not, and are described in the ESI.†
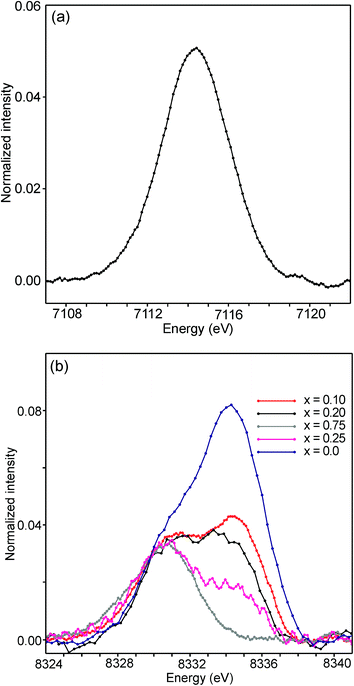 | ||
| Fig. 15 (a) Fe pre-edge peak for the as-prepared x = 0.1 and (b) Ni pre-edge peaks for the as-prepared samples. | ||
The pre-edge peaks for Ni consisted, for all the air-annealed samples and as-prepared samples with x ≥ 0.5, of essentially one major component with a half-width of ∼4–5 eV. For the as-prepared samples with x ≤ 0.4, however, a second component appeared at ∼3.7(1) eV higher energy, as shown in Fig. 15b.
The intensity of this second peak increases with decreasing x, reaching a relative intensity of ∼68% for x = 0.0, while the intensity of the first peak remains constant. We are not able to explain the origins of the two Ni peaks and we find their energy difference of ∼3.7 eV to be large. It seems natural to associate the two peaks with different coordination polyhedra of Ni.
Discussion and conclusions
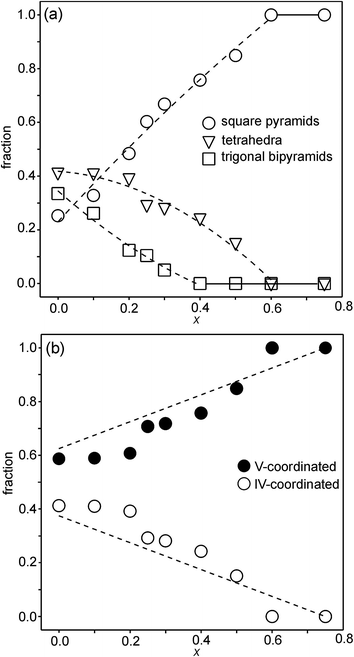
For the as-prepared samples the overall picture looks relatively clear. The Ni pre-edge and main edge intensities suggest that, with decreasing x, the CN for Ni changes from V to IV. The Ni edge position remains constant at 8345.7 eV and agrees with Ni2+. The total O content derived from the NPD data suggests that the oxidation state of Fe is mainly +3, but that some Fe2+ is present for x-values ≤0.4, in particular for x ∼ 0.1–0.25. The maximum content of the indicated Fe2+ is, however, too small, ∼20%, to influence the Fe pre-edge and main edge positions significantly, although they do show for x = 0.25 a slight shift towards lower energies, c.f.Fig. 14a and b. The pre-edge area intensity also remains constant and agrees with a CN of V for Fe. Furthermore, the EXAFS data are consistent with Ni2+ and Fe3+ in square pyramidal coordination for the as-prepared x = 0.75. The main conclusion here is that the coordination changes that take place when x is decreased, i.e., the O content decreases, are mainly of the Ni atoms. Indeed, if the compositions are idealized to contain only Ni2+ and Fe3+, and Fe remains V-coordinated for all x, and then for x = 0 the only coordination possible for Ni is tetrahedral (strictly speaking IV-coordinated). One explanation why solely Ni changes the CN could be that V-coordinated Ni2+ is larger than V-coordinated Fe3+, whereas IV-coordinated Ni2+ is of similar size to V-coordinated Fe3+. This is similar to the finding that in oxides with mixed valence ions a lower oxidation state ion generally prefers a lower CN.The distribution of the considered coordination polyhedra of the B atoms for the as-prepared samples cannot be derived from the determined O1 and O3 occupancies without making assumptions. However, if it is assumed that octahedra are not present they can be derived; the fraction of bipyramids is given by the O1 occupancy, the fraction of tetrahedra from the O3 occupancy minus the O3 vacancies from the bipyramids, and the fraction of square pyramids from the oxygen content and fractions of bipyramids and tetrahedra. The fact that octahedra are not present in significant numbers is suggested by the XANES/EXAFS data; for Ni, they indicate a coordination number between IV and V and for Fe dominantly V. The accordingly derived distribution of polyhedra is shown in Fig. 16a. With decreasing x, the fraction of square pyramids steadily decreases, the fraction of trigonal bi-pyramids increases for x < 0.6, and the fraction of tetrahedra increases for x < 0.4. The corresponding fractions of IV- and V-coordinated B-atoms are given in Fig. 16b. The dashed lines in the figure show expected fractions if (i) no octahedra are present and (ii) Fe remains V-coordinated throughout. The agreement between the deduced and expected fractions is rather good. Several explanations can be invoked for why it is not better, including that there is also Fe2+ present at low x or that a smaller fraction of octahedra are present.
When the as-prepared x = 0.75 is annealed in air the oxidation state of the fraction of the B atoms increases and the oxygen content increases from 6.0 to 6.41. The oxidation is accompanied by a shift of the position of the Ni main K-edge by 1.46 eV. In comparison with the difference of 3.00 eV given by Wooley et al. between Ni3+ and Ni2+, it is concluded that the air-annealed x = 0.75 contains ∼50% of Ni3+. This oxidation of Ni accounts, however, only roughly for half of the increase in the oxygen content and a part of the Fe3+ must thus also be oxidized to Fe4+. This is further proved by the shift of the Fe main edge and pre-edge to higher energies. From the determined oxygen content, the fraction of Fe that is oxidized to Fe4+ can be calculated to be ∼35%. The corresponding cation composition of the air-annealed sample should then be around Fe0.813+Fe0.444+Ni0.382+Ni0.383+. The EXAFS data suggest that the coordination number is higher for Ni than for Fe. Furthermore, the Fe pre-edge intensity does not indicate any significant change in the CN for Fe. The data thus indicate that both Ni2+ and Fe3+ are oxidized upon air-annealing of x = 0.75.
For the air-annealed series of samples, the oxygen content increases slightly with decreasing x, from 6.41 for x = 0.75 to 6.55 for x = 0. Because of this, and the decreasing Y content, the oxidation states of the Ni and/or Fe ions must increase with decreasing x, on average by +0.52. The oxygen content for x = 0 for the hypothetical case of only Ni3+ and Fe4+ is 6.63, only slightly larger than the observed content of 6.55, which suggests that ∼90% of the ions are Ni3+ and Fe4+ for x = 0. The intensities of the Ni main edge and pre-edge show no significant variations with x, indicating no or small variations in the coordination, and neither do those of the main edge of Fe. The intensities of the Fe pre-edge, however, increase with decreasing x, see the ESI,† from 0.20 for x = 0.75 to 0.27 for x = 0.10, indicative of an increasing non-centrosymmetry of the coordination. We cannot offer a good explanation for this, but it can be noted that the coordination of B atoms in octahedra becomes increasingly non-centrosymmetric as x decreases because of a significant increase in the B–O1 distance, see Fig. 6b.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the “Consortium for Crystal Chemistry, C3” within the Röntgen-Ångström cluster, Swedish Research Council, project 1215219, for providing financial support.References
- V. V. Kharton, A. P. Viskup, E. N. Naumovich and F. M. B. Marques, J. Mater. Sci., 1999, 9, 2623 CAS.
- S. J. Skinner and J. A. Kilner, Solid State Ionics, 2000, 135, 709 CrossRef CAS.
- S. Y. Istomin and E. V. Antipov, Russ. Chem. Rev., 2013, 7, 686 CrossRef.
- E. Kravchenko, D. Khalayavin, K. Zakarchul, J. Grins, G. Svensson, V. Pankov and A. Yeremchenko, J. Mater. Chem. A, 2015, 3, 23852 CAS.
- D. C. Peets, J.-H. Kim, P. Dosanjh, M. Reehuis, A. Maljuk, N. Aliouane and C. Ulrich, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 214410 CrossRef.
- L. Samain, P. Amshoff, J. J. Biendicho, F. Tietz, A. Mahmoud, R. P. Hermann, S. Y. Istomin, J. Grins and G. Svensson, J. Solid State Chem., 2015, 227, 45 CrossRef CAS.
- S. N. Ruddlesden and P. Popper, Acta Crystallogr., 1958, 11, 54 CrossRef CAS.
- F. Prado, T. Armstrong, A. Caneiro and A. Manthiram, J. Electrochem. Soc., 2001, 148, J7 CrossRef CAS.
- Y. Bréard, C. Michel, M. Hervieu, F. Studer, A. Maignan and B. Raveau, Chem. Mater., 2002, 14, 3128 CrossRef.
- V. V. Kharton, M. V. Patrakeev, E. V. Tsipis, M. Avdeev, E. N. Naumovich, P. V. Anikina and J. C. Waerenborgh, Solid State Ionics, 2010, 181, 1052 CrossRef CAS.
- L. Mogni, F. Prado, A. Caneiro and A. Manthiram, Solid State Ionics, 2006, 177, 1807 CrossRef CAS.
- L. Mogni, F. Prado and A. Caneiro, Chem. Mater., 2006, 18, 4163 CrossRef CAS.
- L. V. Mogni, F. D. Prado, G. J. Cuello and A. Caneiro, Chem. Mater., 2009, 21, 2614 CrossRef CAS.
- A. Coelho, Topas Academic Version 4.1. Computer Software, Topas Academic, Coelho Software, Brisbane, 2007 Search PubMed.
- G. N. George and I. J. Pickering, EXAFSPAK – A Suite of Computer Programs for EXAFS Analysis, SSRL, Stanford University, CA, 1993 Search PubMed.
- S. I. Zabinsky, J. J. Rehr, A. Ankudinov, R. C. Albers and M. J. Eller, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 2995 CrossRef CAS.
- M. Wojdyr, J. Appl. Crystallogr., 2010, 43, 1126 CrossRef CAS.
- M. V. Lobonov, L. Siwen and M. Greenblatt, Chem. Mater., 2003, 15, 1302 CrossRef.
- P. D. Battle, D. E. Cox, M. A. Green, J. E. Millburn, L. E. Spring, P. G. Radaelli, J. E. Rosseinsky and J. F. Vente, Chem. Mater., 1997, 9, 1042 CrossRef CAS.
- D. N. Argyriou, J. F. Mitchell, J. D. Jorgensen, J. B. Goodenough, P. G. Radaelli, D. E. Cox and H. N. Bordallo, Aust. J. Phys., 1999, 52, 279 CrossRef CAS.
- D. N. Argyriou, J. F. Mitchell, P. G. Radaelli, H. N. Bordallo, D. E. Cox, M. Medarde and J. D. Jorgensen, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 8695 CrossRef CAS.
- R. Seshardi, M. Hervieu, C. Martin, A. Maignan, B. Domenges and B. Raveau, Chem. Mater., 1997, 9, 1778 CrossRef.
- T. Proffen and R. B. Neder, J. Appl. Crystallogr., 1999, 32, 838 CrossRef CAS.
- I. D. Brown, Acta Crystallogr., Sect. B: Struct. Sci., 1992, 48, 553 CrossRef.
- V. S. Urusov and I. P. Orlov, Crystallogr. Rep., 1999, 44, 686 Search PubMed.
- A. Kuzmin and P. Parent, J. Phys.: Condens. Matter, 1994, 6, 4395 CrossRef CAS.
- P. Ravindran, R. Vidya, H. Fjellvåg and A. Kjekshus, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 134448 CrossRef.
- L. Galoisy and G. Calas, Mater. Res. Bull., 1993, 28, 221 CrossRef CAS.
- L. Galoisy and G. Calas, Geochim. Cosmochim. Acta, 1993, 57, 3613 CrossRef CAS.
- J. R. Wooley, B. N. Illy, M. P. Ryan and S. J. Skinner, J. Mater. Chem., 2011, 21, 18592 RSC.
- M. Wilke, F. Farges, P.-M. Petit, G. E. Brown Jr and F. Martin, Am. Mineral., 2001, 86, 714 CrossRef CAS.
- T. E. Westre, P. Kennepohl, J. G. DeWitt, B. Hedman, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 1997, 119, 6297 CrossRef CAS.
- O. Haas, U. F. Vogt, C. Soltmann, A. Braun, W.-S. Yoon, X. Q. Yang and T. Graule, Mater. Res. Bull., 2009, 44, 1397 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Structural parameters, inter-atomic distances, O contents, EXAFS fits and refined parameters, XANES pre-edge and edge parameters, and fits of XANES pre-edge peaks. See DOI: 10.1039/c7ta07113b |
| This journal is © The Royal Society of Chemistry 2018 |