An oxidized magnetic Au single atom on doped TiO₂(110) becomes a high performance CO oxidation catalyst due to the charge effect

Abstract

Catalysis using gold nanoparticles supported on oxides has been under extensive investigation for many important application processes. However, how to tune the charge state of a given Au species to perform a specific chemical reaction, e.g. CO oxidation, remains elusive. Here, using first-principles calculations, we show clearly that an intrinsically inert Au anion deposited on oxygen-deficient TiO₂(110) (Au@TiO₂(110)) can be tuned and optimized into a highly effective single atom catalyst (SAC), due to the depletion of the d-orbital by substrate doping. Particularly, Ni- and Cu-doped Au@TiO₂ complexes undergo a reconstruction driven by one of the two dissociated O atoms upon CO oxidation. The remaining O atom heals the surface oxygen vacancy and results in a stable bow-shaped surface “O–Au–O” species; thereby the highly oxidized Au single atom now exhibits magnetism and dramatically enhanced activity and stability for O₂ activation and CO oxidation, due to the emergence of high density of states near the Fermi level. Based on further extensive calculations, we establish the “charge selection rule” for O₂ activation and CO oxidation on Au: the positively charged Au SAC is more active than its negatively charged counterpart for O₂ activation, and the more positively charged the Au, the more active it is.

---

Introduction

Gold (Au) is considered to be extremely catalytically inert in many chemical processes, as manifested by the high resistance to oxidation of the surface Au atoms and the weak binding with many other gas phase molecules.^1,2 However, since the discovery of the excellent catalysis of Au nanoparticles (NPs)³ on metal oxide substrates, extensive studies have been devoted to the understanding of the underlying mechanisms operative for the high activities of the supported Au NPs for a variety of important catalytic reactions.^4–10 Accordingly, a number of mechanisms have been proposed to elucidate the enhanced activities of Au NPs, including an odd number of electrons,¹¹ the quantum size effect,^11,12 metal–nonmetal transitions in a given cluster size regime,¹³ and the presence of poorly coordinated edge or corner atoms.^14–16 Moreover, it is also widely recognized that the interactions between the Au and the support, including the strain effect,¹⁷ the charge state^18–21 of the Au atom, and particularly the charge transfer between the Au NPs and the substrates²² have been regarded to be crucial in determining the performance of the Au NPs. For instance, Au clusters located at the F-centers on MgO(001) were reported to be negatively charged and highly active for CO oxidation.^5,21,23 In contrast, recent investigations suggest that the active sites for CO oxidation are comprised of positively charged Au atoms and metallic Au nanoparticles appear to be spectators that do not participate in the reaction.^8,24–26 In addition, there are also several reports indicating that metallic Au is the active species that is highly reactive for O₂ activation and CO oxidation.^19,27 Therefore, a fundamental question regarding the catalysis mechanism of a given Au structure is whether the negatively or positively charged state is more favorable for O₂ activation. The answer to this question is important for highly efficient catalyst design for many industrial processes, such as CO oxidation. Intuitively, a negatively charged Au species with excessive electron charge may be more favorable for O₂ binding via electron charge transfer, facilitating the O₂ activation and CO oxidation. However, such a scenario has so far not been rigorously examined using state-of-the-art theoretical and/or experimental approaches, especially when several other factors as mentioned above cannot be convincingly excluded from Au NPs.

A gold single-atom catalyst with a well-defined simple structure and a highly dispersed single active center provides an ideal platform for illustrating the above question, i.e., the charge effect in Au catalysis. Note that as a new concept in heterogeneous catalysis, SACs are now widely expected to maximize the efficiency of noble metals and offer great potential for enhanced chemical activity and selectivity. Recently, various highly efficient SACs with excellent stability and selectivity have been fabricated and theoretically investigated, such as Pt, Ti, Rh, Pd, and Ru on FeO_x supports for CO oxidation^28,29 and an Fe SAC on a silica matrix for methane activation.³⁰ It has been reported that, as the ultimate small size limit of noble Au, a single Au atom supported on rutile TiO₂(110) was rather inert to CO oxidation,^21,29,31 like its bulk Au counterpart. Despite complete experimental and theoretical analysis, the charge state effect on its chemical activity still remains unclear, whilst the system also offers a contrasting case for further understanding, design and development of effective SACs.

Using first-principles calculations on the simple model of Au SACs, we clearly demonstrate the role of charge state in determining the activities of the Au species supported on oxide substrates with the Au SAC on rutile TiO₂(110) as a prototype example. Here, the Au SAC is confirmed to preferably occupy the surface oxygen vacancy (V_O) site of the TiO₂(110) substrate³² and its charge states and chemical activity toward O₂ activation and CO oxidation can be tuned via the substrate doping approach. The results show that the catalytically inert Au SAC on rutile TiO₂(110) is negatively charged, i.e., Q(Au) = −0.38 e. Intriguingly, the catalysis of the essentially inert Au SAC can be triggered by substitution of a neighboring Ti atom by another transition metal element with a relatively large electronegativity (such as Ru, Rh, Pt, Cu, or Ni). The key point is that such a dopant gradually tunes the Au anion to become a positively charged cation with a significantly reduced occupation of the d orbital. Consequently, a monotonically increased activity of the Au SAC as a function of its charge state can be established, that is, the more positively charged the Au SAC, the higher the d-band of the Au SAC, and consequently the more active the Au SAC. More specifically, upon the first CO oxidation via an adsorbed O₂ molecule, the Ni-doped Au@TiO₂(110) complex (denoted as Au@(Ni)TiO₂(110) (Q(Au) = +0.03 e)) undergoes a local reconstruction, driven by one of the dissociated O atoms, healing the surface oxygen vacancy and resulting in a novel bow-shaped surface O–Au–O species. Thus, such an oxidized Au cation in O–Au–O (Q(Au) = +0.64 e) exhibits much enhanced activity and stability for continued CO oxidation, in contrast to previous observations that the healing of the oxygen vacancy usually reduces the catalysis capability of the adsorbed transition metal SACs because of clustering.^29,33,34

Methods

The present work was carried out using first-principles calculations within the density functional theory³⁵ adopting the spin-polarized generalized gradient approximation as implemented in the VASP code. The interactions of the valence electrons with the ionic cores were described by the projector augmented wave (PAW) method.³⁶ For the exchange–correlation functional, we used the generalized gradient approximation of Perdew, Burke, and Ernzerhof.³⁷ The electronic wave functions were expanded in a plane wave basis with an energy cutoff of 500 eV. To obtain the correct band gap of the TiO₂, we used the DFT + U method with U = 4.5 eV, leading to a band gap of about 2.4 eV. Note that our tests show that the choice of U values around 5.0 eV leads to negligible differences for the calculated results, such as the adsorption energy of the O₂ molecule and reaction barrier for CO oxidation. The calculated lattice parameters for the primitive rutile TiO₂ unit cell are a = b = 4.662 Å and c = 2.959 Å, respectively, in good agreement with experimental results.³⁸ The rutile TiO₂(110) surface was simulated by a periodic four-layer c (4 × 2) slab model consisting of 192 atoms with ∼13 Å of vacuum in between the slabs (for details, see Fig. S1 and the structural data in S1, ESI†). The k-space integration was carried out using a Monkhorst–Pack grid of 2 × 3 × 1 k points in the surface Brillouin zone of the c (4 × 2) unit cell. All atoms except those in the bottom layer were allowed to relax along the calculated forces until all the residual force components were lower than 0.01 eV Å⁻¹. In consideration of the experimental conditions and previous calculations, we performed calculations which showed that the Au adatom is located in the vicinity of the surface oxygen vacancy (V_O) site of the rutile TiO₂(110) which is denoted as Au@TiO₂(110) throughout the document. For the interaction of the O₂(CO) molecule with the Au@TiO₂(110) catalyst, we initially placed the O₂(CO) molecule about 4.5 Å away from the Au atom followed by full structural optimization. Bader charge analysis³⁹ is applied to evaluate the charge transfer.

Results and discussion

As a starting point, we confirm that the Au atom prefers to occupy the surface V_O site on TiO₂(110) with binding energy E_b(Au) = 206.093 kJ mol⁻¹ (for details, see Fig. S2 in the ESI†), which is in accordance with the experimental observation that surface V_O sites play a dominant role in stabilizing Au atoms³² and Pd atoms.^40–42

Based on this, we examined the adsorption and activation of an O₂ molecule on Au@TiO₂, which is usually the rate-determining step for CO oxidation. Our results show that the O₂ molecule can only very weakly adsorb on the supported Au monomer (see Fig. S3, ESI†), with an exothermic energy of 5.114 kJ mol⁻¹. The bond length of the adsorbed O₂ molecule remains almost the same as compared with that in its gas phase, 1.24 Å, indicating that the Au SAC is highly inert to O₂. In addition, an incoming CO will further push the weakly adsorbed O₂ away from the Au atom, and occupy the top site of the Au atom, with an exothermic energy of 48.725 kJ mol⁻¹. Therefore, the preference of the CO adsorption on the Au SAC thoroughly blocks the O₂ activation and hence prevents the CO from being oxidized by O₂, in line with experimental observations.³¹

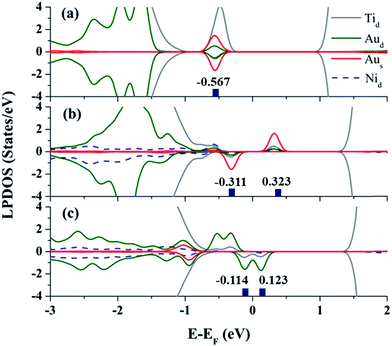
To understand the highly inert nature of the Au atom on TiO₂(110) for O₂ activation, we analyzed its local projected density of states (LPDOS) in Fig. 1(a). Evidently, the main peaks of the d-orbital are positioned below −1.6 eV, and the highest-occupied molecular orbital (HOMO) hybridizes with its neighboring Ti atoms at about 0.57 eV below the Fermi level. Furthermore, the symmetric spin-majority and spin-minority LPDOS confirm that there are no unpaired electrons located on the Au atom. All these features strongly indicate that the Au monomer is negatively charged, and the Bader analysis³⁹ further confirms that the Au anion is charged by about 0.38 e, which shifts the d-orbital of the Au downward relative to the Fermi level. Additional calculations show that the energy gap between the HOMO(Au) and the lowest-unoccupied molecular orbital of the incoming O₂ (LUMO(O₂)) is very large, about 1.527 eV, prohibiting their orbital hybridization and charge transfer from the HOMO(Au) to the 2pπ*-like LUMO(O₂).⁴¹ Therefore, the O₂ can be hardly activated because of the repulsion between orbitals of the adsorbate,¹ and the Au monomer acting as a “spectator” in CO oxidation.³¹

Fig. 1 Local projected density of states (LPDOS) of Au@TiO₂(110), (a); Au@TiO₂(110) doped with Ni, i.e., Au@(Ni)TiO₂(110), (b); and Au@TiO₂(110) doped with O–Ni, i.e., Au@(O–Ni)TiO₂(110), (c). The dark blue bars show the energies at which the HOMO/LUMO are located.

Next, inspired by our central question, we examined the possibility of modifying the catalytic performance of the Au SAC on TiO₂(110) by tuning the charge states of the Au SAC site via the substrate doping approach. For doing this, first, a relatively electronegative Ni atom was employed as a substitutional dopant for the Ti atom.^43–45 It was found that the Ni dopant favors the substitution of a Ti atom close to the V_O site, and this configuration is about 13.508 kJ mol⁻¹ more stable than the case when the Ni atom substitutes for one of the subsurface Ti atoms (see Fig. S4, ESI†). Significantly, Ni-doping modulates the electronic structure of the Au@TiO₂(110) around the Fermi level, as seen in the LPDOS in Fig. 1(b). First, the orbital hybridization between Au and Ni considerably broadens the LPDOS of the Au atom and shifts its d-orbitals upward to the Fermi level. Second, the HOMO of the Au SAC is spin-minority dominated, and the spin-majority orbitals are totally unoccupied. Such features strongly indicate that the electron charge accumulated on the Au single atom is significantly reduced; indeed, Bader charge analysis confirms that the Au monomer is now slightly oxidized and positively charged by about 0.03 e.

To examine whether the anion–cation transition of the Au single atom can promote the catalytic activity, we then further investigated the adsorption and activation of an O₂ molecule on the Au SAC supported on an Ni-doped TiO₂(110) substrate. Based on further extensive calculations, we identified the most stable adsorption configuration of the O₂ molecule on the oxidized Au SAC. The O₂ molecule prefers an end-on structure, forming an angle ∠O–O–Au = 107.63° (see Fig. S5(A), ESI†). The binding of the O₂ molecule with the Au SAC is mainly accompanied by the hybridization of the oxygen 2pπ* orbital with the HOMO of Au. Note that part of the antibonding 2pπ* electronic state of O₂ is now shifted downward below the E_F (for more details, see Fig. S5(B and C) and S5†), confirming a charge transfer from the Au SAC to the O₂ molecule, which results in an extended O–O bond length (1.31 Å) and leads to an exothermic adsorption energy of 97.643 kJ mol⁻¹. Furthermore, the calculated stretching vibrational frequency of the adsorbed O₂ species has been red-shifted to 1158.9 cm⁻¹ from a value of 1560.8 cm⁻¹ for the case of the gas phase. Convincingly, these results demonstrate that the O–O bond is considerably activated on the positively charged Au cation due to Ni-doping in the substrate.

Having clearly illustrated the critical step for O₂ activation by the Au cation on the Ni-doped TiO₂(110) complex, we now investigate the kinetic processes of CO oxidation using the optimized NEB method.⁴⁶ Note that three CO oxidation mechanisms proposed by recent theoretical investigations^47,48 have been examined in the present study. We confirmed that the CO oxidation surprisingly prefers a quasi-Langmuir–Hinshelwood (L–H) process in this case, namely, CO can adsorb relatively weakly on the single Au atom close to the adsorbed O₂ molecule and the co-adsorbed molecules undergo a bimolecular reaction through the formation of a CO₂ precursor, which is subsequently released upon further activation, and the optimized substrate structure upon CO₂ desorption is shown as the initial state (IS) configuration in Fig. 3. The minimum energy path (MEP) and energetics for the oxidation of the first CO molecule on the Au single atom catalyst is shown in Fig. 2. Specifically, we identified that the first CO molecule adsorbs in the vicinity of the O₂ molecule on the Au catalyst via the well-known back-donation charge transfer mechanism,^49,50i.e., donation of CO 5σ electrons to the Au@TiO₂(110) substrate and back-donation from the Au SAC into the unoccupied 2π* orbital of CO, as confirmed by the additional electronic charge density analysis detailed in Fig. S6, ESI.† We emphasize that one important issue in the CO oxidation on Au clusters supported on metal oxides is the formation of carbonate species that poison the active sites.⁵¹ However, one can see that the formation of a carbonate-like species (see the TS state in Fig. 2) is 385.652 kJ mol⁻¹ less stable than the formation of CO₂ on Au@(Ni)TiO₂(110), indicating good catalytic properties of the present system.

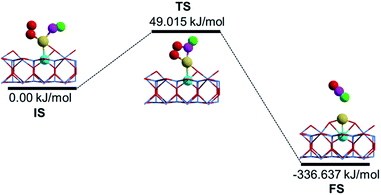Fig. 2 Schematic view of the minimum energy path (MEP) of CO oxidation on Au@TiO₂(110) doped with Ni, i.e., Au@(Ni)TiO₂(110).

Here, we note that, upon Ni-doping, the oxidized Au atom contributes significantly to the LPDOS by the Fermi level, which promotes such a back-donation process for CO adsorption with an exothermic adsorption energy of 12.157 kJ mol⁻¹, see Fig. 2. Consequently, the bond length of the adsorbed CO species is slightly enlarged to 1.15 Å from 1.14 Å of the gas phase, and correspondingly the C–O vibrational frequency is red shifted to 2069.5 cm⁻¹ from 2120.6 cm⁻¹. For the transition state (TS), a low activation barrier of E_bar = 49.015 kJ mol⁻¹ is identified in the process of CO₂ formation, as shown in Fig. 2. Subsequently, a linear CO₂ product can be readily released with an exothermic energy of 336.637 kJ mol⁻¹, as shown in the final state (FS). It is clear that even such a modest activation⁵² of the CO by Au@TiO₂(110) doped with Ni renders the Au monomer a good SAC candidate in avoiding the important issue of CO poisoning in heterogeneous catalysis.

More intriguingly, a novel stable SAC surface structure is generated after the release of the first CO₂ molecule, see FS in Fig. 2. Specifically, the surface V_O is spontaneously “healed” by the remaining O atom from the O₂ reactant, and now the whole catalyst complex can be viewed as Au@TiO₂(110) doped with an O–Ni pair, i.e., Au@(O–Ni)TiO₂(110). Here, we note that a previous investigation also predicted a similar phenomenon on a defective oxide surface,²⁹ where the healing of the oxygen vacancy is believed to promote the adsorbed metal SAC clustering, and hence to reduce the selectivity and performance of the SAC.³⁴ On the contrary, in the present case, the remaining O atom healing the V_O renders the Au atom to form a very stable bow-shaped surface O–Au–O species, with an exothermic energy of 300.069 kJ mol⁻¹. Therefore, the Au atom is now highly stabilized and oxidized, i.e., Q(Au) = +0.64 e. Note that, recently, Wang et al.⁵³ found that single Au cation active sites can be generated from adsorbed Au₂₀ clusters on TiO₂(110), exhibiting excellent catalysis for CO oxidation. In the present structure, the d-orbital-dominated HOMO (LUMO) of the Au cation is located right below (above) the Fermi level, as presented in Fig. 1(c). The Au cation is now surprisingly spin polarized, i.e., possessing a magnetic moment about 0.5 μB. Consequently, the high LPDOS assigned to the HOMO (Au) strongly implies that the magnetic and oxidized Au atom with unpaired electron in the O–Au–O may exhibit high preference in catalysis for successive rounds of O₂ activation and CO oxidation from the spin-selection point of view,^54,55i.e., a system with high spin state is generally more active toward spin-triplet O₂ activation.

The catalytic cycle of CO oxidation over the bow-shaped magnetic Au cation in Au@(O–Ni)TiO₂(110) (see Fig. 3(i)) obtained by NEB calculations is summarized in Fig. 3. The extensive calculations show that the first incoming CO oxidation prefers the L–H process, see Fig. 3(ii). Similarly, the O₂ molecule is first significantly activated on the Au@(O–Ni)TiO₂(110), with an exothermic energy of 72.460 kJ mol⁻¹, which is slightly smaller than that calculated for a previous structure shown in Fig. S5(A).† However, we note that the relatively smaller binding energy of the O₂ molecule in the present bow-shaped O–Au–O SAC case is due to the energy cost compensating the local structural O–Au–O reconstruction upon O₂ adsorption (see also Fig. S7(A)–(C) in S7†). In fact, the extended O–O bond length (1.32 Å) and distinctly red-shifted stretching vibrational frequency (ν(O₂) = 1128.6 cm⁻¹) suggest that the adsorbed oxygen molecule is well activated over the Au active site of the Au@(O–Ni)TiO₂(110) complex. The incoming CO on the single Au atom shows a binding energy of 112.791 kJ mol⁻¹ (step (ii)). Our calculations show that, in the minimum energy path, to form a CO₂ precursor, a CO₃ species (carbonate, see Fig. 3(iv)) will be firstly formed as a local minimum which is only 6.561 kJ mol⁻¹ higher in energy than the configuration shown in (ii), by overcoming a small energy barrier of 60.40 kJ mol⁻¹ (see Fig. 3(iii) denoted as TS1). Based on that, when further overcoming an activation barrier of 37.919 kJ mol⁻¹ (see Fig. 3(v) denoted as TS2), a linear CO₂ species can be formed. When finishing the above steps, an O atom dissociated from the adsorbed O₂ molecule is still left on the Au monomer, as seen from step (vi). When the second CO molecule approaches the deposited Au site (step (vii)), a new reaction of CO_ad + O_ad = CO₂ process (step (vii) and TS3) can readily proceed via the Eley–Rideal (E–R) reaction mechanism. The calculated barrier of this reaction is only 54.418 kJ mol⁻¹, shown in TS3. After releasing the second CO₂ upon overcoming a negligible energy barrier (around 14.473 kJ mol⁻¹), the catalyst system is recovered to the initial bow-shaped Au SAC (step i). Here, we emphasize that the high performance of the above Au@(O–Ni)TiO₂(110) SAC in CO catalytic oxidation, to the negatively charge Au anion counterpart in Au@TiO₂(110), is essentially due to the positively charged electronic state (of the Au single atom), which effectively contributes to the d-orbital-dominated LPDOS near the Fermi level and facilitates O₂ activation via the charge transfer mechanism. These findings on the one hand illustrate that Au single cations rather than anions can exhibit excellent catalysis for O₂ activation and CO oxidation, and on the other hand support previous statement that the active sites of Au NPs should be localized on these positively charged Au atoms.^{8,22,24–26,53}

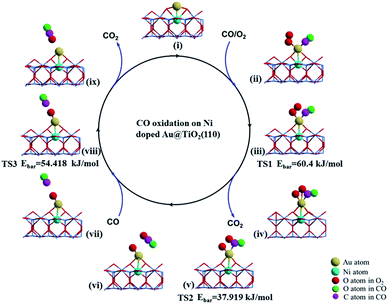Fig. 3 Catalytic circle of CO oxidation, based on the stable structure (i) upon releasing the first CO₂ product in the final state (FS) shown in Fig. 2. Subsequently, structure (i) is denoted as Au@(Ni–O)TiO₂(110). For the transition states (TS), the activation barriers (E_bar) are also presented.

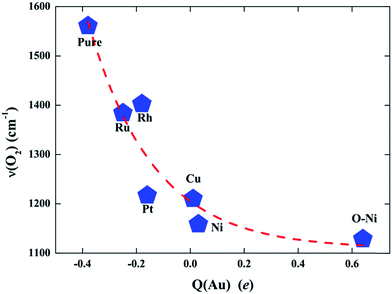
To further validate such a charge state effect on the activity of the Au SAC on TiO₂(110) and figure out a simple approach for further optimizing its catalysis in O₂ activation and CO oxidation, we carried out more extensive calculations to examine the effects of doping with other transition metals on the capability of Au@TiO₂(110) for O₂ activation. Here, four additional TM elements (Ru, Rh, Pt, and Cu) with different values of electronegativity were considered as the dopants. Similar to the structures presented in Fig. S8,† these elements are found to prefer the same site to stabilize the Au atom. As expected, we note that, with Bader charge analysis, these dopants result in different charge states for the Au atom. Therefore, the doped Au@(TM)TiO₂(110) complexes can serve as an ideal platform to demonstrate the trend of the charge-state effect on catalysis. Briefly, we show that the activation rate of the O₂ molecule is almost exactly monotonically increased as a function of the charge depletion of the Au atom. Specifically, the more positively charged the Au atom, the stronger the activation of the O₂ molecule on it, as reflected by the values of the red-shifted ν(O–O) shown in Fig. 4.

Fig. 4 Stretching vibrational frequency of the O₂ molecule adsorbed on Au@TiO₂(110) and those due to dopants of Ru, Rh, Pt, Cu, Ni, and the O–Ni pair as a function of the level of charged electrons on the Au SAC active site (Q(Au)). A negative (positive) value means that the Au is an anion (cation).

Finally, we note that there are already many experimental studies establishing various approaches for improving the photocatalysis of TiO₂(110), such as by doping metal^56–59 and non-metal elements,⁴³ and co-doping methods as well.⁶⁰ In addition, in the ESI (Fig. S9 and S8†), we have also presented a comparison of the formation energies of the dopant elements in TiO₂(110); one can see that all the investigated elements (Pt, Ru, Rh, Cu, and Ni) possess comparable formation energies lying between those of Co and Al which can be readily doped in both anatase and rutile TiO₂.^58,61 Here, we note that both Cu and Ni dopants possess relatively low formation energies relative to Pt, Ru, and Rh, and only the former two can stabilize the bow-shaped O–Au–O structure. These interesting results indicate that Cu and Ni are much preferred dopants for enhancing the chemical activity of Au on TiO₂(110). Correspondingly, we expect that the present theoretical work will motivate future experimental efforts in this field.

Conclusions

Herein, by means of extensive first-principles calculations on a very simple Au SAC model, we have clearly elucidated the role of charge state in determining the activity of the Au species supported on a TiO₂(110) oxide substrate for O₂ activation and CO oxidation. Intriguingly, the intrinsically inert Au anion SAC on rutile TiO₂(110) can be tuned into a highly efficient Au cation SAC by the depletion of the d-orbital of the Au atom via substrate doping with a transition metal atom, whilst the more positively charged the Au atom, the higher its activation of the O₂ molecule, supporting the most recent findings that the catalytically active site of Au NPs should be localized on these poorly coordinated Au cations. Such findings shed new insight into gold catalysis and are expected to be instrumental in the design of highly efficient and cost-effective noble-metal-based catalysts for many O₂-involved chemical reactions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Prof. Z. Y. Zhang and Prof. X. G. Gong for helpful discussion. This work was supported by the NSFC (Grants No. 11674289 and 11074223) and partly by the UK EPSRC (EP/K021192/1) and US NSF (CMMI 1300223).

References

1. B. Hammer and J. K. Norskov, Nature, 1995, 376, 238–240.
2. A. G. Sault, R. J. Madix and C. T. Campbell, Surf. Sci., 1986, 169, 347–356.
3. M. Haruta, T. Kobayashi, H. Sano and N. Yamada, Chem. Lett., 1987, 16, 405–408.
4. M. Haruta, S. Tsubota, T. Kobayashi, H. Kageyama, M. J. Genet and B. Delmon, J. Catal., 1993, 144, 175–192.
5. B. Yoon, H. Häkkinen, U. Landman, A. S. Wörz, J.-M. Antonietti, S. Abbet, K. Judai and U. Heiz, Science, 2005, 307, 403–407.
6. I. N. Remediakis, N. Lopez and J. K. Nørskov, Angew. Chem., Int. Ed., 2005, 44, 1824–1826.
7. J. L. C. Fajín, M. N. D. S. Cordeiro and J. R. B. Gomes, J. Catal., 2012, 289, 11–20.
8. Q. Fu, H. Saltsburg and M. Flytzani-Stephanopoulos, Science, 2003, 301, 935–938.
9. L. B. Vilhelmsen and B. Hammer, ACS Catal., 2014, 4, 1626–1631.
10. J. G. Wang and B. Hammer, Top. Catal., 2007, 44, 49–56.
11. M. Valden, X. Lai and D. W. Goodman, Science, 1998, 281, 1647–1650.
12. O. Lopez-Acevedo, K. A. Kacprzak, J. Akola and H. Häkkinen, Nat. Chem., 2010, 2, 329–334.
13. G. Mills, M. S. Gordon and H. Metiu, Chem. Phys. Lett., 2002, 359, 493–499.
14. J. K. Norskov, T. Bligaard, B. Hvolbaek, F. Abild-Pedersen, I. Chorkendorff and C. H. Christensen, Chem. Soc. Rev., 2008, 37, 2163–2171.
15. N. Lopez and J. K. Nørskov, J. Am. Chem. Soc., 2002, 124, 11262–11263.
16. S. F. Li, X. J. Zhao, X. S. Xu, Y. F. Gao and Z. Zhang, Phys. Rev. Lett., 2013, 111, 115501.
17. M. Mavrikakis, P. Stoltze and J. K. Nørskov, Catal. Lett., 2000, 64, 101–106.
18. G. J. Hutchings, M. S. Hall, A. F. Carley, P. Landon, B. E. Solsona, C. J. Kiely, A. Herzing, M. Makkee, J. A. Moulijn, A. Overweg, J. C. Fierro-Gonzalez, J. Guzman and B. C. Gates, J. Catal., 2006, 242, 71–81.
19. N. Weiher, A. M. Beesley, N. Tsapatsaris, L. Delannoy, C. Louis, J. A. van Bokhoven and S. L. M. Schroeder, J. Am. Chem. Soc., 2007, 129, 2240–2241.
20. J. Guzman and B. C. Gates, J. Am. Chem. Soc., 2004, 126, 2672–2673.
21. A. Sanchez, S. Abbet, U. Heiz, W. D. Schneider, H. Häkkinen, R. N. Barnett and U. Landman, J. Phys. Chem. A, 1999, 103, 9573–9578.
22. Y.-G. Wang, Y. Yoon, V.-A. Glezakou, J. Li and R. Rousseau, J. Am. Chem. Soc., 2013, 135, 10673–10683.
23. Z. Yan, S. Chinta, A. A. Mohamed, J. P. Fackler and D. W. Goodman, J. Am. Chem. Soc., 2005, 127, 1604–1605.
24. P. Frondelius, H. Häkkinen and K. Honkala, Angew. Chem., Int. Ed., 2010, 49, 7913–7916.
25. J. G. Wang and B. Hammer, Phys. Rev. Lett., 2006, 97, 136107.
26. R. J. Davis, Science, 2003, 301, 926–927.
27. J. T. Calla, M. T. Bore, A. K. Datye and R. J. Davis, J. Catal., 2006, 238, 458–467.
28. B. Qiao, A. Wang, X. Yang, L. F. Allard, Z. Jiang, Y. Cui, J. Liu, J. Li and T. Zhang, Nat. Chem., 2011, 3, 634–641.
29. F. Li, Y. Li, X. C. Zeng and Z. Chen, ACS Catal., 2015, 5, 544–552.
30. X. Guo, G. Fang, G. Li, H. Ma, H. Fan, L. Yu, C. Ma, X. Wu, D. Deng, M. Wei, D. Tan, R. Si, S. Zhang, J. Li, L. Sun, Z. Tang, X. Pan and X. Bao, Science, 2014, 344, 616–619.
31. S. Lee, C. Fan, T. Wu and S. L. Anderson, J. Am. Chem. Soc., 2004, 126, 5682–5683.
32. D. Matthey, J. G. Wang, S. Wendt, J. Matthiesen, R. Schaub, E. Lægsgaard, B. Hammer and F. Besenbacher, Science, 2007, 315, 1692–1696.
33. X.-F. Yang, A. Wang, B. Qiao, J. Li, J. Liu and T. Zhang, Acc. Chem. Res., 2013, 46, 1740–1748.
34. S. F. J. Hackett, R. M. Brydson, M. H. Gass, I. Harvey, A. D. Newman, K. Wilson and A. F. Lee, Angew. Chem., Int. Ed., 2007, 46, 8593–8596.
35. P. Hohenberg and W. Kohn, Phys. Rev. B, 1964, 136, B864.
36. P. E. Blochl, Phys. Rev. B, 1994, 50, 17953.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
38. J. K. Burdett, T. Hughbanks, G. J. Miller, J. W. Richardson and J. V. Smith, J. Am. Chem. Soc., 1987, 109, 3639–3646.
39. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
40. W. E. Kaden, T. Wu, W. A. Kunkel and S. L. Anderson, Science, 2009, 326, 826–829.
41. S. Li, X. Zhao, J. Shi, Y. Jia, Z. Guo, J.-H. Cho, Y. Gao and Z. Zhang, Phys. Chem. Chem. Phys., 2016, 18, 24872–24879.
42. J. L. Shi, J. H. Wu, X. J. Zhao, X. L. Xue, Y. F. Gao, Z. X. Guo and S. F. Li, Nanoscale, 2016, 8, 19256–19262.
43. R. Asahi, T. Morikawa, T. Ohwaki, K. Aoki and Y. Taga, Science, 2001, 293, 269–271.
44. Y. Matsumoto, M. Murakami, T. Shono, T. Hasegawa, T. Fukumura, M. Kawasaki, P. Ahmet, T. Chikyow, S. Koshihara and H. Koinuma, Science, 2001, 291, 854–856.
45. M. Esakkimuthuraju, R. Mahesh, T. Sreekanth and P. V. Reddy, J. Supercond. Novel Magn., 2016, 29, 2641–2650.
46. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
47. H. Y. Kim, H. M. Lee and G. Henkelman, J. Am. Chem. Soc., 2012, 134, 1560–1570.
48. C. Zhang, A. Michaelides and S. J. Jenkins, Phys. Chem. Chem. Phys., 2011, 13, 22–33.
49. R. Hoffmann, Rev. Mod. Phys., 1988, 60, 601–628.
50. L. P. A. Nilsson, and J. K. Nørskov, Chemical Bonding at Surfaces and Interfaces, Elsevier, Amsterdam, 2008.
51. Y. Hao, M. Mihaylov, E. Ivanova, K. Hadjiivanov, H. Knözinger and B. C. Gates, J. Catal., 2009, 261, 137–149.
52. Y.-G. Wang, D. Mei, V.-A. Glezakou, J. Li and R. Rousseau, Nat. Commun., 2015, 6, 6511.
53. Y.-G. Wang, D. C. Cantu, M.-S. Lee, J. Li, V.-A. Glezakou and R. Rousseau, J. Am. Chem. Soc., 2016, 138, 10467–10476.
54. E. Wigner and E. E. Witmer, Z. Phys., 1928, 51, 859.
55. J. Behler, B. Delley, S. Lorenz, K. Reuter and M. Scheffler, Phys. Rev. Lett., 2005, 94, 036104.
56. W. K. Park, R. J. Ortega-Hertogs, J. S. Moodera, A. Punnoose and M. S. Seehra, J. Appl. Phys., 2002, 91, 8093–8095.
57. Y. Yamada, K. Ueno, T. Fukumura, H. T. Yuan, H. Shimotani, Y. Iwasa, L. Gu, S. Tsukimoto, Y. Ikuhara and M. Kawasaki, Science, 2011, 332, 1065–1067.
58. L. Kernazhitsky, V. Shymanovska, T. Gavrilko, V. Naumov, V. Kshnyakin and T. Khalyavka, J. Solid State Chem., 2013, 198, 511–519.
59. L. A. Errico, M. Rentería and M. Weissmann, Phys. Rev. B, 2005, 72, 184425.
60. W. Zhu, X. Qiu, V. Iancu, X.-Q. Chen, H. Pan, W. Wang, N. M. Dimitrijevic, T. Rajh, H. M. Meyer, M. P. Paranthaman, G. M. Stocks, H. H. Weitering, B. Gu, G. Eres and Z. Zhang, Phys. Rev. Lett., 2009, 103, 226401.
61. Z. Li, D. Ding and C. Ning, Nanoscale Res. Lett., 2013, 8, 25.

---

Footnote

† Electronic supplementary information (ESI) available: Additional data are presented in Fig. S1–S6. See DOI: 10.1039/c7ta05483a

---