Charge storage at the nanoscale: understanding the trends from the molecular scale perspective
Abstract
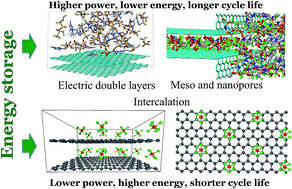
Supercapacitors or electrical double layer (EDL) capacitors store charge via rearrangement of ions in electrolytes and their adsorption on electrode surfaces. They are actively researched for multiple applications requiring longer cycling life, broader operational temperature ranges, and higher power density compared to batteries. Recent developments in nanostructured carbon-based electrodes with a high specific surface area have demonstrated the potential to significantly increase the energy density of supercapacitors. Molecular modeling of electrolytes near charged electrode surfaces has provided key insights into the fundamental aspects of charge storage at the nanoscale, including an understanding of the mechanisms of ion adsorption and dynamics at flat surfaces and inside nanopores, and the influence of curvature, roughness, and electronic structure of electrode surfaces. Here we review these molecular modeling findings for EDL capacitors, dual ion batteries and pseudo-capacitors together with available experimental observations and put this analysis into the perspective of future developments in this field. Current research trends and future directions are discussed.
- This article is part of the themed collection: Recent Review Articles


 Please wait while we load your content...
Please wait while we load your content...