Ionic thermoelectric paper

Abstract

Ionic thermoelectric materials, for example, polyelectrolytes such as polystyrene sulfonate sodium (PSSNa), constitute a new class of materials which are attracting interest because of their large Seebeck coefficient and the possibility that they could be used in ionic thermoelectric SCs (ITESCs) and field effect transistors. However, pure polyelectrolyte membranes are not robust or flexible. In this paper, the preparation of ionic thermoelectric paper using a simple, scalable and cost-effective method is described. After a composite was fabricated with nanofibrillated cellulose (NFC), the resulting NFC–PSSNa paper is flexible and mechanically robust, which is desirable if it is to be used in roll-to-roll processes. The robust NFC–PSSNa thermoelectric paper combines high ionic conductivity (9 mS cm⁻¹), high ionic Seebeck coefficient (8.4 mV K⁻¹) and low thermal conductivity (0.75 W m⁻¹ K⁻¹) at 100% relative humidity, resulting in overall figure-of-merit of 0.025 at room temperature which is slightly better than that for the PSSNa alone. Fabricating a composite with cellulose enables flexibility and robustness and this is an advance which will enable future scaling up the manufacturing of ITESCs, but also enables its use for new applications for conformable thermoelectric devices and flexible electronics.

---

Introduction

Access to clean and sustainable energy is of paramount importance for the development of human society. Typically, 60% of fossil energy is lost in waste heat. Today, various technologies have been proposed to harvest electricity from the largest energy source, the sun, but neither solar thermal plants nor photovoltaic power plants are that efficient and a large proportion of the solar radiation is lost in heat. Thus, several strategies are currently being explored beyond the use of heat engines in order to convert heat into electricity. One of these approaches is the thermoelectric generator (TEG).^2,3 TEGs are defined as solid state devices that can convert heat (temperature differences) directly into electrical energy through a phenomenon called the Seebeck effect arising from the thermo-diffusion of electronic charge carriers in a material. The efficiency of a thermoelectric material is evaluated using a dimensionless quantity called the figure-of-merit, ZT = α²σT/κ, where α, σ, T and κ represent the Seebeck coefficient, the electrical conductivity, the absolute temperature and the thermal conductivity, respectively. Among the various types of material classes,³ organic electronic conducting polymers have attracted increased attention because they are based on abundant atomic elements and thus are potentially scalable at low cost. Despite the tremendous efforts and accomplishments of recent years,^4–12 the efficiency of organic thermoelectric devices remains quite low because of their relatively small Seebeck coefficient. One possible strategy to increase the Seebeck coefficient of conducting polymers is to add solvent into the polymer to change its morphology.¹³ Whereas, another strategy is the addition of ionic thermodiffusion in mixed ionic-electronic conductors.¹⁴ Indeed, an ionic Seebeck contribution up to several hundreds of μV K⁻¹ can be added to the electronic Seebeck coefficient. However, this effect vanishes with time because of the electronic reorganization. But if the electronic conducting paths are removed, for example, for pure ionic conductors, such as polystyrene sulfonic acid (PSSH), the ionic Seebeck coefficient was found to be extremely large and stable with time (∼a few mV K⁻¹).¹⁵

Recently, two classes of material have been explored for use in thermoelectricity: ionic conductors^16–18 and electrolytes.¹⁹ A thermovoltage is developed in an ionic conductor submitted to a temperature difference because of the so-called Soret effect (thermodiffusion of ions). This new research area has been motivated by the use of the large ionic thermovoltage for example to (i) charge a SC leading to the so-called “ionic thermoelectric supercapacitors” (ITESCs)¹⁶ or (ii) to switch on/off transistors in “ionic thermoelectric transistors”.²⁰ The ITESC is a single device comparable to an organic thermoelectric generator (OTEG) coupled in series with a supercapacitor (SC) of equivalent capacitance C. Importantly, because the ionic Seebeck coefficient of ionic conducting polymers (5 mV K⁻¹)¹⁷ is about 100 times higher than the electronic Seebeck coefficient in electronic conducting polymers (50 μV K⁻¹),⁴ the electrical energy E stored in an ITESC is 10 000 times higher than in a SC coupled to an OTEG [E = 1/2C (αΔT)²]. A recent study shows that charging an ITESC can be compared with charging a TEG-SC based on the thermoelectric figure-of-merit ZT, which in the case of an ionic conductor implies that the electrical conductivity is solely because of ionic transport and the Seebeck coefficient is because of the thermodiffusion of ions.¹ Interestingly, high ionic Seebeck coefficients were found for wet solid state polyelectrolytes such as polystyrene sulfonate sodium (PSSNa)¹ and PSSH.¹⁷

Ideally the ionic thermoelectric material should be flexible, so that the ITESC is able to conform to the shape of any hot/cold objects (for example a pipe). Unfortunately polyelectrolytes are fragile and brittle. Also, making ionic thermoelectric materials robust would enable the use of a roll-to-roll machine for the production and assembly of the ITESC. ITESC and TEG are devices that produce a voltage proportional to the temperature difference. Thus, high voltage, i.e., high energy storage, is achievable if the material is thick and of low thermal conductivity. All these requirements need to be met as well as having a high ionic conductivity and high ionic Seebeck coefficient. One approach already demonstrated to strengthen the mechanical properties of materials is to make a composite with cellulose. Cellulose is attractive because it is a cheap, renewable and biodegradable material with good mechanical properties and is scalable for mass implementation.²¹ There have been many reports about fabricating composites with cellulose for use with electrical conductors for SC electrode,²² and electrolyte²³ applications with excellent electronic and ionic conductivity. But no one has ever studied the thermoelectric properties of the cellulose-electrolyte.

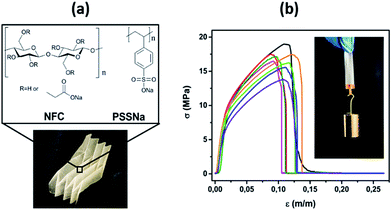
In this research, a polymer nano-composite was fabricated using nanofibrillated cellulose (NFC), and the polyelectrolyte PSSNa and then its thermoelectric properties were characterized. The chemical structure of the biopolymer cellulose²⁴ and PSSNa are illustrated in Fig. 1a. NFC is composed of cellulose polymer chains aggregated in nanofibers.^25,26 They have several key properties which are of interest here: extraordinary mechanical properties,²⁷ high transparency,²⁸ lightweight²⁹ and a large specific surface area.³⁰ The NFC–PSSNa composite is mechanically robust and flexible compared to PSSNa. Despite the presence of NFC, the ionic conductivity and the ionic Seebeck coefficient of NFC–PSSNa is similar to PSSNa. Thus, this new composite is the first demonstration of ionic thermoelectric paper.

Fig. 1 (a) Photograph of flexible NFC–PSSNa paper as well as the chemical structure of nanofibrillated cellulose (NFC) and polystyrene sulfonate sodium (PSSNa). (b) Tensile strength versus strain for eight different NFC–PSSNa samples with the same composition and thickness. Inset is the photograph of 80 μm thick NFC–PSSNa strip subjected to a weight of 100 g. The photographs were taken by Thor Balkhed (Linköping University).

Results and discussion

The PSSNa films were prepared by simply casting a water solution and letting the solvent evaporate. The NFC–PSSNa composite of same thickness (∼60 μm) as the PSSNa film was prepared from a NFC water dispersion, with addition of PSSNa and high boiling point solvents [glycerol, dimethylsulfoxide (DMSO)], then followed by casting and evaporation of the solvents. After peeling off the film, the estimated weight percent ratio of the composite film was 24.8% NFC, 53% PSSNa, and 22.2% of the remaining solvents. The role of the high boiling solvent was to remain in the film so that the nanofibers did not aggregate strongly with each other, but interstitial nanovoids remained filled with the high boiling point solvent in order to create percolation paths for the transport of ions.³¹

The pure PSSNa film was extremely brittle, and it would crack even after drying. The addition of NFC as well as high boiling point solvents to PSSNa leads to a composite of improved mechanical properties: it was now flexible, foldable, and robust (Fig. 1a). Fig. 1b shows the tensile strength of NFC–PSSNa film at different strains and reaching a high value of tensile strength of σ_T = 16.6 ± 1.5 MPa. The calculated Young's modulus was E = 0.9 ± 0.1 GPa and the strain at break was ε_T = 10.2% ± 1.2, and the details are shown in Table S1 (ESI†). Although the parameter specification of the composite film is weaker than typical copy paper, the mechanical properties of the NFC–PSSNa film were sufficient for practical handling and could be processed in roll-to-roll machines.

The atomic force microscopy (AFM) images of both films are shown in Fig. 2. The topography image displays a flat surface on the PSSNa film (Fig. 2a) whereas the NFC–PSSNa film is rough and likely to be porous (Fig. 2c). The phase image of the composite shows that the long chains of the cellulose nanofibrils arranged in parallel with the film surface with an individual diameter of about 10–20 nm. Note that the AFM images were taken on samples that had been dried to remove the high boiling point solvents. At the same time, the composite film was relatively transparent (60%), although this value was less than that of pure PSSNa (90%). This indicated that there was a low amount of aggregates which cause light scattering, and that the sample was homogeneous at the submicron scale (details for transparency see Fig. S1, ESI†).

Fig. 2 AFM topography (a and c) and phase image (b and d) of PSSNa and NFC–PSSNa composite film with a thickness of 60 μm. All images have a scale bar of 1 μm.

Furthermore, impedance spectroscopy was used to study the ion transport in the paper. The impedance spectrum of composite films under different humidities was measured at room temperature (impedance and phase angle versus frequency as well as a Nyquist plot see Fig. S2 and S3, ESI†). Ionic conductivity was obtained from the real part of the impedance where the phase angle was near zero and was compared with the ionic conductivity of pure PSSNa.¹ As shown in Fig. 3a, at 50% relative humidity (RH%), the ionic conductivity of NFC–PSSNa was about 0.04 mS cm⁻¹, which was six times lower than that for PSSNa (0.26 mS cm⁻¹). But the difference in ionic conductivity between these two materials decreased with the increase of humidity, reaching a value of 9 and 12 mS cm⁻¹ for NFC–PSSNa and PSSNa, respectively. Thus, in spite of the introduction of NFC, the ionic conductivity of NFC–PSSNa still remained high. The ionic conductivity in PSSNa increased exponentially with the percentage of humidity in the chamber but was saturated at high humidity levels. This saturation has been explained by the formation of water percolation channels at high humidity.³² Because the ionic conductivity in NFC–PSSNa is as high as that of PSSNa in a humid environment, the ionic transport also occurred in the water percolation paths, but the absence of saturation suggested that the presence of NFC modified the formation of these percolation water channels.

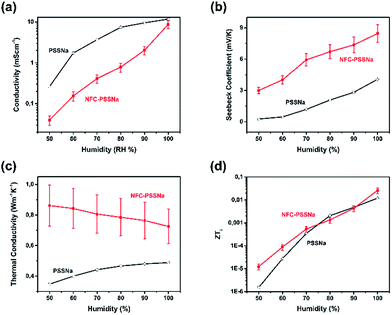Fig. 3 Thermoelectric properties of NFC–PSSNa composite film versus humidity and comparison with pure PSSNa. (a) Ionic conductivity (σ_i), (b) Seebeck coefficient (α_i), (c) thermal conductivity (λ), and (d) ZT_i. All measurements were performed at room temperature and the data for PSSNa are extracted from the paper of Wang et al.¹

The ionic Seebeck coefficient was also studied at room temperature with humidity from 50 to 100 RH%. At a fixed humidity, the open voltage of different temperature differences, ΔT, was measured and the Seebeck coefficient was calculated from the slope of the fitted curve (for details on open voltage and temperature differences as well as the linear fitting of the Seebeck coefficient see Fig. S4 and S5, ESI†). At ΔT = 0 K, the voltage was extremely small with NFC–PSSNa, whereas there was a residual voltage for PSSNa.¹ As shown in Fig. 3b, the ionic Seebeck coefficient of NFC–PSSNa increased from 3 to 8.4 mV K⁻¹ whereas the humidity increased from 50 to 100 RH%. This value was twice as large as that of pure PSSNa¹ and was almost two orders higher than the electronic Seebeck coefficient of normal organic thermoelectric materials such as poly(3,4-ethylenedioxythiophene):polystyrene sulfonate (PEDOT:PSS).⁷

The in-plane thermal conductivity of NFC–PSSNa film was evaluated to obtain a comprehensive understanding of its thermoelectric properties. The room temperature specific heat, measured using differential scanning calorimetry (DSC),³³ and thermal diffusivity,^34,35 measured with AC-calorimetry, were found to be c_P = (1.15 ± 0.10) J g⁻¹ K⁻¹ and D = (8.0 ± 0.8) × 10⁻³ cm² s⁻¹, respectively (see Fig. S6, ESI†). The uncertainties in D and c_P reflected sample dependence, although for a given sample, values were found to be independent of heat treatment and it was assumed that the samples were essentially dehydrated. With the density ρ = (0.97 ± 0.04) g cm⁻³, the calculated value of the thermal conductivity was κ = Dc_Pρ = (0.9 ± 0.2) W m⁻¹ K⁻¹. Although it was difficult to measure the thermal conductivity under different humidity conditions by these methods, the effects of hydration were estimated by assuming that water entered the films in microdomains large enough to use an effective medium theory^36,37 for the composite, in particular assuming that the water domains primarily separate the nanofibers, leading to parallel paths of thermal transport. Then the composite thermal conductivity of hydrated NFC–PSSNa samples was given by κ_c ≈ κ_pϕ_p + κ_wϕ_w (κ and ϕ are the thermal conductivity and volume fraction of each material, respectively, and the subscripts c, p and w correspond to the composites, dry NFC–PSSNa, and water, respectively, where κ_w = 0.6 W m⁻¹ K⁻¹ (ref. 34)). The water content in the composite was measured under different humidity conditions (see Table S2, ESI†), and the water weight and volume fractions were taken to be essentially equal because the density of NFC–PSSNa ≈1 g cm⁻³. The calculated thermal conductivity of the composite and its comparison with pure PSSNa at 50–100 RH% are shown in Fig. 3c. The evolution of the thermal conductivity versus humidity level of PSSNa and NFC–PSSNa were opposite, reflecting the fact that PSSNa was more thermally insulating than water whereas NFC–PSSNa was less insulating. Finally, ZT_i was plotted for both NFC–PSSNa and PSSNa¹versus the humidity level and the plots are shown in Fig. 4d. The ZT_i increased by more than three orders of magnitude with humidity. At low humidity, the ZT_i of NFC–PSSNa (∼10⁻⁵) was almost 10 times larger than that of PSSNa because of its large α_i. Whereas at higher humidity, the ZT_i values of the two materials were similar and about 10⁻².

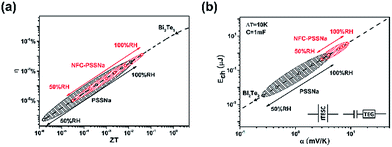Fig. 4 (a) Heat to electricity efficiency and (b) the energy transfer to SC from charging (ΔT = 10 K, C = 1 mF) of NFC–PSSNa composite film and comparison with pure PSSNa film and commercial Bi₂Te₃. The red circle denotes the NFC–PSSNa composite, and the black circle denotes the PSSNa film and the black triangle denotes Bi₂Te₃. The inset in (b) is the structure of the device for ITESC and the structure of the device by connecting the TEG with a SC. The data for PSSNa were extracted from the paper of Wang et al.¹

Although ions cannot pass through an external circuit as electrons can, heat could be converted to electrical energy using the concept of ITESC. The performance of ionic thermoelectric materials can be compared with electronic thermoelectrics because an ITESC of capacitance C corresponds to the equivalent circuit of a TEG connected in series with a SC of same capacitance (see the inset of Fig. 4b). It has been demonstrated that the charging efficiency of the ITESC was related to the traditional thermoelectric figure-of-merit including the ionic conductivity and the ionic Seebeck coefficient.¹ Thus, the two relevant device quantities were calculated: the efficiency η and the energy stored E as a function of ZT_i. As shown in Fig. 4a, the efficiency of the NFC–PSSNa composite was slightly better than that of pure PSSNa, although still much lower than that of commercial bismuth telluride (Bi₂Te₃) (ZT = 1) because of its relatively small ZT_i. But for the comparison of energy transferred to the SC with same ΔT (10 K) and same capacitance (1 mF), the NFC–PSSNa composite performances were much better than those of pure PSSNa and around three orders higher than those with Bi₂Te₃, as shown in Fig. 4b. The energy transferred to the SC is shown quadratically by α_i (E = 1/2CV² = 1/2C(ΔTα_i)²), and the α_i of NFC–PSSNa is much larger than that of the PSSNa over the whole range of humidity.

Conclusions

In conclusion, the first ionic thermoelectric paper has been demonstrated by making a composite from nanofibrillated cellulose and a polyelectrolyte. The introduction of nanofibers of cellulose led to a robust nanocomposite, not fragile nor brittle as was the pure polyelectrolyte. The thermoelectric properties of the paper composite were as good as the pure polyelectrolyte (ZT_i = 0.025 at room temperature). The ionic conductivity of the composite was almost the same as that of pure PSSNa at high humidity and its Seebeck coefficient was higher than that of pure PSSNa. The fabrication of ionic thermoelectric paper opens up new possibilities in term of mass manufacturing of materials for large area ionic thermoelectric SCs. Those devices are designed to convert thermal energy from intermittent heat sources into stored electricity.

Experimental

Materials

Glycerol, DMSO and PSSNa [molecular weight (M_w): 70 000 g mol⁻¹] were purchased from Sigma-Aldrich and used as received. NFC (1 wt%) was produced at Innventia AB, Sweden.

NFC manufacturing

Carboxymethylated NFC was produced by chemically pre-treating wood pulp (trade name Dissolving Plus, supplier Domsjö Fabriker) followed by high-shear mechanical delamination. It was found that through carboxymethylation, anionic carboxymethyl groups were chemically grafted onto the nanofibrils. The charge density of the modified pulp was about 500 μmol g⁻¹, as determined using conductometric studies.

Composites preparation

The concentration of the NFC dispersion was diluted to 0.3 wt% before use. A NFC–PSSNa composite film was prepared by mixing PSSNa, NFC solution, glycerol and DMSO at a solid content (excluding water) weight ratio of 13.9/6.5/8.5/71.1. The mixture was homogenized for several minutes using a T10 basic ULTRA-TURRAX (IKA). The blend was then mixed ultrasonically in an ultrasonic bath for 10 min which was then followed by degassing for 1 h in a vacuum desiccator. Free-standing composite films were then prepared by pouring the NFC–PSSNa dispersions into plastic dishes with a diameter of 5.5 cm and then drying them at 60 °C for 24 h. After drying, the films were peeled off and cut into different shapes for the various measurements.

Characterization

The in-plane ionic conductivity of the NFC–PSSNa composite films were measured using an Alpha high-resolution dielectric analyzer for the impedance spectrometry (Novocontrol Technologies GmbH) with a two-probe method. The impedance spectra were recorded with an AC voltage of 5 mV while sweeping the frequency from 1 MHz to 0.1 Hz. The samples were put inside a humidity chamber and the measurement was done at room temperature at humidity levels from 50 to 100 RH%. The ionic conductivity was calculated from the real part of the impedance where the phase angle was near zero.

The Seebeck coefficient of the composite films was measured at different humidities inside a humidity chamber at room temperature. The voltage difference between the two electrodes was recorded using a model 2182A nanovoltmeter (ΔV) (Keithley Instruments, Inc) and the temperature difference (ΔT) between the two electrodes was evaluated using the thermocouples and measured using a Model 2000 multimeter (Keithley Instruments, Inc). At each humidity, different sets of high and low temperatures with an average of 22.5 °C were applied and the Seebeck coefficient was extracted from the slope of the linear fitted voltage versus temperature difference curves.

The specific heats of the samples were measured using DSC at room temperature and the thermal diffusivity, D ≡ κ/ρc_P and thermal conductivity κ (in the plane of the film) were measured using the AC-calorimetric technique of Hatta et al.³⁴ In this technique, the sample was heated with chopped white light, which was partly blocked by a screen and the oscillating temperature on the reverse surface was measured with a thermocouple. Because the samples were white and translucent, a 0.3 μm film of lead sulfide was evaporated on the front surface to absorb the light. The diffusivity was determined by the variation of the oscillating thermocouple voltage with position, D = πf/(dln(V_ac)/dx)² (the saturation of the signal for large x₀ − x which was because of the edge of the screen reaching the thermocouple glue and the deviations from the linear behavior for small x₀ − x were because of the signal approaching the noise level).

The transmittance spectra were acquired with a Lambda 900 UV-vis spectrophotometer (PerkinElmer instruments) at room temperature in the range of 400–800 nm.

AFM measurement was performed using a Dimension 3100 microscope (Bruker) under ambient conditions with a scan size of 1 × 1 μm.

For tensile testing, 30 μm thick samples were cut into 30 × 15 mm test pieces which were measured in a tensile tester (MTS) with the pulling speed of 30 mm (100%)/min = 0.5 mm s⁻¹ at 23 °C and 50 RH%. Data for eight separate samples were collected to monitor statistical variations.

Acknowledgements

A. N., H. J., J. S. and T. L. contributed to the support of NFC gel and mechanical measurement. D. Z. contributed to AFM. J. S., M. S. and J. B. contributed to the thermal conductivity measurements. J. E. and U. A. contributed to composite preparation and impedance measurements. The authors acknowledge the European Research Council (ERC Starting Grant 307596), the Swedish Foundation for Strategic Research (SSF), the Knut and Alice Wallenberg foundation (KAW), the Swedish Energy Agency, the Advanced Functional Materials Centre at Linköping University and the United States National Science Foundation (Grant No. DMR-1262261). The authors also wish to thank Thor Balkhed from Linköping University for help with the photography.

References

1. H. Wang, D. Zhao, Z. U. Khan, S. Puzinas, M. P. Jonsson, M. Berggren and X. Crispin, Adv. Electron. Mater., 2017, 1700013,  DOI:10.1002/aelm.201700013.
2. F. J. DiSalvo, Science, 1999, 285, 703–706.
3. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114.
4. O. Bubnova, Z. U. Khan, A. Malti, S. Braun, M. Fahlman, M. Berggren and X. Crispin, Nat. Mater., 2011, 10, 429–433.
5. Q. Zhang, Y. M. Sun, W. Xu and D. B. Zhu, Adv. Mater., 2014, 26, 6829–6851.
6. G. H. Kim, L. Shao, K. Zhang and K. P. Pipe, Nat. Mater., 2013, 12, 719–723.
7. O. Bubnova and X. Crispin, Energy Environ. Sci., 2012, 5, 9345–9362.
8. Y. Sun, P. Sheng, C. Di, F. Jiao, W. Xu, D. Qiu and D. Zhu, Adv. Mater., 2012, 24, 932–937.
9. Y. Sun, L. Qiu, L. Tang, H. Geng, H. Wang, F. Zhang, D. Huang, W. Xu, P. Yue, Y. S. Guan, F. Jiao, Y. Sun, D. Tang, C. A. Di, Y. Yi and D. Zhu, Adv. Mater., 2016, 28, 3351–3358.
10. N. Toshima, K. Oshima, H. Anno, T. Nishinaka, S. Ichikawa, A. Iwata and Y. Shiraishi, Adv. Mater., 2015, 27, 2246–2251.
11. B. T. McGrail, A. Sehirlioglu and E. Pentzer, Angew. Chem., Int. Ed., 2015, 54, 1710–1723.
12. N. Toshima, Synth. Met., 2017, 225, 3–21.
13. Q. Wei, M. Mukaida, K. Kirihara, Y. Naitoh and T. Ishida, Appl. Phys. Express, 2014, 7, 031601.
14. H. Wang, U. Ail, R. Gabrielsson, M. Berggren and X. Crispin, Adv. Energy Mater., 2015, 5, 1500044.
15. U. Ail, M. J. Jafari, H. Wang, T. Ederth, M. Berggren and X. Crispin, Adv. Funct. Mater., 2016, 26, 6288–6296.
16. D. Zhao, H. Wang, Z. U. Khan, J. C. Chen, R. Gabrielsson, M. P. Jonsson, M. Berggren and X. Crispin, Energy Environ. Sci., 2016, 9, 1450–1457.
17. S. L. Kim, H. T. Lin and C. Yu, Adv. Energy Mater., 2016, 6, 1600546.
18. W. B. Chang, C. M. Evans, B. C. Popere, B. M. Russ, J. Liu, J. Newman and R. A. Segalman, ACS Macro Lett., 2016, 5, 94–98.
19. M. Bonetti, S. Nakamae, M. Roger and P. Guenoun, J. Chem. Phys., 2011, 134, 114513.
20. D. Zhao, S. Fabiano, M. Berggren and X. Crispin, Nat. Commun., 2017, 8, 14214.
21. M. M. Perez-Madrigal, M. G. Edo and C. Aleman, Green Chem., 2016, 18, 5930–5956.
22. K. Gao, Z. Shao, J. Li, X. Wang, X. Peng, W. Wang and F. Wang, J. Mater. Chem. A, 2013, 1, 63–67.
23. Y. N. Sudhakar, M. Selvakumar and D. K. Bhat, Mater. Renew. Sustain. Energy, 2015, 4, 10.
24. Z. Gui, H. Zhu, E. Gillette, X. Han, G. W. Rubloff, L. Hu and S. B. Lee, ACS Nano, 2013, 7, 6037–6046.
25. H. P. Abdul Khalil, Y. Davoudpour, M. N. Islam, A. Mustapha, K. Sudesh, R. Dungani and M. Jawaid, Carbohydr. Polym., 2014, 99, 649–665.
26. S. Kalia, S. Boufi, A. Celli and S. Kango, Colloid Polym. Sci., 2014, 292, 5–31.
27. T. Saito, R. Kuramae, J. Wohlert, L. A. Berglund and A. Isogai, Biomacromolecules, 2013, 14, 248–253.
28. Y. Y. Li, H. L. Zhu, H. B. Gu, H. Q. Dai, Z. Q. Fang, N. J. Weadock, Z. H. Guo and L. B. Hu, J. Mater. Chem. A, 2013, 1, 15278–15283.
29. N. T. Cervin, L. Andersson, J. B. Ng, P. Olin, L. Bergstrom and L. Wagberg, Biomacromolecules, 2013, 14, 503–511.
30. H. Sehaqui, Q. Zhou, O. Ikkala and L. A. Berglund, Biomacromolecules, 2011, 12, 3638–3644.
31. A. Malti, J. Edberg, H. Granberg, Z. U. Khan, J. W. Andreasen, X. Liu, D. Zhao, H. Zhang, Y. Yao, J. W. Brill, I. Engquist, M. Fahlman, L. Wagberg, X. Crispin and M. Berggren, Adv. Sci., 2016, 3, 1500305.
32. J. Feng, Y. Q. Huang, Z. K. Tu, H. N. Zhang, M. Pan and H. L. Tang, Sci. Rep., 2014, 4, 6225.
33. Y. Q. Wang, M. Chung, T. N. Oneal and J. W. Brill, Synth. Met., 1992, 46, 307–316.
34. I. Hatta, Y. Sasuga, R. Kato and A. Maesono, Rev. Sci. Instrum., 1985, 56, 1643–1647.
35. H. Zhang, Y. Yao, M. M. Payne, J. E. Anthony and J. W. Brill, Appl. Phys. Lett., 2014, 105, 073302.
36. L. L. Gong, Y. H. Wang, X. D. Cheng, R. F. Zhang and H. P. Zhang, Int. J. Heat Mass Transfer, 2014, 68, 295–298.
37. A. Leach, J. Phys. D: Appl. Phys., 1993, 26, 733.

---

Footnote

† Electronic supplementary information (ESI) available: Transparency, mechanical properties and details of ionic conductivity, Seebeck coefficient and thermal conductivity characterization. See DOI: 10.1039/c7ta03196c

---