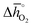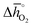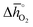Open Access Article
Open Access ArticleDesign principles of perovskites for solar-driven thermochemical splitting of CO2†
Miriam
Ezbiri
,
Michael
Takacs
,
Boris
Stolz
,
Jeffrey
Lungthok
,
Aldo
Steinfeld
 and
Ronald
Michalsky
and
Ronald
Michalsky
 *
*
Department of Mechanical and Process Engineering, ETH Zürich, 8092 Zürich, Switzerland. E-mail: michalskyr@ethz.ch
First published on 3rd July 2017
Abstract
Perovskites are attractive redox materials for thermo/electrochemical fuel synthesis. To design perovskites with balanced redox energetics for thermochemically splitting CO2, the activity of lattice oxygen vacancies and stability against crystal phase changes and detrimental carbonate formation are predicted for a representative range of perovskites by electronic structure computations. Systematic trends in these materials properties when doping with selected metal cations are described in the free energy range defined for isothermal and temperature-swing redox cycles. To confirm that the predicted materials properties root in the bulk chemical composition, selected perovskites are synthesized and characterized by X-ray diffraction, transmission electron microscopy, and thermogravimetric analysis. On one hand, due to the oxidation equilibrium, none of the investigated compositions outperforms non-stoichiometric ceria – the benchmark redox material for CO2 splitting with temperature-swings in the range of 800–1500 °C. On the other hand, certain promising perovskites remain redox-active at relatively low oxide reduction temperatures at which ceria is redox-inactive. This trade-off in the redox energetics is established for YFeO3, YCo0.5Fe0.5O3 and LaFe0.5Ni0.5O3, identified as stable against phase changes and capable to convert CO2 to CO at 600 °C and 10 mbar CO in CO2, and to being decomposed at 1400 °C and 0.1 mbar O2 with an enthalpy change of 440–630 kJ mol−1 O2.
1. Introduction
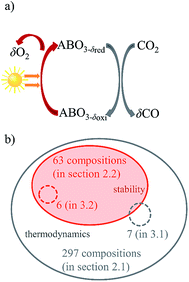
The solar-driven thermochemical splitting of CO2 into CO and O2 operates at high temperatures and utilizes the entire solar spectrum and, thus, can potentially yield high solar-to-fuel energy conversion efficiencies.1–11 It can be realized by a 2-step redox cycle, comprising the endothermic reduction of the metal oxide yielding O2, followed by the exothermic oxidation of a metal oxide with CO2 yielding CO. This is shown schematically in Fig. 1a for perovskite-type metal oxides of ABO3 stoichiometry, with A and B representing metals at the twelve- and six-fold coordinated crystal lattice sites, respectively. Given its crystallographic stability, favorable oxidation thermodynamics, and fast fuel production kinetics, nonstoichiometric ceria (CeO2−δ) has emerged as the benchmark redox material for the thermochemical splitting of CO2 and H2O.3,5,12–23 The use of CeO2−δ is however limited to solar reactors that can withstand the relatively high temperatures required for accessing moderate oxygen exchange capacities. Even at 1723 K and an oxygen partial pressures pO2 below 10−3 bar O2, oxygen nonstoichiometries δ remain typically below 0.03.3,6,24,25 To circumvent these limitations, perovskites have recently attracted attention as an alternative class of redox materials with possibly higher oxygen nonstoichiometries and typically high oxygen vacancy conductivities.5,24,26–38 The vast number of possible metal cation combinations in the perovskite structure may allow for control over the temperature and pO2 requirements of the redox cycle.Previous experimental studies with perovskites have focused mostly on lanthanum manganites.24,26–28,30–33 For instance, McDaniel et al.24 demonstrated that reduction of La0.6Sr0.4Mn0.6Al0.4O3−δ at 1623 K and 0.2 mbar O2 and re-oxidation at 1273 K under 40 vol% H2O or CO2 in Ar results in nine or six times greater H2 and CO yields, respectively, relative to ceria.24 Analogously, Takacs et al.32 showed that La0.6Ca0.4Mn0.6Al0.4O3−δ reduced at 1700 K and 10−3 bar O2 releases up to five times more O2 per unit mass of redox material relative to ceria. However, the authors highlighted that although the reduction extents of the tested perovskites are higher than those of CeO2−δ, oxidation extents with H2O and CO2 are lower.32 Choosing appropriate reduction and oxidation operating conditions for optimal performance is complicate since the thermodynamics and kinetics vary strongly with temperature, pressure, and the composition of the redox material.32,33 Furthermore, given the vast amount of possible materials compositions, experimental evaluation of metal oxide redox materials is limited by trial-and-error.
A computational approach to the design of metal oxide redox materials was presented by Emery et al.,39 calculating the thermodynamic stability and the oxygen vacancy formation energy for 5329 cubic and distorted ABO3 perovskites via high-throughput density functional theory (HT-DFT). The stability of a perovskite was calculated by subtracting the convex hull energy for ABO3 from the DFT-computed formation enthalpy of the perovskite, defined as the energy difference between the total energy of the ABO3 structure and the chemical potentials of A, B and oxygen.39 With this approach, the authors identified 139 compositions suitable for water splitting, such as CeCoO3 and BiVO3.39 Other computational screening efforts for perovskite redox materials include the works by Deml et al.,40,41 correlating the oxygen vacancy formation energy, the enthalpy of metal oxide formation, and the position of the band gap for binary (one cation-type oxides) and ternary systems (with two cations, such as perovskites). Michalsky et al.42 quantified scaling of the free energy and enthalpy of bulk metal oxide formation with the free energy of forming oxygen vacancies at the surface across various metal oxide structures, including three selected perovskites. Furthermore, Calle-Vallejo et al.43 computed perovskite bulk formation energies using DFT and Meredig et al.44 showed that a low enthalpy of reduction and a large positive entropy of reduction of the solid bulk metal oxide are thermodynamically favorable for two-step thermochemical splitting of CO2 and H2O. Noteworthy, Curnan et al.45 showed that the oxygen vacancies formation across LaBO3, SrBO3, (B = 3d transition metals) and similar materials is thermodynamically more favorable in perovskite models with larger unit cell size.45 The energetics of the oxygen vacancy formation are found less favorable in the non-cubic perovskites.45
The present work screens perovskites for thermochemical CO2 splitting by: (1) choosing process conditions for perovskite reduction and oxidation comparable to those used for state-of-the-art ceria based materials; (2) computing the thermochemical stability of cubic perovskites relative to that of possibly formed binary metal oxides and metal carbonates; (3) expanding the range of screened perovskites generally to quinternary compositions; and (4) validating the computed trends in the redox activity and thermochemical stability for selected compositions experimentally. DFT is used to screen ABO3, AA′BO3, ABB′O3 and AA′BB′O3 perovskites for two-step temperature-swing and isothermal thermochemical splitting of CO2 splitting. We considered combinations of non-toxic, inexpensive, and stable metals at the twelve-fold (A, A′ = Mg, Ca, Sr, Ba, Y, La, Ce) and six-fold (B, B′ = Ti, Cr, Mn, Fe, Co, Ni, Cu, Zr, Al) coordinated crystal lattice sites. As a guide, Fig. 1b illustrates which set or subset of perovskite compositions was chosen in a specific section of this article for computational screening (orange) and experimental evaluation (grey), respectively.
2. Electronic structure trends of perovskites
2.1 Redox activity
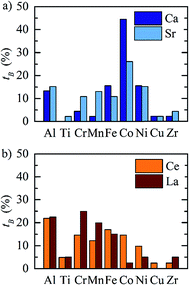
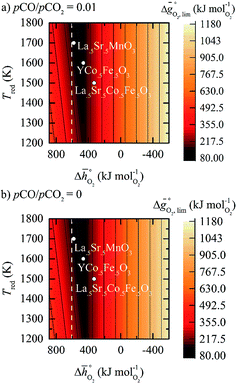
The redox energetics of 297 perovskites were computed for the thermochemical splitting of CO2, of which 63 compositions had basic ternary ABO3 stoichiometry, while the 77, 67, and 90 compositions contained metal cation dopants at the A and/or B lattice sites resulting in AA′BO3, ABB′O3, and AA′BB′O3 stoichiometry, respectively. Fig. 2 shows the tendency of the most stable surfaces with (010) geometry to contain a specific B-cation, as an example for perovskites containing either Ca and Sr (cf.Fig. 2a) or Ce and La (cf.Fig. 2b) at the A-site, respectively. As a trend, we find that surfaces containing alkaline earth metals at the A-site (cf.Fig. 2a) frequently contain B-cations with intermediate periodic number, those with lanthanides at the A-site (cf.Fig. 2b) more frequently contain B-cations with relatively low periodic number.Making use of scaling relations for the free energy of forming oxygen vacancies at metal oxide surfaces, ΔGv[O], and the free energy and enthalpy of bulk metal oxide formation,42 we determined the Gibbs free energy changes for bulk perovskite reduction (liberating O2) and oxidation (reducing CO2 into CO). Generally, the more endergonic reaction limits the oxygen exchange capacity of a perovskite.46Fig. 3 shows the limiting free energy change of a CO2-splitting cycle (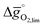 , at process conditions) as a function of the standard partial molar enthalpy change for metal oxide reduction (
, at process conditions) as a function of the standard partial molar enthalpy change for metal oxide reduction (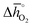 , at ambient conditions), estimated as the reaction of perovskites into their brownmillerite analogs and O2. With other words, we employ the enthalpy change for metal oxide reduction, a measure of the bulk metal–oxygen bond strength, as a single general descriptor of the application-specific redox energetics. Given the resulting volcano-type curve for metal oxide redox materials,42 we find the materials with the least-endergonic limiting free energy changes at the intersection of both correlations. Dependent on reaction temperatures and pressures, balance of the redox energetics indicates a favorable intermediately strong binding of oxygen, that is, strong enough to facilitate oxide oxidation but weak enough to allow for reduction of the oxidized oxide. Ideally, this intersection is located in the exergonic reaction space. To approach this, Fig. 3 shows the redox energetics at reasonable process conditions, that is, oxide reduction between 1200 and 1800 K and 10−4 bar O2 and oxide oxidation at 900 K in an atmosphere of either 1% CO in CO2 (Fig. 3a) or 100% CO2 (Fig. 3b). For the following discussion, the positions of YCo0.5Fe0.5O3, La0.5Sr0.5Co0.5Fe0.5O3 and La0.5Sr0.5MnO3 are marked along with the position of CeO2−δ as a reference. As indicated by their position relative to the top of the volcano-type curve, yields of redox cycles using YCo0.5Fe0.5O3 and La0.5Sr0.5Co0.5Fe0.5O3 are limited by the oxidation thermodynamics, while that of a process using La0.5Sr0.5MnO3 is limited by the reduction thermodynamics.
, at ambient conditions), estimated as the reaction of perovskites into their brownmillerite analogs and O2. With other words, we employ the enthalpy change for metal oxide reduction, a measure of the bulk metal–oxygen bond strength, as a single general descriptor of the application-specific redox energetics. Given the resulting volcano-type curve for metal oxide redox materials,42 we find the materials with the least-endergonic limiting free energy changes at the intersection of both correlations. Dependent on reaction temperatures and pressures, balance of the redox energetics indicates a favorable intermediately strong binding of oxygen, that is, strong enough to facilitate oxide oxidation but weak enough to allow for reduction of the oxidized oxide. Ideally, this intersection is located in the exergonic reaction space. To approach this, Fig. 3 shows the redox energetics at reasonable process conditions, that is, oxide reduction between 1200 and 1800 K and 10−4 bar O2 and oxide oxidation at 900 K in an atmosphere of either 1% CO in CO2 (Fig. 3a) or 100% CO2 (Fig. 3b). For the following discussion, the positions of YCo0.5Fe0.5O3, La0.5Sr0.5Co0.5Fe0.5O3 and La0.5Sr0.5MnO3 are marked along with the position of CeO2−δ as a reference. As indicated by their position relative to the top of the volcano-type curve, yields of redox cycles using YCo0.5Fe0.5O3 and La0.5Sr0.5Co0.5Fe0.5O3 are limited by the oxidation thermodynamics, while that of a process using La0.5Sr0.5MnO3 is limited by the reduction thermodynamics.
The thermodynamic equilibrium for the reduction and oxidation with CO2 are given by eqn (1) and (2), respectively:
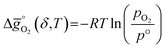 | (1) |
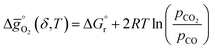 | (2) |
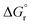 is the standard Gibbs free energy change of CO2 dissociation (CO2 = CO + 0.5O2), and pCO2 and pCO are the partial pressures of CO2 and CO, respectively. Evidently, the reduction of a metal oxide is favorable at high temperatures and low pO2, while its oxidation is favorable at low temperatures and high pCO2 and low pCO. Fig. 3 quantifies this for perovskites, for which thermochemical data is typically not available from experiments. We note, while Fig. 3 gives the computed thermochemical trends at selected process conditions, the analysis can be reiterated for any set of process conditions using the raw data and scaling relations given with ESI.†
is the standard Gibbs free energy change of CO2 dissociation (CO2 = CO + 0.5O2), and pCO2 and pCO are the partial pressures of CO2 and CO, respectively. Evidently, the reduction of a metal oxide is favorable at high temperatures and low pO2, while its oxidation is favorable at low temperatures and high pCO2 and low pCO. Fig. 3 quantifies this for perovskites, for which thermochemical data is typically not available from experiments. We note, while Fig. 3 gives the computed thermochemical trends at selected process conditions, the analysis can be reiterated for any set of process conditions using the raw data and scaling relations given with ESI.†
Guiding the design of perovskites, Fig. 3 identifies materials with the most-favorable redox activity (marked in dark red) with an enthalpy change for perovskite reduction of 440–630 kJ molO2−1 at the chosen process conditions. As expected, CeO2−δ with 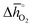 of 606 kJ molO2−1, computed for reduction of the thermodynamically most stable mixed-terminated CeO2(111) facet yielding stable oxygen vacancies in the subsurface of CeO1.75(111),49 is found favorably near the top of the volcano-type plot. While the exact location of this reference depends on the oxygen nonstoichiometry, we find ceria typically exhibits well-balanced redox energetics at high-temperature redox conditions. These trends in the redox energetics indicate further increasing the reduction temperature or decreasing pO2 will yield exergonic limiting free energy changes with perovskites that are characterized by slightly stronger metal–oxygen bonding.
of 606 kJ molO2−1, computed for reduction of the thermodynamically most stable mixed-terminated CeO2(111) facet yielding stable oxygen vacancies in the subsurface of CeO1.75(111),49 is found favorably near the top of the volcano-type plot. While the exact location of this reference depends on the oxygen nonstoichiometry, we find ceria typically exhibits well-balanced redox energetics at high-temperature redox conditions. These trends in the redox energetics indicate further increasing the reduction temperature or decreasing pO2 will yield exergonic limiting free energy changes with perovskites that are characterized by slightly stronger metal–oxygen bonding.
Comparison of Fig. 3a and b shows that 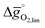 for the perovskites is less endergonic in a pure CO2 atmosphere, as compared to a more realistic environment of solar receiver–reactors for CO2 splitting, i.e., 1% CO in CO2.6 Analogously, we find at the selected conditions 63%, that is, the majority of the studied perovskites are characterized by oxide oxidation-limited redox energetics (cf. Fig. S17†). This confirms, as a trend, previous observations for selected perovskites, as outlined above.26,27,31–33 To validate these trends, we chose seven attractive perovskites (cf.Fig. 4, marked in blue), that are located near the top of the volcano-type curve with oxide reduction at 1600 K and 10−4 bar O2 and oxide oxidation at 900 K and an atmosphere of 1% CO in CO2. These conditions were chosen as realistic process conditions relevant to an industrial implementation.26,27,31,32 In particular, we chose to investigate reduction at 1600 K, that is, below typically 1723 K with CeO2−δ,6 since this would alleviate thermal and mechanical stresses in solar receiver–reactors and decrease volatilization of the redox material. For the seven chosen perovskites, Fig. 4 shows that YFeO3, LaCo0.5Fe0.5O3, LaFeO3 and YMnO3 exhibit reduction-limited energetics, while LaFe0.5Ni0.5O3, LaCo0.5Ni0.5O3 and YCo0.5Fe0.5O3 are exhibit oxidation-limited energetics. Compositions marked with grey symbols were considered unstable, concluded from unsuccessful synthesis attempts. For example, synthesis of CeCoO3 (with
for the perovskites is less endergonic in a pure CO2 atmosphere, as compared to a more realistic environment of solar receiver–reactors for CO2 splitting, i.e., 1% CO in CO2.6 Analogously, we find at the selected conditions 63%, that is, the majority of the studied perovskites are characterized by oxide oxidation-limited redox energetics (cf. Fig. S17†). This confirms, as a trend, previous observations for selected perovskites, as outlined above.26,27,31–33 To validate these trends, we chose seven attractive perovskites (cf.Fig. 4, marked in blue), that are located near the top of the volcano-type curve with oxide reduction at 1600 K and 10−4 bar O2 and oxide oxidation at 900 K and an atmosphere of 1% CO in CO2. These conditions were chosen as realistic process conditions relevant to an industrial implementation.26,27,31,32 In particular, we chose to investigate reduction at 1600 K, that is, below typically 1723 K with CeO2−δ,6 since this would alleviate thermal and mechanical stresses in solar receiver–reactors and decrease volatilization of the redox material. For the seven chosen perovskites, Fig. 4 shows that YFeO3, LaCo0.5Fe0.5O3, LaFeO3 and YMnO3 exhibit reduction-limited energetics, while LaFe0.5Ni0.5O3, LaCo0.5Ni0.5O3 and YCo0.5Fe0.5O3 are exhibit oxidation-limited energetics. Compositions marked with grey symbols were considered unstable, concluded from unsuccessful synthesis attempts. For example, synthesis of CeCoO3 (with 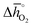 of about 500 kJ molO2−1, resulting in
of about 500 kJ molO2−1, resulting in 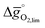 of 97 kJ molO2−1) was unsuccessful, as the solid synthesis product contained only CeO2−δ and Co3O4 (cf. Fig. S1†), in line with previous studies.47,48
of 97 kJ molO2−1) was unsuccessful, as the solid synthesis product contained only CeO2−δ and Co3O4 (cf. Fig. S1†), in line with previous studies.47,48
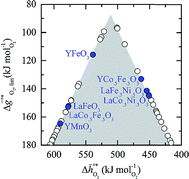 | ||
Fig. 4 A detail of Fig. 3, limiting standard partial molar Gibbs free energy for thermochemical splitting of CO2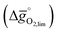 for oxide reduction at 1600 K and 10−4 bar O2 and oxide oxidation at 900 K and in an atmosphere of 1% CO in CO2 plotted vs. for oxide reduction at 1600 K and 10−4 bar O2 and oxide oxidation at 900 K and in an atmosphere of 1% CO in CO2 plotted vs.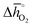 . Perovskites shown with blue symbols (YFeO3, LaCo0.5Fe0.5O3, LaFeO3, YMnO3, LaFe0.5Ni0.5O3, LaCo0.5Ni0.5O3, and YCo.5Fe0.5O3) are further examined experimentally. Perovskites shown with grey symbols were considered unstable, as discussed in Section 2.2. . Perovskites shown with blue symbols (YFeO3, LaCo0.5Fe0.5O3, LaFeO3, YMnO3, LaFe0.5Ni0.5O3, LaCo0.5Ni0.5O3, and YCo.5Fe0.5O3) are further examined experimentally. Perovskites shown with grey symbols were considered unstable, as discussed in Section 2.2. | ||
2.2 Thermochemical stability of the perovskite phase
Thermochemical stability is fundamental for a stable performance of a metal oxide redox material throughout multiple fuel synthesis cycles. In this work, we differentiate between the stability of the cubic perovskite phase in general and the stability against metal carbonate formation in particular. To avoid time- and resource-demanding computations of solid-state entropies, we define as a descriptor of phase stability in an inert atmosphere rphase = ∑Ep,phase/∑Er,phase, with ∑Ep,phase and ∑Er,phase being the sums of the DFT-calculated electronic energies of the stoichiometry-dependent reaction products (possible phases in the A–B–O ternary phase diagram, such as binary metal oxides) and reactants (the perovskite and the balance O2) at 0 K. Analogously, we define as a descriptor of the thermochemical stability of a perovskite against carbonate formation in presence of CO2rcarb = ∑Ep,carb/∑Er,carb, with ∑Ep,carb and ∑Er,carb being the sums of the DFT-calculated electronic energies of the stoichiometry-dependent reaction products (ACO3 carbonates and binary metal oxides) and reactants (the perovskite and CO2) at 0 K. Both stability descriptors indicate stronger stability of the perovskite with lower values. Details of this analysis are given with ESI† (cf. eqn (6) and (7)).
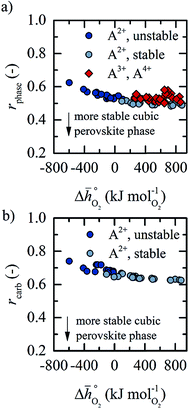
Fig. 5 shows rphase for 63 ABO3-type perovskites (cf.Fig. 5a) and rcarb for 36 ABO3-type perovskites (cf.Fig. 5b) as a function of 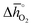 . Since experimental data for Y and La carbonates is very limited (neither the NIST nor Barin's database59 provide thermochemical data for these compounds and their lattice constants are unknown to the best of our knowledge), we focused our analysis of carbonate formation on perovskites containing divalent alkaline earth metals (A = Mg2+, Ca2+, Sr2+ and Ba2+). We find perovskites with divalent A cations exhibit decreasing stability (Fig. 5a and b) with increasing
. Since experimental data for Y and La carbonates is very limited (neither the NIST nor Barin's database59 provide thermochemical data for these compounds and their lattice constants are unknown to the best of our knowledge), we focused our analysis of carbonate formation on perovskites containing divalent alkaline earth metals (A = Mg2+, Ca2+, Sr2+ and Ba2+). We find perovskites with divalent A cations exhibit decreasing stability (Fig. 5a and b) with increasing 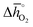 . That is, a stable perovskite phase and an unstable carbonate phase correlate both with strong metal–oxygen binding within the perovskite. The stability of perovskites containing trivalent and tetravalent A cations do not show such a clear trend (red square symbols in Fig. 5a). Furthermore, we find both stability descriptors for perovskites with divalent A cations reach a plateau at
. That is, a stable perovskite phase and an unstable carbonate phase correlate both with strong metal–oxygen binding within the perovskite. The stability of perovskites containing trivalent and tetravalent A cations do not show such a clear trend (red square symbols in Fig. 5a). Furthermore, we find both stability descriptors for perovskites with divalent A cations reach a plateau at 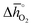 of about 200 kJ
of about 200 kJ ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) molO2−1. That is, we can expect that the thermochemical stability of perovskites containing A2+ cations will not further increase when the metal–oxygen bond becomes stronger than 200 kJ
molO2−1. That is, we can expect that the thermochemical stability of perovskites containing A2+ cations will not further increase when the metal–oxygen bond becomes stronger than 200 kJ ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) molO2−1. Therefore, we consider perovskites containing divalent A cations and with rcarb < 0.66 and rphase < 0.51 as thermochemically stable (cf. light blue circles round symbols in Fig. 5a and b). We note this self-consistent analysis is limited to the cubic perovskite phase. Other descriptors, such as the Goldschmidt tolerance factor, can be employed to further investigate perovskite stability.
molO2−1. Therefore, we consider perovskites containing divalent A cations and with rcarb < 0.66 and rphase < 0.51 as thermochemically stable (cf. light blue circles round symbols in Fig. 5a and b). We note this self-consistent analysis is limited to the cubic perovskite phase. Other descriptors, such as the Goldschmidt tolerance factor, can be employed to further investigate perovskite stability.
In Section 2.1 we describe superior redox energetics for perovskites with 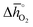 in the range of 440–630 kJ molO2−1 (cf.Fig. 3). This range describes materials with metal–oxygen bonding stronger than 200 kJ
in the range of 440–630 kJ molO2−1 (cf.Fig. 3). This range describes materials with metal–oxygen bonding stronger than 200 kJ ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) molO2−1, indicating that all analyzed perovskites that contain A2+ cations and that show attractive redox energetics are thermochemically stable at the chosen process conditions. This is assuming that the AA′BO3-, ABB′O3- and AA′BB′O3-type compositions follow the correlation established here for ABO3-type compositions.
molO2−1, indicating that all analyzed perovskites that contain A2+ cations and that show attractive redox energetics are thermochemically stable at the chosen process conditions. This is assuming that the AA′BO3-, ABB′O3- and AA′BB′O3-type compositions follow the correlation established here for ABO3-type compositions.
2.3 Choosing a reasonable set of redox conditions
Choosing a reasonable set of process conditions is fundamental for consistent materials screening yielding results that are comparable to experiments with metal oxides tested at their specific set of favorable process conditions, as outlined in Section 2.1. For instance, given the often poor perovskite oxidation energetics, we find exergonic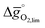 for reduction at 1600 K and 10−5 bar O2 and oxidation at 900 K with a molar ratio of CO2 feed to oxygen vacancies present in the solid of 10
for reduction at 1600 K and 10−5 bar O2 and oxidation at 900 K with a molar ratio of CO2 feed to oxygen vacancies present in the solid of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. At these conditions, LaNiO3, CeNiO3, and YCoO3 reach
000. At these conditions, LaNiO3, CeNiO3, and YCoO3 reach 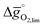 desirably negative values of −6.40, −5.62 and −1.78 kJ
desirably negative values of −6.40, −5.62 and −1.78 kJ ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) molO2−1, respectively. However, these process conditions are unfavorable and would lead to a significant drop of the overall solar-to-fuel energy conversion efficiency of the redox cycle. Both, the low concentrations of O2 during the reduction and the excess of oxidant imply additional energy penalties for gas separations and heat exchange, increasing the net-energy penalties.49 Analogously, for realization of isothermal CO2 splitting with perovskites we find exergonic redox energetics at Tred = Tox = 1600 K, a molar CO2 to oxygen vacancy ratio of 1000, and 10−7 bar O2. This agrees well with the analysis by Meredig et al.,44 who showed that large temperature differences between oxidation and reduction are required for thermodynamically favorable redox cycles. The authors further demonstrated that this advantage of relatively large temperature swings is material-independent and driven solely by the temperature difference and the entropy of the O2.44 The product of these two driving forces must be equal or larger than twice the free energy of formation of H2O or CO2, which is the barrier to a thermodynamically favorable two-step redox cycle.44
molO2−1, respectively. However, these process conditions are unfavorable and would lead to a significant drop of the overall solar-to-fuel energy conversion efficiency of the redox cycle. Both, the low concentrations of O2 during the reduction and the excess of oxidant imply additional energy penalties for gas separations and heat exchange, increasing the net-energy penalties.49 Analogously, for realization of isothermal CO2 splitting with perovskites we find exergonic redox energetics at Tred = Tox = 1600 K, a molar CO2 to oxygen vacancy ratio of 1000, and 10−7 bar O2. This agrees well with the analysis by Meredig et al.,44 who showed that large temperature differences between oxidation and reduction are required for thermodynamically favorable redox cycles. The authors further demonstrated that this advantage of relatively large temperature swings is material-independent and driven solely by the temperature difference and the entropy of the O2.44 The product of these two driving forces must be equal or larger than twice the free energy of formation of H2O or CO2, which is the barrier to a thermodynamically favorable two-step redox cycle.44
In summary, perovskites do not outperform state-of-the-art nonstoichiometric ceria for solar thermochemical fuel production at the high-temperature process conditions which are required to render ceria redox-active. However, perovskites offer the possibility to decrease the maximum temperature of a redox cycle, which may alleviate thermal and mechanical stress in solar receiver–reactors and may diminish volatilization of solids. Realization of such redox cycles at lower temperatures with perovskite redox materials comes, however, at the costs of additional energy penalties for providing low O2 partial pressures during oxide reduction and/or excess oxidant during oxide oxidation. An energy balance and calculation of the theoretical solar-to-fuel energy conversion efficiency assuming thermodynamic equilibrium is found in Takacs et al.32
3. Experimental validation
3.1 Oxygen nonstoichiometry measurements
To assess the trends of the redox energetics established above via DFT, we evaluated the redox activity of selected perovskites (i.e., YFeO3, LaCo0.5Fe0.5O3, LaFeO3, YMnO3, LaFe0.5Ni0.5O3, LaCo0.5Ni0.5O3 and YCo0.5Fe0.5O3, as marked with blue symbols in Fig. 4) by continuous redox cycling with a thermogravimetric analyzer (TGA). As all investigated perovskites are nonstoichiometric, Fig. S5† provides a detailed analysis of the oxygen nonstoichiometry, while we identify the discussed materials within the manuscript for simplicity with their stoichiometric compositions. In these studies perovskite reduction was at 1573 K and 1 bar of 10−4, 3.04 × 10−4, and 5.07 × 10−4 bar O2 in Ar, respectively, and perovskite oxidation was at 873, 1073, and 1273 K and 1 bar of 1% CO in CO2. To facilitate comparison with experiments that use O2 as oxidant, we note these oxidation conditions correspond to O2 partial pressures of 1.88 × 10−21, 3.79 × 10−15, and 7.75 × 10−11 bar O2, respectively, determined from the relation between the activities of CO2, CO, and O2.50 The results of the TGA measurements are shown with Fig. S2 and S3† and are utilized here to calculate the oxygen nonstoichiometries with: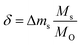 | (3) |
To assess the thermodynamics of the oxygen exchange, Fig. 6 shows the oxygen exchange capacity for reduction at 1573 K in 10−4 bar O2 and oxidation at 873 K in 1% CO in CO2 (equivalent to 1.88 × 10−21 bar O2), respectively. For comparison, Δδ of CeO2−δ, marked with a grey line, was calculated from Panlener et al.25 for oxidation at 1073 K in 3.79 × 10−15 bar O2 (equivalent to 1% CO in CO2) and reduction at 1773 K in 10−4 bar O2, which are typical conditions for thermochemical splitting of CO2 with CeO2−δ. The analysis shows that all perovskites, except YCo0.5Fe0.5O3, have a smaller Δδ than CeO2−δ (found here with Δδ = 0.07, which is comparable to the values reported by previous experimental investigations of ceria25). Furthermore, after perovskite oxidation, YCo0.5Fe0.5O3 does not fully reoxidize using 0.2 bar O2, (cf. Fig. S3 and S6†), which will result in smaller Δδ established in consecutive redox cycles. LaCo0.5Fe0.5O3, LaFe0.5Ni0.5O3, and LaCo0.5Ni0.5O3 show nominally negative Δδ, owing to their strong loss of O2 (that is, perovskite reduction) at oxidation conditions. The relatively large errors originate from drift corrections in the reduction and oxidation runs, from which the oxygen exchange capacities were calculated.
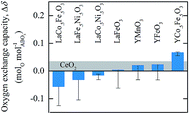 | ||
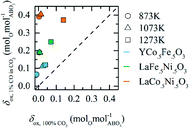
| Fig. 6 Experimentally measured oxygen exchange capacity, Δδ, of LaCo0.5Fe0.5O3, LaFe0.5Ni0.5O3, LaCo0.5Ni0.5O3, LaFeO3, YMnO3, YFeO3, and YCo.5Fe0.5O3 for oxide oxidation at 873 K in 1% CO in CO2 (pO2 = 1.88 × 10−21 bar) and oxide reduction at 1573 K in 10−4 bar O2. As a reference, the grey area marks Δδ for CeO2−δ, as calculated from Panlener et al.25 for oxidation at 1073 K in 3.79 × 10−15 bar O2 (corresponding to 1% CO in CO2) and reduction at 1773 K in 10−4 bar O2 (which are typical redox cycle conditions for ceria). Error bars are calculated as the sum of the experimental uncertainties for the oxidation and reduction runs, arising from minor mass changes of the samples at a stabilization temperature of 873 K and drift corrections. | ||
To demonstrate how crucial the choice of a reasonable set of redox conditions is, we oxidized YCo0.5Fe0.5O3, LaCo0.5Ni0.5O3, and LaFe0.5Ni0.5O3 at 873 K with 100% CO2, which corresponds to a pO2 (3.67 × 10−9 bar O2) that is by several orders of magnitude higher than that of 1% CO in CO2 at the same temperature (1.88 × 10−21 bar O2). To assess the sensitivity of the perovskites to these oxidation conditions, Fig. 7 shows the oxygen nonstoichiometry for perovskite oxidation, δox, measured in 1% CO in CO2 and plotted as a function of that measured in 100% CO2. Parity indicates materials that are insensitive to this difference in the oxidation potential of the gas composition. At all investigated temperatures, all investigated perovskites are located above parity, indicating a high sensitivity to the oxidation potential of the gas composition. This observation agrees well with the DFT-derived trends discussed above with Fig. 3. As a trend, we find perovskites with poor oxidation energetics are most sensitive to the presence of CO in the CO2 oxidant. That is, YCo0.5Fe0.5O3, LaCo0.5Ni0.5O3, and LaFe0.5Ni0.5O3 are (comparing the set of three perovskites) least, intermediately, and most sensitive to the presence of CO in CO2 (cf.Fig. 7), and show positive, negative, and most negative Δδ (cf.Fig. 6), which correlates well with the average electronegativity of the metals at their B-type interstitials, that is 1.86, 1.87, and 1.90, respectively. Analogously, CeO2−δ, with Ce having a much lower electronegativity of 1.12, exhibits redox energetics that are essentially insensitive to the presence of CO.6,25 For example, oxidation of CeO2−δ at 873 K in 100% CO2 and 1% CO in CO2 is reported with δox = 0.0001 and δox = 0.0006 molO molCeO2−1, respectively.25 Compared to this difference in δox within the same order of magnitude for CeO2−δ, we find an increase of δox for YCo0.5Fe0.5O3, LaCo0.5Ni0.5O3, and LaFe0.5Ni0.5O3 from −0.011, 0.004, and 0.003 molO molABO3−1 to 0.066, 0.190, and 0.392 molO molABO3−1 (for 873 K and 100% CO2vs. 1% CO in CO2), respectively. That is a difference in δox by two to three orders of magnitude.
This inferior oxidation performance of the perovskites in the presence of CO in the CO2 oxidant is a major downside, since the CO product is present in a solar receiver–reactor throughout the entire oxidation period at conditions relevant for industrial implementation.6 Alternatively, the oxidation performance of perovskites can be augmented by flooding the reactor with inert gas and/or excess CO2 to decrease CO concentrations, but this may be energetically costly, as it introduces additional energy penalties for gas separation and heat exchange.
3.2 Fine-tuning the oxygen exchange capacity
To evaluate the possibility to fine-tune the oxygen exchange capacity of perovskites, the following discusses the trends in the redox energetics with varying metal cation concentrations. The discussion above focused on perovskite compositions with A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A′ and B
A′ and B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B′ cation ratios equal to unity. To estimate trends in the oxygen exchange capacity of perovskites with metal cation ratios that differ from unity, Fig. 8a shows the volcano-type curve for three selected materials: YFeO3, YCo0.5Fe0.5O3, and YCoO3. The plot indicates oxidation-limited redox thermodynamics for YCo0.5Fe0.5O3 and YCoO3 (since both materials are located on the right side of the volcano) and reduction-limited redox thermodynamics for YFeO3 (located on the left side of the volcano). Thus, we hypothesize increasing the concentration of the Fe dopant in YCo0.5Fe0.5O3 stabilizes metal–oxygen bonds and, in turn, yields compositions located closer to the top of the volcano.
B′ cation ratios equal to unity. To estimate trends in the oxygen exchange capacity of perovskites with metal cation ratios that differ from unity, Fig. 8a shows the volcano-type curve for three selected materials: YFeO3, YCo0.5Fe0.5O3, and YCoO3. The plot indicates oxidation-limited redox thermodynamics for YCo0.5Fe0.5O3 and YCoO3 (since both materials are located on the right side of the volcano) and reduction-limited redox thermodynamics for YFeO3 (located on the left side of the volcano). Thus, we hypothesize increasing the concentration of the Fe dopant in YCo0.5Fe0.5O3 stabilizes metal–oxygen bonds and, in turn, yields compositions located closer to the top of the volcano.
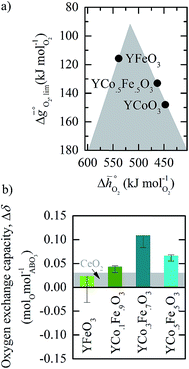 | ||
| Fig. 8 (a) Volcano-type curve for YFeO3, YCo0.5Fe0.5O3, and YCoO3. (b) Oxygen exchange capacity, Δδ, for YFeO3, YCo0.1Fe0.9O3, YCo0.3Fe0.7O3, and YCo0.5Fe0.5O3 for oxide oxidation at 873 K in 1% CO in CO2 at 873 K (pO2= 1.88 × 10−21 bar) and oxide reduction at 1573 K in 10−4 bar O2. As a reference, the grey area marks Δδ for CeO2−δ (equivalent to that shown with Fig. 6). Error bars are the sum of the experimental uncertainties for the oxidation and reduction runs. | ||
To evaluate this hypothesis, we performed TGA experiments for YFeO3, YCo0.1Fe0.9O3, YCo0.3Fe0.7O3, and YCo0.5Fe0.5O3 with reduction at 1573 K in 10−4 bar O2 and oxidation at 873 K in 1% CO in CO2 (1.88 × 10−21 bar O2). Fig. 8b shows the oxygen exchange capacities obtained for these materials. We find increasing the Fe concentration in YCo0.5Fe0.5O3 increases its oxygen exchange capacity from 0.07 molOmolABO3−1 for YCo0.5Fe0.5O3 to 0.11 molOmolABO3−1 for YCo0.3Fe0.7O3, which confirms our hypothesis. Further increasing the Fe concentration of YCo0.3Fe0.7O3 decrease Δδ, which we suggest indicates increasing energetic limitations arising from the unfavorable thermodynamic equilibrium of the perovskite reduction, analogous to that of YFeO3 (cf.Fig. 8a). This trend in the bonding strength of the lattice oxygen in metal-doped bulk perovskites is analogous to the trend in the adsorption energy of molecular fragments at bimetallic surfaces,51 which describes the similarity between the bonding of the gaseous reactant with varying coordination at the surface vs. in the bulk. Generally, these results demonstrate the utility of the presented electronic structure calculations to guide the rational design of perovskites. The presented methodology facilitates screening for redox-active materials at selected process conditions and fine-tuning of the oxygen exchange capacity for this highly versatile class of metal oxides for solar-driven thermochemical fuel synthesis.
3.3 Crystal phase stability and carbonate formation
This section validates the DFT-predicted trend that stronger endothermic perovskite reduction, that is, more positive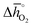 values, indicates increasing thermochemical stability of the perovskite against a phase change yielding binary metal oxides and against carbonate formation. These electronic structure calculations are discussed in detail in Section 2.2, with trends in the metal carbonate formation predicted only for perovskites with ABO3 stoichiometry. To this end, we evaluated the stability of selected perovskites using TGA, room-temperature X-ray diffraction (RT-XRD), high-temperature X-ray diffraction (HT-XRD), and transmission electron microscopy (TEM). The following discusses results that are representative for the investigated materials. The complete data is provided with ESI, including Fig. S9 and S10† showing HT-XRD spectra for SrTiO3, SrCoO3, SrMnO3, LaAlO3, BaCoO3 and BaMnO3 at 310, 675, 875, 1075, and 1275 K, in 100% CO2 (to assess carbonate formation) and in 0.2 bar O2 (to assess the stability of the cubic perovskite phase), respectively.
values, indicates increasing thermochemical stability of the perovskite against a phase change yielding binary metal oxides and against carbonate formation. These electronic structure calculations are discussed in detail in Section 2.2, with trends in the metal carbonate formation predicted only for perovskites with ABO3 stoichiometry. To this end, we evaluated the stability of selected perovskites using TGA, room-temperature X-ray diffraction (RT-XRD), high-temperature X-ray diffraction (HT-XRD), and transmission electron microscopy (TEM). The following discusses results that are representative for the investigated materials. The complete data is provided with ESI, including Fig. S9 and S10† showing HT-XRD spectra for SrTiO3, SrCoO3, SrMnO3, LaAlO3, BaCoO3 and BaMnO3 at 310, 675, 875, 1075, and 1275 K, in 100% CO2 (to assess carbonate formation) and in 0.2 bar O2 (to assess the stability of the cubic perovskite phase), respectively.
Regarding the thermochemical stability against decomposition of the cubic perovskite phase, the HT-XRD spectra, given with Fig. S9 and S10,† show segregation of SrCoO3 into lower-symmetry metal oxides. As expected, SrTiO3 remains stable, independent of temperature and pressure. This confirms the DFT-predicted stability trend, given that the lattice oxygen binds significantly stronger in SrTiO3 (with 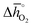 of about 760 kJ molO2−1) than in SrCoO3 (
of about 760 kJ molO2−1) than in SrCoO3 (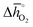 of 151 kJ molO2−1). Similarly, SrMnO3 (
of 151 kJ molO2−1). Similarly, SrMnO3 (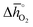 of 314 kJ molO2−1) and LaAlO3 (
of 314 kJ molO2−1) and LaAlO3 (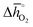 of 860 kJ molO2−1) are thermochemically stable, as they do not show phase changes upon heating in either 0.2 bar O2 or CO2, opposed to less stable BaCoO3 (
of 860 kJ molO2−1) are thermochemically stable, as they do not show phase changes upon heating in either 0.2 bar O2 or CO2, opposed to less stable BaCoO3 (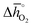 of 92 kJ molO2−1) and BaMnO3 (
of 92 kJ molO2−1) and BaMnO3 (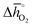 of 237 kJ molO2−1). The enthalpy change of BaMnO3 reduction is near 200 kJ molO2−1, which prohibits conclusive interpretation (cf. Section 2.2) within an uncertainty of this guide in the order of 10 kJ molO2−1, partly due to the approximate nature of the perovskite models (that may converge to the actual extend and distribution of oxygen nonstoichiometries at infinitely large size) and structural differences between the synthesized perovskites (such as those in crystal phase or surface morphology).
of 237 kJ molO2−1). The enthalpy change of BaMnO3 reduction is near 200 kJ molO2−1, which prohibits conclusive interpretation (cf. Section 2.2) within an uncertainty of this guide in the order of 10 kJ molO2−1, partly due to the approximate nature of the perovskite models (that may converge to the actual extend and distribution of oxygen nonstoichiometries at infinitely large size) and structural differences between the synthesized perovskites (such as those in crystal phase or surface morphology).
Regarding the thermochemical stability against metal carbonate formation, Fig. 9a shows the mass gain for BaCoO3, SrCoO3, BaMnO3, SrMnO3 and SrTiO3 exposed in a TGA to pure CO2 at 973, 873, and 773 K (cf. Fig. S9†). We assume this mass gain is solely due to carbonate formation, which is discussed critically further below. As a general trend, we find the extent of apparent carbonate formation increases with less endothermic 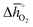 , as predicted. This can be seen in Fig. 9a, for instance by the relative weight changes for SrCoO3 (
, as predicted. This can be seen in Fig. 9a, for instance by the relative weight changes for SrCoO3 (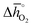 of 151 kJ
of 151 kJ ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) molO2−1), BaMnO3 (
molO2−1), BaMnO3 (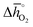 of 237 kJ
of 237 kJ ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) molO2−1) and SrTiO3 (
molO2−1) and SrTiO3 (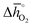 of 760 kJ
of 760 kJ ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) molO2−1) of +1.5, +0.15 and −0.047 wt%, respectively. SrCoO3 and BaCoO3 deviate from this trend, which may reflect differences in the crystal phase between the prepared samples (hexagonal BaCoO3vs. cubic SrCoO3, both shown with Fig. S12†) and the models (cubic perovskites), as well as differences in the oxygen nonstoichiometries between the prepared samples (possibly with δ > 0, as we reported previously for simpler compositions, such as BaCoO2.58 and SrCoO2.95)46 and the models (which assume at oxidizing conditions δ = 0).
molO2−1) of +1.5, +0.15 and −0.047 wt%, respectively. SrCoO3 and BaCoO3 deviate from this trend, which may reflect differences in the crystal phase between the prepared samples (hexagonal BaCoO3vs. cubic SrCoO3, both shown with Fig. S12†) and the models (cubic perovskites), as well as differences in the oxygen nonstoichiometries between the prepared samples (possibly with δ > 0, as we reported previously for simpler compositions, such as BaCoO2.58 and SrCoO2.95)46 and the models (which assume at oxidizing conditions δ = 0).
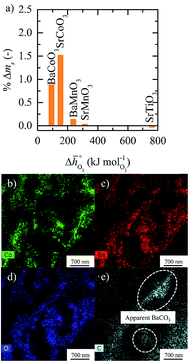 | ||
Fig. 9 (a) Percent mass change as a function of 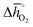 for BaCoO3, SrCoO3, BaMnO3, SrMnO3, and SrTiO3. (b–e) Drift-corrected elemental maps and their overlays for BaCoO3 obtained by TEM analysis. for BaCoO3, SrCoO3, BaMnO3, SrMnO3, and SrTiO3. (b–e) Drift-corrected elemental maps and their overlays for BaCoO3 obtained by TEM analysis. | ||
To obtain evidence for the assumption that the weight gain recorded in presence of CO2 is indeed due to metal carbonate formation, we analyzed selected samples using RT-XRD. This data is shown with Fig. S12,† which confirms formation of SrCO3 by SrCoO3 and of BaCO3 by BaCoO3. This is expected, in particular for these two perovskites that show the highest weight gains in the oxidation runs (cf.Fig. 9). To visualize and locate metal carbonate formation at the perovskite surface, TEM measurements are given with Fig. S13–S16.† As it can be concluded from the spatial distribution of the signals for carbon, oxygen, and the A-site metals, the analysis indicates formation of metal carbonates by SrCoO3 and BaCoO3, more so than by SrTiO3 and SrMnO3. This is shown with Fig. 9b–e, showing as an example the TEM data for BaCoO3. We conclude apparent formation of BaCO3 in surface regions with signals for Ba, C and O, but not for Co (as indicated in Fig. 9e). Equivalent regions we find for SrCoO3 (cf. Fig. S15†), but neither for SrTiO3 (cf. Fig. S14†) nor for SrMnO3 (cf. Fig. S16†), which is in agreement with the trend in the weight changes discussed above (cf.Fig. 9a).
4. Conclusions
We used density functional theory to screen a large range of perovskites for their redox activity and thermochemical stability for solar-driven thermochemical splitting of CO2. The computationally predicted trends are validated experimentally and employed for the fine-tuning of the oxygen exchange capacity of selected perovskite compositions. Our major findings are, firstly, perovskites with thermodynamically favorable redox energetics at reasonable process conditions can be identified with an enthalpy of metal oxide reduction at ambient conditions in the range of 440 to 630 kJ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) molO2−1. Secondly, ABO3-type perovskites containing divalent metal cations at the A-site exhibit a stable cubic crystal phase in an inert atmosphere and thermochemical stability against metal carbonate formation in presence of CO2, provided their enthalpy of metal oxide reduction is equal to or larger than 200 kJ
molO2−1. Secondly, ABO3-type perovskites containing divalent metal cations at the A-site exhibit a stable cubic crystal phase in an inert atmosphere and thermochemical stability against metal carbonate formation in presence of CO2, provided their enthalpy of metal oxide reduction is equal to or larger than 200 kJ ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) molO2−1. This descriptor-based guide for the rational design of perovskites is useful for predicting redox-activity of a perovskite at a selected set of process conditions, fine-tuning of the oxygen exchange capacity via metal cation doping, and for assessing the thermochemical stability of the perovskite phase in an inert or CO2 atmosphere. These properties of this class of highly versatile metal oxides is particularly important for designing redox materials for thermochemical fuel synthesis, but as well central to related high-temperature applications, such as carbonate-free solid oxide fuel cells.
molO2−1. This descriptor-based guide for the rational design of perovskites is useful for predicting redox-activity of a perovskite at a selected set of process conditions, fine-tuning of the oxygen exchange capacity via metal cation doping, and for assessing the thermochemical stability of the perovskite phase in an inert or CO2 atmosphere. These properties of this class of highly versatile metal oxides is particularly important for designing redox materials for thermochemical fuel synthesis, but as well central to related high-temperature applications, such as carbonate-free solid oxide fuel cells.
Furthermore, we demonstrated the importance of choosing an appropriate set of redox cycle conditions for the screening of perovskite redox materials, as this class of materials with typically oxidation-limited redox energetics exhibits a significantly higher sensitivity to the composition of the oxidant, very different to the reduction-limited redox energetics of nonstoichiometric ceria. In this regard, we conclude perovskites do not outperform nonstoichiometric ceria for solar-driven thermochemical fuel synthesis applications at the high-temperature swing conditions used most beneficially with ceria. However, certain perovskites are found redox-active at lower oxide reduction temperatures, offering an option to alleviate thermal and mechanical stress in solar receiver–reactors and to diminish volatilization of solids. This, however, comes at the costs of additional energy penalties for providing low O2 partial pressures and/or excess oxidant.
5. Experimental section
5.1 Electronic structure calculations
All DFT calculations were performed using the Grid-based projector-augmented wave (GPAW) code.52,53 Atomic configurations were handled in the atomic simulation environment (ASE),54 with exchange–correlation interactions treated by the revised Perdew–Burke–Ernzerhof (RPBE) functional.55 The atomic geometries were optimized employing the line search Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm until the maximum force was less than 0.05 eV Å−1. Convergence was achieved using a Fermi–Dirac smearing of 0.1 eV. The results were extrapolated to 0 K. Analogous to previous studies,33,42,46,56–58 all DFT calculations reported here use the generalized gradient approximation (GGA) without a Hubbard U correction, as previous studies demonstrated that this does not improve the description of surface activity with the employed perovskite models.42 AA′BB′O3 perovskites were modeled with A2B2O6 models containing two cubic ABO3 unit cells with the same or two different metals (Mg, Ca, Sr, Ba, Y, La or Ce) at the twelve-fold coordinated A-site interstices, and the same or two different metals (Ti, Cr, Mn, Fe, Co, Ni, Cu, Zr or Al) at the six-fold coordinated B-site interstices. All atoms of the bulk models were allowed to optimize their positions (relax). In total, 297 compositions were modeled, with either ABO3- (63 compositions), AA′BO3- (77 compositions), ABB′O3- (67 compositions), or AA′BB′O3-type stoichiometry (90 compositions). The Brillouin zone of the bulk models with periodic boundary conditions in all directions was sampled with 4 × 4 × 4 k-points. Compositions containing Mn, Fe, Co, or Ni were modeled using spin-polarized calculations. The DFT-computed lattice constants are found within 0.07 to 2.17% of the experimental values. The minimum and maximum values of the computed lattice constants of the ABO3, AA′BO3, ABB′O3 and AA′BB′O3 perovskites are given along with the related magnetic moments with ESI.†Perovskite surfaces were modeled using the (010) facet with AO-termination, which is geometrically symmetric with the (001) and (100) facet, dependent on composition, based on previous work suggesting that this is the thermodynamically most stable surface.42 The surface models contained the same number of atoms as the bulk models, that is with A2B2O6 stoichiometry, of which the upper ABO3(010) layer parallel to the surface was allowed to relax, while the lower ABO3 layer was constrained to the bulk geometry. All surface models were periodically repeated in the directions parallel to the surface, used 10 Å of vacuum perpendicular to the surface, and employed a k-point sampling of 4 × 4 × 1. To model reduced perovskite surfaces, one third of the stoichiometric lattice oxygen in the upper surface layer was removed yielding A2B2O5(010) stoichiometry with δ = 0.5.
The Gibbs free energy of oxygen vacancy formation (ΔGv[O]) was computed with:42
| ΔGv[O] = Gv − (Gs − GrO) | (4) |
We employ the standard enthalpy of bulk metal oxide decomposition into the metals and O2, computed at 298 K and 1 bar total pressure (Δ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) °), as a descriptor of redox-activity. For a limited number of mostly stoichiometric binary metal oxides, Δ
°), as a descriptor of redox-activity. For a limited number of mostly stoichiometric binary metal oxides, Δ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) ° can be computed from tabulated thermochemical data.59 To estimate Δ
° can be computed from tabulated thermochemical data.59 To estimate Δ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) ° for the investigated perovskites without the need for resource-demanding phonon calculations to determine solid-state entropies, we utilized previously established scaling relations describing the correction between Δ
° for the investigated perovskites without the need for resource-demanding phonon calculations to determine solid-state entropies, we utilized previously established scaling relations describing the correction between Δ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) ° and ΔGv[O].42 As discussed in detail with ESI,† we employed:
° and ΔGv[O].42 As discussed in detail with ESI,† we employed:
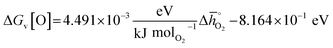 | (5) |
Thermodynamic properties obtained using eqn (5) are per mole O2. Detailed descriptions of converting the DFT-derived ΔGv[O] values into Gibbs free energy changes at a specific set of reaction temperature and pO2, and of the utilized reference energies are provided with ESI.†
5.2 Sample preparation
All perovskites were synthesized with a modified Pechini method, using stoichiometric amounts of La(NO3)3·H2O (Sigma Aldrich, 99.999%), Sr(NO3)2 (Sigma Aldrich, 98%), Mn(NO3)2·4H2O (Alfa Aesar, 98%), Al(NO3)3·9H2O (Alfa Aesar, 98%), Ca(NO3)2·4H2O (Alfa Aesar, 99%), Y(NO3)3·6H2O (Alfa Aesar, 99.9%), Co(NO3)2·6H2O (Sigma Aldrich, 98%), Ni(NO3)2·6H2O (Sigma Aldrich, 97%), C2H6O (Alcosuisse, >96.1% vol) and C6H8O7 (Fluka Chemika, ≥99.5%). The ratio between the metal cations and citric acid was 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3. SrTiO3 (99%) was purchased from Sigma-Aldrich. Solid products were ground using mortar and pestle and sintered for 24 h in air at 1573 K with heating and cooling at 2.5 K min−1.
3. SrTiO3 (99%) was purchased from Sigma-Aldrich. Solid products were ground using mortar and pestle and sintered for 24 h in air at 1573 K with heating and cooling at 2.5 K min−1.
5.3 Solid-state analysis
RT-XRD and HT-XRD were performed in the Bragg Brentano geometry using Cu Kα radiation (20–80° 2θ, 0.01° min−1 scan rate, 45 kV/20 mA output, PANalytical/X'Pert MPD/DY636, Philips). The HT-XRD experiments were performed at 673, 873, 1073, and 1273 K, with heating at 10 K min−1 and a gas flow of 1 L min−1. All volumes are given at standard conditions, here 1 bar and 20 °C. Before each HT-XRD scan, the temperature was held for one hour to establish thermodynamic equilibrium. TEM analyses were performed for SrTiO3, SrCoO3, SrMnO3, and BaCoO3 employing the high angle annular dark field detector used in scanning transmission electron microscopy (HAADF STEM) imaging mode and complemented by elemental distribution analyses using the SuperX EDX system of a FEI TalosF200X instrument, operated at 200 kV acceleration voltage. The surfaces of SrTiO3, BaCoO3, SrMnO3, and SrCoO3 were sampled at 17, 8, 9, and 9 different locations, respectively.5.4 Thermal analysis
Perovskite reduction and oxidation were performed using a TGA (Setaram Setsys Evolution) to measure oxygen nonstoichiometries (δ). Samples with a mass of about 100 mg were finely ground and placed into an Al2O3 crucible which was covered with a platinum sheet. Heating and cooling were at 10 and 20 K min−1, respectively. Reduction was carried out at 1573 K and used a gas flow of 175 mL min−1 with a pO2 of 10−4, 3.04 × 10−4, and 5.07 × 10−4 bar O2, adjusted using a mixture of 500 ppm O2 in Ar and pure Ar. Reduction conditions were held for 60 min. Oxidation was carried out at 873, 1073, and 1273 K and used a gas flow of 192 mL min−1 with a pO2 of 1.88 × 10−21, 3.79 × 10−15, and 7.75 × 10−11 bar, respectively. These pO2 values correspond to 1% CO in CO2, simulating a typical gas composition at the end of the oxidation run in a solar receiver–reactor.6 To assess the sensitivity of the perovskites to the gas composition during oxidation, oxidation was carried out also in pure CO2 and 873, 1073, and 1273 K, corresponding to a pO2 of 3.67 × 10−9, 4.63 × 10−7, and 1.27 × 10−5 bar O2. Oxidation conditions were held for 80 min. For complete re-oxidation before and after each reduction and oxidation experiment, the samples were exposed for 30 min at 873 K to a gas flow of 175 mL min−1 with 0.2 bar O2. The gas composition at the TGA outlet was monitored with a gas chromatograph (GC, CP-4900 System, Agilent Technologies). To account for buoyancy effects, blank runs were conducted for all specific measurement conditions without the perovskite samples.Acknowledgements
We gratefully acknowledge the financial support by the Swiss National Science Foundation (Ambizione Energy Grant No. 166883), the Helmholtz-Gemeinschaft Deutscher Forschungszentren (Virtuelles Institut SolarSyngas), and the European Research Council under the European Union's ERC Advanced Grant (SUNFUELS-No. 320541). The DFT calculations were performed at the High-Performance Computation cluster of ETH Zürich.References
- M. Romero and A. Steinfeld, Energy Environ. Sci., 2012, 5, 9234 CAS.
- W. C. Chueh and S. M. Haile, Chemsuschem, 2009, 2, 735 CrossRef CAS PubMed.
- W. C. Chueh and S. M. Haile, Philos. Trans. R. Soc., A, 2010, 368, 3269 CrossRef CAS PubMed.
- E. A. Fletcher, J. Sol. Energy Eng., 2001, 123, 63 CrossRef CAS.
- J. R. Scheffe and A. Steinfeld, Mater. Today, 2014, 17, 341–348 CrossRef CAS.
- D. Marxer, P. Furler, J. Scheffe, H. Geerlings, C. Falter, V. Batteiger, A. Sizmann and A. Steinfeld, Energy Fuels, 2015, 29, 3241 CrossRef CAS.
- T. Nakamura, Sol. Energy, 1977, 19, 467 CrossRef CAS.
- T. Kodama, Prog. Energy Combust. Sci., 2003, 29, 567 CrossRef CAS.
- M. Roeb, M. Neises, N. Monnerie, F. Call, H. Simon, C. Sattler, M. Schmucker and R. Pitz-Paal, Materials, 2012, 5, 2015 CrossRef CAS.
- G. P. Smestad and A. Steinfeld, Ind. Eng. Chem. Res., 2012, 51, 11828 CrossRef CAS.
- Z. Wang, R. R. Roberts, G. F. Naterer and K. S. Gabriel, Int. J. Hydrogen Energy, 2012, 37, 16287 CrossRef CAS.
- W. C. Chueh, A. H. McDaniel, M. E. Grass, Y. Hao, N. Jabeen, Z. Liu, S. M. Haile, K. F. McCarty, H. Bluhm and F. El Gabaly, Chem. Mater., 2012, 24, 1876 CrossRef CAS.
- S. Ackermann, J. R. Scheffe and A. Steinfeld, J. Phys. Chem. C, 2014, 118, 5216 CAS.
- S. Abanades, A. Legal, A. Cordier, G. Peraudeau, G. Flamant and A. Julbe, J. Mater. Sci., 2010, 45, 4163 CrossRef CAS.
- A. Le Gal, S. Abanades and G. Flamant, Energy Fuels, 2011, 25, 4836 CrossRef CAS.
- P. Singh and M. S. Hegde, Chem. Mater., 2010, 22, 762 CrossRef CAS.
- H. Kaneko, T. Miura, H. Ishihara, S. Taku, T. Yokoyama, H. Nakajima and Y. Tamaura, Energy, 2007, 32, 656 CrossRef CAS.
- Q. L. Meng, C. I. Lee, T. Ishihara, H. Kaneko and Y. Tamaura, Int. J. Hydrogen Energy, 2011, 36, 13435 CrossRef CAS.
- S. G. Huang, L. Li, J. Vleugels, P. L. Wang and O. Van der Biest, J. Eur. Ceram. Soc., 2003, 23, 99 CrossRef CAS.
- K. Otsuka, M. Hatano and A. Morikawa, Inorg. Chim. Acta, 1985, 109, 193 CrossRef CAS.
- S. Abanades, P. Charvin, G. Flamant and P. Neveu, Energy, 2006, 31, 2805 CrossRef CAS.
- P. Furler, J. Scheffe, M. Gorbar, L. Moes, U. Vogt and A. Steinfeld, Energy Fuels, 2012, 26, 7051 CrossRef CAS.
- W. C. Chueh, C. Falter, M. Abbott, D. Scipio, P. Furler, S. M. Haile and A. Steinfeld, Science, 2010, 330, 1797 CrossRef CAS PubMed.
- A. H. McDaniel, E. C. Miller, D. Arifin, A. Ambrosini, E. N. Coker, R. O'Hayre, W. C. Chueh and J. H. Tong, Energy Environ. Sci., 2013, 6, 2424 CAS.
- R. J. Panlener, R. N. Blumenthal and J. E. Garnier, J. Phys. Chem. Solids, 1975, 36, 1213 CrossRef CAS.
- C. K. Yang, Y. Yamazaki, A. Aydin and S. M. Haile, J. Mater. Chem. A, 2014, 2, 13612 CAS.
- J. R. Scheffe, D. Weibel and A. Steinfeld, Energy Fuels, 2013, 27, 4250 CrossRef CAS.
- A. Demont, S. Abanades and E. Beche, J. Phys. Chem. C, 2014, 118, 12682 CAS.
- S. Dey, B. S. Naidu, A. Govindaraj and C. N. R. Rao, Phys. Chem. Chem. Phys., 2015, 17, 122 RSC.
- A. Demont and S. Abanades, RSC Adv., 2014, 4, 54885 RSC.
- T. Cooper, J. R. Scheffe, M. E. Galvez, R. Jacot, G. Patzke and A. Steinfeld, Energy Technol., 2015, 3, 1130 CrossRef CAS.
- M. Takacs, M. Hoes, M. Caduff, T. Cooper, J. R. Scheffe and A. Steinfeld, Acta Mater., 2016, 700 CrossRef CAS.
- M. Ezbiri, M. Takacs, D. Theiler, R. Michalsky and A. Steinfeld, J. Mater. Chem. A, 2017, 5, 4172–4182 CAS.
- L. Nalbandian, A. Evdou and V. Zaspalis, Int. J. Hydrogen Energy, 2009, 34, 7162 CrossRef CAS.
- A. Demont and S. Abanades, J. Mater. Chem. A, 2015, 3, 3536 CAS.
- A. H. Bork, M. Kubicek, M. Struzik and J. L. M. Rupp, J. Mater. Chem. A, 2015, 3, 15546 CAS.
- S. Dey, B. S. Naidu and C. N. R. Rao, Chem.–Eur. J., 2015, 21, 7077 CrossRef CAS PubMed.
- P. M. Geffroy, J. Fouletier, N. Richet and T. Chartier, Chem. Eng. Sci., 2013, 87, 408 CrossRef CAS.
- A. A. Emery, J. E. Saal, S. Kirklin, V. I. Hegde and C. Wolverton, Chem. Mater., 2016, 28, 5621 CrossRef CAS.
- A. M. Deml, A. M. Holder, R. P. O'Hayre, C. B. Musgrave and V. Steyanovic, J. Phys. Chem. Lett., 2015, 6, 1948 CrossRef CAS PubMed.
- A. M. Deml, V. Stevanovic, C. L. Muhich, C. B. Musgrave and R. O'Hayre, Energy Environ. Sci., 2014, 7, 1996 CAS.
- R. Michalsky, V. Botu, C. M. Hargus, A. A. Peterson and A. Steinfeld, Adv. Energy Mater., 2014, 4, 1401082 Search PubMed.
- F. Calle-Vallejo, J. I. Martinez, J. M. Garcia-Lastra, M. Mogensen and J. Rossmeisl, Angew. Chem., 2010, 49, 7699 CrossRef CAS PubMed.
- B. Meredig and C. Wolverton, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 245119 CrossRef.
- M. T. Curnan and J. R. Kitchin, J. Phys. Chem. C, 2014, 118, 28776–28790 CAS.
- M. Ezbiri, K. M. Allen, M. E. Gàlvez, R. Michalsky and A. Steinfeld, Chemsuschem, 2015, 8, 1966 CrossRef CAS PubMed.
- M. Ghiasi, A. Malekzadeh and Y. Mortazavi, “Effect of the cation of site A on the formation of (Ce, La or Sr)CoO3 nano-perovskites”, presented at Proceedings of the 4th International Conference on Nanostructures (ICNS4), 2012 Search PubMed.
- K. Umemoto, Y. Seto and Y. Masuda, Thermochim. Acta, 2005, 431, 117 CrossRef CAS.
- M. Takacs, J. R. Scheffe and A. Steinfeld, Phys. Chem. Chem. Phys., 2015, 17, 7813 RSC.
- HSC Chemistry 5.0, Outokumpu Research Oy, 2002 Search PubMed.
- C. J. H. Jacobsen, S. Dahl, B. S. Clausen, S. Bahn, A. Logadottir and J. K. Norskov, J. Am. Chem. Soc., 2001, 123, 8404 CrossRef CAS PubMed.
- J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dulak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola, H. A. Hansen, H. H. Kristoffersen, M. Kuisma, A. H. Larsen, L. Lehtovaara, M. Ljungberg, O. Lopez-Acevedo, P. G. Moses, J. Ojanen, T. Olsen, V. Petzold, N. A. Romero, J. Stausholm-Moller, M. Strange, G. A. Tritsaris, M. Vanin, M. Walter, B. Hammer, H. Hakkinen, G. K. H. Madsen, R. M. Nieminen, J. Nørskov, M. Puska, T. T. Rantala, J. Schiotz, K. S. Thygesen and K. W. Jacobsen, J. Phys.: Condens. Matter, 2010, 22, 253202 CrossRef CAS PubMed.
- J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035109 CrossRef.
- S. R. Bahn and K. W. Jacobsen, Comput. Sci. Eng., 2002, 4, 56 CrossRef CAS.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413 CrossRef.
- A. J. Medford, J. Wellendorff, A. Vojvodic, F. Studt, F. Abild-Pedersen, K. W. Jacobsen, T. Bligaard and J. K. Norskov, Science, 2014, 345, 197 CrossRef CAS PubMed.
- M. García-Mota, A. Vojvodic, H. Metiu, I. C. Man, H. Y. Su, J. Rossmeisl and J. K. Nørskov, ChemCatChem, 2011, 3, 1607 CrossRef.
- R. Michalsky, D. Neuhaus and A. Steinfeld, Energy Technol., 2015, 3, 784 CrossRef CAS.
- I. Barin, Thermochemical Data of Pure Substances, 1993 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ta02081c |
| This journal is © The Royal Society of Chemistry 2017 |