Effective potentials induced by self-assembly of patchy particles
Abstract
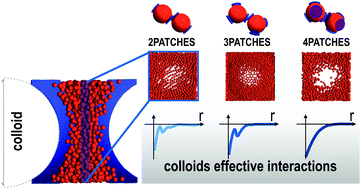
Effective colloid–colloid interactions can be tailored through the addition of a complex cosolute. Here we investigate the case of a cosolute made by self-assembling patchy particles. Depending on the valence, these particles can form either polymer chains or branched structures. We numerically calculate the effective potential Veff between two colloids immersed in a suspension of reversible patchy particles, exploring a wide region of the cosolute phase diagram and the role of valence. In addition to well-known excluded volume and depletion effects, we find that, under appropriate conditions, Veff is completely attractive but shows an oscillatory character. In the case of polymerizing cosolute, this results from the fact that chains are efficiently confined by the colloids through the onset of local order. This argument is then generalized to the case of particles with higher valence, under the condition that they are still able to maintain a fully bonded organization upon confinement. The resulting effective potentials are relevant for understanding the behavior of complex mixtures in crowded environments, but may also be exploited for tuning colloidal self-assembly at preferred target distances in order to build desired superstructures.
- This article is part of the themed collection: Celebrating Excellence in Research: 100 Women of Chemistry


 Please wait while we load your content...
Please wait while we load your content...