DOI:
10.1039/C7SM00616K
(Paper)
Soft Matter, 2017,
13, 6988-7000
Application of the Eckart frame to soft matter: rotation of star polymers under shear flow
Received
27th March 2017
, Accepted 30th August 2017
First published on 5th September 2017
Abstract
The Eckart co-rotating frame is used to analyze the dynamics of star polymers under shear flow, either in melt or solution and with different types of bonds. This formalism is compared with the standard approach used in many previous studies on polymer dynamics, where an apparent angular velocity ω is obtained from the relation between the tensor of inertia and angular momentum. A common mistake is to interpret ω as the molecular rotation frequency, which is only valid for rigid-body rotation. The Eckart frame, originally formulated to analyze the infrared spectra of small molecules, dissects different kinds of displacements: vibrations without angular momentum, pure rotation, and vibrational angular momentum (leading to a Coriolis cross-term). The Eckart frame co-rotates with the molecule with an angular frequency Ω obtained from the Eckart condition for minimal coupling between rotation and vibration. The standard and Eckart approaches are compared with a straight description of the star's dynamics taken from the time autocorrelation of the monomer positions moving around the molecule's center of mass. This is an underdamped oscillatory signal, which can be described by a rotation frequency ωR and a decorrelation rate Γ. We consistently find that Ω coincides with ωR, which determines the characteristic tank-treading rotation of the star. By contrast, the apparent angular velocity ω < Ω does not discern between pure rotation and molecular vibrations. We believe that the Eckart frame will be useful to unveil the dynamics of semiflexible molecules where rotation and deformations are entangled, including tumbling, tank-treading motions and breathing modes.
1 Introduction
Soft matter and, in particular, polymers exhibit quite rich dynamics under non-equilibrium conditions. A plethora of collective motions has been described in the literature, not only of polymers, but also of vesicles and more. In a shear flow, a steady state conformation is not possible, and linear polymers perform wild conformational changes, stretching and tumbling.1–6 Star molecules, dendrimers and also vesicles face the shear flow in a different way. They perform internal rotations around the molecule’s center of mass (CoM), while keeping their overall shape and orientation roughly fixed. This motion has been called tank-treading.6–12 The case of ring polymers, whose properties have recently been extensively studied,6,13–15 is probably in between and recent works have indicated that they tumble or tank-tread depending on the value of the shear rate.16–18 Recently, we have observed that star molecules under large enough shear flow perform another collective oscillation, with successive extensions and contractions in their overall length. We called this mode “breathing”19 and showed that its characteristic frequency ΩB has the same physical origin as the tumbling frequency in linear and ring chains, the difference being that soft stars do not tumble, but rather let their arms rotate. A similar breathing mode (probably with a different mechanical origin) is also observed in vesicles.7–9 It could, however, well be that star molecules with attractive inter-monomer interactions (i.e. in bad solvent) would not only tank-tread, but also occasionally tumble (a rotation of the overall molecular shape) like a rugby ball does. One could speculate that the stiffer the intermonomer interactions, the larger the resemblance with a rigid body would be, with some dynamic transition (tank-tread-to-tumble) taking place at moderate attractive energies. Would still those semi-rigid stars breath? These sort of questions on the mechanics of soft deformable macromolecules are difficult to study in clean ways. The reason is clear: at a given time, in the laboratory (inertial) frame, it is not possible to discern between pure rotations and vibrations of the molecule. The simple shear flow is a paradigm of such duality because it is a mix of pure rotation and pure shear strain (stretching in one direction and compressing over the perpendicular line). Hybrid affine deformations combining shear and pure elongational flows have also been studied,20 enriching the dynamic panorama. The complications of using the laboratory frame to study the rotation of non-rigid molecules have been overlooked in many previous works on polymer dynamics. In particular, a simple estimation of the molecular angular velocity ω based on the polymer shape was first proposed in ref. 21. Such a relation stems from the rotation dynamics in the laboratory frame, where the angular velocity ω is related to the total angular momentum L and inertia tensor J as L = J·ω. A particularly simple estimation of ω involving the gyration tensor components was proposed as a rotational-optic rule.10,21 Since many works have reported values of ω and used it to interpret the polymer rotational dynamics, this has led to erroneous interpretations which are still very much alive in the literature.10,11,22–25
We have recently completed a series of works on star polymer dynamics.19,26,27 This series started by a study of the effect of open boundaries compared with closed systems in the rheology of melts under shear (simulations using Open Boundary Molecular Dynamics (OBMD)26–28 permit fixing the pressure load and shear stress, instead of the density and shear velocity). As a continuation of such work, we studied the dynamics of stars in solution and melt19 and observed that the tank-treading frequency of monomers around the molecule's CoM, ωR, was completely different from the “apparent” angular velocity obtained from the standard (lab-frame) analysis, ω. We also noted that the origin of such strong differences was not explained in previous works. Motivated by these observations, we decided to tackle the problem of soft molecule rotational dynamics using an old and robust formalism, which apparently has been largely forgotten by the soft matter community: the Eckart co-rotating frame.
The Eckart frame formalism, derived in 1935,29 uses a non-inertial frame, which rotates with the molecule. It allows disentangling translation, rotations, and vibrations. Aside from vibrations without angular momentum contribution (which can be detected in the inertial frame), the non-inertial frame allows revealing vibrations with angular momentum. These are the displacements with respect to a purely rotating (rigid-body) reference configuration. The Eckart condition determines the rotation frequency of the reference configuration by minimizing the coupling between vibrational angular momentum and pure rotation.30 The calculus of the so called “Eckart angular velocity” Ω can be carried out by the Eckart frame formalism and has been mostly used to study the infrared and Raman spectra of small molecules31,32 as well as in a variety of other applications, such as structural isomerization dynamics of atomic clusters33 or molecular dynamics (MD) integration.34–37 The “apparent” angular velocity ω extracted from the total angular momentum in the inertial frame mixes up pure rotation and vibrational angular momentum. A misinterpretation of this apparent angular velocity had, as a consequence, some large discrepancies in the polymer literature on shear flow.11,16
While the Eckart formalism is traditionally used in equilibrium states, here we use it to describe a situation which is far away from equilibrium. Although the Eckart condition is first-order accurate, we show that it is robust enough to capture the correct physics. In particular, we show that the Eckart frame is independent of the reference configuration chosen (see Appendix) and that, for any shear rate, the resulting frequency Ω equals within error bars the monomer rotation frequency about the molecule’s CoM, ωR. Star polymers are particularly interesting for this sort of study because of their rich dynamics in shear flow (with tank-treading and breathing modes19) and also because they represent a bridge between the physics of polymers and colloids.38–40 More generally, we expect this work will foster the use of the Eckart frame as another useful tool in the analyses of flowing macromolecules' dynamics.
The rest of the paper is structured as follows: first, we describe the standard (laboratory frame) analysis and the Eckart frame. Then, we describe our working models (star polymer in melt and solution under shear flow). Results and discussion are then presented, followed by Conclusions.
2 Dynamics description in the laboratory frame
A standard approach to describe the rotation of molecules is based on the inertial frame (laboratory frame) and follows from a straight generalization of the rigid body rotation, allowing for vibrations without angular momentum contribution ṽ. The kinetic equation for the time evolution of the position of the α monomer rα is,| | | ṙα = ṙcm + ω × (rα − rcm) + ṽα. | (1) |
In the standard (lab frame) description, the vibrational motion is angular momentum free, and it is denoted by ṽα. It is particularly strong in soft molecules such as polymers. The corresponding angular frequency is then10,11,25Here, 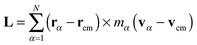 is the angular momentum of the rotating molecule and J its moment-of-inertia tensor with respect to the position of its CoM rcm, defined as
is the angular momentum of the rotating molecule and J its moment-of-inertia tensor with respect to the position of its CoM rcm, defined as| | 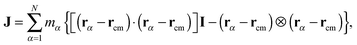 | (3) |
with I being a 3 × 3 identity matrix, rα the coordinate vector of monomer α of the molecule, and mα its mass (here mα = 1).
A common mistake is to interpret ω as the molecular angular velocity. However, ω does not describe the pure rotational component of the molecule and in fact, it is called the apparent angular velocity in the literature dealing with the Eckart formalism.32 Only in the case of rigid-body motion (ṽ = 0) does ω coincide with the rotational angular velocity. The reason will become clear in the next section.
3 Description using the co-rotating Eckart frame
The Eckart formalism permits dissecting yet another kind of vibration u, which contributes to the total angular momentum, but does not contribute to the molecular rotation frequency. The Eckart frame is a non-inertial frame, which co-rotates with the molecule attached to its CoM. The pure rotation frequency Ω is obtained by minimizing the coupling between pure rotation and this vibrational angular momentum: the Coriolis coupling is minimal in this internal moving frame.29–31
The first step of the Eckart frame formalism is to choose some rigid molecular configuration, which is taken as the reference one.31 The Eckart frequency and kinetic energy are, however, independent of the rigid reference configuration chosen. This fact is illustrated in the Appendix, where we compare three different reference configurations. Once the reference configuration is chosen, we introduce the initial internal coordinate system, defined by the three right-handed base vectors f1, f2, and f3 with the origin in the CoM of the molecule. The initial internal coordinate frame (f1, f2, f3) can be chosen arbitrarily, i.e. its initial orientation is arbitrary. The components of the position vector of the α-th monomer of the reference configuration expressed in the initial internal coordinate system are denoted as cαi, i = 1, 2, 3. Once defined, the cαis remain constant during the computation of the angular velocity and fulfill the equation:29,31
| | 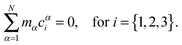 | (4) |
The CoM velocity in the defined internal coordinate frame is 0.
29,31 From the instantaneous positions of the monomers in the polymer and with the
cαis, we define the three Eckart vectors
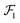
,
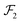
, and
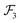
, which are given by:
29,31| | 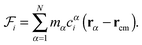 | (5) |
From the Eckart vectors, we define a symmetric positive definite Gram matrix
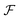
with the
ij-component defined as
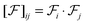
. The unit base vectors of the instantaneous Eckart frame (defined by the instantaneous positions of monomers) are computed as:
29,31| | 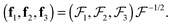 | (6) |
Here,
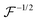
represents a positively defined matrix, for which the following relation holds:
| | 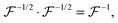 | (7) |
where
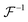
is a positively defined inverse of the Gram matrix
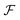
.
The reference components cαis are in the instantaneous Eckart frame given as:
| | 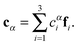 | (8) |
This means that the dynamics of the reference configuration is governed by the time evolution of the positions of the monomers. As mentioned above, the
cαis are in general constant and the reference configuration is rigid. Besides, as will be shown below, there is no angular momentum with respect to the internal coordinate system in the zero-th order of displacement of monomers from their reference positions.
30 Consequently, the dynamics of the reference configuration is nothing but the overall rotation of the molecule, which is described by the angular velocity
Ω.
The rotation of the polymer is defined by the rotation of the base vectors of the Eckart frame:
The combination of
eqn (8) and (9) yields the following relation:
32
It must be emphasized that there are different ways to attach the initial internal coordinate system to the reference configuration. Each of these yields different
cαis and a different Eckart frame. Nevertheless, once the initial internal coordinate system is chosen, the Eckart frame is defined in a unique way.
34 The independence on the choice of the fixed reference configuration is illustrated in the Appendix, where we report results for three completely different reference configurations: (i) a fixed configuration taken from a frozen
T = 0 state; (ii) a fixed configuration adapted to the average molecular shape found at each shear rate
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)
and (iii) a mobile configuration which adapts over time to the average molecular conformation upon a pre-determined “averaging” time
τw. We find that the two fixed configurations give the same Eckart rotation frequency
Ω while the third one consistently converges to the outcome of the fixed references for
τw → ∞ while for
τw → 0, it provides the apparent frequency
ω obtained from the standard approach.
The reference positions of every monomer in the laboratory frame are computed as:
and their instantaneous displacement vectors are defined as
The unit base vectors of the Eckart frame
f1,
f2, and
f3 satisfy the Eckart conditions
29,31| | 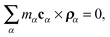 | (13) |
which state that there is no angular momentum with respect to the internal coordinate system in the zero-th order of displacements of the monomers from their equilibrium positions.
30 The sketch of the Eckart frame for a star polymer is depicted in
Fig. 1.
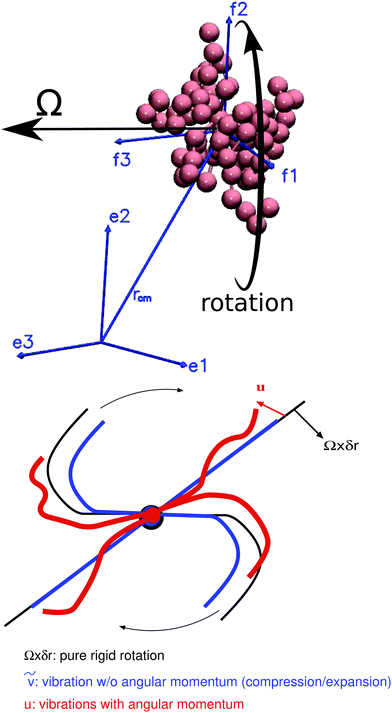 |
| | Fig. 1 (top) A sketch of internal and laboratory frames. The unit base vectors f1, f2, and f3 span the internal coordinate system, i.e. the Eckart frame, which translates and rotates together with the molecule. The laboratory frame's base vectors are e1, e2, and e3. The arrows indicate the rotation of the molecule. (bottom) The sketch gradually introduces the different types of displacements resolved by the Eckart formalism. The black line corresponds to pure rigid rotation (monomer velocity Ω × δr) which does not introduce molecular deformation. The blue line (velocity ṽ) introduces vibrations without angular momentum contribution (e.g. compression and expansion) and the red line introduces vibrations with angular momentum (fluctuations with velocity u) which deform the molecule's shape (e.g. due to Brownian diffusion). Note that u·Ω × δr < 0 (Coriolis term). The different velocities are explained in the text (see e.g.eqn (16) and (17)). | |
The angular velocity of the Eckart's coordinate system is given by:
| | 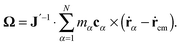 | (14) |
The tensor
J′ is defined as
| | 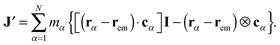 | (15) |
In the limit of a rigid molecule,
eqn (15) becomes
eqn (3) and both definitions of angular velocity (given by
eqn (2) and (14)) are equivalent.
The velocity of a given monomer α can be written as:30,34
| | | ṙα = ṙcm + Ω × (rα − rcm) + Δvα. | (16) |
The first term on the right hand side of
eqn (16) represents the velocity of the molecule's CoM, the second term is the contribution due to the rotation of the molecule, and the third one,
i.e. Δ
vα, is due to molecular vibrations. The latter can be expressed as:
32where
uα represents the angular motion part and
ṽα (the same as in
eqn (1)) the angular motion free part of the vibrational motion. Comparing the expressions in
eqn (1) and (16), one derives the following equation:
32
| | |
u
α
= (ω − Ω) × δrα,
| (18) |
with δ
rα ≡
rα −
rcm. This means that
uα is the part of
α-th monomer's vibrational motion, which is coupled with rotations if the angular velocity is calculated by the standard approach. It can be decoupled from rotations by using the Eckart frame formalism.
According to, eqn (1) the kinetic energy 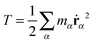 of any rotating molecule can be written as:
of any rotating molecule can be written as:
| | 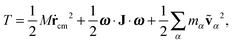 | (19) |
where
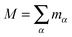
is the molecule's mass. These three terms on the right hand side are collected into,
| | | T = Ttrans + Tlabrot + Tlabvib, | (20) |
with
Ttrans,
Tlabrot, and
Tlabvib the translational, rotational, and vibrational contributions to the kinetic energy.
On the other hand, using the Eckart frame, the velocity of each monomer is expressed by eqn (16) and the kinetic energy of a molecule is decomposed as32
| | 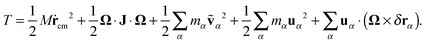 | (21) |
One can now distinguish the following terms (in order of appearance on the RHS of
eqn (21)):
| | | T = Ttrans + TEckrot + TEckvib-non-ang + TEckvib-ang + TEckCori. | (22) |
Here,
TEckrot denotes pure rotational contribution. The vibrational contribution consists of two parts: the first, emerging from the angular free part of the vibrational motion, is denoted by
TEckvib-non-ang, and the second,
i.e. TEckvib-ang, represents the angular part of vibrations. The last contribution is the Coriolis coupling, which is denoted by
TEckCori. Comparing both kinetic energy expressions (
i.e. in
eqn (19) and (21)), we observe that the following relations hold
| | | Tlabvib = TEckvib-non-ang, | (23) |
| | | Tlabrot = TEckrot + TEckvib-ang + TEckCori. | (24) |
and obviously, the translational kinetic energy
Ttrans is the same in both frames. In order to alleviate the notation, we define the pure rotational energy
TEckrot, the angular-momentum free vibrational energy
Tṽ, and the net vibrational angular momentum energy
Tu as,
| | | TΩ ≡ ½Ω·J·Ω = TEckrot, | (25) |
| | 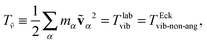 | (26) |
| | 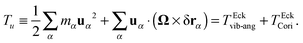 | (27) |
In the next section, we resort to the Eckart frame formalism in the analysis of the rotational and vibrational behavior of star polymers in solution and melt. Differences with respect to the laboratory frame will be highlighted.
4 Results and discussion
In this section, we present results from two different types of systems: (i) a single star polymer in solution (representing a dilute polymer suspension) and (ii) a melt of star polymers, with polymer volume fraction ϕ = 0.2 under isothermal conditions. The molecular model of the star polymer is the same in both types of simulations. In the solution case, we consider two types of bonds between monomers (blobs): harmonic bonds and finitely extensible non-linear elastic (FENE) bonds. In melt simulations, we use harmonic bonds to build up the star molecule.
We have so far introduced two frequencies (i.e. ω and Ω) describing rotation in polymers. In what follows, we will introduce two additional frequencies and for the sake of clarity and reference, we list them all in Table 1.
Table 1 The different frequencies mentioned in this work
To present the results in non-dimensionalized form, we use the Weissenberg numbers Wi and Wirot. The latter is based on the rotational diffusion time of the star. This is defined as Wirot = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τrot where τrot is the time for rotational diffusion, τrot = R2/Dr, of the molecule in equilibrium (see ref. 19 and 27 for details). The Wi, on the other hand, is based on the largest relaxation time (τrel) of the molecule, i.e. Wi =
τrot where τrot is the time for rotational diffusion, τrot = R2/Dr, of the molecule in equilibrium (see ref. 19 and 27 for details). The Wi, on the other hand, is based on the largest relaxation time (τrel) of the molecule, i.e. Wi = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τrel. It has to be said that the molecular rotational diffusion is the slowest relaxation process for stars with harmonic bonds, while for star molecules with FENE bonds, the slowest relaxation is the process of arm disentanglement. The corresponding relaxation times (rotational and arm-disentanglement) for simulations in solution and in melt are given in Table 2.
τrel. It has to be said that the molecular rotational diffusion is the slowest relaxation process for stars with harmonic bonds, while for star molecules with FENE bonds, the slowest relaxation is the process of arm disentanglement. The corresponding relaxation times (rotational and arm-disentanglement) for simulations in solution and in melt are given in Table 2.
Table 2 The rotational diffusion and arm-disentanglement relaxation times for our star model, with 12 arms and 6 monomers per arm. We define Wirot = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τrot and Wi =
τrot and Wi = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τrel with τrel = max[τrot,τdis]
τrel with τrel = max[τrot,τdis]
| System |
τ
rot
|
τ
dis
|
| Closed melt: γ∥ = 1.0, γ⊥ = 1.0 |
710 ± 40 |
390 ± 10 |
| Open melt: γ∥ = 1.0, γ⊥ = 1.0 |
700 ± 40 |
390 ± 10 |
| Solution harmonic bonds |
270 ± 20 |
180 ± 20 |
| Solution FENE bonds |
370 ± 30 |
950 ± 90 |
4.1 Star polymer models
The star polymer model is taken from ref. 41. We use the standard Lennard-Jones units, taking the monomer mass m0, unit length σ0 and energy ε0 as reference. We consider stars with f = 12 arms and m = 6 beads per arm, with a total of 73 monomers (including the central one). Excluded volume interactions of monomers are modeled by the repulsive Weeks–Chandler–Anderson interaction (σ = 2.415 and ε = 1). The bonds between adjacent monomers i and j are modelled by either harmonic springs or FENE bonds. In the case of harmonic bonds, with a recovery force −K(rij − reqij), the spring constant is K = 20 and the equilibrium distance reqij = 2.77 (the equilibrium distance between the central monomer and the first monomer of an arm is larger, reqij = 3.9). Finitely extensible bonds are modeled by the FENE potential,42 with a spring constant K = 20 and maximum length of the bond rmax = 1.5reqij.
Before entering into details, some general comments on the star molecule model are due. The main purpose of this work is to illustrate how the Eckart formalism can be used to provide information about the dynamics of soft molecules under rotation. The same type of analysis could be applied to any other star-molecule model or to other soft molecules (vesicles, semi-flexible linear polymers, or rings, etc.). Here, we have just deployed some relatively simple star molecule models (with short arms m = 6) in two quite different scenarios (melt and solution). It has to be said that some properties of this star molecule model depend on the arm length m, particularly at large Weissenberg numbers. As shown in Fig. 1 of the paper in ref. 11 by Ripoll et al., the elongational parameter G11(Wi)/G11(0) − 1 decreases with m at large shear rates. However, it is relevant to say that the resistance parameter mG, which is directly related to the breathing rotational frequency (see ref. 19 and 27), exhibits a master relation, independent of m (see Fig. 3 of Ripoll et al.). Concerning the simulations in melt, we have recently shown that the type of friction between monomers somewhat alters the melt rheology. The calculation of the “proper” friction kernel representing a particular atomistic model requires expensive Green–Kubo type evaluations of force–force cross-correlations.41 Here, we use a given friction kernel, a la DPD, and notice that the results should slightly vary with the kernel type. The reader is referred to ref. 19 and 27 where we present some studies on how the rheology and dynamic properties of this model of star molecules' melt vary with the friction kernel.
4.2 Melt simulations
For the melt case, we use stars made of harmonic bonds. Simulations are carried out at fixed temperature T = 4 using molecular dynamics with a dissipative particle dynamic (DPD) thermostat.43,44 We solve systems with constant volume (closed setup) and also open systems under constant normal load (see reference for details27). The simulation box is of size 390 × 117 × 117 and the density of the melt in equilibrium corresponds to the occupational factor Φ = 0.2, with about 2000 molecules. In the closed periodic setup, the shear flow is imposed by the SLLOD algorithm implemented with the Lees–Edwards boundary conditions.45–47 Constant load simulations in an open system, are performed using OBMD,26,28,48,49 which permits imposing an external shear stress at the open ends of the system. We shall use the following coordinates: x1 refers to the flow direction, x2 to the direction of the velocity gradient and x3 to the direction of flow vorticity (sometimes called neutral direction). The DPD thermostat used here introduces friction along the normal and tangential directions of any pair of monomers27,41,43,44 which come closer than the DPD-cutoff radius RDPD = 2 × 21/6σ (we use a Heaviside kernel for the DPD interaction). The friction coefficients in normal and tangential directions equal γ∥ = 1.0 and γ⊥ = 1.0. The equations of motion are integrated by the Velocity-Verlet algorithm50 with the integration step 0.01τ for small and moderate shear, and 0.005τ for high shear rates. A sketch of the star-polymer melt under shear flow from the perspective of one of its constituent polymers is depicted in Fig. 2.
 |
| | Fig. 2 Snapshot of the star-polymer melt under shear flow, drawn from the perspective of one polymer. The latter is depicted in purple and its surrounding polymers are colored in gray. The blue arrows correspond to the direction of the imposed shear, while the black arrows indicate the tank-treading rotation of the polymer. The coordinate unit vectors e1, e2, and e3 define the flow (x1), the gradient (x2), and the neutral (x3) direction, respectively. | |
4.3 Star in solution
We simulate a single star polymer in solution using Brownian hydrodynamics.51,52 The monomers (representing a coarse description of the molecule) interact via conservative forces (bonds and excluded volume interactions) and also via hydrodynamic interactions. The displacement of monomer α in direction i over time dt has the form drαi = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) xα2δi,1dt + μαβij(rαβ)Fβjdt + d
xα2δi,1dt + μαβij(rαβ)Fβjdt + d![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) αi where the first term indicates the shear flow (acting in 1-direction) and the mutual drag arises from the mobility tensor μαβij which in present calculations consists of the Rotne–Prager–Yamakawa (RPY) approximation.51,52 The Brownian displacement d
αi where the first term indicates the shear flow (acting in 1-direction) and the mutual drag arises from the mobility tensor μαβij which in present calculations consists of the Rotne–Prager–Yamakawa (RPY) approximation.51,52 The Brownian displacement d![[r with combining tilde]](https://www.rsc.org/images/entities/b_char_0072_0303.gif) satisfies a fluctuating dissipation (FD) relation for its covariance 〈d
satisfies a fluctuating dissipation (FD) relation for its covariance 〈d![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) αid
αid![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) βj〉 = 2kBTμαβijdt and to solve d
βj〉 = 2kBTμαβijdt and to solve d![[r with combining tilde]](https://www.rsc.org/images/entities/b_char_0072_0303.gif) we use the Fixman method.52 The integration scheme is an explicit Euler scheme with the time step dt = 0.01τ. In the present study, all simulations are run for 10
we use the Fixman method.52 The integration scheme is an explicit Euler scheme with the time step dt = 0.01τ. In the present study, all simulations are run for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ.
000τ.
4.4 Monomer rotation dynamics
To provide direct connection with the monomer dynamics, we calculate the angular velocity of rotation of molecules from the autocorrelation function of the gradient-direction coordinate of the last monomer of every arm of the star, relative to the CoM, (rα − rcm)·![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) 2. This signal is similar to an underdamped oscillator (Fig. 3) which can be fitted with the following function:53
2. This signal is similar to an underdamped oscillator (Fig. 3) which can be fitted with the following function:53| | C(t) = A2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωRt + ψ)exp(−Γt), cos(ωRt + ψ)exp(−Γt), | (28) |
where the damping rate Γ represents the decorrelation rate, ωR is the rotation frequency, and ψ is a phase constant. Two issues are noticeable from this graph: first, the decorrelation rate Γ only starts to significantly increase above Wirot > 50. Second, as Wi increases, the quality factor q = ωR/Γ becomes quite large, in particular, compared with what happens in linear polymers under shear53 (which tumble by compressing, as in a tube). Fig. 3 (bottom panel) compares the quality factor q for star polymers in solution (S) and melt (M) (with either FENE or harmonic bonds) and that measured in ref. 53 for FENE linear chains with N = 60 and dumbbells. In the case of star molecules, the arms rotate almost like in a “wheel” and a monomer turns around several times (q) before decorrelating its initial “rigid-body” position. At large shear rates, the differences in values of q are significant [see Fig. 3 (bottom)]. The quality factor is significantly smaller in melts, indicating the hindrance arising from steric interaction amongst close-by molecules. In what follows, we will compare ωR with ω and Ω and discuss the origin of the decorrelation Γ, according to the Eckart analysis.
 |
| | Fig. 3 (top) Autocorrelation function of position of the final monomers of each polymer's arm in the gradient direction, fitted by eqn (28) with parameters: A = 0.93, ωR = 0.35, Γ = 0.0084, and Ψ = 0.0025. (middle panels) The tank-treading frequency ωR and decorrelation rate Γ obtained from the fits (stars in solution and in melt). (bottom) The quality factor q = ωR/Γ for the dynamics of monomer rotations, comparing our 12-6 stars with linear FENE chains (N = 60) (with excluded volume interactions) and dumbbells, from ref. 53. | |
4.5 Kinetic energies
The kinetic energy balance is illustrated in Table 3 for star molecules in solution (having harmonic or FENE bonds) and some values of the shear rate. Displacements describing pure rotations have kinetic energy TΩ but coherent (collective) vibrations without angular momentum contribute with the largest energy Tṽ. These are related to the overall shape deformations (and in particular, compression/expansion does not introduce angular momentum). Other types of molecular deformations (affine or not) are collected in the velocity uα which does provide angular momentum (see eqn (18)) and feeds the (negative) kinetic energy contribution Tu (see Table 3 and eqn (24)). Eqn (27) confirms that this energy can only be negative because of the Coriolis term. So, on average, u·(Ω × δr) < 0; in other words u contributes in opposite direction to the pure rotation velocity Ω × δr. Note that |Tu| is subtracted from the pure rotation energy TΩ to yield the total rotation kinetic energy in the lab frame Tlabrot (see eqn (24)). To clarify matters, a sketch illustrating the different types of displacements is drawn in Fig. 1 (bottom panel). In what follows, we analyze these kinetic energies separately.
Table 3 Kinetic energy balance for solution of star polymers with harmonic and FENE bonds. The error bar of the reported values is approximately 5%
| Solution harmonic bonds |
Solution FENE bonds |
| Wi |
T
|
T
Ω
|
T
ṽ
|
T
u
|
Wi |
T
|
T
Ω
|
T
ṽ
|
T
u
|
| 13.25 |
1102 |
412 |
1028 |
−338 |
9.5 |
875 |
303 |
794 |
−222 |
| 53 |
1117 |
517 |
1042 |
−442 |
95 |
876 |
365 |
793 |
−282 |
| 106 |
1135 |
464 |
1058 |
−387 |
570 |
912 |
498 |
808 |
−394 |
| 424 |
1363 |
1189 |
1275 |
−1101 |
1520 |
1086 |
763 |
919 |
−596 |
4.6 Pure rotation: tank-treading
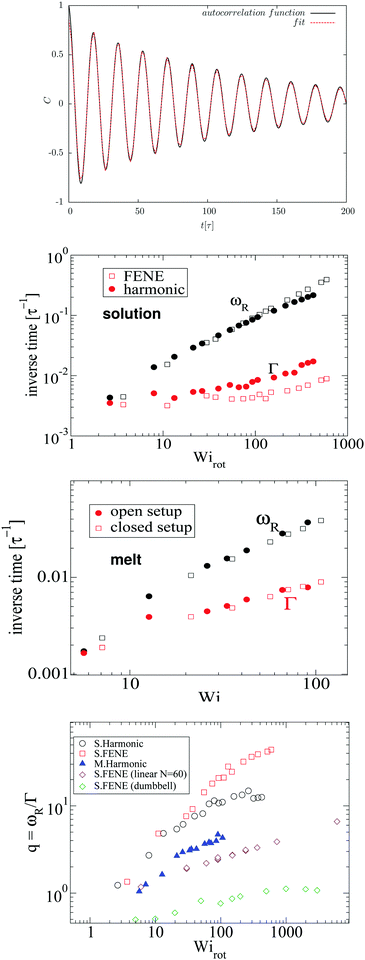
Fig. 4 compares the results for the apparent angular velocity ω, the Eckart angular velocity Ω and the frequency of monomer rotation about the CoM ωR. In all considered cases (polymers with either harmonic or FENE bonds in solution, and the melt case), we find that Ω = ωR within error bars while Ω > ω. Whenever vibrational angular momentum is present, the apparent angular velocity ω does not correctly represent molecular rotation.32 The difference between ω and Ω is larger for stars with Hookean-bonds in solution (see Fig. 4). From eqn (18), this simply indicates that the vibrational angular momentum (uα) has a larger contribution if the molecule is softer (harmonic versus FENE bonds) or has more free space to deform (as in the case of solution compared to melt).
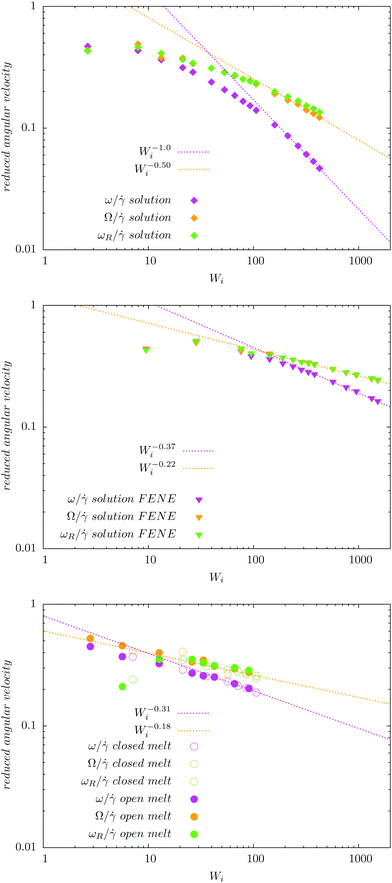 |
| | Fig. 4 Comparison of the angular velocity computation by the Eckart frame formalism (Ω/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) – colored in orange), by the standard approach (ω/ – colored in orange), by the standard approach (ω/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) – colored in magenta), and by the autocorrelation function of the position of the final monomers in every polymer's arm in the gradient direction (ωR/ – colored in magenta), and by the autocorrelation function of the position of the final monomers in every polymer's arm in the gradient direction (ωR/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) – colored in green). We study rotations in the solution of star polymers with Hookean (top) and FENE bonds (middle) and in the melt of star polymers with Hookean springs (bottom). In all three systems, the angular velocity obtained by the Eckart frame formalism is higher than the one calculated by the standard approach. In all cases, ωR matches well with Ω while the difference ω − ωR is larger in the Hookean spring solution case, followed by the solution of molecules with the FENE bonds and the melt. The reasons for these facts are explained in the text. – colored in green). We study rotations in the solution of star polymers with Hookean (top) and FENE bonds (middle) and in the melt of star polymers with Hookean springs (bottom). In all three systems, the angular velocity obtained by the Eckart frame formalism is higher than the one calculated by the standard approach. In all cases, ωR matches well with Ω while the difference ω − ωR is larger in the Hookean spring solution case, followed by the solution of molecules with the FENE bonds and the melt. The reasons for these facts are explained in the text. | |
Stars with harmonic bonds in solution seem to reach the scaling ω/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∼ Wi−1 (i.e. ω → cte) as the shear rate is increased (although, in fact, at very large
∼ Wi−1 (i.e. ω → cte) as the shear rate is increased (although, in fact, at very large ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , ω decreases). This apparent scaling was attributed in ref. 11 (and subsequent citations) to a universal limiting trend for tank-treading rotation of star polymers. However, although the apparent angular velocity ω reaches a maximum value, the tank-treading frequency, ωR, keeps increasing with
, ω decreases). This apparent scaling was attributed in ref. 11 (and subsequent citations) to a universal limiting trend for tank-treading rotation of star polymers. However, although the apparent angular velocity ω reaches a maximum value, the tank-treading frequency, ωR, keeps increasing with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , like ωR ∼ Wiα with α = 0.5 ± 0.02. This is shown in Fig. 4 where one can see that ω and ωR differ significantly.
, like ωR ∼ Wiα with α = 0.5 ± 0.02. This is shown in Fig. 4 where one can see that ω and ωR differ significantly.
Finally, in melts (bottom panel of Fig. 4), we observe that the molecular rotational frequencies are similar in the open and closed environments. This is in agreement with our previous studies (ref. 19 and 27) and indicates that the rheological differences measured in open and closed environments are of thermodynamic origin (density decreases when an open polymer enclosure is sheared).
4.7 Vibrational angular momentum and decoherence of rotational motion
Along this line, eqn (24) indicates that the total kinetic energy coming from displacements with angular momentum can be decomposed into a pure rotational part TΩ and contributions from vibrational angular momentum. It is noted that TΩ contains contributions from collective displacements and also from fluctuations. Eqn (25) indicates that| | 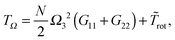 | (29) |
where ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) rot introduces a significant contribution from the covariances involving zero-average components of the rotational frequency Ω, like
rot introduces a significant contribution from the covariances involving zero-average components of the rotational frequency Ω, like ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) rot = 〈NΩ12G22〉 +⋯. Here, Gii represents the diagonal gyration tensor component in the i-th direction.
rot = 〈NΩ12G22〉 +⋯. Here, Gii represents the diagonal gyration tensor component in the i-th direction.
The energy of vibrations with angular momentum corresponds to deformations of the arms away from pure rigid body rotation (see eqn (18)). In solution, these motions arise from Brownian diffusion so we expect that the kinetic energy |Tu| is proportional to ΓDarm where Darm is the diffusion coefficient of the center of mass of one star's arm (which is independent of the shear rate). The scaling this hypothesis predicts is validated in Fig. 5 where |Tu| (normalized with its value at zero shear rate) is compared with Γτrot for increasing Weissenberg number. Results for different types of star polymers (harmonic and FENE bonds) confirm that both magnitudes are proportional and indicate that our intuition contains physical insight. In melts, however, both quantities differ significantly (see Fig. 5 bottom panel) indicating that, in this case, molecular deformations are also determined by other (non-Brownian) mechanisms, like inter-molecular collisions.
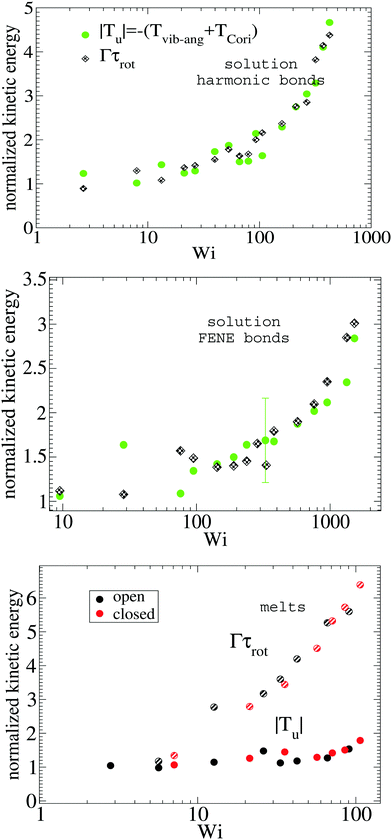 |
| | Fig. 5 The absolute value of kinetic energy related to the vibrational non-angular momentum |Tu| compared with the rate of decorrelation (Γ) of the monomer pure rotation around the molecule’s center (see Fig. 3). Both quantities are normalized with their values at zero shear rate. Top and middle panels show results for solution and the bottom panel, for the melt. | |
4.8 Vibrations without angular momentum and breathing mode
As stated (see Table 3), vibrations without angular momentum Tṽ have the largest contribution to the kinetic energy of the star molecule. This kinetic energy has also a thermal and a coherent contribution. The thermal energy includes the fluctuations in bond length, whose average kinetic energy scales as NspK〈δ2〉, with δ = rα,β − req the bond length, Nsp = 72 the number of springs in our star molecules and K their spring constant. Excluded volume forces are also central forces Fα,β ∝ ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) α,β (
α,β (![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) α,β being the unit distance vector between monomers α and β) so in the absence of hydrodynamic interactions they strictly do not contribute to the total angular momentum. It is noted that hydrodynamics spreads over internal forces, and contributes to the angular momentum, with monomer displacements drα = μαβFβdt, where μαβ is the mobility tensor. However, as shown in ref. 19, the major source of angular momentum comes out from the mean flow. We assume that thermal contribution to Tṽ is independent of the shear rate. The remaining contribution to Tṽ is assumed to be associated with overall deformations of the molecular shape and should increase with
α,β being the unit distance vector between monomers α and β) so in the absence of hydrodynamic interactions they strictly do not contribute to the total angular momentum. It is noted that hydrodynamics spreads over internal forces, and contributes to the angular momentum, with monomer displacements drα = μαβFβdt, where μαβ is the mobility tensor. However, as shown in ref. 19, the major source of angular momentum comes out from the mean flow. We assume that thermal contribution to Tṽ is independent of the shear rate. The remaining contribution to Tṽ is assumed to be associated with overall deformations of the molecular shape and should increase with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . This separation between thermal and coherent vibrations is clearly revealed in the fit Tṽ(Wi) = Tṽ(0) + ΔTṽ(Wi), which is shown in Fig. 6, with Tṽ(0) = 1029 ± 5 and ΔTṽ(Wi) = 0.021 Wi1.54 for harmonic springs, while Tṽ(0) = 792 ± 2 and ΔTṽ(Wi) = 2.32 × 10−5 Wi2.12 for FENE bonds (both in solution). In the case of melts we find Tṽ(0) = 426 and ΔTṽ(Wi) = 4.60 × 10−4 Wi2.00.
. This separation between thermal and coherent vibrations is clearly revealed in the fit Tṽ(Wi) = Tṽ(0) + ΔTṽ(Wi), which is shown in Fig. 6, with Tṽ(0) = 1029 ± 5 and ΔTṽ(Wi) = 0.021 Wi1.54 for harmonic springs, while Tṽ(0) = 792 ± 2 and ΔTṽ(Wi) = 2.32 × 10−5 Wi2.12 for FENE bonds (both in solution). In the case of melts we find Tṽ(0) = 426 and ΔTṽ(Wi) = 4.60 × 10−4 Wi2.00.
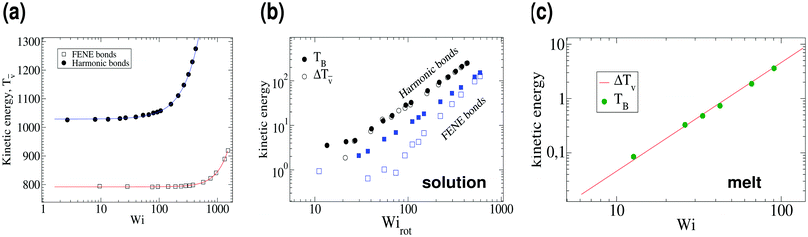 |
| | Fig. 6 (a) The angular momentum free vibrational kinetic Tṽ (symbols) and the fit Tṽ(Wi) = Tṽ(0) + aWiβ with ΔTṽ = aWiβ the coherent part and Tṽ(0) the thermal contribution (results for stars in solution). (b) The coherent contribution ΔTṽ is compared with the breathing mode energy estimated as 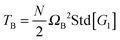 , where G1 is the principal eigenvalue of the gyration tensor and ΩB is the breathing frequency, reported in ref. 19 (results for solution). (c) The same as (b) but for the melt case, and , where G1 is the principal eigenvalue of the gyration tensor and ΩB is the breathing frequency, reported in ref. 19 (results for solution). (c) The same as (b) but for the melt case, and 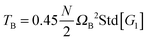 . . | |
We expect that the coherent part of the vibrational energy ΔTṽ(Wi) comes out from a collective “oscillation” of the molecular shape. Such type of collective vibration was discussed in a previous work on star polymers,19 and was referred to as a “breathing mode”. The dynamics of the breathing mode is revealed in the time correlation of the components of the gyration tensor (Gij), given by,3,16,19
| | 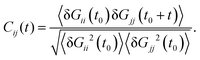 | (30) |
where δ
Gii =
Gii − 〈
Gii〉. These are damped oscillatory signals with a characteristic frequency
ΩB. In previous works,
16,19 the cross-correlation
C12 has been used to extract the “tumbling” time
τt (as twice the difference between the first maximum and the first minimum). We define
ΩB = 2π/
τt. As explained in
ref. 19, these types of dynamics have been called “tumbling” in linear and ring chains, while the word “breathing” is more appropriate to describe the star overall shape oscillation, while they perform tank-treading. The energy of “breathing” can be estimated from the largest fluctuation in the gyration tensor, taken from the standard deviation of the principal eigenvalue of the gyration tensor
G,
i.e. Std[
G1] = 〈(
G1 − 〈
G1〉)
2〉
1/2. A rough estimation of the breathing kinetic energy is then,
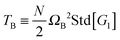
, and it is compared with Δ
Tṽ in
Fig. 6. In passing, we note that a quite similar outcome is obtained by
TB ∝
ΩB2Std[
V2/3] which is based on fluctuations (expansion/contraction) of the overall molecular volume
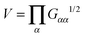
. Interestingly, we find excellent agreement (even quantitative) in all cases involving stars with harmonic bonds (solution and melt). However, in the FENE case, the values of
TB and Δ
Tṽ differ at small and moderate shear rates, and become similar as Wi increases. For moderate and small Wi we find Δ
Tṽ <
TB, indicating that the stronger excluded volume forces in FENE bonds (arm elongations are confined to a fixed value) tend to reduce collective vibrations (breathing) of the star molecules.
4.9 Intrinsic viscosity
One of the major tasks of polymer physics is to relate individual chain dynamics to macroscopic rheological properties. We make such an exercise in this section, taking the shear viscosity as our target macroscopic quantity. In a previous work, we analyzed in some detail the rheology of these stars in melt19 and reported in particular their shear viscosity under shear. Here, we calculate the contribution to the shear viscosity of star polymers in solution from their contribution to the virial part of the shear stress tensor,54| | 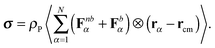 | (31) |
Here, Fnbα represents the force on the α-th monomer, originating from the non-bonded interactions (i.e. the Weeks–Chandler–Anderson interaction), and Fbα are the forces of the bonds (i.e. either harmonic or FENE). The polymer contribution to the stress tensor is proportional to ρP, the number density of polymer molecules, and the polymer contribution to the shear viscosity is ref. 54| | 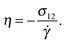 | (32) |
Using the Carreau fit,55,56 we estimate the zero-shear rate viscosity η0 and present the normalized viscosity η/η0. We note that η0 is about 1.8 times larger in the case of the harmonic-bond model compared with the FENE bonds. As the shear rate is increased, we find shear thinning η ∼ Wi−β with shear thinning exponents β = 0.25 for FENE bonds and β = 0.32 for harmonic bonds. These values are somewhat smaller than those found in melt, β = 0.49 (see Fig. 7). Viscous dissipation is related to decorrelation times and in fact, the intrinsic viscosity can be expressed as a sum of relaxation times.57 For an isolated star in dilute solution, one expects that the main mechanism for dissipation comes from the decorrelation in arm lengths, which takes place at an average rate Γ (see Fig. 3). Thus, as a first estimate, we seek a relation of the form η ∝ Γ−1. Fig. 7 shows that such a relation holds relatively well, both in solution and melts. For instance, in solution we see that the softer harmonic bonds lead to faster decorrelation rates and smaller intrinsic viscosity, compared with the more rigid FENE chains. As we indicated in Fig. 5, we found that, in solution, Γ scales as the kinetic energy |Tu| and consistently, |Tu| is larger in the case of harmonic bonds compared with FENE-stars. In melts, however, one expects that the departure from rigid-body rotation (measured by the velocity u and its kinetic energy Tu) arises also from inter-molecular collisions (and not only from Brownian diffusion). This is revealed in the different trends followed by Tu and Γ in melts: unlike what is observed in solution, Tu and Γ do not correlate (see Fig. 5 bottom).
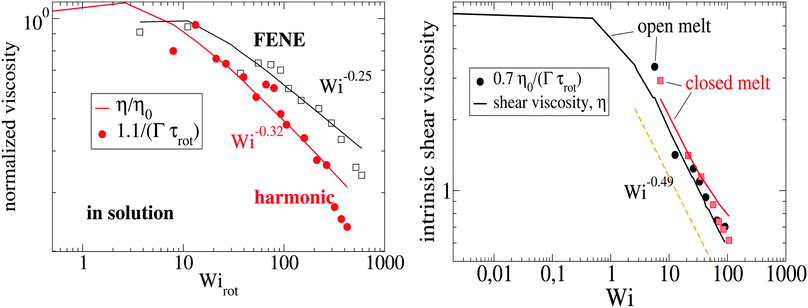 |
| | Fig. 7 The intrinsic shear viscosity η is compared with the normalized decorrelation rate of the arm (center-to-end) distance Γτrot. The left panel corresponds to stars in dilute solution (here, we normalize with the viscosity at zero shear rate η0) and the right panel corresponds to stars in melt (polymer volume fraction 0.2). In solution, the shear stress scales as σ12 = c![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) /Γ with c = 15 for harmonic and c = 7 for FENE bonds. /Γ with c = 15 for harmonic and c = 7 for FENE bonds. | |
5 Conclusions
The main purpose of this work is to show that the Eckart formalism can be used to unveil the complex dynamics of soft molecules in flow. The application of the Eckart formalism to the dynamics of star molecules in shear flow permitted us to warn about the incorrect interpretation of the rotation dynamics of soft molecules (polymers) based on a standard (lab frame) analysis. In particular, the apparent angular velocity ω resulting from such an analysis does not have a clear dynamical interpretation (it is not the rotation frequency of the molecule). We have shown that the Eckart co-rotating frame correctly extracts the different types of motions in the rotating and vibrating molecule: pure rotation, vibration with no-angular momentum and vibrational angular momentum. Star molecules in shear flow perform a tank-treading motion11 whereby monomers rotate around the center of the molecule, but for a given fixed shear rate, the molecule keeps a roughly fixed ellipsoidal overall shape (more precisely, they do not tumble). At large shear rates, the molecule performs another collective motion, which we called the “breathing mode”,19 whereby the gyration tensor of the molecule oscillates in time with a characteristic frequency ΩB. We have shown that each of these dynamics is associated with a different type of displacement in the Eckart frame. The pure rotational component of the Eckart frame, with a frequency Ω, describes the tank-treading frequency of the star ωR. By extracting the thermal (incoherent) part of the kinetic energy of vibrations without the angular momentum component, we find that the kinetic energy of the breathing mode coincides with the energy of “breathing” vibrations. Finally, in solution, we find that the decorrelation of the end-to-end arm distance, driven by Brownian diffusion at a rate Γ, correlates with the kinetic energy associated with vibrations (or more properly, fluctuations) with angular momentum, Tu. In melt, such a correlation is not observed, and it seems that the energy |Tu| of molecular deformations is mainly determined by intermolecular collisions (and thus density dominated).
In this work, we just consider star polymers with f = 12 arms and m = 6 monomers per arm. According to a recent analysis,58 star molecules become chain-like for f < 6, so our stars are within the “colloidal-like” regime. But, what would be the dynamics of more massive stars? While this question is open to future works, we have good reasons to believe that they will be quite similar to that found for f = 12, m = 6. In fact, several computational works on star polymers under dilute11 and semidilute16 conditions, covered a relatively large range of values of f ≤ 50 and m < 50 and (by defining the proper Weissenberg number) they found that all data for ω collapse in a master curve, indicating that the length of the arms or the functionality was not essentially changing the polymer dynamics. The dynamics would surely change in the case of a semidilute solution (or melt) if the stars had very long arms (m > 100), because entanglements should play a major role in distorting their rotation dynamics. However, we emphasize that the Eckart framework would be still applicable in such regimes and provide valuable dynamic information.
It also has to be noted that the present analysis can be complementary to the more detailed normal mode analysis of vibrations, within the framework of the theory of molecular vibrations.29 In the latter, each internally rotating part of the molecule would require the introduction of additional internal coordinate systems inside the translating and rotating Eckart frame.34–37,59–63 Presently, we leave this discussion for future work, since the main aim of this paper is the separation of rotations from vibrations, or the consequences such decomposition brings up in the interpretation of molecular rotations. The objective of this work is to show that the Eckart frame, successfully and routinely used to describe infrared and Raman spectra of small molecules, is also a robust and useful tool to investigate the complex dynamics of soft, semiflexible macromolecules.
Conflicts of interest
There are no conflicts to declare.
Appendix: the Eckart reference configuration
In the Eckart frame formalism of eqn (14) and (15), one needs to define a reference configuration which fixes cαi over time. These are the components of the monomer positions of the reference configuration in the initial internal coordinate system. We choose cαi in three different ways: (i) from an equilibrium configuration of a star polymer at temperature 0 K. (ii) The reference configuration is obtained by Metropolis Monte Carlo (MC) simulation at the desired temperature T = 4, which enforces by additional terms in the Hamiltonian that the configuration matches the average gyration tensor components at every shear rate. (iii) The cαis are not constant. Instead, they are changed after a certain number of sampled configurations in the trajectory. An instantaneous configuration is taken as a reference configuration for the following τw in time, i.e. this configuration is used to evaluate the angular velocity of rotation (using the Eckart frame formalism) from all the following trajectory snapshots within the time window τw. Next, the first following configuration in the trajectory is taken as the new reference configuration. This procedure is thus repeated from the start until the end of the sampled trajectory. We analyze the rotation of molecules for different lengths of the time window and thus give the result for this third characterization of rotation by the Eckart frame formalism in the form of 3-dimensional plots (Fig. 8).
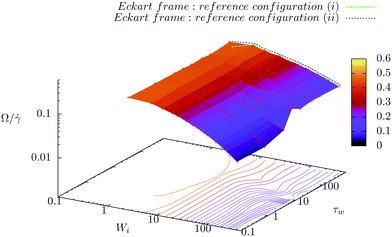 |
| | Fig. 8 Three definitions of reference configuration to calculate the angular velocity by the Eckart frame formalism for star polymers in solution: (i) the reference configuration is the equilibrium configuration at temperature 0 K (green line). (ii) We obtain the reference configuration at every shear rate separately by the Monte Carlo simulation so that it matches the average steady state shape of a polymer (i.e. gyration tensor) at that particular shear rate (blue line). (iii) The reference configuration is taken to be an instantaneous one, but in this way defined cαis are used in the computation of the angular velocity only for the following τw in time. Afterwards, the reference configuration is replaced with the next instantaneous configuration, from which we define new cαis. | |
In all three described definitions of cαis, the unit base vectors of the internal coordinate system f1, f2, and f3 and the origin of the Eckart frame, defined by rcm, are different in every snapshot of the sampled trajectory. Only the reference components cαis remain constant throughout the whole trajectory in (i) and (ii), while in (iii) also cαis change in time, as described above. Molecules rotate in the flow-gradient plane. Therefore, the only component of the molecules' angular velocity with non zero-average is in the neutral direction and we denote, ω = (ω1, ω2, ω3) and Ω = (Ω1, Ω2, Ω3), where indices 1, 2, and 3 denote the flow, gradient, and neutral direction, respectively.
To determine the optimal way to define cαis, we plot, in Fig. 8, angular velocities obtained by the Eckart formalism using definitions (i), (ii), and (iii) for solution of star polymers with 12 arms of 6 monomers (connected by Hookean springs). Plots for the melt are qualitatively similar and are not shown here. We observe that approach (iii), in which cαis change every τw, gives the angular velocity surface that at the shortest τw corresponds to the standard approach (i.e. using eqn (2) and (3)). With increasing τw, it approaches the values obtained by approaches (i) and (ii). At a certain value of τw, we observe a sharp crossover in angular velocity of polymers at very high shear rates, which results in qualitatively different dependencies Ω/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (Wi) emerging only due to the different reference frames. A similar crossover is also observed in melts, but is more prominent in solutions. Furthermore, we observe that this crossover occurs at higher τw for the star polymers with longer arms.
(Wi) emerging only due to the different reference frames. A similar crossover is also observed in melts, but is more prominent in solutions. Furthermore, we observe that this crossover occurs at higher τw for the star polymers with longer arms.
Importantly, we find that definitions (i) and (ii) yield basically the same results, which are also similar to the results obtained by definition (iii) after the crossover. Therefore, in the manuscript, we present only results obtained by definition (ii).
Acknowledgements
J. S. and M. P. acknowledge financial support through grants P1-0002 and J1-7435 from the Slovenian Research Agency. J. S. acknowledges financial support from Slovene Human Resources Development and Scholarship Fund (186. JR). R. D.-B. acknowledges support from the Spanish government under national MINECO project FIS2013-47350-C5-1-R. Partial support from COST Action MP1305 is kindly acknowledged. We thank Raul Pérez Pelaez for his help with the cover figure.
References
- D. E. Smith, H. P. Babcock and S. Chu, Science, 1999, 283, 1724–1727 CrossRef CAS PubMed.
- R. E. Teixeira, H. P. Babcock, E. S. G. Shaqfeh and S. Chu, Macromolecules, 2005, 38, 581–592 CrossRef CAS.
- C.-C. Huang, G. Sutmann, G. Gompper and R. G. Winkler, Europhys. Lett., 2011, 93, 54004 CrossRef.
- S. Costanzo, Q. Huang, G. Ianniruberto, G. Marrucci, O. Hassager and D. Vlassopoulos, Macromolecules, 2016, 49, 3925–3935 CrossRef CAS.
- R. G. Winkler, Soft Matter, 2016, 12, 3737–3749 RSC.
- W. Chen, K. Zhang, L. Liu, J. Chen, Y. Li and L. An, Macromolecules, 2017, 50, 1236–1244 CrossRef CAS.
- M. Abkarian, M. Faivre and A. Viallat, Phys. Rev. Lett., 2007, 98, 188302 CrossRef PubMed.
- A. Z. K. Yazdani and P. Bagchi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 026314 CrossRef PubMed.
- W. R. Dodson and P. Dimitrakopoulos, Biophys. J., 2010, 99, 2906–2916 CrossRef CAS PubMed.
- C. Aust, S. Hess and M. Kröger, Macromolecules, 2002, 35, 8621–8630 CrossRef CAS.
- M. Ripoll, R. G. Winkler and G. Gompper, Phys. Rev. Lett., 2006, 96, 188302 CrossRef CAS PubMed.
- M. Ripoll, R. Winkler and G. Gompper, Eur. Phys. J. E: Soft Matter Biol. Phys., 2007, 23, 349–354 CrossRef CAS PubMed.
- Z.-C. Yan, S. Costanzo, Y. Jeong, T. Chang and D. Vlassopoulos, Macromolecules, 2016, 49, 1444–1453 CrossRef CAS.
- K.-W. Hsiao, C. M. Schroeder and C. E. Sing, Macromolecules, 2016, 49, 1961–1971 CrossRef CAS.
- J. Yoon, J. Kim and C. Baig, J. Rheol., 2016, 60, 673–685 CrossRef CAS.
- W. Chen, J. Chen and L. An, Soft Matter, 2013, 9, 4312–4318 RSC.
- W. Chen, H. Zhao, L. Liu, J. Chen, Y. Li and L. An, Soft Matter, 2015, 11, 5265–5273 RSC.
- W. Chen, Y. Li, H. Zhao, L. Liu, J. Chen and L. An, Polymer, 2015, 64, 93–99 CrossRef CAS.
- J. Sablić, M. Praprotnik and R. Delgado-Buscalioni, Soft Matter, 2017, 13, 4971–4987 RSC.
- A. Jain, C. Sasmal, R. Hartkamp, B. Todd and J. R. Prakash, Chem. Eng. Sci., 2015, 121, 245–257 CrossRef CAS.
- R. Cerf, J. Chim. Phys. Phys.-Chim. Biol., 1969, 68, 479 CrossRef.
- S. P. Singh, D. A. Fedosov, A. Chatterji, R. G. Winkler and G. Gompper, J. Phys.: Condens. Matter, 2012, 24, 464103 CrossRef PubMed.
- S. P. Singh, A. Chatterji, G. Gompper and R. G. Winkler, Macromolecules, 2013, 46, 8026–8036 CrossRef CAS.
- T. Yamamoto and N. Masaoka, Rheol. Acta, 2015, 54, 139–147 CrossRef CAS.
- X. Xu and J. Chen, J. Chem. Phys., 2016, 144, 244905 CrossRef PubMed.
- R. Delgado-Buscalioni, J. Sablić and M. Praprotnik, Eur. Phys. J.: Spec. Top., 2015, 224, 2331–2349 CrossRef CAS.
- J. Sablić, M. Praprotnik and R. Delgado-Buscalioni, Soft Matter, 2016, 12, 2416–2439 RSC.
- G. De Fabritiis, R. Delgado-Buscalioni and P. Coveney, Phys. Rev. Lett., 2006, 97, 134501 CrossRef CAS PubMed.
- C. Eckart, Phys. Rev., 1935, 47, 552–558 CrossRef CAS.
-
E. Wilson, J. Decius and P. Cross, Molecular Vibrations: The Theory of Infrared and Raman Vibrational Spectra, Dover Publications, 1955 Search PubMed.
- J. D. Louck and H. W. Galbraith, Rev. Mod. Phys., 1976, 48, 69–106 CrossRef.
- Y. M. Rhee and M. S. Kim, J. Chem. Phys., 1997, 107, 1394–1402 CrossRef CAS.
- T. Yanao and K. Takatsuka, J. Chem. Phys., 2004, 120, 8924–8936 CrossRef CAS PubMed.
- D. Janežič, M. Praprotnik and F. Merzel, J. Chem. Phys., 2005, 122, 174101 CrossRef PubMed.
- M. Praprotnik and D. Janežič, J. Chem. Inf. Model., 2005, 45, 1571–1579 CrossRef CAS PubMed.
- M. Praprotnik and D. Janežič, J. Chem. Phys., 2005, 122, 174102 CrossRef PubMed.
- M. Praprotnik and D. Janežič, J. Chem. Phys., 2005, 122, 174103 CrossRef PubMed.
- C. N. Likos, H. Löwen, M. Watzlawek, B. Abbas, O. Jucknischke, J. Allgaier and D. Richter, Phys. Rev. Lett., 1998, 80, 4450–4453 CrossRef CAS.
- C. N. Likos, Phys. Rep., 2001, 348, 267–439 CrossRef CAS.
-
G. S. Grest, L. J. Fetters, J. S. Huang and D. Richter, Star Polymers: Experiment, Theory, and Simulation, John Wiley and Sons, Inc., 2007, pp. 67–163 Search PubMed.
- C. Hijon, P. Español, E. Vanden-Eijnden and R. Delgado-Buscalioni, Faraday Discuss., 2010, 144, 301–322 RSC.
- A. A. Veldhorst, J. C. Dyre and T. B. Schrøder, J. Chem. Phys., 2015, 143, 194503 CrossRef PubMed.
- P. Español and P. Warren, Europhys. Lett., 1995, 30, 191 CrossRef.
- T. Soddemann, B. Dünweg and K. Kremer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 046702 CrossRef PubMed.
- A. W. Lees and S. F. Edwards, J. Phys. C: Solid State Phys., 1972, 5, 1921 CrossRef.
- D. J. Evans and G. P. Morriss, Phys. Rev. A: At., Mol., Opt. Phys., 1984, 30, 1528–1530 CrossRef CAS.
- A. J. Ladd, Mol. Phys., 1984, 53, 459–463 CrossRef CAS.
-
R. Delgado-Buscalioni, Numerical Analysis of Multiscale Computations, 2011 Search PubMed.
- E. G. Flekkoy, R. Delgado-Buscalioni and P. V. Coveney, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 026703 CrossRef PubMed.
-
M. Tuckerman, Statistical Mechanics: Theory and Molecular Simulation, OUP Oxford, 2010 Search PubMed.
- R. M. Jendrejack, M. D. Graham and J. J. de Pablo, J. Chem. Phys., 2000, 113, 2894–2900 CrossRef CAS.
- R. M. Jendrejack, J. J. de Pablo and M. D. Graham, J. Chem. Phys., 2002, 116, 7752–7759 CrossRef CAS.
- F. B. Usabiaga and R. Delgado-Buscalioni, Macromol. Theory Simul., 2011, 20, 466–471 CrossRef CAS.
-
P. S. Doyle and P. T. Underhill, in Brownian Dynamics Simulations of Polymers and Soft Matter, ed. S. Yip, Springer Netherlands, Dordrecht, 2005, pp. 2619–2630 Search PubMed.
- K. Yasuda, J. Text. Sci. Eng., 2006, 52, 171–173 CrossRef.
-
J. Aho, Rheological Characterization of Polymer Melts in Shear and Extension: Measurement Reliability and Data for Practical Processing, Tampere University of Technology, 2011 Search PubMed.
-
M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Clarendon Press, Oxford, 1994 Search PubMed.
- A. Chremos and J. F. Douglas, J. Chem. Phys., 2015, 143, 111104 CrossRef PubMed.
- J. B. Howard, J. Chem. Phys., 1937, 5, 442–450 CrossRef CAS.
- J. B. Howard, J. Chem. Phys., 1937, 5, 451–459 CrossRef CAS.
- B. Kirtman, J. Chem. Phys., 1962, 37, 2516–2539 CrossRef CAS.
- B. Kirtman, J. Chem. Phys., 1964, 41, 775–788 CrossRef CAS.
- B. Kirtman, J. Chem. Phys., 1968, 49, 2257–2260 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2017 |
 Open Access Article
Open Access Article *bc and
Matej
Praprotnik
*bc and
Matej
Praprotnik
 *ad
*ad
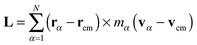 is the angular momentum of the rotating molecule and J its moment-of-inertia tensor with respect to the position of its CoM rcm, defined as
is the angular momentum of the rotating molecule and J its moment-of-inertia tensor with respect to the position of its CoM rcm, defined as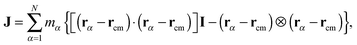
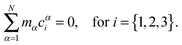
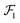 ,
, 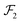 , and
, and 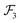 , which are given by:29,31
, which are given by:29,31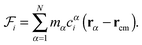
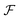 with the ij-component defined as
with the ij-component defined as 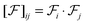 . The unit base vectors of the instantaneous Eckart frame (defined by the instantaneous positions of monomers) are computed as:29,31
. The unit base vectors of the instantaneous Eckart frame (defined by the instantaneous positions of monomers) are computed as:29,31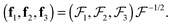
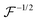 represents a positively defined matrix, for which the following relation holds:
represents a positively defined matrix, for which the following relation holds: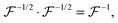
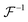 is a positively defined inverse of the Gram matrix
is a positively defined inverse of the Gram matrix 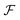 .
.
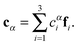
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and (iii) a mobile configuration which adapts over time to the average molecular conformation upon a pre-determined “averaging” time τw. We find that the two fixed configurations give the same Eckart rotation frequency Ω while the third one consistently converges to the outcome of the fixed references for τw → ∞ while for τw → 0, it provides the apparent frequency ω obtained from the standard approach.
and (iii) a mobile configuration which adapts over time to the average molecular conformation upon a pre-determined “averaging” time τw. We find that the two fixed configurations give the same Eckart rotation frequency Ω while the third one consistently converges to the outcome of the fixed references for τw → ∞ while for τw → 0, it provides the apparent frequency ω obtained from the standard approach.
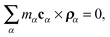

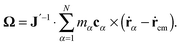
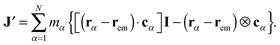
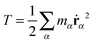 of any rotating molecule can be written as:
of any rotating molecule can be written as: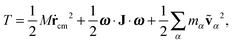
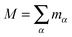 is the molecule's mass. These three terms on the right hand side are collected into,
is the molecule's mass. These three terms on the right hand side are collected into,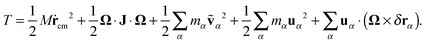
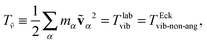
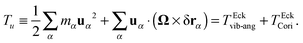
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τrot where τrot is the time for rotational diffusion, τrot = R2/Dr, of the molecule in equilibrium (see ref. 19 and 27 for details). The Wi, on the other hand, is based on the largest relaxation time (τrel) of the molecule, i.e. Wi =
τrot where τrot is the time for rotational diffusion, τrot = R2/Dr, of the molecule in equilibrium (see ref. 19 and 27 for details). The Wi, on the other hand, is based on the largest relaxation time (τrel) of the molecule, i.e. Wi = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τrel. It has to be said that the molecular rotational diffusion is the slowest relaxation process for stars with harmonic bonds, while for star molecules with FENE bonds, the slowest relaxation is the process of arm disentanglement. The corresponding relaxation times (rotational and arm-disentanglement) for simulations in solution and in melt are given in Table 2.
τrel. It has to be said that the molecular rotational diffusion is the slowest relaxation process for stars with harmonic bonds, while for star molecules with FENE bonds, the slowest relaxation is the process of arm disentanglement. The corresponding relaxation times (rotational and arm-disentanglement) for simulations in solution and in melt are given in Table 2.![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τrot and Wi =
τrot and Wi = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τrel with τrel = max[τrot,τdis]
τrel with τrel = max[τrot,τdis]
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) xα2δi,1dt + μαβij(rαβ)Fβjdt + d
xα2δi,1dt + μαβij(rαβ)Fβjdt + d![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) αi where the first term indicates the shear flow (acting in 1-direction) and the mutual drag arises from the mobility tensor μαβij which in present calculations consists of the Rotne–Prager–Yamakawa (RPY) approximation.51,52 The Brownian displacement d
αi where the first term indicates the shear flow (acting in 1-direction) and the mutual drag arises from the mobility tensor μαβij which in present calculations consists of the Rotne–Prager–Yamakawa (RPY) approximation.51,52 The Brownian displacement d![[r with combining tilde]](https://www.rsc.org/images/entities/b_char_0072_0303.gif) satisfies a fluctuating dissipation (FD) relation for its covariance 〈d
satisfies a fluctuating dissipation (FD) relation for its covariance 〈d![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) αid
αid![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) βj〉 = 2kBTμαβijdt and to solve d
βj〉 = 2kBTμαβijdt and to solve d![[r with combining tilde]](https://www.rsc.org/images/entities/b_char_0072_0303.gif) we use the Fixman method.52 The integration scheme is an explicit Euler scheme with the time step dt = 0.01τ. In the present study, all simulations are run for 10
we use the Fixman method.52 The integration scheme is an explicit Euler scheme with the time step dt = 0.01τ. In the present study, all simulations are run for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000τ.
000τ.
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) 2. This signal is similar to an underdamped oscillator (Fig. 3) which can be fitted with the following function:53
2. This signal is similar to an underdamped oscillator (Fig. 3) which can be fitted with the following function:53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωRt + ψ)exp(−Γt),
cos(ωRt + ψ)exp(−Γt),
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∼ Wi−1 (i.e. ω → cte) as the shear rate is increased (although, in fact, at very large
∼ Wi−1 (i.e. ω → cte) as the shear rate is increased (although, in fact, at very large ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , ω decreases). This apparent scaling was attributed in ref. 11 (and subsequent citations) to a universal limiting trend for tank-treading rotation of star polymers. However, although the apparent angular velocity ω reaches a maximum value, the tank-treading frequency, ωR, keeps increasing with
, ω decreases). This apparent scaling was attributed in ref. 11 (and subsequent citations) to a universal limiting trend for tank-treading rotation of star polymers. However, although the apparent angular velocity ω reaches a maximum value, the tank-treading frequency, ωR, keeps increasing with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , like ωR ∼ Wiα with α = 0.5 ± 0.02. This is shown in Fig. 4 where one can see that ω and ωR differ significantly.
, like ωR ∼ Wiα with α = 0.5 ± 0.02. This is shown in Fig. 4 where one can see that ω and ωR differ significantly.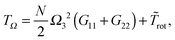
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) rot introduces a significant contribution from the covariances involving zero-average components of the rotational frequency Ω, like
rot introduces a significant contribution from the covariances involving zero-average components of the rotational frequency Ω, like ![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) rot = 〈NΩ12G22〉 +⋯. Here, Gii represents the diagonal gyration tensor component in the i-th direction.
rot = 〈NΩ12G22〉 +⋯. Here, Gii represents the diagonal gyration tensor component in the i-th direction.

![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) α,β (
α,β (![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) α,β being the unit distance vector between monomers α and β) so in the absence of hydrodynamic interactions they strictly do not contribute to the total angular momentum. It is noted that hydrodynamics spreads over internal forces, and contributes to the angular momentum, with monomer displacements drα = μαβFβdt, where μαβ is the mobility tensor. However, as shown in ref. 19, the major source of angular momentum comes out from the mean flow. We assume that thermal contribution to Tṽ is independent of the shear rate. The remaining contribution to Tṽ is assumed to be associated with overall deformations of the molecular shape and should increase with
α,β being the unit distance vector between monomers α and β) so in the absence of hydrodynamic interactions they strictly do not contribute to the total angular momentum. It is noted that hydrodynamics spreads over internal forces, and contributes to the angular momentum, with monomer displacements drα = μαβFβdt, where μαβ is the mobility tensor. However, as shown in ref. 19, the major source of angular momentum comes out from the mean flow. We assume that thermal contribution to Tṽ is independent of the shear rate. The remaining contribution to Tṽ is assumed to be associated with overall deformations of the molecular shape and should increase with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . This separation between thermal and coherent vibrations is clearly revealed in the fit Tṽ(Wi) = Tṽ(0) + ΔTṽ(Wi), which is shown in Fig. 6, with Tṽ(0) = 1029 ± 5 and ΔTṽ(Wi) = 0.021 Wi1.54 for harmonic springs, while Tṽ(0) = 792 ± 2 and ΔTṽ(Wi) = 2.32 × 10−5 Wi2.12 for FENE bonds (both in solution). In the case of melts we find Tṽ(0) = 426 and ΔTṽ(Wi) = 4.60 × 10−4 Wi2.00.
. This separation between thermal and coherent vibrations is clearly revealed in the fit Tṽ(Wi) = Tṽ(0) + ΔTṽ(Wi), which is shown in Fig. 6, with Tṽ(0) = 1029 ± 5 and ΔTṽ(Wi) = 0.021 Wi1.54 for harmonic springs, while Tṽ(0) = 792 ± 2 and ΔTṽ(Wi) = 2.32 × 10−5 Wi2.12 for FENE bonds (both in solution). In the case of melts we find Tṽ(0) = 426 and ΔTṽ(Wi) = 4.60 × 10−4 Wi2.00.

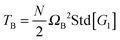 , where G1 is the principal eigenvalue of the gyration tensor and ΩB is the breathing frequency, reported in ref. 19 (results for solution). (c) The same as (b) but for the melt case, and
, where G1 is the principal eigenvalue of the gyration tensor and ΩB is the breathing frequency, reported in ref. 19 (results for solution). (c) The same as (b) but for the melt case, and 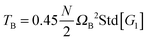 .
.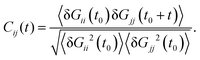
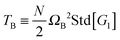 , and it is compared with ΔTṽ in Fig. 6. In passing, we note that a quite similar outcome is obtained by TB ∝ ΩB2Std[V2/3] which is based on fluctuations (expansion/contraction) of the overall molecular volume
, and it is compared with ΔTṽ in Fig. 6. In passing, we note that a quite similar outcome is obtained by TB ∝ ΩB2Std[V2/3] which is based on fluctuations (expansion/contraction) of the overall molecular volume 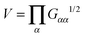 . Interestingly, we find excellent agreement (even quantitative) in all cases involving stars with harmonic bonds (solution and melt). However, in the FENE case, the values of TB and ΔTṽ differ at small and moderate shear rates, and become similar as Wi increases. For moderate and small Wi we find ΔTṽ < TB, indicating that the stronger excluded volume forces in FENE bonds (arm elongations are confined to a fixed value) tend to reduce collective vibrations (breathing) of the star molecules.
. Interestingly, we find excellent agreement (even quantitative) in all cases involving stars with harmonic bonds (solution and melt). However, in the FENE case, the values of TB and ΔTṽ differ at small and moderate shear rates, and become similar as Wi increases. For moderate and small Wi we find ΔTṽ < TB, indicating that the stronger excluded volume forces in FENE bonds (arm elongations are confined to a fixed value) tend to reduce collective vibrations (breathing) of the star molecules.
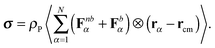
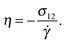
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (Wi) emerging only due to the different reference frames. A similar crossover is also observed in melts, but is more prominent in solutions. Furthermore, we observe that this crossover occurs at higher τw for the star polymers with longer arms.
(Wi) emerging only due to the different reference frames. A similar crossover is also observed in melts, but is more prominent in solutions. Furthermore, we observe that this crossover occurs at higher τw for the star polymers with longer arms.



