Micro- and nano-patterned elastin-like polypeptide hydrogels for stem cell culture

Abstract

We show that submicron-sized patterns can be imprinted into soft, recombinant-engineered protein hydrogels (here elastin-like proteins, ELP) by transferring wavy patterns from polydimethylsiloxane (PDMS) molds. The high-precision topographical tunability of the relatively stiff PDMS is translated to a bio-responsive, soft material, enabling topographical cell response studies at elastic moduli matching those of tissues. Aligned and unaligned wavy patterns with mold periodicities of 0.24–4.54 μm were imprinted and characterized by coherent anti-Stokes Raman scattering and atomic force microscopy. The pattern was successfully transferred down to 0.37 μm periodicity (width in ELP: 250 ± 50 nm, height: 70 ± 40 nm). The limit was set by inherent protein assemblies (diameter: 124–180 nm) that formed due to lower critical solution temperature behavior of the ELP during molding. The width/height of the ELP ridges depended on the degree of hydration; from complete dehydration to full hydration, ELP ridge width ranged from 79 ± 9% to 150 ± 40% of the mold width. The surface of the ridged ELP featured densely packed protein aggregates that were larger in size than those observed in bulk/flat ELP. Adipose-derived stem cells (ADSCs) oriented along hydrated aligned patterns with periodicities ≥0.60 μm (height ≥170 ± 100 nm), while random orientation was observed for smaller distances/amplitudes, as well as flat and unaligned wavy ELP surfaces. Hence, micro-molding of ELP is a promising approach to create tissue-mimicking, hierarchical architectures composed of tunable micron-sized structures with nano-sized protein aggregates, which opens the way for orthogonal screening of cell responses to topography and cell-adhesion ligands at relevant elastic moduli.

---

Introduction

The impact of surface structural features on cellular responses has been studied predominantly using engineered substrates that differ from the native extracellular matrix (ECM) in at least one of the following ways: they tend to be much stiffer than the ECM, they often lack cell-adhesion ligands, and they typically have angular, repetitive surface structures rather than the undulating surfaces commonly found in the ECM.¹ To address these limitations, we developed a reactive ion etching (RIE) protocol to create wavy topographical patterns of varying periodicity that are then micro-molded into a recombinant elastin-like protein (ELP) biomaterial with tissue matrix-like mechanical properties and cell-adhesion ligands. To overcome the challenges of characterizing such soft, hydrated, patterned interfaces, we report the use of coherent anti-Stokes Raman scattering (CARS) microscopy to evaluate the topographical features of the biomaterial without introducing any foreign contrast agents or physical manipulation of the sample.

To better understand the dynamic interaction between environmental cues and cell behavior, bio-responsive materials with elastic properties similar to those of soft tissues are needed.² One such class of materials is recombinant engineered ELPs, which are composed of amino acid sequences derived from the ECM protein elastin. Interspersing these elastin-derived sequences with a fibronectin-derived, extended cell-adhesion sequence that includes the tripeptide arginine-glycine-aspartic acid (RGD)^3,4 offers precise and reproducible control over cell adhesion at the amino acid level. ELPs are typically crosslinked into hydrogels^5–9 with independent tunability over several biologically relevant properties, including cell-adhesion ligand density and matrix stiffness.^10–12

While ELP hydrogels mimic several important properties of the ECM, their homogeneous textures differ significantly from the in vivo matrix, which is composed of hierarchical structures with feature sizes ranging from a few nanometers to multiple microns.¹³ One common material used to study cell responses to substrate structural features is polydimethylsiloxane (PDMS). While PDMS offers ease of fabrication, it lacks cell-adhesion ligands and typically has an elastic modulus of around 3 MPa,¹⁴ which is much stiffer than the native ECM. PDMS has been shaped both on the nano- and microscale,¹⁵ forming controlled repeating patterns supporting growth of human pluripotent stem cell-derived cardiomyocytes¹⁶ and alignment of smooth muscle cells.¹⁷

Structural hydrogels, as reviewed by Ma et al.,¹⁸ have attracted increasing interest with a broad range of applications that goes well beyond cell scaffolds (e.g. intelligent actuators, microfluidic units, synthetic adhesives, etc.). However, these materials typically rely on synthetic polymers without integrated cell-adhesion ligands. Structural biopolymers with inherent cell-adhesion ligands, such as collagen or fibronectin, can also be patterned by two-photon lithography, resulting in structured, bio-responsive, soft materials.¹⁹ Unfortunately, the dyes used in the lithography process tend to remain in the matrix and may influence cell behavior. Electrospinning has successfully been used to form collagen²⁰ and, more recently, fibrous ELP²¹ scaffolds. While the diameter of the electrospun fibers can be controlled across a broad size range, precise alignment at well-defined distances is difficult. Altogether, this leaves a need for a soft, tissue-mimicking platform where the dimensions of structural features, elasticity, and cell-adhesion ligand densities can all be controlled and orthogonally varied.

The challenge in creating such patterned soft materials is not just in their production, but also in their characterization. A conductive coating is needed for scanning electron microscopy (SEM), which may change the surface structure of soft samples. For transmission electron microscopy (TEM), the samples need to be cooled to subfreezing temperatures and handled in vacuum, which can influence structures and introduce new topographies. Thus, less invasive techniques such as atomic force microscopy (AFM) and laser-scanning microscopy are needed for characterization of hydrogel surface topography. AFM is a non-destructive tool to precisely monitor surface topographies at the nanoscale.^22,23 For wet samples with cells, laser scanning microscopy is a more convenient choice, where fluorescent dyes can be used to generate contrast. However, the dyes may affect the properties of the hydrogel and/or associated cells, and the spatial distribution of the fluorophores may be affected by chemical and structural properties of the hydrogel. A label-free method like CARS microscopy,^24,25 which generates chemical contrast based on inherent molecular vibrations, here the CH₃ vibration of proteins, has the capability to provide information about the natural state of the proteins in the hydrogel at physiological conditions.^26,27 Being an optical technique, CARS microscopy enables investigations of soft materials even under hydrated conditions and requires no physical contact, which is challenging for most AFM probes. Furthermore, it is easily combined with two-photon excited fluorescence (TPEF) microscopy, which allows simultaneous observations of living cells and their dynamic interaction with the hydrogel scaffolds at short integration times.

To address the need for a soft, cell-responsive platform with a tissue-mimicking hierarchical architecture, we employed RIE micromolding to introduce reproducible structural features into ELP. PDMS molds with aligned (1D) and unaligned (2D) wavy patterns were used as stamps to imprint features in the ELP with tunable wavelengths spanning nano- to micro-ranges (here between 0.37–4.32 μm on the ELP).²⁸ Because the PDMS mold can be re-used to generate new hydrogels, a high number of samples can be produced at low cost. We investigate the pattern transfer to the ELP hydrogel by advanced microscopy, via AFM and CARS. Combining these microscopy techniques enables high resolution characterization without the need for foreign contrast agents to investigate the detailed chemical (CARS) and structural (AFM) composition of the hydrogels. Finally, we probe the ability of the patterned ELP hydrogels to induce alignment of adipose tissue-derived stem cells (ADSCs). ADSCs are a cell source with potential relevance for regenerative medicine applications as they are relatively easy to isolate in a patient-specific manner and in high abundance, can differentiate into various cell types, and secrete several paracrine growth factors.²⁹ ADSCs are known to be sensitive to a broad range of environmental cues^30–33 including matrix mechanical cues and topographical patterning.^34,35

Experimental

Elastin-like protein (ELP) production and purification

The amino acid sequence for the ELP biomaterial is shown in Table S1 (ESI†). The construction of the plasmid, the expression of ELP in Escherichia coli, and the ELP purification steps have been described in detail elsewhere.³⁶ Briefly, the pET15b plasmid containing the ELP sequence was transformed by heatshock at 42 °C into competent BL21(DE3)pLysS Escherichia coli (Invitrogen). The ELP contained either a fibronectin-derived, cell-adhesion ligand (RGD) or a scrambled version of that amino acid sequence (RDG). The transformed bacteria were cultured in Terrific Broth containing 100 μg ml⁻¹ ampicillin until an optical density of 0.8 at 600 nm has been reached, at which point protein expression was induced with 1 mM isopropyl β-D-1-thiogalactopyranoside. After 5–7 h of expression, the cells were lysed by freeze–thaw cycles with the addition of DNase and 1 mM phenylmethylsulfonyl fluoride. The protein was purified by iterative inverse temperature cycling, which exploits the lower critical solution temperature (LCST) behavior of ELP (Fig. S1, ESI†).³ As a final step, the protein was dialyzed three times against deionized water with a 3.5 kDa membrane at 4 °C and then lyophylized at −56 °C for 24 hours.

Preparation of patterned ELP

Polystyrene (PS) masters with the desired pattern were formed via reactive ion etching (RIE) as described before by Huntington et al.³⁷ Polydimethylsiloxane (PDMS) molds³⁸ were created by mixing degassed vinyl PDMS prepolymer (3.4 g, (7.0–8.0% vinylmethylsiloxane)-dimethylsiloxane copolymer, VDT-731, Gelest, Inc.), 10 μL of a Pt catalyst (platinum-divinyltetramethyldisiloxane, SIP6831.2, Gelest, Inc.), one drop of a modulator (2,4,6,8-tetramethyl-2,4,6,8-tetravinylcyclotetrasiloxane, 396281, Sigma-Aldrich, delivered from a 19 G, 1.5 inch, thin-wall needle), and 1 g of a hydrosilane prepolymer ((25–30% methylhydrosiloxane)-dimethylsiloxane copolymer, HMS-301, Gelest, Inc.). The PDMS (30–40 μm) was spin-coated onto the PS master (1000 rpm, 40 s) and cured for 30 min at 60 °C. Afterwards, an uncured layer of Sylgard 184 PDMS (mixture of base polymer and curing agent at 10 : 1 mass ratio, Dow Corning) was poured onto the thin patterned PDMS layer to a height of 3 mm and then cured for 2 hours at 60 °C. After cooling to room temperature, the PDMS negative was carefully peeled off from the PS master.

To form patterned ELP, a 12.5 wt% stock solution of the lyophilized protein in phosphate-buffered saline (PBS) was prepared overnight at 4 °C. Round cover slips (#1.5 glass, diameter: 5 and 12 mm) were aminated in water with 2% (3-aminopropyl)triethoxysilane in 5% glacial acetic acid for 1 h at room temperature, rinsed with ethanol, and stored in ethanol until use. The lysines in the backbone of the protein were chemically crosslinked with tetrakis(hydroxymethyl)phosphonium chloride (THPC) to form an ELP hydrogel on the pre-chilled PDMS molds. The crosslinking ratio between hydroxyl groups in THPC and primary amines in the ELP was chosen to be 1 : 1 for all experiments, and the final ELP polymer concentration was chosen to be 5 wt%. Both variables can, however, be adjusted to tune the stiffness of the hydrogel (Fig. S2, ESI†) as also previously reported.⁹ The hydrogel was sandwiched against the mold with an aminated glass coverslip, which enables crosslinking of the ELP to the glass for ease of handling. The crosslinking reaction was allowed to proceed for 1 h at 4 °C, and then the hydrogels were dried on the molds for 24 h at 37 °C prior to removal and rehydration in PBS at 37 °C for 72 h. For each PDMS mold a minimum of 5 replicated ELP samples were prepared.

Adipose-derived stem cell (ADSC) culture

All procedures were approved by the ethics board at Gothenburg University and were performed in accordance with the Declaration of Helsinki. ADSCs were extracted from minced and collagenase-digested rat inguinal white adipose tissue via centrifugation²⁹ and then passaged once before being seeded onto the ELP substrates at a concentration of 500 cells per cm². Before each cell experiment the hydrogels were submerged in complete cell culture medium (Dulbecco's Modified Eagle Medium with 4.5 g L⁻¹D-glucose, L-glutamine, 10% fetal calf serum, and 1% penicillin–streptomycin) for 1 h at room temperature. Afterwards the medium was removed and the ADSCs were seeded on top of the scaffolds in replicates. The cells were allowed to attach for 45 min at 37 °C before the well was filled with medium. Cells were either stained after 24 h or kept in culture with medium changes every second day.

Cell staining

Cytosol staining of live cells was performed with CellTracker™ RedCMTPX Dye (MolecularProbes, 3 μM in serum-free medium) or Calcein-AM (live/dead viability/cytotoxicity kit, MolecularProbes, 2 μM in PBS). The cells were incubated for 45 min at 37 °C and then washed twice with serum- and phenol-red free medium before immediate imaging. Cell migration data were collected from six different microscopic regions on two independent samples. More than 20 living cells were tracked. For the alignment analysis, 10 microscopic regions were imaged in total on four independent samples. For F-actin analysis, cells were fixed with formaldehyde, permeabilized with 0.1% Triton X-100 in PBS for 5 minutes, washed twice with PBS, stained with 0.17 μM phalloidin-Alexa 488 conjugate in PBS containing 1% bovine serum albumin for 25 min at room temperature, and finally washed twice again. 2 μM Hoechst 33342 (LifeTechnologies) was used to stain nuclei in formaldehyde-fixed cells with 10 min incubation at room temperature followed by two washes with PBS.

Nonlinear microscopy

Mapping molecular vibrations by the nonlinear optical CARS process requires high peak powers, as well as temporal and spatial alignment of two laser beams. The homebuilt microscopy setup has been described in detail elsewhere.³⁹ In brief, a ps-pulsed laser source (HighQ PicoTrain, SpectraPhysics, 7 ps, 76 MHz) generates 1064 nm and frequency doubled 532 nm beams. The 532 nm beam is in turn guided into an optical parametric oscillator (OPO, Levante Emerald, APE GmbH, Berlin) to generate a tunable output between 690 and 900 nm. In the conducted experiments a wavelength of 811 nm was used and overlapped with the 1064 nm beam from the pump laser to address the CH₃ vibration at 2930 cm⁻¹ for label-free imaging of ELP. To confirm the resonance at this vibration a CARS spectrum was collected from the ELP and compared with a corresponding Raman spectrum (Fig. S3, ESI†). The spontaneous Raman scattering was excited at 730 nm and the spectrum was collected with a CCD camera (Pixis: 400 mounted on an Acton SP2300 spectrometer, Princeton Instruments). The CARS spectrum was collected in the relevant CH region by sequentially tuning the OPO output wavelength. For CARS microscopy the OPO output beam at 811 nm and the 1064 nm beam from the pump laser were spatially and temporally overlapped and then guided into an inverted microscope (Nikon, TE2000-U) through a C1 mirror scanner and focused on the sample by either a 40× oil immersion (Nikon, 1.49 NA) or air (Nikon, 0.95 NA) objective. The lateral and longitudinal dimensions of the focal spot were estimated to be ∼0.45 μm and 1.4 μm, respectively.⁴⁰ Typically, laser powers of approximately 10–20 mW after the objective were used for excitation. Dry ELP samples and PDMS molds were placed on a cover slip and measured with the oil immersion objective. Hydrated samples and samples with cells in well plates were measured with the air objective. Measurements on living cells were conducted with a stage-top incubator (Bold Line, Okolab) keeping a temperature of 37 °C and 5% CO₂ at 95% humidity. CARS signals were detected in transmission mode after filtering out the laser wavelengths by a 661/20 nm bandpass filter (Semrock, FF01-661/20) and collected with a single-photon counting detector (Becker&Hickl, Berlin). TPEF (two-photon excited fluorescence) from labeled cells was collected simultaneously in backward reflection mode using a 514/30 nm (Semrock, FF01-514/30) (Phalloidin-Alexa 488, Calcein) or a 609/57 nm (Semrock, FF01-609/57) (Celltracker Red) bandpass filter. Images were taken with 5 μs pixel dwell time (512 × 512 or 1024 × 1024 pixels per 2D image plane) and summed over 5 acquisitions. Multiple (21–100) sections were scanned in depth (separated by 0.2–1 μm) to form 3D images.

Atomic force microscopy (AFM)

The AFM (NTERGRA, NT-MDT) was equipped with N-type single crystal silicon tips (Sb doped, 3.4 × 1.6 × 0.3 mm, NSG10) and operated in semi-contact mode. Images of exemplary PS master molds, PDMS molds, and dry ELP hydrogels were taken, with 512 × 512 or 1024 × 1024 pixels per 2D image plane to have a certain minimum of steps per wave. The total resolution of AFM depends on the geometry of the tip, which in this setup had an opening cone of about 30° with an end curvature of less than 10 nm.

Image analysis

The Raman spectrum of ELP (Fig. S3, ESI†) was background corrected according to the method published by Beier and Berger.⁴¹ CARS and TPEF images were analyzed using Fiji.⁴² The CARS stacks (before and after rehydration) were summed up over slices between maximum and half-maximum mean intensity, forming a projection of the wrinkles. Then, by applying Otsu local thresholding, which has proven to be more efficient than other segmenting methods for CARS microscopy,⁴³ an estimate of the full-width-at-half-maximum (FWHM) of the wrinkles was obtained. The validity of this approach was confirmed for the dehydrated wrinkles by comparing FWHM values of corresponding wrinkles obtained from AFM, showing excellent agreement (within 6% on average). The widths of the wrinkles were computed from profile plots drawn perpendicular to the wrinkle orientation in the Otsu local thresholded images, covering on average 23 wrinkles per wavelength. AFM images were processed with Gwyddion⁴⁴ using (1) align rows: matching and (2) level data by mean plane subtraction protocols. For the amplitude values, the average amplitude over at least 10 waves was measured. To determine the periodicity of the wrinkles, the fast Fourier transform (FFT) function as described by Huntington et al.³⁷ was used. Briefly, the topographical images were first converted to grayscale and then transformed into a binary mask for FFT analysis. The FFT algorithm converted this spatial domain image to the frequency domain, which enables the determination of the main frequencies of the sample and hence the wavelength of the repeating unit. Detailed procedure of this analysis can be found in the Supplementary Methods S1 (ESI†).

For the analysis of protein aggregates, AFM height profiles along the wrinkles were extracted. The widths of 20–31 aggregates per wavelength were determined as FWHM.

Cell alignment on scaffolds was analyzed with the OrientationJ plugin⁴⁵ using the orientation distribution algorithm.⁴⁶ From these angular distribution curves a FWHM was determined in Fiji, and the results were plotted in GraphPad Prism 6.0.

Statistical significance

A two-tailed t-test was performed to investigate differences in the amplitude/wavelength of the patterns on ELP relative to the ones on PDMS, as well as to compare ELP aggregate widths. 2-Way ANOVA was used to compare wrinkle width on PDMS, dehydrated and hydrated ELP. Statistical difference in actin filament angles was investigated using GraphPad Prism 6.0 and a Kolmogorov–Smirnov test. The FWHM of the actin orientation distribution was analyzed with a Kuskal–Wallis test using Dunn's multiple comparison in groups: 1D (0.60–3.73 μm), 0.37 μm 1D, flat, RDG, 2D (0.40–4.32 μm). P values were ranked: P > 0.05 (ns), P ≤ 0.05 (*), P ≤ 0.01 (**), P ≤ 0.001 (***), and P < 0.0001 (****).

Results and discussion

Fabrication of patterned ELP via micromolding

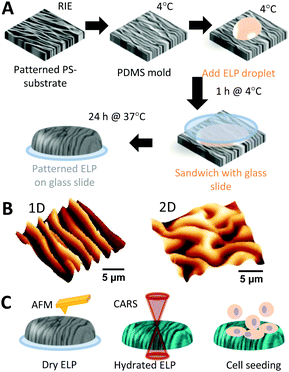
Fig. 1A illustrates the process of imprinting nano- and micro-scale wavy patterns (aligned and unaligned, Fig. 1B) into ELP, as well as their characterization (Fig. 1C). The patterns were fabricated by treating a polystyrene (PS) substrate with CHF₃ reactive ion etching (RIE) and relieving the strain. The wavelength (λ) of the resulting wrinkles on the PS could be controlled from tens of nanometers to multiple microns by simply changing the RIE time.³⁷ Poly(dimethylsiloxane) (PDMS) was molded against the patterned PS to create wrinkled molds for imprinting a covalently crosslinked hydrogel of recombinant ELP polymers, which consist of alternating amino acid sequences of elastin-like domains and fibronectin-derived domains.³ Transferring a polymer solution to a structured substrate by micro/nano-molding consists of a series of challenges.⁴⁷ For example, common challenges include (i) overcoming van der Waals/capillary forces as well as polymer–mold interfacial energies to completely fill the nanostructures of the mold, (ii) the comparable size of the macromolecular unit of the polymer relative to the dimensions of the nanostructured mold, (iii) local thermal and entropic/hydrophobic/hydrophilic effects resulting in local condensation, aggregation, and re/unfolding of the polymer unit, (iv) adhesion of the polymer to the mold, and (v) shrinkage, swelling, or collapse of the polymer structure after detaching the mold. Thus, thorough characterization of the micro-molded polymer is needed to determine how well the pattern has transferred in terms of periodicity and ridge height/width.

Fig. 1 (A) Schematic of the preparation of patterned ELP hydrogels; reactive ion etching (RIE) was employed to create a polystyrene (PS) master, which in turn was used to fabricate a PDMS mold. A droplet of ELP solution with a covalent crosslinking reagent was sandwiched against the PDMS mold with a glass coverslip. After crosslinking and dehydration for 24 h, the PDMS mold was removed to release the patterned ELP substrate. (B) Two wavy patterns were investigated: aligned (1D) and unaligned (2D). (C) The pattern transfer and nanostructure of the imprinted, dehydrated ELP were investigated by AFM, and the response to de/rehydrated conditions as well as the ability of ADSCs to align with the patterns were visualized by CARS microscopy.

Heights of patterns of dehydrated ELP are in general smaller than those of the PDMS molds

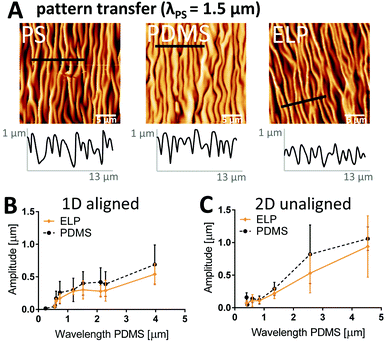
We first investigate to what extent the height (amplitude) and overall pattern of the imprinted structures in dehydrated ELP substrates corresponds to those defined by the PDMS molds and the PS masters for both aligned (i.e. 1D) and unaligned (i.e. 2D) wavy patterns with wavelengths spanning 0.30–4.50 μm (PS master values). AFM images in Fig. 2A confirm that the lateral dimension and the morphology of the dehydrated ELP pattern (λ = 1.35 μm) in general correspond well to that of the PS master (λ = 1.50 μm) with the PDMS as an intermediate negative mold (λ = 1.52 μm) (Fig. 2A). In addition, the AFM profiles show that the amplitude of the ridges vary significantly within one sample already for the PDMS mold and the PS master, with standard deviations as large as 50% of the mean amplitude values.

Fig. 2 (A) AFM images comparing the PS master (left) with the PDMS mold (middle) and the patterned, dehydrated ELP substrate (right) (scale bar: 5 μm). The PDMS mold is a negative of the other two. Heights (0–1 μm) along the lines covering 10 waves (13 μm) are shown in the profile plots below images. (B and C) The heights (plotted versus PDMS wavelength) of the dehydrated ELP (orange) are on average 23% smaller than that of the PDMS (black) for both aligned, 1D (B) and unaligned, 2D (C) samples and all wavelengths, indicating a shrinkage associated with the dehydration (not statistically significant).

Moreover, the profile plots illustrate a trend of decreasing wave amplitude after each transfer step. For the 1.50 μm wavelength pattern, 90% of the amplitude is retained in the transfer from the PS master to the PDMS negative, but only 70% remains on the dehydrated ELP substrate relative to the PS master. Since the major loss of amplitude seems to occur between the transfer step from PDMS to ELP, amplitudes were extracted from profile plots of all PDMS molds as well as corresponding ELP samples and plotted versus PDMS wavelength for aligned (Fig. 2B) and unaligned (Fig. 2C) patterns. First, it can be noted that the amplitude of the waves on the PDMS molds is related to the wavelength as a natural consequence of the RIE process; smaller wavelength results in smaller amplitude. Further, these data confirm that the amplitude in dehydrated ELP was typically less than that of the PDMS mold (with an average decrease of 23%), although no statistically significant differences could be concluded due to the large variability in amplitude. We hypothesize that these decreases in ELP wave amplitude are likely a result of dehydration after crosslinking. As with all hydrogels, ELP substrates are known to undergo significant shrinking and swelling upon dehydration and rehydration, respectively.⁴⁸

The periodicity of the pattern is successfully transferred down to 0.37 μm and unaffected by dehydration

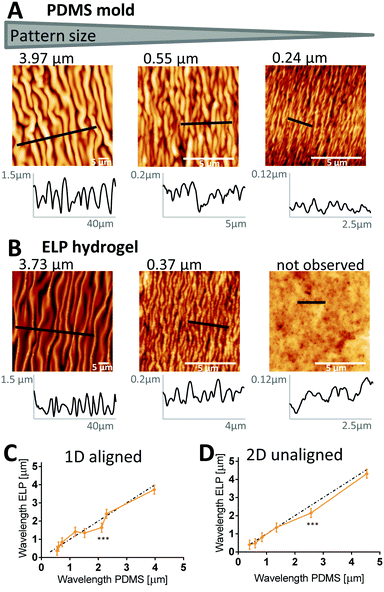
To determine the precision of the micro-molding technique, we first used AFM to confirm the periodicity of PDMS molds made from PS masters, and then investigated how well it is transferred to the ELP and remains after dehydration (24 hours at 37 °C, see Fig. 1). A set of representative images is shown in Fig. 3A and B (PDMS and ELP samples for all wavelengths are shown in Fig. S4, aligned, and S5, unaligned, ESI†). Periodicities were quantified from the AFM images using a 2D fast Fourier transform (FFT) algorithm (for detailed description, see Supplementary Method S1, ESI†). The wavelengths of the PDMS molds ranged between 0.24–4.54 μm. For both aligned (Fig. 3C) and unaligned (Fig. 3D) patterns, good transfer of the mold periodicity to the ELP substrate was achieved; the deviation was on average 2.5%. Thus, unlike wave height and width, wave periodicity is unaffected by the dehydration of the ELP substrate. The FFT algorithm successfully extracted wavelengths from all AFM images of the 1D ELP samples, except for the one originating from the PDMS mold with smallest wavelength (0.24 μm). For the 0.24 μm wavelength PDMS mold, the valley depth was merely 16 ± 10 nm and the average width less than 160 nm – note different scales on x- and y-axes in the profile plots in Fig. 3A and B depending on wavelength. For the 0.24 μm wavelength ELP sample, no wrinkles can be observed (Fig. 3B) and the variations in the profile plot have no repetitive wave-like character. Instead, protein aggregates seem to dominate the surface topography with diameters in the range of 124–180 nm (25–75% quartiles). A similar trend can be noted for the 2D patterns, where a mold with a wavelength of 0.40 μm with 160 nm valley depth can produce a pattern in ELP, while a mold with wavelength 0.43 μm and 48 nm valley depth results in no defined pattern on the ELP (Table S2 and Fig. S5, ESI†). ELPs are known to undergo lower critical solution temperature (LCST) behavior due to hydrophobic interactions between neighboring polymer chains, resulting in self-assembly into protein-dense aggregates at higher temperatures.⁴⁹ These aggregates are here formed during the crosslinking process and may prevent complete filling of the 0.24 μm (1D) and 0.43 μm (2D) wavelength PDMS valleys, since the average aggregate size is comparable to the dimensions of the PDMS valleys. From this we conclude that inherent protein assemblies may define the minimum size of the wrinkles that can be imprinted into ELP.

Fig. 3 (A and B) AFM images of aligned (1D) waves on the PDMS molds (A) and ELP hydrogels (B). Profile plots below images show that waves are successfully imprinted in the ELP samples with wavelengths of 0.37 μm and larger (scale bar: 5 μm). Inherent structures (average diameter 160 nm, i.e. larger than wrinkle width) dominate the topography of the ELP molded on the 0.24 μm PDMS (B, right). (C and D) Quantitative analysis confirms that the wavelength of the PDMS mold is transferred with good fidelity (significant deviations indicated with stars) and that there is on average no significant impact from the dehydration process on the pattern periodicity. Data from 1D (C) and 2D (D) ELP samples are plotted with orange lines (mean ± SD). Perfect transfer of the wavelength from the mold is illustrated by dashed lines in black.

ELP ridge width varies in a broad range with degree of hydration

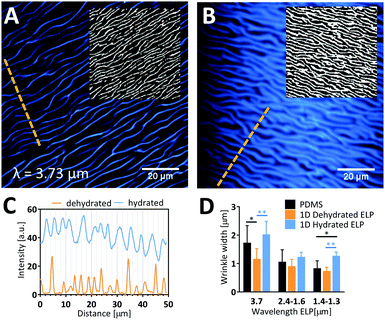
As these patterned ELP materials are intended for use as cell culture substrates in the presence of liquid medium, we next studied the ability of the dehydrated ELP to retain the imprinted pattern upon rehydration and potential swelling. We studied the significant shrinkage/swelling capacity of ELP and its implications on wrinkle dimensions by comparing the widths of wrinkles at dehydrated and hydrated conditions using CARS microscopy (Fig. 4). A clear swelling of the hydrated waves was observed by visual inspection of the raw data images, which was further confirmed by Otsu local thresholding (insets in Fig. 4A and B) and profile plots (Fig. 4C). Wave widths (Fig. 4D) of the dehydrated ELP obtained by CARS microscopy were found to correlate well with width data obtained by AFM (typically less than 6% difference). Since the lateral resolution of CARS is estimated to be about 0.45 μm,⁴⁰ we limited the analysis to samples with pattern widths in the order of 1 μm and greater. Due to the undulating, wrinkled nature of the wavy patterns, large variability in wave width was obtained. Still, there is a clear trend across all samples that the PDMS valley width is larger than the dehydrated ELP ridge and smaller than the rehydrated ELP ridge. On average, a 21 ± 9% decrease in wrinkle width is obtained following dehydration compared to the PDMS mold, which corresponds well to the degree of shrinkage observed for the wrinkle heights. Upon full rehydration, the wrinkle widths swell to a factor of 1.8 ± 0.5 compared to the dehydrated widths, i.e. a factor of 1.5 ± 0.4 larger than the original width measured from the PDMS mold. Due to the large variability in height, there is space for the wrinkles with largest amplitude to expand their width beyond half the wavelength. This shows that while the PDMS mold sets the range of possible wrinkle widths for the patterned ELP, the precise value is determined and can be dynamically altered by changing the degree of dehydration.

Fig. 4 (A and B) CARS microscopy images of aligned (1D) ELP patterns, intensity averaged over the full depth of the waves under both dehydrated (A) and rehydrated (B) conditions (72 h at 37 °C), illustrating that waves shrink under dehydration. Insets show masks obtained by Local Otsu thresholding for quantitative image analysis. (C) Profile plots along the dashed lines in A and B confirm thinner wrinkles for the dehydrated hydrogel. The overall higher CARS intensities for the hydrated sample could be explained by influence of the OH vibrational resonances. (D) Compared to the dehydrated condition, the ELP wrinkles have a capacity to swell with a factor of on average 1.8 (blue vs. orange bars. mean ± SD). Significant differences are indicated with stars.

Presence of the PDMS molds seems to promote protein aggregation in ELP

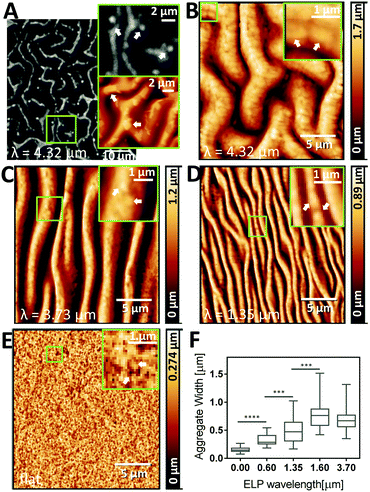
While the wrinkle width and distance determine the micro-scale topography and substrate interactions at the whole cell length-scale, the observation of protein-rich aggregates in ELP is important since they set the nano-scale topography and substrate interactions at the length-scale of cell-surface receptors. Protein assemblies are formed as a result of phase separation, above the LCST of ELP, here upon the temperature shift to physiological temperature, 37 °C.⁴⁹ For this particular ELP sequence (Table S1, ESI†), the LCST is 33.3 °C (Fig. S1, ESI†).³ Above the LCST, hydrophobic interactions between the individual protein molecules dominate, causing aggregation into protein-rich assemblies and depleting the surrounding area.⁵⁰ This liquid–liquid phase separation is influenced by the local temperature, protein concentration, and pH, hence the assemblies can vary in size and shape across samples due to changes in the microenvironment.²⁶ The size of the ELP aggregates is then “locked” into place by the covalent crosslinking chemistry. Thus, we next evaluated to what extent protein assembly size is impacted by the micro-molding technique. High-resolution AFM images and local contrast enhancement indeed showed protein aggregates in samples prepared using PDMS mold with a range of wavelengths (Fig. 5). For example, in unaligned (2D) patterns with the largest wavelength (4.32 μm), aggregates as large as 1–3 μm were observed by both CARS and AFM (Fig. 5A and B). Since CARS microscopy provides chemical contrast by probing the CH₃ vibration at 2930 cm⁻¹, which is characteristic of proteins (see CARS spectrum of ELP in Fig. S3, ESI†), this confirms that the corresponding aggregates observed in the AFM images are indeed high-density regions of protein, i.e. ELP aggregates. Qualitatively, as the pattern size decreases, the size of the ELP aggregates was also decreased (Fig. 5C and D), with unpatterned ELP having the smallest ELP aggregates (Fig. 5E). By analyzing profile plots along the wrinkles, the diameters of the ELP protein domains forming the nano-scale topography were measured (Fig. 5F), confirming the general trend of increasing ELP aggregate size with increasing wavelength. Taken together, it appears that confinement by PDMS valleys promotes ELP aggregation, resulting in larger assemblies than those formed without the patterns, potentially due to locally enhanced concentrations of proteins, which in turn could be due to the hydrophobic character of the PDMS⁵¹ and/or differences in local temperature due to increased surface area. This is supported by the observation that increased concentration of ELP reduces the LCST.⁵² It is likely that the width of the wrinkles then sets a physical limit of how large the protein aggregates can become. These observations motivate future investigations of the details of ELP aggregate formation under nanoscale confinement.

Fig. 5 (A) Micron-sized aggregates (white arrows) are observed in CARS (grey) and AFM (orange) images of unaligned (2D) wrinkled ELP patterns (scale bar: 10 μm, inset: 2 μm). (B–D) High-resolution AFM images with enhanced local contrast confirm that ELP aggregates (white arrows) are present in wrinkles made with several different pattern sizes (scale bar: 5 μm, inset: 1 μm). (E) Unpatterned ELP samples display surface roughness due to inherent protein aggregates (scale bar 5 μm, aggregate diameter 160 nm ± 60 nm). (F) ELP aggregate size as measured from AFM scans on dehydrated hydrogels appears to depend on wrinkle wavelength (median, 25% and 75% quartile, maximum and minimum). Significance indicated with stars.

Stem cells align on 1D patterned ELP with wavelengths between 0.60–4.32 μm

We next evaluated the ability of the patterned ELP substrates to induce alignment of ADSCs. To avoid influence from the underlying glass substrate, the thickness of the hydrogel was kept well beyond the cell perception thickness of 2–20 μm.^53,54 Therefore, we could relate the response of cells solely to the patterned ELP hydrogels. From calculations based on the total hydrogel volume and glass coverslip area, we estimate the thickness of the hydrogel to be between 50 and 100 μm. All samples were prepared with the same polymer concentration and crosslinking density although, they could be readily varied in future studies. ADSCs from rat inguinal white adipose tissue were seeded at 500 cells per cm² onto the scaffolds with no pattern, with aligned (1D) patterns, and with unaligned (2D) patterns, exhibiting wavelengths ranging from 0.37–4.32 μm (Fig. S6, ESI†). After 24 h, ADSCs on aligned (1D) patterns demonstrate elongated cell spreading with actin cytoskeletal fibers arranged parallel to the imprinted ELP pattern for wavelengths 0.60 μm and larger (Fig. 6A, top). In contrast, on unaligned (2D) ELP patterns, no cellular alignment was observed (Fig. 6A, bottom). In order to probe if the RGD cell-binding site is required for this cellular attachment, cells were also seeded on ELP hydrogels that contained a scrambled, non-adhesive version of the peptide sequence – RDG. On these RDG-containing ELP substrates, fewer cells were observed, and the cells demonstrated less cell spreading and grouped together into clusters compared to cells seeded on the RGD-containing substrates (Fig. 6B). These data are consistent with previous studies on embryonic stem cells⁵⁵ and human aortic smooth muscle cells⁵⁶ seeded on protein-coated PDMS surfaces with aligned wrinkles with wavelengths spanning sub-micron to 60 μm. On those relatively stiff substrates, smooth muscle cells could not follow a pattern with 100 nm wavelength and 20 nm depth.⁵⁶ On the patterned ELP the cells did not align on wrinkles with 0.37 μm wavelength and 50 ± 30 nm in amplitude. Here the width of the wrinkles is 260 ± 60 nm under dehydrated conditions, but due to the large swelling capacity of the ELP hydrogel, the hydrated wrinkles may completely fill the spacing between them, which then significantly reduces the effect of the pattern. Taking the ELP swelling factor relative to the PDMS mold into account (1.5 ± 0.4), patterned structures should be hence imprinted at a distance of ∼1.5 times the width of the pattern in order to ascertain that it remains after full rehydration. For the 0.60 μm wavelength pattern, the height of the hydrated wrinkles is significantly larger (130 ± 40 nm), leaving a wrinkled pattern with maintained periodicity on the very top, sufficient to induce cell alignment. This indicates that relatively shallow and narrow spacing between soft patterns still can induce cellular alignment. Cells were then cultured on the ELP substrates in expansion medium until confluency, 96 hours after seeding. During this period of time, the attached cells kept their aligned orientation on the 1D samples as well as their random orientation on the 2D samples (Fig. 6C). We evaluated the angular distribution of actin filament orientations at confluency (Fig. 6D and Fig. S6D, ESI†) to quantify the degree of alignment induced by the surface topography. As the cells align in one direction, their actin filaments also point towards that direction, which causes a decrease in the variability of angles for the actin filaments and thus a narrower distribution.

Fig. 6 (A) Actin cytoskeletal filaments of ADSCs 24 h after seeding on ELP patterns of aligned, 1D waves (top) and unaligned, 2D waves (bottom). (B) Cells also adhere to unpatterned ELP substrates (left, random cell orientation), but show minimal adhesion to negative control hydrogels containing RDG-ELP (right, 1D wrinkles with a 3.73 μm wavelength). (C) Cells become confluent after 96 h on both 1D and 2D ELP patterned substrates and keep their distinct orientation on 1D patterns. (D) Normalized angle distribution of actin filaments on the confluent samples indicating statistically significant (P = 0.007, **) higher organization on the 1D samples. (Scale bar: 40 μm).

As expected, actin fibers tended to align with the orientation of the 1D patterns (i.e. had alignment angles around 0), while cells on 2D patterns had no preferred angular alignment (Fig. 6D). Statistical difference between the two angular distributions could be found. The full width at half-maximum (FWHM) of the angular distribution, a measure of the broadness of the angular distribution and therefore actin filament unalignment, was significantly smaller by a factor of three to four on the aligned, 1D ELP samples, as compared to the 2D samples (Fig. S6D, ESI†). The degree of alignment was similar on all 1D ELP patterns except those with the smallest wavelength 0.37 μm (Fig. S6D, ESI†), which is consistent with the qualitative evaluation based on visual inspection of the images.

ADSCs migrate actively on the ELP scaffolds

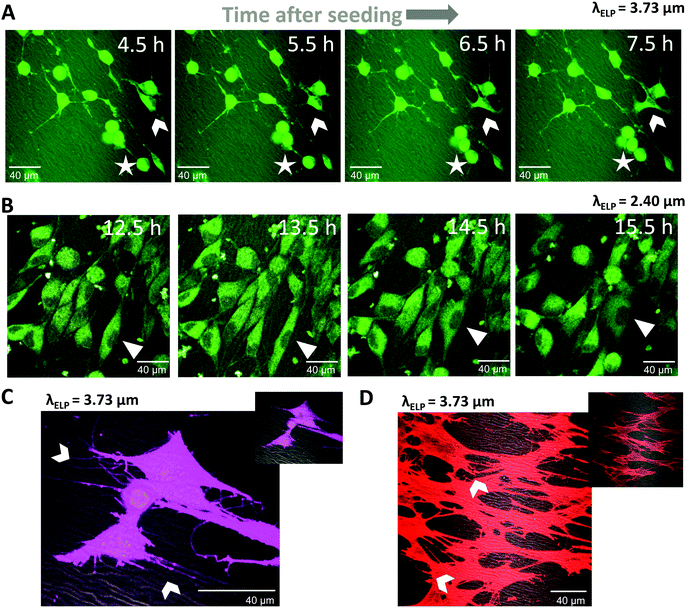
Living cells were studied on the scaffolds in order to verify the suitability of the wrinkled surfaces for studies of cell behavior in, for example, mechanotransduction,⁵⁷ cancer cell migration,⁵⁸ or angiogenesis.⁵⁹ CellTracker Red was used for long-term tracking of cellular migration, since it is well retained across generations of cells and displays low cytotoxicity.⁶⁰ Time-lapse imaging at 30 minute intervals was started 4 hours after cell seeding using an on-stage incubation chamber on the microscope. At early times (4–8 hours) most cells still exhibited a relatively loosely adherent phenotype with a rounded cell shape and long, thin cellular protrusions (Fig. 7A, see cell marked with a star). Over the course of three hours, this cell migrated about 15 μm in a pseudopodal amoeboid form of movement⁶¹ bringing it in closer contact to a cell cluster. Other cells (Fig. 7A, arrowhead) have already attached to the ELP substrate and migrated with the whole cell body adherent to the scaffold by the help of cytoplasmic projections. The cell marked with an arrowhead undergoes a mesenchymal-like migration pattern, where the cell body leads the motion.⁶¹ These two migration patterns can be found in mature connective tissue.⁶² Twelve hours after seeding, most cells had fully attached and appeared well spread (Fig. 7B). The cells continued to be motile at this stage; for example, the cell marked with a triangle first followed the pattern direction along its motion path, stretched and adapted its shape to fit in between two wrinkles, followed by mesenchymal-like migration over the wrinkled pattern.

Fig. 7 (A) Living ADSCs (green, CellTracker Red) can migrate on the patterned ELP scaffolds at early times (A, arrowhead for attached cell and star for unattached cell, 4.5 h after seeding) and at later times (B, triangle denotes migrating adherent cell, 12.5 h after seeding) on aligned 1D patterns with λ = 3.73 μm. (C and D) Cytoplasmic protrusions (arrowheads) visualized with calcein staining (C, magenta) and actin staining (D, red) 24 h after seeding on patterned ELP substrates (grey). These projections are low in intensity relative to the cell body; therefore, in order to see them better they are presented at an increased contrast setting (C and D insets: normal contrast). (Scale bar: 40 μm).

After 24 hours of culture on the ELP patterns, even more cell spreading was observed with several small, distinct cytoplasmic projections protruding from each cell, as evidenced by live cytoplasmic staining (Fig. 7C). Many of these projections were observed to form connections between neighboring cells, while others follow the substrate topography (arrows in Fig. 7C). As expected, these protrusions include F-actin filaments (Fig. 7D), typical for filopodia. In summary, these cell studies demonstrate that (1) cells can survive and migrate during simultaneous fluorescence and CARS microscopy and (2) the patterned ELP substrates induce cell migratory behaviors that are typical for these cells. Taken together, these data suggest an experimental platform that is well suited for in vitro studies of topographical effects on cell behavior.

Conclusions

We show that surface (sub-) micron sized aligned and unaligned wavy patterns can be imprinted in soft, cell-adhesive hydrogels for a wide range of periodicities, widths, and amplitudes by micromolding with PDMS molds. A limit for the smallest possible transferable pattern is set by the formation of inherent protein assemblies, here 124–180 nm in diameter, resulting from the LCST behavior of ELP. The confined space and/or hydrophobicity of the nano-valleys of the PDMS molds promote protein aggregation in ELP. Samples with wavelengths spanning the range of 0.37–4.32 μm could be imprinted, and their pattern periodicity was preserved during substrate dehydration. During rehydration, pattern widths and heights increased beyond the original mold dimensions. ADSCs migrated over the patterned ELP during the first 24 hours after seeding and showed active interaction with the scaffold via cytoplasmic projections. They oriented along 1D aligned patterns and took on a stretched cell morphology on patterns with wavelengths of 0.6 μm and larger, where the periodicity of the pattern remained despite the swelling of the hydrated ridges, while the cells kept a random orientation on the unaligned 2D waves. The cells reach confluency on both scaffolds and maintain their corresponding orientation. Taken together, these micro-molded ELP scaffolds open up new possibilities to study multiple aspects of (stem) cell behavior on patterned, soft, hydrated, cell-adhesive matrices using an engineered biomaterial that enables tuning of substrate mechanics and concentration of cell-adhesion ligands.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We would like to thank Cecilia Brännmark and Charlotta Olofsson, Gothenburg University, for the kind donation of the rat adipose-derived stem cells; Rebecca DiMarco for AFM mechanical measurements of ELP substrates; and Pernilla Wittung-Stafshede, Chalmers University of Technology, for fruitful discussions. The research leading to these results has received funding from the European Union Seventh Framework Program ([FP7/2007–2013]) under grant agreement no. [607842] and the Swedish Research Council. D. R., W.-K. L. and T. W. O. acknowledge the National Science Foundation (CMMI-1462633) and the Office of Naval Research (N00014-13-1-0172) for funding. S. C. and S. C. H. acknowledge funding from the Stanford ChEM-H Institute (SICB-112878), National Science Foundation (DMR 1508006), and National Institutes of Health (U19-AI116484).

References

1. C. J. Bettinger, R. Langer and J. T. Borenstein, Angew. Chem., Int. Ed., 2009, 48, 5406–5415.
2. J. H. Choi, J. M. Gimble, K. Lee, K. G. Marra, J. P. Rubin, J. J. Yoo, G. Vunjak-Novakovic and D. L. Kaplan, Tissue Eng., Part B, 2010, 16, 413–426.
3. K. S. Straley and S. C. Heilshorn, Soft Matter, 2009, 5, 114.
4. E. Ruoslahti, Annu. Rev. Cell Dev. Biol., 1996, 12, 697–715.
5. K. J. Lampe, A. L. Antaris and S. C. Heilshorn, Acta Biomater., 2013, 9, 5590–5599.
6. M. K. Hale, L. A. Setton and A. Chilkoti, Tissue Eng., 2005, 11, 1768–1779.
7. N. Annabi, S. M. Mithieux, E. A. Boughton, A. J. Ruys, A. S. Weiss and F. Dehghani, Biomaterials, 2009, 30, 4550–4557.
8. H. Betre, S. R. Ong, F. Guilak, A. Chilkoti, B. Fermor and L. A. Setton, Biomaterials, 2006, 27, 91–99.
9. C. Chung, K. J. Lampe and S. C. Heilshorn, Biomacromolecules, 2012, 13, 3912–3916.
10. S. Gobaa, S. Hoehnel, M. Roccio, A. Negro, S. Kobel and M. P. Lutolf, Nat. Methods, 2011, 8, 949–955.
11. J. Lee, A. A. Abdeen, D. Zhang and K. A. Kilian, Biomaterials, 2013, 34, 8140–8148.
12. K. Ye, X. Wang, L. Cao, S. Li, Z. Li, L. Yu and J. Ding, Nano Lett., 2015, 15, 4720–4729.
13. F. M. Watt and W. T. S. Huck, Nat. Rev. Mol. Cell Biol., 2013, 14, 467–473.
14. Z. Wang, A. A. Volinsky and N. D. Gallant, J. Appl. Polym. Sci., 2014, 41050.
15. B. K. K. Teo, S. Ankam, L. Y. Chan and E. K. F. Yim, Nanotopography/Mechanical Induction of Stem-Cell Differentiation, Elsevier Masson SAS, 2010, vol. 98.
16. A. Chen, D. K. Lieu, L. Freschauf, V. Lew, H. Sharma, J. Wang, D. Nguyen, I. Karakikes, R. J. Hajjar, A. Gopinathan, E. Botvinick, C. C. Fowlkes, R. A. Li and M. Khine, Adv. Mater., 2011, 23, 5785–5791.
17. J. S. Choi, Y. C. Choi, J. D. Kim, E. J. Kim, H. Y. Lee, I. C. Kwon and Y. W. Cho, Macromol. Res., 2014, 22, 932–947.
18. S. Ma, B. Yu, X. Pei and F. Zhou, Polymer, 2016, 98, 516–535.
19. J. Torgersen, X. H. Qin, Z. Li, A. Ovsianikov, R. Liska and J. Stampfl, Adv. Funct. Mater., 2013, 23, 4542–4554.
20. J. A. Matthews, G. E. Wnek, D. G. Simpson and G. L. Bowlin, Biomacromolecules, 2002, 3, 232–238.
21. P. L. Benitez, S. Mascharak, A. C. Proctor and S. Heilshorn, Integr. Biol., 2015, 8, 50–61.
22. H.-G. Park, H.-C. Jeong, Y. H. Jung and D.-S. Seo, Sci. Rep., 2015, 5, 12356.
23. J.-Y. Park, H. Y. Chae, C.-H. Chung, S. J. Sim, J. Park, H. H. Lee and P. J. Yoo, Soft Matter, 2010, 6, 677–684.
24. A. Zumbusch, G. R. Holtom and X. S. Xie, Phys. Rev. Lett., 1999, 82, 4142–4145.
25. J. Cheng, A. Volkmer, L. D. Book, X. S. Xie, Y. K. Jia and G. Zheng, Biophys. J., 2002, 83, 502–509.
26. H. Wang, L. Cai, A. Paul, A. Enejder and S. C. Heilshorn, Biomacromolecules, 2014, 15, 3421–3428.
27. F. Fleissner, M. Bonn and S. H. Parekh, Sci. Adv., 2016, 2, e1501778.
28. M. D. Huntington, C. J. Engel and T. W. Odom, Angew. Chem., Int. Ed., 2014, 53, 8117–8121.
29. J. M. Gimble, A. J. Katz and B. A. Bunnell, Circ. Res., 2007, 100, 1249–1260.
30. C. Brännmark, A. Paul, D. Ribeiro, B. Magnusson, G. Brolen, A. Enejder and A. Forslöw, PLoS One, 2014, 9, e0113620.
31. L. E. Flynn, Biomaterials, 2010, 31, 4715–4724.
32. E. Bellas, K. G. Marra and D. L. Kaplan, Tissue Eng., Part C, 2013, 19, 745–754.
33. D. H. Stacey, S. E. Hanson, G. Lahvis, K. A. Gutowski and K. S. Masters, Tissue Eng., Part A, 2009, 15, 3389–3399.
34. S. D. Subramony, B. R. Dargis, M. Castillo, E. U. Azeloglu, M. S. Tracey, A. Su and H. H. Lu, Biomaterials, 2013, 34, 1942–1953.
35. R. McBeath, D. M. Pirone, C. M. Nelson, K. Bhadriraju and C. S. Chen, Dev. Cell, 2004, 6, 483–495.
36. K. S. Straley and S. C. Heilshorn, Soft Matter, 2009, 5, 114.
37. M. D. Huntington, C. J. Engel, A. J. Hryn and T. W. Odom, ACS Appl. Mater. Interfaces, 2013, 5, 6438–6442.
38. T. W. Odom, J. C. Love, D. B. Wolfe, K. E. Paul and G. M. Whitesides, Langmuir, 2002, 18, 5314–5320.
39. A. Enejder, C. Brackmann and F. Svedberg, IEEE J. Sel. Top. Quantum Electron., 2010, 16, 506–515.
40. J.-X. Cheng and X. S. Xie, Coherent Raman Scattering Microscopy, CRC Press, 2013.
41. B. D. Beier and A. J. Berger, Analyst, 2009, 134, 1198–1202.
42. J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J.-Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Nat. Methods, 2012, 9, 676–682.
43. J. Hagmar, C. Brackmann, T. Gustavsson and A. Enejder, J. Opt. Soc. Am. A, 2008, 25, 2195–2206.
44. D. Nečas and P. Klapetek, Cent. Eur. J. Phys., 2012, 10, 181–188.
45. Z. Püspöki, M. Storath, D. Sage and M. Unser, Advances in Anatomy, Embryology and Cell Biology, 2016, pp. 69–93.
46. R. Rezakhaniha, A. Agianniotis, J. T. C. Schrauwen, A. Griffa, D. Sage, C. V. C. Bouten, F. N. Van de Vosse, M. Unser and N. Stergiopulos, Biomech. Model. Mechanobiol., 2011, 11, 461–473.
47. B. D. Gates, Q. Xu, M. Stewart, D. Ryan, C. G. Willson and G. M. Whitesides, Chem. Rev., 2005, 105, 1171–1196.
48. K. Trabbic-Carlson, L. A. Setton and A. Chilkoti, Biomacromolecules, 2003, 4, 572–580.
49. A. W. Clarke, E. C. Arnspang, S. M. Mithieux, E. Korkmaz, F. Braet and A. S. Weiss, Biochemistry, 2006, 45, 9989–9996.
50. J. C. Rodriguez-Cabello, S. Prieto, J. Reguera, F. J. Arias and A. Ribeiro, J. Biomater. Sci., Polym. Ed., 2007, 18, 269–286.
51. K. Regehr, M. Domenech and J. Koepsel, Lab Chip, 2009, 9, 2132–2139.
52. D. E. Meyer and A. Chilkoti, Biomacromolecules, 2004, 5, 846–851.
53. A. Buxboim, K. Rajagopal, A. E. X. Brown and D. E. Discher, J. Phys.: Condens. Matter, 2010, 22, 194116.
54. S. Sen, A. J. Engler and D. E. Discher, Cell. Mol. Bioeng., 2009, 2, 39–48.
55. A. Chen, E. Lee, R. Tu, K. Santiago, A. Grosberg, C. Fowlkes and M. Khine, Biomaterials, 2014, 35, 675–683.
56. J. S. Choi, Y. Piao and T. S. Seo, Biotechnol. Bioprocess Eng., 2014, 19, 269–275.
57. M. P. Lutolf, P. M. Gilbert and H. M. Blau, Nature, 2009, 462, 433–441.
58. A. G. Clark and D. M. Vignjevic, Curr. Opin. Cell Biol., 2015, 36, 13–22.
59. A. L. Bauer, T. L. Jackson and Y. Jiang, PLoS Comput. Biol., 2009, 5, e1000445.
60. T. Sun, J. Haycock and S. Macneil, Biomaterials, 2006, 27, 3459–3465.
61. P. Friedl and K. Wolf, J. Cell Biol., 2010, 188, 11–19.
62. P. Friedl, Curr. Opin. Cell Biol., 2004, 16, 14–23.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sm00487g

‡ Equal contribution.

---