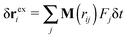Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Deciphering the dynamics of star molecules in shear flow
Jurij
Sablić
a,
Matej
Praprotnik
 *ab and
Rafael
Delgado-Buscalioni
*ab and
Rafael
Delgado-Buscalioni
 *cd
*cd
aDepartment of Molecular Modeling, National Institute of Chemistry, Hajdrihova 19, SI-1001 Ljubljana, Slovenia. E-mail: praprot@cmm.ki.si
bDepartment of Physics, Faculty of Mathematics and Physics, University of Ljubljana, Jadranska 19, SI-1000 Ljubljana, Slovenia
cDepartamento Física Teórica de la Materia Condensada, Universidad Autónoma de Madrid, Campus de Cantoblanco, E-28049 Madrid, Spain. E-mail: rafael.delgado@uam.es
dCondensed Matter Physics Center, IFIMAC, Campus de Cantoblanco, E-28049 Madrid, Spain
First published on 30th May 2017
Abstract
This work analyses the rotation of star polymers under shear flow, in melts, and in good solvent dilute solution. The latter is modeled by single molecule Brownian hydrodynamics, while melts are modeled using non-equilibrium molecular dynamics in closed (periodic) boxes and in open boundaries. A Dissipative Particle Dynamics (DPD) thermostat introduces pairwise monomer friction in melts at will, in directions normal and tangent to the monomer–monomer vectors. Although tangential friction is seldom modeled, we show that it is essential to control hydrodynamic effects in melts. We analyze the different sources of molecular angular momentum in solution and melts and distinguish three dynamic regimes as the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is increased. These dynamic regimes are related with the disruption of the different relaxation mechanisms of the star in equilibrium. Although strong differences are found between harmonic springs and finitely extensible bonds, above a critical shear rate the star molecule has a “breathing” mode with successive elongations and contractions in the flow direction with frequency Ω. The force balance in the flow direction unveils a relation between Ω and the orientation angle. Using literature results for the tumbling of rings and linear chains, either in melt or in solution, we show that the relation is general. A different “tank-treading” dynamics determines the rotation of monomers around the center of mass of the molecule. We show that the tank-treading frequency does not saturate but keeps increasing with
is increased. These dynamic regimes are related with the disruption of the different relaxation mechanisms of the star in equilibrium. Although strong differences are found between harmonic springs and finitely extensible bonds, above a critical shear rate the star molecule has a “breathing” mode with successive elongations and contractions in the flow direction with frequency Ω. The force balance in the flow direction unveils a relation between Ω and the orientation angle. Using literature results for the tumbling of rings and linear chains, either in melt or in solution, we show that the relation is general. A different “tank-treading” dynamics determines the rotation of monomers around the center of mass of the molecule. We show that the tank-treading frequency does not saturate but keeps increasing with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . This is at odds with previous studies which erroneously calculated the molecular angular frequency, used as a proxy for tank-treading.
. This is at odds with previous studies which erroneously calculated the molecular angular frequency, used as a proxy for tank-treading.
1 Introduction
After the pioneering theoretical work by Grest et al.1 in 1989, the interest in star polymers in applied and fundamental science2 has been steadily growing, with theoretical2,3 and experimental contributions.4 More recently, the field is flourishing (see citations in ref. 5 and 6) with new simulations under shear flow,6,7 response under oscillatory perturbation,8 experiments to elucidate their rich spectra of relaxation times5 and studies to elucidate their dual behavior, between polymer and particles.9 Star polymers consist of several linear polymeric chains attached to a central monomer.2 They behave like linear chains if the number of arms or functionality f is small (a linear chain has f = 2) while they tend to be colloid-like for large f.2,5,9,10 The role of the arm length m has been more recently highlighted5,9 to be one of the relevant parameters of such polymer-colloid crossover, showing that short-arm dynamics in stars with f > 6 leads to cooperative relaxation, and different rheological properties than long-armed stars, where entanglements are relevant.Star polymers have a wide range of technical applications such as medical and pharmaceutical applications, wetting, lubrication, coating, binders in toners for copying machines, oil industry, etc.11 The synthesis of monodisperse (in number of arms and degree of polymerisation) star molecules, such as polyisoprene and polybutadiene, by anionic polymerisation enabled the experimental study of static as well as collective and single-molecule dynamic properties of these substances using various microscopic techniques.2,5,11
However, the number of theoretical studies and simulations of star molecules under shear flow is scarce. Gompper’s group has published several papers on the dynamics of star molecules in a sheared solution using the multiparticle collision dynamics (MCD). Ripoll et al. studied individual star molecules with f ∈ [5,50] and m = 30 under shear flow3 and then Singh et al. conducted a study of dilute to semidilute solution ranging from c = 0.19c* to c ∼ 2.5c*12,13 (here, c* is the overlap concentration). More recently, Xu and Chen7 have presented a numerical study of star polymers with a range of functionality f ∈ [3,60] and m = 20 in melts under shear, and Yamamoto et al. have revisited the problem of sheared star polymers in solution.14
At large enough shear rates, any measure of the polymer extension in the flow plane reveals the onset of alternating extensions and contractions of the molecule, typically analyzed from the cross correlation of the molecular elongations in the flow and gradient directions CXY(t).15,16 This behavior is quite general and it has also been studied in linear chains (either free17,18 or tethered16) and in polymer rings under shear.15,19 But how these signals are interpreted as motion depends on the molecule’s architecture. Clearly, in shear flow, a rigid ellipsoid tumbles (turns around) with a precise frequency.20 A linear flexible chain also tumbles because one can assign a “head” and a “tail” and precisely determine a tumbling event (a turn around). However, this is not possible in star polymers and the determination of one tumbling event becomes somewhat arbitrary. A possible criterion is a zero crossing of the molecule’s orientation θ evaluated from its gyration tensor, as it was done for ring polymers15 where tumbling and tank-treading seem to coexist.15 Although a similar study has not been performed in the case of star molecules, for this architecture a discussion on the transition from tumbling to tank-treading dominated dynamics7,13 seems somewhat artificial. In any case, star molecules do not (or seldom) “tumble” but rather keep their flow orientation angle more or less stable, while the arm monomers rotate around the molecule’s CoM following a sort of “tank-treading” motion. The term tank-treading was invented to describe the dynamics of soft visco-elastic objects (e.g. red-blood cells) which rotate with frequency ωR ∝ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) around their center of mass (CoM) but without tumbling, i.e. without essentially altering their orientation against the flow direction.21–23 Later, this term was extrapolated to star polymers.3 To determine the rotation of the monomers around the CoM previous works have used the molecular angular momentum L as a proxy for the angular frequency ω.24 This route is based on the rigid-body relation L = JωL and involves the inertia tensor J. The instantaneous rotation frequency would be strictly that of a rigid-body having the instantaneous configuration of the polymer, then one averages over configurations to obtain 〈ω〉.24 This analogy still makes sense for a linear chain24 which, after all, tumbles like a rigid body does (but certainly with different frequency and dynamics). In the case of star molecules, Ripoll et al.3 and subsequent works12,13 also measured ωL and report that, in dilute and semidilute solutions, it reaches a plateau (ωL → const.) at large shear rates. In melts, Xu et al.7 recently reported ωL ∼
around their center of mass (CoM) but without tumbling, i.e. without essentially altering their orientation against the flow direction.21–23 Later, this term was extrapolated to star polymers.3 To determine the rotation of the monomers around the CoM previous works have used the molecular angular momentum L as a proxy for the angular frequency ω.24 This route is based on the rigid-body relation L = JωL and involves the inertia tensor J. The instantaneous rotation frequency would be strictly that of a rigid-body having the instantaneous configuration of the polymer, then one averages over configurations to obtain 〈ω〉.24 This analogy still makes sense for a linear chain24 which, after all, tumbles like a rigid body does (but certainly with different frequency and dynamics). In the case of star molecules, Ripoll et al.3 and subsequent works12,13 also measured ωL and report that, in dilute and semidilute solutions, it reaches a plateau (ωL → const.) at large shear rates. In melts, Xu et al.7 recently reported ωL ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) α where α ∈ [0.5 − 0.75] increases with the functionality f ∈ [3,60]. These works assign ωL to the tank-treading frequency ωR or, in other words, assume that ωR = ωL. However, if star molecules do not tumble (but rather keep their orientation stable), is it still judicious to interpret ωL as the frequency of the monomer's rotation around the molecule’s CoM? Moreover, the tank-treading frequency in vesicles scales linearly with the shear rate21 instead of saturating to a constant shear-independent value. We believe these questions should be revised. Chen et al.15,19 also used MCD simulations in an attempt to discern tank-treading in ring polymers. They conclude that ring chains mostly tumble at large shear rates but have a significant probability to tank-tread (Ptt ≃ 0.2) with a frequency ωR ∼
α where α ∈ [0.5 − 0.75] increases with the functionality f ∈ [3,60]. These works assign ωL to the tank-treading frequency ωR or, in other words, assume that ωR = ωL. However, if star molecules do not tumble (but rather keep their orientation stable), is it still judicious to interpret ωL as the frequency of the monomer's rotation around the molecule’s CoM? Moreover, the tank-treading frequency in vesicles scales linearly with the shear rate21 instead of saturating to a constant shear-independent value. We believe these questions should be revised. Chen et al.15,19 also used MCD simulations in an attempt to discern tank-treading in ring polymers. They conclude that ring chains mostly tumble at large shear rates but have a significant probability to tank-tread (Ptt ≃ 0.2) with a frequency ωR ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0.6. They obtain ωR from the time correlation of the angle between the CoM-monomer direction and the direction of the chain tilt in flow. This measure captures the individual monomer rotation more precisely. Interestingly, Chen et al. found that tumbling and tank-treading scale similarly with
0.6. They obtain ωR from the time correlation of the angle between the CoM-monomer direction and the direction of the chain tilt in flow. This measure captures the individual monomer rotation more precisely. Interestingly, Chen et al. found that tumbling and tank-treading scale similarly with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) .
.
Aside from this tank-treading or monomer rotation about the molecule’s CoM, another collective motion is observed in star molecules: the overall shape of the star fluctuates in time indicating alternating extensions and contractions with concomitant fluctuations in the instantaneous tilt angle. Following the vesicle dynamics analogy, these would correspond to “breathing” and “swinging” motions,22,23 rather than tumbling. In the case of stars, we have seen that breathing and swinging (tilt fluctuations) have the same origin. We will use the term “breathing” to indicate global molecular expansion/contraction cycles, which are different from tank-treading dynamics. The relation between the breathing frequency (or tumbling in ring and linear chains) Ω and the molecular architecture is also a question that has been posed in the literature.15 Do ring, linear, and star polymers fluctuate in extension in essentially different ways due to their different form? We present a general argument based on the average force balance in the flow direction, showing that the compression/expansion frequency is just determined by the ratio of average molecular extensions in the flow and gradient directions. Thus, the physical origin of tumbling in linear chains and rings and that of “breathing” in stars are the same, and the difference is almost a question of nomenclature. The gradient-to-flow ratio of average extensions is closely related to the tilt angle θ, which decreases with ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and depends on the environment (solution quality), bond type (the harmonic versus the FENE) and hydrodynamics, being also quite different in melts.7 Thus, for the expansion/contraction frequency, differences in the environment and bond type are more determinant than the architecture.
and depends on the environment (solution quality), bond type (the harmonic versus the FENE) and hydrodynamics, being also quite different in melts.7 Thus, for the expansion/contraction frequency, differences in the environment and bond type are more determinant than the architecture.
Another question that this work treats concerns the role of friction in melts. Comparison between single molecules in solution and melts led us to the conclusion that tangential friction enhances the hydrodynamic character of the melt. We checked the “microscopic” origin of such coincidence and found that tangential friction increases the screening length of momentum spreading in the melt. This observation strengthens the message that friction should be an essential part of any coarse-graining model of polymer melts,6,25 and not just a way to extract heat from a non-equilibrium simulation.
We start by presenting the methods used in Section 2 and calibrate the models' relaxation times in equilibrium in Section 2.1. Then, in Section 3, we present the results on the molecular orientation angle θ in flow. Sections 4 and 5 present an analysis of the molecule’s breathing frequency Ω and the “rotation” frequency ωL. Comparison of both frequencies leads to a discussion of the dynamic regimes in Section 6. Although we defer the study of the tank-treading frequency for future work, in Section 6.2, we show that, contrary to the common assumption, ωL does not represent the “tank-treading” frequency. This observation leads to our concluding remarks in Section 7.
2 Setup and simulation details
We consider star polymers under a shear flow along the direction-1, which varies over the gradient direction-2. The mean flow velocity is vflow =![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) x2e1, where
x2e1, where ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the shear rate and e1 is the unit vector in the flow direction. The vorticity of the mean flow points in the direction-3, sometimes called the neutral direction. The star polymers have a central monomer connected with a number of arms f, each arm having m monomers. The total number of monomers of a single chain is N = fm + 1. The polymer model (monomer sizes and bond distances in equilibrium) is taken from ref. 25. In all cases, we model excluded volume interactions between monomers by the repulsive Weeks–Chandler–Anderson (WCA) potential. We shall use σr = 1 and εr = 1 as length and energy units. In these units, the WCA parameters are σ = 2.415 as diameter and ε = 1 as the energy parameter. Melt simulations are carried out at kBT = 4 (i.e. ε = 0.25kBT). The equilibrium distance between non-central monomers is reqij = 2.77 and the equilibrium distance between the central monomer and the first monomer of an arm is reqij = 3.9. Bond interactions are constructed with harmonic springs with stiffness k0 = 20.0ε/σr2 and also consider finitely extensible bonds, using the finite extensible nonlinear elastic (FENE) potential bonds. The spring constant parameter of the FENE potential equals the spring constant stiffness of the harmonic one and the maximum length of the bond is set to rmax = 1.5reqij.
is the shear rate and e1 is the unit vector in the flow direction. The vorticity of the mean flow points in the direction-3, sometimes called the neutral direction. The star polymers have a central monomer connected with a number of arms f, each arm having m monomers. The total number of monomers of a single chain is N = fm + 1. The polymer model (monomer sizes and bond distances in equilibrium) is taken from ref. 25. In all cases, we model excluded volume interactions between monomers by the repulsive Weeks–Chandler–Anderson (WCA) potential. We shall use σr = 1 and εr = 1 as length and energy units. In these units, the WCA parameters are σ = 2.415 as diameter and ε = 1 as the energy parameter. Melt simulations are carried out at kBT = 4 (i.e. ε = 0.25kBT). The equilibrium distance between non-central monomers is reqij = 2.77 and the equilibrium distance between the central monomer and the first monomer of an arm is reqij = 3.9. Bond interactions are constructed with harmonic springs with stiffness k0 = 20.0ε/σr2 and also consider finitely extensible bonds, using the finite extensible nonlinear elastic (FENE) potential bonds. The spring constant parameter of the FENE potential equals the spring constant stiffness of the harmonic one and the maximum length of the bond is set to rmax = 1.5reqij.
Hydrodynamic interactions (HI) between monomers in dilute solution (single chain limit) are introduced implicitly, using a standard Brownian hydrodynamic scheme (overdamped Langevin dynamics) equipped with the Rotne–Prager–Yamakawa mobility matrix.26,27 The hydrodynamic radius of each monomer is set to a = 0.5σ and the Fixman’s method is used to approximate the square root of the mobility appearing in the noise term of the overdamped Langevin equation.27 The monomer diameter σ and WCA energy ε are the same as in melt simulations. The time integration scheme is explicit, using the Euler scheme with the time step 0.01τ. The viscosity is set to η = 0.25, the temperature T = 4, the monomer bare diffusion coefficient D0 = kT/ξm = 0.703 with ξm = 6πηa = 5.69. In terms of the reference monomer diffusion time τ = a2/D0 = 2.07, the time step is dt = 0.01τ. Some of the simulations of single stars in solution are carried out without hydrodynamic interactions (mobility matrix set to a scalar), so as to clearly observe HI effects by comparison. In solution, HI are long ranged (1/r) and induce an Oseen-like perturbative back-flow which is superimposed onto the mean shear. In particular, under shear, HIs expand the chain in the neutral direction and tend to reduce its extension along the flow direction. We shall see that the latter effect has consequences in its rotation dynamics.
In the melt, hydrodynamics arises from the fully resolved, momentum conserving, molecular dynamics (MD). In melts, hydrodynamic interactions are exponentially screened;28 however, we shall see that the back-flow exists and also introduces inter-chain interactions; its shape crucially depends on the monomer–monomer friction forces. In fact, an essential part of a coarse-grained model, like the present one, requires implementation of friction forces between monomers. Here, such friction is introduced in a pair-wise fashion by a DPD thermostat so as to preserve momentum conservation. We consider two pair-wise friction models: one where friction acts only along the vector joining two monomers (normal friction) and another model adding friction also along the perpendicular direction (tangential friction). These generalized DPD thermostats were initially developed by Español29 and then used in ref. 6, 30 and 31. Their relevance in coarse-graining modeling was justified from rigorous bottom-up theory by Hijon et al.25 The DPD thermostat used in this work is explained in ref. 6 and here we just recall the relevant details. In units of m0/τ0 (where m0 = 1 is the monomer mass and τ0 = σr(m0/εr)1/2 is the reference time), the normal friction coefficient γ∥ and the tangential one γ⊥ are γ∥ = 1.0 and γ∥ = 0 for normal friction and γ∥ = 1.0 and γ⊥ = 1.0 for the tangential friction case. In both models, the friction coefficient is constant within a cut-off distance RDPD (we used 27/6σ and 1.5 × 21/6σ) and vanishes beyond (i.e. Heaviside friction kernel).
Melt simulations are performed in a closed periodic environment using the SLLOD dynamics and Lees–Edwards boundary conditions and also in an open (non-periodic) environment using Open Boundary Molecular Dynamics (OBMD).32 In the OBMD setup, the simulation box is open in at least one direction. The system can thus exchange mass with the surroundings. Moreover, OBMD also enables the imposition of the external boundary conditions (e.g. constant normal load and shear flow) on the system, without the modification of Newton’s equations of motion. We refer to ref. 6 for a comparison between these two boundary conditions in terms of rheological properties and pressure–density relations. In melt simulations, the box is 390 × 117 × 117σr3 and the f = 12, m = 6 star polymers occupy a volume fraction of Φ = 0.2, corresponding to a molecular concentration above overlapping c = 1.42c*, where c* = (4πRg3)−1 and the gyration radius Rg = 7.65 (recall that the monomer WCA diameter is σ = 2.415). The equations of motion are integrated by the velocity-Verlet algorithm with time step 0.01τ0 for small and moderate shear rates, and 0.005τ0 for high shear rates.
Table 1 summarizes the models considered in this work.
| Melt (M) | Bonds | Boundaries | Friction |
|---|---|---|---|
| MN-op | Harmonic | Open | γ ∥ = 1.0, γ⊥ = 0.0; RDPD = 1.5σ0 |
| MN-cl | Harmonic | Closed | γ ∥ = 1.0, γ⊥ = 0.0; RDPD = 1.5σ0 |
| MT-op | Harmonic | Open | γ ∥ = γ⊥ = 1.0; RDPD = 2σ0 |
| MT-cl | Harmonic | Closed | γ ∥ = γ⊥ = 1.0, RDPD = 2σ0 |
| Solution (S) | Bonds | Interactions | f–m |
|---|---|---|---|
| SH+HI | Harmonic (H) | Hydrodynamics (+HI) | 12–3; 12–6; 12–11 |
| SH−HI | Harmonic | No-hydrodynamics (−HI) | 12–6 |
| SF+HI | FENE (F) | Hydrodynamics | 12–6 |
2.1 Thermodynamic equilibrium
The different models, in Table 1, are compared by modeling star polymers with f = 12 arms and m = 6 monomers per arm. We also briefly consider the dependence on the arm length in the case of stars with harmonic springs in solution, using f = 12 and m = 3, 6, 11. Our results are consistent with theoretical scaling for star molecule size in equilibrium.1,12 The gyration radius in equilibrium is consistent with the expected scaling Rg2 = b2m2νf1−ν with the excluded volume Flory exponent ν = 0.58. The effective bond distance results to be b = 1.85 for m = 3 while it is consistently closer for longer arms (m = 6 and m = 11), i.e. 1.76 and 1.75, respectively.Star polymers have several relaxation mechanisms,1 which are still under debate.5 We consider three main relaxation mechanisms, which determine the rotation of the whole molecule τrot, the single-arm length decorrelation τarm, and the arm–arm decorrelation τdis. The latter time has also been called disentanglement time; however in this work, the arms are short and entanglements are negligible. In fact, τdis is more properly related to the collective or coordinated motion of the arms, which is known to be enhanced in stars with short arms.5 The time correlation of these mechanisms is expressed in eqn (1)–(3). And their characteristic times can be estimated from the integral of the corresponding normalized autocorrelation function (ACF), via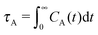 :
:
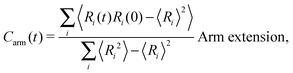 | (1) |
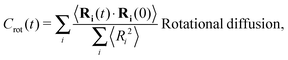 | (2) |
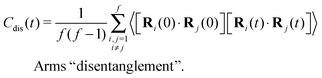 | (3) |
| System | τ rot | τ arm | τ dis |
|---|---|---|---|
| MT, 12–6 | 700 ± 40 | 60 ± 6 | 390 ± 10 |
| MN, 12–6 | 59 ± 5 | 3 ± 1 | 33 ± 2 |
| SH+HI, 12–3 | 95 ± 10 | 10 ± 1 | 67 ± 6 |
| SH+HI, 12–6 | 270 ± 20 | 20 ± 2 | 180 ± 20 |
| SH+HI, 12–11 | 700 ± 70 | 55 ± 5 | 490 ± 50 |
| SH−HI, 12–6 | 500 ± 30 | 25 ± 2 | 260 ± 20 |
| SF+HI, 12–6 | 370 ± 30 | 11 ± 1 | 950 ± 90 |
In the case of SH+HI stars, the rotational diffusion for different arm lengths scales like τrot ≃ σ3m1.65. This exponent is consistent but a bit smaller than 3ν = 1.74, which would result from the relation τr = Rg2/Drot ∼ Rg3 ∼ m3ν and Drot ∼ kBT/(ηRg) the rotation diffusion coefficient.
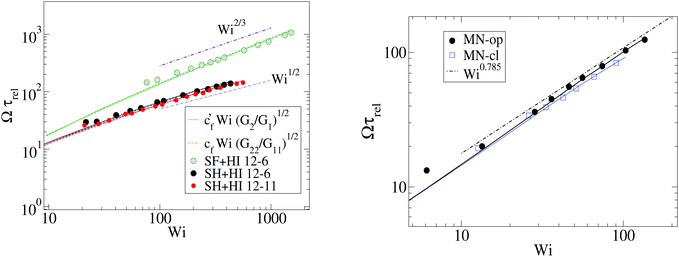
We now define the Weissenberg number for our molecules. Following the standard protocol, we use the longest relaxation time of the molecule (and quote it as τrel) to define the Weissenberg number as Wi = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τrel. Here,
τrel. Here, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −1 represents the time needed to deform a fluid element in shear flow, which is compared with the time needed for the polymer to relax back to its equilibrium shape. We warn, however, that the polymer relaxation time τrel does not have the same physical meaning in the case of harmonic and FENE stars. The stiffer arms of the FENE star present a much larger arm–arm decorrelation time τdis, compared with those observed in harmonic bonds (see Table 2). This large τdis is consistent with the enhanced cooperative motion of short arms recently discussed in ref. 5. Thus, we use τrel = τdis for the FENE model while τrel = τrot is used for harmonic bonds. This is the reason why in some of the graphs below the FENE model data are shifted towards larger values of Wi (about 3 times larger), compared with those cases modeled with harmonic springs. We also plot some of the graphs against WiROT = τrot
−1 represents the time needed to deform a fluid element in shear flow, which is compared with the time needed for the polymer to relax back to its equilibrium shape. We warn, however, that the polymer relaxation time τrel does not have the same physical meaning in the case of harmonic and FENE stars. The stiffer arms of the FENE star present a much larger arm–arm decorrelation time τdis, compared with those observed in harmonic bonds (see Table 2). This large τdis is consistent with the enhanced cooperative motion of short arms recently discussed in ref. 5. Thus, we use τrel = τdis for the FENE model while τrel = τrot is used for harmonic bonds. This is the reason why in some of the graphs below the FENE model data are shifted towards larger values of Wi (about 3 times larger), compared with those cases modeled with harmonic springs. We also plot some of the graphs against WiROT = τrot![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) to reveal this fact.
to reveal this fact.
3 Molecular orientation, θ
The molecular orientation in the flow direction is a quite relevant parameter related to rheological properties33–35 and, as shown in the previous section, connected to the dynamics of the polymer. The average orientation with respect to the flow direction θ is a function of the gyration tensor components,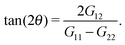 | (4) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −1/3, which can also be analytically obtained for a dumbbell in shear flow, using the Fokker–Planck equation (FPE) for its orientation.17,38
−1/3, which can also be analytically obtained for a dumbbell in shear flow, using the Fokker–Planck equation (FPE) for its orientation.17,38
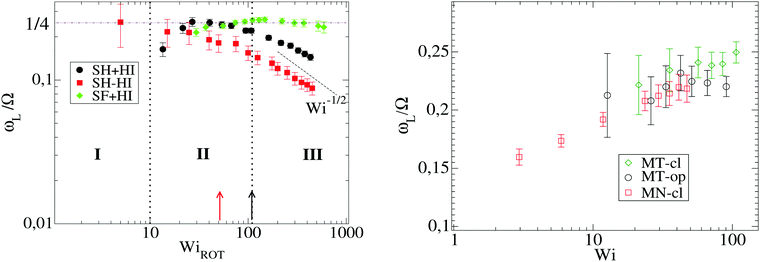
Because the case of star molecules has been relatively less studied, the present results provide new insights into the important relation θ = θ(Wi). These results are shown in Fig. 1 for both solution and melt, for which we have also analyzed the raw data in ref. 7. Let us first consider the polymer dilute solution. The first clear observation is that hydrodynamic's mutual drag forces tend to “compact” the monomers' distribution by increasing the flow-gradient coupling G12, reducing G11 − G22, and also increasing G33 (see below). This leads to larger tilt angles and larger orientational resistances mg = Wi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan(2θ). The trend for θ with Wi is also seen to depend on the presence of HI and the type of bonds. In the case of SH+HI (hydrodynamics included) we observe θ ≃ Wi−1/3 for a broad range of Wi >1. Under no-HI, we find θ ∼ Wi−1/2. However, if the bonds are modeled by harmonic springs, above Wi > 100 cases with HI also converge to the 1/2 exponent. This indicates that at large Wi HIs are reduced along with the increase of the average intermonomer distance (large molecular elongations). By contrast, in the FENE stars the trend is approximately θ ∼ Wi−1/4 and it is comparatively less sensitive to hydrodynamics. The larger exponent is a consequence of the stronger excluded volume interactions (the FENE bonds make less compressible molecules).
tan(2θ). The trend for θ with Wi is also seen to depend on the presence of HI and the type of bonds. In the case of SH+HI (hydrodynamics included) we observe θ ≃ Wi−1/3 for a broad range of Wi >1. Under no-HI, we find θ ∼ Wi−1/2. However, if the bonds are modeled by harmonic springs, above Wi > 100 cases with HI also converge to the 1/2 exponent. This indicates that at large Wi HIs are reduced along with the increase of the average intermonomer distance (large molecular elongations). By contrast, in the FENE stars the trend is approximately θ ∼ Wi−1/4 and it is comparatively less sensitive to hydrodynamics. The larger exponent is a consequence of the stronger excluded volume interactions (the FENE bonds make less compressible molecules).
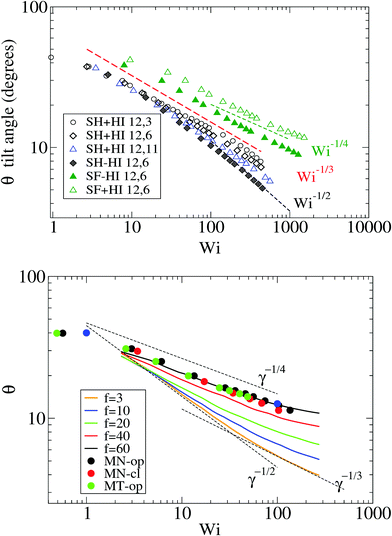 | ||
| Fig. 1 The molecular orientation angle (in degrees) given by eqn (4) for stars in solution (top panel) and in melt (bottom panel). For melts, we compare our results with those of ref. 7. The longest relaxation time was not provided in ref. 7, but just the arm relaxation. For comparison, we multiply the shear rate in ref. 7 by 5500, which is about 10 times the arm elastic relaxation reported therein. | ||
In melts, the trend for θ is highly dependent on the number of arms, as revealed by analysis of the data presented in the recent work of Xu and Chen.7 Our results for f = 12 and m = 6 are consistent with these data (approximately θ ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −1/4). Singh et al.13 have also presented results for the molecular orientation θ of star polymers (with harmonic bonds) in dilute and semidilute solutions c/c* ∈ [0.2,2.4] obtained by multiparticle collision dynamics (MCD) simulations. Their results fit into a master curve upon scaling the shear rate with a molecular relaxation time given by τrel = ϕ(f)τarm, where ϕ(f) ∼ f−2/3 is a functionality dependent function (τrel is proportional to rotation relaxation). They found a scaling θ ∼ Wi−0.43 at large shear rates, which is not quite different from that in Fig. 1 (top, in solution). We have verified that the data of Xu and Chen7 for melts (Fig. 1) do not obey this scaling law: their results for θ (or tan(2θ)) cannot be set in a master curve by scaling with the relaxation time. This disagreement might be due to solvent effects, although one might expect that a dense enough solution should converge to a melt. This disagreement indicates that further revision of the results for melts and dense solutions of star molecules in shear is needed. Another important conclusion is that the tilt angle in stars is very much dependent on hydrodynamics, excluded volume, bond stiffness and environment (solution or melts). Understanding how molecular orientation changes with the shear rate requires more detailed analyses which should incorporate force balances in the gradient and normal directions, taking into account all these contributions. Such analysis will be the subject of our future work.
−1/4). Singh et al.13 have also presented results for the molecular orientation θ of star polymers (with harmonic bonds) in dilute and semidilute solutions c/c* ∈ [0.2,2.4] obtained by multiparticle collision dynamics (MCD) simulations. Their results fit into a master curve upon scaling the shear rate with a molecular relaxation time given by τrel = ϕ(f)τarm, where ϕ(f) ∼ f−2/3 is a functionality dependent function (τrel is proportional to rotation relaxation). They found a scaling θ ∼ Wi−0.43 at large shear rates, which is not quite different from that in Fig. 1 (top, in solution). We have verified that the data of Xu and Chen7 for melts (Fig. 1) do not obey this scaling law: their results for θ (or tan(2θ)) cannot be set in a master curve by scaling with the relaxation time. This disagreement might be due to solvent effects, although one might expect that a dense enough solution should converge to a melt. This disagreement indicates that further revision of the results for melts and dense solutions of star molecules in shear is needed. Another important conclusion is that the tilt angle in stars is very much dependent on hydrodynamics, excluded volume, bond stiffness and environment (solution or melts). Understanding how molecular orientation changes with the shear rate requires more detailed analyses which should incorporate force balances in the gradient and normal directions, taking into account all these contributions. Such analysis will be the subject of our future work.
4 Molecular angular momentum and its effective frequency
The angular momentum of the molecule with respect to its center of mass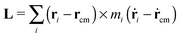 has been considered as an important quantity to understand the molecule’s dynamics under shear. Although for a soft and highly deformable molecule it is not clear how to connect L with the monomer rotations around the molecule’s center of mass (CoM), many works in the past have used decomposition of the monomer velocity based on the following form:
has been considered as an important quantity to understand the molecule’s dynamics under shear. Although for a soft and highly deformable molecule it is not clear how to connect L with the monomer rotations around the molecule’s center of mass (CoM), many works in the past have used decomposition of the monomer velocity based on the following form:| ṙi = ṙcm + ω × (ri − rcm) + ṽ, | (5) |
| ωL = J−1L. | (6) |
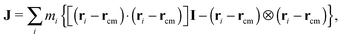 | (7) |
The average effective “rigid body” rotation frequency 〈ωL〉 can be obtained either from 〈ωL〉 = 〈J−1L〉 or from 〈J−1〉 〈L〉. The average is a temporal average. As discussed by Aust et al.24 for the case of linear chains, both evaluations are quite close, reflecting the scarce correlation between J and L. This has also been observed for stars.12 We use the first one, but their differences were found to be negligible. In what follows, we will skip the brackets to alleviate notation and indicate that ωL → 〈ωL〉. We are interested in the component of ωL along the neutral (vorticity) direction ω(3)L, as ω(1)L = ω(2)L ≃ 0. Therefore, we will write ωL to indicate ω(3)L.
The angular velocity ωL for a single chain has been analyzed in many works,12,13,24,39–43 in the search for a connection between the chain structure and its dynamics. An approximate relation between ωL and the components of the molecule’s gyration tensor (here ri = xi,αêα),
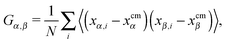 | (8) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) x2,ie1 and an “excess” velocity vexi, which contains contributions from the intra-chain forces (monomer–monomer interaction), inter-chain forces, and hydrodynamic interactions. The total angular momentum of a molecule can thus be expressed as
x2,ie1 and an “excess” velocity vexi, which contains contributions from the intra-chain forces (monomer–monomer interaction), inter-chain forces, and hydrodynamic interactions. The total angular momentum of a molecule can thus be expressed as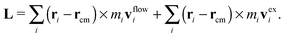 | (9) |
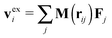 , where Fj is the force acting on monomer-j.† The hydrodynamic contribution stems from the mutual mobility Mij = M(rij) with i ≠ j, while (within the Rotne–Prager–Yamakawa approximation to the mobility26,27) the self-mobility is just a scalar Mii = (6πηa)−1. Velocity contributions from self-mobilities include those coming from internal central forces, which preserve angular momentum and do not contribute to L. The only relevant contributions to L coming from excess velocities are due to hydrodynamic interactions and inter-molecular collisions, only present in melts (or dense solutions). Neglecting the contribution of the excess velocities in eqn (6) and using eqn (7) and (9) immediately leads to a simple relation between the angular velocity ωL (here, indicating its component in the neutral direction) and the components of the gyration tensor Gα,β,
, where Fj is the force acting on monomer-j.† The hydrodynamic contribution stems from the mutual mobility Mij = M(rij) with i ≠ j, while (within the Rotne–Prager–Yamakawa approximation to the mobility26,27) the self-mobility is just a scalar Mii = (6πηa)−1. Velocity contributions from self-mobilities include those coming from internal central forces, which preserve angular momentum and do not contribute to L. The only relevant contributions to L coming from excess velocities are due to hydrodynamic interactions and inter-molecular collisions, only present in melts (or dense solutions). Neglecting the contribution of the excess velocities in eqn (6) and using eqn (7) and (9) immediately leads to a simple relation between the angular velocity ωL (here, indicating its component in the neutral direction) and the components of the gyration tensor Gα,β,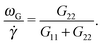 | (10) |
From its very derivation, ωG in eqn (10) should be equal to ωL in eqn (6) if polymer–polymer friction and hydrodynamic couplings between monomers were absent (free draining or Rouse regime). However, ωG ≃ ωL also holds in the case of linear chains in solution with hydrodynamics.24 And, as shown in Fig. 2, we also observe an excellent agreement between ωG and ωL in the case of sheared star polymers in solution. This indicates that hydrodynamic interactions do not seem to directly contribute to the molecular angular momentum. Note, however, that HIs indirectly modify ωL because they modify the gyration tensor Gαα (see eqn (10)). In particular, the effective (rigid body) rotation is faster when HIs are activated [see Fig. 2(a)] because the molecule is made shorter in the flow direction (smaller G11). This fact [shown in Fig. 3(a)] is due to the increased monomer friction induced by mutual hydrodynamic interactions. The other effect of HIs on the molecular shape is to increase its dimension in the vorticity direction G3 (see Fig. 3). This is due to the carrier fluid incompressibility, a condition which is present in the Oseen mobility tensor. However, the expansion in the neutral direction has no direct consequence in the rotation dynamics.
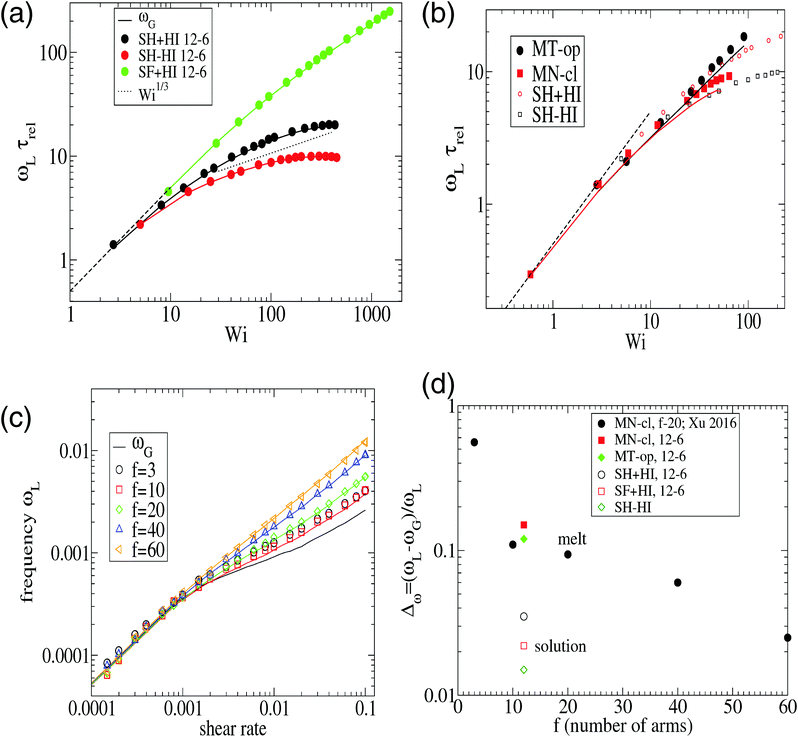 | ||
Fig. 2 The frequency ωL defined in eqn (6) compared with that of eqn (10). Panel (a) corresponds to star polymers in solution, and the results corresponding to the melt are shown in (b) and (c). In (a–c), the symbols correspond to ωL and the lines to ωG ≡ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) G22/(G11 + G22). Panel (b) corresponds to our results for [f,m] = [12,6] stars in the melt (polymer volume fraction ϕ = 0.2 and T = 4ε) (the trends for the same star in solution have been included for comparison). Panel (c) corresponds to the results of Xu and Chen7 for melts of stars with different number of arms f and arm length m = 20. Panel (d) compares the relative difference Δω = (ωL − ωG)/ωL obtained at large shear rates (Wi ∼ 30) for different cases in solution and melt. G22/(G11 + G22). Panel (b) corresponds to our results for [f,m] = [12,6] stars in the melt (polymer volume fraction ϕ = 0.2 and T = 4ε) (the trends for the same star in solution have been included for comparison). Panel (c) corresponds to the results of Xu and Chen7 for melts of stars with different number of arms f and arm length m = 20. Panel (d) compares the relative difference Δω = (ωL − ωG)/ωL obtained at large shear rates (Wi ∼ 30) for different cases in solution and melt. | ||
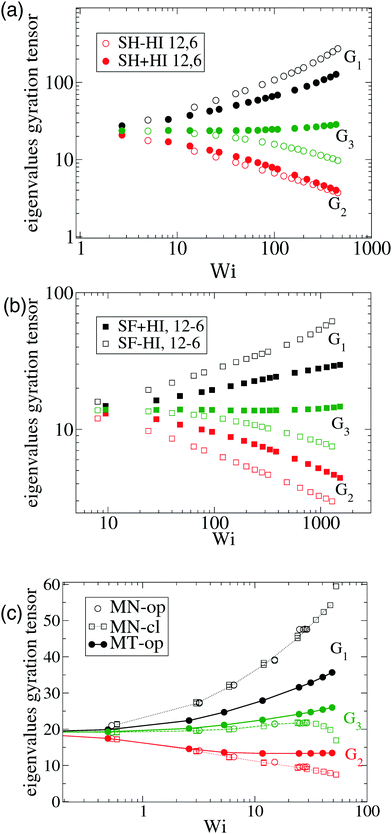 | ||
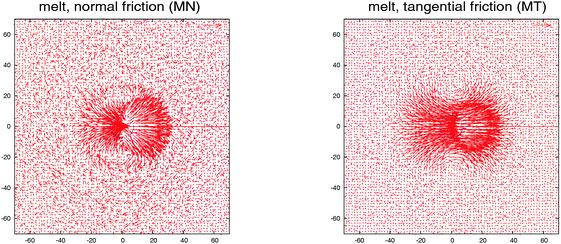
| Fig. 3 The eigenvalues of the gyration tensor defined in eqn (8) for a single star molecule in solution with harmonic bonds (a) and with FENE bonds (b) and in melt (c). In (a and b), we compare hydrodynamic interactions (+HI) with the free draining limit (−HI). In melts (c), we compare the cases where monomers bear only normal friction (MN) and added tangential friction (MT). | ||
A systematic, although small, increase in the deviation of ωG and ωL is observed in passing from a purely Brownian polymer (without HI) to the same molecule (the harmonic bonds) with HI. This can be seen in Fig. 2(d), where we plot the relative deviation Δω ≡ (ωL − ωG)/ωL for Wi ∼ 30. In the SH−HI case (harmonic bonds and no HI), one expects ωL = ωG, so the value of Δω might reflect the noise contribution; meanwhile, cases with HI show small deviations, yet above this noise level. The somewhat smaller deviation found for the FENE bonds (SF+HI), compared with the harmonic ones (SH+HI), might be consistent with the stiffer (more rigid-like) molecular structure although, admittedly, this is a hand-waving argument.
The case of melts is illustrated in Fig. 2(b). We observe that the effective rotation of molecules with added tangential friction (via the DPD thermostat, see above and ref. 6) is faster than that of molecules with just normal friction. In ref. 6, it was also shown that tangential friction has some measurable effect on the polymer rheology: tangential friction contributes to decrease the melt viscosity at similar Wi (a counter-intuitive effect related to the reduction of the monomer kinetic stress when tangential friction is added). The present observation for ωL speed-up goes in the same line. Interestingly, the trend for tangential friction [MT in Fig. 2(b)] resembles the trend obtained in solution with hydrodynamics, while the MN (normal friction) case seems to follow the no-HI trend in solution. Motivated by this coincidence, we revise the trend for the eigenvalues of the gyration tensor in solution (with and without HI) and melt (with normal and tangential friction). Such comparisons can be analyzed in Fig. 3(a)–(c). Interestingly, the dominant eigenvalue of G (approximately the extension in the flow direction, G1) becomes smaller if tangential friction is added, but this is similar to what the HI induce in a dilute solution. In melts, tangential friction also increases the extension of the molecules in the vorticity direction G3, and the molecules breath in the “gradient” direction G2. And this is exactly what the mutual hydrodynamic mobility brings up in solution, as seen in Fig. 3(a) and (b) (note that the HI-induced increase of G2 is particularly relevant for the FENE bonds).
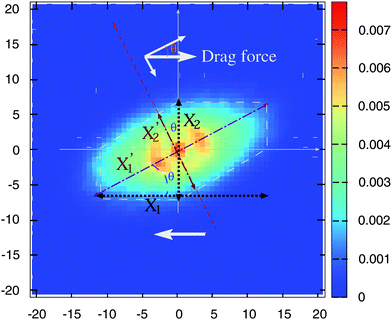
Is there any mechanical justification for such coincidence between HIs in solution and tangential friction in melts? To inspect this issue, we calculate the mutual mobility between molecules in the melt by evaluating the ensemble average of the relative velocity between a tagged molecule 1 and another one “i” at a relative position R1i. This is, 〈V1i〉Ri1, with V1i = Vi − V1 the relative center of mass velocities. The result for a case in equilibrium (no shear flow) is shown in Fig. 4. We see that the mutual (molecular) mobility is more “hydrodynamic like” if tangential friction is present leading to larger screening distances (about a factor two). The larger hydrodynamic coupling between molecules is the reason for the faster rotation in melts with added tangential-monomer-friction.
In melts, inter-chain collisions leading to friction forces introduce a significant amount of angular momentum to each star which reflects in a deviation of ωL from ωG. The intermolecular drag contributes to fasten up the effective rotation frequency ωL with respect to the mean flow approximation ωG. One expects that such difference Δω > 0 should be reduced in compact stars (large f) because of the reduction of the surface-to-volume ratio, while being larger in melts of linear chains. In passing, we note that such inequality Δω > 0 is also observed in solution, see Fig. 2(d). As Fig. 2(b) illustrates, the deviation between ωG (lines) and ωL (filled symbols) increases with the shear rate, which is to be expected, due to increasing inter-molecular friction. An interesting point is that Δω does not substantially depend on tangential friction. We could extract another interesting conclusion by analyzing the data presented in a recent work by Xu and Chen7 on star polymer melts. The results, presented in Fig. 2(c) and (d), permit us to further explore the implications of eqn (10) for architectures with increasing “compactness”, in terms of number of arms f and arm length m. Stars are known to behave like colloids in the limit of large functionality f and transit to “polymeric” behavior for small f. As expected, the values of Δω obtained for Wi ∼ 30 in melts indicate an increasing deviation (Δω > 0) for small f, as the stars become more polymer-like and less colloid like. Even with f as few as 10, the relative deviation Δω remains at just about ten percent, while for f = 3, it suddenly jumps to more than 50 percent. Interestingly, the value of f, where this jump takes place (f ≃ 6), is consistent with that reported in recent work on the transition from polymer to colloidal behavior of star molecules.9 Our results with m = 6 and f = 12 are consistent with those of Xu and Chen,7 with a much larger arm size m = 20. This indicates that the important variable here is the number of arms, rather than the arm length (however, stars with very long arms probably behave differently in this respect).
4.1 Comparison with multiparticle collision dynamics (MCD)
At this point, it is interesting to compare our results and those of Xu and Chen7 (obtained with standard MD) with those obtained from the MCD method (see e.g.ref. 12 and references therein). The published MCD studies considered stars with harmonic springs and various functionalities f, in infinitely dilute solutions3 and moderately dense suspensions.12 For single molecules in the MCD solvent both works3,12 find a master curve for ωL/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) against a scaled shear rate WiMCD = ϕ(f)Wic (in their notation Wic is related to the arm relaxation) collapsing stars of quite different functionalities. It has to be said that the Schmidt numbers (Sc) used in ref. 3 and 12 are Sc = 8 and 17, respectively. Fig. 5 compares the ratio ωL/
against a scaled shear rate WiMCD = ϕ(f)Wic (in their notation Wic is related to the arm relaxation) collapsing stars of quite different functionalities. It has to be said that the Schmidt numbers (Sc) used in ref. 3 and 12 are Sc = 8 and 17, respectively. Fig. 5 compares the ratio ωL/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) obtained from MCD and our results. This figure shows some interesting features. First, contrary to our results and those of Xu’s data, in MCD simulations the difference Δω results to be negative and significant in the case of a single star polymer in solution.3 If ωL < ωG, it seems that hydrodynamic interactions in the MCD model create some extra “drag” which creates angular momentum against the mean flow (whose value is L0 ≡ N
obtained from MCD and our results. This figure shows some interesting features. First, contrary to our results and those of Xu’s data, in MCD simulations the difference Δω results to be negative and significant in the case of a single star polymer in solution.3 If ωL < ωG, it seems that hydrodynamic interactions in the MCD model create some extra “drag” which creates angular momentum against the mean flow (whose value is L0 ≡ N![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) G22) and slows down the molecule’s effective rotation. The same happens in dilute solution (Singh’s result for c = 0.19c*) (see Fig. 5). Note that, in this case, the relative difference (Δω < 0) is, however, smaller (in absolute value) than the single molecule case of Ripoll et al.3 This could be due to a reduction of the solvent fraction, or to the larger Sc used (Sc = 17). In fact, according to Singh et al.’s paper,12 the negative lag Δω < 0 disappears if the solution is made denser (for c/c* = 2.4), i.e. when the volume fraction of the MCD solvent is reduced, probably as L is increased by intermolecular friction. As a second observation, MCD’s single molecule results for ωG by Ripoll et al. are in perfect agreement with the values of ωL obtained here. As ωG is strictly based on the molecular shape, this indicates that the average structure of the MCD molecule in shear flow is similar to ours, but having different dynamics. It has to be said that the definition of the Weissenberg number by Ripoll et al.3 is based on an analytic expression1 and seems to contain an order-one prefactor with respect to our scaling for Wi. In particular, in Fig. 5, we have multiplied their Weissenberg WiMCD = ϕ(f)Wic by 1.7. In doing so, a perfect agreement is found between our ωL and their ωG, while ωL for the MCD simulation is close to our result for the free draining limit (no hydrodynamics). A tentative explanation of the discrepancy with MCD resides in the small Sc the MCD works with. Notably, ref. 3 and 12 report Schmidt numbers of Sc = 8 and 17 respectively, which is unrealistic for polymers. A small value of Sc introduces a finite lag time to unfold hydrodynamic interactions between monomers, which is strictly zero in the Stokes limit (Sc → ∞) we simulate here. A recent work shows that the Stokes limit is only recovered for about Sc > 100.44 Although MCD might also suffer from depletion from point-wise solvent particles, depletion is probably ruled out, because the molecular structure (at least in the flow plane) seems to be similar for MCD and the results hereby. The relation ωL ≃ ωG has been also verified for linear chains in solution,24 indicating that MCD might be suffering from some limitation, probably related to its strong deviation from the Stokes limit Sc → ∞. The MCD has been extensively used for polymer research, so this issue certainly deserves further study.
G22) and slows down the molecule’s effective rotation. The same happens in dilute solution (Singh’s result for c = 0.19c*) (see Fig. 5). Note that, in this case, the relative difference (Δω < 0) is, however, smaller (in absolute value) than the single molecule case of Ripoll et al.3 This could be due to a reduction of the solvent fraction, or to the larger Sc used (Sc = 17). In fact, according to Singh et al.’s paper,12 the negative lag Δω < 0 disappears if the solution is made denser (for c/c* = 2.4), i.e. when the volume fraction of the MCD solvent is reduced, probably as L is increased by intermolecular friction. As a second observation, MCD’s single molecule results for ωG by Ripoll et al. are in perfect agreement with the values of ωL obtained here. As ωG is strictly based on the molecular shape, this indicates that the average structure of the MCD molecule in shear flow is similar to ours, but having different dynamics. It has to be said that the definition of the Weissenberg number by Ripoll et al.3 is based on an analytic expression1 and seems to contain an order-one prefactor with respect to our scaling for Wi. In particular, in Fig. 5, we have multiplied their Weissenberg WiMCD = ϕ(f)Wic by 1.7. In doing so, a perfect agreement is found between our ωL and their ωG, while ωL for the MCD simulation is close to our result for the free draining limit (no hydrodynamics). A tentative explanation of the discrepancy with MCD resides in the small Sc the MCD works with. Notably, ref. 3 and 12 report Schmidt numbers of Sc = 8 and 17 respectively, which is unrealistic for polymers. A small value of Sc introduces a finite lag time to unfold hydrodynamic interactions between monomers, which is strictly zero in the Stokes limit (Sc → ∞) we simulate here. A recent work shows that the Stokes limit is only recovered for about Sc > 100.44 Although MCD might also suffer from depletion from point-wise solvent particles, depletion is probably ruled out, because the molecular structure (at least in the flow plane) seems to be similar for MCD and the results hereby. The relation ωL ≃ ωG has been also verified for linear chains in solution,24 indicating that MCD might be suffering from some limitation, probably related to its strong deviation from the Stokes limit Sc → ∞. The MCD has been extensively used for polymer research, so this issue certainly deserves further study.
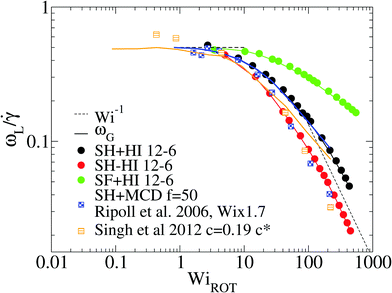 | ||
Fig. 5 Effective rotation frequency ωL (defined in eqn (6)) scaled with the shear rate. We compare the results of multiparticle collision dynamics (MCD) in dilute solution with the present results. The results of stars with f = 50 and m = 30 obtained via MCD are extracted from Ripoll et al.3 (single star molecule) and from Singh et al.12 (dilute solution, c = 0.19c*). The solid lines correspond to ωG in eqn (10) and symbols to ωL in eqn (6). Note that we scale the shear rate with the molecular rotational relaxation time WiROT = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τrot. τrot. | ||
5 Molecular breathing: expansion and contraction
Polymers under shear flow are known to experience large and fast conformation changes3,15,45 in the flow and gradient directions. In linear and ring chains, one can assign a molecule “head” and clearly determine a tumbling event. In the case of stars, these alternating extensions and contractions are probably better described by the term “breathing”. In any case, either tumbling or breathing are the ways to describe the same mechanism: the successive extensions and contractions of the molecule over time. Such information is given by the time-correlation of the gyration tensor components,15,45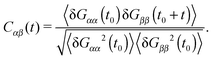 | (11) |
Above a certain shear rate, C12(t) becomes an underdamped signal, i.e. presents negative anticorrelation peaks. The physical meaning is clear: a large fluctuation of the polymer breath in the gradient direction induces an increase in the overall flow drag ξ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) X2 (we denote Xα as the average chain breath in the α direction), which has the consequence of a subsequent large fluctuation (elongation) in the flow direction. As it elongates in the flow direction, the molecule becomes less exposed to the flow drag and, at some stage, it coils back owing to the entropic penalty of being elongated above its equilibrium shape (entropic compression). This “cycle” is not purely periodic but has a characteristic frequency, often called tumbling frequency in the case of free linear chains.18,37 In fact, the same type of dynamics has also been observed in linear chains tethered to a surface and exposed to shear flow.46 In these cases (linear chains), the onset of tumbling takes place above a certain shear rate, which is about the inverse of the rotation relaxation time of the chain. Star molecules, however, have different characteristic times related to different relaxation mechanisms. These times are indicated in Table 2 for our molecular models: τrot molecular rotation, τdis arm disentanglement and τarm individual arm relaxation. It is thus pertinent to ask what is the relaxation mechanism which is altered upon shearing, eventually leading to the onset of expansion/contraction cycles (here we call them “breathing”).
X2 (we denote Xα as the average chain breath in the α direction), which has the consequence of a subsequent large fluctuation (elongation) in the flow direction. As it elongates in the flow direction, the molecule becomes less exposed to the flow drag and, at some stage, it coils back owing to the entropic penalty of being elongated above its equilibrium shape (entropic compression). This “cycle” is not purely periodic but has a characteristic frequency, often called tumbling frequency in the case of free linear chains.18,37 In fact, the same type of dynamics has also been observed in linear chains tethered to a surface and exposed to shear flow.46 In these cases (linear chains), the onset of tumbling takes place above a certain shear rate, which is about the inverse of the rotation relaxation time of the chain. Star molecules, however, have different characteristic times related to different relaxation mechanisms. These times are indicated in Table 2 for our molecular models: τrot molecular rotation, τdis arm disentanglement and τarm individual arm relaxation. It is thus pertinent to ask what is the relaxation mechanism which is altered upon shearing, eventually leading to the onset of expansion/contraction cycles (here we call them “breathing”).
Such a question requires a precise determination of the “transition” based on the form of time-correlation of the gyration tensor components. Fortunately, the time correlation of the gyration tensor components in eqn (11) offers a clear distinction of such transition, which is illustrated in Fig. 6 (corresponding to stars with harmonic bonds). At small shear rates (Wi < 10), the molecule is slightly strained by the flow drag and according to the decay of C12(t) is able to exponentially relax its shape. Above Wi > 10, we observe an oscillatory component in C12(t) with a pronounced maximum at t− < 0 and minimum negative correlation at t+ > 0.15,17 The lapse τt = 2(t+ − t−) should be interpreted as the characteristic time for one “breathing” event, in other words the average time between two stretched molecular configurations (stretched-contracted-stretched). The corresponding angular frequency is noted as Ω = 2π/τt. We can now answer the question we posed above; according to our results the transition to breathing dynamics takes place for τrot![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∼ 10. A glance of Table 2 reveals that this corresponds to τarm
∼ 10. A glance of Table 2 reveals that this corresponds to τarm![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) > 1 and this indicates that the molecular expansion and contraction cycle starts to happen when the shear rate is faster than the arm relaxation time τarm (needed by elastic entropic forces to recover its most probable configuration).
> 1 and this indicates that the molecular expansion and contraction cycle starts to happen when the shear rate is faster than the arm relaxation time τarm (needed by elastic entropic forces to recover its most probable configuration).
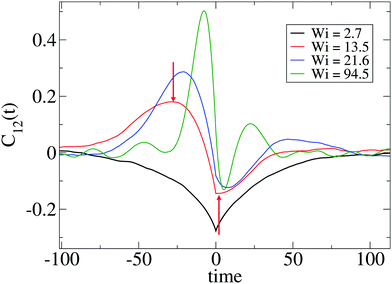 | ||
| Fig. 6 Cross-correlation of polymer extension in the flow (1) and gradient (2) directions, C12(t) defined in eqn (11) for several values of Wi and the SH+HI 12–6 case (see Table 1). The arrows correspond to the first extremes of C12 from which we obtain the time lapse τt/2 (see text). The breathing frequency is defined as Ω = 2π/τt. | ||
Fig. 6 indicates that the non-equilibrium dynamics have several characteristic times. A better determination of these dynamics might require fitting the time correlation of the gyration tensor components with at least two mechanisms (recovery and damping), using for instance C12(t) ∼ exp[−Γt]cos[Ωt + ψ] (as some of us used in linear chains17). Such simple fit (which, by the way, fails in the case of stars) would reveal the characteristic frequency Ω and another non-equilibrium relaxation rate Γ related to dissipation under flow.17 Such dissipative mode is already present before the “tumbling” or “breathing” transition (see Fig. 6 for Wi < 10). Here, we will just analyze the oscillatory component of the time-correlation of the gyration tensor, Ω, and defer its decorrelation envelope Γ (related to the quality factor of the corresponding power spectra) for future work.
5.1 A scaling relation for the breathing frequency
We now seek a relation between the expansion/contraction rate (i.e. the tumbling frequency in linear chains or the breathing rate used hereby) and the chain average shape. To that end, we use an order of magnitude analysis for the force balance in the flow direction based on the average molecular properties: extensions Xα, tension K and friction coefficient ξ. In general, K and ξ depend on the molecular size, shape and Wi; however, the present analysis will only need the ratio K/ξ because we focus on the expansion/contraction frequency Ω.First, a relation between the average extension in the flow X1 and gradient directions X2 can be determined from the balance of the drag force ξ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) X2 and the molecular tension KX1,
X2 and the molecular tension KX1,
KX1 ∼ ξ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) X2 X2 | (12) |
| ξẊ1 ∼ ξΩX1 ∼ KX1, |
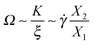 | (13) |
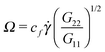 | (14) |
Before falsifying eqn (14) against simulation results, it is interesting to consider the force-balance in the molecular frame coordinates, given by the eigenvectors of the gyration tensor. In this frame, the molecular elongations can be taken as the square root of the eigenvalues of G, and we note them as Xα′ = Gα1/2. The eigen-directions in the flow-gradient plane are rotated by an angle θ with respect to the laboratory frame (x1′,x2′) = ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) θ(x1,x2)T with
θ(x1,x2)T with ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) θ being the rotation unitary orthogonal matrix and the primes denoting coordinates in the molecular frame. Second rank tensors transform as G′ = RθGRTθ and the average molecular tilt θ in eqn (4) is precisely the angle providing G12′ = 0.
θ being the rotation unitary orthogonal matrix and the primes denoting coordinates in the molecular frame. Second rank tensors transform as G′ = RθGRTθ and the average molecular tilt θ in eqn (4) is precisely the angle providing G12′ = 0.
We find that approximately for θ < 0.4 rad the tilt is roughly proportional to the width-to-length ratio X2/X1. In particular, (G22/G11)1/2 ≃ 1.8θ. A similar relation is found for the eigenvalues of the gyration tensor, (G2/G1)1/2 ≃ 2.0θ. In fact, for any shear rate both ratios (G2/G1 and G22/G11) are close and proportional to each other (G2/G1 ≃ 0.88G22/G11 for the FENE while the constant is 0.85 for the harmonic chains). This indicates that the force-balance in the longest molecular direction x1′ has also the form of eqn (12). A simple geometrical argument supporting this claim is given in the Appendix.
5.2 Breathing frequency in star polymers
Fig. 7 shows that the relation, given by eqn (14), correctly describes the relation between breathing dynamics and average molecular shape in all the cases considered (solution and melt). For the range of sizes studied here, we observe that for star polymers in solution (with hydrodynamic interactions, SH+HI) Ω is roughly independent of the molecular size N. This would imply that in this case K and ξ scale similarly with N (this is not the case in linear chains). We find that the constant cf in eqn (14) is indeed quite similar for all the star sizes and cases considered: in solution the best fit corresponds to cf = 1.75 while cf = 2.0 in melts. Fig. 7 also shows that the eigenvalues of the gyration tensor can also be used to forecast the breathing frequency, Ω = cf′![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (G2/G1)1/2 where cf′ = 2.0 in solution and cf′ = 2.3 in melt.
(G2/G1)1/2 where cf′ = 2.0 in solution and cf′ = 2.3 in melt.
5.3 Tumbling frequency in ring and linear polymers
Eqn (14) stems from a quite general relation, which is independent of the polymer architecture. We expect that it should hold for linear chains and ring polymers, two cases for which we found published results. For Wi > 10, we observe that G22/G11 ≃ c2θ2 so that eqn (14) becomes| Ω ≃ cθθ(Wi)Wi. | (15) |
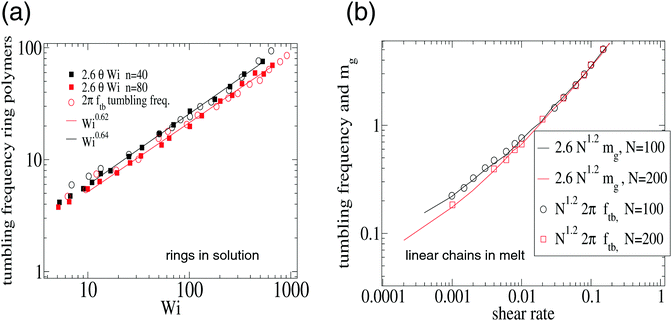 | ||
| Fig. 8 Validation of eqn (15) for the tumbling frequency Ω = 2πftb in (a) ring polymers in solution and (b) linear (FENE) chains in melt. The results in (a) were analyzed from the multiparticle collision dynamics (MCD) simulations of Chen et al.15 on ring polymers with n = 40 and n = 80 beads in shear flow. And the results in (b) are from Xu et al.47 corresponding to a melt of FENE linear chains at volume fraction ϕ = 0.45 (non-equilibrium MD using a DPD thermostat). In (b) we plot the tumbling frequency and the resistance parameter mg (see text). In both cases, the agreement is excellent. | ||
This result is important because it means that the differences in tumbling frequencies observed between different polymer architectures, polymer type and environment (excluded volume, hydrodynamics, melt vs. solution, etc.) can be explained from the force balance in the flow direction, being ultimately determined by the group ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (G2/G1)1/2. This group scales like the orientation resistance mg. We consistently observe that
(G2/G1)1/2. This group scales like the orientation resistance mg. We consistently observe that
| Ω = cmmg |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0.75 at large shear rates). In fact, as mg is a standard parameter in polymer physics we have used it to collect, in Table 3, our findings for different polymer architectures. The quotient cm = Ω/mg is independent of the shear rate for all the studied cases (polymers in solution with or without hydrodynamics or in melt). In Table 3, we have included results in solution and melt and different architectures and models. Remarkably, Ω ∝ mg holds for all the range of shear rates reflecting that the ratio cm = Ω/mg stems from material (K) and environment (ξ) properties (see eqn (13)) and, depending on the polymer architecture, it might lead to (mass-independent) universal ratios. We thus suggest future studies to report values of such ratio. For star and ring polymers and linear chains in melt cm seems to be roughly independent of the molecular weight N. However, this seems not to be the case of linear chains in solution, as deduced from the data obtained in previous work.17
0.75 at large shear rates). In fact, as mg is a standard parameter in polymer physics we have used it to collect, in Table 3, our findings for different polymer architectures. The quotient cm = Ω/mg is independent of the shear rate for all the studied cases (polymers in solution with or without hydrodynamics or in melt). In Table 3, we have included results in solution and melt and different architectures and models. Remarkably, Ω ∝ mg holds for all the range of shear rates reflecting that the ratio cm = Ω/mg stems from material (K) and environment (ξ) properties (see eqn (13)) and, depending on the polymer architecture, it might lead to (mass-independent) universal ratios. We thus suggest future studies to report values of such ratio. For star and ring polymers and linear chains in melt cm seems to be roughly independent of the molecular weight N. However, this seems not to be the case of linear chains in solution, as deduced from the data obtained in previous work.17
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan(2θ), obtained from fits to simulation results. The values of cm for rings come from the analysis of the results in ref. 15 for n = 40 and n = 80 beads using multiparticle collision dynamics (MCD) and those for stars correspond to the present work. The results for linear (FENE) chains are obtained from the analysis of the results of the study published by one of us in ref. 17, corresponding to chains of length N ∈ [2,90]. The results for linear FENE chains in melt were analyzed from the results of Xu et al.47 using non-equilibrium MD and DPD thermostat (note that ref. 15 and 47 report values of Ω/(2Π)). The present results correspond to melts of star molecules with harmonic bonds. The polymer volume fraction ϕ is indicated
tan(2θ), obtained from fits to simulation results. The values of cm for rings come from the analysis of the results in ref. 15 for n = 40 and n = 80 beads using multiparticle collision dynamics (MCD) and those for stars correspond to the present work. The results for linear (FENE) chains are obtained from the analysis of the results of the study published by one of us in ref. 17, corresponding to chains of length N ∈ [2,90]. The results for linear FENE chains in melt were analyzed from the results of Xu et al.47 using non-equilibrium MD and DPD thermostat (note that ref. 15 and 47 report values of Ω/(2Π)). The present results correspond to melts of star molecules with harmonic bonds. The polymer volume fraction ϕ is indicated
| Linear (FENE) | Solution | Melt | |||
|---|---|---|---|---|---|
| Rings | Star-harmonic | Star-FENE | Linear ϕ = 0.45 | Star ϕ = 0.2 | |
| 0.4N−1/3 | 1.20 | 1.41 | 1.57 | 2.6 | 1.73 |
The present findings shed light on recent literature discussions3,13,15,19 about the different polymer architectures concerning tumbling dynamics. The conclusion is that such structure–dynamic relation is controlled by the aspect ratio G2/G1. A deeper understanding of this ratio (or equivalently mg) requires unveiling the force balance in the gradient and neutral directions in different polymers and environments.
6 Dynamic regimes
The frequency ratio ωL/Ω can be a useful quantity for determining different dynamic regimes of the sheared molecules. We find that Ω (in eqn (14)) and ωL (or more precisely ωG in eqn (10)) are directly connected with the polymer shape. Combining both relations one gets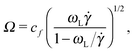 | (16) |
6.1 Low shear rates
For![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τrot < 1 the molecule has a spheroid shape with G11 ≃ G22 so that the angular velocity scales like ωL ≃
τrot < 1 the molecule has a spheroid shape with G11 ≃ G22 so that the angular velocity scales like ωL ≃ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) /2. Monomers move affinely with the flow and the angular frequency coincides with half the fluid vorticity. The polymer shape relaxes exponentially (see Fig. 6) without any expansion/contraction event. In the range τrot−1 <
/2. Monomers move affinely with the flow and the angular frequency coincides with half the fluid vorticity. The polymer shape relaxes exponentially (see Fig. 6) without any expansion/contraction event. In the range τrot−1 < ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) < τarm−1, ωL starts to be smaller than
< τarm−1, ωL starts to be smaller than ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) /2 but the molecule still does not experience expansion/contraction cycles.
/2 but the molecule still does not experience expansion/contraction cycles.
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a2.gif) τarm > 1.
Approximately for
τarm > 1.
Approximately for ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τarm > 1 a transition to a “breathing” dynamics (expansion/contraction of the gyration tensor) takes place. Note that τarm is the arm elastic relaxation time, given in Table 2 (for a linear chain case f = 2 this transition would correspond to the chain “tumbling”). Using the relation ωL ∼
τarm > 1 a transition to a “breathing” dynamics (expansion/contraction of the gyration tensor) takes place. Note that τarm is the arm elastic relaxation time, given in Table 2 (for a linear chain case f = 2 this transition would correspond to the chain “tumbling”). Using the relation ωL ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) /2 valid for immediately smaller shear rates in eqn (16) one gets
/2 valid for immediately smaller shear rates in eqn (16) one getsΩ ≃ 2cfωL ≃ cf![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a2.gif) τlag > 1.
At large shear rates,
τlag > 1.
At large shear rates, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) /ωL ≫ 1 (see eqn (10) for G11 ≫ G22) and eqn (16) becomes
/ωL ≫ 1 (see eqn (10) for G11 ≫ G22) and eqn (16) becomesΩ ≃ cf(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ωL)1/2. ωL)1/2. | (17) |
At larger shear rates, the molecule becomes highly elongated G11 ≫ G22 so that ωL ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) G22/G11. In the particular case of harmonic bonds, we observe that G22/G11 ∼
G22/G11. In the particular case of harmonic bonds, we observe that G22/G11 ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −1. As a consequence, ωL ∼
−1. As a consequence, ωL ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) G22/G11 reaches a plateau (see Fig. 2(a)) and, consistent with eqn (16), Ω ∼
G22/G11 reaches a plateau (see Fig. 2(a)) and, consistent with eqn (16), Ω ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 1/2. This is observed for both HI and non-HI simulations, indicating that above a certain molecular elongation the effect of HIs becomes negligible.
1/2. This is observed for both HI and non-HI simulations, indicating that above a certain molecular elongation the effect of HIs becomes negligible.
However, we stress that this regime with ωL → cte (III in Fig. 9, left panel) is not observed in the FENE chains (neither in melts), so contrary to that claimed in ref. 3, the saturation of the monomer’s angular rotation (ωL ∼ cte) is not a property of the star molecule’s architecture, but rather depends on the bond stiffness, excluded volume and environment (melt or solution).
We tried to understand what molecular time characterizes this large shear-rate regime, by thinking over the fastest molecular response time. The sequence of motion of the molecule in shear flow is first to elongate in the velocity gradient direction and after some time lapse τlag to stretch in the flow direction. This response time, τlag, is defined as the phase-lag between the gradient–gradient and flow–flow time-correlations of the gyration components [see ref. 17 and Fig. 10(a)] and it has been related with dissipation.17 It is quite sensitive to molecular material properties: a rigid molecule presents τlag = 0 while softer molecules have a finite response time. But, how this lag time changes with the shear rate? Fig. 10 illustrates the problem and presents the definition of τlag obtained from the phase difference between C22(t) and C11(t) which lags behind (more precisely they were obtained from τlag = t1 − t2 with Cii(ti) = c, and we tried c = {0.1,0.2,0.3} to verify that τlag is not sensitive to the cut-off c). The response time τlag is seen to increase from zero at small shear (obviously τlag = 0 for the molecule in equilibrium, as there is no cause preceding consequence), up to a maximum value τmaxlag. Interestingly, we find that the ratio τlag/τrot converges at large Weissenberg number to a certain value which only depends on the molecule’s “stiffness”. For SH stars (harmonic bonds), we find τlag/τrot → 0.01 [see Fig. 10(b)], while for the FENE bonds (SF) this value is much smaller. The monomer relaxation time is τm = ξm/k0 and equals 0.28 for harmonic bonds with spring constant k0 (see Section 2). Scaling the lag time with this monomer time, one gets τlag/τm = 17 for SH−HI 12–6 stars and τlag/τm = 8 for SH+HI 12–6 stars. Assuming that one of the 6 linear chains forming two arms, which cross the star through its center (having Nl = 2m = 12 beads), has a relaxation spectrum of τp = (Nl/p)ντm, with ν = 2 for free-draining chains (no hydrodynamics) and ν = 3/2 when hydrodynamic interactions are present, one concludes that in both cases (with or without HI), τlag corresponds to a mode with p = 4. This means that the limit value of τlag at large shear rates is roughly equal to the relaxation time of 12/4 = 3 consecutive monomers of one arm. In the case of the SH+HI 12–3 star, we get τlag/τm ≃ 3.6 and p ≃ 2, also resulting in a mode with 6/2 = 3 monomers. Although these are gross estimations, the good agreement indicates that at some large enough shear rate, the flow strain might become even faster than the response time of a few consecutive monomers. In such a case, above a certain Wi, τlag saturates to the fastest possible molecular response time (a Rouse mode for consecutive monomers). The saturation of τlag is illustrated in Fig. 10(b) and the limiting shear rate can be deduced from the condition ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τlag > 1 illustrated in Fig. 10(c). For
τlag > 1 illustrated in Fig. 10(c). For ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τlag > 1, monomers are advected collectively and the length distribution of the individual harmonic bonds shows strong deviations from the equilibrium value req. The condition
τlag > 1, monomers are advected collectively and the length distribution of the individual harmonic bonds shows strong deviations from the equilibrium value req. The condition ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τlag = 1 occurs at Wi ≃ 100 (SH+HI 12–6 case) and at Wi ≃ 45 (for SH−HI 12–6). Above these values [indicated with vertical lines in Fig. 9(a)], ωL reaches a plateau and Ω ∼
τlag = 1 occurs at Wi ≃ 100 (SH+HI 12–6 case) and at Wi ≃ 45 (for SH−HI 12–6). Above these values [indicated with vertical lines in Fig. 9(a)], ωL reaches a plateau and Ω ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 1/2. Around Wi ∼ 400, (G22/G11)
1/2. Around Wi ∼ 400, (G22/G11)![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) reaches a maximum value [see SH cases in Fig. 2(a)]. In fact, at even larger shear rates (Wi > 103) we observed that ωL ∼
reaches a maximum value [see SH cases in Fig. 2(a)]. In fact, at even larger shear rates (Wi > 103) we observed that ωL ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −1 (not shown). The reason is the following (see eqn (10)): for these extreme shear rates, the highly deformed molecular bonds weakly connect the molecular displacements in flow with contractions and expansions in the gradient direction. The molecule then approaches the limit of a Gaussian polymer under shear flow, for which G22 is constant and G11 ∝
−1 (not shown). The reason is the following (see eqn (10)): for these extreme shear rates, the highly deformed molecular bonds weakly connect the molecular displacements in flow with contractions and expansions in the gradient direction. The molecule then approaches the limit of a Gaussian polymer under shear flow, for which G22 is constant and G11 ∝ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 2. Thus, the conclusion ωL → cte for large Wi, made in previous works (ref. 3 and 12–14), is not exact and it is due to a limited window of observation. Here we present results for Wi < 400 (which is also the range of Wi analyzed in ref. 3) and defer an exploration of larger Wi for future work.
2. Thus, the conclusion ωL → cte for large Wi, made in previous works (ref. 3 and 12–14), is not exact and it is due to a limited window of observation. Here we present results for Wi < 400 (which is also the range of Wi analyzed in ref. 3) and defer an exploration of larger Wi for future work.
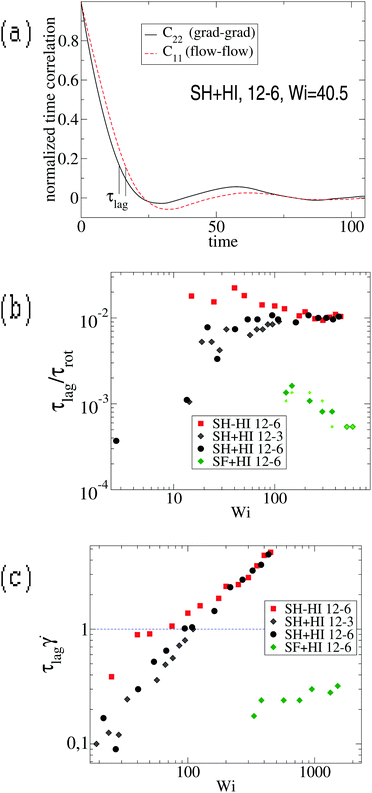 | ||
Fig. 10 (a) Time correlation of the star extensions in the flow–flow (C11) and gradient–gradient (C22) directions indicating the meaning of the lag time τlag: the time between a fluctuation in molecular extension along the gradient direction and the subsequent elongation in the flow direction. (b) The lag time scaled with the longest relaxation (rotational) time. (c) The lag time τlag scaled with the shear rate τlag![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) against the Weissenberg number for several types of stars in solution. The Weissenberg numbers at which τlag against the Weissenberg number for several types of stars in solution. The Weissenberg numbers at which τlag![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1 are indicated with vertical arrows in Fig. 9. = 1 are indicated with vertical arrows in Fig. 9. | ||
In any case, when bonds of finite extensibility (FENE) are considered (SF+HI case) ωL keeps increasing with Wi: consistent with the picture above [see Fig. 10(b)], the flow is not able to strain faster than its fastest (“bond”) response (i.e. τlag![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) < 1 probably for any shear rate; here, we reached Wi ∼ 103). A similar comment could be made in the case of melts; however, in this case, we could only reach Wi ∼ 100 due to strong heat dissipation.
< 1 probably for any shear rate; here, we reached Wi ∼ 103). A similar comment could be made in the case of melts; however, in this case, we could only reach Wi ∼ 100 due to strong heat dissipation.
6.2 Tank-treading rotation
It is interesting to compare the relation in eqn (17) with the results for ring polymers by Chen et al.15 In particular, following previous comments in the literature, one could be tempted to relate ωL with their tank-treading frequency ftt ∼ Wi0.6. In doing so, eqn (17) completely fails, leading to ftb ∼ Wi0.80 instead of ftb ∼ Wi0.64 (see Fig. 8). However, we have verified that the relation, given by eqn (17), holds, so it seems that the way ωL and ftt (in ref. 15) are measured corresponds to very different dynamics. In particular, the frequency ftt, defined in ref. 15, properly follows the “real” monomer rotation around its molecular CoM. By contrast ωL is a way to measure the total angular momentum of the molecule, but it is not really connected with the monomer rotation frequency.This issue is relevant because in many previous papers3,7,12–14ωL appearing in eqn (6) has been taken to represent the monomer rotation frequency around the soft molecule’s CoM and thus related to “tank-treading” dynamics. This interpretation is incorrect and comes out from the fact that ωL in eqn (6) (and its approximation ωG in eqn (10)) corresponds to the tumbling frequency of a rigid spheroid having the average shape of the soft molecule. But the tumbling motion of a rigid spheroid and the tank-treading rotation of the soft molecule are completely different! The “real” rotation frequency of the monomers around the molecule’s CoM can be measured, for instance, from the time correlation Crot(t) in eqn (2) which considers the vector between the center monomer and the end-monomer of each arm. This vector rotates with the monomers with a frequency ωR which can be measured from a fit to a decaying sinusoidal function. We used a similar function (using the projection in the flow direction) to show that ωR differs a lot from ωL, particularly as the shear rate is increased. This fact is illustrated in Fig. 11 for the SH+HI case, but it is observed in all cases (either solution or melt). Fig. 11 compares Ω, ωR and ωL for the SH+HI case, showing that ωG < ωR < Ω. Unlike that stated in ref. 3 and more recent works,12–14 the “tank-treading” frequency does not saturate at large ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , but keeps monotonically increasing. Here, we focus on the origin of the breathing frequency Ω, so it has to be stressed that, so far, the tank-treading frequency of star molecules ωR remains to be theoretically or experimentally studied. Such study should probably reveal strong similarities between tank-treading in star-molecules, in ring polymers15,19 and also in vesicles,21,23 even at large shear rates (see the comparison made in ref. 12).
, but keeps monotonically increasing. Here, we focus on the origin of the breathing frequency Ω, so it has to be stressed that, so far, the tank-treading frequency of star molecules ωR remains to be theoretically or experimentally studied. Such study should probably reveal strong similarities between tank-treading in star-molecules, in ring polymers15,19 and also in vesicles,21,23 even at large shear rates (see the comparison made in ref. 12).
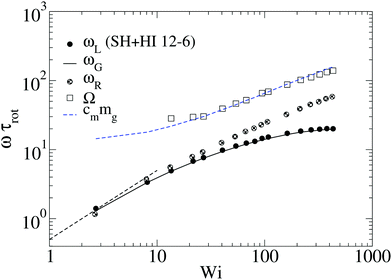 | ||
| Fig. 11 The frequency of monomer rotations around the star molecule’s center (tank-treading) ωR, obtained from the time autocorrelation of the end-monomer-center distance in the flow direction Xi = (x1,i − xcm). We compare ωR with ωL and ωG in eqn (6) and (10) and also with the breathing frequency Ω and cmmg where mg is the orientational resistance, see Table 3. | ||
In view of this fact, ωL should be just taken as a proxy for the angular momentum imparted by the mean flow to the molecule and not as a way to understand how a soft molecule rotates. Indeed, the soft-body analogous of ωL appearing in eqn (5) cannot be deduced from the simple relation in eqn (6) but would require a special theoretical framework for soft rotating bodies, which will be the focus of our future work.
7 Conclusions
This work studied the dynamics of star polymer molecules under shear flow, in both dilute solution and melts, focusing on the sources of molecular angular momentum and expansion/contraction dynamics under shear flow. The standard and widely used route to evaluate the molecular angular frequency ωL consists in neglecting other sources of angular momentum rather than the mean flow L ≃ L0 ≃ N![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) G22 and uses a relation between ωL and L inspired in a rigid-body equation, eqn (6). This approximation to ωL (see Eqn (10)) is denoted as ωG because it only depends on the molecular gyration tensor.24 We found that, in solution, ωG ≃ ωL, indicating that hydrodynamics does not add significant intra-molecular angular momentum, which is in agreement with that found in linear chains.24 However, in melts, intermolecular friction adds molecular-L and we found ωL > ωG. Interestingly, the deviation Δω = 1 − ωG/ωL was found to be indicative of the compactness of the star in the melt. The deviation Δω decreases for stars with smaller surface-to-volume ratios (increasing number of arms f > 10) because of the smaller fraction of intermolecular forces. But a sudden jump was observed for stars with few arms (f < 6) which is another expression of the transition between compact and linear polymer molecules.9 We also studied the effect of tangential friction between monomers in melts. Tangential friction was seen to increase the “hydrodynamic character” of the melt, as revealed from the comparison between melt and single star molecules in solution. As an aside, we warned that simulations using the multiparticle collision dynamics (MCD) present peculiar negative deviations Δω < 0, which are not observed in any of the previous works using standard Brownian hydrodynamics in solution. This might well be a consequence of the small values of the Schmidt numbers used in MCD simulations, or a consequence of the lack of conservation of angular momentum in the MCD scheme. In whatever case, this fact certainly requires a more detailed study.
G22 and uses a relation between ωL and L inspired in a rigid-body equation, eqn (6). This approximation to ωL (see Eqn (10)) is denoted as ωG because it only depends on the molecular gyration tensor.24 We found that, in solution, ωG ≃ ωL, indicating that hydrodynamics does not add significant intra-molecular angular momentum, which is in agreement with that found in linear chains.24 However, in melts, intermolecular friction adds molecular-L and we found ωL > ωG. Interestingly, the deviation Δω = 1 − ωG/ωL was found to be indicative of the compactness of the star in the melt. The deviation Δω decreases for stars with smaller surface-to-volume ratios (increasing number of arms f > 10) because of the smaller fraction of intermolecular forces. But a sudden jump was observed for stars with few arms (f < 6) which is another expression of the transition between compact and linear polymer molecules.9 We also studied the effect of tangential friction between monomers in melts. Tangential friction was seen to increase the “hydrodynamic character” of the melt, as revealed from the comparison between melt and single star molecules in solution. As an aside, we warned that simulations using the multiparticle collision dynamics (MCD) present peculiar negative deviations Δω < 0, which are not observed in any of the previous works using standard Brownian hydrodynamics in solution. This might well be a consequence of the small values of the Schmidt numbers used in MCD simulations, or a consequence of the lack of conservation of angular momentum in the MCD scheme. In whatever case, this fact certainly requires a more detailed study.
We analyzed the different dynamic regimes as the shear rate increased, and related the different dynamics with the cross-over of the shear rate above each one of the equilibrium rates of the star molecule (see Table 2). These relaxation times are star rotation τrot, arm elastic relaxation τarm and τlag related to the fastest response of consecutive bonds. For ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τrot > 1, the molecule begins to rotate with a frequency smaller than about ωL ∼
τrot > 1, the molecule begins to rotate with a frequency smaller than about ωL ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) /2. For
/2. For ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τarm > 1, the molecules start to expand/contract in an underdamped fashion, with an (angular) frequency Ω. At larger shear rates,
τarm > 1, the molecules start to expand/contract in an underdamped fashion, with an (angular) frequency Ω. At larger shear rates, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) τlag > 1, the flow strains faster than the bond–bond interaction time. Hydrodynamic interactions delay the onset of the large
τlag > 1, the flow strains faster than the bond–bond interaction time. Hydrodynamic interactions delay the onset of the large ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) regime. In this high-shear regime, the aspect ratio of the molecule scales like G22/G11 →
regime. In this high-shear regime, the aspect ratio of the molecule scales like G22/G11 → ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −1, the molecular tilt as θ ∼
−1, the molecular tilt as θ ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −1/2 and the molecular angular momentum seems to saturate ωL → cte, while Ω ∼ (ωL
−1/2 and the molecular angular momentum seems to saturate ωL → cte, while Ω ∼ (ωL![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) )1/2. The apparent “saturation” of ωL is, however, only observed for stars with Hookean springs, but certainly not when using the FENE bonds. Moreover, the plateau of ωL is not real because, at even larger shear rates, a star with harmonic springs behaves like a Gaussian polymer, for which ωL ∼
)1/2. The apparent “saturation” of ωL is, however, only observed for stars with Hookean springs, but certainly not when using the FENE bonds. Moreover, the plateau of ωL is not real because, at even larger shear rates, a star with harmonic springs behaves like a Gaussian polymer, for which ωL ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −1. The situation in melts is much more complex. We analyzed the recent results of Xu and Chen7 along with those in the present work to show that ωL ∼
−1. The situation in melts is much more complex. We analyzed the recent results of Xu and Chen7 along with those in the present work to show that ωL ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) α with exponents increasing with the functionality f (α ∈ [0.52,0.79] for f ∈ [3,60]). A definitive explanation of rotation and molecular breathing, stemming from the molecular architecture and mechanical properties, should take into account the force balance in the gradient and normal directions, including excluded volume and hydrodynamics.
α with exponents increasing with the functionality f (α ∈ [0.52,0.79] for f ∈ [3,60]). A definitive explanation of rotation and molecular breathing, stemming from the molecular architecture and mechanical properties, should take into account the force balance in the gradient and normal directions, including excluded volume and hydrodynamics.
The second part of the work concerned the expansion/contraction dynamics of the star molecules in shear. A relation for Ω was derived based on the force balance in the flow direction, leading to Ω ≃ cf![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (G22/G11)1/2 (with Gij the components of the gyration tensor and 1-flow and 2-gradient directions). We also showed that this relation can be expressed in terms of the molecular tilt angle θ and, alternatively, in terms of the orientational resistance parameter Ω = cmmg, with mg = Wi
(G22/G11)1/2 (with Gij the components of the gyration tensor and 1-flow and 2-gradient directions). We also showed that this relation can be expressed in terms of the molecular tilt angle θ and, alternatively, in terms of the orientational resistance parameter Ω = cmmg, with mg = Wi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan(2θ). Using our results in solution and melt along with those in the recent literature, we suggest that this relation is general, as it holds excellently well in stars, rings and linear chains. The ratio cm = Ω/mg is of order one and slightly depends on polymer properties and environment (melt or solution, bond type, molecular architecture). In view of the present results, it would be interesting to study collective vibrations in dendrimers under shear flow. Our guess is that their dynamics would be similar to the “breathing” mode of star molecules, but the higher coordination required for “arms” and monomer displacements in dendrimers might somehow modify these collective dynamics. Another aspect to have in mind is that this study focuses on star molecules with relatively short arms, where entanglement is irrelevant. Previous studies3 indicate that entanglements do not qualitatively alter the star structure or dynamics at least for arms with m ≤ 30 Kuhn lengths. However, it would be interesting to study if the entanglements created in star molecules with very long arms m > 102 (and large enough functionality) might lead to qualitatively different dynamics under shear flow, at very dilute concentration (below overlap).
tan(2θ). Using our results in solution and melt along with those in the recent literature, we suggest that this relation is general, as it holds excellently well in stars, rings and linear chains. The ratio cm = Ω/mg is of order one and slightly depends on polymer properties and environment (melt or solution, bond type, molecular architecture). In view of the present results, it would be interesting to study collective vibrations in dendrimers under shear flow. Our guess is that their dynamics would be similar to the “breathing” mode of star molecules, but the higher coordination required for “arms” and monomer displacements in dendrimers might somehow modify these collective dynamics. Another aspect to have in mind is that this study focuses on star molecules with relatively short arms, where entanglement is irrelevant. Previous studies3 indicate that entanglements do not qualitatively alter the star structure or dynamics at least for arms with m ≤ 30 Kuhn lengths. However, it would be interesting to study if the entanglements created in star molecules with very long arms m > 102 (and large enough functionality) might lead to qualitatively different dynamics under shear flow, at very dilute concentration (below overlap).
As a final relevant contribution, we showed that, contrary to what is stated in relatively recent works,3,7,12–14 the angular frequency ωL evaluated from the mean-flow approximation of a “rigid-body-like” equation for the molecular angular momentum L is not related with the rotation frequency of the monomers around their center of mass, ωR. This frequency, ωR, is the one determining the tank-treading motion of star-polymers and also ring chains.15 The error in previous works was to directly relate the rotation equation for a rigid-body with the much more complex rotation of soft-bodies, which would require a more elaborate framework.
Appendix: force balance in the long molecular axis
It is useful to consider the force balance in the molecular frame coordinates, given by the eigenvectors of the gyration tensor. A simplified geometrical description of the relation between elongations in the laboratory and molecular frame is given in Fig. 12. The figure shows the probability cloud of the monomers' location in the flow-gradient plane (for a SH+HI 12–6 star at Wi = 30). The ellipsoidal shape of the probability cloud is simplified in the figure (dashed white lines) to propose an approximated relation between elongations in the laboratory and molecular frame based on projections: X1 ∼ X1′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ) while X2′ ∼ X2
cos(θ) while X2′ ∼ X2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ).
cos(θ).
The flow drag pushes in the x1 (lab) direction (Ff = Ffx1) but its components in the molecular frame are Ff′ = Ff[cos(θ)x1′ − sin(θ)x2′] (see Fig. 12). When observed from the (tilted) molecular frame, the drag force stretches the molecule in the x1′ direction and compresses it in the x2′ direction. Such compression reduces the polymer width G2 according to another force balance, to be studied in a subsequent work. Here, we consider the balance in the most elongated molecular x1′-direction, where the average elastic force KX1′ should be balanced by the projected drag force ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) X2
X2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ). Now, if X2 ∼ X2′/cos(θ), one concludes that
cos(θ). Now, if X2 ∼ X2′/cos(θ), one concludes that
KX1′ ∼ ξ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) X2′, X2′, |
Acknowledgements
J. S. and M. P. acknowledge financial support through grants P1-0002 and J1-7435 from the Slovenian Research Agency. J. S. acknowledges financial support from Slovene Human Resources Development and Scholarship Fund (186. JR). R. D.-B. acknowledges support from the Spanish government under the national MINECO project FIS2013-47350-C5-1-R. Partial support from COST Action MP1305 and PRF-ACS grant 54312-ND9 is kindly acknowledged. We thank Raul Pérez Pelaez and Marc M. Schofield for their work on the cover figure.References
- G. S. Grest, K. Kremer, S. T. Milner and T. A. Witten, Macromolecules, 1989, 22, 1904–1910 CrossRef CAS.
- C. N. Likos, Phys. Rep., 2001, 348, 267–439 CrossRef CAS.
- M. Ripoll, R. G. Winkler and G. Gompper, Phys. Rev. Lett., 2006, 96, 188302 CrossRef CAS PubMed.
- D. Vlassopoulos, G. Fytas, T. Pakula and J. Roovers, J. Phys.: Condens. Matter, 2001, 13, R855 CrossRef CAS.
- K. J. Johnson, E. Glynos, G. Sakellariou and P. Green, Macromolecules, 2016, 49, 5669–5676 CrossRef CAS.
- J. Sablić, M. Praprotnik and R. Delgado-Buscalioni, Soft Matter, 2016, 12, 2416–2439 RSC.
- X. Xu and J. Chen, J. Chem. Phys., 2016, 144, 244905 CrossRef PubMed.
- B. W. Fitzgerald, H. Lentzakis, G. Sakellariou, D. Vlassopoulos and W. J. Briels, J. Chem. Phys., 2014, 141, 114907 CrossRef PubMed.
- A. Chremos and J. F. Douglas, J. Chem. Phys., 2015, 143, 111104 CrossRef PubMed.
- C. N. Likos, H. Löwen, M. Watzlawek, B. Abbas, O. Jucknischke, J. Allgaier and D. Richter, Phys. Rev. Lett., 1998, 80, 4450–4453 CrossRef CAS.
- G. S. Grest, L. J. Fetters, J. S. Huang and D. Richter, Star Polymers: Experiment, Theory, and Simulation, John Wiley and Sons, Inc., 2007, pp. 67–163 Search PubMed.
- S. P. Singh, D. A. Fedosov, A. Chatterji, R. G. Winkler and G. Gompper, J. Phys.: Condens. Matter, 2012, 24, 464103 CrossRef PubMed.
- S. P. Singh, A. Chatterji, G. Gompper and R. G. Winkler, Macromolecules, 2013, 46, 8026–8036 CrossRef CAS.
- T. Yamamoto and N. Masaoka, Rheol. Acta, 2015, 54, 139–147 CrossRef CAS.
- W. Chen, J. Chen and L. An, Soft Matter, 2013, 9, 4312–4318 RSC.
- G. De Fabritiis, R. Delgado-Buscalioni and P. V. Coveney, Phys. Rev. Lett., 2006, 97, 134501 CrossRef CAS PubMed.
- F. B. Usabiaga and R. Delgado-Buscalioni, Macromol. Theory Simul., 2011, 20, 466 CrossRef CAS.
- R. E. Teixeira, H. P. Babcock, E. S. G. Shaqfeh and S. Chu, Macromolecules, 2005, 38, 581 CrossRef CAS.
- W. Chen, H. Zhao, L. Liu, J. Chen and Y. Li, Soft Matter, 2015, 11, 5265 RSC.
- E. J. Hinch and L. Leal, J. Fluid Mech., 1979, 92, 591 CrossRef.
- D. P. Dodson WR, Biophys. J., 2010, 99, 2906–2916 CrossRef PubMed.
- M. Abkarian, M. Faivre and A. Viallat, Phys. Rev. Lett., 2007, 98, 188302 CrossRef PubMed.
- A. Z. K. Yazdani and P. Bagchi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 026314 CrossRef PubMed.
- C. Aust, S. Hess and M. Kröger, Macromolecules, 2002, 35, 8621–8630 CrossRef CAS.
- C. Hijon, P. Español, E. Vanden-Eijnden and R. Delgado-Buscalioni, Faraday Discuss., 2010, 144, 301–322 RSC.
- R. M. Jendrejack, M. D. Graham and J. J. de Pablo, J. Chem. Phys., 2000, 113, 2894–2900 CrossRef CAS.
- R. M. Jendrejack, J. J. de Pablo and M. D. Graham, J. Chem. Phys., 2002, 116, 7752–7759 CrossRef CAS.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Oxford University Press, Oxford, UK, 1990 Search PubMed.
- P. Español and P. Warren, Europhys. Lett., 1995, 30, 191 CrossRef.
- T. Soddemann, B. Dünweg and K. Kremer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 046702 CrossRef PubMed.
- C. Junghans, M. Praprotnik and K. Kremer, Soft Matter, 2008, 4, 156–161 RSC.
- R. Delgado-Buscalioni, J. Sablić and M. Praprotnik, Eur. Phys. J.: Spec. Top., 2015, 224, 2331–2349 CrossRef CAS.
- K. S. Kumar and J. R. Prakash, J. Chem. Phys., 2004, 121, 3886–3897 CrossRef CAS PubMed.
- J. G. H. Cifer and J. G. de la Torre, Macromol. Theory Simul., 2004, 13, 273–279 CrossRef.
- M. Kröger, W. Loose and S. Hess, J. Rheol., 1993, 37, 1057–1079 CrossRef.
- S. Gerashchenko and V. Steinberg, Phys. Rev. Lett., 2006, 96, 038304 CrossRef PubMed.
- C. M. Schroeder, R. Teixeira, E. S. G. Shaqfeh and S. Chu, Phys. Rev. Lett., 2005, 95, 018301 CrossRef PubMed.
- M. Chertkov, I. Kolokolov, V. Lebedev and K. Turitsyn, J. Fluid Mech., 2005, 531, 251 CrossRef CAS.
- R. Cerf, J. Chim. Phys., 1969, 68, 479 CrossRef.
- E. R. Bazúa and M. C. Williams, J. Polym. Sci., 1974, 12, 825–848 Search PubMed.
- E. R. Bazúa and M. C. Williams, J. Polym. Sci., 1974, 12, 2397 Search PubMed.
- S. Hess and G. P. Morriss, in Computer Simulations of Liquid Crystals and Polymers Proceedings of the NATO Advanced Research Workshop on Computational Methods for Polymers and Liquid Crystalline Polymers Erice, Italy 16–22 July 2003, ed. P. Pasini, C. Zannoni and S. Žumer, Springer Netherlands, Dordrecht, 2005, ch. Rotation and Deformation of Polymer Molecules in Solutions Subjected to a Shear Flow, pp. 269–293 Search PubMed.
- P. Debye, J. Chem. Phys., 1946, 14, 636–639 CrossRef CAS.
- F. Balboa Usabiaga, X. Xie, R. Delgado-Buscalioni and A. Donev, J. Chem. Phys., 2013, 139, 214113 CrossRef PubMed.
- C.-C. Huang, G. Sutmann, G. Gompper and R. G. Winkler, Europhys. Lett., 2011, 93, 54004 CrossRef.
- R. Delgado-Buscalioni, Phys. Rev. Lett., 2006, 96, 088303 CrossRef PubMed.
- X. Xu, J. Chen and L. An, J. Chem. Phys., 2014, 140, 174902 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2017 |