High-voltage aqueous supercapacitors based on NaTFSI

Abstract

Ultra-high salt concentration has recently been reported to extend the kinetic stability of aqueous electrolytes up to 3 V. However, the low ionic conductivity of these systems makes them unsuitable for high power devices such as supercapacitors. In this study, an 8 mol kg⁻¹ NaTFSI aqueous electrolyte is reported that displays a high stability of 1.8 V on activated carbon during a stringent stability test and a conductivity of 48 mS cm⁻¹ at 20 °C, the latter being comparable to the one of state-of-the-art acetonitrile-based non-aqueous electrolytes. A 1.8 V carbon/carbon supercapacitor employing 8 mol kg⁻¹ NaTFSI displays a high maximum energy density of 14.4 W h kg⁻¹ on the activated carbon mass level and stable cycling for 100 000 cycles. By addition of the redox additive potassium iodide to the electrolyte, the maximum specific energy could be increased to an extremely high value of 37.8 W h kg⁻¹, comparable to the performance of the current generation of commercial non-aqueous supercapacitors.

---

Introduction

Supercapacitors based on aqueous electrolytes are potentially safer and environmentally more benign than their non-aqueous electrolyte counterparts which typically employ highly flammable acetonitrile as the electrolyte solvent.¹ The low thermodynamic stability of water of 1.23 V puts aqueous double-layer capacitors at a natural disadvantage in terms of volumetric and gravimetric energy (E) and power (P) densities as both metrics scale with the square of the maximum operating voltage (V) (E = 1/2CV² and P = V²/(4R) with capacitance (C) and equivalent series resistance (R)).² In comparison, commercial non-aqueous supercapacitors are currently rated at up to 3.0 V.

The lower voltage of aqueous supercapacitors is partly offset by higher capacitance values of activated carbon (AC) in aqueous electrolytes due to the higher relative permittivity of water compared to acetonitrile.² In addition, the capacitance of AC in aqueous electrolytes benefits from typically smaller ion sizes and pseudocapacitive contributions from fast redox reactions between surface functional groups and e.g. hydronium ions.² Redox active electrolyte additives like halogenides or quinone based organics have been employed to further increase the capacitance of aqueous AC/AC supercapacitors.^3–5

To increase the operating voltage and thus strongly increase the energy density of aqueous supercapacitors, several strategies have been proposed. Near pH-neutral electrolytes have improved kinetic stability compared to strongly basic or acidic solutions based on e.g. KOH or H₂SO₄, for which the cell voltage is limited to about 1 V. For 1 mol L⁻¹ Li₂SO₄, initial results suggested stable long-term cycling up to 2.2 V using gold current collectors.⁶ However, later studies revealed several stability issues for this system arising from water oxidation/reduction at high cell voltages. For example, carbon oxidation on the positive electrode by water oxidation products, resulting in continuous capacitance fading, has been observed in 1 mol L⁻¹ Li₂SO₄ when the cell voltage exceeded values as low as 1.5 V.^7,8 On the negative side, hydrogen formation is accompanied by an increase in local pH which can be detrimental to the stability of the current collector.⁹ Furthermore, hydrogen evolution during operation of such systems at high voltages also raises safety concerns.

A possible solution for these stability and safety issues is the use of highly concentrated aqueous electrolytes. Recently very large stability windows of up to 3 V have been reported for ultra-highly concentrated aqueous electrolytes such as the water-in-salt system, 21 mol kg⁻¹ LiTFSI (TFSI = N(SO₂CF₃)₂), by the battery community.^10–12 The increased apparent stability window is a consequence of the very small water-to-salt ratio in these systems leading to low fractions of free water molecules and increased average oxidative stability of water molecules and electrolyte anions. In addition, the formation of a passivation layer from reductive decomposition of electrolyte anions that further reduces the kinetics of the hydrogen evolution reaction has been reported for these systems.^10,12 Furthermore, suppressed Al current collector dissolution has been reported for the water–LiTFSI system at very high salt concentration.¹³ First studies using such highly concentrated electrolytes in supercapacitors indeed indicate improved stability compared to the Li₂SO₄ system. Gambou-Bosca and Bélanger reported a useable voltage window of 2.3 V for an AC-MnO₂ pseudocapacitor containing 5 mol L⁻¹ (≈20 mol kg⁻¹) LiTFSI.¹⁴ Hasegawa et al. demonstrated stable cycling of an AC/AC supercapacitor based on 5 mol L⁻¹ LiTFSI for 10 000 cycles at 5 A g⁻¹ when cycled up to 2.4 V.¹⁵ Tomiyasu et al. claimed even 3.2 V stability for a supercapacitor based on a saturated NaClO₄ solution.¹⁶ However, the low conductivity of these highly concentrated aqueous electrolytes presents a major impediment to their use in high power devices such as supercapacitors.^14,17

Inspired by the trend of increasing conductivity with increasing cationic radius for other aqueous alkali metal salt solutions,¹⁸ we explore the solubility, conductivity and electrochemical stability of different alkali metal TFSI salts in aqueous solutions on AC. The results are compared to values for the widely studied Li₂SO₄ system. Interestingly, we find conditions very suitable for supercapacitors at a NaTFSI concentration of 8 mol kg⁻¹. This electrolyte displays a room temperature conductivity of ∼50 mS cm⁻¹ compared to <10 mS cm⁻¹ for 21 mol kg⁻¹ LiTFSI, while the electrochemical stability window on AC of 1.8 V is only 200 mV smaller than the one for 21 mol kg⁻¹ LiTFSI. A double-layer capacitor based on 8 mol kg⁻¹ NaTFSI shows excellent rate performance and stability for 100 000 cycles when charged up to 1.8 V. Finally, we present results for a cell with the redox additive potassium iodide added to the NaTFSI electrolyte. This device displays an extremely high maximum energy density of 37.8 W h kg⁻¹ on the activated carbon mass level, reaching the performance of commercial non-aqueous electrolyte supercapacitors.

Experimental methods

The electrolytes were prepared by dissolving the as-received salts LiTFSI (99.95%, Sigma-Aldrich or 99.9%, Solvionic), NaTFSI (99.5%, Solvionic), KTFSI (99.5%, Solvionic), Li₂SO₄ (99.99%, Alfa Aesar) and KI (≥99.5%, Sigma-Aldrich), respectively, in high purity water (prepared with a Millipore Milli-Q water purification system). Neutral pH was established by addition of appropriate amounts of a suitable hydroxide solution, and the electrolytes were degassed with argon or nitrogen prior to their use.

Ionic conductivity was determined by impedance spectroscopy in sealed 2-electrode cells equipped with Pt electrodes (Materials Mates HTCC) using a Bio-Logic VMP3 electrochemical workstation. The temperature was controlled with a climatic chamber (Binder MK53). The electrolyte resistance was extracted from the intersection of the complex impedance curve with the x-axis in a Nyquist plot.

Raman spectra of selected electrolytes sealed in NMR tubes were collected at room temperature on a Renishaw Ramascope between 100 and 4000 cm⁻¹ using a laser with a wavelength of 633 nm.

All supercapacitors were assembled in stainless steel T-type Swagelok cells in a 3-electrode configuration and characterized using a Bio-Logic VMP3 electrochemical workstation. A Ag/AgCl miniature electrode (eDAQ) was used as the reference. For the half-cell tests, oversized AC pellets served as the counter electrode.

AC (MTI AB-520, coconut-derived, BET surface area: 2000 ± 100 m² g⁻¹, pore volume: 0.9 ± 0.1 cm³ g⁻¹, carbon content: > 95%) electrodes were prepared by casting a slurry consisting of 85% AC, 10% carbon black (IMERYS Graphite & Carbon C-NERGY SUPER C65) and 5% polyvinylidene difluoride (PVdF) binder (Arkema Kynar HSV900) suspended in N-methyl-2-pyrrolidone (NMP) on stainless steel (grade 1.4310; thickness: 25 μm) or nickel (grade 2.4068; thickness: 20 μm) foils. The stainless steel foils were etched in 4 mol kg⁻¹ KOH heated to 60 °C for 30 s and both foils were roughened (further) with sandpaper before casting to improve adhesion. The electrode sheets were then dried overnight at 80 °C in air and electrode discs with a diameter of 12 mm were punched out. The electrodes were then pressed at 15 t for 30 s before a final drying step at 120 °C under vacuum overnight. The AC mass loading was about 1–2 mg for all tests except for the full cell tests, where the combined mass loading of both electrodes was about 6 mg.

The stability window of the electrolytes on AC was determined in a half-cell configuration by cyclic voltammetry with a scan rate of 1 mV s⁻¹. After five conditioning cycles between ±0.2 V vs. Ag/AgCl, the cut-off potential was increased in 100 mV steps to ±1.5 V vs. Ag/AgCl and the second vertex potential was fixed at 0 V vs. Ag/AgCl. Three cycles were recorded for each potential window to reduce the influence of wetting phenomena and first cycle effects. Separate measurements were conducted for the negative and positive electrode, respectively.

Rate tests in a half-cell configuration at specific currents ranging from 0.5 to 20 A g⁻¹ were conducted separately for both electrodes in the respective potential windows. Balanced full cells were assembled for the long-term cycling tests and the Ragone plot by adapting the mass loadings of the positive and negative electrodes in a way that the potentials of electrodes would not significantly exceed their determined stability limits.

Self-discharge tests in a half-cell configuration were conducted separately for the negative and positive electrodes. After 250 cycles of activation cycling at 1 A g⁻¹, the working electrode potentials were kept constant for 3 h at −1.1 or 0.7 V vs. Ag/AgCl, respectively. Subsequently, the potential evolution over time was monitored for 24 h under open-circuit conditions.

Results and discussion

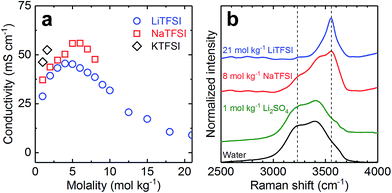
Fig. 1a shows the concentration dependent conductivity at 20 °C of aqueous solutions of LiTFSI, NaTFSI, and KTFSI. We find that for a given molality the conductivity (σ) increases in the order σ_LiTFSI < σ_NaTFSI < σ_KTFSI. For example, at 1 mol kg⁻¹ the conductivities are 29, 37, and 46 mS cm⁻¹ for LiTFSI, NaTFSI, and KTFSI, respectively. The same trend has been observed for other aqueous solutions of alkali metal salts and can be rationalized with the effective radii of the solvated cations.¹⁸ With increasing cation radius (r) (in crystals: r_c^Li+ < r_c^Na+ < r_c^K+), the charge density decreases and hence ion-dipole forces between cation and water molecules weaken. As a consequence, at least for dilute solutions, the effective radii (r_h) of the corresponding hydrated cations decrease within increasing r_c, i.e. r_h^Li+ > r_h^Na+ > r_h^K+.¹⁹ And the smaller the effective radius of the hydrated ion, the larger is the conductivity.

Fig. 1 (a) Concentration-dependence of the conductivity of aqueous solutions of LiTFSI, NaTFSI, and KTFSI at 20 °C. (b) Raman spectra of pure water, 1 mol kg⁻¹ Li₂SO₄, 8 mol kg⁻¹ NaTFSI, and 21 mol kg⁻¹ LiTFSI in the wavenumber range corresponding to the OH stretching modes of water.

Another consequence of the differences in charge density is the difference in solubility. Fig. 1a reports conductivity values up to the approximate room temperature solubility limit of each salt. The maximum solubility (c) decreases in the order c_LiTFSI > c_NaTFSI > c_KTFSI from ca. 21 to 8 to 1.5 mol kg⁻¹. Solubility is determined by the competition between the energy needed to break-up the crystal lattice and the energy and entropy gains during hydration of the ions. Within a family of similar compounds, the melting points can often be used as a proxy for their relative lattice energies.²⁰ For the family of TFSI salts investigated here, the cations must determine the differences as the anions are identical. The high solubility of LiTFSI (∼21 mol kg⁻¹) is due to a combination of low lattice energy, as indicated by the low melting point of this salt (233 °C),²¹ and high charge density of Li⁺, which leads to a high hydration energy contribution. The melting point of NaTFSI is only slightly higher (257 °C),²¹ indicating that the lattice energies are comparable. However, the 75% lower charge density of Na⁺ compared to Li⁺ indicates significantly lower hydration energy for NaTFSI compared to LiTFSI. The melting point of KTFSI (199 °C)²¹ is slightly lower than the one of LiTFSI, indicating that the charge density of K⁺, which is 64% lower than the one of Na⁺, is the cause for the lowest solubility in the series. Due to the relatively low solubility of KTFSI, solutions based on this salt were not further investigated in this study.

The conductivity of LiTFSI and NaTFSI solutions shows similar concentration dependences. At low concentration, the conductivity strongly increases with concentration, reaching maximum conductivities of 46 and 56 mS cm⁻¹ for LiTFSI and NaTFSI at similar concentrations of 4 and 6 mol kg⁻¹, respectively. When further increasing the concentration, the conductivity decreases faster for NaTFSI till reaching its solubility limit. The conductivity function of the LiTFSI solutions beyond the concentration of maximum conductivity monotonically decreases with increasing concentration and shows an inflection point at about 12 mol kg⁻¹. For 21 mol kg⁻¹ LiTFSI, we measured a conductivity of 9 mS cm⁻¹, in line with previous reports.¹⁰ At 8 mol kg⁻¹, close to the solubility limit of NaTFSI, the LiTFSI and NaTFSI solutions display conductivities of 39 and 48 mS cm⁻¹, respectively. The latter value is very similar to the one of 1 mol L⁻¹ Et₄N–BF₄ in acetonitrile (53 mS cm⁻¹), the standard non-aqueous electrolyte for supercapacitors and comparable to the one of 1 mol kg⁻¹ Li₂SO₄ (62 mS cm⁻¹). Due to its high conductivity at a relatively high concentration, we selected 8 mol kg⁻¹ NaTFSI as the electrolyte for supercapacitors.

Raman spectra were recorded to compare the structure of pure water, 1 mol kg⁻¹ Li₂SO₄, 8 mol kg⁻¹ NaTFSI, and 21 mol kg⁻¹ LiTFSI. The bands observed between 2500 and 4000 cm⁻¹ (Fig. 1b) correspond to the OH stretching modes of water.²² The various hydrogen bonding environments in water result in a broad Raman band between 2900 and 3700 cm⁻¹.²² Upon salt addition, a distinct peak at ∼3550 cm⁻¹ emerges (see the right dashed line in Fig. 1b) that increases in intensity with increasing salt concentration.²³ At the same time, the broad signal of free water molecules vanishes.²³ Such a sharp OH stretching peak is typical of crystalline hydrates, indicating that a large fraction of water molecules is strongly interacting with Li⁺.^10,12 Indeed the fraction of free water molecules in 21 mol kg⁻¹ LiTFSI has been estimated from molecular dynamics simulations to be only ca. 15%.¹⁰ The spectrum of 1 mol kg⁻¹ Li₂SO₄ resembles the one of pure water, corresponding to a large fraction of free water in this electrolyte. In contrast, the fraction of free water in 8 mol kg⁻¹ NaTFSI appears to be significantly smaller. Compared to pure water, the intensity of the peak at ∼3230 cm⁻¹ (see the left dashed line in Fig. 1b) is significantly reduced and the sharp component at ∼3550 cm⁻¹ corresponding to water molecules strongly interacting with solution cations is clearly present.

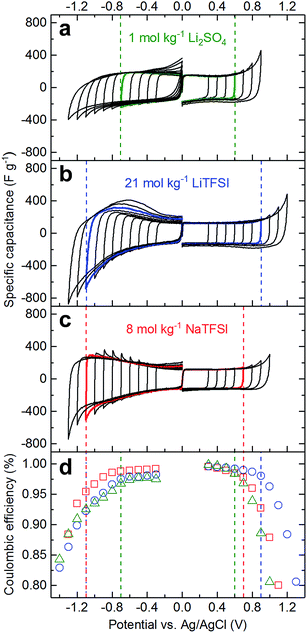
Cyclic voltammetry (CV) in a 3-electrode configuration with an oversized AC pellet as the counter electrode was carried out to assess the electrochemical stability of 21 mol kg⁻¹ LiTFSI, 8 mol kg⁻¹ NaTFSI, and 1 mol kg⁻¹ Li₂SO₄ on AC working electrodes. We followed the potential opening approach, for both electrodes separately, and used a criterion based on coulombic efficiency (η) to determine the stability limits.²⁴ We define stability as the last vertex potential (E_v) for which the modulus of the second derivative of η vs. E_v remains below 0.05 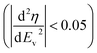. The rationale put forward by Weingarth et al. for stability criteria based on the second derivative of coulombic efficiency is to be able to distinguish between constant background currents, leakage currents that increase linearly with potential and currents corresponding to faradaic processes, i.e. electrolyte decomposition.²⁴ The latter currents should increase exponentially with the potential as faradaic processes generally follow the Butler–Volmer equation and can hence be detected as a change in the slope of η.²⁴ The CV curves and the corresponding η values are plotted in Fig. 2.

Fig. 2 Cyclic voltammograms used to determine the stability windows of (a) 1 mol kg⁻¹ Li₂SO₄, (b) 21 mol kg⁻¹ LiTFSI, and (c) 8 mol kg⁻¹ NaTFSI. The scan rate was set to 1 mV s⁻¹. (d) Corresponding coulombic efficiency vs. vertex potential plot. The vertical dashed lines correspond to the stability limits of the electrolytes according to the second derivative of the efficiency criterion used in this work.

The positive effects of highly concentrated solutions are prominently observable for the positive electrode, where oxygen evolution is apparently pushed to higher potentials. The positive potential stability limit according to the second derivative of the η criterion increases from 0.6 V vs. Ag/AgCl for 1 mol kg⁻¹ Li₂SO₄ to 0.7 V for 8 mol kg⁻¹ NaTFSI to 0.9 V for 21 mol kg⁻¹ LiTFSI. The increased stability can also be seen when comparing the coulombic efficiencies for a fixed vertex potential. For example, for a vertex potential of 0.8 V vs. Ag/AgCl, the efficiencies are 98.8% for 21 mol kg⁻¹ LiTFSI, 96.1% for 8 mol kg⁻¹ NaTFSI and only 94.2% for 1 mol kg⁻¹ Li₂SO₄. This can be explained with the higher energy of the highest occupied molecular orbital (HOMO) of water when coordinated to Li⁺, i.e. higher oxidative stability of coordinated water molecules.¹² As the fraction of free water molecules strongly decreases from 1 mol kg⁻¹ Li₂SO₄ to 8 mol kg⁻¹ NaTFSI to 21 mol kg⁻¹ LiTFSI as demonstrated above, the average HOMO energy of water increases and hence the oxidation kinetics decrease.

The positive effects of high concentration are also observable on the negative side. Here, the negative potential stability limit according to the second derivative of the η criterion decreases from −0.7 V vs. Ag/AgCl for 1 mol kg⁻¹ Li₂SO₄ to −1.1 V for 8 mol kg⁻¹ NaTFSI and 21 mol kg⁻¹ LiTFSI. Interestingly, we find the highest coulombic efficiencies for 8 mol kg⁻¹ NaTFSI and not for 21 mol kg⁻¹ LiTFSI. As previously shown both experimentally and theoretically, TFSI⁻ reduction is shifted to more positive potentials at ultra-high concentration as a consequence of the proximity of Li⁺ and TFSI⁻ at such high concentration.^10,12 This has been described as a positive effect of ultra-high salt concentration for batteries, leading to the formation of LiF-based passivation layers that reduce the kinetics of hydrogen formation on the anode side. However, for a supercapacitor we suspect that this could lead to pore clogging and hence reduced capacitance over time. At 8 mol kg⁻¹, at least for NaTFSI, the reductive stability of TFSI⁻ seems not to be altered significantly judging from the higher efficiency between −0.7 and −1.1 V vs. Ag/AgCl and the similarity in peak position of the major TFSI⁻ Raman band at ∼745 cm⁻¹ for diluted (1 mol kg⁻¹) compared to 8 mol kg⁻¹ NaTFSI (Fig. S1†). For 21 mol kg⁻¹ LiTFSI, the peak position is more similar to the one of crystalline LiTFSI, indicative of a stronger average interaction between Li⁺ and TFSI⁻ at this concentration, which leads to the change in reductive stability.

Subtracting the potential limits for the negative from the limits for the positive electrodes, we obtain stability windows of 2.0 V, 1.8 V and 1.3 V for 21 mol kg⁻¹ LiTFSI, 8 mol kg⁻¹ NaTFSI and 1 mol kg⁻¹ Li₂SO₄, respectively. When comparing the stability window on activated carbon of 2.0 V for 21 mol kg⁻¹ LiTFSI with literature data obtained using other working electrodes, it is interesting to note that the stability window strongly depends on the nature of the electrode, i.e. on the electrocatalytic properties with respect to the hydrogen and oxygen evolution reactions. Consequently, stability windows of 2.3, 2.8 and even 4.1 V were measured on platinum, gold, and glassy carbon electrodes, respectively.²⁵ The narrower window of 2.0 V obtained by us can be rationalized with differences in experimental parameters: we used a two orders of magnitude lower scan rate and AC has a much larger surface area compared to the flat electrodes used in the cited study. Furthermore, we apply a particularly stringent stability criterion.

In the literature, somewhat larger stability windows of ≥1.5 V have been reported for Li₂SO₄ solutions using other stability criteria. The decreasing coulombic efficiency with decreasing potential beyond −0.7 V vs. Ag/AgCl for 1 mol kg⁻¹ Li₂SO₄ is due to irreversible hydrogen formation. A higher upper cut-off potential than the 0 V vs. Ag/AgCl we used during the CV measurements might render this reaction more reversible, i.e. might allow partial re-oxidation of hydrogen. However, this would require an open circuit potential of AC in such solutions that is significantly higher than 0 V vs. Ag/AgCl, which is not the case for our AC on stainless steel or nickel electrodes. Furthermore, a high open circuit potential would complicate the electrode mass balancing as it would shrink the available potential range for the positive electrode.

Rate tests were performed in a half-cell configuration for 1 mol kg⁻¹ Li₂SO₄, 8 mol kg⁻¹ NaTFSI, and 21 mol kg⁻¹ LiTFSI (Fig. 3). Separate tests were carried out for the negative and positive electrodes and the cells were charged up to/down to the respective potential limits of the electrolytes determined in Fig. 2, respectively. As expected from the differences in conductivity, the rate performance using 8 mol kg⁻¹ NaTFSI and 1 mol kg⁻¹ Li₂SO₄ is much better than when using 21 mol kg⁻¹ LiTFSI. The capacitance for the former electrolytes shows only weak rate dependence, while it is very pronounced for the latter one. For example, when comparing the performance at 1 and 5 A g⁻¹, the capacitance retention is ≥88% for the highly conductive electrolytes and only ≤64%, and starting from lower absolute values, for 21 mol kg⁻¹ LiTFSI. The results clearly demonstrate the poor power capabilities of supercapacitors based on super-concentrated LiTFSI solutions. Even at 20 A g⁻¹, 8 mol kg⁻¹ NaTFSI and 1 mol kg⁻¹ Li₂SO₄ still deliver ≥82% and ≥92% of the capacitance values at 1 A g⁻¹ for the negative and positive electrodes, respectively. Overall, the capacitance retention is slightly better for 1 mol kg⁻¹ Li₂SO₄ compared to 8 mol kg⁻¹ NaTFSI due to the higher conductivity of the former electrolyte (62 vs. 48 mS cm⁻¹ at 20 °C).

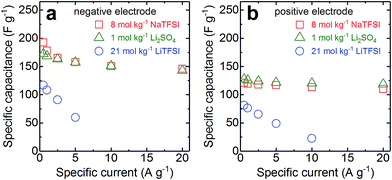Fig. 3 Rate-dependent capacitance of activated carbon in 1 mol kg⁻¹ Li₂SO₄, 8 mol kg⁻¹ NaTFSI, and 21 mol kg⁻¹ LiTFSI for the (a) negative and (b) positive electrodes.

The absolute capacitance values for 8 mol kg⁻¹ NaTFSI and 1 mol kg⁻¹ Li₂SO₄ are very similar. We find higher maximum capacitance values for the negative (>170 F g⁻¹) compared to the positive electrodes (<130 F g⁻¹) in line with the cyclic voltammograms shown in Fig. 2. We attribute this to the differences in ion size. For both electrolytes, the cations are smaller than the anions. The smaller Li⁺ and Na⁺ cations can access smaller pores than the bulkier SO₄²⁻ and TFSI⁻ anions, giving rise to an ion sieving effect and additional capacitance for the negative electrode where the properties of the cations dominate.²⁶

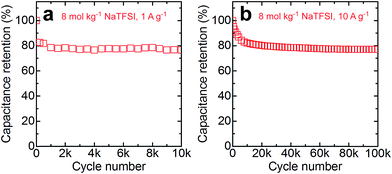
Among the investigated electrolytes, 8 mol kg⁻¹ NaTFSI shows the best combination of high conductivity (∼50 mS cm⁻¹ at room temperature) and wide electrochemical stability window (1.8 V). We therefore assembled full cells based on this electrolyte and carried out long-term cycling tests to assess the stability of the system. We used nickel as the current collector material for the negative electrodes of these cells in light of a recent report that stainless steel is more prone to corrosion in such aqueous electrolytes than nickel under conditions where the local pH might increase due to hydrogen formation.⁹ Aluminum current collectors cannot be used in combination with 8 mol kg⁻¹ NaTFSI as we observe strong anodic aluminum dissolution in this electrolyte. We assign the lower stability of aluminum in 8 mol kg⁻¹ NaTFSI compared to 8 mol kg⁻¹ LiTFSI to the higher fraction of free water molecules in the former electrolyte due to the lower charge density of Na⁺ compared to Li⁺.¹³ The tests were carried out at two different current densities, 1 and 10 A g⁻¹ (referring to the total mass of AC) in order to study both the low and high rate stability. The capacitance retention for the two different loads is plotted in Fig. 4. Both cells show an initial capacitance fading of about 20% during the first ca. 1000 cycles at 1 A g⁻¹ and 15 000 cycles at 10 A g⁻¹. We assign the initial capacitance loss to irreversible oxidation/reduction of functional groups of the AC. After the initial fading, the capacitance loss per cycle is significantly reduced and the cells only loose further ca. 3% during the remaining cycles, demonstrating the feasibility of 8 mol kg⁻¹ NaTFSI as the electrolyte for high-voltage aqueous supercapacitors.

Fig. 4 Capacitance retention obtained during long-term cycling of 1.8 V activated carbon full cells containing 8 mol kg⁻¹ NaTFSI as the electrolyte. The cells were subjected to (a) 1 A g⁻¹ and (b) 10 A g⁻¹.

Commercial non-aqueous electrolyte supercapacitors currently reach up to about 35 W h kg⁻¹ on the activated carbon mass level. In comparison, our cell based on 8 mol kg⁻¹ NaTFSI shows a maximum specific energy of 14.4 W h kg⁻¹. In order to close the gap in energy density and also to facilitate the mass balancing of the electrodes (for 8 mol kg⁻¹ NaTFSI, the positive electrode has to be massively oversized to compensate for its lower capacitance and smaller useable potential window compared to the negative electrode), a redox additive active at the positive electrode was added to the electrolyte. We chose potassium iodide (KI) because the reversible redox reactions of the iodine system take place around 0.3 V vs. Ag/AgCl, well within the stability window of 8 mol kg⁻¹ NaTFSI.^3,27,28 Potassium was selected as the counter ion to avoid a common ion effect and thus precipitation of NaTFSI.

We prepared a solution containing 8 mol kg⁻¹ NaTFSI and 0.5 mol kg⁻¹ KI, and carried out the same rate test for this electrolyte as the one shown in Fig. 3. As expected, the performance of the negative electrode is almost unaffected by KI addition to the electrolyte. In contrast, the positive electrode benefits significantly, especially at low rates. For redox additive-enhanced supercapacitors, capacity is usually a more suitable performance metric than capacitance because the voltage profile differs significantly from the one of a pure double-layer capacitor. With KI, the capacity of the positive electrode reaches a very high value of 140 mA h g⁻¹ at 0.5 A g⁻¹ compared to 23.5 mA h g⁻¹ without KI. At high currents, the performance of the positive electrode converges to the one operated without the redox additive. This suggests that the kinetics of the redox reactions of the iodine species are significantly slower than double-layer formation for this system.

We also assembled a full cell with this electrolyte, which enables a balancing close to 1 : 1 due to the much improved capacitance of the positive electrode. Our preliminary results show that such a cell has a very high maximum specific energy of 37.8 W h kg⁻¹ on the activated carbon mass level, reaching or even exceeding the level of commercial non-aqueous electrolyte systems. However, due to the very different rate-dependence of the capacitance for the positive and negative electrodes, the optimal balancing is strongly rate dependent and a cell that is optimized for one rate tends to be less stable when cycled at other rates.

Increased self-discharge rates have been observed in the presence of certain redox additives.²⁹ However, a recent study reported that the self-discharge behavior of aqueous supercapacitors is not affected by the addition of KI to the electrolyte.³ To confirm that this also applies to our system, we carried out self-discharge tests for cells containing 8 mol kg⁻¹ NaTFSI with and without the addition of 0.5 mol kg⁻¹ KI (see the Experimental section for details). Fig. S2† shows the time evolution of the potential under open-circuit conditions after the AC electrodes were kept for 3 h at the potential stability limits determined above corresponding to a cell voltage of 1.8 V. The self-discharge of the negative electrode is not affected by the addition of KI. The potential of the positive electrode initially decays slightly faster with KI, but stabilizes at comparable (in fact even slightly higher) potentials than without KI after 24 h in agreement with results reported in ref. 3.

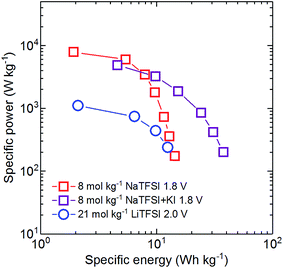
To compare the performance of supercapacitors based on 8 mol kg⁻¹ NaTFSI, 8 mol kg⁻¹ NaTFSI + 0.5 mol kg⁻¹ KI and 21 mol kg⁻¹ LiTFSI, we constructed a Ragone plot (Fig. 5). The reported specific energy and power values are those of balanced full cells cycled within the electrochemical stability windows determined above. It is important to note that the AC electrodes used in all experiments were not optimized. Hence, only the maximum reported specific energies are realistic, while there is much room for improvement in the power performance.

Fig. 5 Ragone plot on the activated carbon mass level comparing the specific energy and power of full cells containing 8 mol kg⁻¹ NaTFSI (1.8 V), 8 mol kg⁻¹ NaTFSI + 0.5 mol kg⁻¹ KI (1.8 V), and 21 mol kg⁻¹ LiTFSI (2.0 V) as the electrolyte, respectively.

The outstanding maximum energy density of the cell based on the KI enhanced electrolyte (37.8 W h kg⁻¹) even surpasses those of commercial systems at low currents. However, the power performance of this system suffers from the strong load dependence of the pseudocapacitive contribution of KI to the total capacitance of the positive electrode. The device based on 21 mol kg⁻¹ LiTFSI also displays a relatively high maximum specific energy of 12.5 W h kg⁻¹ on the activated carbon mass level during our test, benefiting from the largest maximum cell voltage of 2.0 V. However, due to the low conductivity of the electrolyte, the energy that can be stored in such a device is very load dependent and the maximum power performance of the system is relatively poor. The supercapacitor based on 8 mol kg⁻¹ NaTFSI shows the most balanced behavior. Although the maximum energy density is limited to 14.4 W h kg⁻¹, it shows the best energy retention with increasing current and the highest maximum power of all investigated systems.

Conclusions

Alkali metal TFSI solutions of a concentration of 8 mol kg⁻¹ are promising aqueous electrolytes for supercapacitors due to their comparably high conductivity but improved electrochemical stability compared to standard concentration (∼1 mol kg⁻¹) pH-neutral aqueous electrolytes. We demonstrated that the stability window on AC is enhanced by several hundred millivolts to 1.8 V for 8 mol kg⁻¹ NaTFSI compared to 1 mol kg⁻¹ Li₂SO₄.

In addition, 8 mol kg⁻¹ NaTFSI exhibits a room temperature conductivity of ∼50 mS cm⁻¹, comparable to the one of state-of-the-art non-aqueous electrolytes based on acetonitrile. Ultra-highly concentrated electrolytes like 21 mol kg⁻¹ LiTFSI not only suffer from low conductivity (<10 mS cm⁻¹) as pointed out previously,¹⁴ but our tests also show lower coulombic efficiencies on the negative electrode for this electrolyte compared to 8 mol kg⁻¹ NaTFSI.

We also demonstrate that the combination with a redox additive further narrows the gap in energy density between aqueous and non-aqueous supercapacitors. An AC/AC full cell based on 8 mol kg⁻¹ NaTFSI + 0.5 mol kg⁻¹ KI displays a very high maximum energy density of 37.8 W h kg⁻¹ on the activated carbon mass level when charged up to 1.8 V, comparable to the performance of state-of-the-art non-aqueous supercapacitors. However, electrode balancing for such a system remains challenging because the pseudocapacitive contribution of the redox additive to the capacitance of the positive electrode is very rate dependent and hence the optimal balancing strongly depends on the target load. The balancing issue could be eased by the use of a second redox additive active at the negative electrode that would lead to more similar capacitance retention for the two electrodes, bringing the performance of aqueous to the level of organic electrolyte supercapacitors.

Conflicts of interest

There are no conflicts to declare.

References

1. F. Béguin, V. Presser, A. Balducci and E. Frackowiak, Adv. Mater., 2014, 26, 2219–2251.
2. B. E. Conway, Electrochemical Supercapacitors, Springer Science+Business Media, New York, 1999.
3. Q. Abbas, P. Babuchowska, E. Frąckowiak and F. Béguin, J. Power Sources, 2016, 326, 652–659.
4. D. Gastol, J. Walkowiak, K. Fic and E. Frackowiak, J. Power Sources, 2016, 326, 587–594.
5. J. Menzel, K. Fic and E. Frackowiak, Prog. Nat. Sci.: Mater. Int., 2015, 25, 642–649.
6. K. Fic, G. Lota, M. Meller and E. Frackowiak, Energy Environ. Sci., 2012, 5, 5842–5850.
7. P. Ratajczak, K. Jurewicz and F. Béguin, J. Appl. Electrochem., 2014, 44, 475–480.
8. M. He, K. Fic, E. Frąckowiak, P. Novák and E. J. Berg, Energy Environ. Sci., 2016, 9, 623–633.
9. Q. Abbas, P. Ratajczak, P. Babuchowska, A. L. Comte, D. Bélanger, T. Brousse and F. Béguin, J. Electrochem. Soc., 2015, 162, A5148–A5157.
10. L. Suo, O. Borodin, T. Gao, M. Olguin, J. Ho, X. Fan, C. Luo, C. Wang and K. Xu, Science, 2015, 350, 938–943.
11. L. Suo, O. Borodin, W. Sun, X. Fan, C. Yang, F. Wang, T. Gao, Z. Ma, M. Schroeder, A. von Cresce, S. M. Russell, M. Armand, A. Angell, K. Xu and C. Wang, Angew. Chem., Int. Ed., 2016, 55, 7136–7141.
12. Y. Yamada, K. Usui, K. Sodeyama, S. Ko, Y. Tateyama and A. Yamada, Nat. Energy, 2016, 1, 16129.
13. R.-S. Kühnel, D. Reber, A. Remhof, R. Figi, D. Bleiner and C. Battaglia, Chem. Commun., 2016, 52, 10435–10438.
14. A. Gambou-Bosca and D. Bélanger, J. Power Sources, 2016, 326, 595–603.
15. G. Hasegawa, K. Kanamori, T. Kiyomura, H. Kurata, T. Abe and K. Nakanishi, Chem. Mater., 2016, 28, 3944–3950.
16. H. Tomiyasu, H. Shikata, K. Takao, N. Asanuma, S. Taruta and Y.-Y. Park, Sci. Rep., 2017, 7, 45048.
17. P. Simon, Y. Gogotsi and B. Dunn, Science, 2014, 343, 1210–1211.
18. H. A. Mosqueda, O. Crosnier, L. Athouël, Y. Dandeville, Y. Scudeller, P. Guillemet, D. M. Schleich and T. Brousse, Electrochim. Acta, 2010, 55, 7479–7483.
19. E. R. Nightingale, J. Phys. Chem., 1959, 63, 1381–1387.
20. R. Gopal, Z. Anorg. Allg. Chem., 1955, 278, 42–45.
21. R. Hagiwara, K. Tamaki, K. Kubota, T. Goto and T. Nohira, J. Chem. Eng. Data, 2008, 53, 355–358.
22. J. D. Smith, C. D. Cappa, K. R. Wilson, R. C. Cohen, P. L. Geissler and R. J. Saykally, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 14171–14174.
23. J. Yin, C. Zheng, L. Qi and H. Wang, J. Power Sources, 2011, 196, 4080–4087.
24. D. Weingarth, H. Noh, A. Foelske-Schmitz, A. Wokaun and R. Kötz, Electrochim. Acta, 2013, 103, 119–124.
25. L. Coustan, G. Shul and D. Bélanger, Electrochem. Commun., 2017, 77, 89–92.
26. L. Eliad, G. Salitra, A. Soffer and D. Aurbach, J. Phys. Chem. B, 2001, 105, 6880–6887.
27. G. Lota and E. Frackowiak, Electrochem. Commun., 2009, 11, 87–90.
28. S. T. Senthilkumar, R. Kalai Selvan, Y. S. Lee and J. S. Melo, J. Mater. Chem. A, 2013, 1, 1086–1095.
29. L. Chen, H. Bai, Z. Huang and L. Li, Energy Environ. Sci., 2014, 7, 1750–1759.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7se00423k

---