Open Access Article
Open Access ArticleFrom cellulose to kerogen: molecular simulation of a geological process†
Lea
Atmani
ab,
Christophe
Bichara
b,
Roland J.-M.
Pellenq
abc,
Henri
Van Damme
a,
Adri C. T.
van Duin
d,
Zamaan
Raza
a,
Lionel A.
Truflandier
e,
Amaël
Obliger
a,
Paul G.
Kralert
f,
Franz J.
Ulm
ac and
Jean-Marc
Leyssale
 *ag
*ag
aCNRS/MIT Joint Lab “MultiScale Materials Science for Energy and Environment”, MIT Energy Initiative, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
bCNRS, Centre Interdisciplinaire des Nanosciences de Marseille, Campus de Luminy, Case 913, 13288 Marseille Cedex 9, France
cDepartment of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
dDepartment of Mechanical and Nuclear Engineering, The Pennsylvania State University, University Park, Pennsylvania 16802, USA
eInstitut des Sciences Moléculaires, Univ. Bordeaux, CNRS UMR 5255, 351 Cours de la Libération, 33405 Talence, France
fSpecialist Geoscience, Upstream Development, Projects & Technology, Shell Global Solutions International BV, Kessler Park 1, 2288 GS Rijswijk, The Netherlands
gCNRS, Laboratoire des Composites Thermostructuraux, UMR 5801 CNRS-Safran-CEA-Université de Bordeaux, 3 allée de la Boetie, 33600 Pessac, France. E-mail: jean-marc.leyssale@u-bordeaux.fr
First published on 10th October 2017
Abstract
The process by which organic matter decomposes deep underground to form petroleum and its underlying kerogen matrix has so far remained a no man’s land to theoreticians, largely because of the geological (Myears) timescale associated with the process. Using reactive molecular dynamics and an accelerated simulation framework, the replica exchange molecular dynamics method, we simulate the full transformation of cellulose into kerogen and its associated fluid phase under prevailing geological conditions. We observe in sequence the fragmentation of the cellulose crystal and production of water, the development of an unsaturated aliphatic macromolecular phase and its aromatization. The composition of the solid residue along the maturation pathway strictly follows what is observed for natural type III kerogen and for artificially matured samples under confined conditions. After expulsion of the fluid phase, the obtained microporous kerogen possesses the structure, texture, density, porosity and stiffness observed for mature type III kerogen and a microporous carbon obtained by saccharose pyrolysis at low temperature. As expected for this variety of precursor, the main resulting hydrocarbon is methane. The present work thus demonstrates that molecular simulations can now be used to assess, almost quantitatively, such complex chemical processes as petrogenesis in fossil reservoirs and, more generally, the possible conversion of any natural product into bio-sourced materials and/or fuel.
1 Introduction
Thermal annealing, or cracking, of organic matter results in the production of carbon-rich solids as well as hydrogen- and oxygen-rich fluids. This very fundamental process can be used to turn biomass products into various types of carbon-based material – microporous adsorbents or catalysts1,2 and carbon fibers3 – or biofuels.4 In nature, organic matter degradation begins on the earth surface but only significantly proceeds when organic residues are buried in sedimentary basins, a few km deep, where increased temperature and pressure can activate the process. From this geological decomposition originates petroleum and a carbonaceous residue called kerogen, the most abundant form of organic matter on the planet (∼a thousand time larger in mass than coal and petroleum in conventional reservoirs).5Kerogen formation operates at moderate depths, i.e. under mild conditions (below ∼350 K), where the remains of the most resistant tissues of living organisms combine with smaller moieties coming from the microbial or chemical degradation of less resistant biopolymers.6–12 At the end of a process called diagenesis7 this proto-kerogen turns into immature kerogen, a truly macromolecular hydrogen-rich solid, by further losing oxygen in the form of water, CO or CO2.
Kerogen “maturation” – actually, thermal decomposition – is considered to start when immature kerogen encounters more stressful geothermal conditions and becomes metastable,7i.e. above ∼350 K. Weak C–S and C–O bonds break first, producing bitumen that is highly enriched in polar compounds. C–C bonds start breaking immediately after, within the evolved polar compounds and in the residual kerogen, yielding a hydrocarbon-rich fluid.9 By convention, the term catagenesis refers to the stages of kerogen decomposition during which oil and “wet gas” (C1–C6) are produced. Catagenesis ends around 450 K. It may be followed by metagenesis and late methane (or “dry gas”) production if more severe geothermal conditions are encountered.
Kerogens are usually classified into three main families, noted type I, II and III, depending on the origin of their parent organic matter: marine for type I, lacustrine for type II and terrestrial for type III. On a more chemical ground, hydrogen content decreases and oxygen content increases when going from type I to type III. Hydrogen-rich type I and type II organic matters generally retain a high aliphatic content in their corresponding kerogen and are prone to produce oil during catagenesis. Conversely, type III organic matter generally has low oil potential and essentially produces methane during catagenesis. It is also worth noting that in the late stages of maturity, the end of catagenesis and metagenesis, all kerogen residues become chemically very similar, whatever the type of living cell they are derived from. The principal difference between these aromatic chars is that those arising from type I or type II organic matter will show extended graphene domains up to hundreds of nanometers, whilst graphene domains in type III chars will only grow, at best, to around 10 nm.12,13
Both time and temperature are critical for kerogen maturation, each one of the two parameters being able to compensate for the other,7 as shown by laboratory pyrolysis experiments14–16 and by numerous field observations relating hydrocarbon generation to subsidence depth and/or geothermal gradient.7–10 Quantitatively, the rate of petroleum formation and the kerogen maturity indicators are exponentially related to temperature and linearly related to time. Whereas pressure only has a second order influence, it was demonstrated16 that confinement effects are crucial in order to accurately reproduce the maturation pathway in a van Krevelen diagram (H/C versus O/C). Transition state theory of rate processes is the perfect framework to account for these features and it is extensively used in petroliferous basin modeling.17 The most popular formalism is a matrix of parallel first-order kinetic reactions, the parameters of which – primarily the distributions of activation energies and the frequency factors to a lesser extent – are determined by artificially heating immature source rock samples in far from equilibrium conditions, at heating rates (∼1 to 50 K min−1, up to 825 K (ref. 11)) or at isothermal temperatures (550–625 K) much higher than those found in sedimentary basins (∼1 to 10 K per My, up to ∼525 K (ref. 7 and 11)), and fitting the data to the kinetic model. Remarkably, as it was early recognized, when geological heating rates are imposed, the kinetic model yields kerogen maturity results comparable to what is observed in the field.14,18
Aside from these efforts to investigate maturation kinetics and the nature and quantities of produced hydrocarbons, very little attention has been paid to the structure and properties of the corresponding kerogen. The first structural models of kerogen were hand-drawings based on chemical analysis and/or microscopy observations.19–21 Of particular interest was the series of models proposed by Béhar and Vandenbroucke for the three types of kerogen at different maturities.20 The recent exploration and extraction of shale hydrocarbons has brought interest back into kerogen modeling, with characterization of their porosity, mechanical and hydrocarbon transport properties as the main aim. 3D atomistic kerogen models22–26 were first generated by digitalization and migration into 3D of the early 2D models of Béhar and Vandenbroucke20 and Siskin et al.21 More recently, models of type II kerogen of various maturities were produced by Bousige et al.27 using a purely reconstructive approach, hybrid reverse Monte Carlo, which has the advantage of not having to presuppose any structural or chemical elements other than the composition and density of the material. All these models have shown undeniable success in reproducing structural properties, such as pair distribution functions (g(r))26,27 and spectroscopic (NMR) signatures26 as well as volumetric and rheological observables.23,25 Most recent investigations have also allowed the prediction of transport properties of various hydrocarbons in the microporosity of kerogen28,29 and the ductile to brittle fracture transition induced by maturation.27
In spite of these important achievements, two important unresolved questions could still largely benefit from modeling studies. First, the relatively limited amount of experimental data (especially g(r)), and probably also of computational resources, does not allow for a proper model of kerogen growth and maturation pathways, even though the latter would constitute a crucial step in connecting kerogen maturity and properties. Second, experimentally fed kerogen models do not allow for the prediction of their hydrocarbon potential, i.e. the nature and amounts of hydrocarbon than can be produced upon further maturation, an obvious aim in the context of unconventional hydrocarbon extraction. Despite the apparent conflict between geological time scales of oil and gas generation (10 s to 100 Myears) and those accessible to molecular simulations (milliseconds at best30), 20 orders of magnitude lower, a few recent studies based on reactive molecular dynamics simulations report on the early stages of pyrolysis of various kinds of organic matter.31–36 In these works, reactive processes are considerably accelerated by performing simulations at temperatures well above 1000 K,32–36 thus significantly affecting the thermodynamic conditions, or using accelerated sampling approaches.31 However, because of timescale limitations, the apparition of kerogen remains entirely unexplored so far. In what follows, we use reactive molecular dynamics37 within an accelerated simulation framework, replica exchange molecular dynamics (REMD),38,39 and large scale computational resources (∼one million hours CPU time40) to report on the decomposition of cellulose, one of the principal constituents of terrestrial plants (type III organic matter), under typical geological conditions: 150 °C and 10–100 MPa. As we will demonstrate in the following sections, we have been able to simulate the process up to a relatively advanced maturation stage, typical of the later stages of catagenesis, and to observe the formation of methane, the most expected hydrocarbon for such a nonaliphatic precursor.7
2 Methods
The present work is based on well-known molecular dynamics methods,41 either in the canonical (NVT) or isothermal–isobaric (NPT) ensembles, where N, V, P and T refer to the number of atoms, the volume, the pressure and the temperature, respectively. The velocity-verlet scheme42 is used with a 0.1 fs timestep to integrate the equations of motion and the Nosé–Hoover and Nosé–Hoover–Andersen thermostat and barostat43 are used to fix temperature and pressure, respectively. Time constants of 0.05 and 0.5 ps are used for temperature and pressure relaxations, respectively. Interatomic interactions are computed using ReaxFF37 by combining the Reax2013 C–C interaction parameters,44 which have demonstrated significant improvement in the description of carbonaceous solids, with the C–O, C–H, O–O, O–H and H–H interaction parameters used in ref. 45 and 46. Periodic boundary conditions are always applied in the three cartesian directions and all the simulations are performed using LAMMPS.47More precisely, the REMD technique is used to study the complete transformation of cellulose into kerogen and its associated fluid phase. REMD is an accelerated MD scheme that was initially developed to investigate the transformation of a protein from a non-folded out of equilibrium state to its equilibrium folded state – a microsecond to millisecond process – from picosecond to nanosecond long MD simulations.38,48 It is based on the parallel simulation of many replicas of the same system, each operating at a different temperature using canonical (NVT) MD. Monte Carlo attempts are then performed at regular time intervals to exchange configurations between replicas operating at close temperatures. Accepting these attempts with probability 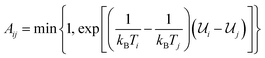 – where i and j are the IDs of two adjacent replicas, Ti and Tj their temperatures, and
– where i and j are the IDs of two adjacent replicas, Ti and Tj their temperatures, and ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) i and
i and ![[scr U, script letter U]](https://www.rsc.org/images/entities/char_e534.gif) j their potential energies – ensures that each replica will be driven towards its canonical equilibrium distribution. This is where REMD significantly differs from conventional MD or MC methods. Although all of these methods tend to progressively decrease the prevailing thermodynamic potential (Helmholtz free energy in the case of simulations in the canonical ensemble) until equilibrium is reached, MD and MC operate by crossing successively all the free energy barriers separating the initial and equilibrium states, generating a kinetic path to equilibrium. In REMD, most of these barriers are crossed at higher temperatures. This has the advantage of being considerably faster but the trajectory to equilibrium may deviate from the kinetic trajectory as individual barriers are crossed on a different (high-temperature) free energy landscape. For this reason the path followed by any replica in REMD can only be considered as a thermodynamic path (i.e. a path of progressively decreasing free energy) as opposed to a kinetic path.
j their potential energies – ensures that each replica will be driven towards its canonical equilibrium distribution. This is where REMD significantly differs from conventional MD or MC methods. Although all of these methods tend to progressively decrease the prevailing thermodynamic potential (Helmholtz free energy in the case of simulations in the canonical ensemble) until equilibrium is reached, MD and MC operate by crossing successively all the free energy barriers separating the initial and equilibrium states, generating a kinetic path to equilibrium. In REMD, most of these barriers are crossed at higher temperatures. This has the advantage of being considerably faster but the trajectory to equilibrium may deviate from the kinetic trajectory as individual barriers are crossed on a different (high-temperature) free energy landscape. For this reason the path followed by any replica in REMD can only be considered as a thermodynamic path (i.e. a path of progressively decreasing free energy) as opposed to a kinetic path.
A first REMD simulation is run for 750 ps in which all of the replicas are initiated with a 4200-atom I-β cellulose crystal, constructed using the “Cellulose-builder” package49 at an initial density of 1.29 g cm−3. It uses 96 parallel replicas run in the (NVT) ensemble with an exponential spacing of temperatures between adjacent replicas, from 423 to 3502 K. The maximum temperature has been chosen using the experimental activation energy (47 kcal mol−1) and prefactor (6 × 1014 s−1) for cellulose pyrolysis50 to provide a decomposition time in the 1–100 ps range, easily accessible to MD. Note that this corresponds to timescales of around 1013 years and a few thousand years at room and geological (150 °C) temperatures, respectively. Temperature swaps between two adjacent replicas, selected at random among all the replicas, are attempted every 10 fs. The average acceptance rates for these attempts are found around 20%, with low variability among the different replicas, indicative of a successful spacing of replicas in temperature space. This is also confirmed by visualization of the potential energy histograms, showing reasonable overlap between replicas. As cellulose conversion into kerogen produces an important amount of fluid, and because of the constant volume condition, the system pressure significantly increases during the process. In order to maintain reasonable pressure conditions the REMD process is interrupted every time the pressure rises above 200 MPa and the configuration of the 423 K replica is relaxed at this temperature and at an imposed pressure of 25 MPa for 100 ps using NPT MD. The resulting configuration is then attributed to all of the replicas and the REMD run resumed.
After this first REMD run, all of the created fluid molecules are removed from the system and the resulting macromolecular phase (kerogen) is relaxed for 1 ns at 423 K and 25 MPa, during which the kerogen densifies. A subsequent REMD run is launched for 1.8 ns on this solid phase, using the exact same simulation parameters. During this run, configurations of the 423 K replica are stored every 200 ps for analysis. The latter are relaxed for 100 ps, again at 423 K and 25 MPa, prior to structural and volumetric characterizations.
Chemical analysis is based on the identification of independent molecular clusters, achieved using the following cutoffs for covalent bonding: 1.9 Å for C–C, C–O and O–O bonds, 1.4 Å for O–H bonds, and 1.1 Å for H–H bonds. These values produce reliable results as they fall in very low population areas of the corresponding partial pair distribution functions for most couples. The only difficulty is the O–H case because of the complexity arising from hydrogen bonds, with some hydrogen atoms being, in some particular configurations, difficult to associate to one or another O atom, especially in water–hydronium couples. This difficulty does not affect any conclusions of the present work. Aside from standard coordination statistics, clustering algorithms are used to infer some textural elements from the macromolecular phase present in the atomistic configurations.
All primitive rings are identified using the shortest path analysis method51 and atom-sharing rings are regrouped into ring clusters. Similarly, all atoms that do not belong to any ring are designated as “chain” atoms and regrouped into chain clusters. Note that, even though related to the aromatic/aliphatic content, nothing guarantees here, for instance, that the rings are aromatic.
Some volumetric and structural properties, such as density, bulk modulus (B), and g(r), require time-averaging for such small systems. These data are computed using 1 ns long NPT simulations. Density and g(r) calculations are trivial. Bulk moduli are computed from the volume fluctuation method,41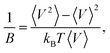 where kB is the Boltzmann’s constant and 〈…〉 stands for a time average.
where kB is the Boltzmann’s constant and 〈…〉 stands for a time average.
Pore space properties, here including porosity fraction and pore size distributions (PSDs), should also, in theory, be time-averaged, however, as these calculations are associated with high computational cost, they are obtained here from single, equilibrated configurations. Porosity is computed as the fraction of the volume available to a CO2 molecule based on the van der Waals diameters of CO2 (3.74 Å) and of the kerogen atoms (3.36, 3.17 and 2.42 Å for C, O and H, respectively). It is obtained by sampling 2 × 105 random locations within the volume. As in earlier works,27,29 PSDs are calculated using the Gelb and Gubbins technique52 on this porous space, using about 104 pore size investigations at each location.
High-resolution transmission electron microscopy (HRTEM) images are simulated from atomistic models using a multislice HRTEM simulation software53 and standard microscope parameters: Philips CM30ST microscope operated at 300 kV; −58 nm Scherzer defocus; 1.2 mm spherical aberration; 1.5 mm chromatic aberration; 7 nm spread of focus and aperture radius of 4 nm−1.
3 Results and discussion
3.1 Cellulose decomposition and kerogen formation
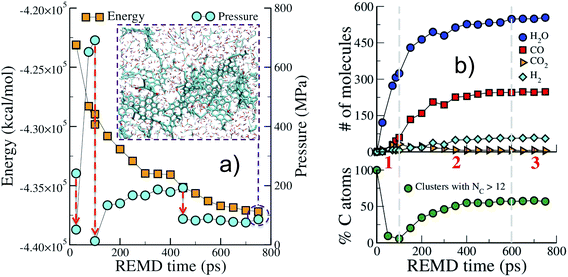
We start by describing the evolution of the low temperature replica (423 K), typical of geological conditions, during the first REMD simulation. Fig. 1 shows that the crystal decomposes quickly and separates into a carbon-rich macromolecular (or solid) phase, with high aromatic content, immersed in a hydrogen- and oxygen-rich fluid phase comprised of small molecular species (see the inset in Fig. 1(a)). The huge potential energy release and the massive production of fluid, increasing the system entropy, confirm the scenario of an irreversible process. Also noticeable is the significant increase in pressure due to fluid production (Fig. 1(a)). This excess pressure was released using short NPT MD simulations after 25 ps, 100 ps and 450 ps to maintain reasonable reservoir conditions. In the final part of the simulation, energy and pressure reach a plateau that is indicative of convergence to an equilibrium state, i.e. a state at which no macroscopic observable evolves in time. This could either be the true thermodynamic equilibrium state or (most probably) a metastable equilibrium state.Fig. 1(b) shows the evolution with time of the numbers of common volatile molecules (water, carbon monoxide and dioxide, and hydrogen) as well as the size of the macromolecular (solid) phase, arbitrarily defined as molecules with more than 12 carbon atoms. Even though care must be taken as the path followed by the system may be different from the true kinetic path (see discussion in the Methods section), this allows breaking down the process into three main steps. In agreement with the commonly accepted mechanism of cellulose pyrolysis,54,55 we first observe, in the initial 100 ps (REMD time), the fragmentation of the cellulose crystal into small molecular units associated with the production of a large amount (around 300 molecules) of water. Then, from 100 ps to approximately 600 ps, a carbon-rich macromolecular phase appears and progressively grows until it includes around 60% of the carbon atoms. In this second phase, a high amount of carbon monoxide and water, ∼250 molecules each, are produced as well as around 50 hydrogen molecules. Carbon dioxide, on the other hand, is only obtained at a low concentration (around 5 molecules), although a peak in its production is visible at 100 ps, when the carbon-rich phase starts growing. Noticeably, the amount of produced H2O, CO and CO2 and their order of appearance are in very fair agreement with results from pyrolysis experiments at temperatures below 1000 K.55 Above 600 ps, the system seems to have reached an equilibrium state.
The maturation of organic residues, excluding volatile molecules, is usually described in a so-called van Krevelen diagram, plotting atomic H/C against atomic O/C. Such a diagram is provided in Fig. 2 for the carbonaceous residue obtained at 423 K at different times of the REMD simulation and compares experimental data for type III kerogen precursors. Interestingly, we observe that, although departing slightly from the average trend, the simulation data are found well within the data cloud reported for Mahakam coals, a reference type III kerogen.12 Especially, the change in slope characterizing the transition between late diagenesis and early catagenesis observed after ∼150 ps of REMD simulation (O/C ∼0.14 and H/C ∼0.8 (ref. 7)) is fairly well reproduced. Experimental data for cellulose pyrolysis by Tang and Bacon54 show the same trend, yet at slightly downshifted H/C, that arises from open system conditions, as later demonstrated by Monthioux et al.16 Data for type III organic matter pyrolysis in confined conditions – where the produced fluid molecules remain in contact with the solid residue (in nano- or sub-nanopores) and can assist reactivity – by Monthioux et al. indeed follow almost the same path as found in the present simulation. The slight difference observed between the natural maturation on one side and the confined system pyrolysis and REMD modeling on the other side remains difficult to explain. Our work and the confined pyrolysis experiments taking into account both equilibrium with the fluid and the pressure effects give as the main plausible explanations either a kinetic effect or a modification of equilibrium conditions due to partial fluid release in the fossil sample. It is nonetheless important to recall that the important spread of experimental data for the natural maturation, as shown by the colored area in Fig. 2 and the somehow limited size of our model, and thus its statistical significance, do not allow further comparison.
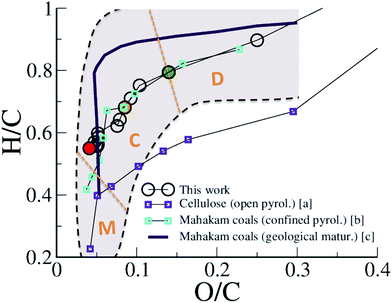 | ||
| Fig. 2 van Krevelen plot of the evolution of the macromolecular phase (kerogen). H/C versus O/C atomic ratios of the 423 K replica during the first REMD simulation are compared to experimental data of cellulose pyrolysis in an open system (a: ref. 54), confined pyrolysis (b: ref. 16) and geological maturation (c: ref. 12) of a type III kerogen/coal. The shadowed area roughly depicts the spread of the data cloud for the natural maturation. Orange dotted lines and characters indicate the domains of diagenesis (D), catagenesis (C) and metagenesis (M) according to Tissot and Welte.7 Colored circles correspond to 150 ps (green), 300 ps (orange) and 750 ps (red). | ||
We now describe the structure and texture evolution of the kerogen during this simulation. Fig. 3 shows some snapshots of the growing kerogen at different times of the first REMD simulation. Fig. 4 provides quantitative data on the carbon atom hybridization, texture (rings vs. chains) and ring topology.
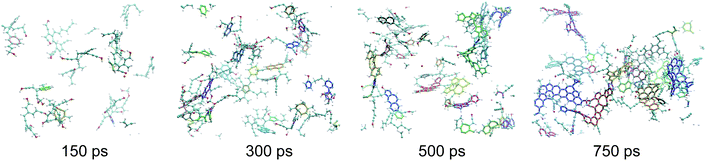 | ||
| Fig. 3 Snapshots of the macromolecular (kerogen) phase at 150, 300, 500 and 750 ps. The color code is the same as in Fig. 1. In addition every independent ring cluster is highlighted with thicker sticks with a unique color. All data are from the 423 K replica of the first REMD simulation. The first, second and last snapshots correspond to the green, orange and red circles in Fig. 2, respectively. | ||
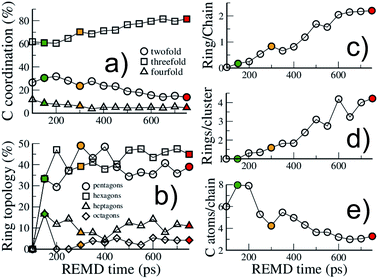 | ||
| Fig. 4 Structural evolution of the macromolecular (kerogen) part during growth. Evolution with REMD time of (a) the carbon atom coordination, (b) the ring topology, (c) the ratio of carbon atoms in rings over carbon atoms in chains, (d) the size of ring clusters (in number of rings) and (e) the size of chains (in number of carbon atoms). The colored symbols are equivalent to Fig. 2. All data are from the 423 K replica. | ||
First, as shown in Fig. 4(a), the macromolecular phase is essentially composed of threefold (sp2) carbon atoms, increasing from ∼60% in the early stages to ∼80% at the end of the simulation. The fraction of fourfold (sp3) carbon atoms is low and decreases during the whole process (from ∼10% to less than 5%). This low sp3 content is somewhat expected as the considered precursor does not possess any alkyl chain in its structure. However, a surprisingly high amount of twofold (sp) carbon atoms is obtained in the early stages of the process, with a maximum of about 30% at the onset of catagenesis, before decreasing down to 13%. We do not have any definitive explanation for this high amount of sp bonded C atoms. We can only suggest that this environment may be over-stabilized by the current ReaxFF parameterization.
As can be seen in Fig. 3, at 150 ps, which seems to correspond to late diagenesis according to Fig. 2, the proto-kerogen is composed of small, essentially (unsaturated) aliphatic moities (see the ring over chain ratio in Fig. 4(c)), forming clusters of on average 7C atoms (Fig. 4(e)). At this stage, only a few (five) isolated rings (see the number of rings per cluster ∼1 in Fig. 4(d)) are visible, in agreement with the classical picture of immature type III kerogen.20
The catagenesis regime, which according to Fig. 2 starts after around 200 ps of simulation, corresponds to the development of rings and ring clusters in the material. As shown in Fig. 3 and 4(d) (see also Fig. S1†) the amount of rings and their aggregation into clusters drastically increases from 150 to 750 ps. Conversely, the average chain length is reduced down to ∼3 atoms (Fig. 4(e)). Overall, the ratio of carbon atoms in rings over carbon atoms in chains increases from very close to zero at the onset of catagenesis to more than 2 after 750 ps (Fig. 4(c)). At this time, the average cluster size is of about 4 rings (Fig. 4(d)), slightly lower than the usual picture of mature type III kerogen (6–7 rings),20 even though clusters up to 14 rings can be detected (see Fig. 3). Note that we do not distinguish between aromatic and non-aromatic ring structures here, an algorithmically delicate and complex task for such small units, especially in the absence of electronic structure in the calculations. As shown in Fig. S1(a),† the number of C atoms in the kerogen significantly increases up to ∼400 ps, the proper growth phase, at which it stabilizes. Above this, we essentially observe a conversion from chain atoms to ring atoms, which can already be considered as a maturation stage. Interestingly, although the number of rings constantly increases up to almost the end of the simulation, the number of ring clusters plateaus around 30 clusters after 400 ps (Fig. S1(b)†). Finally, as can be seen in Fig. 4(b), the ring topology remains relatively constant during the simulation (note that at 100 ps, the first point displayed in Fig. 4(b), there is no ring in the system, and hence all values are zero), with around 40–45% of both hexagons and pentagons, 10% of heptagons and a few % of octagons, typical of fullerenic, or non-graphitizing, amorphous carbons.56
Tables 1 and 2 give some more details on the compositions of the fluid and solid phases, respectively, including temperature effects by comparison with replicas simulated at higher temperatures. First, we observe that, in addition to the molecules discussed in Fig. 1, many other molecular species are obtained (see Table 1). This includes two acetylene-based alcohols, acetylenediol and ethynol, as well as hydronium and ketenium cations, methanediol, methanol and methane. Even though the thermal cracking of type III organic matter, especially cellulose, is expected to produce very short molecular species,12,55 as obtained here, their precise nature and distributions may be surprising at first sight. Table S1† compares the formation energies at 0 K (with respect to isolated atoms) computed with ReaxFF and plane waves density functional theory (PW-DFT) for the eleven molecules listed in Table 1. As can be seen, the error with respect to PW-DFT is within 6% for all of the neutral molecules but CO2, which we believe is accurate enough to grant a reasonable description of the potential energy surface for this set of 8 molecules. Note that it does not exclude the fact that other molecules (possibly containing other functional groups like acids, ketones, ethers, etc.) could be destabilized by ReaxFF and hence are not observed. Nevertheless, this work suggests that the obtained high amounts of hydroxylated methane and acetylene (methanol, methanediol, ethynol and acetylenediol) with respect to methane and acetylene result from the high oxygen concentration in the fluid phase (O/C = 1.9 and O/H = 0.6). Such conditions do not apply in the reported pyrolysis experiments, either because of the open-system conditions54 or because of the use of a pre-matured precursor, much poorer in oxygen.16
| Molecule formula | Usual name | Temperature (K) | |||
|---|---|---|---|---|---|
| 423 | 604 | 901 | 1407 | ||
| H2O | Water | 554 | 563 | 552 | 577 |
| CO | Carbon monoxide | 248 | 245 | 245 | 302 |
| H2 | Dihydrogen | 55 | 57 | 59 | 155 |
| C2H2O2 | Acetylenediol | 30 | 28 | 29 | 20 |
| H3O+ | Hydronium | 14 | 11 | 13 | 17 |
| C2H3O+ | Ketenium | 12 | 10 | 12 | 3 |
| C2H2O | Ethynol | 9 | 12 | 10 | 15 |
| CH4O2 | Methanediol | 8 | 6 | 7 | 2 |
| CH4O | Methanol | 6 | 9 | 9 | 3 |
| CO2 | Carbon dioxide | 5 | 7 | 7 | 0 |
| CH4 | Methane | 5 | 5 | 5 | 6 |
The formation energy of CO2, 13% larger with ReaxFF than with PW-DFT, also possibly explains the extremely low amounts of produced CO2, especially with respect to CO. Furthermore, the presence of many cations (hydronium and ketenium) in the fluid phase is clearly an artifact of the ReaxFF potential which induces a strong overestimation of the charge transfer in the system. A detailed analysis of charges reveals that the average net charges on hydronium and ketenium are only of 0.34e and 0.13e, respectively, and are essentially neutralized by a small artificial net negative charge of −0.14e on the CO molecules. Note also that, unlike usual classical non-reactive force fields for instance, electrostatics is here a limited contribution to the total ReaxFF potential energy in which the highest contribution is from chemical bonds. A further discussion on the chemistry obtained with the used ReaxFF parameters, including a DFT evaluation of REMD/ReaxFF configurations, is presented in Table S2 and Fig. S5 and S6.†
As shown in Table 1, the composition of the fluid at 750 ps does not show much dependence on temperature until 1407 K, the temperature at which we observe a significant evolution towards a more mature state, corresponding to an important additional production of, by decreasing importance, H2, CO and water, as well as a decrease in the amounts of carbon dioxide and all of the hydroxylated compounds but ethynol. As for the fluid, the solid phase is relatively constant in composition up to 1407 K (see Table 2). Below this temperature the system is composed of 3–5 molecular fragments of various sizes, while at 1407 K a transition occurs towards a unique fragment with lower overall O/C and H/C ratios typical of a higher maturation level. We note that the transition temperature between these two degrees of advancement along the decomposition path is not totally established at the end of the 750 ps simulation as replicas obtained at temperatures larger than 1407 K show alternate occurrence of these more mature and less mature configurations. This clearly results from an insufficient convergence of the REMD simulation and of course the configuration exchange moves.
| T (K) | Composition | O/C | H/C | Molecules |
|---|---|---|---|---|
| 423 | C682H375O28 | 0.041 | 0.550 | C434H229O16, C235H136O11, C13H10O1 |
| 604 | C693H388O31 | 0.045 | 0.560 | C522H283O25, C113H61O3, C40H29O3, C18H15O |
| 901 | C688H383O33 | 0.048 | 0.557 | C289H148O13, C238H141O13, C113H62O3, C35H22O3, C13H10O |
| 1407 | C748H273O19 | 0.025 | 0.364 | C748H273O19 |
A last item provided by this REMD simulation is the hydrocarbon potential of cellulose that can be computed as the mass ratio of the produced hydrocarbon fluid phase at 423 K (excluding other molecules as H2, H2O, H3O+, CO and CO2) over the initial mass of cellulose. We obtain a value of 180 mg g−1, typically in the range of values obtained experimentally with rock analysis methods, ∼100 mg g−1 C12. Interestingly the only alkane produced is methane (5 molecules at 423 K), which along with acetylene (2 molecules) is the only true hydrocarbon obtained in this work. The absence of long alkanes is actually expected for type III kerogen,7 especially when derived from the structural elements of plants such as cellulose, lignin or hemicellulose as they do not contain saturated aliphatic chains. Methane is also known as the main hydrocarbon product of cellulose pyrolysis.55
3.2 Kerogen maturation
Even though it has a chemical nature typical of a type III kerogen at an intermediate maturation state, the macromolecular phase obtained at the end of the REMD simulation does not really form a proper solid, strictly speaking, as it is highly dispersed in the fluid phase. We indeed expect a phase separation to occur at some point, especially considering the prominence of water in the fluid and the hydrophobicity of the solid. However, this diffusive process could be extremely long to occur in a simulation, and would certainly be thermodynamically hindered due to the free energy cost for the creation of a solid/fluid interface in a system with a necessarily huge surface over volume ratio. We have thus decided to overcome this limitation by removing all of the fluid from the system in order to observe how further the macromolecular phase can mature within its bulk (i.e. far from any such interface).A second system, consisting of the macromolecular phase at 423 K at the end of the 750 ps REMD run, with no fluid molecules, was first relaxed at 423 K and 50 MPa for 1 ns, giving rise to a dense kerogen model, labeled A in Fig. 5. This model was then subjected to an additional 1800 ps of REMD to produce another more mature kerogen model labeled B in Fig. 5. As can be seen in Fig. 5, both O/C and H/C are slightly further reduced, down to 0.018 and 0.5, respectively, due to the progressive production of 10H2O, 6CO and 5H2 molecules, yet remain typical of the late catagenesis stage. From a structural point of view, the three large unconnected molecules constituting the initial system quickly coalesce (in around 100 ps) to form a unique macromolecular entity. The snapshots in Fig. 5 also clearly show an increase of the ring (aromatic) content in the system.
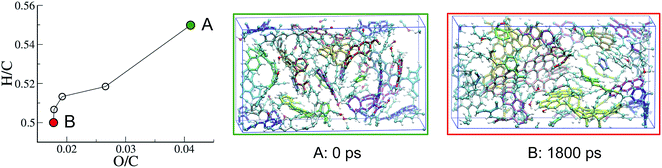 | ||
| Fig. 5 Evolution with REMD time of the kerogen composition plotted in a van Krevelen diagram and snapshots of the system (A) after the 1 ns NPT relaxation and (B) at the end of the second (1800 ps) REMD simulation. All data refer to the 423 K replica of the second REMD simulation and the color code is as in Fig. 3. | ||
Interestingly, the application of REMD to model A, which appeared as an equilibrium structure in the presence of the fluid, leads to a significant structural and chemical evolution in absence of the fluid phase, resulting in model B and a few extra molecules. It thus seems that removing the fluid considerably accelerates the maturation of the system. However, we do not know whether this is due to an important modification of the thermodynamic equilibrium (recalling that both the system composition and density are changed) or to the removal of a kinetic hindrance (one can argue that the presence of the fluid hinders the agglomeration of the solid phase and thus the possibility of different solid residues to react with each other).
Fig. 6 allows one to quantify the texture and structure evolution a little more. First, we see in Fig. 6(a) that the density remains around 1.3 g cm−3, even though it passes through a maximum, close to 1.4 g cm−3 during the process, which corresponds to a state of no porosity (Fig. 6(b)). Apart from this extreme case, the porosity remains at around 10%, with pore diameters in the 0.35–0.75 nm range, characteristic of ultramicropores, as shown in the pore size distributions (PSD) presented in Fig. S3.†Fig. 6(c) shows that the chain to ring conversion is pushed a little further during this second REMD with the number of ring C atoms reaching 3.5 times the number of chain C atoms and the average size of ring clusters increasing up to around 6 rings per ring cluster. In the mean time the chain clusters are reduced to on average 2.6 C atoms (see Fig. S2†). The structure of model B is thus very close to the one accepted for mature (end of catagenesis) type III kerogen: coronene (7 rings) as the prototypal aromatic cluster and 2–3 C atoms per chain according to Béhar and Vandenbroucke.20 We note that the largest ring clusters count 14 and 24 rings for models A and B, corresponding to 48 and 73 C atoms, respectively. Chemical representations of the three largest ring clusters in model B, given in Fig. S4,† show that more than half of the rings are aromatic and form extended aromatic cores in these clusters. Also, the proportion of hexagonal rings significantly increases, from 45 (A) to 60 (B)%, while that of pentagonal rings decreases from 40 (A)% to 30 (B)%, indicating an increase in stability (see Fig. S2†) and, probably, in planarity of the clusters. The final state of the system (model B), however, is not advanced enough on the maturation path to conclude on the nature – graphitizing or non-graphitizing – of the kerogen.13 Finally, as shown in Fig. 6(e), the bulk modulus of the kerogen progressively increases from 2 to 8 GPa between models A and B. We note, by comparing the evolutions of the different quantities reported in Fig. 6, that the increase in stiffness seems to be more related to the structure of the carbon backbone, with the conversion from chain to rings increasing the stiffness, than to the volumetric properties (including porosity) as postulated earlier.27
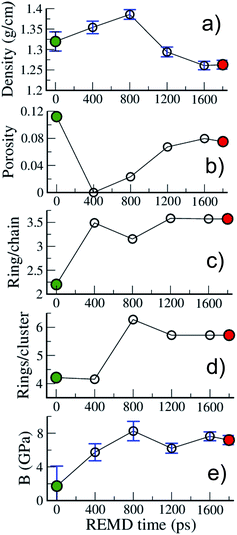 | ||
| Fig. 6 Evolution with REMD time of the kerogen (a) density, (b) porosity, (c) ring/chain ratio, (d) number of rings per ring cluster and (e) bulk modulus. All data refer to the 423 K replica. | ||
Some of the properties reported in Fig. 6 can also be compared to a few experimental or modeling values reported for type II and type III kerogens23–25 and for the well-characterized CS400 material, a porous carbon derived from the pyrolysis of saccharose at low temperature (400 °C),57 which constitutes an excellent lab-based proxy for the present work. First, the density values obtained in this work (1.25–1.4 g cm−3) are close to the reported experimental values for Green River kerogen23 (1.11 g cm−3), type II and type III kerogens25 (1.15–1.30 g cm−3), or CS400 (1.28 g cm−3). Data regarding porosity and stiffness are scarcer. Collell et al.24 have predicted a porosity of 0.15% for a kerogen model of density 1.42 g cm−3, in other words, very close to the value of 0% found in the present work at the maximum density of 1.4 g cm−3. On the other hand, Pikunic et al.57 have reported a porosity of 12% for CS400, which corresponds to the maximum value reported in the present work. It is also worth noting that the extent of the PSDs (Fig. S3†) corresponds well to those reported for type II kerogen27 and CS400.57 Finally, the values of the bulk modulus reported in this work (2–8 GPa) are of the same order as those of 3.7 and 5 GPa obtained for mature type II kerogen models.24,27
Few other properties can be gathered from the kerogen models and compared to available data, either resulting from experiments or former atomistic models. Fig. 7 compares C–C contributions to g(r) obtained for models A and B to experimental (full g(r)) data from an immature type II kerogen sample and a post-metagenesis (overmature) pyrobitumen obtained by Bousige et al.27 We can see that the produced kerogen models both share the short-range order of aromatic carbons, as opposed to aliphatic immature kerogens, yet do not possess the long-range order of pyrobitumen, a high-stiffness (∼40 GPa) almost heteroelement free aromatic carbon. Recalling that the integrated first peak intensity is proportional to the number of C–C bonds per C atom (2.35, 2.51 and ≈3 for model A, model B and pyrobitumen, respectively) divided by the carbon atom number density, one easily deduces that the density of the pyrobitumen sample is significantly (20–30%) larger than those of models A and B. In addition to having its area affected by density, the first peak can also significantly be broadened, especially at such low r values, because of the finite Q range of the diffraction apparatus used in the experiments. Broadening corrections should be applied to simulated g(r) for a quantitative comparison to the experiments58 but we unfortunately do not have the necessary experimental inputs. Finally, the g(r) values for models A and B are actually also very close to that for CS400 (see Fig. 2(a) in the original publication57), even though the first peak in the present work appears significantly thinner.
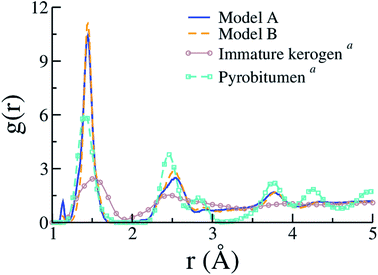 | ||
| Fig. 7 Pair distribution functions (C–C only) of models A and B compared to the experimental data (including contributions from heteroelements) for an immature type II kerogen and a post-metagenesis pyrobitumen from (a) Bousige et al.27 (the well-known experimental broadening at short r (ref. 58) is not accounted for in the simulation data). | ||
In Fig. 8 we compare HRTEM images simulated from models A and B to an experimental image of CS400 taken from Pikunic et al.57 A few dark fringes, indicative of aromatic domains well-aligned with the beam direction, are clearly visible for the three samples. For all of them, these fringes are short (below 1 nm), randomly oriented in the plane, and do not show any layer stacking as would appear under the form of parallel fringes distant by ∼0.34 nm. These images further confirm that both kerogen models possess the texture of low temperature saccharose-based char.
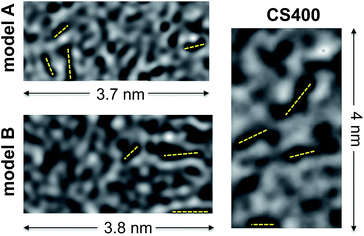 | ||
| Fig. 8 Simulated HRTEM images of models A and B compared to an experimental HRTEM micrograph of CS400 (reprinted with permission from the original ACS publication57). Dark fringes in the micrographs (a few of them are highlighted with dashed yellow lines) indicate the presence of aromatic domains aligned with an electron beam. | ||
In spite of a significant structural evolution during the second REMD simulation, it is important to recall that the produced kerogen model (B) remains at a pre-metagenesis state, even though it is sitting at the border between catagenesis and metagenesis according to the van Krevelen diagram. During metagenesis, the extent of parallel aromatic domains should considerably increase, up to tens of nm for type III kerogens, which is definitely not observed in the present work. Note that other types of kerogen (types I and II) would see these domains grow considerably larger during metagenesis: hundreds to thousands of nm upon further pyrolysis as shown by Oberlin and coworkers.59,60 The presence of many pentagonal rings, especially if isolated, could be an explanation for the non-graphitizability of type III kerogen.
Nevertheless, the absence of metagenesis in the simulation indicates that the activation energy for metagenesis is certainly significantly higher than that for diagenesis and catagenesis, and certainly too high to be activated in the current simulation setup in a reasonable amount of time, even in the high temperature (3500 K) replica. This hypothesis is supported by the fact that metagenesis usually takes place at a much deeper depth, and hence higher temperatures, than diagenesis and catagenesis.12 A much larger maximum temperature would thus certainly be required to observe metagenesis in a REMD simulation.
4 Conclusion
By combining reactive molecular dynamics and the replica exchange method, we have been able, for the first time, to simulate the complete geological conversion of some organic matter into a fluid and a kerogen at an advanced maturation state.The simulated kerogen formation and maturation plotted in the van Krevelen diagram follow with great accuracy those observed for natural specimens or for samples obtained in the laboratory under confined volume conditions. The nature of the produced fluid phase, especially the high water content, also agrees well with experiments. As expected, methane is the main alkane produced (actually the only one, certainly because of the small system size).
The resulting kerogen model (model B in Fig. 5) shares most of the known, or hypothesized, properties of mature type III kerogen. It is a dense, relatively stiff, ultramicroporous aromatic carbon with short aromatic domains and a low degree of texture, as highlighted by the absence of well-stacked aromatic domains. Besides the fact that the final outcome of this work enriches the so far extremely limited database of atomistic kerogen representations,25,27 we should emphasize that the key result of this work is that the mimetic nature of the employed methodology allows the simulation of the entire generation process, from the precursor to the kerogen and its associated fluid production.
Whereas the quantitative character of our results remains questionable, especially regarding: (i) the degree of convergence of the simulations, (ii) the ability of the ReaxFF potential to accurately capture the chemistry, and (iii) the limited size of the model, we believe that this work demonstrates the possibility of simulating, at least qualitatively, a complex chemical process like the conversion of an organic precursor into a char and a fluid.
Generalizing this study to other forms of organic matter, especially oil-prone type II precursors, will certainly provide invaluable data on the relationship between the nature of the precursor, the structure and properties of the obtained kerogen and the nature and quantity of the produced fluid phase, with potential impact on the development of non-conventional hydrocarbon resources. Finally, the methods used here can also be applied to other current technological issues like the prediction of structure/property relationships for bio-sourced materials or the conversion of organic waste into bio-fuels.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Game-Changer Shell project enabled through MIT’s Energy Initiative. Additional support was provided by ICoME2 Labex (ANR-11-LABX-0053) and the Aix-Marseille University AMIDEX foundation. ACTvD acknowledges funding from AFOSR FA9550-14-1-0355. Most REMD and MD simulations presented here were performed using the facilities of the Extreme Science and Engineering Discovery Environment (XSEDE) platform,40 which is supported by the National Science Foundation grant number ACI-1053575. DFT calculations discussed in the ESI† were achieved using the facilities of the Mésocentre de Calcul Intensif en Aquitaine (MCIA).References
- H. Marsh and F. Rodríguez-Reinoso, Activated carbon, Elsevier, 2006 Search PubMed.
- F. Rodriguez-Reinoso and M. Molina-Sabio, Carbon, 1992, 30, 1111–1118 CrossRef CAS.
- A. A. Ogale, M. Zhang and J. Jin, J. Appl. Polym. Sci., 2016, 133, 43794 CrossRef.
- A. J. Ragauskas, C. K. Williams, B. H. Davison, G. Britovsek, J. Cairney, C. A. Eckert, W. J. Frederick, J. P. Hallett, D. J. Leak, C. L. Liotta, J. R. Mielenz, R. Murphy, R. Templer and T. Tschaplinski, Science, 2006, 311, 484–489 CrossRef CAS PubMed.
- J. M. Hunt, Am. Assoc. Pet. Geol. Bull., 1972, 56, 2273–2277 CAS.
- D. W. Waples, in Geochemistry in Petroleum Exploration, D. Reidel Pub. Co. and IHRDC, Boston, 1985, p. 35 Search PubMed.
- B. P. Tissot and D. H. Welte, Petroleum Formation and Occurrence. A New Approach to Oil and Gas Exploration, Springer-Verlag, 1978 Search PubMed.
- J. M. Hunt, Petroleum Geochemistry and Geology, W. H. Freeman, New York, 1996 Search PubMed.
- C. C. Walters, in Practical Advances in Petroleum Processing, ed. C. S. Hsu and P. R. Robinson, Springer, 2006, ch. 2, pp. 79–101 Search PubMed.
- A.-Y. Huc, Geochemistry of Fossil Fuels, Editions Technip, Paris, 2013 Search PubMed.
- A. Hood, C. Gutjahr and R. Heacock, Am. Assoc. Pet. Geol. Bull., 1975, 59, 986–996 Search PubMed.
- M. Vandenbroucke and C. Largeau, Org. Geochem., 2007, 38, 719–833 CrossRef CAS.
- A. Oberlin, J. Boulmier and M. Villey, in Kerogen, Insoluble Organic Matter from Sedimentary Rocks, ed. B. Durand, Editions Technip, Paris, 1980, ch. 7, pp. 191–241 Search PubMed.
- B. Tissot, Rev. Inst. Fr. Pet., 1969, 24–4, 470–501 Search PubMed.
- J. Connan, AAPG Bull., 1974, 58, 2516–2521 Search PubMed.
- M. Monthioux, P. Landais and J.-C. Monin, Org. Geochem., 1985, 8, 275–292 CrossRef CAS.
- T. Hantschel and A. I. Kauerauf, Fundamentals of Basin and Petroleum Systems Modeling, Springer, 2009 Search PubMed.
- B. Tissot, R. Pelet and P. Ungerer, AAPG Bull., 1987, 71, 1445–1466 CAS.
- A. Burlingame, P. Haug, H. Schnoes and B. Simoneit, in Advances in Organic Geochemistry, ed. P. Schenck and I. Havenaar, Pergamon Press, Paris, 1969, pp. 85–129 Search PubMed.
- F. Béhar and M. Vandenbroucke, Org. Geochem., 1987, 11, 15–24 CrossRef.
- M. Siskin, C. Scouten, K. Rose, T. Aczel, S. Colgrove and R. Pabst Jr, in Composition, Geochemistry and Conversion of Oil Shales, ed. C. Snape, Kluwer Academic Publishers, Dordrecht, 1995, pp. 143–158 Search PubMed.
- M. Vandenbroucke and C. Largeau, Oil & Gas Science and Technology, Rev.IFP (Institut Français du Pétrole), 2007, vol. 38, pp. 719–833 Search PubMed.
- L. Zhang and E. J. LeBoeuf, Org. Geochem., 2009, 40, 1132–1142 CrossRef CAS.
- J. Collell, P. Ungerer, G. Galliero, M. Yiannourakou, F. Montel and M. Pujol, Energy Fuels, 2014, 28, 7457–7466 CrossRef CAS.
- P. Ungerer, J. Collell and M. Yiannourakou, Energy Fuels, 2015, 29, 91–105 CrossRef CAS.
- A. M. Orendt, I. S. Pimienta, S. R. Badu, M. S. Solum, R. J. Pugmire, J. C. Facelli, D. R. Locke, K. W. Chapman, P. J. Chupas and R. E. Winans, Energy Fuels, 2013, 27, 702–710 CrossRef CAS.
- C. Bousige, C. M. Ghimbeu, C. Vix-Guterl, A. E. Pomerantz, A. Suleimenova, G. Vaughan, G. Garbarino, M. Feygenson, C. Wildgruber, F.-J. Ulm, R. J. M. Pellenq and B. Coasne, Nat. Mater., 2016, 15, 576–582 CrossRef CAS PubMed.
- J. Collell, G. Galliero, R. Vermorel, P. Ungerer, M. Yiannourakou, F. Montel and M. Pujol, J. Phys. Chem. C, 2015, 119, 22587–22595 CAS.
- A. Obliger, R. Pellenq, F.-J. Ulm and B. Coasne, J. Phys. Chem. Lett., 2016, 7, 3712–3717 CrossRef CAS PubMed.
- K. Lindorff-Larsen, S. Piana, R. O. Dror and D. E. Shaw, Science, 2011, 334, 517–520 CrossRef CAS PubMed.
- V. Agarwal, P. J. Dauenhauer, G. W. Huber and S. M. Auerbach, J. Am. Chem. Soc., 2012, 134, 14958–14972 CrossRef CAS PubMed.
- X. Liu, J.-H. Zhan, D. Lai, X. Liu, Z. Zhang and G. Xu, Energy Fuels, 2015, 29, 2987–2997 CrossRef CAS.
- C. Zou, S. Raman and A. C. T. van Duin, J. Phys. Chem. B, 2014, 118, 6302–6315 CrossRef CAS PubMed.
- M. Zheng, Z. Wang, X. Li, X. Qiao, W. Song and L. Guo, Fuel, 2016, 177, 130–141 CrossRef CAS.
- E. Salmon, A. C. van Duin, F. Lorant, P.-M. Marquaire and W. A. Goddard III, Org. Geochem., 2009, 40, 1195–1209 CrossRef CAS.
- Y. Zhang, X. Wang, Q. Li, R. Yang and C. Li, Energy Fuels, 2015, 29, 5056–5068 CrossRef CAS.
- A. van Duin, S. Dasgupta, F. Lorant and W. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS.
- Y. Sugita and Y. Okamoto, Chem. Phys. Lett., 1999, 314, 141–151 CrossRef CAS.
- D. J. Earl and M. W. Deem, Phys. Chem. Chem. Phys., 2005, 7, 3910–3916 RSC.
- J. Towns, T. Cockerill, M. Dahan, I. Foster, K. Gaither, A. Grimshaw, V. Hazlewood, S. Lathrop, D. Lifka, G. D. Peterson, R. Roskies, J. R. Scott and N. Wilkins-Diehr, Comput. Sci. Eng., 2014, 16, 62–74 CrossRef.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, 1987 Search PubMed.
- W. C. Swope, H. C. Andersen, P. H. Berens and K. R. Wilson, J. Chem. Phys., 1982, 76, 637–649 CrossRef CAS.
- W. Shinoda, M. Shiga and M. Mikami, Phys. Rev. B, 2004, 69, 134103 CrossRef.
- S. G. Srinivasan, P. Ganesh and A. C. T. van Duin, J. Phys. Chem. A, 2015, 119, 571–580 CrossRef CAS PubMed.
- Y. K. Shin, L. Gai, S. Raman and A. C. T. van Duin, J. Phys. Chem. A, 2016, 120, 8044–8055 CrossRef CAS PubMed.
- F. Tavazza, T. P. Senftle, C. Zou, C. A. Becker and A. C. T. van Duin, J. Phys. Chem. C, 2015, 119, 13580–13589 CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- J. W. Pitera and W. Swope, Proc. Natl. Acad. Sci., 2003, 100, 7587–7592 CrossRef CAS PubMed.
- T. C. F. Gomes and M. S. Skaf, J. Comput. Chem., 2012, 33, 1338–1346 CrossRef CAS PubMed.
- Y.-C. Lin, J. Cho, A. Tompsett, P. R. Westmoreland and G. W. Huber, J. Phys. Chem. C, 2009, 113, 20097–20107 CAS.
- D. S. Franzblau, Phys. Rev. B, 1991, 44, 4925–4930 CrossRef CAS.
- L. D. Gelb and K. E. Gubbins, Langmuir, 1999, 15, 305–308 CrossRef CAS.
- R. Kilaas, Proceedings of the 22nd Annual Conference of the Microbeam Aanalysis Society, 1987, pp. 293–300 Search PubMed.
- M. M. Tang and R. Bacon, Carbon, 1964, 2, 211–220 CrossRef CAS.
- M. R. Hajaligol, J. B. Howard, J. P. Longwell and W. A. Peters, Ind. Eng. Chem. Process Des. Dev., 1982, 21, 457–465 CAS.
- P. J. F. Harris and C. Tsang, Philos. Mag. A, 1987, 76, 667–677 CrossRef.
- J. Pikunic, C. Clinard, N. Cohaut, K. E. Gubbins, J.-M. Guet, R. J.-M. Pellenq, I. Rannou and J.-N. Rouzaud, Langmuir, 2003, 19, 8565–8582 CrossRef CAS.
- B. Farbos, P. Weisbecker, H. E. Fischer, J.-P. Da Costa, M. Lalanne, G. Chollon, C. Germain, G. L. Vignoles and J.-M. Leyssale, Carbon, 2014, 80, 472–489 CrossRef CAS.
- M. Villey, A. Oberlin and A. Combaz, Carbon, 1979, 17, 77–86 CrossRef CAS.
- A. Oberlin, M. Villey and A. Combaz, Carbon, 1980, 18, 347–353 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1–S6 and Tables S1 and S2. See DOI: 10.1039/c7sc03466k |
| This journal is © The Royal Society of Chemistry 2017 |