Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Size and charge effect of guest cations in the formation of polyoxopalladates: a theoretical and experimental study†‡
Zhongling
Lang§
a,
Peng
Yang§
b,
Zhengguo
Lin
 b,
Likai
Yan
b,
Likai
Yan
 c,
Ming-Xing
Li
d,
Jorge J.
Carbó
c,
Ming-Xing
Li
d,
Jorge J.
Carbó
 a,
Ulrich
Kortz
a,
Ulrich
Kortz
 *b and
Josep M.
Poblet
*b and
Josep M.
Poblet
 *a
*a
aDepartament de Química Física i Inorgànica, Universitat Rovira i Virgili, c/Marcel lí Domingo 1, 43007 Tarragona, Spain. E-mail: josepmaria.poblet@urv.cat
bDepartment of Life Sciences and Chemistry, Jacobs University, Campus Ring 1, 28759 Bremen, Germany. E-mail: u.kortz@jacobs-university.de
cInstitute of Functional Material Chemistry, Faculty of Chemistry, Northeast Normal University, Changchun 130024, P. R. China
dDepartment of Chemistry, College of Sciences, Shanghai University, Shanghai 200444, P. R. China
First published on 25th September 2017
Abstract
The development of rational synthetic procedures with desired nuclearity and high selectivity is a critical issue in inorganic chemistry. Here we demonstrate a comprehensive understanding of the template effect induced by metal cations in the formation mechanism of the class of polyoxopalladates ({MPd12L8} nanocube and {MPd15L10} nanostar) by combining computational and experimental techniques. The capture of a Mn+ guest ion by a peripheral palladium(II)-oxo shell leads to a competition between the parent Pd2+ addenda ion and the respective guest metal ion. The present study reveals that (i) the selection of the incorporated guest ion has a thermodynamic control, (ii) the main factors governing the formation of a particular polyanion are the charge and size of the guest cation, (iii) the electrostatic interaction between the cation and the surrounding oxo ligands and (iv) the dehydration ability of the cation. As expected from the number of observed {Mn+Pd12L8} species, trivalent cations M3+ were found to be good templates resulting in several examples of {M3+Pd12L8}, whereas monovalent cations M+ are much less prone to form {M+Pd12L8}. For tetravalent cations the dehydration energies are very large, however, the formation of {M4+Pd12L8} nanocubes is found to be still energetic favourable. Fully consistent with computational predictions, four novel polyoxo-12-palladates were synthesized: the La3+-centered nanocube [LaPd12O8(PhAsO3)8]5− (LaPd12-closed), the La3+-centered “open” nanocube [LaPd12O6(OH)3(PhAsO3)6(OAc)3]3− (LaPd12-open), the Ga3+-centered [GaPd12O8(PhAsO3)8]5− (GaPd12), and the In3+-analogue [InPd12O8(PhAsO3)8]5− (InPd12). All four compounds were fully characterized in the solid state and in solution by a multitude of physicochemical techniques, including 71Ga and 115In NMR as well as mass spectrometry. The experimentally observed selective incorporation of only In3+ ions in the presence of Ga3+ and In3+ confirmed the thermodynamic control of the formation mechanism, which we had predicted by theory.
1. Introduction
In recent years significant advances have been made in the control of different variables involved in the formation mechanism of polyoxometalates (POMs). However, there is a lack of systematic studies that aim at identifying unambiguously the driving forces related to the self-assembly or aggregation processes. The “template-directed” method is one popular and extremely important synthetic strategy for obtaining novel POMs. The nuclearity and topology of the products are strongly dependent on the size, shape, and charge of the template ions. For example, anions such as Cl− and SO42− could be encapsulated in the central cavities of discrete polyoxovanadates to form templated host–guest complexes.1 On the other hand, many different heterogroups (e.g., AsIIIO33−, SbIIIO33−, SiIVO44−, GeIVO44−, PVO43−, AsVO43−, and IVIIO65−) can efficiently control the shape, size, and structure of high-nuclearity heteropolytungstates.2Besides classical POMs,3 in the last decade or so an “unconventional” POM family based exclusively on PdII, PtIII, or AuIII addenda has been developed.4 Since noble metals are well-known active ingredients of many catalysts, the study of noble metal-containing POMs is a particularly interesting topic. In 2004, Wickleder's group synthesized the first polyoxoplatinate exclusively based on d7 addenda ions, [PtIII12O8(SVIO4)12]4−.5 Since then the Kortz group has pioneered the class of polyoxopalladates(II) in 2008,6 and the class of polyoxoaurates(III) in 2010.7a The first polyoxopalladate was the [H6Pd13O8(AsO4)8]8− (Pd13) nanocube, prepared by simple condensation of Pd2+ and arsenate (AsVO43−) ions in aqueous medium.6 In the following years it was demonstrated that the eight arsenate capping groups can be easily replaced by other heterogroups, such as selenite ([Pd13O8(SeO3)8]6−, Pd13Se) or phenylarsonate ([Pd13O8(PhAsO3)8]6−, Pd13AsPh).8 Interestingly, substitution of the capping groups is accompanied by an increase of the coordination number of the central Pd2+ ion from 4 (Pd13) to 6 (Pd13Se) and even 8 (Pd13AsPh).
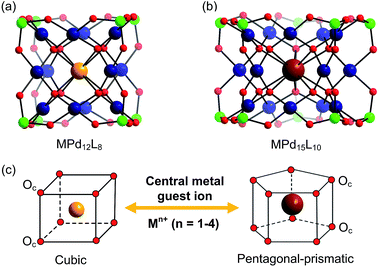
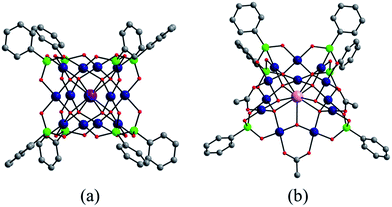
In addition to the capping groups the central palladium(II) ion in the nanocube {MPd12L8} (Fig. 1a) can also be replaced by other metal ion guests, including trivalent lanthanide ions (Ln3+ = Y, Pr, Nd, Sm, Eu, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu) and 3d transition metal ions (Sc3+, Mn2+, Fe3+, Co2+, Ni2+, Cu2+, Zn2+).9 Interestingly, the nanostar {MPd15L10} (Fig. 1b) can be formed only in the presence of Na+, K+, Ag+, or Ba2+,10 whereas in the presence of Sr2+ ions the “open” nanocube {SrPd12L6L′3} (L = phenylarsonate, L′ = acetate) is formed.10e Such observations bear similarities with the important template role of alkali and alkaline earth ions in the formation of various organic macrocycle-based structures (crown ethers etc.).11 In addition to the above-mentioned nanocube, nanostar and open-nanocube structural types, some additional polyoxopalladates with unexpected geometries have been obtained, such as the bowl-shaped palladovanadate {Pd7V6},12a the double cuboid-shaped 22-palladates {Cu2Pd22}12b and {Na2Pd22},12c as well as palladate macrocycles {Pdn} (n = 60, 72, 84, 96, 108).13
It is evident that the central metal ion guest as well as the capping groups play a key role in the formation mechanism of polyoxopalladates, but details remain unknown. Hence the rational synthesis of novel polyoxopalladate structural types of desired shape, size and composition is virtually impossible. On the other hand, density functional theory (DFT) methods have been applied to POMs significantly in the last two decades, in particular with respect to (i) electronic structure, (ii) rationalization of physicochemical properties, and (iii) reactivity as a function of shape and composition.14 In order to obtain more insight into polyoxopalladate chemistry, in particular with respect to factors that govern guest metal ion encapsulation and to perhaps shed more light on selectivity issues, we have decided to perform systematic theoretical analysis for a series of 35 metal ion guests M involved in the formation of the {MPd12L8} nanocube and {MPd15L10} nanostar polyoxopalladate structural types.
The encapsulated cations were selected by considering both their charge and size, which range from alkali and alkaline earth ions to transition metal ions, as well as trivalent and tetravalent main group cations. We have discovered a remarkable competition between Pd2+ ions and other cations, which is key for the formation of a specific polyoxopalladate structural type. With a focus on eventually being able to computationally predict experimental results, we have carefully studied experimentally (i) the capture of the largest trivalent cation La3+ inside a polyoxopalladate, and (ii) the selective incorporation of In3+vs. Ga3+ in a polyoxopalladate.
2. Computational and experimental details
2.1 Computational method
All calculations were performed with the Gaussian 09 package.15 The computational scheme consists of two steps. Geometry optimizations of all nanocube {MPd12L8} and nanostar {MPd15L10} polyoxopalladates were carried out at the B3LYP level without symmetry restrictions.16 The SDD effective core pseudopotential (ECP) basis set was used for La, Yb, Lu, Eu, Ce, Th, and U,17 the small core potential (CRENBL ECP) was used for Ra,18 whereas the LANL2DZ basis set was employed for the main group metals (Rb, Cs, Sr, Ba, Ga, In, Tl, Sn) and transition metals (Sc, Mn, Fe, Co, Ni, Cu, Zn, Y, Zr, Pd, Ag, Cd, Hf) with Los Alamos relativistic core potentials (ECPs).19 In addition, the 6-31G** basis set was used for O, C, As, Se, H, and the encapsulated small metal ions (Li, Na, K, Be, Mg, Ca).20 From these calculations, we obtained the energies at the B3LYP level. In order to include the long-range interaction and dispersion effects, single point calculations were performed for all optimized polyanions with two additional functionals, M06 and ωB97XD.21,22 For all steps, the continuum SMD implicit solvation model was used to simulate the effect of the aqueous solution.23As shown in Fig. 1, the nanocube {MPd12L8} and nanostar {MPd15L10} were selected, in which the central metal ion usually has an oxo-coordination number of 8 and 10, respectively. In order to evaluate the selective encapsulation of different guest metal ions, the reaction mechanism is simulated by scheme (1), and the complexation energy (Ecom) was calculated by eqn (2) and (3):
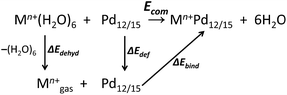 | (1) |
| Ecom = E(Mn+Pd12/15) + E(6H2O) − E(Pd12/15) − E(Mn+(H2O)6) | (2) |
| Ecom = ΔEbind + ΔEdef + ΔEdehyd | (3) |
2.2 Synthesis of Na5[LaPd12O8(PhAsO3)8]·31H2O (Na-LaPd12-closed)
Pd(CH3COO)2 (0.023 g, 0.102 mmol), PhAsO3H2 (0.020 g, 0.099 mmol) and LaCl3·7H2O (0.009 g, 0.024 mmol) were dissolved in 2 mL of 0.5 M NaOAc solution (pH 7.0). While stirring, the solution was heated to 80 °C. After dissolution of all components, the pH of the reaction mixture was adjusted to 7.3 by addition of 6 M NaOH. The resulting solution was heated at 80 °C for 1 hour. Then it was cooled to room temperature, filtered and allowed to crystallize at room temperature in an open vial. Dark red, block-shaped crystals of Na-LaPd12-closed were obtained after one week, which were filtered off and air dried. Yield: 0.008 g (25%, based on Pd). Elemental analysis calcd (%): Na 3.01, C 15.10, La 3.64, Pd 33.45, As 15.70; found: Na 3.28, C 15.51, La 3.76, Pd 33.44, As 15.43. IR (2% KBr pellet, ν/cm−1): 1627 (m), 1479 (w), 1439 (m), 1093 (m), 792 (s), 742 (w), 694 (m), 592 (m), 547 (s).2.3 Synthesis of Na3[LaPd12O6(OH)3(PhAsO3)6(OAc)3]·40H2O (Na-LaPd12-open)
This compound was prepared by exactly the same procedure as Na-LaPd12-closed. The initially formed Na-LaPd12-closed was removed by filtration. The filtrate was left for further evaporation, which resulted in another portion of dark red, needle-like crystals of Na-LaPd12-open within a few days, which were filtered off and air dried. Yield: 0.006 g (19% based on Pd). Elemental analysis calcd (%): Na 1.85, C 13.52, La 3.72, Pd 34.24, As 12.05; found: Na 1.94, C 13.75, La 3.51, Pd 34.69, As 12.66. IR (2% KBr pellet, ν/cm−1): 1633 (m), 1539 (m), 1439 (w), 1419 (m), 1093 (m), 814 (s), 744 (m), 694 (m), 536 (s).2.4 Synthesis of Na5[GaPd12O8(PhAsO3)8]·36H2O (Na-GaPd12)
Pd(CH3COO)2 (0.023 g, 0.102 mmol), PhAsO3H2 (0.020 g, 0.099 mmol) and Ga(NO3)3 (0.006 g, 0.024 mmol) were dissolved in 2 mL of 0.5 M NaOAc solution (pH 7.0). While stirring, the solution was heated to 80 °C for 1 hour. Then it was cooled to room temperature, filtered and allowed to crystallize at room temperature in an open vial. Red, block-shaped crystals of Na-GaPd12 were obtained after three days, which were filtered off and air dried. Yield: 0.014 g (43% based on Pd). Elemental analysis calcd (%): Na 2.99, C 15.02, Ga 1.82, Pd 33.27, As 15.62; found: Na 2.90, C 15.71, Ga 1.96, Pd 32.34, As 16.14. IR (2% KBr pellet, ν/cm−1): 1631 (m), 1479 (w), 1438 (m), 1094 (m), 804 (s), 744 (w), 694 (m), 657 (m), 538 (s).2.5 Synthesis of Na5[InPd12O8(PhAsO3)8]·30H2O (Na-InPd12)
This compound was prepared by exactly the same procedure as Na-GaPd12, but with InCl3 (0.005 g, 0.025 mmol) instead of Ga(NO3)3. Red, block-shaped crystals of Na-InPd12 were obtained after three days, which were filtered off and air dried. Yield: 0.014 g (44% based on Pd). Elemental analysis calcd (%): Na 3.04, C 15.27, In 3.04, Pd 33.22, As 15.88; found: Na 2.82, C 15.89, In 3.80, Pd 32.30, As 16.06. IR (2% KBr pellet, ν/cm−1): 1628 (m), 1479 (w), 1439 (m), 1093 (m), 802 (s), 744 (w), 694 (m), 629 (m), 540 (s).3. Results and discussion
3.1 Size matching between guest Mn+ cations and the Pd12/15 cages
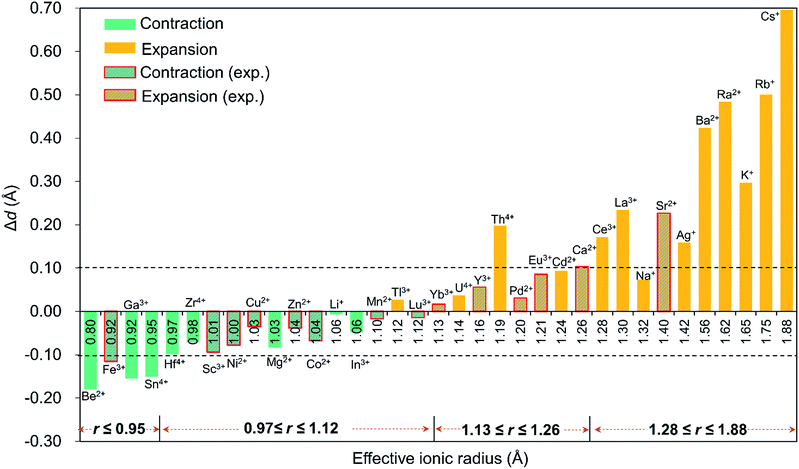
Since the discovery in 2008 of the first member of the Pd12 family, Pd13,6 Kortz's group has synthesized a large number (ca. 50) of palladate nanocube derivatives {MPd12L8} by systematically substituting the arsenate capping groups by selenite, phenylarsonate and phenylphosphonate, and the central Pd2+ ion by s, d and f block metal ions.4,6–9 In order to better understand the templating role of the guest cation, systematic DFT calculations were performed by introducing different metal ions into the Pd12 and Pd15 cages. The empty “host” cages Pd12 and Pd15 and the corresponding host (Pd12/Pd15 cage) – guest (cation M) systems capped by PhAsVO32− ({MPd12(AsPh)8}) were optimized at the B3LYP level. The molecular electrostatic potential (MEP, Fig. S2‡) analysis for the free Pd12 cage revealed an interesting distribution of most negative partial atomic charges at the centre of the inner {O8} cage, indicating that electrophiles such as metal ions are most likely to be located at the central position of the palladate nanocube. This prediction is in line with the experimental results, which show that the guest cation indeed occupies such position. As shown in Table S1,‡ the computed distances (Oc–Oc, M–Oc, and M–Pd) for a series of palladates reproduced fairly well the reported XRD data, although they are found systematically slightly longer than observed experimentally. It is worth mentioning that when M = Pd2+, Fe3+, Co2+, Ni2+, and Eu3+ ions occupy the central site, the DFT calculations suggested that the high-spin state for M in {MPd12(AsPh)8} is more favourable than the low-spin state. Such result was indeed confirmed experimentally by magnetic and EPR studies.9bFor efficient encapsulation, the guest cation and the cavity in the palladate cage should match well. Due to the small flexibility of the {O8} coordination shell, all guest cations are optimally located in the centre of the cube. The average Oc–Oc distance generally elongates as the effective ionic radius of Mn+ increases, and this trend is perfectly in line with an increase of the M–Oc bond distances. To gain insight into the effect of cation size on the geometry of the cage, the Oc–Oc distortions after encapsulation of the cation are plotted in Fig. 2, by referring to the distance in the empty cage Pd12 (dOc–Oc = 2.728 Å). We found that guest cations with a radius smaller than 1.12 Å could induce a contraction of the {O8} cavity (e.g. Co2+, Ni2+, Cu2+, Zn2+, Mn2+, Sc3+, Fe3+, Lu3+) and also guest ions that have not yet been incorporated in the Pd12 cage experimentally, such as Li+, Be2+, Mg2+, Ga3+, In3+, Sn4+, Zr4+, and Hf4+. In particular, Be2+, Fe3+, Ga3+, and Sn4+ seem too small to be hosted efficiently, and consequently a large contraction occurs to maximize the M–Oc interactions. When the ion size is between 1.13 and 1.26 Å, a small expansion with Δd less than 0.1 Å is needed, except for Th4+. However, a significant distortion of {O8} was detected for ions larger than 1.28 Å, such as Ce3+, La3+ Sr2+, Ag+, K+, Rb+, Cs+, Ba2+, and Ra2+, where for some cases elongations larger than 0.4 Å were observed.
It is remarkable that for most of the experimentally observed palladate nanocubes, the distortion induced by guest metal ion encapsulation is no larger than 0.1 Å, and therefore the size matching between the cation guests and the cavity of the Pd12 cage is an important factor that must be considered. Fig. 2 also suggests that guest cations with a size ranging from 0.97–1.26 Å fit well within the {O8} cavity in Pd12 regardless of the charge (except Th4+). In contrast, smaller (r ≤ 0.95 Å) and larger (r ≥ 1.28 Å) cations are probably poor candidates for constructing {MPd12L8} palladate nanocubes from a size-matching point of view, with the optimal cation size being in the 0.97–1.26 Å range.
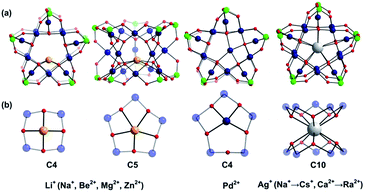
Large guest cations are more likely to accommodate themselves in larger polyoxopalladate assemblies with larger cavities. In order to compare with our computational results on the Pd12 nanocube, we inserted some selected cations (Li+, Na+, K+, Rb+, Cs+, Ag+, Be2+, Mg2+, Ca2+, Sr2+, Ba2+, Zn2+, Pd2+) also in the Pd15 nanostar cage. The Pd15 host provides a pentagonal-prismatic {O10} inner coordination sphere, which appears too large for encapsulation of small guest cations, such as Li+, Be2+, Mg2+, and Zn2+ (r < 1.2 Å). In this case the cations move away from the C5 symmetry axis of the Pd15 cage and coordinate to less than 10 oxo-ligands. Two types of such off-center coordination modes were observed from our DFT calculations, C4 and C5 as depicted in Fig. 3. For example, Li+ could coordinate to five Oc from a Pd5O5 fragment (2.107, 2.276, 2.261, 2.457, 2.336 Å) or to four Oc from a Pd4O4 fragment (2.002, 2.023, 2.005, 2.022 Å). Although the former configuration includes five coordinated oxygen atoms, the shorter bonds in the latter situation indicate stronger interactions. As expected, the energy differences illustrate that the C4 mode is more stable than C5 by 6.1 kcal mol−1 (Table S2‡). On the other hand, encapsulation of Na+, K+, Rb+, Cs+, Ag+ Ca2+, Sr2+, Ba2+, and Ra2+ (r > 1.2 Å) is expected to work well for the Pd15 nanostar cage. Some of them are strongly supported by experiments, which show that NaPd15, KPd15, BaPd15, and AgPd15 can be easily observed in the presence of Na+, K+, Ba2+, and Ag+.10 It is worth mentioning that Na+ prefers to coordinate to a Pd5O5 face (C5) rather than sitting at the body centre of Pd15, as suggested by experiment.10a Interestingly, Pd2+ prefers a C4 mode, binding to only four Oc of the Pd5O5 face, as shown by XRD.10a,c The good reproducibility of the experimental results by DFT reemphasizes that the size of the cation guest indeed plays an important role in the formation mechanism of the resulting palladate structure.
3.2 Complexation energy and competition between Pd2+ and other metal cations
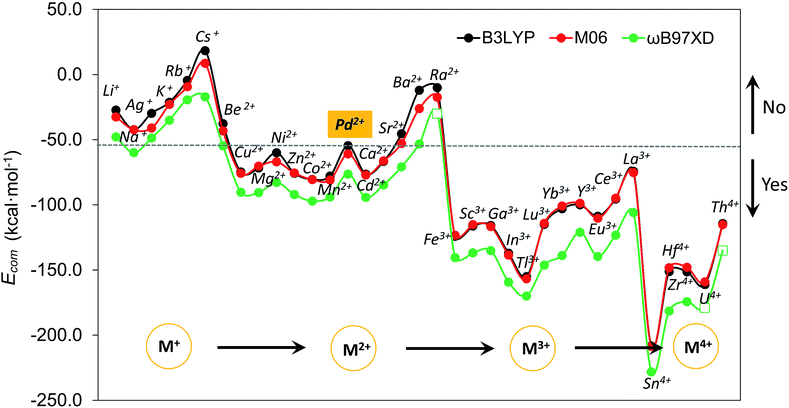
Although size-matching has been established as an essential factor during palladate formation, we have to be aware that (i) the cation–cavity interaction and (ii) the dehydration ability of the cation is not included in the analysis. Thus, we next analyse why the reported cations can be encapsulated by the Pd12/15 cages and predict some potential candidates from an energetic point of view. To rationalize this point, the complexation energy (Ecom) of Pd12 and Pd15 for the different guest cations was computed as described in the Computational section, and the results at B3LYP level (black points) are shown in Fig. 4, as well as the energy corrections with M06 (red points) and ωB97XD (green points) functionals. The results for M06 give virtually identical values as those of B3LYP functional, whereas adding the dispersion correction in ωB97XD increases the values of the complexation energies, without changing the overall trends. Therefore, the results at B3LYP level can reasonably identify the trend analysis. Generally, the Ecom becomes more negative (exothermic) as the formal charge of the guest cation increases from +1 to +4. For alkali and alkaline earth ions the Ecom is affected significantly by the size of the cations. All encapsulations seem to be thermodynamically favourable, except for Cs+, which shows a positive Ecom of 18.3 kcal mol−1. It is illustrative that the first reported polyoxopalladate was Pd13 with a Pd2+ ion located at the center,6 and that the synthesis occurred in the presence of both Na+ and Pd2+ ions. Encapsulation of Pd2+ in the {Pd12(AsPh)8} nanocube cage is predicted to be very exothermic with a complexation energy of −54.6 kcal mol−1, whereas Na+ is much less competitive with −42.2 kcal mol−1. Thus, it is not surprising that the Na+ ions are not incorporated in the palladate structure, but rather act just as counter cations.Following such strategy, all cations were divided into two domains with Ecom of Pd2+ as a reference (dashed grey line). The Ecom values below the reference line indicate that from a thermodynamic point of view, the respective ions are more favourable to stabilize the Pd12 host cage than the reference ion Pd2+. Thus, polyanion nanocubes of the type {MPd12(AsPh)8} are preferentially formed as compared to {Pd13(AsPh)8} (Pd13AsPh). For instance, encapsulation of Fe3+ and Sc3+ ions inside the Pd12 shell has associated complexation energies of −124.1 ({FePd12(AsPh)8}) and −116.2 kcal mol−1 ({ScPd12(AsPh)8}), respectively, both being significantly more exothermic than Pd2+ (−54.6 kcal mol−1, Pd13AsPh). Indeed, the nanocube family {MPd12(AsPh)8} with M = Ca2+, Co2+, Cu2+, Ni2+, Zn2+, Mn2+, Sc3+, Fe3+, Y3+, Yb3+, Lu3+, and Eu3+ has already been synthesized by using similar synthetic procedures.9 In contrast, encapsulation of M = alkali metal ions, Ag+, Be2+, Sr2+, Ba2+, and Ra2+ in {MPd12(AsPh)8} is expected to be difficult due to the less favourable complexation energy with respect to Pd2+, in spite of some of them (Li+) having a suitable size. In fact, these hypothetical polyoxopalladates have not been synthesized yet in the laboratory. Such conclusions are also valid for nanocube derivatives with other capping groups, such as arsenate (AsO43−) and selenite (SeO32−), see Fig. S3.‡ The absolute values of Ecom seem to be influenced by the charge of the capping group. Interestingly, almost identical complexation energies were obtained when replacing PhAsO32− by SeO32−, which have the same charge and the AsV–O and SeIV–O distances are similar. As based on size only, Ag+, K+, Rb+, Cs+, and Ba2+ can be excluded as guests for the nanocube cage Pd12.
We also decided to consider computationally the encapsulation of large guest cations by the 15-palladate nanostar cage {MPd15(AsPh)10} (Fig. S4‡), and then compare to Pd12. As expected, the larger guest ions Na+, Ag+, K+, Rb+, Ba2+, and Ra2+ ions were calculated to be both geometrically and energetically suitable for the Pd15 nanostar rather than the Pd12 nanocube, and these results are in full agreement with the experimental facts.10 Most of the smaller cations such as Mg2+ and Zn2+ do not fit geometrically and are also energetically unfavourable in Pd15. On the other hand, Pd2+ shows a similar ability to be encapsulated by the Pd12 nanocube and the Pd15 nanostar, which is consistent with the experimentally observed nanocube Pd13AsPh,8 as well as the mono- and di-palladium-centered nanostar derivatives {Pd ⊂ Pd15(PhAsO3)10} and {Pd2 ⊂ Pd15(PhAsO3)10}.10a,c The medium-sized Sr2+ ion was shown experimentally to form an unexpected ‘open-nanocube’ structure [SrPd12O6(OH)3(PhAsO3)6(OAc)3]4− (SrPd12-open),10e which inspired us to compute the complexation energies for both the open and closed nanocubes Pd12, see Table 1. The energy required for encapsulating Sr2+ into the open form SrPd12-open was computed to be −50.0 kcal mol−1, and for the closed form [SrPd12O8(PhAsO3)8]6− (SrPd12-closed) it was slightly less exothermic, −45.4 kcal mol−1. Therefore, computationally it is predicted that the open form SrPd12-open is preferentially formed compared to SrPd12-closed. Amongst the unfavourable guest ions for the closed nanocube shell Pd12-closed, Sr2+ shows the smallest Ecom difference compared to Pd2+ with only 9.2 kcal mol−1 (and only 4.6 kcal mol−1 for Pd12-open) at the B3LYP level, and even smaller differences at the M06 and ωB97XD levels. Thus, a competition between Pd2+ and Sr2+ guest ions is predicated computationally for such reactions. Experiments showed that only 2% of SrPd12-closed is formed, and that the Sr2+ ion can be substituted by Pd2+ to form Pd13AsPh by simply increasing the pH of the solution.10e On the other hand, SrPd12-open can indeed be isolated in clean form, but to date the Pd13-open structural type has not been prepared yet.
| B3LYP | M06 | ωB97XD | Exp. ratio% | ||
|---|---|---|---|---|---|
| Pd2+ | Closed | −54.6 | −60.8 | −76.4 | 100% |
| Sr2+ | Open | −49.9 | −61.0 | −75.8 | 98% |
| Closed | −45.4 | −52.9 | −70.9 | 2% | |
| La3+ | Open | −70.6 | −74.7 | −105.7 | 40% |
| Closed | −74.2 | −75.2 | −105.9 | 60% | |
It is interesting to note that Ecom for La3+ is very close to that calculated for Pd2+, which may lead to mixed products LaPd12-closed and Pd13AsPh. In contrast to Sr2+, calculations suggest that for La3+ the closed nanocube (LaPd12-closed) is slightly more favourable than the open one (LaPd12-open), see Table 1. Accordingly, the nature and size of the guest cation directly influences the shape of the resulting poly-oxopalladate and this in turn strongly suggests a template effect of the cation in polypalladate synthesis.
3.3 Potential new candidates for the 12-palladate family
The systematic study of the complexation energies for different cation guests has revealed that competition with Pd2+ plays a critical role when trying to determine the structure-type of the respective product. Although the energy trend should not be taken quantitatively, it appears to be qualitatively useful in the design of synthetic parameters for discovering new polyoxopalladates.To date there is a dominance of 3d transition metal and lanthanide elements as central guests of the polyoxo-12-palladate nanocube family {MPd12L8}. Much less attention has been paid on p-block elements. We calculated the encapsulation of Ga3+, In3+, and Tl3+ as very exothermic with energies of −115.8, −137.1 and −155.1 kcal mol−1, respectively. For all three cations, the encapsulation is predicted to be more favourable than for the already reported Sc3+ derivative [ScPd12O8(PhAsO3)8]5−.9b In addition, there is a clear trend of increasing encapsulation ability going down group IIIA (B, Al, Ga, In, Tl).
On the other hand, to date no cation with a charge larger than 3+ has been encapsulated in the Pd12 nanocube shell. Therefore, we analysed computationally the encapsulation of several tetravalent cations, such as Sn4+, Zr4+, Th4+, U4+, and Hf4+. As expected, all tetravalent cations exhibit much favourable complexation energies due to the large anion–cation electrostatic interactions. The small Sn4+ ion has the lowest energy of all computed tetravalent ions and is hence the most promising candidate for encapsulation.
In order to verify the various theoretical predictions experimentally, we designed several key experiments, which concern mainly (i) encapsulation of p-block elements in the Pd12 nanocube shell, (ii) synthesis of open- and closed-nanocube isomers for La3+, and (iii) competition of three guest cations for Pd12 nanocube shell.
3.4 Synthesis and structural characterization of nanocubes LaPd12-closed, GaPd12, InPd12 and open-nanocube LaPd12-open
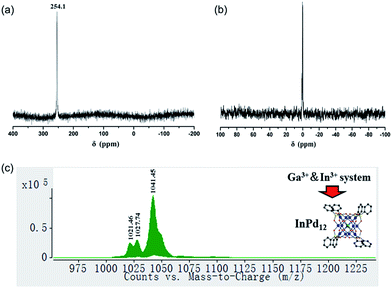
We have synthesized three new members of the {MPd12L8} nanocube family, the lanthanum-derivative [LaPd12O8(PhAsO3)8]5− (LaPd12-closed), as well as the first examples of main group III derivatives, namely the gallium-containing [GaPd12O8(PhAsO3)8]5− (GaPd12) and the indium-containing [InPd12O8(PhAsO3)8]5− (InPd12), see Exp. section for details. Single-crystal X-ray analysis revealed that all three polyoxopalladates are isostructural (Fig. 5a, Tables S3 and S4‡). The main differences between LaPd12-closed, GaPd12, and InPd12 are the central M–O bond distances with La–O = 2.459(5) Å, Ga–O = 2.211(4) Å, and In–O = 2.293(4) Å, respectively. Notably, La3+ is the largest trivalent cation ever encapsulated inside a Pd12 nanocuboid cage and together with the relatively low complexation energy (Table S4‡). LaPd12-closed presents a good test case for the present study. Interestingly, we are also able to synthesize the open nanocube [LaPd12O6(OH)3(PhAsO3)6(OAc)3]3− (LaPd12-open, see Fig. 5b). This structure had so far only been observed for strontium(II) in the center, [SrPd12O6(OH)3(PhAsO3)6(OAc)3]4−.10e This result perfectly supports the above mentioned calculations (Fig. 4 and Table 1), as the energetically lower closed structure LaPd12-closed is indeed isolated in higher yields compared to the open structure LaPd12-open. However, our efforts to prepare additional analogues of MPd12-open (M = La3+, Sr2+) with other large lanthanide ions have not been successful, suggesting that La3+ is a unique template amongst all lanthanide ions.The 13C and 1H NMR spectra indicate good aqueous stability of all four polyanions (Fig. S5 and S6‡). Moreover, we also performed 71Ga and 115In NMR studies on solutions of Na-GaPd12 and Na-InPd12, respectively. The observed singlets in 71Ga NMR centred at 48.9 ppm (GaPd12, Fig. S7‡) and the singlet in 115In NMR centred at 247.7 ppm (InPd12, Fig. S8‡) are in full agreement with the solid-state structures. The spectra are clean, indicating that no impurities are present, and the signals are rather narrow, in spite of the quadrupolar nature of both isotopes (71Ga, S = 3/2; 115In, S = 9/2), which is a result of the cubic coordination environment around the metal ions combined with the highly symmetrical (cuboctahedral) structure of the overall polyanion, rendering the electric field gradient virtually zero.
We also performed ESI-MS studies in order to study the solution and gas phase properties of GaPd12 and InPd12. All peaks shown in the spectra can be assigned to species related to GaPd12 and InPd12, with different numbers of protons or sodium ions attached. For instance, the major envelopes centred at m/z = 1025.45 (Fig. S9a‡) and m/z = 1041.45 (Fig. S9b‡) can be attributed to the triply negatively charged [H2GaPd12]3− and [H2InPd12]3−. Additional MS assignments are summarized in Table S5.‡
3.5 Selective encapsulation of Ga3+ or In3+ in {MPd12(AsPh)8} nanocube
To date around 60–70 polyoxopalladates are known, and by far most of them belong to the {MPd12L8} class of nanocubes with being usually d or f block metal ions.9 However, a competitive study using two or more potential guest cations has never been reported before. Considering that both GaPd12 and InPd12 can be followed by NMR in solution, we decided to perform competition studies for this system on fresh reaction solutions. Interestingly, we observed that if equimolar amounts of Ga3+ and In3+ ions were present, then only InPd12 was formed, as confirmed by 71Ga (no signal) and 115In NMR (singlet at 254.1 ppm, Fig. 6a). This result indicates that a strong preference exists for InPd12 compared to GaPd12. The free Ga3+ ions were detectable by 71Ga NMR at 0 ppm after the solution had been acidified to pH 1 by 1 M HNO3 (Fig. 6b).For the same mixed, equimolar Ga/In system, the filtrated mother solution was allowed to evaporate until the maximum amount of crystals had formed, which were isolated when still covered by mother liquor. These crystals were analysed by ESI-MS and the spectrum obtained showed peaks corresponding exclusively to InPd12-related species (Fig. 6c). Notably, the envelopes appearing at m/z = 1021.46 and 1027.74 can be unequivocally ascribed to {Na[InPd12O8(C6H5AsO3)7(AsO3)+]}3− and {Na[InPd12O8(C6H5AsO3)7(AsO3)+](H2O)}3−, which may form from the plenary InPd12 cluster by losing one (C6H5)− fragment, perhaps during the electrospray ionization processes.
We also performed additional competition experiments, for example for the template pairs Ga3+/Sc3+ and In3+/Sc3+, respectively. Both 71Ga and 45Sc NMR signals could be detected for the Ga3+/Sc3+ system after the reaction, indicating that GaPd12 and ScPd12 are both formed and coexist in solution (Fig. S10 and S11‡). For the In3+/Sc3+ system, the 115In NMR signal for InPd12 could be detected after a few seconds; whereas the 45Sc signal for ScPd12 could only be obtained overnight. These results indicate that selective encapsulation features exist for the central cation guest M of the Pd12 nanocube, which fit well with the trends of the computed complexation energies shown in Fig. 4. Combining the theoretical and experimental results, we obtain a selectivity order of In3+ > Ga3+ ≈ Sc3+. The apparent Ecom difference between In3+ (−137.1 kcal mol−1) and Ga3+/Sc3+ (−116.2/−115.8 kcal mol−1) leads indeed to a pronounced encapsulation selectivity for In3+, whereas Sc3+ and Ga3+ are more difficult to be separated by polyoxopalladate formation, due to similar complexation energies.
3.6 Factors governing encapsulation of metal ion templates in different polyoxopalladate shells
In the above mentioned theoretical and experimental studies, we have mainly addressed the two main factors that control incorporation of metal ion guests in the polyoxopalladate nanocube shell Pd12: (i) the energy associated with the complexation of a given cation by the empty Pd12 cage (Ecom) and (ii) how the guest fits inside the host cage. In order to gain a deeper understanding of the intrinsic factors governing formation of {MPd12L8}, we decided to perform an energy decomposition analysis for Ecom. From an energetic point of view, we can subdivide the encapsulation process of the cation guest in three steps: (i) dehydration of the cation, (ii) deformation of the Pd12 host shell, and (iii) binding between the cation and the Pd12 host. Thus, Ecom can be expressed as the sum of ΔEdef + ΔEdehyd + ΔEbind. In Fig. 7, the values computed for ΔEdef, ΔEdehyd, and ΔEbind for a series of cation guests are classified according to the cation charge. It becomes apparent that in absolute values ΔEdef is much smaller than ΔEdehyd and ΔEbind, and that these two latter terms are very dependent on the cation charge. The complexation energy for di- and trivalent cation guests is respectively two or three times more exothermic than for monovalent cations, due to increasing charge–dipole and charge–charge interactions.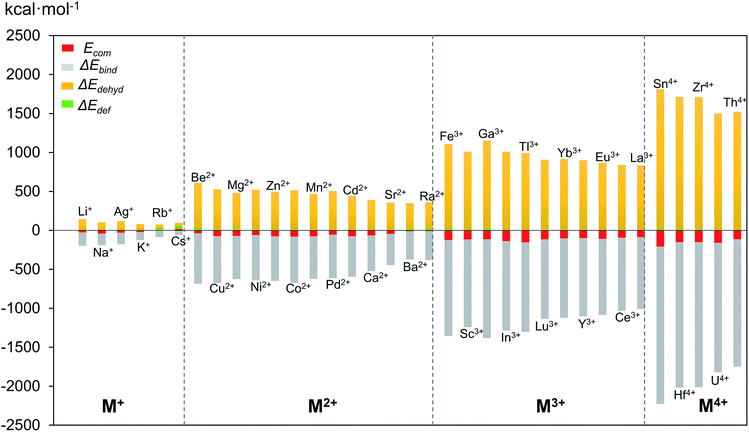 | ||
| Fig. 7 Complexation energy Ecom (in kcal mol−1) of Mn+ encapsulated in Pd12L8 (L = PhAs) host shell and its decomposition terms ΔEdehyd, ΔEbind and ΔEdef. | ||
The dehydration energy (ΔEdehyd) of the cation guest M and the electrostatic interaction (ΔEbind) between M and the Pd12 nanocage exhibit large values, and in all cases ΔEbind is larger than the sum ΔEdehyd + ΔEdef, consequently, the Ecom term is always negative and hence exothermic. However, this does not mean that ΔEbind alone is sufficient to describe the Ecom trend. In Table 2 three examples are shown indicating that in absolute value ΔEbind is indeed dominant, but this term alone does not allow predicting the correct trend for Ecom. For example, let us consider the cation guest pair Ga3+/In3+, for which experiments clearly demonstrated that In3+ is captured preferentially over Ga3+. The more negative value for Ecom for In3+ originates essentially from the large deformation energy of 25.7 kcal mol−1 for Ga3+ (vs. 8.4 kcal mol−1 for In3+). The other two energy terms (ΔEbind and ΔEdehyd) are significantly larger in absolute terms for Ga3+ than In3+, but they cancel each other out. Notice that the Pd12 host cage deforms significantly more for Ga3+ than In3+, because the former is rather small.
| Mn+ | E com | ΔEdef | ΔEbind | ΔEdehyd | Ionic radius | Critical energy term |
|---|---|---|---|---|---|---|
| Ga3+ | −115.8 | 25.7 | −1267.1 | 1125.5 | 0.92 | ΔEdef |
| In3+ | −137.1 | 8.4 | −1146.9 | 1001.5 | 1.06 | |
| Lu3+ | −115.0 | 5.7 | −1021.2 | 900.5 | 1.12 | ΔEdehyd |
| Yb3+ | −103.0 | 4.9 | −1018.4 | 910.5 | 1.13 | |
| Ce3+ | −95.5 | 5.8 | −935.2 | 833.9 | 1.28 | ΔEbind |
| La3+ | −86.3 | 3.9 | −920.6 | 830.4 | 1.30 |
For the Lu3+/Yb3+ pair, it can be noticed from the values in Table 2 that Lu3+ has a more negative complexation energy by 12 kcal mol−1. The radii of both ions are virtually identical and the deformation and binding energies are rather similar, and so it can be concluded that the dehydration energy is the critical term in this case.
Finally, the third ion pair Ce3+/La3+ allows to identify the relevance of electronic structure. The La3+ and Ce3+ ions have the same charge and essentially identical ionic radii, but the larger atomic number for Ce3+ leads to a higher effective nuclear charge and due to the low shielding of f electrons Ce3+ has a larger (more negative) binding energy than La3+, which in turn leads to a higher (more negative) complexation energy for the former.
In summary, Ecom depends mainly on the following four properties of the metal ion guest: (i) effective ionic radius, (ii) valence state, (iii) dehydration ability, and (iv) electronic configuration and resulting charge-accepting ability. The selectivity for a given cation guest is the result of a delicate balance between the cation–polyoxopalladate and the cation–solvent interactions.
4. Conclusions
In host – guest or template-based chemistry, one of the challenges is to know the exact role that ions or small fragments play in the formation of a given species. Ever since the discovery in 2008 of the archetypal polyoxopalladate [H6PdII13O8(AsVO4)8]8− (Pd13), which can be described as a {Pd12O8(AsO4)8} nanocube encapsulating a central Pd2+ ion with square-planar coordination geometry, about 50 more polyoxopalladate nanocubes {MPd12L8} with different central metal ion guests M and capping groups L have been reported. However, the main factors that govern the experimental formation of a particular polyoxopalladate (and the non-formation of others) are not well understood. Here, combining experimental and computational chemistry, we have been able to rationalize why a polyoxopalladate shell self-assembles around a particular cation template guest more preferentially than others.The prototype Pd13 is formed by condensation of [Pd(H2O)4]2+ complex cations in the presence of arsenate anion heterogroups. Nevertheless, if the solution contains other cations Mn+, then in principle {MPd12L8} type species may also be formed, determined by the favourable complexation energy and the relative competition with respect to Pd2+ ions. After an exhaustive computational analysis of complexation and dehydration energies for a series of cation guests we were able to identify the most promising cations to be encapsulated inside the Pd12 nanocube shell. Trivalent and tetravalent cations are easily trapped inside Pd12, whereas monovalent cations are largely elusive. As based on the calculations, we also performed target-oriented synthetic studies and we were able to isolate four novel polyoxopalladates: (i) the La3+-centered nanocube [LaPd12O8(PhAsO3)8]5− (LaPd12-closed), the La3+-centered “open” nanocube [LaPd12O6(OH)3(PhAsO3)6(OAc)3]3− (LaPd12-open), the Ga3+-centered [GaPd12O8(PhAsO3)8]5− (GaPd12), and the In3+-analogue [GaPd12O8(PhAsO3)8]5− (InPd12). All four compounds were fully characterized in the solid state, in solution, and in the gas phase. In particular 115In and 75Ga NMR combined with mass spectrometry were very useful, as these techniques allowed to perform speciation studies. We demonstrated that in solutions containing In3+ and Ga3+ ions only the former is incorporated in the Pd12 shell, due to its more suitable size and higher complexation energy. DFT method also predicted that the large La3+ ion should fit in the Pd12 host shell. The experimental work following the computations indeed resulted in the successful synthesis of the regular nanocube LaPd12-closed as well as the open-shell structure LaPd12-open. These results reemphasize that size and dehydration energy of the cation guest are the key driving forces in the formation mechanism of nanocuboid polyoxopalladates of the type {MPd12L8}. Our work has demonstrated how powerful the interplay between theory and experiment can be. We predict that other cations such as Cd2+, Tl3+, Sn4+, Zr4+, Hf4+, U4+, and Th4+ amongst others are potential candidates for encapsulation inside the Pd12 host and our efforts are geared in this direction.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. M. P. thanks the Spanish Ministry of Science (CTQ2014-52774-P) and the Generalitat de Catalunya (2009SGR462 and XRQTC), and acknowledges the BSC for a computer grant. J. M. P. also thanks ICREA foundation for an ICREA ACADEMIA award. U. K. thanks the German Research Council (DFG-KO-2288/20-1 and DFG-KO-2288/16-1), Jacobs University, and CMST COST Action CM1006 (EUFEN) for support. U. K. and J. M. P. acknowledge CMST COST Action CM1203 (PoCheMoN). P. Y. sincerely acknowledges CSC (China Scholarship Council) for a doctoral fellowship. We thank Prof. Imre Tóth in Debrecen University (Debrecen, Hungary) for performing elemental analysis.Notes and references
- A. Müller, H. Reuter and S. Dillinger, Angew. Chem., Int. Ed. Engl., 1995, 34, 2328 CrossRef.
- (a) U. Kortz, M. G. Savelieff, B. S. Bassil and M. H. Dickman, Angew. Chem., Int. Ed., 2001, 40, 3384 CrossRef CAS; (b) S. S. Mal and U. Kortz, Angew. Chem., Int. Ed., 2005, 44, 3777 CrossRef CAS PubMed; (c) U. Kortz, F. Hussain and M. Reicke, Angew. Chem., Int. Ed., 2005, 44, 3773 CrossRef CAS PubMed; (d) C. Ritchie, A. Ferguson, H. Nojiri, H. N. Miras, Y. F. Song, D. L. Long, E. Burkholder, M. Murrie, P. Kögerler, E. K. Brechin and L. Cronin, Angew. Chem., Int. Ed., 2008, 47, 5609 CrossRef CAS PubMed; (e) D. L. Long, Y. F. Song, E. F. Wilson, P. Kögerler, S. X. Guo, A. M. Bond, J. S. J. Hargreaves and L. Cronin, Angew. Chem., Int. Ed., 2008, 47, 4384 CrossRef CAS PubMed; (f) X. K. Fang and P. Kögerler, Angew. Chem., Int. Ed., 2008, 47, 8123 CrossRef CAS PubMed; (g) S. Reinoso, M. Giménez-Marqués, J. R. Galán-Mascarós, P. Vitoria and J. M. Gutiérrez-Zorrilla, Angew. Chem., Int. Ed., 2010, 49, 8384 CrossRef CAS PubMed; (h) J. Yan, D. L. Long and L. Cronin, Angew. Chem., Int. Ed., 2010, 49, 4117 CrossRef CAS PubMed; (i) M. Ibrahim, S. S. Mal, B. S. Bassil, A. Banerjee and U. Kortz, Inorg. Chem., 2011, 50, 956 CrossRef CAS PubMed; (j) W. C. Chen, H. L. Li, X. L. Wang, K. Z. Shao, Z. M. Su and E. B. Wang, Chem.–Eur. J., 2013, 19, 11007 CrossRef CAS PubMed.
- M. T. Pope, Heteropoly and Isopoly Oxometalates, Springer-Verlag, New York, 1983 Search PubMed.
- N. V. Izarova, M. T. Pope and U. Kortz, Angew. Chem., Int. Ed., 2012, 51, 9492 CrossRef CAS PubMed.
- M. Pley and M. S. Wickleder, Angew. Chem., Int. Ed., 2004, 43, 4168 CrossRef CAS PubMed.
- E. V. Chubarova, M. H. Dickman, B. Keita, L. Nadjo, F. Miserque, M. Mifsud, I. W. C. E. Arends and U. Kortz, Angew. Chem., Int. Ed., 2008, 47, 9542 CrossRef CAS PubMed.
- (a) N. V. Izarova, N. Vankova, T. Heine, R. Ngo Biboum, B. Keita, L. Nadjo and U. Kortz, Angew. Chem., Int. Ed., 2010, 49, 1886 CrossRef CAS PubMed; (b) Y. Xiang, N. V. Izarova, F. Schinle, O. Hampe, B. Keita and U. Kortz, Chem. Commun., 2012, 48, 9849 RSC; (c) N. V. Izarova, A. Kondinski, N. Vankova, T. Heine, P. Jäger, F. Schinle, O. Hampe and U. Kortz, Chem.–Eur. J., 2014, 20, 8556 CrossRef CAS PubMed.
- N. V. Izarova, M. H. Dickman, R. Ngo Biboum, B. Keita, L. Nadjo, V. Ramachandran, N. S. Dalal and U. Kortz, Inorg. Chem., 2009, 48, 7504 CrossRef CAS PubMed.
- (a) M. Barsukova, N. V. Izarova, R. Ngo Biboum, B. Keita, L. Nadjo, V. Ramachandran, N. S. Dalal, N. S. Antonova, J. J. Carbó, J. M. Poblet and U. Kortz, Chem.–Eur. J, 2010, 16, 9076 CrossRef CAS PubMed; (b) M. Barsukova-Stuckart, N. V. Izarova, R. A. Barret, Z. Wang, J. van Tol, H. W. Kroto, N. S. Dalal, P. Jiménez-Lozano, J. J. Carbó, J. M. Poblet, M. S. von Gernler, T. Drewello, P. de Oliveira, B. Keita and U. Kortz, Inorg. Chem., 2012, 51, 13214 CrossRef CAS PubMed; (c) M. Barsukova-Stuckart, N. V. Izarova, R. Barrett, Z. Wang, J. van Tol, H. W. Kroto, N. S. Dalal, B. Keita, D. Heller and U. Kortz, Chem.–Eur. J, 2012, 18, 6167 CrossRef CAS PubMed; (d) Z. Lin, B. Wang, J. Cao, B. Chen, C. Xu, X. Huang, Y. Fan and C. Hu, Eur. J. Inorg. Chem., 2013, 20, 3458 CrossRef.
- (a) N. V. Izarova, R. Ngo Biboum, B. Keita, M. Mifsud, I. W. C. E. Arends, G. B. Jameson and U. Kortz, Dalton Trans., 2009, 43, 9385 RSC; (b) M. Delferro, C. Graiff, L. Elviri and G. Predieri, Dalton Trans., 2010, 39, 4479 RSC; (c) F. Xu, R. A. Scullion, J. Yan, H. N. Miras, C. Busche, A. Scandurra, B. Pignataro, D. L. Long and L. Cronin, J. Am. Chem. Soc., 2011, 133, 4684 CrossRef CAS PubMed; (d) Z.-G. Lin, B. Wang, J. Cao, B.-K. Chen, Y.-Z. Gao, Y.-N. Chi, C. Xu, X.-Q. Huang, R.-D. Han, S.-Y. Su and C.-W. Hu, Inorg. Chem., 2012, 51, 4435 CrossRef CAS PubMed; (e) P. Yang, Y. X. Xiang, Z. G. Lin, B. S. Bassil, J. Cao, L. Y. Fan, Y. Fan, M. Li, P. Jiménez-Lozano, J. J. Carbó, J. M. Poblet and U. Kortz, Angew. Chem., Int. Ed., 2014, 53, 11974 CrossRef CAS PubMed; (f) P. Yang, Y. X. Xiang, Z. G. Lin, Z. L. Lang, P. Jiménez-Lozano, J. J. Carbó, J. M. Poblet, L. Y. Fan, C. W. Hu and U. Kortz, Angew. Chem., Int. Ed., 2016, 55, 15766 CrossRef CAS PubMed.
- B. R. Bowsher and A. J. Rest, J. Chem. Soc., Dalton Trans., 1981, 1157 RSC.
- (a) N. V. Izarova, N. Vankova, A. Banerjee, G. B. Jameson, T. Heine, F. Schinle, O. Hampe and U. Kortz, Angew. Chem., Int. Ed., 2010, 49, 7807 CrossRef CAS PubMed; (b) M. Barsukova-Stuckart, N. V. Izarova, G. B. Jameson, V. Ramachandran, Z. Wang, J. van Tol, N. S. Dalal, R. Ngo Biboum, B. Keita, L. Nadjo and U. Kortz, Angew. Chem., Int. Ed., 2011, 50, 2639 CrossRef CAS PubMed; (c) N. V. Izarova, Z. Lin, P. Yang, A. Kondinski, N. Vankova, T. Heine and U. Kortz, Dalton Trans., 2016, 45, 2394 RSC.
- (a) F. Xu, H. N. Miras, R. A. Scullion, D.-L. Long, J. Thiel and L. Cronin, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 11609 CrossRef CAS PubMed; (b) R. Scullion, A. J. Surman, F. Xu, J. S. Mathieson, D.-L. Long, F. Haso, T. Liu and L. Cronin, Angew. Chem., Int. Ed., 2014, 53, 10032 CrossRef CAS PubMed; (c) L. G. Christie, A. J. Surman, R. A. Scullion, F. Xu, D.-L. Long and L. Cronin, Angew. Chem., Int. Ed., 2016, 55, 12741 CrossRef CAS PubMed.
- (a) X. López, P. Miró, J. J. Carbó, A. Rodríguez-Fortea, C. Bo and J. M. Poblet, Theor. Chem. Acc., 2011, 128, 393 CrossRef; (b) X. López, J. J. Carbó, C. Bo and J. M. Poblet, Chem. Soc. Rev., 2012, 41, 7537 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian09W, Revision A02, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- (a) L. v. Szentpály, P. Fuentealba, H. Preuss and H. Stoll, Chem. Phys. Lett., 1982, 93, 555 CrossRef; (b) X. Y. Cao and M. Dolg, J. Chem. Phys., 2001, 115, 7348 CrossRef CAS; (c) X. Y. Cao and M. Dolg, J. Mol. Struct.: THEOCHEM, 2002, 581, 139 CrossRef CASM. Dolg, H. Stoll and H. Preuss, Theor. Chem. Acc., 1993, 85, 441 CrossRef CAS; (d) M. Dolg, H. Stoll, H.-J. Flad and H. Preuss, J. Chem. Phys., 1992, 97, 1162 CrossRef CAS.
- (a) D. Feller, J. Comput. Chem., 1996, 17, 1571 CrossRef CAS; (b) K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045 CrossRef CAS PubMed.
- (a) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270 CrossRef CAS; (b) W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284 CrossRef CAS.
- (a) G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193 CrossRef CAS; (b) J.-P. Blaudeau, M. P. McGrath, L. A. Curtiss and L. Radom, J. Chem. Phys., 1997, 107, 5016 CrossRef CAS; (c) M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. Defrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654 CrossRef CAS; (d) P. C. Hariharan and J. A. Pople, Theor. Chem. Acc., 1973, 28, 213 CrossRef CAS.
- (a) Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2007, 120, 215 CrossRef; (b) Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157 CrossRef CAS PubMed.
- (a) S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS PubMed; (b) A. D. Becke, J. Chem. Phys., 1997, 107, 8554 CrossRef CAS; (c) J. D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC; (d) Q. Wu and W. T. Yang, J. Chem. Phys., 2002, 116, 515 CrossRef CAS.
- (a) J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999 CrossRef CAS PubMed; (b) A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378 CrossRef CAS PubMed.
- D. W. Smith, J. Chem. Educ., 1977, 54, 540 CrossRef CAS.
Footnotes |
| † Dedicated to Professor Walter Klemperer on the occasion of his 70th birthday. |
| ‡ Electronic supplementary information (ESI) available: Details on experimental methods; the experimental and computational related tables and figures. CCDC 1555480–1555483. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7sc03441e |
| § Z. L. and P. Y. equally contributed to the work. |
| This journal is © The Royal Society of Chemistry 2017 |