HOMO inversion as a strategy for improving the light-absorption properties of Fe(II) chromophores

Abstract

A computational study of a series of [Fe(tpy)₂]²⁺ (tpy = 2,2′:6′,2′′-terpyridine) complexes is reported, where the tpy ligand is substituted at the 4, 4′, and 4′′ positions by electron donor (furan, thiophene, selenophene, NH₂) and acceptor (carboxylic acid, NO₂) groups. Using DFT and TD-DFT calculations, we show that the substitution of heterocyclic π donor groups onto the tpy ligand scaffold leads to marked improvement of the [Fe(tpy)₂]²⁺ absorption properties, characterized by increased molar extinction coefficients, shift of absorption energies to longer wavelengths, and broadening of the absorption spectrum in the visible region. The observed changes in the light absorption properties are due to destabilization of ligand-centered occupied π orbital energies, thus increasing the interactions between the metal t_2g (HOMO) and ligand π orbitals. Substitution of extended π-conjugated groups, such as thienothiophene and dithienothiophene, further destabilizes the ligand π orbital energies, resulting in a fully ligand-localized HOMO (i.e., HOMO inversion) and additional improvement of the light absorption properties. These results open up a new strategy to tuning the light absorption properties of Fe(II)-polypyridines.

---

1. Introduction

Metal polypyridines have been at the forefront of numerous experimental and computational studies focusing on the design of molecular systems that could serve as sensitizers or photocatalysts in various assemblies for solar energy conversion, such as dye-sensitized solar cells (DSSCs)^1,2 and dye-sensitized photoelectrosynthesis cells (DSPECs).³ Among these, Ru(II)-polypyridines have been examined in the most detail as they are typical sensitizers employed in DSSCs due to their stability, tunability, optimal redox properties, and solar-to-electric power conversion efficiencies (PCE) of over 11%.^2,4–8 Unfortunately, ruthenium is a relatively rare and expensive metal, which limits its wide application in photovoltaic and photocatalytic assemblies on a large scale.

Significant attention has been recently focused on Fe(II)-polypyridines as a replacement for Ru(II)-polypyridine sensitizers. While it was known since about 1998 that Fe(II)-polypyridines are in principle capable of sensitizing TiO₂ semiconductors thanks to the work of Ferrere and Gregg,^9–12 as well as Meyer and coworkers,¹³ the first report of a successful, high-yield sensitization of TiO₂ with an iron complex did not appear until recently.¹⁴ The main obstacle to utilization of Fe(II)-polypyridines as photosensitizers is the short lifetime of their photoactive metal-to-ligand charge transfer (MLCT) states, that undergo ultrafast intersystem crossing into low-lying metal-centered (MC) ligand field states.^15–18 Therefore, much effort has been expended on designing iron complexes with increased ligand field strength, with the intention to destabilize the low-lying ligand field states and decrease the rate of intersystem crossing.^19–27 Until now, introduction of strongly σ donating carbene ligands proved to be the most successful strategy for increasing the lifetime of the photoactive MLCT states in Fe(II)-polypyridines.^28–31 An interesting and counter-intuitive approach was also taken by Damrauer and coworkers who designed a highly strained Fe(II)-bis(terpyridine) based complex with a quintet ground state and long-lived lifetime of the excited thermalized^5,7 MLCT state.^32,33 A downside of this approach is, however, a weak absorption of visible light in the quintet ground state. Thus, while great strides were made in designing viable Fe-based sensitizers, there is still significant room for improvement.^34–36

Besides the chemical stability and tunability mentioned earlier, an ideal photosensitizer (1) displays panchromatic absorption across all wavelengths of the visible spectrum, including the near infrared (NIR) region, (2) possesses long-lived charge-separated (MLCT) states, (3) undergoes efficient electron injection into the semiconductor, and (4) is amenable to efficient regeneration by the redox mediators typically used in DSSCs. Until now, most studies of iron sensitizers have focused on increasing the lifetime of the photoactive MLCT states^19,30,31,33 or rational design of semiconductor surface anchoring groups³⁷ with the aim to increase the efficiency of interfacial electron transfer (IET) between the excited dye and semiconductor.^14,31,36,38 Comparably little attention has been paid to improving light absorption properties of iron sensitizers or to regeneration of oxidized iron dyes by standard electrolytes, both of which are essential for increasing the external quantum efficiency of DSSCs.

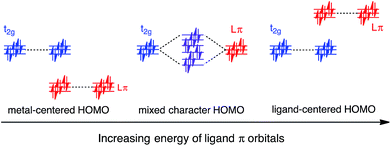
In this work, a computational study focused on improving light absorption properties of Fe(II) polypyridines is reported. A series of [Fe(tpy)₂]²⁺ (tpy = 2,2′:6′,2′′-terpyridine) based complexes is investigated (see Fig. 1), substituted with different electron donor and acceptor groups along the tpy scaffold. Improvement in the absorption properties and progress toward panchromatic absorption is achieved by destabilization of the occupied ligand π orbitals via substitution of π-conjugated electron donating groups onto the terpyridine scaffold. While the highest occupied molecular orbital (HOMO) in traditional Fe(II)-polypyridine complexes possesses metal-localized t_2g character with separate ligand π orbitals at lower energy, destabilization of the ligand π orbitals causes extensive mixing between the ligand π orbitals and metal t_2g levels (see Fig. 2). Further destabilization can invert the ordering of metal t_2g levels and ligand π based orbitals (i.e., causing HOMO inversion), making the HOMO ligand-localized. This leads to dramatic changes in the light absorption properties of substituted Fe(II)-polypyridines, resulting in near panchromatic absorption. We propose that HOMO inversion is an effective strategy for tuning the absorption properties of Fe(II)-polypyridines as well as other metal polypyridine systems.

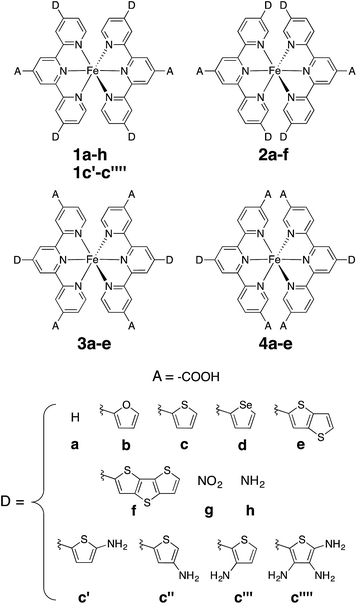Fig. 1 Substituted [Fe(tpy)₂]²⁺ investigated in this work. Note that complexes 1a and 2a are identical (D = H case).

Fig. 2 Interactions between the t_2g orbital set on Fe with ligand-centered π orbitals. Increased interactions between the ligand π orbitals and the t_2g orbitals destabilize the HOMO and decrease the electron density on the Fe center. Further increase in the energy of the ligand π orbitals inverts the character of the HOMO to that of a ligand-centered π orbital.

2. Methods

2.1 Structure optimization

All complexes investigated in this study (Fig. 1) were optimized in the singlet ground state employing the B3LYP functional^39,40 and Grimme's D2 dispersion correction.⁴¹ The SDD effective core potential and associated basis set for Fe⁴² and the 6-311G* basis set for all other atoms (C, H, O, N, S, Se)^43,44 were utilized along with a polarizable continuum (PCM)⁴⁵ model to include water as implicit solvent. Vibrational frequency analysis was performed for each optimized structure to confirm the local minima at their respective potential energy surfaces. Optimized geometries are provided in the ESI.† All calculations on the molecular complexes were carried out using the Gaussian 09 software package (revision D).⁴⁶

2.2 Absorption spectra and electron density on the linker group

Absorption spectra were calculated with linear-response time dependent DFT (TD-DFT)^47–49 at the same level of theory as described for optimization. Solvent effects (water) were included in the TD-DFT calculations via the polarizable continuum model (PCM).⁵⁰ Singlet excitations for the 50 lowest excited states were computed for the complexes without any donor groups. Seventy singlet excitations were included for complexes containing donor groups in order to obtain the high energy ligand centered (LC) π–π* transitions. The stick spectra were broadened using Lorentzian functions with a half-width-at-half-maximum (HWHM) of 0.12 eV. Excited states with a significant oscillator strength, f_osc ≥ 0.01, were characterized for wavelength greater than 350 nm. Each transition in the UV-vis spectrum can be represented by a set of hole and electron pairs. Only the hole and electron pairs whose contributions add up to 70% were considered for identification of the excited states. While the B3LYP functional tends to overestimate the calculated absorption energies relative to experiment, it was previously shown to provide a good qualitative description of the absorption spectra of metal polypyridine complexes, as well as of the excitation energy trends in a series of related compounds.^51,52 Absorption spectra for selected complexes (1a, 1c, 1e, 1f, 1h and 1c′′′′) were also obtained with the CAM-B3LYP⁵³ functional to eliminate any ambiguity in the analysis based on the choice of functional, as it is more reliable in describing excitations with the charge transfer character.⁵⁴

Electron densities on the carboxylic acid substituents that can serve as anchoring groups binding the dye to TiO₂ semiconductor surface were calculated from Mulliken population analysis for the lowest degenerate set of unoccupied orbitals (LUMO).⁵⁵ The amount of electron density on the linker in the degenerate LUMO set is directly correlated with the electronic coupling between the conduction band (CB) of the semiconductor and the excited state of the dye characterized by the population of the LUMO.⁵⁶ This percent of electron density on the linker can therefore serve as a means to qualitatively determine the impact of donor group substitutions on the initial IET rate due to the choice and position of donor groups as well as position of the carboxylic acid linker on the terpyridine scaffold.

The magnitude of interactions between the metal-based t_2g orbital set and ligand-based π orbitals were estimated by calculating the electron density on the Fe center (ρ^Fe) for the twenty one highest energy occupied Kohn–Sham (KS) orbitals.

2.3 Pyridine-donor model for understanding the effect of donor groups

Perturbations to the KS orbitals of 2,2′:6′,2′′-terpyridine due to various donor groups were investigated using a ligand only model of a pyridine-donor shown in Fig. 3. The role of the type of the donor group was explored by placing the four donor groups (furan, thiophene, and conjugated thiophenes) at the para position of the pyridine ring. Another model with thiophene at the meta position of the pyridine was employed to understand the impact of donor groups substituted at the 5, 5′′ positions of the terpyridine scaffold. Structures of the pyridine-donor models were constrained to the geometry in their respective Fe-complexes in the 1a–c, 1e and 1f series (see Fig. 1).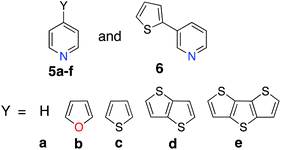

Fig. 3 Model complexes employed to investigate perturbation of the KS orbitals of pyridine due to the presence of donor groups.

3. Results

Photophysical properties of metal polypyridine sensitizers related to their light absorption capabilities, such as the molar extinction coefficients, energies of the lowest energy excited states, and HOMO–LUMO gaps, can be tuned by introducing various donor and acceptor moieties onto their polypyridine ligand scaffold. It is therefore important to determine the ideal positions and types of substituents by studying their effect on the energies and electronic character of the Frontier orbitals (HOMO and LUMO) as well as the HOMO–LUMO gaps. The ability of the photoexcited dye to transfer electrons into the CB of a semiconductor is among other essential properties of dye sensitizers. The amount of electron density on the linker in the excited state is a strong indicator of the strength of electronic coupling between the excited dye and the CB of the semiconductor and consequently the initial IET rate.⁵⁶ Therefore, performance of the donor and acceptor groups was gauged by calculating the HOMO–LUMO gaps, Frontier orbital energies, the electron density on the carboxylic linker of the LUMO, as well as UV-vis absorption spectra of selected complexes.

The following sections describe the impact of the selected donor and acceptor group substitutions on the light absorption. The first section deals with the determination of the best position for the carboxylic acid substituent (i.e., the acceptor group) at the tpy scaffold, while the second section focuses on describing the influence of π-conjugated donor groups on light-harvesting properties of Fe(II) polypyridine sensitizers. The third section investigates a simple model based on substituted pyridine and provides a deeper understanding of perturbations to terpyridine ligand MO energies and shapes in the presence of π conjugated donor groups. The following (fourth) section then delves into the understanding of metal–ligand interactions in the presence of different π-conjugated donor groups, while the fifth section focuses on calculations of absorption spectra for substituted complexes. The final two sections deal with improving the electron density on the carboxylic acid linker group via substitutions of more simple electron donating and withdrawing groups.

3.1 Optimal position of the carboxylic acid substituents

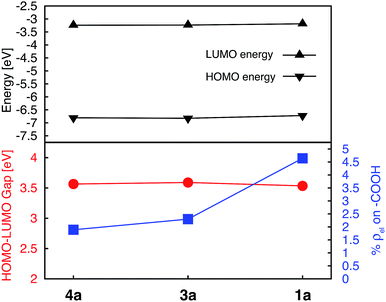
An optimal position of the carboxylic acid group on the terpyridine scaffold was determined by comparing the properties of complexes 1a, 3a, and 4a. Since, as shown in the following sections, the substitution of donor groups affects the electronic structure of [Fe(tpy)₂]²⁺ complexes in the same way irrespective of the position of the carboxylic acid, the optimal substituent position was determined in the absence of the π conjugated donor groups.

For all complexes investigated, position of the carboxylic acid linkers does not change the nodal structures of the HOMO, doubly degenerate HOMO-1 and LUMO orbitals (see Fig. S1 in the ESI†). Consequently, we can compare their orbital energies and distribution of electron densities to understand the perturbation caused by the position of the linking group.

Energies of the HOMO and LUMO orbitals for complexes 1a, 3a, and 4a are shown Fig. 4 (top panel), along with the HOMO–LUMO gap and electron density on the carboxylic acid linker averaged over a set of two degenerate LUMO orbitals (Fig. 4, bottom panel). As can be seen in this figure, the substituent position of the carboxylic acid group has a negligible effect on the HOMO and LUMO energies and subsequently on the HOMO–LUMO gap, which varies by at most 0.06 eV across the set. The smallest HOMO–LUMO gap is observed for complex 1a (3.53 eV).

Fig. 4 Electronic properties for a series of [Fe(tpy)₂]²⁺ complexes substituted with carboxylic acid groups. Top: HOMO and LUMO energies. Bottom: HOMO–LUMO gaps (red), and average % of electron density (%ρ_el) on the linker group in doubly degenerate LUMO (blue).

Interestingly, the amount of electron density on the carboxylic acid linker is more sensitive to the substituent position, varying from 1.9–4.6% across the set. Complex 1a (carboxylic acid substituted at 4′ position) displays the largest amount of the electron density on the linker, approximately double the amount in comparison to complexes 3a and 4a. This trend can be explained based on the number of linking groups attached to the dye. Adding four carboxylic acid groups will delocalize the density on all four linkers, thus significantly lowering densities on individual linkers capable of attaching the dye to the semiconductor surface. In conclusion, the 4′ position on the terpyridine scaffold is the ideal position for the carboxylic acid attachment as it maximizes the electron density on the linker in the low-energy excited states, thus improving the electronic coupling between the excited dye and semiconductor.

3.2 Influence of donor groups

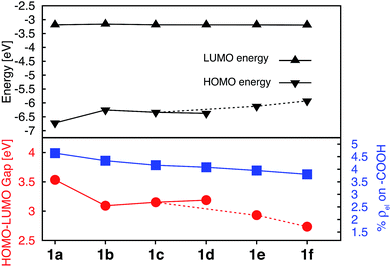
Donor groups with various heteroatoms (O, S, Se) as well as different extent of π conjugation (1–3 fused heterocycles) as shown in Fig. 1 were utilized to understand their impact on the electronic and absorption properties of [Fe(tpy)₂]²⁺ complexes. While only the thiophene heterocycle was utilized to investigate the effect of extended π-conjugation, results obtained should be applicable to donor groups with any heteroatom. Since the presence of π conjugated donor groups impacts the ground state electronic structure in the same way irrespective of the substituent position on the tpy scaffold, only results for series 1a–f are presented in this section. Data for series 2a–f, 3a–e, and 4a–d can be found in the ESI (Fig. S2–S4†). Note that the effect of extending π conjugation was only studied for series 1 and 2, as these have a carboxylic acid group attached at the optimal 4′ position as determined in the previous section.

Fig. 5 summarizes the changes in the most important electronic properties for various donor substituents for the 1a–f series of complexes. Electron donor substituents do not affect the LUMO energy, while they slightly decrease the percent of electron density on the carboxylic acid linker. Negligible effects of donor group on the LUMO energies can be explained by inspecting the nodal structure of the degenerate pair of LUMO orbitals for complex 1a (see Fig. S1 in the ESI†). As the electron density is mostly concentrated on the central pyridine ring of the tpy group, substitution of the electron donor groups on the side pyridine rings does not significantly impact the LUMO energies. The average electron density on the donor groups becomes significant (greater than 10%) in the higher energy unoccupied orbitals (see Fig. S5 and S6 in the ESI†).

Fig. 5 Electronic properties of 1a–f series of complexes. Top: HOMO and LUMO energies. Bottom: HOMO–LUMO gaps (red) and average % of electron density on the carboxylic acid in doubly degenerate LUMO (blue).

While the influence of donor groups on LUMO energies is negligible, they do have a significant impact on the HOMO energies. Substitution of furan (1b), thiophene (1c), and selenophene (1d) raises the HOMO energy by 0.35–0.47 eV with respect to complex 1a. Further increase in the HOMO energies is observed for complexes 1e and 1f with donor groups with extended π conjugation (0.60–0.79 eV). Consequently, the HOMO–LUMO gap decreases significantly in the presence of all donor groups investigated (see Fig. 5, bottom panel). The overall trend in the decrease of the HOMO–LUMO gaps across the series of 1a–1f complexes was also confirmed via TD-DFT calculations utilizing an approach suggested in previous studies (see Fig. S7 and S8 in the ESI†).^57,58

Interestingly, changing the type of donor group from furan to thiophene to selenophene (complexes 1b, 1c, and 1d, respectively) slightly reduces the HOMO energy and increases the HOMO–LUMO gap. This decrease in the HOMO energy with the type of donor atom can be explained on the basis of the variation in the electronic structure of the donor group, as well as the variation in the atomic size (van der Waals radii of O, S and Se are 48, 88 and 103 pm, respectively) utilizing the model complexes shown in Fig. 3, discussed in Section 3.3. As the atom size increases the dihedral angle between the donor and the pyridine ring increases. The dihedral angles between the terpyridine group and heterocycle are 0°, 15.8° and 16.8° for furan, thiophene and selenophene, respectively.

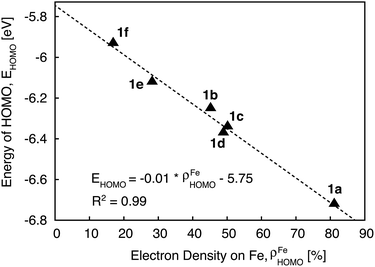
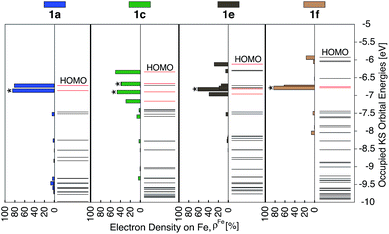
Since the HOMO is the orbital most affected by the donor group substitution, it is crucial to explain the changes in its energy and nodal structure. Nodal structures of HOMO orbitals for complexes 1a–1f are shown in Fig. 6. In the presence of a donor group, electron density delocalizes away from the Fe center onto the ligands. The extent of delocalization can be quantified with the percent of electron density on Fe, ρ^Fe, where larger delocalization results in lower ρ^Fe. Interestingly, the HOMO energy is inversely correlated with the electron density on the Fe center, as seen in Fig. 7. Equal sharing of electron density between the metal center and ligands (ρ^Fe ∼ 50%) corresponds to the strongest interactions between the t_2g set of Fe orbitals and the occupied π orbitals of the substituted tpy ligand, and is accompanied by an increase in the HOMO energy in comparison to the unsubstituted tpy ligand. As the energies of the ligand-centered π orbitals increase further, the interactions between the metal t_2g and ligand π orbitals decrease. Consequently, the HOMO becomes almost entirely ligand-centered and continues to increase in energy (also see Fig. 2).

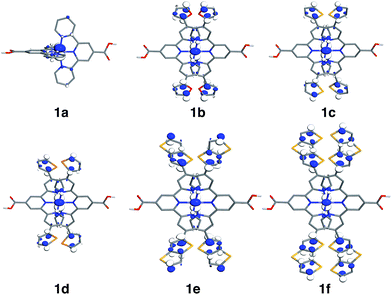Fig. 6 Highest occupied molecular orbitals (HOMO) for 1a–1f complexes. Surfaces are constructed with the isovalue of 0.04 e Å⁻³.

Fig. 7 Correlation between the energy of HOMO and electron density on Fe for complexes 1a–1f.

Based on Fig. 7, the interactions between the metal t_2g set and ligand π orbitals are the strongest for complexes 1b–1d, as ρ^Fe for the HOMO is ∼50% for these complexes, suggesting an equal sharing of electron density between the metal and ligand. Interactions further decrease as the energies of π donor orbitals increase with the extension of π conjugation of the donor groups (complexes 1e and 1f). Note that interactions between the substituted tpy ligands and Fe center are almost identical for complexes 1c and 1d, possibly due to a similar dihedral angles between the donor heterocycle and tpy (15.8° and 16.8° for 1c and 1d, respectively), and similar electronegativities of heteroatoms (2.58 and 2.55 for S and Se, respectively).

3.3 Pyridine-donor models for understanding tpy substitution effects

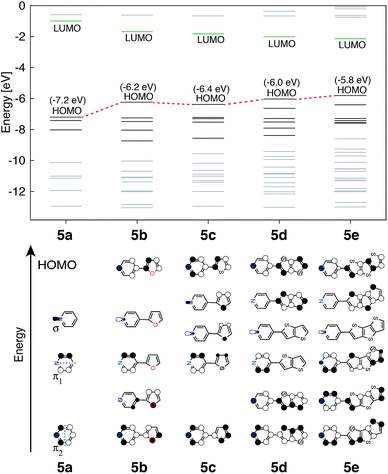
The perturbation to terpyridine ligand orbitals due to donor group substitutions were studied utilizing a simpler model comprised of a single pyridine with a donor substituent at either the para or meta positions (see Fig. 3). MO energy levels and shapes for pyridine and substituted pyridine models are shown in Fig. 8. Only one σ and two π pyridine orbitals that have appropriate symmetry to interact with the Fe d orbital set (d_xy, d_yz, d_xz, d_z² and d_x²−y²) were considered, and variations in their energies due to donor group substitution were monitored.

Fig. 8 Top: KS orbital energies of the pyridine and pyridine-donor models. Energies of HOMO are given in parenthesis. Bottom: Schematics of KS orbitals for the energy levels highlighted in black on the top panel in the order of increasing energy.

In general, donor group orbitals interact with pyridine π orbitals introducing new bonding and antibonding MO combinations and raising the energy of the HOMO. Detailed molecular orbital diagrams of all pyridine-donor models depicting relevant interactions between the donor and pyridine orbitals are provided in the ESI (Fig. S9 and S10†). As seen from the orbital schematics in Fig. 8, there are three relevant pyridine orbitals – σ (HOMO), π₁, and π₂ (HOMO-1 and HOMO-2, respectively). The π₂ orbital of pyridine interacts with a donor π orbital giving a bonding and antibonding pair. The new π antibonding orbital becomes the HOMO of the pyridine-donor system in place of the σ orbital. The same interactions are present between the occupied π orbitals of the tpy and donor groups, raising the energy of the occupied π orbitals of the tpy. Therefore, terpyridine with substituted furan, thiophene, and selenophene groups has occupied π orbitals that are better energetically aligned with the t_2g orbitals on Fe, maximizing their interactions (see Fig. 2).

Two factors are responsible for the HOMO energy decrease going from 5b to 5c. First, the occupied π orbital of the donor group that interacts with the occupied π₂ orbital on the pyridine becomes lower in energy going from furan to thiophene and selenophene, causing a decrease in the energy of HOMO that corresponds to their antibonding combination (see Fig. S11 in the ESI†). Second, the interaction between the occupied π orbital on the donor group and the π₂ orbital on the pyridine decreases with an increase in the dihedral angle (see Fig. S12 in the ESI†). Therefore, lower energy of thiophene's π orbital as well as the 16° dihedral angle between the pyridine and thiophene are both responsible for the decrease in the HOMO energy of 5c compared to that in 5b.

The HOMOs in tpy ligands substituted with more extended π conjugated donor groups are destabilized to a greater extent, thus reducing the interactions with the Fe t_2g set resulting in the HOMO of the Fe(II) complex itself becoming ligand-centered. These interactions explain why higher HOMO energies and lower HOMO–LUMO gaps are observed in complexes 1b–1f relative to 1a (refer to Fig. 5).

Another interesting observation is that the presence of donor groups increases the number of π orbitals at the appropriate energy that could interact with the t_2g orbitals on Fe, symmetry permitting. A further increase in this number is seen with increase in donor group conjugation. In the case of highly conjugated donors, the fraction of higher energy orbitals with density localized on the donor also increases. The trends are identical irrespective of the substituent position (meta vs. para) as can be seen in Fig. S10 and S13 in the ESI.†

3.4 Electron density on Fe and Fe–ligand interactions

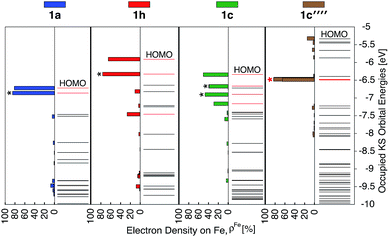
As discussed previously, the interactions of ligand π orbitals with the Fe t_2g orbitals raise HOMO energies and delocalize the electron density away from Fe (also see Fig. 2). To illustrate this point further, Fig. 9 displays histograms of calculated electron density on Fe (ρ^Fe) for a set of highest energy occupied MOs along with the MO energies. Molecular orbitals with significant iron character (ρ^Fe ≥ 20%) are highlighted in red and the doubly degenerate sets are marked with an asterisk. While the figure shows only thiophene-substituted complexes, the histogram profiles found for the other heterocycles considered in this study are very similar as shown in Fig. S14 in the ESI.†

Fig. 9 Electron density on Fe (ρ^Fe) of the 21 highest energy occupied KS orbitals near the frontier region for 1a, 1c, 1e and 1f. The KS orbitals with electron distribution ≥20% on Fe are shown in red and, among these, the doubly degenerate orbitals are labelled with ‘*’.

In the case of complex 1a, the HOMO, HOMO-1 and HOMO-2 orbitals display high electron density on Fe (ρ^Fe ∼ 84%) and correspond to the typical Fe t_2g orbital set. The presence of a heterocyclic donor group such as thiophene (1c) delocalizes the density away from the Fe center (KS orbitals shown in Fig. 6). Consequently, the HOMO, HOMO-1 and HOMO-2 orbitals have ρ^Fe ∼ 43%, while the lower energy orbitals, HOMO-4, HOMO-5 and HOMO-6, have ρ^Fe ∼ 40%. This result is consistent with the analysis of substituted pyridine models (see Section 3.3) suggesting that π orbitals of substituted terpyridine ligands are closer in energy to the Fe t_2g orbitals, resulting in stronger interactions between the two orbital sets.

In addition to the changes observed for ρ^Fe, the HOMO energies are also significantly different between 1c and 1a. Since the energy of the HOMO in 1c is higher and has electron density spread over both metal and ligand, its UV-vis spectrum is expected to be red-shifted in comparison to 1a, with mixed metal-to-ligand and ligand-centered transitions in the lower energy region. When donor group π conjugation increases going from 1c to 1e and 1f, HOMO and neighboring orbitals now display more than 70% of electron density on the ligand. This is expected to introduce ligand-centered transitions into the low energy region of the absorption spectrum.

3.5 UV-vis absorption spectra

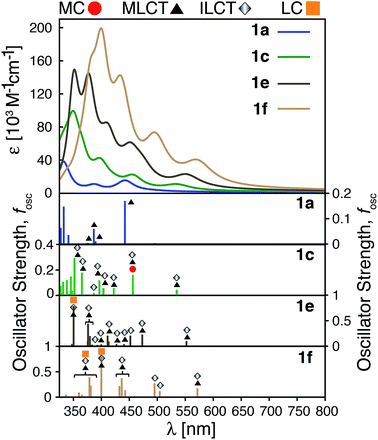
The calculated absorption spectra for 1a, 1c, 1e and 1f are shown in Fig. 10 along with the character of transitions with significant oscillator strength (f_osc ≥ 0.01) in the visible region (λ ≥ 350 nm). Transitions were classified as metal-centered (MC), metal-to-ligand charge transfer (MLCT), intra-ligand charge transfer (ILCT), or ligand-centered (LC) based on visual inspection. Note that several ILCT transitions also possess inter-ligand charge transfer character, but for simplicity they are all labelled as ILCT in Fig. 10. Details for each transition (excitation wavelength, oscillator strength, MO contributions) are provided in the ESI (Fig. S15–S18†). Mixed character was observed for several transitions; most of these displayed features of both MLCT and ILCT character. Two basic cases of mixed transitions were observed, in which the joint MLCT/ILCT assignment can either imply that the electron density in the hole state is delocalized over both metal and ligand moieties (case 1, see Fig. S19 in the ESI†), or that the transition has contributions from several hole–particle pairs that display either MLCT or ILCT character (case 2).

Fig. 10 Top: Calculated UV-vis spectra for complexes 1a, 1c, 1e and 1f. Bottom: Assignments for transitions with λ ≥ 350 nm and oscillator strength f_osc ≥ 0.01 for complexes 1a, 1c, 1e and 1f. MC: metal-centered, MLCT: metal-to-ligand charge transfer, ILCT: intra-ligand charge transfer and LC: ligand-centered.

The calculated UV-vis spectra (see Fig. 10) predict remarkable improvements in absorption properties upon substitution of the tpy ligand by donor groups. The absorption spectra of the substituted complexes shift towards longer wavelengths, with most of their transitions displaying a mixed MLCT/ILCT character (compare transition assignments for 1cvs.1a, see Fig. 10). The substituted complexes also display significant increases in molar absorptivity. Extending the π-conjugation of the substituent groups (going from 1c to 1e and 1f) further enhances the intensity as well as red-shifts the spectrum. New transitions with pure ILCT character are also observed for complexes 1e and 1f. These results are consistent with our predictions of a red shift in the absorption spectrum and rise of new ILCT transitions based on ρ^Fe and the energetics of occupied orbitals discussed in Section 3.4. It is also important to note that observations based on the calculated UV-vis spectra do not rely on the use of a particular DFT functional. Absorption spectra calculated with the CAM-B3LYP functional⁵³ display the same features, i.e., red-shifted absorption spectra and increased molar absorptivities (see Fig. S20 in the ESI†).

Improvements in molar absorptivity observed for substituted Fe(II) complexes are likely due to (1) an increased number of transitions in the lower energy region of the spectrum, and (2) mixed character (MLCT/ILCT) of these transitions. This is supported by the TD-DFT data on the iron–free complex of 1c (i.e., a hypothetical complex consisting of a substituted terpyridine ligand obtained by removal of the central Fe atom and one ligand from complex 1c, labeled as 1c-L) shown in Fig. 11. While the 1c-L complex displays intense transitions in the higher energy region (∼300 nm), the presence of the iron atom is necessary for these transitions to be shifted towards the lower-energy region. Same is true for complexes 1e and 1f – the presence of the metal enhances the ligand-localized transitions and shifts them toward the longer wavelengths (see Fig. S21 and S22 in the ESI†). This clearly demonstrates that the involvement of the metal is critical for enhancing the absorption spectrum in the visible region and the metal-free analogues are not predicted to display the same light-absorption properties.

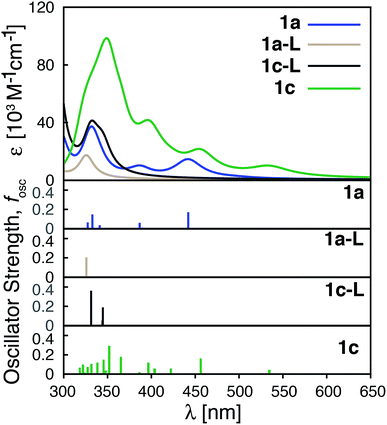Fig. 11 Calculated UV-vis spectra of 1a, 1a-L, 1c-L and 1c. 1a-L and 1c-L denote a ligand only structure obtained from the optimized geometry of 1a and 1c, respectively.

3.6 Improving electron density on the LUMO

While the heterocyclic donor substituents do improve the absorption properties of Fe(II)-bis(terpyridine) complexes, they also slightly decrease the electron density on the carboxylic acid group in the degenerate LUMO set (refer to Fig. 5), which can adversely affect IET. Therefore, strong electron withdrawing (NO₂) and donating (NH₂) groups were substituted onto 1a, with the aim to increase the electron density on the acceptor group. The resulting Frontier MO energies, HOMO–LUMO gaps, and %ρ_el are shown in Fig. 12.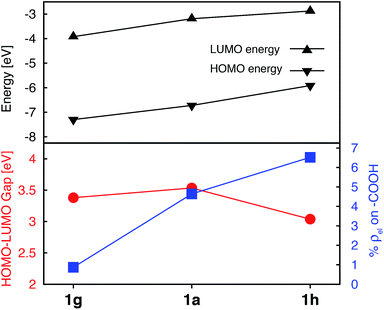

Fig. 12 Electronic properties of 1a, 1g, and 1h. Top: HOMO and LUMO energies. Bottom: HOMO–LUMO gaps (red) and average % of electron density on the carboxylic acid in doubly degenerate LUMO (blue).

Unlike the heterocyclic substituents, strong electron withdrawing (NO₂) and donating (NH₂) substituents change energies of both the HOMO and LUMO. Overall, both substituents decrease the HOMO–LUMO gap. The NH₂ substituent (complex 1h) has a more prominent effect, resulting in a HOMO–LUMO gap comparable to that of the complexes with heterocyclic substituents (see Fig. 5). Both substituents also strongly affect the electron density on the carboxylic acid linker group. While the NO₂ substitution results in a significant decrease of electron density (%ρ_el = 0.87 vs. 4.64 in an unsubstituted complex), substitution of NH₂ has an opposite effect (%ρ_el = 6.52). Moreover, the LUMO energy of NH₂–substituted complex (1h) increases by 0.31 eV compared to 1a. Since the density of states of the TiO₂ conduction band increases non-linearly with energy,⁵⁹ even a 0.31 eV change in the LUMO energy can significantly impact the IET efficiency. Thus, the main advantages of NH₂ over heterocyclic substituents is that it increases the LUMO energy as well as the electron density on the carboxylic acid linking group in the LUMO, while still decreasing the HOMO–LUMO gap. Due to lack of extended π conjugation, however, the NH₂ substituent will not provide the same orbital mixing and destabilization of terpyridine ligand-based π orbitals as seen with the heterocyclic donor groups (see Section 3.2).

3.7 NH₂-functionalized thiophene substituted complexes

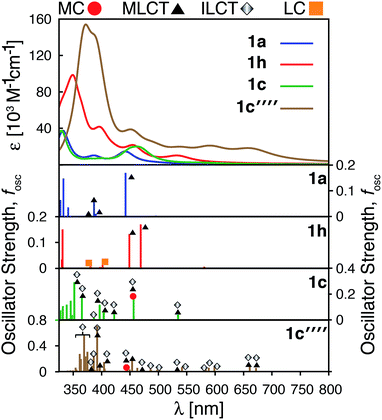
As shown in the previous sections, heterocyclic donor groups significantly improve the light absorption in Fe(II) polypyridine complexes, but are not expected to improve the IET efficiency. On the other hand, the NH₂ substituent favorably modulates the complex's electronic properties (%ρ_el and LUMO energy) that are important for efficient IET. Complexes 1c′-1c′′′′ (see Fig. 1) utilize both NH₂ and thiophene substituents in the molecular design with the aim to improve electronic properties important both for light-absorption and efficient IET. These complexes feature thiophene substituents functionalized with NH₂ at the position 5, 4, or 3 corresponding to complexes 1c′, 1c′′, and 1c′′′′ , respectively, as well as functionalized at all three positions simultaneously (1c′′′′).

Although NH₂-functionalized thiophene substituents do not affect the LUMO energies and %ρ_el to the same extent as direct substitution of NH₂ onto the tpy scaffold, they still improve these properties relative to an unfunctionalized thiophene substituent. Variations in the frontier orbital energies and %ρ_el due to NH₂-functionalized thiophene are more noticeable when all three positions of thiophene are substituted (complex 1c′′′′), refer to Fig. S23 in the ESI.† The LUMO energy increases by 0.24 eV and density on the carboxylic acid linker of LUMO increases by 1.4% in 1c′′′′ relative to 1a. The increases in the LUMO energy and density on the carboxylic acid linker are lower than those for 1h (0.31 eV and 1.9%, respectively) but higher than for 1c (0 eV and −0.5%, respectively). As higher electron density on the carboxylic acid linker and higher LUMO energy are some of the important parameters for efficient IET,^37,56,60 we predict that the IET efficiency from the excited states populating the LUMOs of these complexes will follow the order of 1h > 1c′′′′ > 1c.

The HOMO–LUMO gap of 1c′′′′ is reduced by 0.77 eV relative to 1a, which is a larger change than that for 1c and 1h complexes (0.38 eV and 0.50 eV, respectively). Therefore, the absorption spectrum of 1c′′′′ is expected to red shift more compared to the spectrum of 1c and 1h. The calculated UV-vis spectra shown in Fig. 13 are consistent with this prediction. Additionally, 1c′′′′ absorbs over a wider range of wavelengths with a better intensity compared to 1c and 1h. Panchromatic absorption in the visible region can potentially improve the light harvesting capability of sensitizers and, in turn, enhance the incident photon-to-current efficiency (IPCE). UV-vis spectra calculated employing the CAM-B3LYP functional display similar features and do not alter this analysis (see ESI, Fig. S24†). Fig. 13 also summarizes the character of transitions in the visible region of the absorption spectrum (λ ≥ 350 nm). Molecular orbitals involved in the transitions of 1h and 1c′′′′ can be found in the ESI, Fig. S25 and S26.† The amount of electron density on Fe (ρ^Fe) in the higher energy occupied orbitals for complexes 1a and 1h (see Fig. 14) suggests that the electron distribution does not change significantly upon the NH₂ substitution and that the HOMO, HOMO-1, and HOMO-2 correspond to the t_2g orbital set in both complexes. The main effect of the NH₂ substitution then is the destabilization of MO energies. Therefore, the absorption spectra for 1h and 1a are very similar, with the lowest energy transitions red-shifted for 1h.

Fig. 13 Calculated UV-vis spectra employing TD-DFT for 1a, 1h, 1c and 1c′′′′. Characteristics of the transitions at λ ≥ 350 nm with oscillator strength f_osc ≥ 0.01 for complexes 1a, 1h, 1c, 1c′′′′. MC: metal centered, MLCT: metal–ligand charge transfer, ILCT: intra-ligand charge transfer and LC: ligand centered.

Fig. 14 Electron density on Fe (ρ^Fe) for the 21 highest energy occupied orbitals near the frontier region for 1a, 1h, 1c, 1c′′′′. The KS orbitals with electron distribution ≥20% are shown in red and among these the doubly degenerate orbitals are labeled with *. The red * indicates nearly degenerate orbitals.

In the case of the 1c and 1c′′′′ complexes, mixed MLCT/ILCT transitions are observed in the lower-energy region of their absorption spectra. Additionally, a larger number of ILCT transitions are present in the spectrum of 1c′′′′ in comparison to 1c, since its HOMO–HOMO-5 orbitals are almost entirely ligand localized (see Fig. 14). The presence of a number of ILCT and mixed MLCT/ILCT transitions is likely behind the higher intensity observed for 1c′′′′. Similarly, the NH₂-functionalization of the extended π-conjugated thiophenes in 1f increases the intensity and redshifts the absorption spectrum in the visible region. The UV-vis spectrum of the NH₂-functionalized complex 1f as well as the electron density on Fe (ρ^Fe) for the highest energy occupied orbitals near the frontier region of this complex are shown in Fig. S27 and S28 in the ESI.†

4. Discussion

An ideal photosensitizer will possess multiple desirable properties. First, it will be stable in its ground, excited, and oxidized states, and undergo reversible oxidation and reduction. It will absorb light in the visible and near-IR region of the spectrum with a high molar absorption coefficient. A good photosensitizer will also possess long-lived photoactive excited states, and undergo efficient interfacial electron transfer into the semiconductor, if used in DSSC or DSPEC devices. Designing an ideal photosensitizer is a complex multi-dimensional optimization problem; an improvement in a single property is no guarantee of an overall good performance.⁶¹ It is, however, desirable to determine structure–property relationships for individual properties, as these can help us to formulate useful strategies for rational design of new chromophores.

Modification of metal polypyridine complexes by ligand substitutions is an important and commonly used approach in the molecular design of chromophores with desired properties.^1,62,63 For example, Ru(II) tris-heteroleptic complexes based on substituted bipyridine or 2-phenylpyridine ligands have shown improved absorption properties due to presence of multiple MC, MLCT, and ligand-centered bands in the visible region originating from different ligands.^64,65 Another common approach is to utilize substituents to extend the π-conjugated system of the polypyridines ligands, thus red-shifting the visible transitions and improving their molar extinction coefficients.⁶⁶ This work adopts a similar strategy to explore the impact of electron donor group substitutions on ground and excited state properties of Fe(II)-polypyridine complexes, with the aim to improve their light-absorption properties (i.e., achieve strong and broad absorption in the visible and near-IR region). A strong link between the electronic structure of the dyes, especially the amount of electron density on the semiconductor linker group in the excited state, and the initial IET rates^56,60 also allows us to explore the impact of the ligand modifications on the IET efficiency, albeit to a smaller (and less reliable) extent.

This work provides several important insights into the structure–property relationships in substituted [Fe(tpy)₂]²⁺ complexes. First, only one acceptor group used for the attachment of the dye to a semiconductor should be substituted on each terpyridine ligand, ideally at the 4′ position of the center pyridine ring. This will result in the highest electron density on the linker in the lowest energy MLCT state, in which the excited electron populates the LUMO. Substitution of strong electron donating groups, such as NH₂, onto the terpyridine scaffold further increases the amount of electron density on the acceptor group, which is expected to have a positive impact on the initial IET rates. Substitution of either of these groups does not have a considerable impact on the light-absorption properties of the [Fe(tpy)₂]²⁺ complex.

Second, π-conjugated donor groups, such as thiophene, selenophene, and furan, significantly improve the light absorption profile of the Fe(II)-polypyridine complexes under study. They do so by destabilizing the occupied π orbitals of the terpyridine ligand, making them energetically better aligned with the metal t_2g orbitals, causing a considerable increase in t_2g–π orbital mixing. This results in the presence of multiple mixed MLCT/ILCT transitions in the visible spectrum, shifting the absorption spectrum of the dye toward the lower energies, broadening it, as well as increasing the molar absorption coefficients of the visible transitions. Donor groups with more extended π conjugation (e.g., thienothiophene, dithienothiophene), will cause further destabilization of the ligand π orbitals and result in a ligand-centered HOMO. This type of “inverted ligand field”, in which the occupied antibonding orbitals are localized more on the ligand than the metal, was described previously⁶⁷ and more recently observed in a series of metallacarbatrane complexes of copper.⁶⁸ The “HOMO inversion” in the [Fe(tpy)₂]²⁺ complex introduces new ILCT transitions into the visible spectrum, further increases the intensity of transitions in the visible region, and results in an additional shift of the UV-vis spectrum toward lower energies. Similar improvement in the absorption properties due to the presence of new ILCT absorption bands was recently reported for a [Cr(tpy)₂]³⁺ complex substituted with aryl-based ligands.⁶⁹ It is likely that HOMO inversion is responsible for tuning the photophysical properties of this complex as well, however, electronic structure calculations would be necessary to confirm this. Several heteroleptic cyclometalated ruthenium complexes substituted by π-conjugated groups, such as triphenylamine-thiophene, 4-pyridine, and thiophene-2-carbaldehyde, prepared by Berlinguette and coworkers also displayed either the HOMO inversion⁷⁰ or at least a significant mixing between the metal t_2g and ligand-localized π orbitals.⁷¹ In the present work, the predicted improvement in the light absorption properties is more dramatic, likely due to the presence of a larger number of donor groups (four vs. one) as well as the presence of both electron withdrawing and donating groups in a single ligand.

Interestingly, substitution of π conjugated donor groups in Fe(II)-polypyridine complexes has only a small effect on the energies of the LUMO or the electron density on the carboxylic acid linker group, causing a slight decrease in both properties. Finally, an increase in the electron density on the linker group along with improved absorption profile in the visible region, can be achieved by combining both types of substituents into the NH₂-functionalized thiophenes (see complex 1c′′′′).

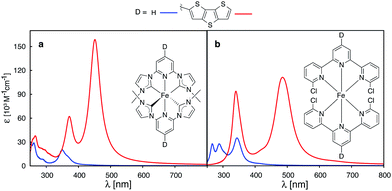
Recently, a great deal of attention has been focused on lengthening the lifetime of the MLCT states of iron polypyridine complexes, with the goal to improve the IET efficiency in Fe(II)-polypyridine sensitized semiconductors.^{14,28–30,72–74} Great strides have been made by utilization of N-heterocyclic carbene (NHC) ligands that significantly destabilize metal e_g σ* orbitals, increase the ligand field strength of the iron complex, and, consequently, lengthen the lifetime of photoactive ³MLCT states.⁷² An interesting question is whether one can further improve Fe–NHC complexes by increasing their ability to absorb sunlight via π-conjugated donor group substitutions. The calculated absorption spectrum for an unsubstituted [Fe(CNC)₂]²⁺ complex designed by Wärnmark and coworkers²⁸ is shown in Fig. 15a along with the spectrum for the same complex substituted with a dithienothiophene donor group (absorption spectra obtained with CAM-B3LYP can be found in the ESI, Fig. S29†). The DFT calculations predict a dramatic increase in the absorption intensity as well as shift to lower energies, in accordance with the calculations on the substituted [Fe(tpy)₂]²⁺ complex. Moreover, electron densities on Fe (ρ^Fe) for the higher energy occupied orbitals (see ESI, Fig. S30†), indicate significant mixing between the Fe t_2g and ligand π orbitals. The combination of improved light absorption and high IET quantum yield¹⁴ could make this complex an interesting synthetic target.

Fig. 15 Calculated UV-vis spectra of (a) [Fe(CNC)₂]²⁺ and (b) [Fe(dctpy)₂]²⁺. The spectra of their corresponding complexes with conjugated thiophenes substituted at the 4′ position of pyridine rings are shown in red.

A different approach to increasing the lifetime of photoactive MLCT states of Fe(II)-polypyridine complexes was taken by Damrauer and coworkers,^32,33 in which halogen substituents at 6 and 6′′ positions of the terpyridine ligand scaffold create a highly strained complex with a long-lived^5,7 MLCT state (∼16 ps). A downside of this approach is a decrease in the ligand field strength of the Fe complex, resulting in a complex with quintet ground state. This reduces the molar absorptivity in the visible region relative to the unsubstituted [Fe(tpy)₂]²⁺,^3,33 due to a smaller spatial overlap between the metal- and ligand-centered orbitals caused by longer metal–ligand bond lengths resulting from the high-spin ground state. Interestingly, the substitution of a conjugated thiophene at the 4′ positions of the terpyridine ligand improves the absorption spectrum of the strained complex as shown in Fig. 15b.

In summary, it is clear that light absorption in Fe(II) polypyridines can be fine-tuned by modifying interactions between the metal t_2g and ligand π orbitals. The occupied π orbitals of the terpyridine ligand are close enough in energy to the Fe t_2g orbitals that the strength of metal–ligand interactions as well as energetic ordering of the metal- and ligand-based orbitals can be adjusted by substitutions on the terpyridine ligand scaffold, resulting in dramatic consequences for light-absorption properties.

5. Conclusions

This work presents a computational study of the absorption properties of a series of [Fe(tpy)₂]²⁺ dyes substituted with various electron donor (furan, thiophene, selenophene, thienothiophene, dithienothiophene, NH₂) and acceptor groups (carboxylic acid, NO₂). The DFT and TD-DFT calculations indicate that the substitution on the tpy ligand scaffold with π-conjugated electron donating groups will shift the absorption spectrum to longer wavelengths, broaden the dye absorption in the visible region, and increase the molar extinction coefficient, leading to dyes that absorb sunlight more efficiently. Dramatic changes in the absorption properties of the substituted [Fe(tpy)₂]²⁺ are primarily due to destabilization of the ligand π orbital energies resulting either in extensive t_2g–π orbital mixing or, ultimately, the HOMO inversion, where the HOMO becomes fully ligand-localized.

Additional analysis suggests that substitution of only one electron acceptor group (i.e., the semiconductor linker group) on each tpy ligand will lead to the greatest increase of the electron density localized on this group in the lowest-energy MLCT state, potentially leading to more efficient IET. The presence of electron donating groups, such as NH₂, will lead to a further increase of electron density on the linker as well as the increase of the ligand-localized LUMO energy.

Finally, preliminary calculations on related complexes, such as [Fe(CNC)₂]²⁺ and [Fe(dctpy)₂]²⁺, indicate that the HOMO inversion is a viable strategy for improving the absorption properties of a wider class of iron polypyridine compounds.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We gratefully acknowledge support from the U.S. Army Research Office under Contract W911NF-15-1-0124. D. E. T. also thanks the ARO High School Research Apprenticeship Program (HSAP) for support.

References

1. S. Ardo and G. J. Meyer, Chem. Soc. Rev., 2009, 38, 115–164.
2. M. Grätzel, Inorg. Chem., 2005, 44, 6841–6851.
3. D. L. Ashford, M. K. Gish, A. K. Vannucci, M. K. Brennaman, J. L. Templeton, J. M. Papanikolas and T. J. Meyer, Chem. Rev., 2015, 115, 13006–13049.
4. A. Hagfeldt, G. Boschloo, L. Sun, L. Kloo and H. Pettersson, Chem. Rev., 2010, 110, 6595–6663.
5. B. O'Regan and M. Gratzel, Nature, 1991, 353, 737–740.
6. M. K. Nazeeruddin, A. Kay, I. Rodicio, R. Humphry-Baker, E. Mueller, P. Liska, N. Vlachopoulos and M. Graetzel, J. Am. Chem. Soc., 1993, 115, 6382–6390.
7. K. Kalyanasundaram and M. Grätzel, Coord. Chem. Rev., 1998, 177, 347–414.
8. C.-Y. Chen, M. Wang, J.-Y. Li, N. Pootrakulchote, L. Alibabaei, C.-h. Ngoc-le, J.-D. Decoppet, J.-H. Tsai, C. Grätzel, C.-G. Wu, S. M. Zakeeruddin and M. Grätzel, ACS Nano, 2009, 3, 3103–3109.
9. S. K. Deb, R. Ellingson, S. Ferrere, A. J. Frank, B. A. Gregg, A. J. Nozik, N. Park, G. Schlichthorl and A. Zaban, AIP Conf. Proc., 1999, 462, 473–482.
10. S. Ferrere, Chem. Mater., 2000, 12, 1083–1089.
11. S. Ferrere, Inorg. Chim. Acta, 2002, 329, 79–92.
12. S. Ferrere and B. A. Gregg, J. Am. Chem. Soc., 1998, 120, 843–844.
13. M. Yang, D. W. Thompson and G. J. Meyer, Inorg. Chem., 2000, 39, 3738–3739.
14. T. C. Harlang, Y. Liu, O. Gordivska, L. A. Fredin, C. S. Ponseca Jr, P. Huang, P. Chabera, K. S. Kjaer, H. Mateos, J. Uhlig, R. Lomoth, R. Wallenberg, S. Styring, P. Persson, V. Sundstrom and K. Warnmark, Nat. Chem., 2015, 7, 883–889.
15. C. Creutz, M. Chou, T. L. Netzel, M. Okumura and N. Sutin, J. Am. Chem. Soc., 1980, 102, 1309–1319.
16. E. A. Juban, A. L. Smeigh, J. E. Monat and J. K. McCusker, Coord. Chem. Rev., 2006, 250, 1783–1791.
17. J. E. Monat and J. K. McCusker, J. Am. Chem. Soc., 2000, 122, 4092–4097.
18. A. L. Smeigh, M. Creelman, R. A. Mathies and J. K. McCusker, J. Am. Chem. Soc., 2008, 130, 14105–14107.
19. L. L. Jamula, A. M. Brown, D. Guo and J. K. McCusker, Inorg. Chem., 2014, 53, 15–17.
20. D. N. Bowman, A. Bondarev, S. Mukherjee and E. Jakubikova, Inorg. Chem., 2015, 54, 8786–8793.
21. I. M. Dixon, F. Alary, M. Boggio-Pasqua and J.-L. Heully, Inorg. Chem., 2013, 52, 13369–13374.
22. I. M. Dixon, G. Boissard, H. Whyte, F. Alary and J.-L. Heully, Inorg. Chem., 2016, 55, 5089–5091.
23. I. M. Dixon, S. Khan, F. Alary, M. Boggio-Pasqua and J. L. Heully, Dalton Trans., 2014, 43, 15898–15905.
24. D. C. Ashley and E. Jakubikova, Coord. Chem. Rev., 2017, 337, 97–111.
25. N. Huse, H. Cho, K. Hong, L. Jamula, F. M. F. de Groot, T. K. Kim, J. K. McCusker and R. W. Schoenlein, J. Phys. Chem. Lett., 2011, 2, 880–884.
26. H. Cho, M. L. Strader, K. Hong, L. Jamula, E. M. Gullikson, T. K. Kim, F. M. F. de Groot, J. K. McCusker, R. W. Schoenlein and N. Huse, Faraday Discuss., 2012, 157, 463.
27. S. Mukherjee, D. N. Bowman and E. Jakubikova, Inorg. Chem., 2015, 54, 560–569.
28. Y. Liu, T. Harlang, S. E. Canton, P. Chabera, K. Suarez-Alcantara, A. Fleckhaus, D. A. Vithanage, E. Goransson, A. Corani, R. Lomoth, V. Sundstrom and K. Wärnmark, Chem. Commun., 2013, 49, 6412–6414.
29. Y. Liu, K. S. Kjær, L. A. Fredin, P. Chábera, T. Harlang, S. E. Canton, S. Lidin, J. Zhang, R. Lomoth, K.-E. Bergquist, P. Persson, K. Wärnmark and V. Sundström, Chem.–Eur. J., 2015, 21, 3628–3639.
30. L. A. Fredin, M. Pápai, E. Rozsályi, G. Vankó, K. Wärnmark, V. Sundström and P. Persson, J. Phys. Chem. Lett., 2014, 5, 2066–2071.
31. L. Liu, T. Duchanois, T. Etienne, A. Monari, M. Beley, X. Assfeld, S. Haacke and P. C. Gros, Phys. Chem. Chem. Phys., 2016, 18, 12550–12556.
32. S. M. Fatur, S. G. Shepard, R. F. Higgins, M. P. Shores and N. H. Damrauer, J. Am. Chem. Soc., 2017, 139, 4493–4505.
33. S. G. Shepard, S. M. Fatur, A. K. Rappé and N. H. Damrauer, J. Am. Chem. Soc., 2016, 138, 2949–2952.
34. T. C. Motley and G. J. Meyer, NPG Asia Mater., 2016, 8, e261.
35. E. Galoppini, Nat. Chem., 2015, 7, 861–862.
36. T. Duchanois, T. Etienne, C. Cebrián, L. Liu, A. Monari, M. Beley, X. Assfeld, S. Haacke and P. C. Gros, Eur. J. Inorg. Chem., 2015, 2015, 2469–2477.
37. D. N. Bowman, S. Mukherjee, L. J. Barnes and E. Jakubikova, J. Phys.: Condens. Matter, 2015, 27, 134205.
38. M. Pastore, T. Duchanois, L. Liu, A. Monari, X. Assfeld, S. Haacke and P. C. Gros, Phys. Chem. Chem. Phys., 2016, 18, 28069–28081.
39. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
40. A. D. Becke, J. Chem. Phys., 1993, 98, 1372.
41. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
42. M. Kaupp, P. v. R. Schleyer, H. Stoll and H. Preuss, J. Chem. Phys., 1991, 94, 1360–1366.
43. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222.
44. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
45. G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110.
46. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, 2009.
47. R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464.
48. M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, J. Chem. Phys., 1998, 108, 4439–4449.
49. R. E. Stratmann, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 1998, 109, 8218–8224.
50. M. Cossi, G. Scalmani, N. Rega and V. Barone, J. Chem. Phys., 2002, 117, 43–54.
51. E. Jakubikova, W. Chen, D. M. Dattelbaum, F. N. Rein, R. C. Rocha, R. L. Martin and E. R. Batista, Inorg. Chem., 2009, 48, 10720–10725.
52. D. N. Bowman, J. H. Blew, T. Tsuchiya and E. Jakubikova, Inorg. Chem., 2013, 52, 8621–8628.
53. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
54. A. D. Laurent and D. Jacquemin, Int. J. Quantum Chem., 2013, 113, 2019–2039.
55. R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833.
56. E. Jakubikova and D. N. Bowman, Acc. Chem. Res., 2015, 48, 1441–1449.
57. G. Zhang and C. B. Musgrave, J. Phys. Chem. A, 2007, 111, 1554–1561.
58. N. S. Mills, A. Levy and B. F. Plummer, J. Org. Chem., 2004, 69, 6623–6633.
59. L. G. C. Rego and V. S. Batista, J. Am. Chem. Soc., 2003, 125, 7989–7997.
60. C. Liu and E. Jakubikova, Chem. Sci., 2017, 8, 5979–5991.
61. C. M. Ip, A. Eleuteri and A. Troisi, Phys. Chem. Chem. Phys., 2014, 16, 19106–19110.
62. A. O. Adeloye and P. A. Ajibade, Molecules, 2014, 19, 12421–12460.
63. H. Shalan, A. Colbert, T. T. Nguyen, M. Kato and L. Cheruzel, Inorg. Chem., 2017, 56, 6558–6564.
64. P. G. Bomben, T. J. Gordon, E. Schott and C. P. Berlinguette, Angew. Chem., 2011, 123, 10870–10873.
65. A. Juris, S. Campagna, V. Balzani, G. Gremaud and A. Von Zelewsky, Inorg. Chem., 1988, 27, 3652–3655.
66. P. Wang, C. Klein, R. Humphry-Baker, S. M. Zakeeruddin and M. Grätzel, J. Am. Chem. Soc., 2005, 127, 808–809.
67. R. Hoffmann, S. Alvarez, C. Mealli, A. Falceto, T. J. Cahill 3rd, T. Zeng and G. Manca, Chem. Rev., 2016, 116, 8173–8192.
68. S. Ruccolo, M. Rauch and G. Parkin, Chem. Sci., 2017, 8, 4465–4474.
69. J. C. Barbour, A. J. I. Kim, E. deVries, S. E. Shaner and B. M. Lovaasen, Inorg. Chem., 2017, 56, 8212–8222.
70. K. C. D. Robson, B. D. Koivisto, A. Yella, B. Sporinova, M. K. Nazeeruddin, T. Baumgartner, M. Grätzel and C. P. Berlinguette, Inorg. Chem., 2011, 50, 5494–5508.
71. P. G. Bomben, B. D. Koivisto and C. P. Berlinguette, Inorg. Chem., 2010, 49, 4960–4971.
72. Y. Liu, P. Persson, V. Sundstrom and K. Warnmark, Acc. Chem. Res., 2016, 49, 1477–1485.
73. W. Zhang, K. S. Kjaer, R. Alonso-Mori, U. Bergmann, M. Chollet, L. A. Fredin, R. G. Hadt, R. W. Hartsock, T. Harlang, T. Kroll, K. Kubicek, H. T. Lemke, H. W. Liang, Y. Liu, M. M. Nielsen, P. Persson, J. S. Robinson, E. I. Solomon, Z. Sun, D. Sokaras, T. B. van Driel, T. C. Weng, D. Zhu, K. Warnmark, V. Sundstrom and K. J. Gaffney, Chem. Sci., 2017, 8, 515–523.
74. L. A. Fredin, K. Wärnmark, V. Sundström and P. Persson, ChemSusChem, 2016, 9, 667–675.

---

Footnotes

† Electronic supplementary information (ESI) available: Electronic properties, molecular orbitals, excited state assignments, and UV-vis spectra calculated with CAM-B3LYP functional. Cartesian coordinates for all complexes provided in an xyz file format. See DOI: 10.1039/c7sc02926h

‡ Current address: North Carolina State University, Raleigh, NC 27695, USA.

---