Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Inside information on xenon adsorption in porous organic cages by NMR†
Sanna
Komulainen
a,
Juho
Roukala
 a,
Vladimir V.
Zhivonitko
b,
Muhammad Asadullah
Javed
a,
Linjiang
Chen
c,
Daniel
Holden
c,
Tom
Hasell
a,
Vladimir V.
Zhivonitko
b,
Muhammad Asadullah
Javed
a,
Linjiang
Chen
c,
Daniel
Holden
c,
Tom
Hasell
 c,
Andrew
Cooper
c,
Perttu
Lantto
c,
Andrew
Cooper
c,
Perttu
Lantto
 a and
Ville-Veikko
Telkki
a and
Ville-Veikko
Telkki
 *a
*a
aNMR Research Unit, University of Oulu, P.O.Box 3000, 90014 Oulu, Finland. E-mail: ville-veikko.telkki@oulu.fi
bLaboratory of Magnetic Resonance Microimaging, International Tomography Center SB RAS, Department of Natural Sciences, Novosibirsk State University, Instututskaya St. 3A, Pirogova St. 2, 630090 Novosibirsk, Russia
cDepartment of Chemistry, Centre for Materials Discovery, University of Liverpool, Crown Street, Liverpool L69 7ZD, UK
First published on 14th June 2017
Abstract
A solid porous molecular crystal formed from an organic cage, CC3, has unprecedented performance for the separation of rare gases. Here, xenon was used as an internal reporter providing extraordinarily versatile information about the gas adsorption phenomena in the cage and window cavities of the material. 129Xe NMR measurements combined with state-of-the-art quantum chemical calculations allowed the determination of the occupancies of the cavities, binding constants, thermodynamic parameters as well as the exchange rates of Xe between the cavities. Chemical exchange saturation transfer (CEST) experiments revealed a minor window cavity site with a significantly lower exchange rate than other sites. Diffusion measurements showed significantly reduced mobility of xenon with loading. 129Xe spectra also revealed that the cage cavity sites are preferred at lower loading levels, due to more favourable binding, whereas window sites come to dominate closer to saturation because of their greater prevalence.
Introduction
Porous materials are ubiquitous and they have a wide range of important applications, including molecular separations and catalysis.1 They provide an alternative means to capture greenhouse gases, such as CO2 and CH4, as well as valuable noble gases (Xe, Ar, Kr), being potentially more energy efficient than traditional cryogenic methods. Zeolites,2 metal–organic frameworks (MOFs),3 covalent organic frameworks (COFs)4 and porous polymers5 have been studied intensively for selective isolation of a certain component in a gas mixture. So far, none of them has supplanted zeolites, although each has their own strengths in specific cases.Xenon is widely used in optics and medical applications, and it plays important role in nuclear fission processes.6 However, its extraction from air is difficult because of the low abundance in the atmosphere (0.087 ppm by volume)6b and its inert nature, leading to a high commercial price. Because of its inertness, the selective isolation of xenon by porous materials requires tight size selectivity.7 Additionally, the adsorbent should have a high adsorption capacity for commercial utilization.
Recently, it was reported that an organic cage molecule, CC3,8 has unprecedented performance in the solid state for the separation of rare gases.9 This selectivity arises from precise size match between the rare gas and the organic cage. Separation of krypton, xenon and argon from air at concentrations of only a few parts per million has become feasible. The tetrahedral CC3 cage is structured by imine bonds that connect rigid aromatic rings to the more flexible cyclohexane linkers (Fig. 1A). The cage molecule packs into a crystalline structure forming an interconnected 3D pore structure via cage windows (Fig. 1B). The molecular framework has the largest inclusion sphere of 4.4 Å in the cage cavity, which is close to the diameter of xenon (4.10 Å) and other higher-mass noble gases. The narrowest point in the pore channels between the cage and window cavities is only 3.6 Å in diameter; that is, smaller than xenon. However, the vibrational motion of the cage molecules allows the movement of xenon between the cavities. Even SF6 with the kinetic diameter of 5.5 Å can enter the cage because of thermal motion and flexibility of these organic crystals.10
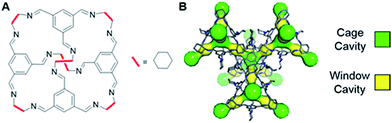 | ||
| Fig. 1 (A) Chemical structure of CC3 cage. (B) 3D crystal and cavity structure of CC3 material. The cage and window cavities are illustrated by green and yellow, respectively. | ||
Xenon has a 129Xe isotope with spin-1/2 as well as relatively high natural abundance (26%) and NMR receptivity. The chemical shift of 129Xe is extremely sensitive to its local environment, and its nuclear spin polarization can be increased by several orders of magnitude by spin-exchange optical pumping (SEOP). Therefore, it is an excellent inert probe molecule in NMR and magnetic resonance imaging (MRI) applications in chemistry, biochemistry, materials science and medicine.11 It has been exploited, for example, in MRI of lungs,12 microfluidic flow imaging,13 investigation of liquid crystals,14 polymers,15 and ionic liquids,16 as well as the determination of pore sizes of porous media.17 Xenon trapped inside of a cage molecule (typically a cryptophane cage), which is functionalized to bind to a specific target, is also used as an NMR biosensor. Combination of hyperpolarization and chemical exchange saturation transfer (CEST)18 techniques enables very high-sensitivity, background-free molecular imaging.19 Finding alternative, optimized and lower cost cages for xenon biosensor applications is also an important branch of research.20 Hyperpolarized CEST technique has also been exploited in materials research, and it enables the observation of Xe-binding sites that are otherwise invisible by direct detection methods in, e.g., spores, proteins, cryptophane and cucurbituril.21
Here, we use xenon, via its rich chemical and dynamical 129Xe NMR information, as an internal probe for adsorption phenomena in CC3. We show that the combination of various experimental 129Xe NMR techniques with the state-of-the-art quantum chemical calculations provide exceptionally versatile information about binding, occupancies, dynamics and equilibrium of xenon in CC3.
Results and discussion
Samples
Three homochiral CC3-R9 samples with different xenon loadings were prepared. The samples contained approximately 4 cm of solid CC3-R powder and Xe gas in a sealed 5 mm sample tube (see details in the ESI†). The Xe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CC3-R molar ratio for the low loading (LL), middle loading (ML) and high loading (HL) samples were 0.10
CC3-R molar ratio for the low loading (LL), middle loading (ML) and high loading (HL) samples were 0.10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 0.52
1, 0.52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2.4
1 and 2.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively. The last sample represents an almost fully saturated material, in which nearly all three binding sites (one in each cage cavity plus four more shared between two cages in the surrounding window cavities) are occupied by xenon.
1, respectively. The last sample represents an almost fully saturated material, in which nearly all three binding sites (one in each cage cavity plus four more shared between two cages in the surrounding window cavities) are occupied by xenon.
129Xe NMR spectra
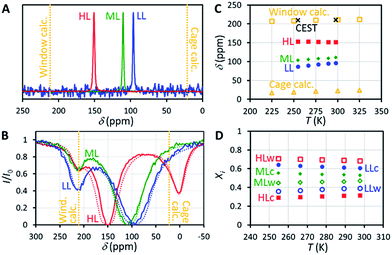
129Xe NMR spectra of the samples measured at 14.1 T (resonance frequency of 129Xe is 166 MHz) at room temperature, shown in Fig. 2A, include a single, relatively narrow (linewidth 1–2 ppm) and symmetrical peak, indicating that the chemical exchange between the cage and window cavities is fast in NMR time scale.22 Even below 160 K, the linewidth is so narrow (about 10 ppm) that the system is clearly in the fast exchange region (see Fig. S2 in the ESI†). No signal of free gas around 0 ppm is visible because of the exceptionally high adsorption affinity of xenon in CC3-R.Chemical shift of 129Xe in CC3-R increases with loading (see Fig. 2C). For the HL sample, the shift is almost constant (slope −0.045 ppm K−1) over the whole measurement temperature region (255–298 K), while for the lower loading samples it increases with temperature, with the slopes of +0.160 and +0.219 ppm K−1 for the ML and LL samples, respectively.
Quantum chemical calculations
In order to understand the experimental observations, we performed quantum chemical density functional theory (DFT) calculations of the chemical shift of xenon (with respect to atomic Xe) inside static model structures of the cage and window cavities (see Fig. S17†). Nonrelativistic (NR) potential energy and NMR shielding calculations were performed using the dispersion-corrected (D3)23 hybrid BHandHLYP24 functional, which has been demonstrated to provide the best estimation for NR shielding contribution to both heavy element chemical shifts in molecules25 and for Xe chemical shift inside cavities.20,26 DFT potential energy and NMR shielding calculations were performed with the Turbomole27 code, whereas the Amsterdam Density Functional28 program package was used for relativistic calculations of the Xe NMR shielding at the zeroth-order regular approximation level of theory including scalar (SR-ZORA) or both scalar and spin–orbit (SO) relativistic effects (SO-ZORA)28 (see details in the ESI†). All-electron co-r20,29/def2-SVP30 (NR) and jpcl/TZP31 (ZORA) basis sets were used for Xe/other atoms.First, the best static (Stat) reference value for Xe chemical shift was computed at the center of the cavity at the SO-ZORA/BHandHLYP level. Thereafter the dynamical contribution (Dyn) due to Xe motion was estimated as a function of temperature via canonical NVT Monte Carlo statistical simulation averaging on three-dimensional surfaces of NR chemical shift and potential energy (see Fig. S21†). The effects due to periodic cage and its dynamics or different Xe loadings in neighboring cavities were not taken into account in these simulations.
The resulting overall chemical shift values are shown in Fig. 2C. Calculated chemical shifts and their dynamic contributions at different temperatures are shown in Tables S5 and S6.† At T = 300 K, the calculated 129Xe chemical shift in the cage cavity is only 22 ppm (total = Stat + Dyn = −21 ppm + 43 ppm), while it is 211 ppm (181 ppm + 30 ppm) in the smaller window cavity. We note that similar 129Xe chemical shift calculations for other cavity systems have proven to be in very good agreement with experiments,20,26a implying good accuracy of current values as well. The relativity is an important phenomenon for the Xe chemical shift in CC3-R, since at SO-ZORA level it increases the cage and window shifts by ca. +3 ppm and +36 ppm, respectively. As the relativity has a larger role in the window cavity, it increases the chemical shift difference between the cavities by ca. +32 ppm (19%). While most of this difference is due to SR, also SO effects are important as their absolute contribution in the window cavity is notable, ca. 10 ppm, and about 29% of the total relativistic effect. This differs from the previously studied cavities, e.g., Buckminster fullerene,26a Fe4L6 metallosupramolecular,20 and fluorophenol clathrate cavities,26b where the SO contributions were small, like in the CC3-R cage cavity. However, the shape of the 3D Xe shift surface and, hence, the thermal effect, are expected not to be affected much by relativity. Thus the temperature dependence of the Xe shift is well estimated around room temperature to be +0.064 ppm K−1 and +0.051 ppm K−1 for the cage and window cavities, respectively. The values are three to four times smaller than the slope of the experimental chemical shift observed for the ML and LL samples, while the slope for the HL sample has a different sign. Therefore, changes in the relative population of the cavities have a dominant role in explaining the temperature dependence of the shift.
The effect of loading, i.e., the occupancy of nearby cavities, on the chemical shift was also modeled. The effect is quite similar in both cavities, ca. −14 ppm (see Table S7†). Therefore, it has an insignificant effect on the chemical shift difference between cavities. The structure of the CC3 material may also change with loading due to the flexibility of the material. This may have some influence on the chemical shift as well.17e
Population of the cage and window cavities
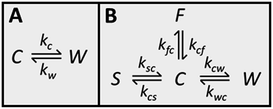
Because CC3-R contains two binding sites for Xe, the cage and window cavities, it is justified to approximate the system by a two-site exchange model (see Fig. 4A).32 In the fast exchange region, the experimentally observed 129Xe chemical shift is the weighted average of the shifts in the cage and window cavities (δC and δW):| δ = XCδC + XWδW. | (1) |
Eqn (1) makes it possible to extract the relative populations of xenon atoms in the cage and window cavities, XC and XW, from the experimental chemical shifts, using the calculated δC and δW values (Fig. 2C). The resulting populations are shown in Fig. 2D. Relative population of Xe in the window cavity increases with loading: at room temperature, the populations are 39%, 47% and 68% for the LL, ML and HL samples, respectively. Consequently, the larger cage cavity is a more favorable adsorption site for xenon, and the window cavity becomes more occupied only at higher loadings.
Exchange between the cage and window cavities
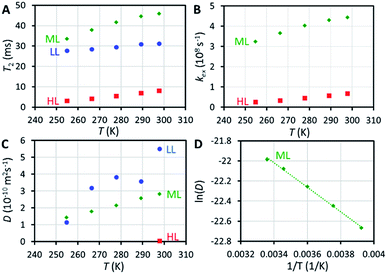
129Xe relaxation measurements provide deeper insight into exchange phenomena. At room temperature, T1 relaxation time of xenon adsorbed in the HL sample (48 s) is significantly longer than in the LL and ML samples (14 and 16 s, respectively), implying significantly reduced mobility of xenon (slower exchange between cage and window cavities) close to the sample saturation, because xenon atoms cannot pass each other in the small cavities. Variable temperature T1 data (Fig. S4†) show an interesting non-linear behavior of T1 of xenon in the HL sample with a maximum around 270 K, deviating from the linearly increasing T1 observed for the LL and ML samples.T 2 relaxation time of xenon in the HL sample (8 ms at room temperature) is significantly shorter than in the LL and ML samples (31 and 46 ms, respectively). Surprisingly, T2 value of the LL sample is between the values of the HL and ML samples. The slope of the T2 with respect to temperature is also smaller in the LL sample than in the ML and HL samples (see Fig. 3A). We interpret that the effect of interparticle exchange on T2 is significant in the LL sample due to the high mobility of xenon (revealed by the diffusion experiments described below), explaining the differing T2 behavior. Because the effect appears to be insignificant in the ML and HL samples, a two-site exchange model (Fig. 4A) can be used in the T2 relaxation time analysis. In the fast exchange limit the transverse relaxation rate constant is given by33
| R2 = XCXWΔω2/kex. | (2) |
Four-site exchange
129Xe CEST spectra18 of the samples reveal additional details of the exchange processes and sample structure. In these experiments, the sample was first irradiated by a long continuous wave (CW) pulse (pulse length 5–10 s), followed by a hard π/2 excitation pulse and signal detection. The amplitudes of the signal as a function of the offset of the CW pulse, i.e., the CEST spectra for LL, ML and HL samples are shown in Fig. 2B. In addition to the main dips at the same chemical shifts with the signals observed in the conventional spectra (Fig. 2A), all the CEST spectra include another dip around 211 ppm. The chemical shift of the dip matches perfectly with the shift of xenon in the window cavity predicted by the calculations (211.1 ppm). Therefore, we interpret that the dip arises from the window cavity. On the other hand, the perfect agreement may be considered to indicate also the high accuracy of the calculations. However, the dip has to arise from such window sites, from which xenon exchange to the cage cavities is slow, because separate signals can be observed in the CEST spectra only in the slow or intermediate exchange region, similarly to the conventional spectra.18 Therefore we call these cavities “stuck window cavities”. The population of the stuck window cavities must be very small, because their signal is not visible even in the conventional spectrum measured with a high number of scans, with signal-to-noise ratio (SNR) of 4000 (see Fig. S1†). The stuck window signal becomes observable in the CEST spectrum because of significant CEST signal amplification effect of a minor site, being several orders of magnitude.18In the case of the HL sample, there is a third dip around 0.6 ppm, which is interpreted to arise from free xenon gas between the particles. In fact, a small free gas signal is observed at the same chemical shift also in the high SNR conventional spectrum (see Fig. S1†). The free gas signal is observable from the HL sample, because of two reasons: firstly, the amount of free gas is higher than in the other samples, and, secondly, the exchange between free and adsorbed sites is slower, because almost all the adsorption sites are occupied in the HL sample.
The CEST observations suggest that, instead of the two-site model, a four-site exchange model is more precisely characterizing the xenon exchange phenomena in CC3-R. As illustrated in Fig. 4B, the cage cavities are connected to three other sites: the window cavities, the stuck window cavities and the free gas pool. On the other hand, these three sites are not directly connected to each other, because xenon can move from one window cavity to another only via a cage cavity. When a free gas atom enters a CC3-R crystal, it has to arrive first in a cage cavity, because window cavities exist only in between the cage molecules. Simulated CEST spectra (see Fig. 2B and ESI†) suggest that the population of the stuck window cavities is between 0.02% and 0.3%, and the exchange rate between the stuck window and cage cavities is about 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s−1. The stuck window cavities may arise from crystal defects, such as dislocations and grain boundaries, in CC3-R,34 and the population of these cavities may reflect the amount of defects in the material. Good agreement between the measured and simulated CEST spectra confirm that the exchange rates determined from the T2 values are reliable. The population of the free gas site is 0.9%, and the exchange rate between the free gas and cage cavities is about 14
000 s−1. The stuck window cavities may arise from crystal defects, such as dislocations and grain boundaries, in CC3-R,34 and the population of these cavities may reflect the amount of defects in the material. Good agreement between the measured and simulated CEST spectra confirm that the exchange rates determined from the T2 values are reliable. The population of the free gas site is 0.9%, and the exchange rate between the free gas and cage cavities is about 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s−1.
000 s−1.
Diffusion of xenon in CC3-R
NMR is one of the rare methods for measuring self-diffusion of molecules without an invasive tracer.35 We investigated the diffusion of xenon in CC3-R by 129Xe pulsed-field-gradient stimulated-echo (PGSTE)36 experiments, using bipolar gradients minimizing the effect of background gradients.37 Diffusion coefficient (D) of xenon in CC3-R is many orders of magnitude smaller than that of free xenon (5.3 × 10−6 m2 s−1),38 and it decreases significantly with loading: at room temperature, D is 5.5 × 10−10, 2.8 × 10−10 and 4.1 × 10−12 m2 s−1 for the LL, ML and HL samples, respectively (see Fig. 3C). D in the HL sample, which is almost saturated, is two orders of magnitude smaller than in the LL sample. This is a consequence of single-file nature of the diffusion:39 xenon atoms cannot pass each other in the small cavities, and therefore high loading significantly restricts the moving of xenon atoms. Mean distance diffused by xenon atoms in the diffusion time Δ, characterized by the square root of the mean-square displacement (MSD), (2DΔ)1/2 = 2–3 μm, is on the same order with the size of smallest particles in the sample (particle sizes between 0.5 and 50 μm). Because of this, the second diffusion component was observed (see Fig. S12 and S13†), arising from interparticle exchange, and characterized by the diffusion coefficient of about 2 × 10−9 m2 s−1. On the other hand, because most of the particles are much larger than the mean diffusion distance, the first diffusion coefficient reflects pure intraparticle diffusion.The activation energy for diffusion of xenon in the ML sample was determined by fitting an Arrhenius function to the variable temperature D values (see Fig. 3D and S14†). The resulting activation energy is (10.1 ± 0.3) kJ mol−1. Chen et al.9 fitted stretched exponential model to adsorption isotherms, and obtained activation energies ranging from 6.0 to 17.5 kJ mol−1 for xenon loading of 0 to 2.0 mmol g−1. Bearing in mind the loading of the ML sample (0.48 mmol g−1), our NMR result is in good agreement with the adsorption measurements.
In long, straight, cylindrical channels, which are not interconnected, single-file diffusion MSD is proportional to square root of time 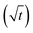 instead of normal Fickian t dependence,39 leading to an apparent D, which is inversely proportional to the square-root of the diffusion time, Δ−1/2. The value of D of the HL sample, however, turned out to be independent of Δ within experimental error. Because CC3-R is composed of three-dimensional interconnected network of pores, instead of straight cylinders, the single-file diffusion is not present itself in the same manner as in the case of non-interconnected straight channels.
instead of normal Fickian t dependence,39 leading to an apparent D, which is inversely proportional to the square-root of the diffusion time, Δ−1/2. The value of D of the HL sample, however, turned out to be independent of Δ within experimental error. Because CC3-R is composed of three-dimensional interconnected network of pores, instead of straight cylinders, the single-file diffusion is not present itself in the same manner as in the case of non-interconnected straight channels.
Equilibrium between bound and free xenon
The equilibrium of xenon between bound and free gas phases was studied in the ML and HL samples at the temperature range of 255–298 K by comparing the integrals of 129Xe signal measured from the CC3-R and gas regions of the sample (see ESI†). The gas region was measured by turning the sample upside down (a piece of glass wool prevented the moving of the cage material). The mole fractions of xenon in the gas phase and cage were calculated from the integrals, using the known overall amounts of Xe and CC3-R added into the samples. Van't Hoff analysis of the equilibrium constants yielded the following values for the changes of Gibbs free energy, enthalpy and entropy, for ML and HL samples, respectively: ΔG = −(30 ± 4) and −(25.9 ± 1.4) kJ mol−1, ΔH = −(9 ± 2) and −(1.8 ± 0.7) kJ mol−1 and ΔS = (71 ± 6) and (81 ± 3) J mol−1 K−1. The binding is both enthalpy and entropy driven. Enthalpy is significantly lower for the HL sample.Equilibrium between xenon in the cage and window cavities
Based on the populations of the cage and window cavities shown in Fig. 2D, we were able to investigate the equilibrium of xenon between the cage and window cavities (see ESI†). In the cases of the LL and ML samples, the cage cavity binding is favored, with the changes of Gibbs free energy, enthalpy and entropy of ΔG = −(4.4 ± 0.3) and −(2.5 ± 0.4) kJ mol−1, ΔH = −(3.7 ± 0.2) and −(1.6 ± 0.2) kJ mol−1 and ΔS = (2.5 ± 0.6) and (2.9 ± 0.6) J mol−1 K−1, respectively. However, in the case of the almost saturated HL sample, the binding affinities of these sites are almost equal, and the corresponding values are ΔG = +(0.9 ± 0.6) kJ mol−1, ΔH = +(8.0 ± 0.3) kJ mol−1 and ΔS = (24 ± 1) J mol−1 K−1.Conclusions
Combined state-of-the-art experimental and computational 129Xe analysis provided extraordinarily versatile inside information on the adsorption of xenon in a crystalline porous organic cage, CC3. It enabled us to determine the populations of the cage and window cavities as well as exchange rates between them, diffusion coefficients and activation energy of diffusion, and thermodynamic parameters of the equilibrium between the bound and free xenon as well as between xenon in the cage and window cavities. Furthermore, the analysis revealed a minor “stuck” window cavity site, which may be associated with crystal defects. The analysis improves significantly the understanding of the extraordinarily high adsorption of noble gases in the organic cages, facilitating their use in gas separation as well as other conceivable applications, such as biosensor applications.Acknowledgements
The authors are grateful to J. Vaara, J. Lounila, A. Kantola, M. E. Briggs, S. Y. Chong, and M. A. Little for useful discussions. V.-V. T. (grant numbers 289649 and 294027) and P. L. (grant number 285666) acknowledge the Academy of Finland for financial support. We acknowledge funding from the Engineering and Physical Sciences Research Council (EPSRC) (grants EP/H000925/1 and EP/N004884/1) and the European Research Council under the European Union's Seventh Framework Programme (FP/2007-2013)/ERC through grant agreement no. 321156 (ERC-AG-PE5-ROBOT). T. H. thanks the Royal Society for a University Research Fellowship.References
- A. G. Slater and A. I. Cooper, Science, 2015, 348, 988 CrossRef CAS PubMed.
- P. A. Wright, Microporous Framework Solids, Royal Society of Chemistry, Cambridge, 2008 Search PubMed.
- (a) M. Kondo, T. Yoshitomi, H. Matsuzaka, S. Kitagawa and K. Seki, Angew. Chem., Int. Ed., 1997, 36, 1725–1727 CrossRef CAS; (b) A. K. Cheetham, G. Férey and T. Loiseau, Angew. Chem., Int. Ed., 1999, 38, 3268–3292 CrossRef CAS; (c) H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444 CrossRef PubMed.
- A. P. Côté, A. I. Benin, N. W. Ockwig, M. O'Keeffe, A. J. Matzger and O. M. Yaghi, Science, 2005, 310, 1166–1170 CrossRef PubMed.
- A. Thomas, Angew. Chem., Int. Ed., 2010, 49, 8328–8344 CrossRef CAS PubMed.
- (a) W. M. Stacey, Nuclear Reactor Physics, Wiley-VCH, Weinheim, 2007 Search PubMed; (b) F. G. Kerry, Industrial Gas Handbook: Gas Separation and Purification, CRC Press, Boca Raton, 2007 Search PubMed.
- T. Mitra, K. E. Jelfs, M. Schmidtmann, A. Ahmed, S. Y. Chong, D. J. Adams and A. I. Cooper, Nat. Chem., 2013, 5, 276–281 CrossRef CAS PubMed.
- T. Tozawa, J. T. A. Jones, S. I. Swamy, S. Jiang, D. J. Adams, S. Shakespeare, R. Clowes, D. Bradshaw, T. Hasell, S. Y. Chong, C. Tang, S. Thompson, J. Parker, A. Trewin, J. Bacsa, A. M. Z. Slawin, A. Steiner and A. I. Cooper, Nat. Mater., 2009, 8, 973–978 CrossRef CAS PubMed.
- L. Chen, L. Chen, P. S. Reiss, S. Y. Chong, D. Holden, K. E. Jelfs, T. Hasell, M. A. Little, A. Kewley, M. E. Briggs, A. Stephenson, K. M. Thomas, J. A. Armstrong, J. Bell, J. Busto, R. Noel, J. Liu, D. M. Strachan, P. K. Thallapally and A. I. Cooper, Nat. Mater., 2014, 13, 954–960 CrossRef CAS PubMed.
- T. Hasell, M. Miklitz, A. Stephenson, M. A. Little, S. Y. Chong, R. Clowes, L. Chen, D. Holden, G. A. Tribello, K. E. Jelfs and A. I. Cooper, J. Am. Chem. Soc., 2016, 138, 1653–1659 CrossRef CAS PubMed.
- (a) K. Bartik, P. Choquet, A. Constantinesco, G. Duhamel, J. Fraissard, J. N. Hyacinthe, J. Jokisaari, E. Locci, T. J. Lowery, M. Luhmer, T. Meersmann, I. L. Moudrakovski, G. E. Pavlovskaya, K. L. Pierce, A. Pines, J. A. Ripmeester, V.-V. Telkki and W. S. Veeman, Actual. Chim., 2005, 287, 16–34 CAS; (b) D. A. Barskiy, A. M. Coffey, P. Nikolaou, D. M. Mikhaylov, B. M. Goodson, R. T Branca, G. J. Lu, M. G. Shapiro, V.-V. Telkki, V. V. Zhivonitko, I. V. Koptyug, O. G. Salnikov, K. V. Kovtunov, V. I. Bukhtiyarov, M. S. Rosen, M. J. Barlow, S. Safavi, I. P. Hall, L. Schröder and E. Y. Chekmenev, Chem.–Eur. J., 2017, 23, 725–751 CrossRef CAS PubMed.
- (a) M. S. Albert, G. D. Cates, B. Driehuys, W. Happer, B. Saam, C. S. Springer Jr and A. Wishnia, Nature, 1994, 370, 199–201 CrossRef CAS PubMed; (b) J. P. Mugler III, T. A. Altes, I. C. Ruset, I. M. Dregely, J. F. Mata, G. W. Miller, S. Ketel, J. Ketel, F. W. Hersman and K. Ruppert, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 21707–21712 CrossRef PubMed.
- (a) C. Hilty, E. E. McDonnell, J. Granwehr, K. L. Pierce, S. Han and A. Pines, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 14960–14963 CrossRef CAS PubMed; (b) V.-V. Telkki, C. Hilty, S. Garcia, E. Harel and A. Pines, J. Phys. Chem. B, 2007, 111, 13929–13936 CrossRef CAS PubMed.
- J. Jokisaari, in NMR of Ordered Liquids, ed. E. E. Burnell and C. A. de Lange, Kluwer, Dordrecht, 2003, pp. 109–135 Search PubMed.
- (a) J. B. Miller, J. H. Walton and C. M. Roland, Macromolecules, 1993, 26, 5602–5610 CrossRef CAS; (b) S. Glöggler, M. Raue, J. Colell, P. Türschmann, A. Liebisch, T. Mang, B. Blümich and S. Appelt, ChemPhysChem, 2012, 13, 4120–4123 CrossRef PubMed.
- G. Saielli, A. Bagno, F. Castiglione, R. Simonutti, M. Mauri and A. Mele, J. Phys. Chem. B, 2014, 118, 13963–13968 CrossRef CAS PubMed.
- (a) J. Demarquay and J. Fraissard, Chem. Phys. Lett., 1987, 136, 314–318 CrossRef CAS; (b) V. V. Terskikh, I. L. Moudrakovski, S. R. Breeze, S. Lang, C. I. Ratcliffe, J. A. Ripmeester and A. Sayari, Langmuir, 2002, 18, 5653–5656 CrossRef CAS; (c) V.-V. Telkki, J. Lounila and J. Jokisaari, J. Chem. Phys., 2006, 124, 034711 CrossRef PubMed; (d) E. Weiland, M.-A. Springuel-Huet, A. Nossov and A. Gédéon, Microporous Mesoporous Mater., 2016, 225, 41–65 CrossRef CAS; (e) M.-A. Springuel-Huet, A. Nossov, F. Guenneau and A. Gédéon, Chem. Commun., 2013, 49, 7403 RSC.
- J. Zhou and P. C. M. van Zijl, Prog. Nucl. Magn. Reson. Spectrosc., 2006, 48, 109–136 CrossRef CAS.
- (a) M. M. Spence, S. M. Rubin, I. E. Dimitrov, E. J. Ruiz, D. E. Wemmer, A. Pines, S. Q. Yao, F. Tian and P. G. Schultz, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 10654–10657 CrossRef CAS PubMed; (b) L. Schröder, T. J. Lowery, C. Hilty, D. E. Wemmer and A. Pines, Science, 2006, 314, 446–449 CrossRef PubMed; (c) G. Huber, T. Brotin, L. Dubois, H. Desvaux, J.-P. Dutasta and P. Berthault, J. Am. Chem. Soc., 2006, 128, 6239–6246 CrossRef CAS PubMed; (d) G. K. Seward, Y. Bai, N. S. Khan and I. Dmochowski, J. Chem. Sci., 2011, 2, 1103–1110 RSC; (e) H. M. Rosea, C. Witte, F. Rossella, S. Klippel, C. Freund and L. Schröder, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 11697–11702 CrossRef PubMed; (f) L. Schröder, Phys. Med., 2013, 29, 3–16 CrossRef PubMed.
- J. Roukala, J. Zhu, C. Giri, K. Rissanen, P. Lantto and V.-V. Telkki, J. Am. Chem. Soc., 2015, 137, 2464–2467 CrossRef CAS PubMed.
- (a) Y. Bai, Y. Wang, A. Driks, M. Goulian and I. J. Dmochowski, Chem. Sci., 2014, 5, 3197–3203 RSC; (b) M. G. Shapiro, R. M. Ramirez, L. J. Sperling, G. Sun, J. Sun, A. Pines, D. V. Schaffer and V. S. Bajaj, Nat. Chem., 2014, 6, 629–634 CrossRef CAS PubMed; (c) Y. Wang, B. W. Roose, E. J. Palovcak, V. Carnevale and I. J. Dmochowski, Angew. Chem., Int. Ed., 2016, 55, 8984–8987 CrossRef CAS PubMed; (d) Y. Bai, A. P. Hill and I. J. Dmochowski, Anal. Chem., 2012, 84, 9935–9941 CrossRef CAS PubMed; (e) Y. Wang and I. J. Dmochowski, Chem. Commun., 2015, 51, 8982–8985 RSC.
- A. Abragam, The Principles of Nuclear Magnetism, Clarendon, Oxford, 1974 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- (a) A. D. Becke, Phys. Rev. A, 1988, 38, 3098 CrossRef CAS; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS; (c) A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS.
- (a) P. Lantto and J. Vaara, J. Chem. Phys., 2007, 127, 084312 CrossRef PubMed; (b) M. Straka, P. Lantto, M. Räsänen and J. Vaara, J. Chem. Phys., 2007, 127, 234314 CrossRef PubMed; (c) J. Roukala, A. F. Maldonado, J. Vaara, G. A. Aucar and P. Lantto, Phys. Chem. Chem. Phys., 2011, 13, 21016 RSC; (d) P. Lantto, S. Standara, S. Riedel, J. Vaara and M. Straka, Phys. Chem. Chem. Phys., 2012, 14, 10944 RSC.
- (a) M. Straka, P. Lantto and J. Vaara, J. Phys. Chem. A, 2008, 112, 2658 CrossRef CAS PubMed; (b) M. Selent, J. Nyman, J. Roukala, M. Ilczyszyn, R. Oilunkaniemi, P. J. Bygrave, R. Laitinen, J. Jokisaari, G. M. Day and P. Lantto, Chem.–Eur J., 2017, 23, 5258 CrossRef CAS PubMed.
- TURBOMOLE V6.5 2013, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, http://www.turbomole.com.
- (a) G. Schreckenbach and T. Ziegler, J. Phys. Chem., 1995, 99, 606 CrossRef CAS; (b) ADF2014, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com; (c) ADF2016, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com.
- M. Hanni, P. Lantto, M. Repiský, J. Mareš, B. Saam and J. Vaara, Phys. Rev. A, 2017, 95, 032509 CrossRef.
- (a) A. Schäfer, H. Horn and R. J. Ahlrichs, Chem. Phys., 1992, 97, 2571 Search PubMed; (b) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- (a) E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597 CrossRef CAS; (b) E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783 CrossRef CAS; (c) E. van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505 CrossRef CAS; (d) S. K. Wolff and T. Ziegler, J. Chem. Phys., 1998, 109, 895 CrossRef CAS; (e) S. K. Wolff, T. Ziegler, E. van Lenthe and E. J. Baerends, J. Chem. Phys., 1999, 110, 7689 CrossRef CAS.
- A. D. Bain, Prog. Nucl. Magn. Reson. Spectrosc., 2003, 43, 63–103 CrossRef CAS.
- (a) Z. Luz and S. Meiboom, J. Chem. Phys., 1963, 39, 366–370 CrossRef CAS; (b) D. Idiyatullin, S. Michaeli and M. Garwood, J. Magn. Reson., 2004, 171, 330–337 CrossRef CAS PubMed.
- T. Hasell, S. Y. Chong, K. E. Jelfs, D. J. Adams and A. I. Cooper, J. Am. Chem. Soc., 2012, 134, 588–598 CrossRef CAS PubMed.
- P. T. Callaghan, Translational Dynamics and Magnetic Resonance: Principles of Pulsed Gradient Spin Echo NMR, Oxford University Press, Oxford, 2011 Search PubMed.
- J. E. Tanner, J. Chem. Phys., 1970, 52, 2523–2526 CrossRef CAS.
- R. M. Cotts, M. J. R. Hoch, T. Sun and J. T. Marker, J. Magn. Reson., 1989, 83, 252–266 CAS.
- M. Pfeffer and O. Lutz, J. Magn. Reson., Ser. A, 1965, 113, 108–113 CrossRef.
- (a) Q.-H. Wei, C. Bechinger and P. Leiderer, Science, 2000, 287, 625–627 CrossRef CAS PubMed; (b) C. R. Bowers, M. Dvoyashkin, S. R. Salpage, C. Akel, H. Bhase, M. F. Geer and L. S. Shimizu, ACS Nano, 2015, 6343–6353 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional details of experimental methods and results as well as computational modelling. See DOI: 10.1039/c7sc01990d |
| This journal is © The Royal Society of Chemistry 2017 |