Single particle tracking-based reaction progress kinetic analysis reveals a series of molecular mechanisms of cetuximab-induced EGFR processes in a single living cell

Abstract

Cellular processes occur through the orchestration of multi-step molecular reactions. Reaction progress kinetic analysis (RPKA) can provide the mechanistic details to elucidate the multi-step molecular reactions. However, current tools have limited ability to simultaneously monitor dynamic variations in multiple complex states at the single molecule level to apply RPKA in living cells. In this research, a single particle tracking-based reaction progress kinetic analysis (sptRPKA) was developed to simultaneously determine the kinetics of multiple states of protein complexes in the membrane of a single living cell. The subpopulation ratios of different states were quantitatively (and statistically) reliably extracted from the diffusion coefficient distribution rapidly acquired by single particle tracking at constant and high density over a long period of time using super-resolution microscopy. Using sptRPKA, a series of molecular mechanisms of epidermal growth factor receptor (EGFR) cellular processing induced by cetuximab were investigated. By comprehensively measuring the rate constants and cooperativity of the molecular reactions involving four EGFR complex states, a previously unknown intermediate state was identified that represents the rate limiting step responsible for the selectivity of cetuximab-induced EGFR endocytosis to cancer cells.

---

Introduction

Cellular processes occur through the orchestration of multi-step molecular reactions.¹ Kinetic analyses of these molecular reactions can illuminate their detailed molecular mechanisms.^2,3 Reaction progress kinetic analysis (RPKA) is a powerful tool for comprehensively elucidating complex catalytic reactions and obtaining kinetic constants from a minimal number of experiments by simultaneously monitoring the reaction courses of multiple substrates.⁴ RPKA can also provide insights into reaction behaviors that are difficult to obtain using classical steady-state kinetic analyses, such as catalyst activation or product acceleration.⁵ Despite these advantages, applying RPKA to living cells has been challenging because the molecular states involved in a cellular process are typically unknown,^6–8 and even when the states have been identified, it is difficult to simultaneously quantify their dynamic changes.^9,10 Furthermore, because a single type of protein can be simultaneously involved in multiple molecular reactions over the progression of a cellular process,¹¹ these heterogeneous molecular states of a protein must be distinguished at the single molecule level.

Single particle tracking (SPT) analysis of membrane proteins provides diffusional information for individual molecules and can reveal diffusional heterogeneity among the molecules on a plasma membrane.¹² However, a simple SPT approach cannot provide a sufficient number of trajectories^8,13,14 to give reliable statistical information about the multiple diffusional states of membrane proteins at the single cell level. This limitation in the number of trajectories has been overcome by use of single particle tracking photoactivated localization microscopy (sptPALM), in which a high density of trajectories is obtained by switching sparse subsets of photoactivatable fluorescent proteins on and off in a single cell.¹⁵ The ability to perform continuous SPT of membrane proteins at a constant density in a single living cell over a long period of time allows the determination of time series distributions of single molecule diffusion coefficients that vary over the reaction course of a cellular process.

In this research, a robust approach was developed to apply RPKA to the investigation of the time-dependent kinetics of cellular processes involving multiple complex states on a plasma membrane in a living cell. The intrinsic diffusivities of the different complex states of a membrane protein were estimated statistically and the amount of each state was extracted from the single molecule diffusion-coefficient distributions acquired by sptPALM over time, which was then subjected to RPKA to obtain kinetic information including reaction models and rate constants. This method was called single particle tracking-based reaction progress kinetic analysis (sptRPKA). This method was capable of simultaneously analyzing a series of molecular reactions involving up to five complex states with rate constants <0.05 s⁻¹. Using sptRPKA, the simultaneous kinetics of the multi-step molecular reactions for epidermal growth factor receptor (EGFR) endocytosis induced by cetuximab were analyzed, which involves four distinct EGFR complex states. Furthermore, a previously unknown intermediate state was identified, that was the rate determining step in cetuximab-induced EGFR endocytosis.

Results and discussion

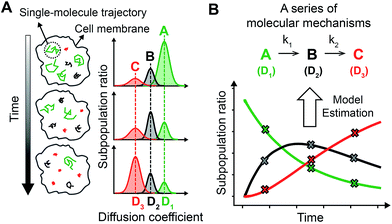
Single particle tracking-based reaction progress kinetic analysis (sptRPKA)

By accurately monitoring the time dependent conversion of the amounts of multiple substrates, the reaction progress can be analyzed kinetically to elucidate the multi-step reaction mechanisms. Because SPT can be used to distinguish multiple complex states of a membrane protein based on their different intrinsic diffusivities,^16,17 the subpopulation ratios of these complex states can be extracted over time from the single molecule diffusion coefficient distribution generated by a sufficient number of trajectories in a single living cell using photoactivatable fluorescent dyes (Fig. 1A). Thus, by acquiring the diffusion coefficient distributions over the entire course of the cellular process of a membrane protein, variations in the subpopulation ratios of multiple complex states of the membrane protein can be kinetically analyzed (Fig. 1B). Use of sptRPKA can provide quantitative kinetic information, including rate constants and rate laws, for a series of molecular reactions involving multiple complex states of a membrane protein in a single living cell.

Fig. 1 (A) By tracking an individual membrane protein in space and time on a living cell, the subpopulation ratio of each state that has a different diffusivity can be extracted from the diffusion coefficient distribution. (B) Observed subpopulation ratios over the cellular process (X) were subjected to RPKA for model estimation. The illustrations shown represent a first-order sequential reaction involving an intermediate state with two rate constants (k₁ = k₂), where the diffusion coefficients (D₁, D₂, and D₃) of each complex state are distinct.

Performance of sptRPKA

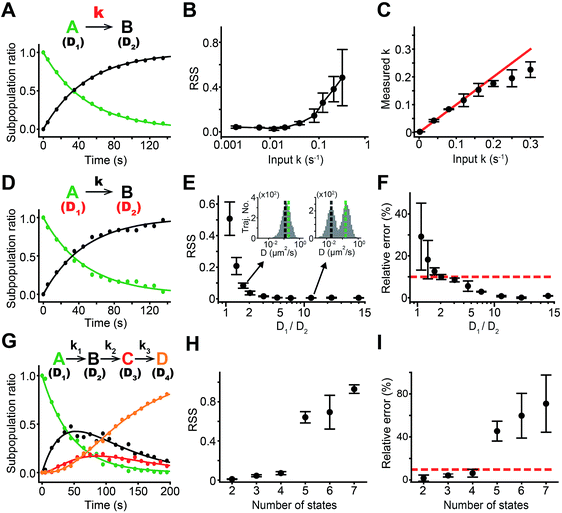
Simulated trajectory data was used to explore the performance of sptRPKA. The simulated trajectories were realistically generated similar to those of trajectories typically observed in SPT experiments with various membrane proteins and in the experiments reported here.¹⁸ Using the simulated trajectories, the effects of three primary parameters for sptRPKA were examined: rate constants, diffusion coefficients of each state, and the number of states for molecular reactions.

First, the rate constants were varied for a first-order reaction with two complex states whose diffusion coefficients were set to 0.2 and 0.004 μm² s⁻¹, which ensured the complete separation of the two states in the trajectories (Fig. 2A). The residual sum of squares (RSS) for the fit increased as the rate constant increased over 0.05 s⁻¹ (Fig. 2B). Interestingly, the estimation of the rate constant was far more stable than that of the RSS, which allowed the accurate determination of rate constants for first-order reactions which were even faster than 0.16 s⁻¹ (Fig. 2C). This result indicates that the overall trend of the reaction progress was preserved despite the presence of inaccuracies in the subpopulation ratio measured at each time point, which were caused by the number of trajectories acquired over a brief period being insufficient to rapidly extract subpopulation ratios of the complex states from the diffusion coefficient distribution.

Fig. 2 Performance of sptRPKA. (A–C) The performance of sptRPKA to estimate various rate constants with given diffusion coefficients of two complex states (D₁ = 0.2 μm² s⁻¹; D₂ = 0.004 μm² s⁻¹) for a first-order sequential reaction. The reaction data of sptRPKA for a rate constant of 0.02 s⁻¹ are shown in (A). The fitting performance was examined using the RSS (B). The rate constants measured with sptRPKA are represented with respect to the input rate constants (C). The red line in (C) indicates the points where the measured rate constants equal the input rate constants. (D–F) The performance of sptRPKA to estimate a rate constant with unknown diffusion coefficients of two complex states for a first-order reaction. The reaction data from sptRPKA for a rate constant of 0.02 s⁻¹ and diffusion coefficients of 0.2 and 0.05 μm² s⁻¹ are shown in (D). The RSS for the fit (E) and the relative error for the estimation of a rate constant (F) are displayed with respect to the ratio of the diffusion coefficients between the two states. Diffusion coefficient distributions with two estimated diffusion coefficients for each state are shown (insets in (E)). The 10% estimation error is indicated as a red dashed line in (F). (G–I) The performance of sptRPKA used to estimate the rate constants for a series of first-order reactions involving multiple complex states with unknown diffusion coefficients. The reaction data from sptRPKA for a rate constant of 0.02 s⁻¹ for all four states and diffusion coefficients of 0.2, 0.05, 0.015, and 0.004 μm² s⁻¹ are shown in (G). The RSS for the fit (H) and the relative error for the estimation of the rate constants (I) are displayed with respect to the number of states. The error bars denote the standard deviation of the measurements for multiple simulations (n = 5).

Next, the effects of the diffusion coefficients of two complex states on determining rate constants were examined (Fig. 2D). The short time diffusion coefficient was determined from trajectories with a duration of eight frames using the mean squared displacement (MSD) relationship, where the MSD = 4DΔτ + 4e² (0 ≤ Δτ < 160 ms). The rate constant estimates were accurate when the diffusion coefficient distribution of each state was well discerned. The RSS for the fitting of the reaction progress data started to increase as the diffusion coefficient distributions of the two states became inseparable (Fig. 2E). The estimation error for the rate constant was within 10% when the mean diffusion coefficients of the two states differed by 40% (Fig. 2F). However, the estimation error for the rate constant was less stable compared to RSS because the uncertainty in the determination of the diffusion coefficient of each state from the diffusion coefficient distribution produced systematic bias for the extraction of the subpopulation ratio over the entire course of the reaction.

Because the uncertainty of the diffusion coefficient depends on the trajectory length, the estimation error for sptRPKA caused by an indistinguishable mixture of two diffusion coefficient distributions could be improved by using trajectories with longer lengths. However, to obtain longer trajectories, the particle density must be lowered to circumvent the high probability that more than one particle would be observed in a diffraction limit during tracking because of the complication of the correct linking of two particles in consecutive frames. Thus, it was expected that the temporal resolution (the fastest rate constant that could be accurately estimated) of sptRPKA would be compromised if longer trajectories were used because the number of trajectories in a given time interval would be decreased. This inversely proportional relationship between the separability of the diffusion coefficient distribution and the temporal resolution of sptRPKA was observed with respect to trajectory length [see Fig. S1 in the ESI†]. This result indicates that interconversion between the temporal resolution and the amount of diffusional information for sptRPKA can be accomplished by simply controlling the trajectory length, which can be adjusted according to the dynamic or static nature of the cellular processes of interest.

Lastly, the effect of the number of complex states on determining rate constants was explored. The first-order sequential reactions were analyzed simultaneously and this involved up to seven complex states (under a condition of maximal separation among the mean diffusion coefficients of multiple states) (Fig. 2G). One of the benefits of using sptRPKA, in which a reaction is examined over an entire time course, is that the diffusion coefficient of each complex state can be determined at a different time point, such point when the complexity of the diffusion coefficient distribution for that state is the lowest (e.g., for a first-order sequential reaction, the diffusion coefficients for the first and last states can be determined at the initial and late periods of the reaction, respectively). With this advantage, the reaction progress data (Fig. 2H) was accurately fitted and was used to determine the rate constants for the reactions involving up to four complex states using the trajectories with a length of eight frames (Fig. 2I). However, it was not feasible to precisely estimate the rate constants for reactions involving more than five complex states because of the generation of inseparable diffusion coefficient distributions when significant amounts of all the complex states appeared simultaneously in the middle of the reaction. It was confirmed that utilizing trajectories longer than 15 frames made it possible to estimate rate constants for the reactions with five complex states (see Fig. S2 in the ESI†), however, the temporal resolution of sptRPKA was sacrificed in this case.

Unlike simulated conditions, the membranes of living cells are structurally and dynamically heterogeneous. It is uncertain whether diffusion coefficient distributions produced by multiple independent measurements of diffusion coefficients from individual trajectories acquired at different points in space and time on the membrane of a living cell can be sufficiently consistent for accurate comparisons over a long period of time.¹⁹ Thus, prior to applying sptRPKA to a cellular process of a membrane protein, the measurement stability of single molecule diffusion coefficient distributions was examined in a living cell. EGFR was analyzed on the membrane of a living COS-7 cell and this was used as a model system. Using EGFR tagged with mEos3.2, a monomeric photoactivatable fluorescent protein,²⁰ >200 000 EGFR molecules with a trajectory duration longer than eight frames were tracked in a single COS-7 cell within 1 h at constant density using 405 nm photoactivation (see Fig. S3a in the ESI†). The cell morphology was not altered after the measurement, confirming that negligible photodamage to the cell occurred during the imaging (see Fig. S3b and c in the ESI†). The diffusion coefficient was calculated from the EGFR trajectories using the following equation: MSD = 4DΔτ + 4e² (0 ≤ Δτ < 160 ms) (see Fig. S4 in the ESI†). Approximately 8.5 s was sufficient to obtain the stable diffusion coefficient distribution of EGFR in COS-7 cells (see Fig. S5 in the ESI†), which was also similar in different cell lines including HEK293, HeLa, and CHO-K1 cells (see Fig. S6 in the ESI†), thus enabling sptRPKA to resolve the sub-minute kinetics of EGFR.

Temporal diffusive dynamics of EGFR subpopulations induced by cetuximab

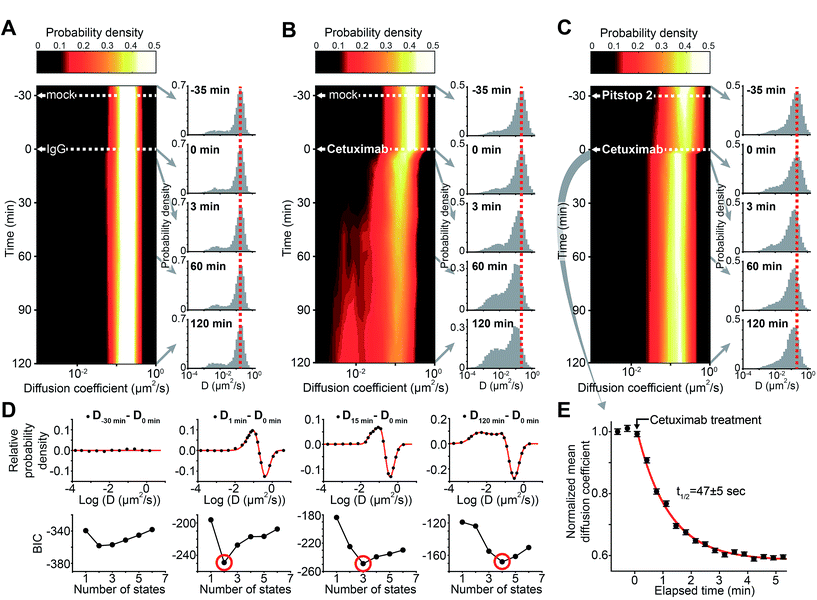
To demonstrate the applicability of sptRPKA, the cellular processing of EGFR induced by cetuximab was investigated. EGFR is highly relevant to various types of cancers,²¹ and cetuximab, a monoclonal antibody targeting EGFR, is an anti-cancer drug in clinical use.²² The individual reactions involved in the cellular processing of EGFR induced by cetuximab have been studied one at a time.²³ However, this process, which involves multi-step molecular reactions, has not been comprehensively investigated because of the lack of an in situ method to simultaneously analyze multiple molecular reactions in a living cell.

Because it had been confirmed statistically that the diffusion coefficient distribution of EGFR could be reliably obtained using trajectories longer than eight frames with a frame rate of 13.3 Hz when accumulated over ∼8.5 s, the trajectories of EGFR-mEos3.2 were divided into 10 s intervals to generate a temporal map of the EGFR diffusion-coefficient distributions. The first such map was generated by treating COS-7 cells with immunoglobulin G (IgG) for 2 h following a mock treatment for 30 min to ensure that the basal steady state of the EGFR diffusional dynamics was not altered by nonspecific treatments (Fig. 3A). IgG treatment did not induce any noticeable changes in the EGFR diffusive dynamics. Next, the cells were treated with cetuximab 30 min after the mock treatment (Fig. 3B). The peak of the diffusion coefficient distribution of the fast diffusive EGFR subpopulation decreased by ∼38% within 3 min and then slowly decreased further by ∼55% after 2 h of cetuximab treatment. The portion of the slow diffusive subpopulation of EGFR increased dramatically after 2 h of cetuximab treatment, to ∼49% of the entire population.

Fig. 3 Temporal diffusion dynamics of EGFR subpopulations induced by cetuximab. (A, B and D) Probability density maps of the temporal dynamics of the diffusion coefficient distribution of EGFR for sptRPKA. COS-7 cells expressing EGFR-mEos3.2 were treated with either mock (A and B) or Pitstop 2 (D) for 30 min followed by IgG (A) or cetuximab (B and D) for 2 h. Histograms showing the diffusion coefficient distributions at −35, 0, 3, 60, and 120 min (the IgG or cetuximab treatment point was set to 0 min) are presented as sections of the temporal axis of the diffusion coefficient distribution maps. (C) The number of states was determined objectively by using BIC. The diffusion coefficient distributions of EGFR from (B) at each time, subtracted from the distribution at 0 min (upper panels). The BIC was calculated from the subtracted distribution with respect to the number of states (lower panels). Red lines indicate the curve fitting generated using the specified number of Gaussian mixtures (red circles). (E) Sub-minute kinetics analysis of the diffusion coefficient distribution of EGFR altered by cetuximab with Pitstop 2 pretreatment. The diffusion coefficient distributions of EGFR were obtained every ∼10 s before and after cetuximab treatment for 5 min following Pitstop 2 preincubation for 30 min. The addition of cetuximab is indicated at 0 min (arrow). The error bars represent the standard error of the mean at the single molecule level (n > 3000). The half-life for the kinetics (t_1/2 = ∼47 s) was obtained by fitting an exponential decay (red line).

To objectively identify the number of EGFR complex states involved in this process, the EGFR diffusion coefficient distributions (probability densities) obtained after cetuximab treatment were subtracted from the distribution obtained before cetuximab treatment, and this representing the change in the distribution caused by cetuximab treatment. Then, based on the Bayesian information criterion (BIC) analysis, the number of Gaussian mixtures were determined from the subtracted distributions that were transformed to a logarithmic scale because diffusion coefficients from a single state follow empirically a log normal distribution when the short trajectories are used.^13,24–28 To avoid the artifacts derived from the noise signals, a fitted Gaussian distribution was counted as a state if the distribution was responsible for more than 3% of the entire EGFR population. With increasing time after cetuximab treatment, the number of EGFR complex states increased from two to four (Fig. 3C and see also Fig. S7 in the ESI†). This result indicates that at least four different EGFR complex states are involved in the cetuximab induced EGFR cellular process for up to 2 h after treatment. Singular value decomposition analysis of the subtracted distribution, which provides a non-parametric criterion to determine the effective rank to properly represent the characteristics in both the diffusion coefficient and time dimension simultaneously, supported the number of states determined (see Fig. S8 in the ESI†).

Identification of four distinct complex states of EGFR induced by cetuximab

It was suspected that the slow diffusive subpopulation of EGFR induced by cetuximab in the late stage of the reaction represented endocytic EGFR because cetuximab is known to induce the endocytosis of EGFR,²³ and a complex of EGFR and the endocytic machinery should diffuse substantially more slowly than free diffusive EGFR. EGFR endocytosis has been reported to be dependent on a clathrin-coated pit (CCP),²⁹ which is observed to be nearly immobilized on the plasma membrane with an average trajectory duration of ∼0.7 s in these measurements.³⁰ Furthermore, the majority of this slow subpopulation underwent sub-diffusion (see Fig. S9 in the ESI†). Thus, it was predicted that this slow diffusive (primarily immobilized) subpopulation might represent a transient state of EGFR inside a CCP before its internalization into the cytosol. To examine whether this slow subpopulation induced by cetuximab was related to CCPs, the cells were pretreated with Pitstop 2, an inhibitor of clathrin-mediated endocytosis,³¹ for 30 min prior to cetuximab treatment (Fig. 3D). Pitstop 2 pretreatment alone slightly altered the diffusion coefficient distribution (Kolmogorov–Smirnov test, p < 0.01) but negligibly altered the mean diffusion coefficient of EGFR. However, the generation of the slow EGFR subpopulation induced by cetuximab treatment was substantially inhibited by the Pitstop 2 pretreatment. Furthermore, the diffusion coefficient of the major fast diffusive subpopulation decreased by ∼36% within 3 min after cetuximab treatment, as observed in the distribution without Pitstop 2 pretreatment, but it did not decrease further for 2 h. The number of EGFR complex states inferred by the BIC analysis also indicated that only two states remained over the entire reaction course (see Fig. S7 in the ESI†). This result confirmed that multiple processes exhibiting at least two different reaction kinetics exist in the alterations of this fast diffusive subpopulation induced by cetuximab.

The kinetics of the ∼36% peak shift of the fast diffusive subpopulation observed within 3 min after cetuximab treatment with Pitstop 2 pretreatment were further examined. By obtaining the EGFR diffusion coefficient distributions approximately every 10 s for 5 min immediately after the addition of cetuximab, the kinetic changes in this subpopulation (t_1/2 = ∼47 s) were resolved (Fig. 3E). Interestingly, the kinetics were similar to the association rate constant (k_on) of cetuximab binding to EGFR,³² suggesting that this immediate decrease in the diffusion coefficient after cetuximab treatment represents the direct binding reaction of cetuximab to EGFR. The dissociation constant (K_d) for cetuximab binding to EGFR after Pitstop 2 pretreatment (∼0.39 nM) was also calculated from the dose-dependent shifts of the diffusion coefficient of EGFR (see Fig. S10 in the ESI†). The K_d value was similar to that previously reported for cetuximab binding to EGFR in vitro.³² Furthermore, the binding of cetuximab to EGFR should be independent of CCPs, which is consistent with the result that this immediate peak shift was resistant to Pitstop 2 pretreatment (Fig. 3D). This interpretation seemed to contradict the traditional Saffman–Delbrück model of membrane protein diffusion.³³ However, a recent study showed that the direct binding of antibodies and their Fab fragments to the extracellular domains of membrane proteins can significantly contribute to the diffusivity of the membrane proteins in living cells,³⁴ which supports the interpretation of the direct binding of cetuximab to EGFR based on the immediate decrease in the diffusion coefficient.

Although the existence of EGFR predimers has been suggested in many cancer cells,^35,36 no discernible changes were detected in the other states indicating the predimers except for the monomeric EGFR and the cetuximab bound EGFR immediately after cetuximab treatment likely because the amount of EGFR predimers in COS-7 cells at its basal status is not significantly high. The predimers might have been detected, if a significant amount exists, because cetuximab plays a role in the dissociation of a dimer to a monomer.³⁷

No previous reports were found concerning the molecular state of EGFR responsible for the further peak shift in the diffusion coefficient distribution induced by cetuximab (∼55% diffusion coefficient shift after 2 h, see Fig. 3B). Considering this additional shift was generated more rapidly (t_1/2 ≈ 8.4 min) than the CCP-trapped state (t_1/2 >32 min) (see Fig. S11 in the ESI†), this previously unknown state may represent an intermediate state that exists before EGFR becomes trapped in a CCP.^38,39

Use of sptRPKA for cetuximab-induced EGFR endocytosis

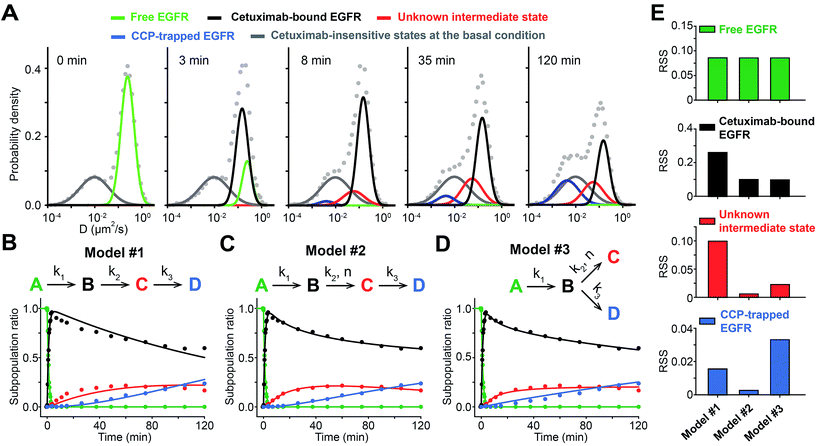
To apply sptRPKA to study cetuximab-induced EGFR endocytosis, the subpopulation ratios of the EGFR complex states must be determined from the time series diffusion coefficient distributions. A global fit was applied with independent (weights of Gaussian mixtures) and shared parameters (mean and variance of Gaussian mixtures) to the log-scaled time series diffusion-coefficient distributions with the distribution at 0 min subtracted. It was assumed that the subpopulation ratio of the state for basal free diffusive EGFR was equal to 1 at the initial time point because the subtracted distribution immediately after cetuximab treatment clearly showed that only the state for basal free-diffusive EGFR was reduced (the upper second panel in Fig. 3C). To determine the initial values for the global fit optimization, the mean diffusion coefficients of the four EGFR complex states were estimated taking into consideration the fixed mean diffusion coefficient of each state throughout the entire time series distribution data (R² > 0.99): 0.25 μm² s⁻¹ for basal free-diffusive EGFR, 0.15 μm² s⁻¹ for cetuximab bound EGFR, 0.056 μm² s⁻¹ for the clathrin dependent unknown state, and 0.005 μm² s⁻¹ (observed as immobilized) for CCP trapped EGFR (Fig. 4A). Then, a temporal profile of the relative subpopulation ratio of each state was generated by calculating the area under the curve of the time series distributions of each state normalized by subtracting the cetuximab insensitive states at the basal condition (see Fig. S12 in the ESI†). Because the change in the total expression level of EGFR in a cell surface was negligible up to 2 h of cetuximab treatment, the sum of subpopulation ratios was kept as one up to 2 h (see Fig. S13 in the ESI†).

Fig. 4 Use of sptRPKA for the cetuximab-induced EGFR endocytosis. (A) The diffusion coefficient distributions of EGFRs fitted with a Gaussian mixture model with the four complex states using global fitting are displayed at the indicated times. (B–D) The subpopulation ratios of the four complex states of EGFR induced by cetuximab (dots) were obtained from the diffusion coefficient distributions of EGFR in (A) after subtracting the cetuximab insensitive states at the basal condition (Dulbecco's Modified Eagle's Medium (DMEM) at 37 °C). Parameter estimation was performed by simultaneously fitting a set of differential equations for a sequential reaction model (B), a sequential reaction with cooperativity model (C), and a parallel reaction with cooperativity model (D) to the reaction progress data for the four states [the states are indicated by the same colors as in (A)]. (E) Objective evaluation of models using the RSS obtained from the optimal fits exhibited in (B–D). The comparisons between the three models were made state-by-state.

Next, a reaction model was determined that explained the dynamic variations in the relative subpopulation ratios involving the four different complex states of EGFR induced by cetuximab for up to 2 h. Based on the results that both the unknown and CCP-trapped states of EGFR were blocked by Pitstop 2 and that the unknown state appeared prior to the CCP-trapped state (Fig. 3B and D), these reactions were likely to be sequential. However, a simple sequential reaction model with first-order kinetics could not explain the measurements (Fig. 4B). The reversible reaction models could also not explain the data (see Fig. S14 in the ESI†), and this was consistent with the fact that the reversible rate is generally negligible compared to its forward rate for high affinity antibodies (<1 nM of K_d) and EGFR trapped in CCPs could not be readily released because CCP seals its structure through dynamin,³⁸ which should make the reversible rate negligible. While searching for a reaction model to best account for this data from the selection of plausible reaction models, it was found that the unknown state required a high order rate law to fit the data. To examine whether the CCP-trapped state was derived from the unknown state, both sequential and parallel reaction models were analyzed for the CCP-trapped state (Fig. 4C and D). Because the number of parameters in these two models was the same, the RSS for each state was utilized as a criterion to determine the best model. As expected, these two models exhibited no significant differences in RSS for the basal EGFR and cetuximab bound EGFR states because the two models were distinguished from the unknown intermediate state. However, the parallel reaction model did not fit the CCP-trapped state well, whereas the sequential reaction model fit it almost perfectly (Fig. 4E). Furthermore, the residuals from the parallel model exhibited a predictive pattern, whereas a random pattern was observed in the sequential model and this implies that the parallel model cannot capture the entire explanatory information of the CCP-trapped state (see Fig. S15 in the ESI†). Taken together, a cooperative sequential reaction model is the most probable model for the cetuximab induced EGFR endocytosis in the membrane of living cells (Fig. 4C). This result was confirmed by analyzing the cooperativity of the intermediate state in EGFR expression dependent manner (see Fig. S16 in the ESI†).

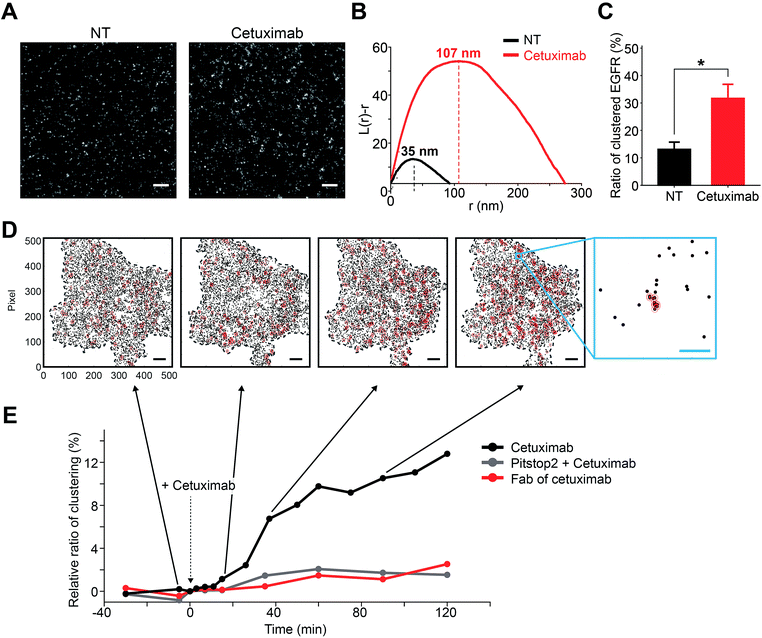
From the sequential model, it could be inferred that the previously unknown intermediate state was responsible for the transition from cetuximab bound EGFR to EGFR inside a CCP. It was found that EGFR in the CCP trapped state was highly clustered with a size similar to CCP (∼120 nm), whereas the cetuximab bound EGFR state was not (Fig. 5). This cetuximab-induced EGFR clustering observed by using super-resolution microscopy was also recently reported by Gao et al.⁴⁰ Considering previous studies showing that EGFR signaling for active trafficking was not involved in cetuximab induced EGFR endocytosis^23,41 and that a Fab fragment of cetuximab did not trigger EGFR internalization,⁴² the previously unknown intermediate state might be EGFR clusters passively associated with pre-existing EGFR oligomers that are held by clathrin through the bivalency of cetuximab (Fig. 6A), which is consistent with the fact that a monovalent Fab fragment of cetuximab did not induce the intermediate state and the CCP-trapped state (see Fig. S17 in the ESI†).

Fig. 5 EGFR clustering induced by cetuximab. (A) Reconstructed PALM images of EGFR-mEos3.2 with or without cetuximab treatment for 2 h. Representative images of 5 μm × 5 μm areas are shown. Scale bar, 500 nm. (B) Ripley's K-function analysis of reconstructed PALM images. The linearly transformed Ripley's K function, L(r)–r, was plotted against the radius of clusters examined. The radius of clusters for no treatment (NT) was 35 nm, whereas that for cetuximab increased to 107 nm. Similar values were observed among independent cells. (C) The ratio of clustered EGFR to the total observed EGFR with or without cetuximab treatment. Clustered EGFR was determined by the k-nearest neighbor analysis. Error bars denote the standard error of the mean of multiple cells (n > 3). *p < 0.05. (D) A total of 7500 immobilized EGFR trajectories (the averaged position of each trajectory is displayed as a black dot) are shown in each image for quantitative comparisons among the images in the same single living cell. An individual EGFR that belongs to the EGFR cluster is indicated by a red circle. The criterion of clustering radius was set at 110 nm. At least three particles were included in the clustering criterion to be classified as belonging to the cluster. Scale bars, 5 μm (black) and 0.5 μm (blue). (E) The normalized relative ratios of EGFR clusters after cetuximab treatment with or without Pitstop 2 pretreatment are shown over time. It was confirmed that the criteria of the clustering radius did not have a significant effect on the trend of the curve or the correlation coefficient from 80 to 200 nm, although the absolute ratio was changed in proportion to the clustering radius or the number of neighbors.

Fig. 6 A series of molecular mechanisms for cetuximab induced EGFR endocytosis. (A) The illustrations for a proposed model to account for a series of molecular mechanisms of cetuximab induced EGFR endocytosis on a living cell membrane. Each kinetic parameter at 37 °C was estimated from a set of rate equations for the sequential reaction with the cooperativity model shown in Fig. 4C. Cetuximab binds to monomeric EGFR with a first-order reaction, followed by a high-order rate law reaction for an unknown intermediate state that may involve clathrin dependent EGFR oligomerization. Finally, cetuximab bound EGFR in the unknown intermediate state is trapped in a CCP with a first-order reaction for clathrin mediated endocytosis. (B) EGFR internalization induced by cetuximab treated for 12 h on cell lines with different surface expression levels of EGFR at 37 °C. The proposed model (A) fits the experimental data (red line).

Although cetuximab is known to inhibit the epidermal growth factor (EGF) dependent activity of EGFR by competing with EGF to bind EGFR,²⁹ the mechanism by which cetuximab selectively targets EGFR-overexpressing cancer cells is still unknown.⁴³ Because the rate limiting step produced by the previously unknown intermediate state is higher than the fifth order of rate law, this model provides kinetic evidence to account for the steep selectivity of cetuximab to the amount of surface EGFR to induce EGFR internalization. It was observed that cetuximab induced EGFR internalization exhibited strong sigmoidal dependence on the surface expression level of EGFR across normal and cancer cell lines, which was predicted well using this model (Fig. 6B). Furthermore, this model indicates that the first-order binding process of cetuximab to EGFR could not be a selective mechanism for both normal and cancer cells, which implies that the binding process represents a side effect, consistent with the phenomena that the affinity of anti-EGFR antibody drugs is directly proportional to the side effects of the drugs.⁴⁴

Discussion

Use of sptRPKA enables the simultaneous analysis of the sub-minute kinetics of multiple complex states of a membrane protein in a living cell. Utilizing the protein's intrinsic diffusivity allows the detection of different complex states without a requirement for specific labeling, which is remarkably advantageous when these states are unknown. A hidden state detected with sptRPKA can be identified further by analyzing the states before and after the hidden state using traditional biochemical or imaging tools, such as chemical inhibitors or co-localization techniques.²⁵

Various kinetic parameters, including reaction models, rate constants, and stoichiometry for a series of molecular reactions in a living cell, can be obtained by performing a minimal number of experiments using sptRPKA. Furthermore, use of sptRPKA guarantees statistical reliability by obtaining one data point for RPKA using tens of thousands of single molecule trajectory data, which is critical because the quality of kinetic analyses largely depends on accurate measurements. Combined with computational simulations generated by the numerical integration of a set of differential equations,^45,46 sptRPKA can be used to determine reaction models for cellular processes occurring in the membrane of living cells with significantly less uncertainty than traditional graphical methods.

By specifically labeling endogenous EGFR using the Fab fragment of an anti-EGFR antibody conjugated to photoswitchable Alexa Fluor 647,⁴⁷ diffusional dynamics were observed for cetuximab induced endogenous EGFR similar to those of EGFR conjugated to mEos3.2 (see Fig. S18 in the ESI†). The acquisition of longer trajectories by adopting brighter and more stable organic dyes can provide additional diffusional information, such as confined and directed motions. This unique diffusional information can be used to classify the more complex states of membrane proteins that are difficult to classify using only a diffusion coefficient.

Conclusions

Single molecule diffusivity was introduced to RPKA for analysing in vivo kinetics of cellular processes in an intact membrane of living cells. Using sptRPKA, demonstrated unprecedented kinetic analysis by revealing a series of molecular mechanisms for the cetuximab induced EGFR endocytosis. A previously unknown intermediate state was identified, which was a clustering of EGFR, essential for the antibody–drug selectivity to EGFR-overexpressing cancer cells. The diffusivity of membrane proteins can be used to monitor different types of cellular processes, including protein oligomerization,⁴⁸ cytoskeletal protein confinement,⁴⁹ focal adhesion organization,²⁵ membrane microdomain formation,⁵⁰ and directed protein transport.⁵¹ Thus, sptRPKA can be utilized to elucidate comprehensive molecular mechanisms of various cellular processes in the crowded membrane of living cells.

Acknowledgements

This work was supported by a National Research Foundation of Korea (NRF) grant funded by the Ministry of Education Science and Technology of Korea (MEST), No. 2015R1A2A1A13001834 and by the Ministry of Science, ICT and Future Planning, Korea, (MSIP) under the “IT Consilience Creative Program” (NIPA-2014-H0201-14-1001) supervised by the National IT Industry Promotion Agency (NIPA).

Notes and references

1. J. M. Berg, J. L. Tymoczko and L. Stryer, Biochemistry, W. H. Freeman, New York, 7th edn, 2012.
2. R. D. Phair and T. Misteli, Nat. Rev. Mol. Cell Biol., 2001, 2, 898–907.
3. S. J. Ullrich, U. A. Hellmich, S. Ullrich and C. Glaubitz, Nat. Chem. Biol., 2011, 7, 263–270.
4. D. G. Blackmond, Angew. Chem., Int. Ed., 2005, 44, 4302–4320.
5. H. Iwamura, D. H. Wells Jr, S. P. Mathew, M. Klussmann, A. Armstrong and D. G. Blackmond, J. Am. Chem. Soc., 2004, 126, 16312–16313.
6. M. J. Parker, J. Spencer and A. R. Clarke, J. Mol. Biol., 1995, 253, 771–786.
7. G. Lee, J. Yoo, B. J. Leslie and T. Ha, Nat. Chem. Biol., 2011, 7, 367–374.
8. S. Matsuoka, T. Shibata and M. Ueda, PLoS Comput. Biol., 2013, 9, e1002862.
9. P. J. Higgins and H. F. Bunn, J. Biol. Chem., 1981, 256, 5204–5208.
10. J. J. Hornberg, B. Binder, F. J. Bruggeman, B. Schoeberl, R. Heinrich and H. V. Westerhoff, Oncogene, 2005, 24, 5533–5542.
11. A. E. Leschziner and E. Nogales, Annu. Rev. Biophys. Biomol. Struct., 2007, 36, 43–62.
12. M. J. Saxton and K. Jacobson, Annu. Rev. Biophys. Biomol. Struct., 1997, 26, 373–399.
13. A. Kusumi, Y. Sako and M. Yamamoto, Biophys. J., 1993, 65, 2021–2040.
14. Y. Shav-Tal, X. Darzacq, S. M. Shenoy, D. Fusco, S. M. Janicki, D. L. Spector and R. H. Singer, Science, 2004, 304, 1797–1800.
15. S. Manley, J. M. Gillette, G. H. Patterson, H. Shroff, H. F. Hess, E. Betzig and J. Lippincott-Schwartz, Nat. Methods, 2008, 5, 155–157.
16. J. Lippincott-Schwartz, E. Snapp and A. Kenworthy, Nat. Rev. Mol. Cell Biol., 2001, 2, 444–456.
17. I. Chung, R. Akita, R. Vandlen, D. Toomre, J. Schlessinger and I. Mellman, Nature, 2010, 464, 783–787.
18. D. A. Jans, The mobile receptor hypothesis: the role of membrane receptor lateral movement in signal transduction, Springer, N. Y., 1st edn, 1997.
19. A. Robson, K. Burrage and M. C. Leake, Philos. Trans. R. Soc., B, 2013, 368, 20120029.
20. M. Zhang, H. Chang, Y. Zhang, J. Yu, L. Wu, W. Ji, J. Chen, B. Liu, J. Lu, Y. Liu, J. Zhang, P. Xu and T. Xu, Nat. Methods, 2012, 9, 727–729.
21. E. K. Rowinsky, Annu. Rev. Med., 2004, 55, 433–457.
22. E. Van Cutsem, C. H. Kohne, E. Hitre, J. Zaluski, C. R. Chang Chien, A. Makhson, G. D'Haens, T. Pinter, R. Lim, G. Bodoky, J. K. Roh, G. Folprecht, P. Ruff, C. Stroh, S. Tejpar, M. Schlichting, J. Nippgen and P. Rougier, N. Engl. J. Med., 2009, 360, 1408–1417.
23. H. Sunada, B. E. Magun, J. Mendelsohn and C. L. MacLeod, Proc. Natl. Acad. Sci. U. S. A., 1986, 83, 3825–3829.
24. M. J. Saxton, Biophys. J., 1997, 72, 1744–1753.
25. O. Rossier, V. Octeau, J. B. Sibarita, C. Leduc, B. Tessier, D. Nair, V. Gatterdam, O. Destaing, C. Albiges-Rizo, R. Tampe, L. Cognet, D. Choquet, B. Lounis and G. Giannone, Nat. Cell Biol., 2012, 14, 1057–1067.
26. S. C. Knight, L. Xie, W. Deng, B. Guglielmi, L. B. Witkowsky, L. Bosanac, E. T. Zhang, M. El Beheiry, J. B. Masson, M. Dahan, Z. Liu, J. A. Doudna and R. Tjian, Science, 2015, 350, 823–826.
27. D. Normanno, L. Boudarene, C. Dugast-Darzacq, J. Chen, C. Richter, F. Proux, O. Benichou, R. Voituriez, X. Darzacq and M. Dahan, Nat. Commun., 2015, 6, 7357.
28. C. Y. Zhen, R. Tatavosian, T. N. Huynh, H. N. Duc, R. Das, M. Kokotovic, J. B. Grimm, L. D. Lavis, J. Lee, F. J. Mejia, Y. Li, T. Yao and X. Ren, eLife, 2016, 5, e17667.
29. M. L. Jaramillo, Z. Leon, S. Grothe, B. Paul-Roc, A. Abulrob and M. O'Connor McCourt, Exp. Cell Res., 2006, 312, 2778–2790.
30. E. Macia, M. Ehrlich, R. Massol, E. Boucrot, C. Brunner and T. Kirchhausen, Dev. Cell, 2006, 10, 839–850.
31. L. von Kleist, W. Stahlschmidt, H. Bulut, K. Gromova, D. Puchkov, M. J. Robertson, K. A. MacGregor, N. Tomilin, A. Pechstein, N. Chau, M. Chircop, J. Sakoff, J. P. von Kries, W. Saenger, H. G. Krausslich, O. Shupliakov, P. J. Robinson, A. McCluskey and V. Haucke, Cell, 2011, 146, 471–484.
32. D. Patel, A. Lahiji, S. Patel, M. Franklin, X. Jimenez, D. J. Hicklin and X. Kang, Anticancer Res., 2007, 27, 3355–3366.
33. P. G. Saffman and M. Delbruck, Proc. Natl. Acad. Sci. U. S. A., 1975, 72, 3111–3113.
34. D. H. Kim, K. Zhou, D. K. Kim, S. Park, J. Noh, Y. Kwon, D. Kim, N. W. Song, J. B. Lee, P. G. Suh, N. K. Lee and S. H. Ryu, Angew. Chem., Int. Ed., 2015, 54, 7028–7032.
35. Y. Teramura, J. Ichinose, H. Takagi, K. Nishida, T. Yanagida and Y. Sako, EMBO J., 2006, 25, 4215–4222.
36. X. Yu, K. D. Sharma, T. Takahashi, R. Iwamoto and E. Mekada, Mol. Biol. Cell, 2002, 13, 2547–2557.
37. A. Talavera, R. Friemann, S. Gomez-Puerta, C. Martinez-Fleites, G. Garrido, A. Rabasa, A. Lopez-Requena, A. Pupo, R. F. Johansen, O. Sanchez, U. Krengel and E. Moreno, Cancer Res., 2009, 69, 5851–5859.
38. H. T. McMahon and E. Boucrot, Nat. Rev. Mol. Cell Biol., 2011, 12, 517–533.
39. J. Z. Rappoport, S. M. Simon and A. Benmerah, Traffic, 2004, 5, 327–337.
40. J. Gao, Y. Wang, M. Cai, Y. Pan, H. Xu, J. Jiang, H. Ji and H. Wang, Nanoscale, 2015, 7, 2511–2519.
41. A. B. Schreiber, T. A. Libermann, I. Lax, Y. Yarden and J. Schlessinger, J. Biol. Chem., 1983, 258, 846–853.
42. Z. Fan, Y. Lu, X. Wu and J. Mendelsohn, J. Biol. Chem., 1994, 269, 27595–27602.
43. G. P. Adams and L. M. Weiner, Nat. Biotechnol., 2005, 23, 1147–1157.
44. M. S. Ramakrishnan, A. Eswaraiah, T. Crombet, P. Piedra, G. Saurez, H. Iyer and A. S. Arvind, mAbs, 2009, 1, 41–48.
45. C. T. Zimmerle and C. Frieden, Biochem. J., 1989, 258, 381–387.
46. B. V. Alekseev and N. I. Kol'tsov, Kinet. Catal., 2002, 43, 34–37.
47. M. Heilemann, S. van de Linde, M. Schuttpelz, R. Kasper, B. Seefeldt, A. Mukherjee, P. Tinnefeld and M. Sauer, Angew. Chem., Int. Ed., 2008, 47, 6172–6176.
48. D. J. Williamson, D. M. Owen, J. Rossy, A. Magenau, M. Wehrmann, J. J. Gooding and K. Gaus, Nat. Immunol., 2011, 12, 655–662.
49. N. L. Andrews, K. A. Lidke, J. R. Pfeiffer, A. R. Burns, B. S. Wilson, J. M. Oliver and D. S. Lidke, Nat. Cell Biol., 2008, 10, 955–963.
50. A. D. Douglass and R. D. Vale, Cell, 2005, 121, 937–950.
51. K. Jaqaman, H. Kuwata, N. Touret, R. Collins, W. S. Trimble, G. Danuser and S. Grinstein, Cell, 2011, 146, 593–606.

---

Footnotes

† Electronic supplementary information (ESI) available: Details in experimental section and supporting figures. See DOI: 10.1039/c7sc01159h

‡ These authors contributed equally.

---