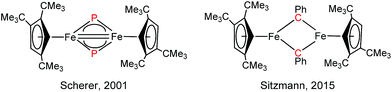Reactivity studies on [Cp′Fe(μ-I)]₂: nitrido-, sulfido- and diselenide iron complexes derived from pseudohalide activation

Abstract

The iron half-sandwich [Cp′Fe(μ-I)]₂ (Cp′ = 1,2,4-(Me₃C)₃C₅H₂, 1) reacts with the pseudohalides NCO⁻, SCN⁻, SeCN⁻ and N₃⁻ to give [Cp′Fe(μ-NCO)]₂ (2), [Cp′Fe(μ-S)]₂ (3), [Cp′Fe(μ-Se₂)]₂ (4) and [Cp′Fe(μ-N)]₂ (5), respectively. Various spectroscopic techniques including X-ray diffraction, solid-state magnetic susceptibility studies and ⁵⁷Fe Mössbauer spectroscopy were employed in the characterization of these species. Mössbauer spectroscopy shows a decreasing isomer shift with increasing formal oxidation state, ranging from Fe(II) to Fe(IV), in complexes 1 to 5. The sulfido-bridged dimer 3 exhibits strong antiferromagnetic coupling between the Fe(III) centers. This leads to temperature-independent paramagnetism (TIP) at low temperature, from which the energy gap between the ground and the excited state can be estimated to be 2J = ca. 700 cm⁻¹. The iron(IV) nitrido complex [Cp′Fe(μ-N)]₂ (5) shows no reactivity towards H₂ (10 atm), but undergoes clean reactions with CO (5 bar) and XylNC (Xyl = 2,6-Me₂C₆H₃) to form the diamagnetic isocyanate and carbodiimide complexes [Cp′Fe(CO)₂(NCO)] (7) and [Cp′Fe(CNXyl)₂(NCNXyl)] (8), respectively. All compounds were fully characterized, and density functional theory (DFT) computations provide useful insights into their formation and the electronic structures of complexes 3 and 5.

---

Introduction

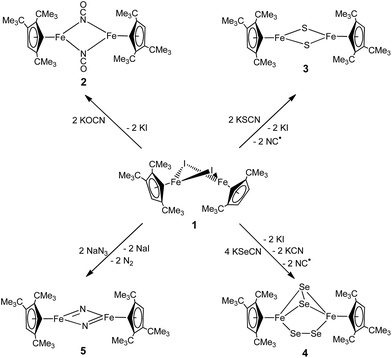
Iron nitrides have been extensively investigated because of their potential in synthetic and biological N₂ activation and functionalization.¹ In general they can be prepared by direct N₂ activation using a low-valent iron species;^1h,1l,1n alternatively N-atom transfer reagents such as Li(dbabh) (dbabh = 2,3:5,6-dibenzo-7-azabicyclo[2.2.1]hepta-2,5-diene² or—more frequently—inorganic azides have been used.^1g,1i,3 However, N₂ elimination from iron azido precursors usually requires forcing conditions such as reduction or photochemical/thermal activation.^1g,1i,3 Nevertheless, surprisingly facile conversion of [Bu₄N]N₃ to the corresponding iron nitride derivative has been observed in the context of trinuclear iron compounds such as [(^tbsL)Fe₃(thf)] (^tbsL = [1,3,5-C₆H₉(NPh-o-NSitBuMe₂)₃]⁶⁻) to yield [Bu₄N][(^tbsL)Fe₃(μ₃-N)].^1j,4

Our laboratory recently reported the synthesis of [Cp′Fe(μ-I)]₂ (Cp′ = η⁵-1,2,4-(Me₃C)₃C₅H₂, 1)⁵ and its reactivity toward KBH₄ to form the metastable, diamagnetic complex [Cp′FeBH₄], which releases H₂ to form a trimeric iron boryl [Cp′FeBH₂]₃.⁶ In contrast, the diiron trihydride and tetrahydride compounds, [Cp′₂Fe₂(μ-H)₃] and [Cp′Fe(μ-H)₂]₂ can be isolated from the reaction of 1 with KHBEt₃.⁷ Although no N₂ activation was achieved with [Cp′Fe(μ-H)₂]₂, it serves under mild conditions as a synthon for reactive iron(I) Cp′Fe-fragments, as illustrated by its facile reaction with white phosphorus (P₄).⁷ These results suggested that the bulky Cp′Fe-fragment provides sufficient steric protection to kinetically hamper [Cp′₂Fe] formation and can also stabilize iron in higher (formal) oxidation states.⁸ The successful synthesis of the phosphido-bridged complex [Cp′Fe(μ-P)]₂ by photochemically induced CO elimination from [Cp′Fe]₂(μ-P₂)(μ-CO) (Chart 1) also supports this assumption.⁹ In this contribution we report on some observations regarding the reactivity and redox chemistry of [Cp′Fe(μ-I)]₂ (1) with pseudohalides such as NCO⁻, SCN⁻, SeCN⁻ and N₃⁻.

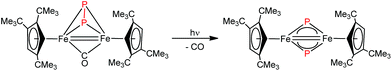Chart 1 Preparation of [Cp′Fe(μ-P)]₂.⁹

Results and discussion

Reaction with pseudohalides

The products formed by the reaction 1 with the KOCN, KSCN, KSeCN and NaN₃ may be divided into three classes; the reactions proceed either with (a) no redox chemistry (OCN⁻), (b) a 2-electron redox process (SCN⁻ and SeCN⁻) or (c) a 4-electron redox process (N₃⁻) to give [Cp′Fe(μ-NCO)]₂ (2), [Cp′Fe(μ-S)]₂ (3) and [Cp′Fe(μ-Se₂)]₂ (4), or [Cp′Fe(μ-N)]₂ (5), respectively (Scheme 1).

Scheme 1 Reaction of 1 with various pseudohalides.

Synthesis of a dimeric μ-NCO iron(II) complex (2)

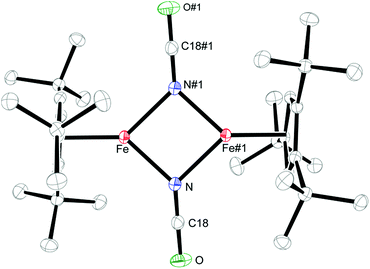
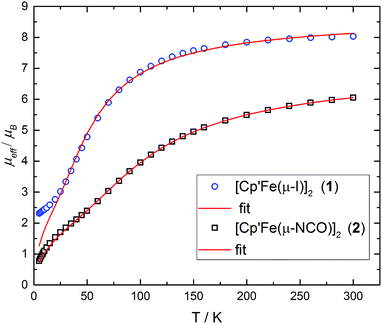
Salt metathesis of 1 with KOCN yields the dimeric iron(II) isocyanate complex [Cp′Fe(μ-NCO)]₂ (2), which is isolated as green crystals in moderate yield (52%). The paramagnetic complex 2 melts intact at 163 °C and shows a molecular ion (662 amu) in the EI-MS spectrum with the correct isotope distribution. The ¹H NMR resonances corresponding to the tBu groups Cp′ ligand (δ = −4.05 (18H) and −7.80 (9H)) are in the same range as those observed for the starting material 1 (δ = −7.8 (18H) and −13.5 (9H)).⁵ Crystals of 2 suitable for an X-ray diffraction experiment were grown from a concentrated pentane solution at −30 °C (see Table S1 in the ESI†) and the molecular structure is shown in Fig. 1. Complex 2 crystallizes in the monoclinic space group P2₁/n with crystallographically imposed inversion symmetry.

Fig. 1 Thermal ellipsoid plot (50% probability) of the molecular structure of 2. H-atoms are omitted for clarity. Selected bond distances (Å) and angles (°): Cp′_cent–Fe 1.919, Cp′_plane–Fe 1.916, Fe–N 2.0425(12), Fe–N#1 2.0840(12), N–C18 1.1904(19), O–C18 1.1824(19), Fe⋯Fe#1 3.002, N–Fe–N#1 86.65(5), Fe–N–Fe#1 93.35(5), O–C18–N 179.36(18). Symmetry transformations used to generate equivalent atoms: #1 −x + 1, −y + 1, −z + 1.

The X-ray data were of sufficient quality to establish exclusive κN-coordination of the ambidentate OCN⁻. Furthermore the iron(II) atoms in 1 and 2 adopt a high-spin configuration with 4 unpaired electrons per Fe(II) atom, as can be inferred from the long Cp′_cent–Fe bond distances in 1 (1.93 Å),⁵2 (1.92 Å) and [Cp′FeOC₆H₃(CMe₃)₂-3,5]₂ (1.94 Å.⁸ For comparison, the Cp′_cent–Fe distances in [Cp′₂Fe] (S = 0) and [Cp′₂Fe][SbF₆] (S = 1/2) are significantly shorter at 1.72 Å (ref. 5) and 1.77 Å,¹⁰ respectively. The spin state assignment in 2 is further substantiated by solid-state magnetic susceptibility data, which indicate antiferromagnetic coupling between the two Fe(II) (S = 2) centers at low temperature (Fig. 2). The magnetic trace for both complexes may be simulated using a Heisenberg exchange Hamiltonian¹¹ and the respective fit parameters are provided in the figure caption. The extent of antiferromagnetic coupling varies significantly between 1 and 2 (J₁₂ = −6.5 cm⁻¹ and J₁₂ = −13.6 cm⁻¹, respectively) which can be rationalized by the difference in the Fe⋯Fe distances in both complexes of 3.526, 3.002 Å, respectively. Furthermore, there are also significant differences in the respective Fe₂X₂-cores. Please note that a butterfly structure is adopted for the Fe₂I₂-core in 1 with afold angle between the two I1–Fe1–I2 and I1–Fe2–I2 planes of 24.49°, whereas a planar Fe₂N₂-core is realized in 2.⁵ Another notable feature is a large negative zero-field splitting parameter D that is required to obtain a suitable simulation of the magnetic trace. Although the model employed is not completely sufficient to describe the low-temperature regime found in complex 1 and no significant improvement is achieved when a paramagnetic impurity is assumed. We also want to mention that this feature has been observed in several independently prepared samples prepared over the time frame of several years and measured on different magnetometers and using different sample containers (quartz tubes or KEL-F buckets).

Fig. 2 Effective magnetic moment μ_effvs. T plots for compounds 1 and 2. Fit parameter for 1: S₁ = S₂ = 2.0; g₁ = g₂ = 2.51; J₁₂ = −6.5 cm⁻¹; D₁ = D₂ = −18.16 cm⁻¹, E/D₁ = E/D₂ = 0.11. Fit parameter for 2: S₁ = S₂ = 2.0; g₁ = g₂ = 2.04; J₁₂ = −13.6 cm⁻¹; D₁ = D₂ = −32.85 cm⁻¹, E/D₁ = E/D₂ = 0.10.

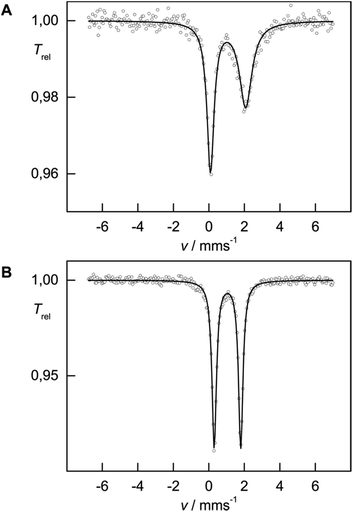
While solid-state magnetic susceptibility studies represent a bulk method, the local electronic structure at the individual Fe nucleus may conveniently be probed by ⁵⁷Fe Mössbauer spectroscopy.¹² The isomer shift (δ_iso) provides information on the s-electron density at the Fe nucleus, which is modulated by the iron oxidation state, the spin state and the covalency in the iron–ligand bonds. However, in strongly covalent compounds unambiguous assignment of the oxidation and spin state exclusively based on δ_iso is not necessarily straightforward, but some trends have emerged from extensive studies on various iron (coordination) compounds, and are well understood.¹² In contrast, Mössbauer investigations on Cp-containing iron complexes, which are more covalent than traditional coordination complexes, have remained relatively rare.¹³ In zero-field ⁵⁷Fe Mössbauer spectra (at 77 K), complexes 1 and 2 show well-resolved doublets with isomer shifts δ_iso = 1.08(1) and 1.05(1) mm s⁻¹ and with a quadrupole splitting ΔE_Q = 1.98(1) and 1.49(1) mm s⁻¹, respectively (Fig. 3), which is in the range commonly observed for high-spin (S = 2) Fe(II) species.^12a The asymmetry in the quadrupole doublet of 1 indicates a dynamic process, for which the spin relaxation time at 77 K is close to the Mössbauer time scale (ca. 10⁻⁷ s) (=intermediate spin relaxation regime).^13c

Fig. 3 Zero field Mössbauer spectra of 1 (A) and 2 (B) recorded at 77 K.

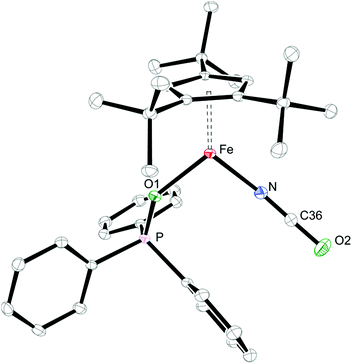
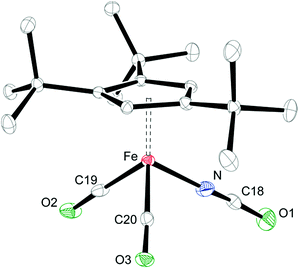
When coordinating ligands such as Ph₃PO and CO are added to 1 and 2, either 16- or 18-valence-electron (VE) complexes are formed (Scheme 2). For example, addition of Ph₃PO results in isolation of the paramagnetic, 16-valence-electron (VE) complexes [Cp′Fe(I)(OPPh₃)] (see ESI† for details) and [Cp′Fe(NCO)(OPPh₃)] (6), respectively. Furthermore, the exchange of free and coordinated Ph₃PO is slow on the NMR time scale and no spin state change occurs when the dimeric structure is broken (see ESI† for details). In contrast, exposure of 1 and 2 to CO (1 atm) immediately forms the diamagnetic, 18VE derivatives [Cp′Fe(CO)₂(I)]¹⁴ and [Cp′Fe(CO)₂(NCO)] (7), respectively. The molecular structures of 6 and 7 are shown in Fig. 4 and 5, respectively; selected bond distances and angles are listed in the corresponding figure captions. The most notable difference in the molecular structures of these compounds are the Cp′_cent–Fe distances of 1.97 Å vs. 1.73 Å for 6 and 7, which reflect their different electronic ground states of S = 2 and S = 0, respectively.

Scheme 2 Adduct formation of 2 with Ph₃PO and CO.

Fig. 4 Thermal ellipsoid plot (30% probability) of the molecular structure of 6. H-atoms are omitted for clarity. Selected bond distances (Å) and angles (°): Cp′_cent–Fe 1.968, Cp′_plane–Fe 1.967, Fe–N 1.9530(17), Fe–O1 2.0164(13), O1–P 1.5074(14), N–C36 1.170(3), C36–O2 1.203(6), O1–Fe–N 101.30(7), Fe–O1–P 137.97(8), Fe–N–C36 154.80(18), N–C36–O2 177.2(2).

Fig. 5 Thermal ellipsoid plot (30% probability) of the molecular structure of 7. H-atoms are omitted for clarity. Selected bond distances (Å) and angles (°): Cp′_cent–Fe 1.732, Cp′_plane–Fe 1.731, Fe–N 1.952(3), Fe–C19 1.785(3), Fe–C20 1.784(2), N–C18 1.108(4), C18–O1 1.248(4), C19–O2 1.147(3), C20–O3 1.151(3), Fe–N–C18 173.1(2), N–C18-01 173.8(3).

Preparation of sulfido- (3) and diselenido-bridged (4) iron(III) complexes from KSCN and KSeCN

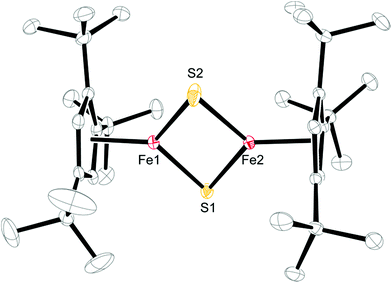
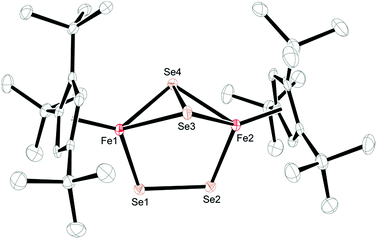
When the heavier homologues KSCN and KSeCN are employed, the Fe(III) compounds 3 and 4 are isolated in low yield (Scheme 1). The formation of these compounds is unexpected, since generally no redox processes are encountered when pseudohalides coordinate to transition metals,¹⁵ which implies that the Cp′Fe-fragment is susceptible to redox chemistry. Furthermore, this redox behavior is apparently facilitated by the synergy between two or more Fe atoms, an effect that also accounts for the facile N₂ release from [Bu₄N]N₃ in the presence of [(^tbsL)Fe₃(thf)].⁴ Furthermore, S–C bond cleavage of a SCN⁻ ligand is a rare event, but has previously been observed in [Pd₃(SCN)(μ₃-CO)(μ-dppm)₃]⁺ to form [Pd₃(μ₃-S)(CN)(μ-dppm)₃]⁺.¹⁶ The FeMoco nitrogenase enzyme also transiently binds SCN⁻ before reduction to HCN and H₂S occurs; but the mechanism of this biological SCN⁻ reduction remains unknown.¹⁷ Cleavage of the S–C and Se–C bond to form 3 and 4 requires that the Fe(II) atoms are oxidized to Fe(III) concomitant with the formation of CN˙ radicals. The remarkable difference between the reactivity of [OCN]⁻ and [XCN]⁻ (X = S, Se) is most likely traced to the inherently weaker C–X bonds for the higher chalcogenide homologues (X = S and Se), which also result in shorter and therefore stronger C–N bonds of 1.15 Å in the free thio- and selenocyanate anions.¹⁸ On coordination of [XCN]⁻ (X = S, Se) to two Fe(II) fragments [Cp′Fe]⁺ (as in complex 2) a redox-process into the σ*-orbitals of the C–X bond can then be initiated leading to the Fe(III) compounds 3 and 4 and CN˙ radicals, which are highly reactive species that readily undergo H atom abstractions from THF to generate HCN,¹⁹ or alternatively they may dimerize to cyanogen (CN)₂. Unfortunately, we have so far been unable to detect either of these side products spectroscopically. Nevertheless, it is conceivable that the formation of HCN or (CN)₂ can induce undesired side reactions, which cause the observed formation of hydrolyzed Cp′ ligand (HCp′) and unidentified paramagnetic species in the reaction mixture. This may also account for the relatively low yields, in which complexes 3 and 4 are isolated as crystalline and analytically pure materials (13% and 15%, respectively). Nevertheless, the formation of the diselenido-bridged complex [Cp′Fe(μ-Se₂)]₂ (4) can be rationalized by the fact that selenocyanate SeCN⁻ can also act as a Se source.²⁰ The formation of the diselenido-bridged complex 4 suggests that it represents a thermodynamic minimum relative to the selenido-bridged species [Cp′Fe(μ-Se)]₂.

Iron–sulfur clusters play an important role as biological cofactors involved in electron transfer processes.²¹ Hence, several bioinorganic model complexes with thiolato ligands have been prepared²² and their electrochemistry studied.²³ Despite significant general interest in these systems,²⁴ well-defined [2Fe–2S] derivatives with other than thiolato co-ligands have remained rare.²⁵ From an organometallic point of view, metal chalcogenido clusters are generally prepared by the thermal reaction of elemental chalcogens with transition metal carbonyls such as [CpFe(μ-CO)(CO)]₂.²⁶ The outcome of these reactions is not very predictable, but some control can be achieved by changing the steric demand on the Cp-ligands, whereby various iron chalcogenides such as [(η⁵-C₅H₅)₄Fe₄S_n] (n = 4–6),²⁷ [(η⁵-C₅Me₅)₂Fe₂S₄],²⁸ [(η⁵-(Me₃Si)C₅H₄)₄Fe₄S₆],²⁹ [(η⁵-1,3-(Me₃Si)₂C₅H₃)₂Fe₂S₄],²⁹ [(η⁵-C₅H₅)₂Fe₄Se₄],³⁰ and [(η⁵-C₅Me₅)₃Fe₃Se₈]³¹ have been isolated. However, the facile and selective formation of [Cp′Fe(μ-S)]₂ (3) from 1 and KSCN provides the first organometallic model of the Rieske [2Fe–2S] cluster, whereas thermolysis of [Cp′Fe(CO)(μ-CO)] in the presence of S₈ only yields the disulfide-bridged compound [Cp′Fe(μ-S₂)]₂ (see ESI† for details).

Crystals of 3 and 4 were obtained from concentrated Et₂O solutions at −30 °C (see Table S1 in the ESI†) and their molecular structures are shown in Fig. 6 and 7. Selected bond distances and angles are listed in the respective figure captions.

Fig. 6 ORTEP of [Cp′Fe(μ-S)]₂ (3) (30% probability ellipsoids). H-atoms are omitted for clarity. Selected bond distances (Å) and angles (°): Cp′_cent–Fe(ave) 1.833, Cp′_plane–Fe(ave) 1.831, Fe1–S1 2.1415(6), Fe1–S2 2.1305(7), Fe2–S1 2.1435(6), Fe2–S2 2.12393(7), Fe1⋯Fe2 2.5873(5), S1⋯S2 2.587, Fe1–S1–Fe2 74.29(2), Fe1–S2–Fe2 74.91(2), S1–Fe1–S2 105.21(3), S1–Fe2–S2 105.37(3).

Fig. 7 ORTEP of [Cp′Fe(μ-Se₂)]₂ (4) (50% probability ellipsoids). H-atoms are omitted for clarity. Selected bond distances (Å): Cp′_cent–Fe(ave) 1.712, Cp′_plane–Fe(ave) 1.710, Fe1–Se1 2.2513(6), Fe1–Se3 2.4055(6), Fe1–Se4 2.4145(6), Fe2–Se2 2.2432(6), Fe2–Se3 2.4213(6), Fe2–Se4 2.4073(6), Se1–Se2 2.2993(5), Se3–Se4 2.3255(5), Fe1⋯Fe2 3.721.

A comparison of the structural parameters for the [2Fe–2S] core in 3 with the biological [2Fe–2S] clusters and their biomimetic models shows some interesting features. Complex 3 has significantly shorter Fe–S bond distances with an average value of 2.1349 ± 0.0093 Å than those found in the structurally characterized biological systems, which range from 2.16–2.23 Å. The latter values are well reproduced in the biomimetic structures (2.185–2.232 Å).^25c,32 In addition, the average Fe–S–Fe and S–Fe–S bond angles of 74.60 ± 0.44° and 105.29 ± 0.11° are also at the lower and upper ends of the literature examples.^25c,32 Consequently the Fe–Fe distance of 2.5873(5) Å is shorter than that in [(meso-phenyl-dibenzimidazolate)₂Fe₂(μ-S)]²⁻ (2.7019(5) Å)^25c or in [(nacnac)Fe(μ-S)]₂ (nacnac = MeC[C(Me)N(2,6-Me₂C₆H₃)]₂) (2.669(1) Å).^32b The more compact [2Fe–2S] core may manifest itself in the physical properties of 3, e.g., the magnetic exchange interaction between the two Fe(III) atoms (vide infra).

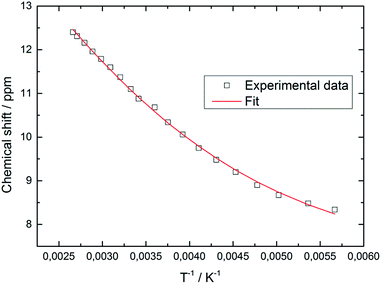
In contrast, the diselenide-bridged compound 4, which displays non-crystallographic twofold symmetry (r.m.s. deviation 0.12 Å), features a rather long Fe⋯Fe distance of 3.721 Å. The Fe–Se distances are 2.2513(6) Å and 2.2432(6) Å for the end-on coordinated [Se₂]²⁻ moiety, while those corresponding to the side-on coordinated [Se₂]²⁻ moiety range between 2.4055(6) Å and 2.4213(6) Å. This leads to Se–Se distances of 2.2993(5) Å and 2.3255(5) Å for the end-on and side-on coordinated [Se₂]²⁻ fragments, respectively. In accord with these different binding modes, two resonances at δ = 2103.2 and 493.2 ppm are found in the ⁷⁷Se NMR spectrum. Unfortunately, we cannot unambiguously assign these chemical shifts to the different coordination modes. Several transition metal polyselenides,³³ are known, such as [{(η⁵-C₅H₅Me)V(μ-Se₂)}₂(μ-Se)],³⁴ but no ⁷⁷Se NMR data have been provided. Nevertheless, complexes 3 and 4 feature significantly shorter average Cp′_cent–Fe distances of 1.83 and 1.71 Å than in their Fe(II) counterparts 1 and 2. This difference of 0.12 Å between 3 and 4 appears unusual, considering that both molecules contain Fe(III) atoms. A d⁵ system can potentially adopt three different spin states of S_Fe = 1/2, S_Fe = 3/2 and S_Fe = 5/2; and in a dimeric structure these iron centers can either be magnetically independent or anti-/ferromagnetically coupled. A closer inspection of the ¹H NMR spectra of 3 and 4 reveals that the resonances of the Cp′ moiety are narrow and occur between δ = 11.0 and 0.4 ppm for 3 and δ = 5.9 and 0.8 ppm for 4. The larger chemical shift window for complex 3 is also found in its ¹³C{¹H} NMR spectrum, which shows very unusual chemical shifts for a diamagnetic compound ranging from δ = 235.3 to 9.7 ppm; the most downfield shifted resonance (δ = 235.3 ppm) is assigned to one of the Cp′ ring-C_ipso positions. This indicates that unpaired spin density is transferred from the iron atoms to the Cp′ ligand.³⁵ These observations prompted us to record variable temperature (VT) ¹H NMR spectra for 3 and 4. While the ¹H NMR resonances in 4 exhibit only a negligible temperature dependence (see ESI† for details), the ring CH resonance in 3 varies from δ = 8.34 to 12.40 ppm in the temperature range 176 K to 376 K, approaching a diamagnetic limit at low temperature (Fig. 8). The different VT behavior can be rationalized by antiferromagnetic coupling between the two Fe(III) atoms in 3 and 4 to form an open-shell singlet ground state, whereby the degree of exchange coupling is significantly different in both materials. While in 4 the Fe(III) atoms undergo strong antiferromagnetic coupling, a smaller energy gap between ground and excited state in 3 allows the thermal population of the (uncoupled) excited state. Based on the underlying Boltzmann distribution the energy gap (2J) between these states can be estimated (Fig. 8).

Fig. 8 Temperature dependence of the ¹H NMR Cp′ ring-CH resonance in 3 and the associated fit.

The fit of the temperature dependence of the ¹H NMR chemical shifts of Cp′ ring CH resonance yields an energy separation of |2J| = 654 cm⁻¹ (0.082 eV or 1.87 kcal mol⁻¹). Similar analyses have previously been applied to model spin-equilibria in [(C₅Me₅)Ni(acac)]³⁶ or [(PNP)RuCl] (PNP = N(CH₂CH₂PtBu₂)₂).³⁷

The effective magnetic moment of 3 increases gradually from 0.95 μ_B at 5 K to 1.98 μ_B at 360 K, consistent with strong antiferromagnetic coupling between the Fe(III) atoms. Fig. 9 shows the experimental data and the fit to the effective spin Hamilitonian Ĥ = −2J(Ŝ₁Ŝ₂) + gβ(ŜB), where J is the coupling constant and g represents the average electronic g value. Since the effective magnetic moment is still increasing at 360 K, we cannot unambiguously establish the spin state of the individual Fe(III) atoms, i.e. S_Fe = 1/2, S_Fe = 3/2, and S_Fe = 5/2. While we prefer the intermediate spin description (S_Fe = 3/2) based on the Cp′_cent–Fe(ave) 1.833 Å, the other possibilities were also evaluated (see ESI† for details). Gratifyingly, the coupling constant J remains almost unaffected by the model employed for the simulation of the experimental data; Fig. 9 shows the results obtained for S_Fe = 3/2. Importantly, the J values determined from solution (NMR, J = −327 cm⁻¹) and solid-state (magnetic susceptibility, J = −354 cm⁻¹) data of 3 are in good agreement with each other. In addition, the antiferromagnetic exchange coupling in 3 is also significantly stronger than in the biomimetic model [(meso-phenyl-dibenzimidazolate)₂Fe₂(μ₂-S)]²⁻ (J = −179 cm⁻¹).^25c This increase may be caused by the shorter Fe–Fe and Fe–S bond distances in 3 facilitating direct and super-exchange coupling.

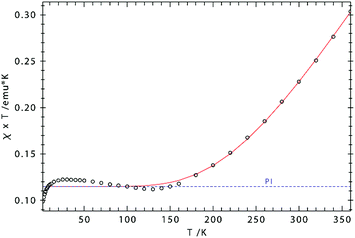Fig. 9 χT vs. T plot for 3. Simulation: S₁ = S₂ = 3/2; g₁ = g₂ = 2.244; J = −354 cm⁻¹ [2J = −708 cm⁻¹], paramagnetic impurity (PI, S = 2) = 2.6%, TIP = 1087 × 10⁻⁶ emu).

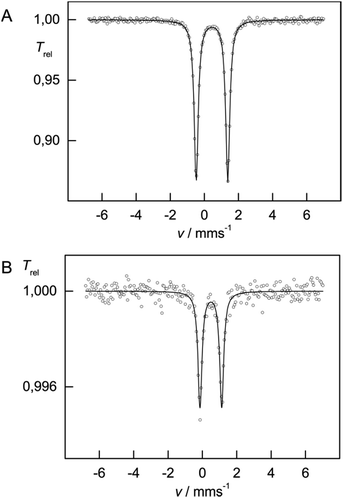
The ⁵⁷Fe Mössbauer spectra recorded at 77 K for complexes 3 and 4 are shown in Fig. 10. In contrast to compounds 1 and 2, the isomer shifts in 3 and 4 are significantly reduced with δ_iso = 0.45(1) mm s⁻¹ [ΔE_Q = 1.85(1) mm s⁻¹] and δ_iso = 0.49(1) mm s⁻¹ [ΔE_Q = 1.26(1) mm s⁻¹], respectively. This reduction is consistent with a change in formal oxidation state from Fe(II) to Fe(III). DFT computations further provide deeper insights into the electronic structure of 3 (vide infra).

Fig. 10 Zero field Mössbauer spectra of 3 (A) and 4 (B) recorded at 77 K. The selenium atoms in 4 act as strong absorber of the Mössbauer γ-radiation, so that only small effects (1.000 to 0.995) could be achieved despite collecting data for 12 days.

Preparation of nitrido- bridged iron(IV) complex (5) from NaN₃

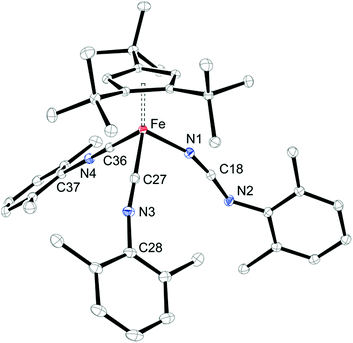
Equally interesting is the reaction of 1 with NaN₃, from which the dinuclear iron nitrido complex [Cp′Fe(μ-N)]₂ (5) is isolated. The formation of 5 was investigated in more detail by ¹H NMR spectroscopy in THF-d₈. When 1 is dissolved in THF-d₈, a yellow solution is formed that shows significantly upfield shifted tBu-resonances in the ¹H NMR spectrum at δ = −22.4 and −27.7 ppm, corresponding to 18H and 9H, respectively. We rationalize this change in chemical shifts relative to those recorded in C₆D₆ solutions of 1 with the formation of a labile mono-THF adduct [Cp′Fe(I)(thf-d₈)].⁵ On addition of NaN₃ the THF-d₈ solution colour gradually changes from yellow to orange and the ¹H NMR resonances of the tBu-groups shift downfield to δ = −15.8 and −22.3 ppm, respectively. Furthermore, a strong IR stretch at 2059 cm⁻¹ indicates the formation of an iron azido intermediate. When the THF solvent is removed under dynamic vacuum, an orange oily residue is initially formed that solidifies and turns olive-green on further exposure to dynamic vacuum. When this olive-green residue is extracted into C₆D₆, only the resonances corresponding to 5 are observed in the ¹H NMR spectrum (see Experimental section for details). Consistent with these observations we propose the following mechanism: initial salt metathesis between 1 and NaN₃ forms a solvent-stabilized iron azido intermediate [Cp′Fe(N₃)(thf)] (A) that loses the coordinated THF on exposure to dynamic vacuum and generates a dimeric iron azido intermediate [Cp′Fe(μ-N₃)]₂ (B). Nevertheless, intermediate B is unstable and readily eliminates N₂ at ambient temperature (even in the absence of light) (Scheme 3) to yield the dimeric iron nitrido species 5. Although our spectroscopic data support this mechanistic proposal, we have so far been unable to provide structural evidence for intermediates A and B. Nevertheless, the isolation of the 2 and its Ph₃PO adduct [Cp′FeI(OPPh₃)] is consistent with this proposal (see ESI† for details).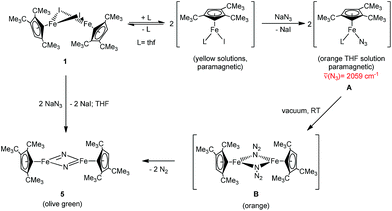

Scheme 3 Proposed mechanism for the formation of [Cp′Fe(μ-N)]₂ (5). Intermediates given in parenthesis were not isolated.

Complex 5 may be crystallized from concentrated Et₂O solution to yield olive-green crystals that decompose at 191–193 °C with gas evolution. In the EI-MS spectrum a molecular ion with the correct isotope distribution is observed, which shows that the Fe₂N₂ core stays intact under EI-MS conditions. When ¹⁵N-enriched sodium azide, Na¹⁵N(¹⁴N)₂ is used, 5 is isolated with a statistical isotopic distribution, that is, a 1 : 1 : 2 mixture of [Cp′Fe(μ-¹⁵N)]₂, [Cp′Fe(μ-¹⁴N)]₂ and [Cp′₂Fe₂(μ-¹⁵N)(μ-¹⁴N)], respectively. In an attempt to probe the stability of the Fe₂N₂-moiety, unlabeled [Cp′Fe(μ-N)]₂ was added to the ¹⁵N-enriched statistical mixture in an 1 : 1 ratio. This mixture was then dissolved in diethyl ether, crystallized and subjected to an EI-MS analysis. However, no enrichment of the mixed [Cp′₂Fe₂(μ-¹⁵N)(μ-¹⁴N)] compound was observed, suggesting that under the chosen conditions no dissociation into monomeric [Cp′FeN]-fragments occurred.

The ¹H and ¹³C{¹H} NMR spectra of 5 show narrow resonances in the diamagnetic region and the ¹H NMR resonances exhibit only negligible temperature dependence (see Experimental section and ESI† for details), which also argues against a dissociation into monomeric species in solution. The ¹⁵N NMR spectrum recorded for ¹⁵N-enriched 5 features a significantly downfield shifted resonance at δ(¹⁵N) = 1118 ppm (relative to NH_3(liq)). Interestingly, the related iron phosphido compound [Cp′Fe(μ-P)]₂ also exhibits a strongly downfield shifted ³¹P NMR resonance at δ(³¹P) = 1406.9 ppm.⁹

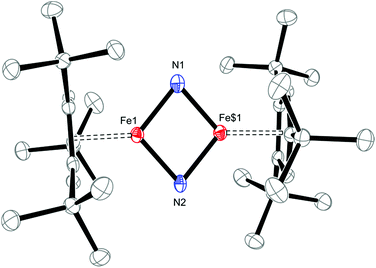
Solid-state structural information on 5 was provided by X-ray diffraction. Fig. 11 shows the molecular structure of 5, which crystallizes in the tetragonal space group P4₁2₁2 (see ESI† for details); and selected bond distances and angles are provided in the figure caption. The planar Fe₂N₂–core in 5 has pseudo-D_2h symmetry and features nearly equal Fe1–N1 and Fe1–N2 bond distances of 1.744(2) and 1.734(2) Å, respectively. This is surprising, since the M–N bond distances in neutral M₂N₂ complexes commonly follow a distinct short-long-short-long pattern.³⁸ The situation realized in 5 more closely resembles that typically observed in Fe₂O₂ complexes with their well-known diamond-core structural motifs.³⁹ This is the first example of a d⁴ system adopting a M₂N₂ core and previous examples of neutral M₂N₂ species are limited to compounds with a formal d⁰ or d¹ electron configuration such as [(η⁵-C₅Me₅)V(Cl)(μ-N)]₂,⁴⁰ [(η⁵-C₅Me₅)V(Cl)(μ-N)]₂,⁴¹ {[(Me₃SiN{CH₂CH₂NSiMe₃}₂)V(μ-N)]₂}ⁿ (n = 0, −1),^38b [(iPr₂N)₂Cr(μ-N)]₂,^38a, [{(anti-O₃)Nb(μ-N)}₂],⁴², [{(η⁵-C₅Me₅)(η³-iPrNC(Me)N_iPr)Ta(μ-N)}₂]⁴³ [(tBuCH₂)(RO)₂W(μ-N)]₂}ⁿ (n = 0, −1)^38c and [{(ArO)₂Nb(μ-N)}₂]ⁿ (n = 0, −1).⁴⁴ Both aspects render 5 and [Cp′Fe(μ-P)]₂ rather unusual, with their formal Fe(IV) d⁴ ground states. The Fe–N bond distances of 1.744(2) and 1.734(2) Å in 5 may also be compared to standard Fe–N single and Fe=N double bonds, which lie in the range 1.9–2.0 Å and 1.6–1.7 Å, respectively.⁴⁵ For comparison, the Fe–N distances in complex 2 (2.0425(12) and 2.0840(12) Å) are significantly longer than those in 5. Furthermore, the very long N⋯N distance of 2.667 Å precludes any direct interactions between the bridging N-atoms in 5, but the short Fe–Fe distance of 2.2325(7) Å raises questions regarding any direct Fe–Fe interactions, e.g., for Fe=Fe double bonds a Fe–Fe distance of 2.316(1) Å was reported.⁴⁶ In the related phosphido derivative [Cp′Fe(μ-P)]₂ the Fe–Fe distance is as expected longer at 2.5005(4) Å, and to fulfil the 18VE rule the authors originally proposed a Fe=Fe double bond.⁹ In contrast, for the iron alkylidyne derivative [Cp′Fe(μ-CPh)]₂, which also features a short Fe–Fe distance of 2.3558(4) Å, DFT computations and NBO analyses indicate no direct Fe–Fe bonding interaction; and the benzylidyne ligands should instead be considered as deprotonated phenylcarbene fragments coordinated to two [Cp′Fe]⁺ fragments; thus, forming a low-spin iron(II) complex (Chart 2).⁴⁷

Fig. 11 ORTEP of [Cp′Fe(μ-N)]₂ (5) (50% probability ellipsoids). H-atoms are omitted for clarity. Selected bond distances (Å) and angles (°): Cp′_cent–Fe 1.744, Cp′_plane–Fe 1.744, Fe1–N1 1.744(2), Fe1–N2 1.734(2), Fe1$1–N1 1.744(2), Fe1$1–N2 1.734, Fe1⋯Fe1$1 2.2325(7), N1⋯N2 2.667, N1–Fe1–N2 100.14(9), Fe1–N1–Fe1$1 79.59(13), Fe1–N2–Fe$1 80.13(14). Symmetry transformations used to generate equivalent atoms: $1 −y, −x, −z + 0.5.

Chart 2 Comparison between [Cp′Fe(μ-P)]₂ (ref. 9) and [Cp′Fe(μ-CPh)]₂.⁴⁷

We will present a more detailed analysis of the bonding in 5, especially in comparison to [Cp′Fe(μ-P)]₂ (ref. 9) and [Cp′Fe(μ-CPh)]₂,⁴⁷ in our computational details section. However, the Cp′_cent–Fe distance of 1.74 Å in 5 compares well with the values found in [Cp′Fe(μ-P)]₂ (1.73 Å)⁹ and [Cp′Fe(μ-CPh)]₂ (1.74 Å);⁴⁷ and it is also consistent with an S = 0 ground state. To further address the electronic structure, the ⁵⁷Fe Mössbauer spectrum and solid-state magnetic susceptibility data for 5 were recorded (vide infra). The Mössbauer spectrum of 5 (at 77 K) features a doublet with an isomer shift of δ_iso = −0.02(1) mm s⁻¹ and a quadrupole splitting ΔE_Q = 0.71(1) mm s⁻¹. Within the investigated series of [Cp′Fe(μ-X)]₂ compounds this value represents the lowest isomer shift, which is consistent with a reduction of δ_iso with increasing oxidation state (Fig. 12).

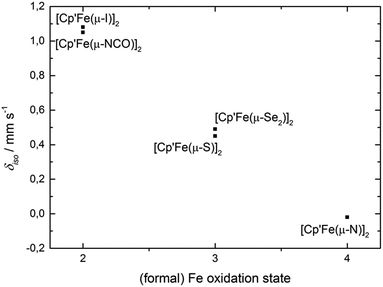Fig. 12 Correlation between the (formal) oxidation state of compounds [Cp′Fe(μ-X)]₂ (1–5) and the Mössbauer isomer shift (δ_iso) at 77 K.

The magnetic susceptibility data show that complex 5 behaves as a temperature-independent paramagnet (TIP) (see ESI† for details) indicating the presence of strong antiferromagnetic coupling between the Fe atoms, mediated either by the nitrido bridges (super-exchange) or an Fe–Fe bond (direct exchange). This is also consistent with the negligible temperature dependence of the ¹H NMR chemical shifts.

Reactivity studies on [Cp′Fe(μ-N)]₂ (5)

In a preliminary study, we further investigated the reactivity of 5 towards H₂, CO, N-heterocyclic carbenes (NHCs) and isonitriles (XylNC, where Xyl = 2,6-Me₂C₆H₃). Complex 5 exhibits no reactivity with H₂ when a hexane solution of 5 is exposed to H₂ (10 bar) at ambient temperature for one week, but on exposure to CO (5 bar) a rapid conversion occurs to yield [Cp′Fe(CO)₂(NCO)] (7) (see Experimental section for details). We assume that in an initial reaction CO reacts with 5 to form the isocyanato-bridged intermediate [Cp′Fe(μ-NCO)]₂ (2), which then rapidly reacts with an excess of CO to form 7. This led us also to probe the reactivity with isonitriles such as XylNC and indeed we isolated the carbodiimido complex [Cp′Fe(CNXyl)₂(NCNXyl)] (8) (Scheme 4) in good yield. The molecular structure of 8 is shown in Fig. 13, and the selected bond distances and angles are provided in the figure caption. We also monitored this reaction upon addition of substoichiometric quantities of XylNC by ¹H NMR spectroscopy. In C₆D₆ solution we detected starting material 5, product 8 and small quantities of a paramagnetic intermediate, which we assume to be [Cp′Fe(μ-NCNXyl)]₂. Unfortunately, every attempt to isolate this intermediate failed, and we attribute this to a slow conversion of 5 to form the proposed [Cp′Fe(μ-NCNXyl)]₂ intermediate, followed by a rapid reaction of this species with excess of XylNC.

Scheme 4 Reactivity of 5 with CO and XylNC.

Fig. 13 ORTEP of [Cp′Fe(CNXyl)₂(NCNXyl)] (8) (30% probability ellipsoids). H-atoms are omitted for clarity. Selected bond distances (Å) and angles (°): Cp′_cent–Fe 1.73, Fe–C27 1.8221(13), Fe–C36 1.8265(13), Fe–N1 1.9555(11), N1–C18 1.1640(18), N2–C18 1.2861(17), N2–C19 1.3895(16), N3–C27 1.1769(18), N3–C28 1.3974(17), N4–C36 1.1716(17), N4–C37 1.3964(16), C27–N3–C28 168.29(13), C36–N4–C37 170.48(14), N1–C18–N2 170.44(14).

We then also screened the reactivity of 5 with a series of N-heterocyclic carbenes (NHCs), but only unreacted starting material was recovered. Presumably the sterically hindered nitrido functionalities in 5 are not accessible to bulky substrates.

Computational studies

Computational investigations have become increasingly popular for experimental chemists to rationalize their findings.⁴⁸ Nevertheless, it is always imperative to calibrate the computational results to experimental data in order to demonstrate the adequacy of the chosen computational method. At the beginning the structure of complex 1 was computed at the B3PW91 level of theory. Gratifyingly, the optimized structure reproduces the experimental data reasonably well (Table 1).

Table 1 Selected computed and experimental bond distances for complex 1

Geometrical data (Å)	Exp	Computed
Cp(centroid)–Fe	1.93	1.94
Fe1–I1	2.6748(5)	2.79
Fe1–I2	2.7088(5)	2.75
Fe2–I1	2.7120(5)	2.75
Fe2–I2	2.6780(5)	2.79
Fe1⋯Fe2	3.5263(8)	3.83

---

For example, the computed and experimental Cp(cent)–Fe(ave) bond distance is in good agreement, while the computed Fe–I bond distances are elongated by 0.04 - 0.12 Å, which is also reflected in a significant elongation of the computed Fe1 Fe2 (3.83 Å, exp.: 3.5263(8) Å) distance. In a next step, the molecular structures and relative energies of the different spin states of [Cp′Fe(μ-NCO)]₂ (2) and of those of the proposed intermediates [Cp′Fe(μ-SCN)]₂ and [Cp′Fe(μ-N₃)]₂ were computed (see ESI† for details). For 2 the computed geometry also compares well with the experimentally determined geometry. In addition, for the cyanato- and isothiocyanato-bridged dimers, the ambiphilic binding modes of these pseudohalides (O vs. N and S vs. N coordination) were also explored and in both cases, the coordination via the N-atom is energetically more favourable (see ESI† for details). While this is indeed consistent with the experiment for compound 2, our computations predict a more complicated situation for the formation of 3, in which μ-κ²-S,N and μ-κ-N coordinated intermediates are suggested to be in equilibrium with each other and may therefore be involved in the formal elimination of CN˙ radicals (see ESI† for details). However, this will require more detailed experimental and computational studies, which are currently ongoing and will be reported in the future.

We then turned our attention to the bonding situation in [Cp′Fe(μ-S)]₂ (3) and [Cp′Fe(μ-N)]₂ (5). For both molecules a series of different spin states was originally considered using the B3PW91 functional (see ESI† for details). For complex 3 four different spin states were found to be close in energy (i.e., within 0.3 eV) (Fig. 14).

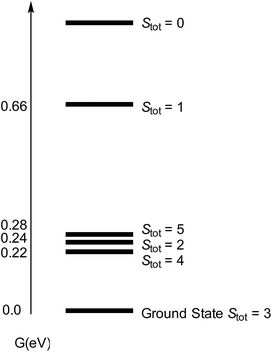Fig. 14 Computed spectrum of electronic spin states (at the B3PW91 level of theory) for [Cp′FeS]₂ (3) with S_tot = S_Fe,1 + S_Fe,2.

However, the ground state configuration of S_tot = 3 (computed at the B3PW91 level of theory) is clearly inconsistent with the experimentally observed TIP and indicates unresolved shortcomings of the DFT description of these open shell systems. Therefore, a more sophisticated approach at a higher level of theory is required (vide supra). A similar situation arises when the bonding situation in the iron nitrido compound [Cp′Fe(μ-N)]₂ (5) is analysed using DFT methods. The computed molecular structure matches the experimental structure (see ESI† for details), and the potential spin isomers were also evaluated. During these investigations, we found that the quintet and singlet spin states are almost degenerate in energy (their Gibbs free energies (ΔG⁰) are equal within 0.07 eV). As shown for complex 3, DFT methods can be problematic when applied to open shell systems, especially when different spin states are very close in energy. Complexes 3 and 5 possess d-electron configurations of 3d^4.58 and 3d^4.33, respectively, which are associated with their formal oxidation states of Fe(III) (3d⁵) and Fe(IV) (3d⁴). In 3, the NBO analysis indicates strongly polarized Fe–S bonds with 70% S and 30% Fe composition. Furthermore, at the second order donor–acceptor NBO, another strong donation (73 kcal mol⁻¹) from a π lone pair on sulphur to an empty d orbital on iron is found. The NBO analysis of 5 also suggests strongly polarized Fe–N bonds; a first order analysis reveals four Fe–N single bonds (with 40% Fe–60% N contributions). This strong polarization of the Fe–N bonds is also reflected in their small Wiberg bond indexes of 0.23 and 0.31, respectively. At the second order, a small donation from the nitrogen lone pair to Fe (20 kcal mol⁻¹) is found, in line with the Lewis structure B illustrated in Chart 3.

Chart 3 Two resonance structures of 5.

To investigate the electronic structure of these compounds in more detail preliminary CASSCF computations were undertaken. For complex 3, six electrons were distributed in 6 orbitals (mainly three 3d orbitals per iron atom that appears as linear combinations between the two iron atoms). Calculations were conducted for the singlet, triplet and quintet spin states. The lowest spin-state is a singlet with a triplet higher in energy (0.14 eV) and a quintet slightly higher (0.28 eV). In the singlet CASSCF wavefunction, two orbitals are doubly occupied whereas two others appear to be singly occupied, yielding an open-shell singlet as ground state. Therefore, in the ground state of 3, the two Fe(III) centres (S_Fe = 1/2) couple antiferromagnetically, which is consistent with the experiment observation. Applying a similar approach for complex 5, four electrons were distributed into 6 orbitals and singlet, triplet and quintet spin states were computed at the CASSCF level. Alike complex 3, the lowest spin state is found to be a singlet with a quintet higher in energy (0.12 eV) and finally the triplet (0.54 eV). Analysing the singlet wavefunction deeply, it appears that the 4 electrons are populating four different orbitals, leading to an open-shell singlet with an S_Fe = 1 electron configuration per Fe atom (M_s = ±1). In other words, two Fe(IV, d⁴) metal atoms with two unpaired electrons on each iron atom are coupled antiferromagnetically with each other (similarly to situation described for 3). At this more sophisticated level of theory it was indeed possible to obtain computational results that match the experimental findings.

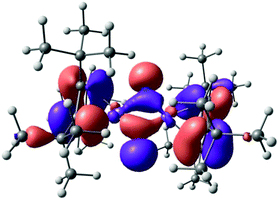
The polarized nature of the Fe–N bond (Chart 3, Lewis structure B) is also reflected in the frontier orbitals of 5, in which the nitrogen lone pairs contribute substantially to the highest molecular orbital (HOMO) (Fig. 15). Consistent with [Cp′Fe(μ-CPh)]₂,⁴⁷ a closer inspection of the NBO orbitals confirmed the absence of any (direct) Fe–Fe bonding interactions in complex 5.

Fig. 15 Highest molecular orbital (HOMO) of complex 5.

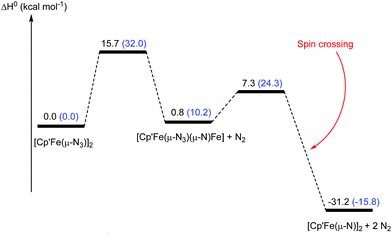
As we have demonstrated above, the commonly employed DFT methodology can describe the geometries and the overall structural features reasonably well, but fails when the electronic structure of these compounds need to be considered in more detail. However, CASSCF computations on these large dinuclear complexes to provide insights in reaction pathways is too time consuming and therefore not feasible. We therefore decided to probe if the DFT methodology is actually sufficient to adequately describe the observed reactivity patterns of these compounds focusing on the formation of complex 5 and its reaction towards CO was probed computationally (Fig. 16 and 17). Starting from the hypothetical [Cp′Fe(μ-N₃)]₂ intermediate, DFT methods predict that the initial step involves the cleavage of the N–N bond in one of the azido ligands yielding a transient azido-nitrido species (Fig. 16). The latter undergoes N₂ release yielding the product 5 followed by a change of spin state. This reaction pathway was computed at the B3PW91 level of theory with and without the inclusion of dispersion (D3BJ) and solvent corrections (THF). Dispersion and solvent corrections have only a minor influence on the structure of the intermediates and transition states involved, but they dramatically reduce the barriers of the overall reaction and also significantly stabilize the final product 5 (Fig. 17) The overall computed barrier for the conversion of the proposed intermediate [Cp′Fe(μ-N₃)]₂ (B) to the dinuclear iron nitrido dimer is ΔH^‡ = 15.7 kcal mol⁻¹, which agrees with the experimentally observed facile N₂ elimination at ambient temperature.

Fig. 16 Enthalpy (ΔH⁰) profile for the formation of [Cp′FeN]₂ (5) from the proposed intermediate [Cp′Fe(μ-N₃)]₂ (B). Values given in parenthesis refer to the values computed at the B3PW91 level of theory without consideration of solvent and dispersion corrections.

Fig. 17 Enthalpy (ΔH⁰) profile for the formation of [Cp′Fe(μ-NCO)]₂ (2) starting [Cp′Fe(μ-N)]₂ (5) and CO. Values given in parenthesis refer to the values computed at the B3PW91 level of theory without consideration of solvent and dispersion corrections.

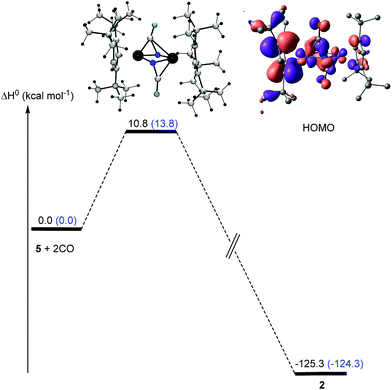
In a next step, the reaction pathway for the reaction of complex 5 with CO was probed. Consistent with the computed HOMO for complex 5 (Fig. 14) the two CO molecules do not attack directly at the lone pair of the N-atoms; instead they approach 5 perpendicularly to the Fe₂N₂ plane (Fig. 17), which is associated with a low barrier of activation (ΔH^‡) of 10.8 kcal mol⁻¹ after consideration of solvent and dispersion corrections. In the transition state electron density is transferred from 5 into the π* orbitals of CO (Fig. 17).

Overall, while the precise electronic structure of compounds 3 and 5 are not adequately described to account for their magnetic properties by standard DFT methods, their molecular structures and the formation and reactivity of 5 can be modeled in sufficient detail yielding reasonable reaction barriers which agree with our experimental observations.

Conclusions

In summary, [Cp′FeI]₂ (1) is a valuable starting material for the activation of pseudohalides such as SCN⁻, SeCN⁻ and N₃⁻ yielding sulfido (3), diselenido (4) and nitrido (5) complexes. These compounds were characterized by various spectroscopic techniques including X-ray diffraction, solid-state magnetic susceptibility studies and zero-field ⁵⁷Fe Mössbauer spectroscopy. Phenomenologically there is a clear correlation between the increasing formal oxidation state in complexes 1 to 5 (ranging from Fe(II) to Fe(IV)) and the decreasing isomer shift observed in their respective Mössbauer spectra. While standard DFT methods reproduce the molecular structures of these complexes reasonably well, their electronic structures require more sophisticated methods to reproduce the data inferred from magnetic susceptibility data of 3 and 5. The iron(IV) nitrido complex 5 shows no reaction towards H₂ (even at elevated pressures), but in the presence of CO it converts to the iron(II) isocyanate complex 6. This represents a rare example of successful CO functionalization of a bridging μ-N fragment. In addition, some useful insights into the formation of 5 and its reactivity with CO can be obtained from DFT computations which justify its use to describe the reaction chemistry of these species. Further investigations on the electronic structure of the compounds 3 and 5 using X-ray absorption near edge studies (XANES) and on their intrinsic reactivity towards electrophiles or organic radicals are ongoing and will be reported in due course.

Experimental details

General considerations

All reactions and product manipulations were carried out under an atmosphere of dry, oxygen free argon or dinitrogen using standard high-vacuum, Schlenk, or drybox techniques. Argon or dinitrogen were purified by passage through BASF R3-11 catalyst (Chemalog) and 4 Å molecular sieves. Dry, oxygen-free solvents were employed throughout. NMR spectra were recorded on Bruker DRX 500 MHz, a Bruker DRX 400 MHz, or a Bruker 400 MHz AVANCE spectrometer. All chemical shifts are reported in δ units and referenced to the residual protons of the deuterated solvents, which are internal standards, for proton chemical shifts. The elemental analyses were performed by the analytical facilities at the University of California at Berkeley, Robertson Microlit Laboratories of Madison, NJ, or at the TU Braunschweig.

Magnetic susceptibility measurements were conducted in a 7 T Quantum Design MPMS magnetometer utilizing a superconducting quantum interference device (SQUID). The samples (10–25 mg) were transferred into a quartz tube and held in place with quartz wool (ca. 5 mg). The quartz tube was flame sealed and transferred into the magnetometer. This method provided a very small and reliable container correction, typically of ca. −2 × 10⁻⁵ emu mol⁻¹. The data were also corrected for the overall diamagnetism of the molecule using Pascal constants.⁴⁹ For a more detailed description see ref. 50. The program package JulX written by Eckhard Bill for exchange coupled systems was used.¹¹

Materials

All solvents were deoxygenated and dried by passage over columns of activated alumina.⁵¹ Tetrahydrofuran dried over sodium/benzophenone and freshly distilled prior to use. Deuterated solvents, C₆D₆, C₇D₈ and THF-d₈ were purchased from Cambridge Laboratories, Inc. or Eurisotope, refluxed for 3 days over sodium metal, vacuum transferred to a Teflon sealable Schlenk flask containing 4 Å molecular sieves, and degassed via three freeze–pump–thaw cycles. [Cp′Fe(μ-I)]₂ (1) was prepared as previously reported.⁵ All other chemicals were purchased from Acros Organics or Sigma Aldrich. KNCO, KSCN, KSeCN and NaN₃ were dried overnight under dynamic vacuum at 90 °C.

Synthesis

[Cp′Fe(μ-NCO)]₂ (2). [Cp′Fe(μ-I)]₂ (0.5 mmol, 416 mg), KOCN (1.0 mmol, 81 mg) and THF (25 mL) were mixed in a Schlenk flask. A green suspension and white precipitate were formed immediately. After 15 min the THF solvent was evaporated and the residue was extracted with pentane (20 mL). After filtration, the extract was concentrated to ca. 5 mL and cooled to −30 °C. The product crystallized as green plates. Yield: 170 mg (0.26 mmol, 52%). Mp: 163 °C. ¹H NMR (400.1 MHz, C₆D₆, 297 K): δ = 42.5 (4H, ν_1/2 = 508 Hz, ring-CH), −4.05 (s, 36H, ν_1/2 = 75 Hz, tBu-H), −7.80 (s, 18H, ν_1/2 = 74 Hz, tBu-H) ppm. The EI mass spectrum showed a molecular ion at m/z = 662 amu. The parent ion isotopic cluster was simulated: (calcd%, observd%): 660(13, 14), 661(6, 7), 662(100, 100), 663(46, 43), 664(12, 11), 665(2, 2). IR (ATR, cm⁻¹): 2952(m), 2866(w), 2176(s), 2030(m), 1974(m), 1460(m), 1391(w), 1360(m), 1236(m), 1201(w), 998(w), 831(m), 665(m), 617(m). UV/Vis (n-hexane, 22 °C, nm): λ(ε, L mol⁻¹ cm⁻¹) = 337 (sh, 1710), 408 (sh, 535), 705 (84). Elemental analysis calcd (%) for C₃₆H₅₈Fe₂N₂O₂: C 65.26, H 8.82, N 4.23; found: C 65.23, H 8.66, N 4.03.

[Cp′Fe(μ-S)]₂ (3). A Schlenk flask was charged with [Cp′Fe(μ-I)]₂ (1.0 mmol, 832 mg), KSCN (2.0 mmol, 65 mg) and THF (50 mL). The suspension was stirred at ambient temperature for 12 h; then the solvent was removed under dynamic vacuum and the residue was extracted with pentane (3 × 20 mL). The extracts were filtered and the solvent was removed under dynamic vacuum. The residue was rinsed with Me₃SiOSiMe₃ (ca. 2 mL) and then dissolved in Et₂O (ca. 3 mL). The solution was cooled to −30 °C to give dark red crystals. Yield: 98 mg (0.15 mmol, 15%). Mp: 224–226 °C (dec). ¹H NMR (400.4 MHz, C₆D₆, 296 K): δ = 10.96 (s, 4H, ring CH), 1.01 (s, 36H, tBu-H), 0.44 (s, 18H, tBu-H) ppm. ¹³C{¹H} NMR (100.9 MHz, C₆D₆, 298 K): δ = 253.3 (br, ν_1/2 = 59 Hz, 2C, ring-C_ipso), 199.2 (br, ν_1/2 = 41 Hz, 4C, ring-C_ipso), 98.5 (4C, ring-CH), 53.8 (6C, tBu-CH₃), 46.1 (12C, tBu-CH₃), 21.6 (4C, tBu-C_ipso), 9.7 (2C, tBu-C_ipso). The EI mass spectrum showed a molecular ion at m/z = 642 amu. The parent ion isotopic cluster was simulated: (calcd%, observd%): 640(12, 13), 641(5, 6), 642(100, 100), 643(50, 45), 644(19, 18), 645(6, 6), 646(1, 1). UV/Vis (n-hexane, 22 °C, nm): λ(ε, L mol⁻¹ cm⁻¹) = 256 (22520), 347 (17170), 389 (sh, 12630), 519 (2020). Elemental analysis calcd (%) for C₃₄H₅₈Fe₂S₂: C 63.55, H 9.10; found: C 63.85, H 8.96.

[Cp′Fe(μ-Se₂)]₂ (4). In a Schlenk flask [Cp′Fe(μ-I)]₂ (1.0 mmol, 832 mg) and KSeCN (4.0 mmol, 576 mg) were dissolved in THF (100 mL). The suspension was stirred at ambient temperature for 15 h and the solvent was evaporated. The residue was extracted with n-hexane (3 × 100 mL). The extracts were filtered and taken to dryness. The residue was dissolved in Et₂O (15 mL) and the solution was slowly concentrated to ca. 5 mL. The product was obtained as dark orange plates. Yield: 132 mg (0.15 mmol, 15%). Mp: 186 °C (dec). ¹H NMR (300.1 MHz, C₆D₆, 27 °C, ppm): δ = 5.89 (s, 4H, ring CH), 1.33 (s, 36H, tBu-H), 0.81 (s, 18H, tBu-H). ¹³C{¹H} NMR (75.5 MHz, C₆D₆, 28 °C, ppm): δ = 104.5 (4C, ring-C_ipso), 102.9 (2C, ring-C_ipso), 84.1 (4C, ring-CH), 33.4 (12C, tBu-CH₃), 33.1 (4C, tBu-C_ipso), 31.4 (6C, tBu-CH₃), 29.4 (2C, tBu-C_ipso). ⁷⁷Se NMR (76.4 MHz, C₆D₆, 24 °C, ppm): δ = 2103.2 (s), 493.2 (s) ppm. The EI mass spectrum showed a molecular ion at m/z = 896 amu. The parent ion isotopic cluster was simulated: (calcd%, observd%): 886(6, 5), 887(8, 8), 888(18, 16), 889(21, 20), 890(41, 42), 891(41, 41), 892(72, 74), 893(59, 57), 894(97, 98), 895(63, 62), 896(100, 100), 897(49, 47), 898(72, 70), 899(30, 26), 900(32, 29), 901(12, 9), 902(8, 7). IR (ATR, cm⁻¹): 2957(s), 2910(m), 2866(m), 2053(m), 1999(m), 1919(m), 1895(m), 1484(s), 1391(m), 1239(m), 1168(s), 1098(w), 1021(w), 994(m), 880(m), 859(m), 823(m), 646(m). Elemental analysis calcd (%) for C₃₄H₅₈Fe₂Se₄: C 45.66, H 6.54; found: C 46.06, H 6.65.

[Cp′Fe(μ-N)]₂ (5). A Schlenk flask was charged with [Cp′Fe(μ-I)]₂ (0.5 mmol, 416 mg), NaN₃ (1.0 mmol, 65 mg) and THF (25 mL). The suspension was stirred at ambient temperature for 16 h, during which time the yellow solution gradually turned orange. The solvent was removed under dynamic vacuum leaving an olive-green residue that was extracted with pentane (3 × ca. 15 mL). The extract was filtered and the solvent was evaporated. The residue was dissolved in Et₂O (3 mL) and cooling this solution to −30 °C formed green crystals. Yield: 171 mg (0.28 mmol, 56%). Mp: 191-193 °C. ¹H NMR (300.1 MHz, C₆D₆, 296 K): δ = 6.45 (s, 4H, ring CH), 1.33 (s, 36H, tBu-H), 0.58 (s, 18H, tBu-H) ppm. ¹³C{¹H} NMR (75.5 MHz, C₆D₆, 297 K): δ = 114.6 (4C, ring-C_ipso), 113.7 (2C, ring-C_ipso), 91.3 (4C, ring-CH), 33.7 (12C, tBu-CH₃), 32.7 (4C, tBu-C_ipso), 30.7 (6C, tBu-CH₃), 29.1 (2C, tBu-C_ipso) ppm. ¹⁵N NMR (40.57 MHz, C₆D₆, 296 K): δ = 1118 ppm. IR (ATR, cm⁻¹): 3005(m), 2962(w), 2907(w), 1482(m), 1459(w), 1418(m), 1359(m), 1246(m), 1169(m), 997(w), 858(s), 828(m), 811(w), 696(vw), 679(vw), 642(vw). UV/Vis (n-hexane, 22 °C, nm): λ(ε, L mol⁻¹ cm⁻¹) = 255 (sh, 21900), 291 (59830), 386 (12100)m, 519 (sh, 820). Elemental analysis calcd (%) for C₃₄H₅₈Fe₂N₂: C 67.33, H 9.64, N 4.62; found: C 67.17, H 9.52, N 4.81.

[Cp′Fe(OPPh₃)(NCO)] (6). To a stirred solution of [Cp′Fe(μ-NCO)]₂ (2, 150 mg, 0.23 mmol, 1 eq.) in toluene (10 mL) a solution of Ph₃PO (126 mg, 0.45 mmol, 2 eq.) was added and stirred for 2 h at ambient temperature. The green solution was dried under oil-pump vacuum, extracted and filtered with pentane. After reducing the solvent to a minimum under oil-pump vacuum, the green residue (ca. 0.5 mL) was filtered and stored at −30 °C to form green crystals. Yield: 110 mg (0.284 mmol, 63%). Mp: 161 °C (dec). ¹H NMR (300 MHz, C₆D₆, 300 K): δ = 20.84 (br s, 6H, ν_1/2 = 46 Hz, ortho-CH Ph₃PO), 10.16 (br s, 6H, ν_1/2 = 550 Hz, meta-CH Ph₃PO), 7.36 (br s, 3H, ν_1/2 = 20 Hz, para-CH Ph₃PO), −10.60 (br s, 18H, ν_1/2 = 260 Hz, tBu-H), −16.00 (s, 9H, ν_1/2 = 210 Hz, tBu-H), −60.63 (s, 2H, ν_1/2 = 2200 Hz, CH Cp) ppm. IR (KBr, cm⁻¹): 2211(NCO). Elemental analysis calcd (%) for C₃₆H₄₄FeNO₂P: C 70.93, H 7.28, N 2.30; found: C 70.87, H 7.23, N 2.32.

[Cp′Fe(CO)₂(NCO)] (7).
Method A. To a stirred solution of [Cp′Fe(μ-NCO)]₂ (2, 100 mg, 0.151 mmol, 1 eq.) in hexane (10 mL), CO (5 bar) was added and the solution stirred for 12 h at ambient temperature. The colour of the solution changed immediately from dark green to red-orange. After removal of the solvent under oil-pump vacuum the red residue was dissolved in a small amount of Et₂O (1 mL), filtered and stored at −30 °C to form red crystals. Yield: 104 mg (0.269 mmol, 89%). Mp: 126–127 °C. ¹H NMR (300 MHz, C₆D₆, 300 K): δ = 4.61 (s, 2H, Cp-CH), 1.08 (s, 18H, tBu-H), 1.04 (s, 9H, tBu-H) ppm. ¹³C{¹H} NMR (75 MHz, C₆D₆, 300 K): δ = 214.7 (CO), 110.0 (C-Cp), 108.0 (C-Cp), 89.2 (CH-Cp), 33.0 (C(CH₃)₃), 32.5 (C(CH₃)₃, 31.1 (C(CH₃)₃), 30.4 (C(CH₃)₃) ppm. IR (KBr, cm⁻¹): 2228(NCO), 2023(CO), 1978(CO). Elemental analysis calcd (%) for C₂₀H₂₉FeNO₃: C 62.02, H 7.55, N 3.62; found: C 61.84, H 7.59, N 3.49.
Method B. To a stirred hexane solution (10 mL) of [Cp′Fe(μ-N)]₂ (5, 100 mg, 0.165 mmol, 1 eq.) CO (5 bar) was added and the solution stirred for 12 h at ambient temperature. The colour of the solution changed immediately from dark green to red-orange. The solvent was removed under dynamic vacuum and the red residue was dissolved in a small amount of Et₂O (1 mL), filtered and stored at −30 °C to form red crystals. Yield: 116 mg (0.300 mmol, 91%).

[Cp′Fe(CNXyl)₂(NCNXyl)] (8). To a stirred solution of [Cp′Fe(μ-N)]₂ (150 mg, 0.247 mmol, 1 eq.) in hexane (25 mL), a solution of XylNC (194 mg, 1.482 mmol, 6 eq.) in hexane (5 mL) was added at ambient temperature. The colour of the solution changed immediately from dark green to red and it was stirred for 12 h. After removal of the solvent under oil-pump vacuum the red residue was dissolved in a small amount of Et₂O (1 mL), filtered and stored at −30 °C, whereby it crystallized as dark red blocks. Yield: 236 mg (0.339 mmol, 69%). Mp: 117 °C (dec). ¹H NMR (600 MHz, C₆D₆, 300 K): δ = 7.04 (d, 2H, NCNXyl meta-CH, ³J_HH = 7.4 Hz), 6.80 (t, 1H, NCNXyl para-CH, ³J_HH = 7.4 Hz), 6.75–6.73 (m, 2H, NCNXyl para-CH), 6.69 (d, 4H, CNXyl meta-CH, ³J_HH = 7.4 Hz), 4.79 (s, 2H, Cp-CH), 2.58 (s, 6H, CH₃-Xyl), 2.39 (s, 12H, CH₃-Xyl) 1.41 (s, 18H, Cp-C(CH₃)₃), 1.26 (s, 9H, Cp-C(CH₃)₃) ppm. ¹³C{¹H} NMR (150 MHz, C₆D₆, 300 K): δ = 184.3 (q, CNXyl), 147.7 (q, NCNXyl), 135.1 (q, CNXyl CN-C_ipso), 130.5 (q, NCNXyl Me-C_ipso), 130.1 (q, CNXyl Me-C_ipso), 128.3 (CH, NCNXyl meta-CH), 128.1 (CH, CNXyl meta-CH), 128.0 (q NCN-C_ipso NCNXyl), 127.3 (CH, CNXyl para-CH), 118.4 (CH, NCNXyl para-CH), 106.3 (q, tBu-C_ipso), 99.6 (q, tBu-C_ipso), 84.8 (CH, Cp-CH), 33.7 (CH₃, Cp-C(CH₃)₃), 33.0 (q, Cp-C(CH₃)₃), 31.6 (CH₃, Cp-C(CH₃)₃), 30.5 (q, Cp-C(CH₃)₃), 20.3 (CH₃, CH₃-Xyl), 19.2 (CH₃, CH₃-Xyl) ppm. Elemental analysis calcd (%) for C₄₄H₅₆FeN₄: C 75.84, H 8.10, N 8.04; found: C 75.54, H 8.237, N 8.00.

Mössbauer spectroscopy

⁵⁷Fe Mößbauer spectra were recorded on a WissEl Mößbauer spectrometer (MRG-500) at 77 K in constant acceleration mode. ⁵⁷Co/Rh was used as the radiation source. WinNormos for Igor Pro software has been used for the quantitative evaluation of the spectral parameters (least-squares fitting to Lorentzian peaks). The minimum experimental line widths were 0.20 mm s⁻¹. The temperature of the samples was controlled by an MBBC-HE0106 MÖSSBAUER He/N₂ cryostat within an accuracy of ±0.3 K. Isomer shifts were determined relative to α-iron at 298 K.

Crystallographic details

X-ray diffraction studies on complex 5 were conducted on a Bruker-AXS SMART APEX-II diffractometer. A suitable crystal was selected and mounted using paratone oil on a MiteGen mylar tip. For all other structures, crystals were mounted on glass fibres in inert oil; data were collected on Oxford Diffraction systems using mirror-focused Cu Kα or monochromatized Mo Kα radiation. Structures were refined anisotropically on F² using SHELXL-97. Hydrogen atoms were included using rigid methyl groups or a riding model. Special features: For 3, two t-butyl groups were disordered over two positions. Crystal and data collection parameters are presented in Table S1 in the ESI.†

Computational details section

All the quantum-chemical calculations were conducted using the Gaussian 09 program suite.⁵² As functional we used the Becke's 3-parameter hybrid, combined with the non-local correlation functional provided by Perdew/Wang, denoted as B3PW91.⁵³ For Fe and I, the relativistic energy-consistent pseudopotential of the Stuttgart-Köln ECP library was used in combination with its adapted segmented basis.⁵⁴ For all other atoms, a standard 6-31G** basis set was used.⁵⁵ All stationary points were identified as minima (number of imaginary frequencies Nimag = 0) or transition states (Nimag = 1).

Acknowledgements

We thank the Alexander von Humboldt Foundation for a Feodor-Lynen Fellowship (M. D. W.) and Prof. Maurice Brookhart for providing financial support (through NSF Grant CHE-0615704) and laboratory facilities (M. D. W.) during the initial phase of this research program. Deutsche Forschungsgemeinschaft (DFG) is acknowledged for generous funding by the Emmy Noether and Heisenberg program (WA 2513/2 and WA 2513/6, respectively). LM is grateful to the Humboldt Foundation for a grant of experienced researcher and the Chinese Academy of Science. CalMip is also gratefully acknowledged for a generous computational grant.

Notes and references

1. (a) C. Ercolani, M. Gardini, G. Pennesi, G. Rossi and U. Russo, Inorg. Chem., 1988, 27, 422–424; (b) S. D. Brown and J. C. Peters, J. Am. Chem. Soc., 2005, 127, 1913–1923; (c) P. J. Chirik, Angew. Chem., Int. Ed., 2006, 45, 6956–6959; (d) J. J. Scepaniak, M. D. Fulton, R. P. Bontchev, E. N. Duesler, M. L. Kirk and J. M. Smith, J. Am. Chem. Soc., 2008, 130, 10515–10517; (e) J. J. Scepaniak, J. A. Young, R. P. Bontchev and J. M. Smith, Angew. Chem., Int. Ed., 2009, 48, 3158–3160; (f) Y. Nishibayashi, Nat. Chem., 2011, 3, 502–504; (g) J. J. Scepaniak, C. S. Vogel, M. M. Khusniyarov, F. W. Heinemann, K. Meyer and J. M. Smith, Science, 2011, 331, 1049–1052; (h) M. M. Rodriguez, E. Bill, W. W. Brennessel and P. L. Holland, Science, 2011, 334, 780–783; (i) J. Hohenberger, K. Ray and K. Meyer, Nat. Commun., 2012, 3, 720; (j) T. M. Powers and T. A. Betley, J. Am. Chem. Soc., 2013, 135, 12289–12296; (k) J. Torres-Alacan, U. Das, A. C. Filippou and P. Vohringer, Angew. Chem., Int. Ed. Engl., 2013, 52, 12833–12837; (l) K. C. MacLeod and P. L. Holland, Nat. Chem., 2013, 5, 559–565; (m) J. M. Smith, Prog. Inorg. Chem., 2014, 58, 417–471; (n) Y. Lee, F. T. Sloane, G. Blondin, K. A. Abboud, R. García-Serres and L. J. Murray, Angew. Chem., Int. Ed., 2015, 54, 1499–1503; (o) M. D. Walter, Adv. Organomet. Chem., 2016, 65, 261–377.
2. (a) T. A. Betley and J. C. Peters, J. Am. Chem. Soc., 2004, 126, 6252–6254; (b) M. P. Hendrich, W. Gunderson, R. K. Behan, M. T. Green, M. P. Mehn, T. A. Betley, C. C. Lu and J. C. Peters, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 17107–17112.
3. (a) J. F. Berry, E. Bill, E. Bothe, S. D. George, B. Mienert, F. Neese and K. Wieghardt, Science, 2006, 312, 1937–1941; (b) M. P. Mehn and J. C. Peters, J. Inorg. Biochem., 2006, 100, 634–643; (c) C. Vogel, F. W. Heinemann, J. Sutter, C. Anthon and K. Meyer, Angew. Chem., Int. Ed., 2008, 47, 2681–2684.
4. T. M. Powers, A. R. Fout, S.-L. Zheng and T. A. Betley, J. Am. Chem. Soc., 2011, 133, 3336–3338.
5. M. D. Walter and P. S. White, New J. Chem., 2011, 35, 1842–1854.
6. M. Maekawa, C. G. Daniliuc, P. G. Jones, J. Hohenberger, J. Sutter, K. Meyer and M. D. Walter, Eur. J. Inorg. Chem., 2013, 2013, 4097–4104.
7. M. D. Walter, J. Grunenberg and P. S. White, Chem. Sci., 2011, 2, 2120–2130.
8. M. D. Walter and P. S. White, Inorg. Chem., 2012, 51, 11860–11872.
9. C. Eichhorn, O. J. Scherer, T. Sögding and G. Wolmershäuser, Angew. Chem., Int. Ed., 2001, 40, 2859–2861.
10. M. Kreye, D. Baabe, P. Schweyen, M. Freytag, C. G. Daniliuc, P. G. Jones and M. D. Walter, Organometallics, 2013, 32, 5887–5898.
11. The program package JulX was used for spin-Hamiltonian simulations and fittings of the data by a full-matrix diagonalization approach, ed. E. Bill, Max-Planck Institute for Chemical Energy Conversion, unpublished results.
12. (a) P. Gütlich and J. Ensling, in Inorganic Electronic Structure and Spectroscopy: Methodology, ed. E. I. Solomon and A. B. P. Lever, J. Wiley & Sons, New York, 1999, vol. 1, pp. 161–213; (b) P. Gütlich, E. Bill and A. X. Trautwein, Mössbauer Spectroscopy and Transition Metal Chemistry, Springer, Heidelberg, 2011.
13. (a) M. L. Good, J. Buttone and D. Foyt, Ann. N. Y. Acad. Sci., 1974, 239, 193–207; (b) J. P. Mariot, F. Varret, P. Michaud, D. Astruc, J. R. Hamon, G. Althoff and P. Batail, J. Phys., Colloq., 1980, 319–320; (c) M. Reiners, D. Baabe, K. Harms, M. Maekawa, C. G. Daniliuc, M. Freytag, P. G. Jones and M. D. Walter, Inorg. Chem. Front., 2016, 3, 250–262; (d) M. Malischewski, M. Adelhardt, J. Sutter, K. Meyer and K. Seppelt, Science, 2016, 353, 678–682.
14. M. Maekawa, C. G. Daniliuc, M. Freytag, P. G. Jones and M. D. Walter, Dalton Trans., 2012, 41, 10317–10327.
15. (a) J. S. Thayer and R. West, Adv. Organomet. Chem., 1967, 5, 169–224; (b) R. A. Bailey, S. L. Kozak, T. W. Michelsen and W. N. Mills, Coord. Chem. Rev., 1971, 6, 407–445; (c) Z. Dori and R. F. Ziolo, Chem. Rev., 1973, 73, 247–254; (d) A. M. Golub, H. Köhler and V. V. Skopenko, Chemistry of pseudohalides, Elsevier, Amsterdam, 1986.
16. G. Ferguson, B. R. Lloyd, L. Manojlovic-Muir, K. W. Muir and R. J. Puddephatt, Inorg. Chem., 1986, 25, 4190–4197.
17. M. E. Rasche and L. C. Seefeldt, Biochemistry, 1997, 36, 8574–8585.
18. A. F. Hollemann, E. Wiberg and N. Wiberg, Lehrbuch der Anorganischen Chemie, de Gruyter, Berlin, 102 edn, 2007.
19. R. A. Rose, S. J. Greaves, F. Abou-Chahine, D. R. Glowacki, T. A. A. Oliver, M. N. R. Ashfold, I. P. Clark, G. M. Greetham, M. Towrie and A. J. Orr-Ewing, Phys. Chem. Chem. Phys., 2012, 14, 10424–10437.
20. (a) P. Nicpon and D. W. Meek, Inorg. Chem., 1966, 5, 1297–1298; (b) W. J. Stec, G. Zon, W. Egan and B. Stec, J. Am. Chem. Soc., 1984, 106, 6077–6079; (c) A. R. Butler, C. Glidewell and A. E. Waddon, Polyhedron, 1989, 8, 2627–2629.
21. H. Beinert, R. H. Holm and E. Münck, Science, 1997, 277, 653–659.
22. P. Venkateswara Rao and R. H. Holm, Chem. Rev., 2004, 104, 527–560.
23. (a) R. H. Holm, P. Kennepohl and E. I. Solomon, Chem. Rev., 1996, 96, 2239–2314; (b) E. I. Solomon, X. Xie and A. Dey, Chem. Soc. Rev., 2008, 37, 623–638.
24. W. Yao, P. Gurubasavaraj and P. Holland, Struct. Bonding, 2014, 160, 1–37.
25. (a) D. Coucouvanis, A. Salifoglou, M. G. Kanatzidis, A. Simopoulos and V. Papaefthymiou, J. Am. Chem. Soc., 1984, 106, 6081–6082; (b) J. Ballmann, A. Albers, S. Demeshko, S. Dechert, E. Bill, E. Bothe, U. Ryde and F. Meyer, Angew. Chem., Int. Ed., 2008, 47, 9537–9541; (c) A. Albers, S. Demeshko, S. Dechert, E. Bill, E. Bothe and F. Meyer, Angew. Chem., Int. Ed., 2011, 50, 9191–9194; (d) Y. Li, Y. Li, B. Wang, Y. Luo, D. Yang, P. Tong, J. Zhao, L. Luo, Y. Zhou, S. Chen, F. Cheng and J. Qu, Nat. Chem., 2013, 5, 320–326; (e) A. Albers, T. Bayer, S. Demeshko, S. Dechert and F. Meyer, Chem.–Eur. J., 2013, 19, 10101–10106; (f) A. Albers, S. Demeshko, S. Dechert, C. T. Saouma, J. M. Mayer and F. Meyer, J. Am. Chem. Soc., 2014, 136, 3946–3954.
26. (a) J. Wachter, Angew. Chem., Int. Ed. Engl., 1989, 28, 1613–1626; (b) J. Wachter, J. Coord. Chem., 1987, 15, 219–236.
27. (a) P. J. Vergamini and G. J. Kubas, Prog. Inorg. Chem., 1976, 261–282; (b) G. J. Kubas and P. J. Vergamini, Inorg. Chem., 1981, 20, 2667–2676.
28. H. Brunner, N. Janietz, W. Meier, G. Sergeson, J. Wachter, T. Zahn and M. L. Ziegler, Angew. Chem., Int. Ed. Engl., 1985, 24, 1060–1061.
29. M. Yamada, H. Tobita, S. Inomata and H. Ogino, Bull. Chem. Soc. Jpn., 1996, 69, 861–867.
30. H. Ogino, H. Tobita, K. Yanagisawa, M. Shimoi and C. Kabuto, J. Am. Chem. Soc., 1987, 109, 5847–5848.
31. S. Inomata, T. Hiruma and H. Ogino, Chem. Lett., 1998, 309–310.
32. (a) I. Bertini, H. B. Gray, E. I. Stiefel and J. S. Valentine, Biological Inorganic Chemistry, University Science Books, Sausalito, CA, 2007; (b) M. E. Reesbeck, M. M. Rodriguez, W. W. Brennessel, B. Q. Mercado, D. Vinyard and P. L. Holland, J. Biol. Inorg Chem., 2015, 20, 875–883.
33. (a) M. A. Ansari and J. A. Ibers, Coord. Chem. Rev., 1990, 100, 223–266; (b) C. Simonnet-Jégat and F. Sécheresse, Chem. Rev., 2001, 101, 2601–2612; (c) M. N. Sokolov, V. P. Fedin and A. G. Sykes, in Comprehensive Coordination Chemistry II, ed. T. J. Meyer, Pergamon, Oxford, 2003, pp. 761–823; (d) S. M. Dibrov, B. Deng, D. E. Ellis and J. A. Ibers, Inorg. Chem., 2005, 44, 3441–3448.
34. (a) C. M. Bolinger, T. B. Rauchfuss and A. L. Rheingold, Organometallics, 1982, 1, 1551–1553; (b) A. L. Rheingold, C. M. Bolinger and T. B. Rauchfuss, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1986, 42, 1878–1880.
35. NMR of Paramagnetic Molecules, ed. G. N. La Mar, W. D. Horrocks and R. H.Holm, Academic Press, New York, 1973.
36. M. E. Smith and R. A. Andersen, J. Am. Chem. Soc., 1996, 118, 11119–11128.
37. B. Askevold, M. M. Khusniyarov, E. Herdtweck, K. Meyer and S. Schneider, Angew. Chem., Int. Ed. Engl., 2010, 49, 7566–7569.
38. (a) A. L. Odom and C. C. Cummins, Organometallics, 1996, 15, 898–900; (b) G. K. B. Clentsmith, V. M. E. Bates, P. B. Hitchcock and F. G. N. Cloke, J. Am. Chem. Soc., 1999, 121, 10444–10445; (c) Z. J. Tonzetich, R. R. Schrock, K. M. Wampler, B. C. Bailey, C. C. Cummins and P. Müller, Inorg. Chem., 2008, 47, 1560–1567.
39. (a) C. Kim, Y. Dong and L. Que Jr, J. Am. Chem. Soc., 1997, 119, 3635–3636; (b) L. Que Jr, Pure Appl. Chem., 1998, 70, 947–954; (c) A. J. Skulan, M. A. Hanson, H.-f. Hsu, L. Que Jr and E. I. Solomon, J. Am. Chem. Soc., 2003, 125, 7344–7356.
40. T. S. Haddad, A. Aistars, J. W. Ziller and N. M. Doherty, Organometallics, 1993, 12, 2420–2422.
41. M. Herberhold, A.-M. Dietel, A. Goller and W. Millius, Z. Anorg. Allg. Chem., 2003, 629, 871–879.
42. F. Akagi, T. Matsuo and H. Kawaguchi, Angew. Chem., Int. Ed., 2007, 46, 8778–8781.
43. M. Hirotsu, P. P. Fontaine, A. Epshteyn and L. R. Sita, J. Am. Chem. Soc., 2007, 129, 9284–9285.
44. K. Searles, P. J. Carroll, C.-H. Chen, M. Pink and D. J. Mindiola, Chem. Commun., 2015, 51, 3526–3528.
45. (a) M. M. Olmstead, P. P. Power and S. C. Shoner, Inorg. Chem., 1991, 30, 2547–2551; (b) S. K. Dutta, U. Beckmann, E. Bill, T. Weyhermüller and K. Wieghardt, Inorg. Chem., 2000, 39, 3355–3364; (c) R. E. Cowley, N. J. DeYonker, N. A. Eckert, T. R. Cundari, S. DeBeer, E. Bill, X. Ottenwaelder, C. Flaschenriem and P. L. Holland, Inorg. Chem., 2010, 49, 6172–6187; (d) R. E. Cowley and P. L. Holland, Inorg. Chem., 2012, 51, 8352–8361; (e) A. K. Verma, T. N. Nazif, C. Achim and S. C. Lee, J. Am. Chem. Soc., 2000, 122, 11013–11014; (f) S. C. Bart, E. Lobkovsky, E. Bill and P. J. Chirik, J. Am. Chem. Soc., 2006, 128, 5302–5303; (g) E. R. King, E. T. Hennessy and T. A. Betley, J. Am. Chem. Soc., 2011, 133, 4917–4923.
46. F. A. Cotton, J. D. Jamerson and B. R. Stults, J. Organomet. Chem., 1975, 94, C53–C55.
47. G. Y. Vollmer, M. W. Wallasch, D. Saurenz, T. R. Eger, H. Bauer, G. Wolmershäuser, M. H. Prosenc and H. Sitzmann, Organometallics, 2015, 34, 644–652.
48. E. R. Davidson, Chem. Rev., 2000, 100, 351–352 , Introduction to a special issue Computational Transition Metal Chemistry.
49. C. J. O'Connor, in Progress in Inorganic Chemistry, ed. S. J. Lippard, J. Wiley & Sons, New York, 1982, vol. 29, pp. 203–285.
50. M. D. Walter, M. Schultz and R. A. Andersen, New J. Chem., 2006, 30, 238–246.
51. (a) P. J. Alaimo, D. W. Peters, J. Arnold and R. G. Bergman, J. Chem. Educ., 2001, 78, 64; (b) A. B. Pangborn, M. A. Giardello, R. H. Grubbs, R. K. Rosen and F. J. Timmers, Organometallics, 1996, 15, 1518–1520.
52. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. J. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, E. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallington CT, 2009.
53. (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652; (b) J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
54. M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872.
55. (a) W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261; (b) P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222.

---

Footnote

† Electronic supplementary information (ESI) available: Crystallographic details, additional experimental and structural details, VT ¹H NMR studies, magnetic susceptibility studies, ⁵⁷Fe Mössbauer spectrum of 5, computational details. CCDC 1531255–1531264. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7sc00570a

---